惯性测量单元(IMU, inertial measurement unit)包括三轴陀螺仪和三轴加速度计。基于微电机系统(MEMS, micro-electro-mechanical-system)的IMU不仅成本低、尺寸小、重量轻和功耗低,而且工作时不受天气、地形和时间的影响,近年来被广泛应用于移动机器人、宇航和导航等领域。利用MEMS-IMU设计惯性导航系统时,通过减小陀螺仪的噪声得到高精度的航姿(即俯仰角:θ、横滚角:φ和航向角:ψ)为设计难点之一。陀螺仪的噪声分为确定性噪声和随机噪声。由于陀螺仪的噪声较大,利用传统的多位置校准算法提取确定性噪声需要借助一种高精度的旋转台,因此较不方便且成本较高[1-4]。针对该不足,大量的研究利用姿态误差模型校准陀螺仪的确定性误差,然而当MEMS-IMU处于动态时,该模型的精度较差[5-8]。另一方面,较多的研究专注于随机误差的建模,例如基于艾伦方差和小波矩广义估算的模型,但是该方法过程繁琐且需要实时统计大量的数据[9-11]。LEE J K报导了一种基于卡尔曼滤波的姿态估算算法,通过加速度计的精确测量减小陀螺仪的噪声对MEMS-IMU姿态的影响[12-13]。该方法需要借助3轴磁力计获取ψ,而机器人的大部分零部件由磁性材料组成,比较容易干扰磁力计的测量精度,因此应用范围具有一定的局限。
笔者提出一种基于陀螺仪噪声实时移除的高精度MEMS-IMU航姿技术,该方法较LEE J K的方法具有2点不同:陀螺仪的偏置被增加到状态向量,用于实时移除陀螺仪的噪声;加速度计的外部加速度和噪声均被设为测量余量,便于动态时,能通过加速度计测量得到重力向量。首先分析了存在的问题,然后介绍了推荐的算法,最后利用一种MEMS-IMU论证了推荐算法并给出了相关的结论。
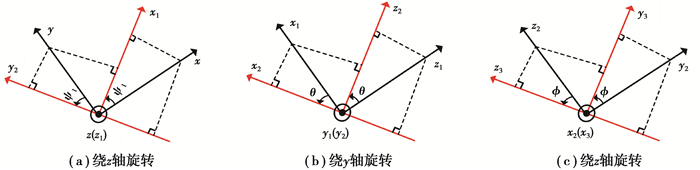
1 关键问题图 1中x-y-z and x3-y3-z3分别表示导航坐标系和载体(MEMS-IMU)坐标系,方向余弦矩阵:Cnb为导航坐标系依次绕z轴、y轴和x轴旋转角度ψ1、θ和φ得到的矩阵,其中ψ等于-ψ1。
| $ \mathit{\boldsymbol{C}}_n^b = \left[ {\begin{array}{*{20}{c}} {{\rm{cos}}\theta {\rm{cos}}\psi }&{ - \cos {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi }&{ - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }\\ {{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi + {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi }&{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi }&{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }\\ { - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi + {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi }&{ - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi }&{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi } \end{array}} \right]。$ | (1) |
|
图 1 导航坐标系到载体坐标系的旋转过程 Fig. 1 The rotation process from navigation frame to body frame |
陀螺仪和加速度计的测量结果yG和yA分别表示为
| $ {{y_{Gx,y,z}} = {\omega _{x,y,z}} + {b_{x,y,z}} + {n_{Gx,y,z}},} $ | (2) |
| $ {{y_{Ax,y,z}} = \mathit{\boldsymbol{C}}_n^b{{[0,0,g]}^{\rm{T}}} + {a_{x,y,z}} + {n_{Ax,y,z}},} $ | (3) |
其中:ω为角速率,b为偏置,nG和nA为测量噪声,[0,0,g]为导航坐标系上的重力向量,a为外部加速度。,下标x, y和z分别表示相关量在x轴、y轴和z轴上的分量。以下通过介绍常用的3种航姿算法说明存在的关键问题。
1) Cnb的转置为Cbn。根据i时刻Cbn和yG的值,得到i+1时刻Cbn的更新值为
| $ \mathit{\boldsymbol{C}}_{b,i + 1}^n = \mathit{\boldsymbol{C}}_{b,i}^n{\mathit{\boldsymbol{A}}_i}, $ | (4) |
Ai为载体坐标系从i时刻到i+1时刻的旋转矩阵,近似为:I3+(yG, i×)Δt,其中I3为单位矩阵,Δt为采样时间间隔,yG, i×表示yG, i的斜对称矩阵。
| $ ({\mathit{\boldsymbol{y}}_{G,i}} \times ) = \left[ {\begin{array}{*{20}{c}} 0&{ - {\mathit{\boldsymbol{y}}_{Gz,i}}}&{{\mathit{\boldsymbol{y}}_{Gx,i}}}\\ {{\mathit{\boldsymbol{y}}_{Gz,i}}}&0&{ - {\mathit{\boldsymbol{y}}_{Gy,i}}}\\ { - {\mathit{\boldsymbol{y}}_{Gx,i}}}&{{\mathit{\boldsymbol{y}}_{Gy,i}}}&0 \end{array}} \right]。$ | (5) |
根据Cb, i+1n和等式(1),i+1时刻θ、φ和ψ的更新结果如下
| $ {{\theta _{i + 1}} = {\rm{arcsin}}( - \mathit{\boldsymbol{C}}_{n,i + 1,13}^b),} $ | (6) |
| $ {{\varphi _{i + 1}} = {\rm{arctan}}{\kern 1pt} {\kern 1pt} 2(\mathit{\boldsymbol{C}}_{n,i + 1,23}^b,\mathit{\boldsymbol{C}}_{n,i + 1,33}^b),} $ | (7) |
| $ {{\psi _{i + 1}} = {\rm{arctan}}{\kern 1pt} {\kern 1pt} 2( - \mathit{\boldsymbol{C}}_{n,i + 1,12}^b,\mathit{\boldsymbol{C}}_{n,i + 1,11}^b),} $ | (8) |
以上等式以及其它地方的数字下标均表示行和列,例如Cn, i+1, 13b表示Cn, i+1b的第1行和第3列元素。此时,i+1时刻的外部加速度为
| $ {[{a_{x,i + 1}},{a_{y,i + 1}},{a_{z,i + 1}}]^{\rm{T}}} = {[{\mathit{\boldsymbol{y}}_{Ax,i + 1}},{\mathit{\boldsymbol{y}}_{Ay,i + 1}},{\mathit{\boldsymbol{y}}_{Az,i + 1}}]^{\rm{T}}} - g\left[ {\begin{array}{*{20}{c}} { - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\theta _{i + 1}}}\\ {{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\theta _{i + 1}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _{i + 1}}}\\ {{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\theta _{i + 1}}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _{i + 1}}} \end{array}} \right]。$ | (9) |
由于陀螺仪的测量噪声和偏置,利用等式(6)、(7)和(8)计算的姿态和航向角具有较大的误差,因此外部加速度也呈现较大的误差。
2) 当外部加速度为0时,MEMS-IMU处于静态或者伪静态,此时等式(3)为
| $ {\mathit{\boldsymbol{y}}_{Ax,y,z}} \approx \mathit{\boldsymbol{C}}_n^b{[0,0,g]^{\rm{T}}} = \left[ {\begin{array}{*{20}{c}} { - g{\kern 1pt} {\kern 1pt} {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }\\ {g{\kern 1pt} {\kern 1pt} {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }\\ {g{\kern 1pt} {\kern 1pt} {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi } \end{array}} \right], $ | (10) |
因此,θ和φ可直接根据加速度计的测量结果计算。
| $ {\theta = {\rm{arctan}}2( - {\mathit{\boldsymbol{y}}_{Ax}},\sqrt {{\mathit{\boldsymbol{y}}_{Ay}}^2 + {\mathit{\boldsymbol{y}}_{Az}}^2} ),} $ | (11) |
| $ {\varphi = {\rm{arctan}}2({\mathit{\boldsymbol{y}}_{Ay}},{\mathit{\boldsymbol{y}}_{Az}})}。$ | (12) |
此时,可以根据如下2种方法计算。第一,根据等式(13)
| $ \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{y}}_{Gx}}}\\ {{\mathit{\boldsymbol{y}}_{Gy}}}\\ {{\mathit{\boldsymbol{y}}_{Gz}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {\dot \varphi }\\ 0\\ 0 \end{array}} \right] + {\mathit{\boldsymbol{C}}_\varphi }\left[ {\begin{array}{*{20}{l}} 0\\ {\dot \theta }\\ 0 \end{array}} \right] + {\mathit{\boldsymbol{C}}_\varphi }{\mathit{\boldsymbol{C}}_\theta }\left[ {\begin{array}{*{20}{l}} 0\\ 0\\ {\dot \psi } \end{array}} \right]。$ | (13) |
得到i+1时刻ψ的更新值为
| $ {\psi _{i + 1}} = {\psi _i} + ({\mathit{\boldsymbol{y}}_{Gy,i}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _i} + {\mathit{\boldsymbol{y}}_{Gz,i}}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _i}){\rm{sec}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\theta _i}, $ | (14) |
尽管θi和φi具有较高的精度,但是yG在y轴和z轴的噪声分量导致ψi+1具有较大的误差。
另一方面,利用磁力计测量可以得到载体坐标系和导航坐标系上的磁场分量分别为mb=[mx, my, mz]T和mn=[a, 0, b]T。使mn绕z轴旋转并且mb分别绕x轴和y轴旋转可以得到导航坐标系水平面x轴的磁场为hx且y轴的磁场为hy,此时ψ可以表示为[14]
| $ \psi = {\rm{arctan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} 2[{h_y},{h_x}]. $ | (15) |
但是,该方法需要用到磁力计,ψ的精度较易受到磁性物质的干扰。
3) 当外部加速度不为0时,载体坐标系的重力向量不能被测量,θ和φ不能根据等式(11)和(12)计算。LEE J K提出的解决方案如下
首先,令Cnb的第3列为状态向量,记为Z=[Cn, 13b, Cn, 23b, Cn, 33b]T。根据陀螺仪在i+1时刻的测量结果,可以得到i+1时刻Z的更新值为
| $ {\mathit{\boldsymbol{Z}}_{i + 1}} \approx [I - \Delta t{\mathit{\boldsymbol{y}}_{G,i + 1}} \times ]{\mathit{\boldsymbol{Z}}_i}, $ | (16) |
然后,通过加速度计测量载体坐标系上重力向量的方法校正Zi+1。i+1时刻外部加速度的估算值为ai+1,可近似为caai+,其中ca为0到1之间的常数,此时载体坐标系上重力向量的测量结果为
| $ {\mathit{\boldsymbol{y}}_{A,i + 1}} - {c_a}a_i^ + \approx [g{I_3}]{\mathit{\boldsymbol{Z}}_{i + 1}}, $ | (17) |
通过卡尔曼滤波器融合陀螺仪和加速度计的测量结果,可实现Zi+1的校正,最终得到高精度的θ和φ。该方法可以在动态环境下获得高精度的姿态,但是ψ的计算需要借助等式(14)或者等式(15)。因此,计算ψ时存在第2种方法中的问题。
以上3种航姿算法为目前较常用的方法,均存在一定的不足。提出一种基于陀螺仪噪声实时移除的航姿技术,该方法具有较高的姿态精度,因此可以测量出较高精度的外部加速度。而且,陀螺仪的偏置被在线移除,根据等式(14),航向角具有更高的精度。
2 核心技术该技术仅采用3轴陀螺仪和3轴加速度计。将Cnb的第3列和陀螺仪的偏置同时设为状态向量X:X=[Cn, 13b, Cn, 23b, Cn, 33b, bx, by, bz]T。则i+1时刻X的更新值为
| $ {\mathit{\boldsymbol{X}}_{i + 1}} = {f_i}({\mathit{\boldsymbol{X}}_i},{y_{G,i}}) = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_3}}&{ - \Delta t[{\mathit{\boldsymbol{Z}}_i} \times ]}\\ {{0_{3 \times 3}}}&{{\mathit{\boldsymbol{I}}_3}} \end{array}} \right]\mathit{\boldsymbol{X}}_i^ + + \left[ {\begin{array}{*{20}{c}} {\Delta t[{\mathit{\boldsymbol{Z}}_i} \times ]}\\ {{0_{3 \times 3}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{y}}_{Gx,i}}}\\ {{\mathit{\boldsymbol{y}}_{Gy,i}}}\\ {{\mathit{\boldsymbol{y}}_{Gz,i}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{l}} { - \Delta t[{\mathit{\boldsymbol{Z}}_i} \times ]\left[ {\begin{array}{*{20}{l}} {{n_{Gx}}}\\ {{n_{Gy}}}\\ {{n_{Gz}}} \end{array}} \right]}\\ {{\sigma _{bx}}}\\ {{\sigma _{by}}}\\ {{\sigma _{bz}}} \end{array}} \right], $ | (18) |
等式(18)右边第3项中nG和σb分别为陀螺仪的测量噪声和偏置,则以上过程噪声协方差矩阵U为
| $ \mathit{\boldsymbol{U}} = \left[ {\begin{array}{*{20}{c}} {{n_G}^2{\mathit{\boldsymbol{I}}_3}}&0\\ 0&{{\sigma _b}^2{I_3}} \end{array}} \right], $ | (19) |
根据等式(18)右边的第1项和第2项,可以计算出i+1时刻X的先验状态:Xi+1,则它的先验误差协方差矩阵Pi+1为
| $ \mathit{\boldsymbol{P}}_{i + 1}^ - = \frac{{\partial {f_i}}}{{\partial {\mathit{\boldsymbol{X}}_i}}}\mathit{\boldsymbol{P}}_i^ + {\left[ {\frac{{\partial {f_i}}}{{\partial {\mathit{\boldsymbol{X}}_i}}}} \right]^{\rm{T}}} + \frac{{\partial {f_i}}}{{\partial ({n_{Gx,y,z}},{\sigma _{bx,y,z}})}}\mathit{\boldsymbol{U}}{\left[ {\frac{{\partial {f_i}}}{{\partial ({n_{Gx,y,z}},{\sigma _{bx,y,z}})}}} \right]^{\rm{T}}} $ | (20) |
另一方面,设定测量矩阵为
| $ \mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{l}} {g{\mathit{\boldsymbol{I}}_3}}&{{0_{3 \times 3}}} \end{array}} \right], $ | (21) |
当外部加速度和测量噪声均被作为测量余量时,载体坐标系的重力向量如下
| $ {\mathit{\boldsymbol{y}}_{Ax,y,z,i + 1}} = \mathit{\boldsymbol{HX}}_{i + 1}^ - + {a_{x,y,z,i + 1}} + \underbrace {{n_{Ax,y,z}}}_{{\rm{测量余量}}}, $ | (22) |
其中,ai+1可根据1阶低通滤波白噪声过程近似为caai[15]。则测量余量协方差矩阵Ri+1为
| $ {\mathit{\boldsymbol{R}}_{i + 1}} = ({\left\| {{a_i}} \right\|^2}{c_a}^2 + {n_A}^2){\mathit{\boldsymbol{I}}_3}。$ | (23) |
当应用卡尔曼滤波器融合陀螺仪和加速度计的测量值,卡尔曼滤波器的增益Ki+1为
| $ {K_{i + 1}} = \mathit{\boldsymbol{P}}_{i + 1}^ - {\mathit{\boldsymbol{H}}^{\rm{T}}}(\mathit{\boldsymbol{HP}}_{i + 1}^ - {\mathit{\boldsymbol{H}}^{\rm{T}}} + {\mathit{\boldsymbol{R}}_{i + 1}}) - 1。$ | (24) |
经过校正的状态向量Xi+1+和误差协方差矩阵Pi+1+分别为
| $ {\mathit{\boldsymbol{X}}_{i + 1}^ + = \mathit{\boldsymbol{X}}_{i + 1}^ - + {\mathit{\boldsymbol{K}}_{i + 1}}({{[{\mathit{\boldsymbol{y}}_{Ax,i + 1}},{\mathit{\boldsymbol{y}}_{Ay,i + 1}},{\mathit{\boldsymbol{y}}_{Az,i + 1}}]}^{\rm{T}}} - \mathit{\boldsymbol{HX}}_{i + 1}^ - ),} $ | (25) |
| $ {\mathit{\boldsymbol{P}}_{i + 1}^ + = [\mathit{\boldsymbol{I}} - {K_{i + 1}}\mathit{\boldsymbol{H}}]\mathit{\boldsymbol{P}}_{i + 1}^ - {{[I - {K_{i + 1}}\mathit{\boldsymbol{H}}]}^{\rm{T}}} + {K_{i + 1}}{\mathit{\boldsymbol{R}}_{i + 1}}{K_{i + 1}}^{\rm{T}}}。$ | (26) |
最后,i+1时刻θ和φ的更新值分别为
| $ {{\theta _{i + 1}} = {\rm{arcsin}}( - \mathit{\boldsymbol{X}}_{i + 1,11}^ + ),} $ | (27) |
| $ {{\varphi _{i + 1}} = {\rm{arctan}}{\kern 1pt} {\kern 1pt} 2(\mathit{\boldsymbol{X}}_{i + 1,21}^ + ,\mathit{\boldsymbol{X}}_{i + 1,31}^ + ),} $ | (28) |
并且,根据等式(9)求出外部加速度。同时,i+1时刻ψ的更新值为
| $ {\psi _{i + 1}} = {\psi _i} + [({\mathit{\boldsymbol{y}}_{Gy,i}} - \mathit{\boldsymbol{X}}_{i,51}^ + ){\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _i} + ({\mathit{\boldsymbol{y}}_{Gz,i}} - \mathit{\boldsymbol{X}}_{i,61}^ + ){\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _i}]{\rm{sec}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\theta _i}, $ | (29) |
其中Xi, 51+和Xi, 61+为陀螺仪在y轴和z轴的偏置。因为偏置被在线移除,ψ具有更高的精度。
3 实验和结果 3.1 测试搭建利用Inven Sense公司生产型号为MPU9250的MEMS-IMU验证提出的算法。MPU9250包括三轴陀螺仪、三轴加速度计和三轴磁力计,角速度的量程为±250°/s、±500°/s、±1 000°/s和±2000°/s;加速度的量程为±2 g、±4 g、±8 g和±16 g,g为9.8 m/s2;磁场的量程范围为±4 800 μT。角速度、加速度和磁场的测量结果由16位的模数转换器量化。本实验陀螺仪和加速度计的量程分别选为±2 000°/s和±16 g,其它量程处的实验同理。将MPU9250沿任意轨迹伪静态旋转,测试基于加速度计和磁力记的航姿、基于陀螺仪的航姿和基于推荐算法的航姿。因为载体处于伪静态,理想的外部加速度为0,同时可将基于加速度计和磁力计的航姿作为参考航姿。
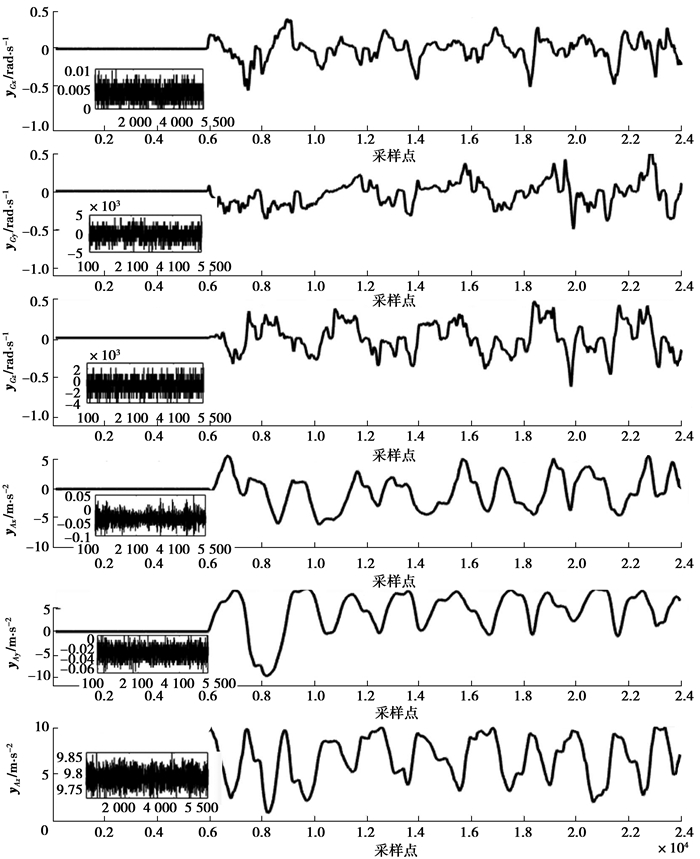
MPU9250的原始数据通过蓝牙协议采集到计算机,然后在Matlab中进行数据处理,用于计算MPU9250的航姿和外部加速度。首先将MPU9250水平静止放置在航向角为0的方向1 min,计算卡尔曼滤波器的初始参数,然后将MPU9250缓慢旋转3 min,计算外部加速度和航姿,用于验证推荐的算法的可行性。陀螺仪和加速度计在x轴、y轴和z轴上的测量数据如图 2所示,该数据为原始数据经过低通滤波器滤波后的结果,其中,第1 min内的数据放大在图 2的左下角。
|
图 2 陀螺仪和加速度计在x轴、y轴和z轴上的测量结果 Fig. 2 The measurement results of gyroscope and accelerometer at x-axis, y-axis and z-axis |
本实验中的采样时间间隔为0.01 s。第1 min内的5500个采样数据用于计算卡尔曼滤波器的初始参数,包括θ1、φ1、ψ1、X1+、P1+、nG2、nA2、σb2和ca2。
根据等式(11)、(12)和(15),可得到初始的θ1、φ1和ψ1分别为0.0165°、-0.412°和-0.1044°。当陀螺仪的初始偏置设为0时,X1+等于[-0.003, -0.007, 1, 0, 0, 0],则P1+为diag([-0.003-rms(Cn13b)]2, [-0.007-rms(Cn23b)]2,[1-rms(Cn33b)]2,[rms(yGx)]2,[rms(yGy)]2,[rms(yGz)]2),diag表示为对角矩阵,其中rms(Cn13, 23, 33b)和rms(yGx, y, z)为均方差值,分别计算为
| $ {\rm{rms }}(\mathit{\boldsymbol{C}}_{n13,23,33}^b) = \sqrt {\mathop \sum \limits_{i = 1}^{5{\kern 1pt} {\kern 1pt} {\kern 1pt} 500} {{\left[ {\mathit{\boldsymbol{C}}_{n13,23,33,i}^b - \left[ {\sum\limits_{i = 1}^{5{\kern 1pt} {\kern 1pt} {\kern 1pt} 500} {C_{n13,23,33,i}^b} /5{\kern 1pt} {\kern 1pt} {\kern 1pt} 500} \right]} \right]}^2}/5{\kern 1pt} {\kern 1pt} {\kern 1pt} 500} , $ | (30) |
| $ {\rm{rms }}({\mathit{\boldsymbol{y}}_{Gx,y,z}}) = \sqrt {\mathop \sum \limits_{i = 1}^{5{\kern 1pt} {\kern 1pt} {\kern 1pt} 500} {{\left[ {{\mathit{\boldsymbol{y}}_{Gx,y,z,i}} - \left[ {\sum\limits_{i = 1}^{5{\kern 1pt} {\kern 1pt} {\kern 1pt} 500} {{\mathit{\boldsymbol{y}}_{Gx,y,z,i}}} /5{\kern 1pt} {\kern 1pt} {\kern 1pt} 500} \right]} \right]}^2}/5{\kern 1pt} {\kern 1pt} {\kern 1pt} 500} , $ | (31) |
nG2x, y, z、σbx, y, z2和nAx, y, z2的值根据等式(31)、(32)和(33)计算
| $ n_G^2x,y,z = \left[ {\mathop \sum \limits_{i = 1}^{5{\kern 1pt} {\kern 1pt} {\kern 1pt} 500} {{\left( {\mathit{\boldsymbol{C}}_{n13,23,33,i}^b - \left( {\left( {\sum\limits_{i = 1}^{5{\kern 1pt} {\kern 1pt} {\kern 1pt} 500} {\mathit{\boldsymbol{C}}_{n13,23,33,i}^b} } \right)/5{\kern 1pt} {\kern 1pt} {\kern 1pt} 500} \right)} \right)}^2}} \right]/5{\kern 1pt} {\kern 1pt} {\kern 1pt} 500, $ | (32) |
| $ \sigma _{bx,y,z}^2 = \left[ {\mathop \sum \limits_{i = 1}^{5{\kern 1pt} {\kern 1pt} {\kern 1pt} 500} {{\left( {{y_{Gx,y,z,i}} - \left( {\left( {\sum\limits_{i = 1}^{5{\kern 1pt} {\kern 1pt} {\kern 1pt} 500} {{y_{Gx,y,z,i}}} } \right)/5{\kern 1pt} {\kern 1pt} {\kern 1pt} 500} \right)} \right)}^2}} \right]/5{\kern 1pt} {\kern 1pt} {\kern 1pt} 500, $ | (33) |
| $ n_{Ax,y,z}^2 = \left[ {\mathop \sum \limits_{i = 1}^{5{\kern 1pt} {\kern 1pt} {\kern 1pt} 500} {{\left( {{y_{Ax,y,z,i}} - \left( {\left( {\sum\limits_{i = 1}^{5{\kern 1pt} {\kern 1pt} {\kern 1pt} 500} {{y_{Ax,y,z,i}}} } \right)/5{\kern 1pt} {\kern 1pt} {\kern 1pt} 500} \right)} \right)}^2}} \right]/5{\kern 1pt} {\kern 1pt} {\kern 1pt} 500。$ | (34) |
卡尔曼滤波器的初始参数总结如表 1所示。其中,ca2为经验参数,设为0.001。
| 表 1 卡尔曼滤波器的初始参数 Table 1 Initial parameters of a kalman filter |
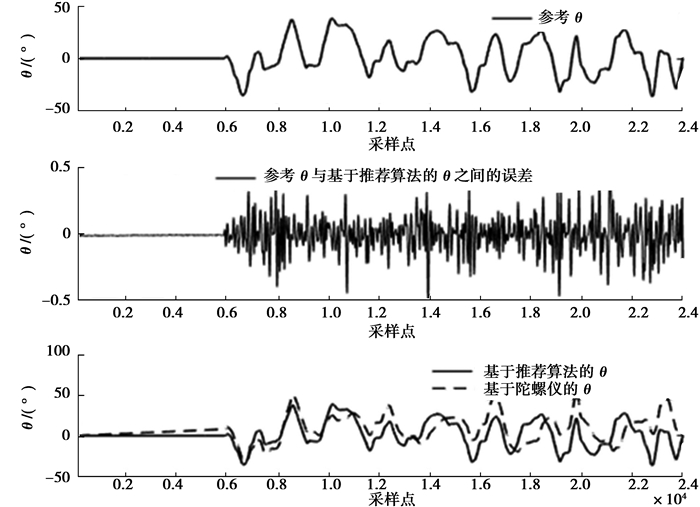
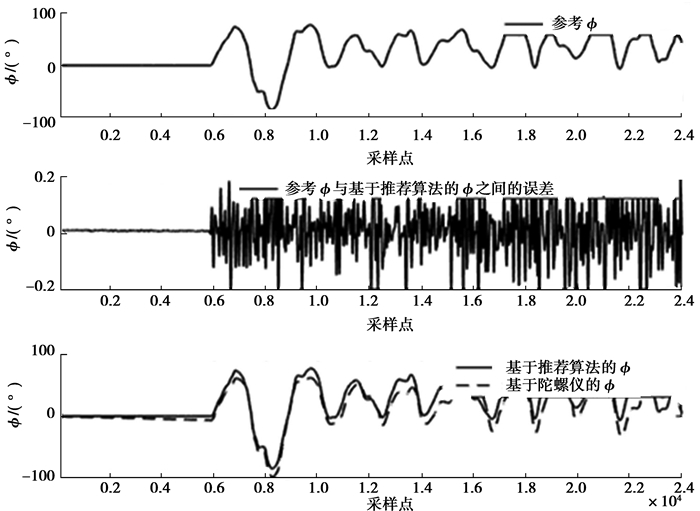
姿态包括θ 和φ。参考姿态、基于陀螺仪的姿态和基于推荐算法的姿态分别如图 3和4。因为IMU处于伪静态,参考的θ和φ采用加速度计算的θ和φ。实验结果表明,因为陀螺仪存在测量噪声和偏置,仅用陀螺仪得到的姿态存在较大偏差。与之对比,因为测量噪声和偏置被实时移除,基于推荐算法的姿态和参考姿态较一致,θ 和φ的最大误差分别仅为0.4°和0.3°。
|
图 3 参考θ、基于陀螺仪的θ和基于推荐算法的θ Fig. 3 The reference θ and the θ based on gyroscope and the proposed algorithm |
|
图 4 参考φ、基于陀螺仪的φ和基于推荐算法的φ Fig. 4 The reference φ and the φ based on gyroscope and the proposed algorithm |
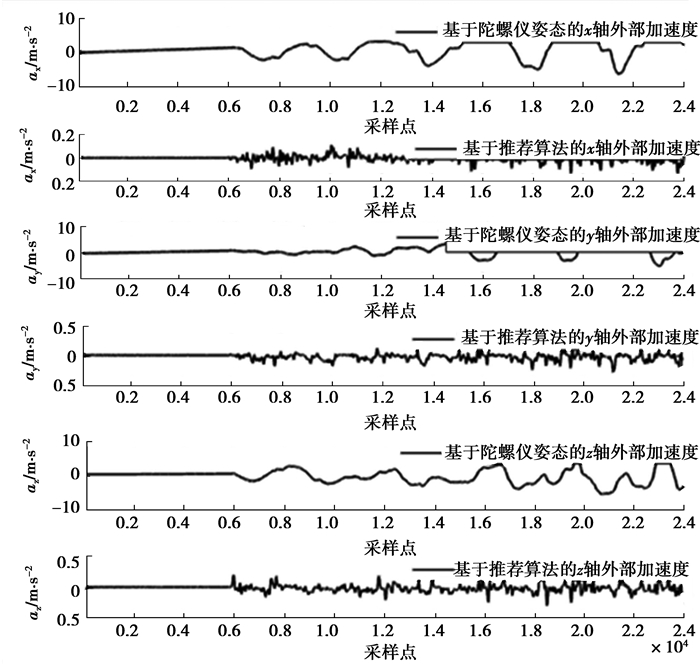
利用基于陀螺仪的姿态解算的外部加速度和基于推荐算法的姿态解算的外部加速度如图 5。因为基于陀螺仪解算的姿态具有较大的误差,其解算的外部加速度完全不正确;另一方面,因为基于推荐算法的姿态具有较高的精度,外部加速度与理想的加速度值一致,其在x轴、y轴和z轴的最大误差仅为0.2 m/s2。
|
图 5 基于陀螺仪姿态和推荐算法姿态的外部加速度 Fig. 5 External accelerations under gyroscope based attitude and the proposed algorithm based attitude |
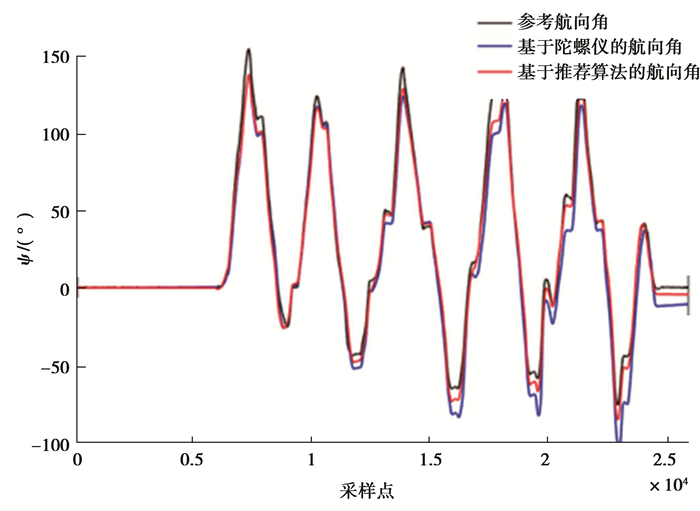
参考航向角,基于陀螺仪的航向角和基于推荐算法的航向角如图 6。根据等式(29),航向角的精度与姿态的精度和偏置有关,因为利用推荐算法的姿态较精确且陀螺仪y轴的偏置Xi, 51+和z轴的偏置Xi, 61+被移除,所以解算得到的航向角较仅用陀螺仪得到的航向角具有较高的精度。
|
图 6 参考航向角、基于陀螺仪的航向角和基于推荐算法的航向角 Fig. 6 The reference ψ and the ψ based on gyroscope and the porposed algorithm |
提出了一种高精度的航姿计算算法,它通过实时移除陀螺仪的噪声实现。笔者给出了相关的理论、卡尔曼滤波的初始参数设计和实验结果分析。实验结果表明本研究工作具有一定的先进性。其中,关键算法解算的航向角的精度远好于仅用陀螺仪解算的航向角,但距离理想的航向角仍有一定的偏差。当该算法应用在基于脚面携带MEMS-IMU的行人定位系统时,可利用零速检测和零角速度技术进一步被减小航向角偏差,因此具有一定的实用性。
| [1] |
Lu J Z, Lei C H. Applied system-level method in calibration validation for personal navigation system in field[J]. IET Science, Measurement & Technology, 2017, 11(1): 103-110. |
| [2] |
Qureshi U, Golnaraghi F. An algorithm for the in-field calibration of a MEMS IMU[J]. IEEE Sensors Journal, 2017, 17(22): 7479-7486. DOI:10.1109/JSEN.2017.2751572 |
| [3] |
Sarkka O, Nieminen T, Suuriniemi S, et al. A multi-position calibration method for consumer-grade accelerometers, gyroscopes, and magnetometers to field conditions[J]. IEEE Sensors Journal, 2017, 17(11): 3470-3481. DOI:10.1109/JSEN.2017.2694488 |
| [4] |
Zhang H L, Wu Y X, Wu M P, et al. A multi-position calibration algorithm for inertial measurement units[C/OL]. AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, Hawaii. Reston, Virigina: AIAA, 2008[2020-05-25]. https://doi.org/10.2514/6.2008-7437.
|
| [5] |
Jiang P, Wang G C, Zhang Y, et al. An improved attitude compensation algorithm in high dynamic environment[J]. IEEE Sensors Journal, 2020, 20(1): 306-317. |
| [6] |
Makni A, Fourati H, Kibangou A Y. Energy-aware adaptive attitude estimation under external acceleration for pedestrian navigation[J]. IEEE/ASME Transactions on Mechatronics, 2016, 21(3): 1366-1375. |
| [7] |
Ahme H, Tahir M. Accurate attitude estimation of a moving land vehicle using low-cost MEMS IMU sensors[J]. IEEE Transactions on Intelligent Transportation Systems, 2017, 18(7): 1723-1739. DOI:10.1109/TITS.2016.2627536 |
| [8] |
Lu J, Lei C. Applied system-level method in calibration validation for personal navigation system in field[J]. Iet Science Measurement & Technology, 2017, 11(1): 103-110. |
| [9] |
Narasimhappa M, Mahindrakar A D, Guizilini V C, et al. MEMS based IMU drift minimization:sage husa adaptive robust kalman filtering[J]. IEEE Sensors Journal, 2020, 20(1): 250-260. |
| [10] |
Radi A, Nassar S, El-Sheimy N. Stochastic error modeling of smartphone inertial sensors for navigation in varying dynamic conditions[J]. Gyroscopy and Navigation, 2018, 9(1): 76-95. |
| [11] |
Radi A, Bakalli G, Guerrier S, et al. A multisignal wavelet variance-based framework for inertial sensor stochastic error modeling[J]. IEEE Transactions on Instrumentation and Measurement, 2019, 68(12): 4924-4936. DOI:10.1109/TIM.2019.2899535 |
| [12] |
Lee J K, Park E J, Robinovitch S N. Estimation of attitude and external acceleration using inertial sensor measurement during various dynamic conditions[J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(8): 2262-2273. DOI:10.1109/TIM.2012.2187245 |
| [13] |
Zihajehzadeh S, Lee T J, Lee J K, et al. Integration of MEMS inertial and pressure sensors for vertical trajectory determination[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(3): 804-814. DOI:10.1109/TIM.2014.2359813 |
| [14] |
Wu Y X, Pei L. Gyroscope calibration via magnetometer[J]. IEEE Sensors Journal, 2017, 17(16): 5269-5275. DOI:10.1109/JSEN.2017.2720756 |
| [15] |
Luinge H J, Veltink P H. Measuring orientation of human body segments using miniature gyroscopes and accelerometers[J]. Medical & Biological Engineering & Computing, 2005, 43(2): 273-282. |
 2020, Vol. 43
2020, Vol. 43


