b. 西安理工大学 自动化与信息工程学院, 西安 710048
b. The Faculty of Automation and Information Engineering, Xi'an University of Technology, Xi'an 710048, P. R. China
随着国民经济的发展,航空出行方式已成为越来越多旅客的选择。但众所周知,飞机航班如果不能按原计划执行,不仅会在经济上造成巨大损失,还会给旅客出行带来极大不便。造成航班不正常的种种因素中,有些是不可抗阻的自然因素:如暴风雪、飓风等;有些是不可预测的突发事件:如突发恐怖袭击、飞机机械故障等;还有些是因为管理手段的落后:比如飞行员缺位、空中管制等。近年来快速增长的航空旅客数量已超过了许多主要机场容量,加上气候变化反常及安全突发事件增多,各国民航管理机构和各大航空公司对航班恢复问题越发重视,因为一旦某个航班出现故障,就有可能造成一系列连锁反应,从而影响成千上万旅客的出行。因此针对不正常航班问题,如何快速合理科学的对其进行恢复,是目前研究的重点方向[1-3]。
不正常航班恢复问题作为一种实时网络优化问题,其约束条件众多且十分复杂,属于NP-Hard问题。国内外学者专家进行了一系列相关研究,Kohla等[4]基于分支定界法,提出以旅客的总延误最小化为目标函数模型,以解决飞机资源短缺问题。Teodorović等[5]提出通过网络流的形式构建以旅客最小总延误为目标函数的航班恢复模型,并通过网络流求解TSP问题从而得到最优解。Eggenberg等[6]采用了一种考虑航班运行约束的列生成算法,通过对最短路径问题进行求解,从而形成新的列(既飞机路线),最终建立航班恢复模型,通过实测数据对模型进行验证。Liang等[7]针对飞机路径问题,提出一种新颖的混合整数线性规划计算公式。Petersen等[8]对旅客行程、机组排班和飞机路线进行一体化整合,并提出相应的优化模型,通过Benders分解及列生成法进行求解,用以解决航班恢复问题。Dunbar等[9]提出一种用于精确计算最小延误传播成本的新方法。Jozefowiez等[10]提出了一种启发式算法解决航班计划的恢复问题。
而中国国内关于不正常航班问题的研究起步相对较晚。唐小卫等[11]基于经典的资源指派模型,考虑放宽流平衡的约束建立了恢复模型,在GRASP算法及模拟退火算法的基础上,提出了一种新的启发式算法。白凤等[12]同时考虑了机场关闭和飞机短缺的因素,通过构建恢复网络,建立多商品网络流模型,采用列生成算法对其进行求解。朱博等[13]采用约束规划的方法,建立一体化恢复模型,对比分析了一体化恢复与分阶段恢复的优异。吴刚等[14]分析了由于飞机资源短缺而导致的不正常航班问题,针对该问题建立了多商品网络流模型,并对列生成算法进行了改进,在算法的效率上有了明显的提高。尽管目前针对不正常航班问题的研究已取得众多成果,但仍存在一些问题,如:没有将航班延误,飞机置换及航班取消等调度策略综合考虑,并且针对此类NP-Hard问题,大多采用启发式算法,无法保证解的质量。
鉴于此,拟采用时空网络技术,对不正常航班问题进行描述,以实现对航班在空间和时间上的追踪。然后在最小费用流的基础上,建立航班最小延误时间模型,该模型同时考虑航班延误,飞机置换及航班取消的调度策略,并采用Floyd-Warshall算法进行求解。最终通过算例计算,得出机场关闭情况下最小延误时间,验证了模型的可行性。
1 不正常航班恢复问题某些突发事件的发生会造成机场关闭,导致航班无法按原计划实行,此时需要尽快对航班计划进行调整,减少损失。针对航班恢复问题,通常有3种调整方法:航班延误、飞机置换和航班取消。航班延误和飞机置换可以同时发生。飞机置换就是将航班安排给不同于原计划执行飞机的其他飞机去执行,如图 1所示。
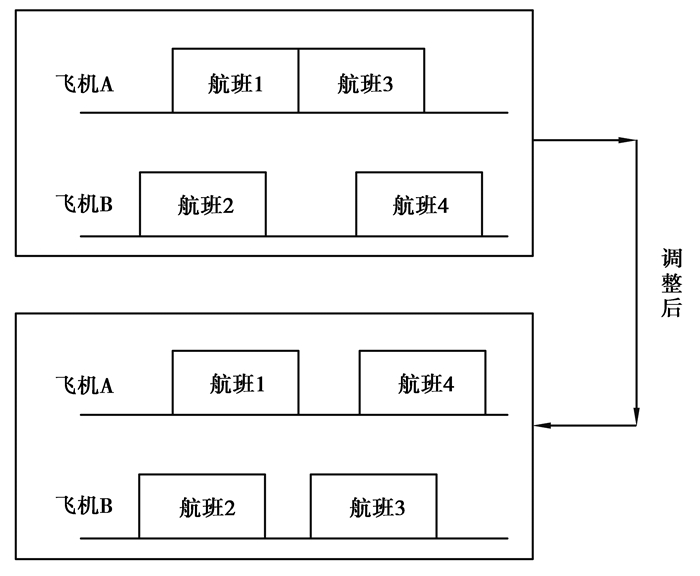
|
图 1 飞机置换示意图 Fig. 1 Aircraft replacement schematic |
由于航班运输的特殊性,在航空规划问题的研究中,经典网络往往不能对问题进行清晰描述,因此,需要借助特殊网络。为了更加直观的在空间和时间上对恢复航班进行跟踪,便有了时空网络[15]。
2.1 时空网络的描述时空网络主要由有向边及节点构成,节点同时包含空间特性和时间特性。首先,以横坐标各坐标点表示各个机场(相互离散),以每一机场为基点作一纵轴,以表示时间轴,其方向由上至下表示时间的进程,起始点为航班最早始发时间,终止点为最晚到达时间[16]。可根据航班的时刻表将连续时间轴离散化,从而得到若干节点,各个节点代表某一航班在某一机场的起飞时间或到达时间,如图 2所示,图中不同颜色直线表示不同航班的具体调度情况。
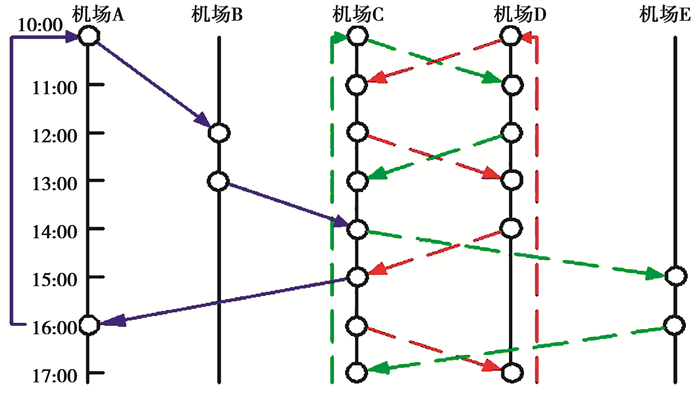
|
图 2 时空网络基本图 Fig. 2 Basic map of space-time network |
在航班恢复问题中,每一个网络节点指代一个特定时间的特定机场,每一条边的连接与网络中不同时间的事件相关联。在航班问题中主要包括三种边:第一,航班边,由每趟航班的起飞节点指向到达节点;第二,过站边,方向由上至下,连接同一机场不同的节点,表示航班在该机场短暂停留;第三,过夜边,方向由下至上,由同一机场的终止节点指向起始节点,表示航班在该机场停留过夜。在时空网络中,流动的是各个机型的飞机,且任一航班边只能有一架飞机,每条过站边及过夜边都可设置容量[17]。
2.2 最小费用流模型不正常航班恢复问题的核心就是在有限的时间内尽快恢复航班秩序,即总延误成本最小。因此,可将此类问题视为最小费用流问题,其基本概念如下:
网络G=(V, E, c, ω)是一个带有始点νs和终点νt的容量—费用网络,在容量—费用网络G中,求一个非负的可行流,当可行流费用最小时,称其为最小费用流。其数学模型基本形式如下[18-19]
| $ {\rm{min}}z = {\sum \omega _{ij}}{f_{ij}}, $ | (1) |
| $ {\rm{s}}.{\rm{t}}.\left\{ \begin{array}{l} \;\;\;\;0 \le {f_{ij}} \le {c_{ij}}, \;\;\;\;\;\;\;\;\;i, j = s, 1, 2, \ldots , n, t, \\ \sum\limits_{i = s}^n {{f_{sj}}} = {\nu _0} = \sum\limits_{i = s}^n {{f_{jt}}} , \\ \sum\limits_{i = s}^n {{f_{ji}}} - \sum\limits_{i = s}^n {{f_{ij}}} = 0, \;\;\;\;i = 2, 3, \ldots , n, t, \\ \;\;\;\;({\nu _i}, {\nu _j}) \in E, \end{array} \right. $ | (2) |
式中:z为网络流中所有弧的流量总费用;ωij为每单位流量通过弧(νi, νj)时的费用;fij为通过弧(νi, νj)的流量;(νi, νj)为从νi到νj的弧;cij为弧(νi, νj)的容量;ν0为通过可行流的流量;E为网络流中所有弧的集合。
目标函数为流过网络流中所有弧的流量费用总和最小。
约束条件1表示流过弧(νi, νj)的流量非负且小于该弧的容量cij;约束条件2表示可行流的流量ν0等于始点νs流入量或终点νt流出量;约束条件3表示中间点νi的净储流量为0;约束条件4表示弧(νi, νj)是网络流弧集合E中的弧。
2.3 航班最小延误时间模型基于最小费用模型,进一步建立了航班最小延误时间模型如下
| $ {\rm{min}}t = \sum\limits_{f \in F} {\sum\limits_{i \in I} {x_f^i} } a_f^i + \sum\limits_{f \in F} {{y_f}} {b_f} + \sum\limits_{f \in F} {\sum\limits_{i \in I} {z_f^i} } c_f^i, $ | (3) |
| $ {\rm{s}}.{\rm{t}}.\left\{ \begin{array}{l} \;\;\;\;\;\;\;\;\;\sum\limits_{i \in I} {x_f^i} + {y_f}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\forall f \in F, \\ \;\;\;\;\;\;\;0 \le x_f^ia_f^i \le {t_a}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\forall f \in F, \forall i \in I, \\ a_f^i = an\left( {n = 1, 2, \ldots , 30} \right), \;\;\;\forall f \in F, \forall i \in I, \\ \;\;\;\;\;\;\;\;\;\sum\limits_{i \in I} {x_f^i} \le 1, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\forall i \in I, \end{array} \right. $ | (4) |
式中:I为飞机集合;F为航班集合;xfi为0-1变量,当航班f被飞机i执行时,取1;否则取0。yf为0-1变量,当航班f被取消时,取1;否则取0。zfi为0-1变量,当飞机i为置换飞机时,取1;否则取0;afi为延误成本;bf为取消成本;cf为置换成本。
目标函数为最小航班总延误时间。其中第一项为因航班延误而导致的延误成本,第二项为因航班取消而导致的取消成本,第三项为因航班置换而导致的置换成本。
约束条件1表示每一个航班只能被执行或者被取消;约束条件2表示如果航班被执行,延误时间需不小于0且不大于ta;约束条件3表示航班延误的决策时间点间隔为a;约束条件4表示一架飞机最多只能指派给一条航班。
3 Floyd-Warshall算法随着科学技术和计算机水平的发展,针对最小费用流问题的求解已有众多算法,不同算法的方式手段或许不同,但最终目的均是找到最小费用流。采用Floyd-Warshall算法对不正常航班的恢复问题进行求解计算,算法基本思路如下。
设图G=(V, E), wij表示边(vi, vj)上的权,若vi与vj不相邻,则wij=+∞;用dij表示顶点vi到顶点vj的最短距离,则对于任何一个顶点vk∈V,从顶点vi到顶点vj的最短路经过vk,或者不经过vk,这样就可以利用动态规划的思想来比较dij和dik+dkj的大小。
当dij>dik+dkj时,令dij=dik+dkj,则使得dij始终为顶点vi到顶点vj的最短距离。重复该步骤搜索全部顶点vk,则最终得到的dij既是顶点vi与顶点vj之间最短距离。该算法称为Floyd-Warshall算法,简称Floyd算法,其步骤如下[20]
Step1:输入图G的权矩阵W,则对所有i, j,有dij=wij,k=1;
Step2:更新dij,对所有的i, j,若dij>dik+dkj,则令dij=dik+dkj;
Step3:若dii<0,则存在一条含有顶点vi的负权值,算法终止;或k=n时算法终止;否则转Step2。
4 算例分析 4.1 数据来源数据来源于2017年全国研究生数学建模竞赛华为杯C题,题目相关信息如下:
由于受到暴风雪的影响,管理部门决定在2016年4月22日的18:00到21:00之间关闭机场OVS。在该时间段内该机场不能起飞或降落任何航班,而该时间段之前的所有航班都处于正常状态,该时间段之后机场可立即恢复正常起降。因此,原定在该日18:00至21:00之间(不包括18:00和21:00这2个时刻)起降的所有航班都需要重新安排,而且它们的重新安排可能造成关闭后其它航班的重新安排。
不考虑旅客信息,如何重新规划机型9(不考虑其他机型)的航班计划,制定起飞时间表(给出延误分钟),使得所有原计划安排给机型9的航班尽可能不被取消,同时保证机型9的所有航班总体延误时间最短?
4.2 模型假设基于不正常航班恢复问题,作出如下几点假设:
1) 所有航班只能延误,不能提前;
2) 不考虑机场可停留飞机的容量;
3) 不考虑OVS机场每5 min内起降飞机的数量;
4) 所有机场可以全天24 h工作;
5) 不考虑机组人员的恢复,也不考虑旅客行程重新规划问题;
6) 飞机的飞行时间不会因延误而受影响;
7) 航班延误的决策时间点间隔为10 min。
4.3 结果分析将航班数据带入本文建立的最小延误时间模型,并采用Floyd-Warshall算法进行求解,利用Matlab软件计算可得航班的调整方案。经统计,在OVS机场关闭时间段内,机型9共有13次航班计划需要进行调整,具体调整计划见表 1,图 3为本次航班调度的时空网络图。
| 表 1 航班延误时间详情表 Table 1 Schedule of flight delays |
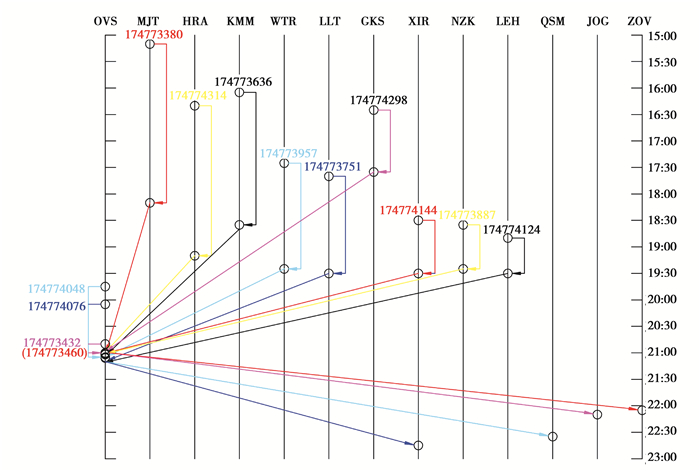
|
图 3 航班时空网络图 Fig. 3 Flight space-time network chart |
从表 1可以看出,174773380、174774314、174773636等13次航班需要延迟,而其中174774048等4次航班的执行飞机需被置换,航班总延误时间为1 110 min。从图 3可知13次航班的具体调度延误情况,在时间和空间上对本次航班调度情况有更加直观的了解。
由表 1可知13次航班的具体延误情况,如下
1) 其中航班174773380、174774314、174773636等9次航班比原计划起飞时间分别延误180 min、170 min、150 min……,主要原因是因为此9次航班原计划到达OVS机场时间该机场处于关闭状态。
2) 其中航班174774048、174774076、174773432、174773460共4次航班比原计划起飞时间分别延误80 min、60 min、10 min、10 min,主要原因是因为此4次航班原计划起飞时间OVS机场处于关闭状态。
5 结论研究了因突发状况导致机场关闭从而造成不正常航班问题的解决方法。通过时空网络对不正常航班进行描述,基于最小费用流模型建立了航班最小延误时间模型,模型同时包含了航班延误,飞机置换及航班取消的调度策略,并提出采用Floyd-Warshall算法对模型进行求解。最终通过算例计算验证模型和算法的有效性。研究思路、模型及方法具有一定的普遍适用性,可用于指导突发情况下不正常航班的快速恢复问题。存在的不足是没有进一步考虑不同机型的置换以及各旅客的实际乘坐情况,这些都是以后的研究方向。
| [1] |
唐小卫, 高强, 朱金福. 不正常航班恢复模型的贪婪模拟退火算法研究[J]. 预测, 2010, 29(1): 66-70. TANG Xiaowei, GAO Qiang, ZHU Jinfu. Research on greedy simulated annealing algorithm of irregular flight schedule recovery model[J]. Forecasting, 2010, 29(1): 66-70. (in Chinese) |
| [2] |
丁建立, 王新茹, 徐涛. 航班延误恢复调度的混合粒子群算法[J]. 交通运输工程学报, 2008, 8(2): 90-95. DING Jianli, WANG Xinru, XU Tao. Hybrid particle swarm optimization arithmetic for recovery scheduling of flight delays[J]. Journal of Traffic and Transportation Engineering, 2008, 8(2): 90-95. (in Chinese) |
| [3] |
Jafari N, Zegordi S H. Simultaneous recovery model for aircraft and passengers[J]. Journal of the Franklin Institute, 2011, 348(7): 1638-1655. DOI:10.1016/j.jfranklin.2010.03.012 |
| [4] |
Kohl N, Larsen A, Larsen J, et al. Airline disruption management:perspectives, experiences and outlook[J]. Journal of Air Transport Management, 2007, 13(3): 149-162. DOI:10.1016/j.jairtraman.2007.01.001 |
| [5] |
Teodorović D, Guberinić S. Optimal dispatching strategy on an airline network after a schedule perturbation[J]. European Journal of Operational Research, 1984, 15(2): 178-182. |
| [6] |
Eggenberg N, Salani M, Bierlaire M. Constraint-specific recovery network for solving airline recovery problems[J]. Computers & Operations Research, 2010, 37(6): 1014-1026. |
| [7] |
Liang Z, Chaovalitwongse W A, Huang H C, et al. On a new rotation tour network model for aircraft maintenance routing problem[J]. Transportation Science, 2011, 45(1): 109-120. |
| [8] |
Petersen J D, Sölveling G, Clarke J P, et al. An optimization approach to airline integrated recovery[J]. Transportation Science, 2012, 46(4): 482-500. DOI:10.1287/trsc.1120.0414 |
| [9] |
Dunbar M, Froyland G, Wu C L. Robust airline schedule planning:minimizing propagated delay in an integrated routing and crewing framework[J]. Transportation Science, 2012, 46(2): 204-216. DOI:10.1287/trsc.1110.0395 |
| [10] |
Jozefowiez N, Mancel C, Mora-Camino F. A heuristic approach based on shortest path problems for integrated flight, aircraft, and passenger rescheduling under disruptions[J]. Journal of the Operational Research Society, 2013, 64(3): 384-395. |
| [11] |
唐小卫, 朱金福, 高强. 流不平衡条件下飞机恢复的优化模型与算法研究[J]. 小型微型计算机系统, 2010, 31(4): 793-796. TANG Xiaowei, ZHU Jinfu, GAO Qiang. Research on optimization model and algorithm of unbalanced aircraft recovery[J]. Mini-Micro Systems, 2010, 31(4): 793-796. (in Chinese) |
| [12] |
白凤, 朱金福, 高强. 基于列生成法的不正常航班调度[J]. 系统工程理论与实践, 2010, 30(11): 2036-2045. BAI Feng, ZHU Jinfu, GAO Qiang. Disrupted airline schedules dispatching based on column generation methods[J]. Systems Engineering-Theory & Practice, 2010, 30(11): 2036-2045. (in Chinese) |
| [13] |
朱博, 朱金福, 高强. 飞机和机组一体化恢复的约束规划模型[J]. 交通运输工程学报, 2013, 13(1): 77-83. ZHU Bo, ZHU Jinfu, GAO Qiang. Constraint programming model of integrated recovery for aircraft and crew[J]. Journal of Traffic and Transportation Engineering, 2013, 13(1): 77-83. (in Chinese) |
| [14] |
吴刚, 严俊. 不正常航班恢复的一种改进的列生成算法[J]. 南京航空航天大学学报, 2014, 46(2): 329-334. WU Gang, YAN Jun. Improved column generation algorithm for disrupted airline schedules recovery[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2014, 46(2): 329-334. (in Chinese) |
| [15] |
乐美龙, 王婷婷, 吴聪聪. 多机型不正常航班恢复的时空网络模型[J]. 四川大学学报(自然科学版), 2013, 50(3): 477-483. LE Meilong, WANG Tingting, WU Congcong. The time-band model for recovery of multi-type aircrafts' disrupted flights[J]. Journal of Sichuan University (Natural Science Edition), 2013, 50(3): 477-483. (in Chinese) |
| [16] |
赵秀丽.航空公司不正常航班恢复模型及算法研究[D].南京: 南京航空航天大学, 2010. ZHAO Xiuli. Research on airline irregular flight recovery model and Algorithm[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10287-1011291558.htm |
| [17] |
Bard J F, Yu G, Arguello M F. Optimizing aircraft routings in response to groundings and delays[J]. ⅡE Transactions, 2001, 33(10): 931-947. |
| [18] |
Atamtürk A, Zhang M H. Two-stage robust network flow and design under demand uncertainty[J]. Operations Research, 2007, 55(4): 662-673. DOI:10.1287/opre.1070.0428 |
| [19] |
Ebrahim R M, Razmi J. A hybrid meta heuristic algorithm for bi-objective minimumcost flow (BMCF) problem[J]. Advances in Engineering Software, 2009, 40(10): 1056-1062. DOI:10.1016/j.advengsoft.2009.03.003 |
| [20] |
谢潜, 武鹏, 周江昕, 等. 基于Floyd-warshall算法的分布式电源孤岛划分[J]. 水电能源科学, 2015, 33(10): 173-177. XIE Qian, WU Peng, ZHOU Jiangxin, et al. Island partition for distributed generation based on floyd-warshall algorithm[J]. Water Resources and Power, 2015, 33(10): 173-177. (in Chinese) |
 2020, Vol. 43
2020, Vol. 43

