2. 四川大学 计算机学院, 成都 610065
2. College of Computer Science, Sichuan University, Chengdu 610065, P. R. China
软件定义网络(SDN, software defined networking)作为一个新型网络架构[1-2],通过解耦网络的数据平面和控制平面,解决了传统网络体系结构中存在的设备配置复杂、管理结构臃肿、管控能力不足及可扩展性差等问题,引起了各界的广泛关注。随着SDN在大规模网络中的应用,单一集中式控制器的单点失效、负载过大等问题突显出来,研究学者们提出分布式控制的可扩展控制平面解决方案。分布式控制方式是多个控制器共同协调管理交换机,而控制器个数和位置影响网络的性能,从而如何部署分布式控制器成为目前SDN研究热点之一。
根据SDN网络应用场景的需求,依据性能尺度对控制器部署问题进行求解。当求解选取的性能尺度不同时,求解的结果也存在明显差异[3]。在不同需求下如何确定控制器个数和位置、交换机与控制器之间的关联是控制器部署的研究关键,已经证明是一个NP难问题[4]。求解控制器部署问题的经典算法包括启发式算法[5-6]、基于最小割算法[7]、贪婪搜索算法[8-9]、聚类问题求解算法[10-13]等。在聚类问题求解算法中,文献[10]首次将控制器部署抽象为聚类问题求解,利用2个代价函数分布表示管理域间连接链路和管理域内控制器与交换机间平均传输时延,通过最小化代价来对网络中管理域进行划分, 算法只考虑传输时延。文献[11]通过对网络进行子域划分, 以改进谱聚类方法来研究控制器的部署问题, 提出在时延和容量限制下,负载均衡的SDN网络多控制器部署算法, 但算法复杂度相对较高,且结果比较随机。文献[12]利用K-critical方法求解,通过选择出来的控制器构建高健壮性和负载均衡的控制网络,存在节点跨域问题。文献[13]提出层次聚类K*-means算法最小化传输时延和控制器负载均衡,但未考虑可靠性问题。目前关于SDN分布式控制器部署研究从时延、可靠性、负载等性能指标进行研究,仍存在求解方法复杂、优化目标和约束条件过于单一等问题。在网络拓扑结构已知情况下,采用聚类思想,从提高网络弹性和可靠性两方面优化目标,提出两阶段部署控制器(TSCP, two-stage controller placement)算法:利用节点相似度划分控制域,增强控制域的网络弹性;选择控制路径平均失效率最小的控制器集合作为控制器的部署,提高网络的可靠性。
1 问题描述及模型 1.1 问题描述SDN分布式控制器部署是考虑网络拓扑结构,根据相关需求,确定控制器的个数和位置,并将网络中的交换机划分到相应控制器下,形成多个控制域。控制器部署的位置实际上是某个交换机的位置附近,该交换机与控制器的传播时延可以忽略。假设SDN抽象为无向图G=(S, E, W)中,S为网络中交换机节点的集合,E为连接网络中交换机的无向边的集合,W为交换机之间传播时延大小的集合,其元素w(i, j)表示交换机节点i与节点j之间时延大小,取0表示两者不可达,反之亦然。建立相应邻接矩阵A,元素a(i, j)表示如下
| $ a(i, j) = \left\{ {\begin{array}{*{20}{l}} 1&{w(i, j) > 0, {\rm{ s}}{\rm{.t}}{\rm{.}}i{\bf{ }}, j \in S, }\\ 0&{{\rm{ others}}, {\rm{ }}} \end{array}} \right. $ | (1) |
其中:a(i, j)=1表示节点i和节点j相邻,a(i, j)=0表示两者不相邻。
为了便于描述问题,用C表示控制器节点集合,且C⊆S。d(s, c)表示网络中交换机s到控制器c的最小传播时延,σ表示交换机与控制器之间传播时延的上限,δ表示控制器与控制器之间的传播时延上限,P(i, j)表示交换机节点i与节点j之间最短路径。
1.2 部署模型分布式控制器部署是确定控制器的个数和位置、交换机与控制器之间关系,与控制器容量大小、网络设备(交换机或控制器)之间传播时延大小等相关。
1.2.1 交换机与控制器之间关联考虑一个交换机只受一个控制器控制,交换机与控制器之间的关系用二维数组X|S|×|C|表示,其中|S|、|C|分别是网络中交换机和控制器的个数,定义如下
| $ x(s, c) = \left\{ {\begin{array}{*{20}{l}} 1&{c \to s, }\\ 0&{{\rm{ others, }}} \end{array}} \right. $ | (2) |
式(2)中x(s, c)=1表示交换机s受控于控制器c,反之,表示两者不存在关系。
1.2.2 相邻控制域控制域是描述控制器所控制的交换机集合,即控制器c对应的控制域D(c)表示为D(c)={ s|x(s, c)=1, ∀s∈S}。
相邻控制域是指2个控制域的交换机之间存在链路,用n(i, j)表示
| $ n(i, j) = \left\{ {\begin{array}{*{20}{l}} 1&{{\rm{ if }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} w(u, v) \ne 0\quad \exists u \in D(i), v \in D(j), }\\ 0&{{\rm{ others, }}} \end{array}} \right. $ | (3) |
式(3)中n(i, j)=1表示控制域i和控制域j相邻,反之,则不相邻。
1.2.3 时延约束传播时延反映了网络设备之间传递消息的快慢。交换机与控制器之间的传播时延越小,控制器处理交换机的消息效率越高。控制器部署时尽量选择与它传播时延较小的交换机,需要约束交换机与控制器之间传播时延,即
| $ d(s, c) \le \sigma \quad \forall s \in S, \forall c \in C, $ | (4) |
控制器与控制器之间需要同步状态等,则相邻控制器之间的传播时延不能过大,否则影响网络的性能。控制器u和控制器v的传播时延大小约束如下
| $ d(u, v) \le \delta \forall u, v \in C, \quad n(u, v) = 1。$ | (5) |
假设网络中部署同种类型的控制器,则控制器的容量相同。控制器容量反映了可管理的交换机个数上限。为了均衡控制域的规模,需约束控制域的交换机个数,即
| $ {\eta _L} \le \sum\limits_{s \in S} x (s, c) \le {\eta _U}, \quad \forall c \in C, $ | (6) |
式(6)中ηL、ηU分别为控制域的规模下限和上限。
2 TSCP算法两阶段控制器部署算法(TSCP, two-stage controller placement)是优化网络弹性和可靠性,分为控制域划分和控制器部署两阶段。控制域划分是先利用节点相似度划分控制域,且满足相关约束,形成初始的控制域;再通过分裂控制域和迁移节点,均衡控制域内交换机个数,优化控制域。控制器部署是在满足相关约束条件下选择可靠性强的节点作为控制器的位置,可靠性用控制路径平均失效率衡量。
2.1 相似度定义网络划分中节点间的相似度是反映网络中节点连接的紧密程度或者节点间的关联程度。定义节点i的邻居节点集(包括自身节点i)记为N(i),即
| $ N(i) = \{ j|a(i, j) = 1\} \cup \{ i\} 。$ | (7) |
节点i的权重记为nw(i),表示节点i的所有邻接边的权重倒数之和,即
| $ nw(i)=\sum\limits_{\begin{smallmatrix} k\in N(i) \\ k\ne i \end{smallmatrix}}{\frac{1}{w(i, k)}}。$ | (8) |
节点i与j的关联权重记为nw(i, j),表示节点i与j的所有公共邻居节点之间的相邻边的权重倒数之和,即
| $ nw(i, j)=\sum\limits_{\begin{smallmatrix} u, v\in N(i)\bigcap N(j) \\ u<v \end{smallmatrix}}{\frac{1}{w(u, v)}}。$ | (9) |
当节点i与j拥有较多的相同的邻居节点或者距离较近时,其相似度相对较大。对于任意节点i与j,如果它们直接相连,则存在较大的相似度,且其相似度随节点i与j之间的距离(即权重w(i, j))增大而减小;如果它们不是直接相连,只是存在共同的邻接点,则节点i与j的相似度与邻接节点相关。权重倒数1/w(i, j)和nw(i, j)分别反映了距离越小相似度越大以及公共节点个数越多相似度越大的关系,结合文献[14]提出的节点相似度模型,提出新的基于权重的节点相似度定义
| $ {\rm{ Sim}} (i, j) = \left\{ {\begin{array}{*{20}{c}} {\frac{{\frac{1}{{{w_{ij}}}} * nw(i, j)}}{{nw(i) + nw(j) - \frac{1}{{{w_{ij}}}}}}}&{i \leftrightarrow j, }\\ {\prod\limits_{ < u, v > \in {P_{ij}}} {{\rm{Sim}}} (u, v), }&{i \to j, }\\ {0, }&{{\rm{ others , }}} \end{array}} \right. $ | (10) |
式(10)中Pij表示节点i与j的最短路径,<u, v>表示路径Pij上有序的节点对。式(10)从2节点直接相连、不相连但存在路径和不存在路径3种情况定义2节点间的相似度:当节点i与j直接相连时,即权重w(i, j)不为0,1/w(i, j)说明节点间距离越大其相似度越小,nw(i, j)反映了公共节点越多其值相对较大。可简单证明分母是大于等于分子的,因分子中nw(i, j)表示2个邻居节点集的交集,分母反映两者的并集。同时1/w(i, j)值小于等于1,从而证明了整个分式的取值范围为(0, 1]。当2节点不是直接相连时,但节点i与j存在路径Pij,其相似度与路径Pij上的节点有关,且任意两节点的相似度相互独立,则选择其最短路径上的节点间的相似度的乘积作为两节点的相似度。当两节点不可达时,其相似度为0。理论证明,式(10)满足非负性、自反性、传递性等特性,且取值区间在[0, 1],满足相似度定义。
节点间的相似度描述了节点之间的紧密关系,则推广到节点与控制域之间的相似度定义。即节点i与控制域D(k)的相似度为[14]
| $ {\rm{ Sim}} (i, D(k)) = \sum\limits_{j \in D(k)} {{\rm{Sim}}} (i, j)。$ | (11) |
初始划分采用聚类思想,初步形成控制域,尽量使得控制域的交换机个数最大化,从而减少控制器个数。
初始划分过程:
Step 1:计算节点间的相似度;初始迭代次数N;初始队列queue为空;初始交换机节点遍历标志为false;
Step 2:获取任意边缘节点,以节点i形成第一个控制域D(i);
Step 3:依次遍历与控制域D(i)相邻的节点,选择与它相似度最大的节点j,且满足条件:1)控制域D(i)与节点j新形成的控制域D(i)中存在某节点v,使得所有节点到某节点v的传播时延均小于等于上限σ;2)新形成的控制域D(i)的交换机总个数满足上限ηU,则将节点j加入控制域D(i),标记节点j为true。重复执行,直到没有任何节点可加入控制域D(i)。
Step 4:选择与控制域D(i)相邻的所有节点,加入队列queue中;
Step 5:若队列queue为空,跳到Step 7;否则,出队列,选择标记为false的节点i且满足当前节点与相邻控制域的控制器传播时延满足上限δ,形成下一个控制域D(i)。
Step 6:依次遍历与控制域D(i)相邻节点j:若节点j已标记,判断节点j与控制域D(i)的相似度是否大于与其他控制域的相似度,从中选择相似度最大的节点j,且满足条件:1)控制域D(i)与节点j新形成的控制域D(i)中存在某节点v,使得所有节点到某节点v的传播时延均小于等于上限σ;2)满足条件(1)节点的同时需要满足控制域D(i)与所有相邻域D(k)对应2个控制器之间传播时延不大于上限δ;3)新形成的控制域D(i)的交换机总个数满足上限ηU,则将节点j加入控制域D(i),并从其他控制域中删除,标记节点j为true。重复执行,直到没有任何节点可加入控制域。跳到Step 4;
Step 7:重置queue为空,以及所有交换机节点标志为false;
Step 8:重复执行N次Step 2到Step 7;选择最优的划分结果,需要优先选择控制域个数最少的,其次选择控制域规模比较均衡的(选择控制器容量利用率方差最小的);
Step 9:输出结果,算法结束。
初始划分结果可能存在控制域的规模小于下限ηL情况,需要优化控制域。
2.2.2 优化划分优化划分是为了减少控制域个数,平衡控制域规模。划分采用分裂和迁移方法,分裂是将可能重叠的控制域的所有交换机分配到邻居控制域,减少控制域个数。迁移是从相邻控制域中迁移部分节点到当前控制域,增加当前控制域的交换机个数,平衡各个控制域的规模。
1) 分裂控制域
Step 1:对初始划分结果按控制域的规模升序排序;
Step 2:遍历控制域D(i),计算当前控制域的相邻控制域;
Step 3:若控制域D(i)的节点划分到其他相邻控制域,使得所有相邻控制域的交换机个数大于上限ηU,则分裂失败,跳到Step 5;
Step 4:将控制域D(i)的所有节点进行集合划分,划分子集个数等于相邻控制域的个数,采用递归思想实现;
Step 5:遍历所有集合划分结果,判断每个集合划分中的子集节点是否可以划分到其他相邻控制域D(k),且新形成的控制域D(k)满足传播时延上限σ、时延上限δ、控制域的规模上限ηU3个约束条件,若满足,则该集合划分满足条件,分裂成功。更新控制域集合,结束遍历;否则,继续遍历直到结束;
Step 6:若控制域遍历未结束,继续Step 2;
Step 7:分裂结束。
分裂可以减少控制域的个数,仍可能存在规模小的控制域,则需从相邻控制域中迁移部分节点,使得控制域的交换机个数均衡。
2) 迁移节点
Step 1:控制域的规模升序排序;
Step 2:遍历控制域D(i),判断相邻控制域D(k)的节点,对于D(k)中节点j,满足条件:1)控制域D(i)与节点j新形成的控制域D(i)中存在某节点v,使得所有节点到某节点v的传播时延均小于等于上限δ;2)满足条件(1)的节点同时需要满足控制域D(i)与所有相邻域对应2个控制器之间传播时延不大于上限δ;3)新形成的控制域D(i)的交换机总个数满足上限ηU;选择与D(i)相似度最大的节点迁移到D(i),且保证被迁移控制域D(k)节点的连通性;对于所有满足条件的节点,构成迁移节点集;
Step 3:遍历迁移节点集,选择与当前控制域相似度最大的节点构成新的控制域,且迁移节点个数至少使得控制域的容量不小于下限ηL,均衡相邻控制域的规模。直到遍历结束;
Step 4:若控制域遍历未结束,继续Step 2;
Step 5:迁移结束。
经过2次控制域划分,控制域内结点连接紧密,控制域交换机个数最大化,控制域个数最小化。
2.3 基于可靠性的控制器部署算法 2.3.1 可靠性描述SDN中网络设备的控制平面和数据平面的控制消息传递主要通过控制路径,网络中交换机与控制器的控制消息、控制器与控制器之间的状态同步消息都需要通过控制路径传递。当某条控制路径失效时,中断的交换机可能处于非控制状态,控制器与其他控制器的消息同步失败。因此,控制路径失效越多,控制流量中断的可能性越大。控制器的个数和位置不同,控制路径也不同,影响网络的可靠性。
用控制路径失效率描述网络的可靠性,失效率越小,可靠性越大。控制路径的失效率与控制路径上的节点和链路有关,任意节点或链路失效,控制路径失效。所指的控制路径是控制器与交换机之间、控制器与控制器之间的最短路由。
定义节点i和节点j通过路径P(i, j)连通失效的概率
| $ q(i, j)=1-\prod\limits_{\begin{smallmatrix} \forall v, e\in P(i, j) \\ v\in S, e\in E \end{smallmatrix}}{(1-{{r}_{v}})}(1-{{r}_{e}}), $ | (12) |
式(12)中re表示链路e失效率,rv表示节点v失效率。
网络控制路径平均失效率是两部分控制路径失效率之和的均值,包括控制器与控制器之间的控制路径失效率和控制域内控制器与交换机的控制路径失效率。其值越小,网络可靠性越强。网络控制路径平均失效率ρ
| $ \rho = \frac{1}{m}\left[ {\sum\limits_{u \in C} {\sum\limits_{\begin{array}{*{20}{c}} {v \in C}\\ {u < v} \end{array}} q } (u, v) + \sum\limits_{u \in C} {\sum\limits_{i \in D(u)} q } (u, i)} \right], $ | (13) |
式(13)中m表示控制路径数,等于控制器与控制器之间的控制路径数和控制域内控制器与交换机之间的控制路径数之和,即m=(|C|2-|C|)/2+|S|。
2.3.2 控制器部署算法考虑到控制域内的控制节点选择不同,控制路径不同,网络控制路径平均失效率ρ不同,网络可靠性也不同,从而控制器节点的选择对网络可靠性影响较大。控制域划分阶段结束之后,形成相对独立的控制域,根据相关需求,选择最优的节点作为控制域的控制器部署位置。当前控制域的控制器选择影响其他控制域的控制器选择,所有控制域对应的控制器是一一对应关系。假设3个控制域,分别从各自控制域的候选控制器节点选择一个节点,若节点i、j、k满足控制器之间的时延约束,而节点i、j、l不满足,说明所有控制域的控制节点是一一对应,只有满足约束条件的每个控制域对应控制器节点组合才是可行解,可能存在多组。控制器部署需要先计算控制域中满足交换机与控制器之间传播时延约束的控制器候选节点,再根据相邻控制域的控制器之间传播时延的约束条件,计算各个控制器可行的控制器节点组合构成一个可行解,最后计算每一个可行解,从中选择可靠性最强的可行解作为控制器的部署位置,完成控制器的部署。
控制器部署算法:
Step 1:初始划分形成控制域,初始化每个控制域的候选控制节点集为空;初始化可行解集合,且每个可行解是所有控制域的控制器节点;
Step 2:遍历每个控制域,计算所有满足交换机与控制器之间传播时延上限σ约束的节点集,加入其候选控制节点集;直到遍历结束;
Step 3:递归计算每个控制域可行的控制器节点组合:遍历控制域D(i)的候选控制器节点u,递归计算每个相邻控制域D(j)满足相邻控制域的控制器与控制器之间的传播时延上限δ约束节点,依次存入可行解集合。
Step 4:遍历每个可行解,计算控制路径平均失效率ρ值,选择ρ最小的可行解作为控制器的部署位置;直到遍历结束;
Step 5:输出结果,算法结束。
2.4 性能指标为了验证部署模型和TSCP算法的有效性,提出相关性能指标分析控制器部署结果。
1) 控制器容量利用率
控制器容量是控制器允许连接交换机的最大个数(即上限ηU),用控制器容量利用率衡量控制域的规模均衡性,等于控制域的交换机个数与控制器容量上限ηU的比值。控制器c容量的利用率R(c)表示如下
| $ R(c) = \frac{{\sum\limits_{s \in S} x (s, c)}}{{{\eta _U}}}, \forall c \in C。$ | (14) |
控制器容量利用率值越大,控制器控制的交换机个数越多,整个网络所需控制器个数越少。控制器容量利用率越高,则控制域的规模越均衡。
控制器容量利用率方差可以衡量全局的控制域规模均衡性,则
| $ H = \frac{1}{{|C|}}\sum\limits_{c \in C} {(R(} c) - \bar R{)^2}, $ | (15) |
式(15)中R表示控制器容量利用率平均值。
2) 连通强度
网络中节点之间的连接边越多,网络的连通性越强,弹性越强。连通强度是指控制域内边的数量与这些节点在网络中的边的数量的比值,其值越大,表示控制域内节点联系越紧密,连通性越强。控制域D(c)的连通强度K(c)
| $ K(c)=\frac{\sum\limits_{i\in D(c)}{\sum\limits_{\begin{smallmatrix} j\in D(c) \\ i<j \end{smallmatrix}}{a}}(i, j)}{\sum\limits_{i\in D(c)}{\sum\limits_{\begin{smallmatrix} j\in S \\ i<j \end{smallmatrix}}{a}}(i, j)}\quad \forall c\in C。$ | (16) |
网络弹性等于各个控制域的连通强度的平均值,即
| $ \varphi = \frac{1}{{|C|}}\sum\limits_{c \in C} K (c)。$ | (17) |
3) 网络覆盖时延
网络覆盖时延表示整个网络的控制时延,其值越小,网络的整体性能越强。网络覆盖时延是指所有控制器覆盖所属交换机的传播时延之和,再加上控制器与控制器之间同步状态所需时延。网络覆盖时延T如下
| $ T = \sum\limits_{c \in C} {\sum\limits_{s \in D(c)} d } (s, c) + \sum\limits_{u \in C} {\sum\limits_{\begin{array}{*{20}{c}} {v \in C}\\ {u < v} \end{array}} d } (u, v)。$ | (18) |
考虑到度较大的节点作为控制器位置的可能性较大,提出一种基于贪婪策略的控制器部署(GCP, greedy controller placement)算法,其算法思想是依次选择未标记节点中度最大的节点作为控制器的位置,在满足相关约束条件下,将距离最近的节点划分到控制域,多次迭代,直到所有节点完成划分。
K*-means算法[13]是基于最小化交换机与控制器之间时延、平衡控制器负载的网络划分算法。算法基本思想:建立时延和负载的目标函数,初始化一定数量的中心节点,划分交换机节点到离聚类中心最近的类中,合并目标函数最小的两个聚类,多次迭代直到结束。
K*-means算法、GCP算法都是划分交换机到距离最近的控制域中,没有考虑节点之间的关系;而TSCP算法以节点相似度为划分条件,将距离最近、关联紧密的节点划分到一个控制域,实现时延最小化和网络弹性最大化。三种算法都考虑负载均衡,K*-means算法将负载均衡作为目标函数最小化,GCP算法、TSCP算法通过约束控制域的规模实现负载均衡,但GCP算法只考虑规模界限,而TSCP算法在初始划分基础上,通过分裂和迁移机制的优化划分,负载均衡效果优于GCP算法。
K*-means算法利用控制域内最小最短路径确定控制器位置,GCP算法是选择节点度最大的节点为控制器,TSCP算法在优化划分基础上,引入可靠性指标,选择可靠性高的位置部署控制器。
对比三种算法的控制域划分和控制器位置确定的过程,从算法理论分析可知,TSCP算法相比其他2种算法,能优化网络时延、网络弹性、可靠性3个性能指标,整体效果较好。
3 实验结果与分析为了验证算法的有效性和性能,笔者用开源的真实网络GEANT网络(22个节点、36条链路)、INTERNET2(34个节点、42条链路)网络数据,对比文献[13]的K*-means算法、GCP算法、TSCP算法的多项性能指标:控制器个数Φ、控制器容量利用率方差H、网络弹性φ、网络覆盖时延T、网络可靠性ρ。实际网络中,利用节点的经度和纬度计算节点之间的距离描述节点之间的传播时延。在不同的网络拓扑运行部署算法,验证算法的普遍性和适用性。实验算法采用Java语言编写,在电脑(CPU Intel Xeon 3.3G 8核,内存16G,Win10操作系统)的运行环境实现。
3.1 TSCP算法分析为了验证算法的稳定性和收敛性,对传播时延、控制域的规模参数进行实验分析。失效参数re、rv只影响网络可靠性ρ值,由式(12)可知,失效参数值的变化与ρ值成反比,但控制器位置选择是不变的,故这里不再分析。
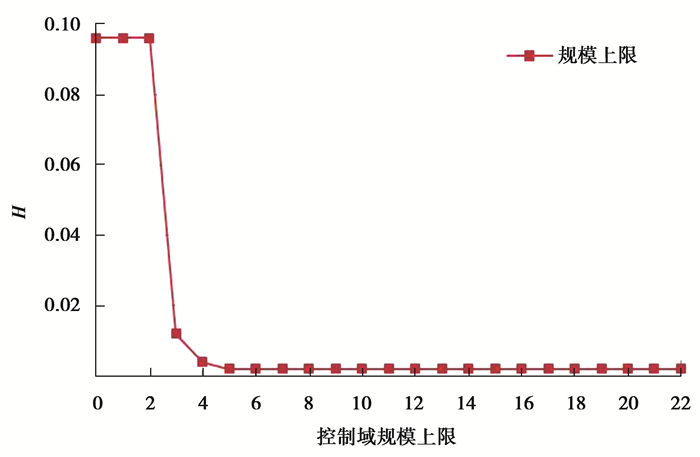
控制域的规模下限ηL会影响控制域负载均衡,从图 1看出ηL小于3时,控制器容量利用率方差H值较高,表明控制域的规模不均衡;当大于4时,H值再无变化,控制域的规模均衡,且不随ηL值增大而变化。
|
图 1 GEANT网络参数ηL分析 Fig. 1 Parameter analysis of ηL in GEANT |
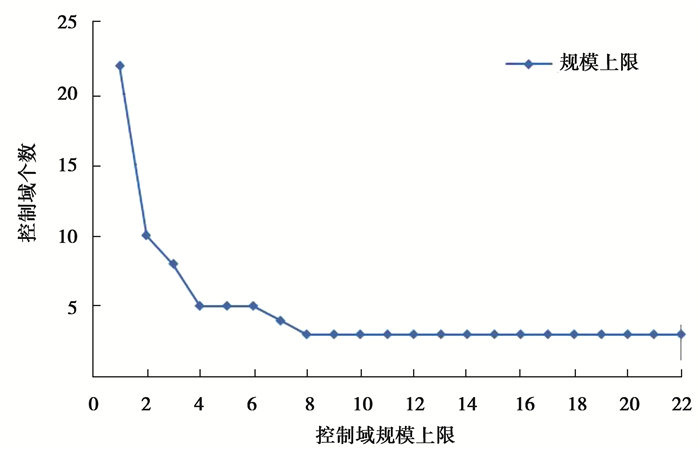
控制域的规模上限ηU会影响控制域划分个数,从图 2可知ηU小于4时,划分较多的控制域;当大于8时,控制域个数再无变化,说明控制域划分恒定,不随ηU值变化。
|
图 2 GEANT网络参数ηU分析 Fig. 2 Parameter analysis of ηU in GEANT |
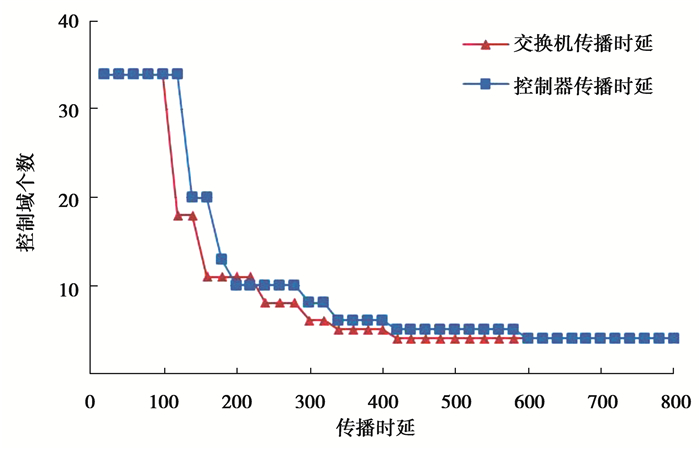
交换机与控制器传播时延上限σ,控制器与控制器的传播时延上限δ影响控制域划分个数。图 3中得知σ、δ值小于240时,控制域个数较多;随着时延上限增大,单个控制域中交换机个数增加,控制域个数减少。当σ大于400,δ大于等于600时,控制域个数不变化。
|
图 3 INTERNET2网络传输时延分析 Fig. 3 Parameter analysis of propagation delay in GEANT |
上述3个实验结果表明,随着传播时延、控制域的规模参数增加,控制域划分结果逐渐变化;变化到一定值时,控制域划分结果不再变化,表明TSCP算法是收敛且稳定的。
通过对传播时延、控制域的规模参数多次测试,根据上述收敛性结论,选择算法收敛时的参数值作为后续测试。则设置参数:传播时延上限σ=400,播时延上限δ=600,控制域的规模下限ηL=4,规模上限ηU=10。失效率取值范围一般为(0, 0.1],为了一致性,节点失效率和链路失效率取值相同,通常rv=0.05,re=0.05。
3.2 控制域划分分析控制器容量利用率R反映控制域内交换机个数与控制器容量上限的比值,其值越大说明控制域的规模越大,控制器的利用率越高。网络所有控制器容量利用率均较高时,所需控制器的个数较少。
从表 1可以看出TSCP算法计算结果中每个控制域的规模是相对均衡的,利用率至少大于等于70%,控制域个数最少,达到算法目的。GCP算法只考虑节点的度,容易出现边缘节点,导致控制域构成不平衡,且控制域个数多。K*-means算法考虑负载均衡,控制器利用率相差不大,但是INTERNET2网络中控制域个数比TSCP算法多。
| 表 1 控制器容量利用率R分析 Table 1 Analysis of R |
表 2可以看出,由于TSCP算法在控制域划分时引入节点相似度,将相似度较大的节点划分到同一个控制域,控制域的连通性较强,连通强度值均大于等于0.57。说明TSCP算法的控制域内节点联系紧密,交换机与控制器之间可以存在多条备份路径,提高网络的弹性。K*-means算法未考虑,使得可能存在某些控制域内节点之间连接不紧密,其效果欠佳。
| 表 2 控制域连通强度K分析 Table 2 Analysis of R |
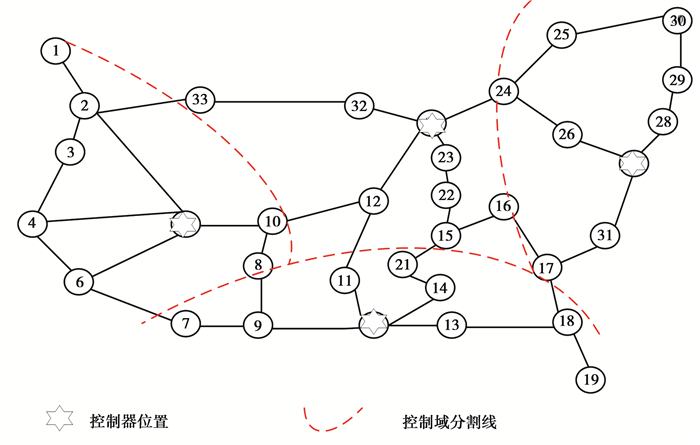
为了对比INTERNET2网络的实际部署结果[15](采用4个控制器控制整个网络),研究采用TSCP算法部署结果如图 4。
|
图 4 INTERNET2网络的部署结果示意 Fig. 4 Deployment result in INTERNET2 |
图 4中TSCP算法在节点5、20、27、34分别部署控制器,所需控制器个数为4个,与INTERNET2网络中实际部署控制器个数一致,每个控制域中的节点数为8到9个,控制域的规模相对均衡。控制器节点分别选择节点5、20、27、34,其控制路径平均失效率ρ=0.235,网络可靠性较高。
3.4 控制器部署结果综合分析为了更全面验证TSCP算法的有效性,分别从控制器个数Φ、控制器容量利用率方差H、网络弹性φ、网络覆盖时延T、网络可靠性ρ的性能指标测验并分析。性能指标具体内容如下
控制器个数Φ与控制域个数一致,选择较少的控制器部署有利于减少网络资源成本。从性能指标Φ可知,TSCP算法通过初始划分和优化划分2步,利用节点相似度的原理,将关联更紧密的交换机划分到一个控制域,减少控制域个数。而GCP算法、K*-means算法未考虑节点关联性,控制域个数比TSCP算法较多。
控制器容量利用率方差H能反映全局控制域的规模均衡性,其值越小说明各个控制域的规模越均衡。TSCP算法和K*-means算法均考虑负载均衡性,H值较小,说明TSCP算法能满足负载均衡要求。而GCP算法未考虑负载均衡指标,H值较大。在INTERNET2网络中K*-means算法控制域个数为5,控制器容量利用率最大和最小相差为0.2,影响H值。
网络弹性φ值的大小说明控制域内处理网络故障的能力,其值越大,节点连通性越强,交换机与控制器之间容错率越高,备份路径越多。从表中可以看出,TSCP算法的φ值均最大,均大于等于0.66,验证节点相似度的有效性,说明TSCP算法能提高网络的弹性。GCP算法以最大节点度为控制器位置,其网络弹性效果在GEANT网络中比K*-means算法较好。
网络覆盖时延T是衡量控制器部署的重要指标之一,反映了控制器部署的好坏。其值越小,网络的整体性能越强。K*-means算法以时延为优化目标,其T值较小。而TSCP算法中节点相似度把时延作为最短路径指标引入,相似度越大,其时延较小。从而说明TSCP算法通过节点相似度划分控制域,能使网络覆盖时延较小。在INTERNET2网络中K*-means算法控制域个数比TSCP算法多,增加了控制器之间时延,影响网络覆盖时延。
控制路径平均失效率ρ衡量网络可靠性,值越小,整个网络可靠性越高。表 3中数据得知GCP算法的可靠性较差,K*-means算法其次,TSCP算法可靠性较高。GCP算法和K*-means算法实现控制器部署时并没有考虑控制路径的失效率。TSCP算法均衡划分控制域,减少控制器个数,从每个控制域中选择全局性的控制路径平均失效率最小的控制器集合确定控制器的位置,提高网络可靠性。
| 表 3 性能指标对比 Table 3 Performance index comparison |
上述实验结果说明TSCP算法通过两阶段划分策略,可以优化控制域的规模,均衡控制域的交换机个数,减少控制器个数,网络弹性和可靠性均表现较好。总之,TSCP算法与其他算法相比,对于SDN控制器部署具有一定的优势和效果。
4 结语只考虑网络拓扑,以优化网络弹性和可靠性为目标,提出两阶段控制器部署方案。首先,分析了约束控制器部署的相关因素,如控制域规模、网络设备(交换机或控制器)之间的传播时延,建立对应的部署模型;其次,定义了节点相似度,提出了控制域划分:初始划分和优化划分。再次,基于控制路径失效率计算可靠性最大的控制器部署位置。最后,提出相关性能指标用于测试算法,举例分析算法的可行性。基于两阶段的控制器部署算法可以有效地提高网络控制器利用率,平衡控制域的交换机个数,尽量减少控制器的个数。然而实际SDN网络是流量动态变化的,如何通过引入流量矩阵实现控制器的动态部署是未来要做的工作。
| [1] |
McKeown N. Software-defined networking[J]. Infocom Keynote Talk, 2009, 17(2): 30-32. |
| [2] |
张朝昆, 崔勇, 唐翯祎, 等. 软件定义网络(SDN)研究进展[J]. 软件学报, 2015, 26(1): 62-81. ZHANG ChaoKun, CUI Yong, TANG HeYi, et al. State-of-the-art survey on software-defined networking (SDN)[J]. Journal of Software, 2015, 26(1): 62-81. (in Chinese) |
| [3] |
高先明, 王宝生, 邓文平, 等. SDN网络中控制器放置问题综述[J]. 通信学报, 2017, 38(7): 155-164. GAO Xianming, WANG Baosheng, DENG Wenping, et al. Survey of controller placement problem in software defined network[J]. Journal on Communications, 2017, 38(7): 155-164. (in Chinese) |
| [4] |
Heller B, Sherwood R, McKeown N. The controller placement problem[C]//Proceedings of the first workshop on Hot topics in software defined networks. New York, USA: ACM Press, 2012: 7-12. https://www.zhangqiaokeyan.com/open-access_resources_thesis/0100056177315.html
|
| [5] |
杨耀通, 汪清, 高丽蓉, 等. 基于蝙蝠算法的SDN多控制器部署[J]. 重庆大学学报, 2018, 41(9): 57-65. YANG Yaotong, WANG Qing, GAO Lirong, et al. A bat inspired controller placement algorithm in software defined network[J]. Journal of Chongqing University, 2018, 41(9): 57-65. (in Chinese) |
| [6] |
Narmanlioglu O, Zeydan E. Network virtualization for mobile operators in software-defined based LTE networks[C/OL]. 2017 IFIP/IEEE Symposium on Integrated Network and Service Management (IM). Piscataway, NJ: IEEE, 2017(2017-07-24)[2020-05-25]. https://doi.org/10.23919/INM.2017.7987334
|
| [7] |
Zhang Y, Beheshti N, Tatipamula M. On resilience of split-architecture networks[C/OL]. 2011 IEEE Global Telecommunications Conference Houston. Piscataway, NJ: IEEE, 2011(2012-01-19)[2020-05-25]. https://doi.org/10.1109/GLOCOM.2011.6134496.
|
| [8] |
Riggio R, Marina M K, Rasheed T. Interference management in software-defined mobile networks[C/OL]. 2015 IFIP/IEEE International Symposium on Integrated Network Management (IM). Piscataway, NJ: IEEE, 2015(2015-07-02)[2020-05-25]. https://doi.org/10.1109/INM.2015.7140347
|
| [9] |
Hu Y N, Wang W D, Gong X Y, et al. On reliability-optimized controller placement for software-defined networks[J]. China Communications, 2014, 11(2): 38-54. DOI:10.1109/CC.2014.6821736 |
| [10] |
Zhang Y, Beheshti N, Tatipamula M. On resilience of split-architecture networks[C/OL]. 2011 IEEE Global Telecommunications Conference-GLOBECOM 2011. Piscataway, NJ: IEEE, 2011(2012-01-19)[2020-05-25]. https://doi.org/10.1109/GLOCOM.2011.6134496.
|
| [11] |
覃匡宇, 黄传河, 王才华, 等. SDN网络中受时延和容量限制的多控制器均衡部署[J]. 通信学报, 2016, 37(11): 90-103. QIN Kuangyu, HUANG Chuanhe, WANG Caihua, et al. Balanced multiple controllers placement with latency and capacity bound in software-defined network[J]. Journal on Communications, 2016, 37(11): 90-103. (in Chinese) |
| [12] |
Aoki H, Shinomya N. Controller placement problem to enhance performance in multi-domain SDN networks[C]//The Fifteenth International Conference on Networks. Lisbon, Portugal: IARIA, 2016: 108-109.
|
| [13] |
Kuang H L, Qiu Y W, Li R F, et al. A hierarchical K-means algorithm for controller placement in SDN-based WAN architecture[C]//2018 10th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA). Piscataway, NJ: IEEE, 2018(2014-04-16)[2020-05-25]. https://doi.org/10.1109/ICMTMA.2018.00070
|
| [14] |
王坤, 吕光宏, 梁召伟, 等. 基于相似度的加权复杂网络社区发现方法[J]. 四川大学学报(自然科学版), 2014, 51(6): 1170-1176. WANG Kun, LV Guanghong, LIANG Zhaowei, et al. Detecting community in weighted complex network based on similarities[J]. Journal of Sichuan University(Natural Science Edition)), 2014, 51(6): 1170-1176. (in Chinese) |
| [15] |
Heller B, Sherwood R, McKeown N. The controller placement problem[C]//Proceedings of the First Workshop on Hot Topics in Software Defined Networks. New York, USA: ACM Press, 2012: 7-12.
|
 2020, Vol. 43
2020, Vol. 43


