b. 武警工程大学 信息工程学院, 西安 710086
b. Information and Communication, Engineering University of PAP, Xi'an 710086, P. R. China
现代装备功能繁多、结构复杂,同一装备中的不同系统之间相互交织、相互依赖。元件的故障会引起部件、系统的故障,系统之间的关联性也可能会造成故障的传播,使故障具有复合性。同时,实验环境下采集到的故障样本难以覆盖全部故障类型,使故障具有未知性,提高故障诊断难度。使用多个传感器进行信号采集,可以多角度、全方位检测装备运行状态,提高故障诊断效果。
传统故障诊断方法往往通过信号处理手段、专家经验、浅层学习等方式提取特征,特征的选择直接影响故障诊断效果,也难以充分利用海量数据。深度学习因其多隐层网络,能够自适应地从海量数据中提取特征,摆脱人为进行特征选择的局限性,其中,CNN在处理海量数据上有独特优势,在轴承[1-2]、旋转机械[3-4]等领域得到应用。文献[1]将迁移学习与CNN相结合,在训练数据与实际数据有不同分布时也能较好诊断。文献[2]用复Morlet小波的连续小波变换处理时域信号,得到时频图像,再输入卷积神经网络,充分利用信号的时频特征。文献[3]提出多尺度深度CNN模型,拓宽、深化神经网络,达到更好的鲁棒性,缩短训练时间。文献[4]将多堆栈胶囊设计为解耦分类器,与CNN结合,准确解耦复合故障。吴魁[5]等人将多传感器信号构建为测量数据帧,输入CNN,完成了多传感器信号的融合。CNN能够实现准确的故障诊断,但只能诊断已知、单一类别的故障,迫切需要其他方法解决未知、复合故障诊断问题。
LSTM对具有前后联系的时间信号更加敏感,可以应用于故障诊断和预测,在锂电池[6]、风冷式冷水机组系统[7]、盾构机[8]、轴承[9]等领域得到应用。文献[6]改进LSTM结构,将输入门和遗忘门进行耦合,对新输入和历史单元状态的元素乘积进行筛选,筛选出更有益的信息;在输出门中加入来自“恒定误差旋转木马”的窥视孔连接,屏蔽了不需要的误差信号。文献[7]增加自适应增强模块,能够自适应地改变反向传播误差,并通过自适应设置学习率减少计算时间。文献[8]利用层规范化方法改进LSTM,使网络的收敛速度更快、精度更高。文献[9]提出了一种改进具有全局性质的并行LSTM。该模型由每个采样点的并行状态组成,通过加入窥视孔连接来提取序列的局部信息和全局信息,通过重用存储单元的信息更好提取序列信息。既充分利用信息,保证了迭代速度。虽然LSTM具有较好故障诊断效果,但是在大量数据的情况下,LSTM网络将难以提取数据的非线性特征,且收敛速度慢。
CNN与LSTM的组合已经在无人机[10]、网络[11]、单元设备[12]、工业[13]、轴承[14-15]等领域得到了应用。该模型首先利用CNN提取特征,然后通过LSTM来探索时间序列数据的内在联系。其中CNN擅长数据处理,可以充分利用海量数据而不丢失数据之间的联系。将提取的特征向量输入LSTM,有利于对时间序列数据的分析。该模型不仅保留了输入数据的特征及其相互关系,且保证模型的时序性。FCM作为模糊分类方法,一个对象可以同时属于多个不同的类,其隶属度在0~1之间,能够应用于故障诊断,但诊断效果不如CNN。
因此,研究将LSTM和FCM与CNN相结合,使其能够有效诊断未知信号,并通过概率分类输出实现复合故障的解耦,最终实现含未知复合故障的多传感器信号故障诊断。
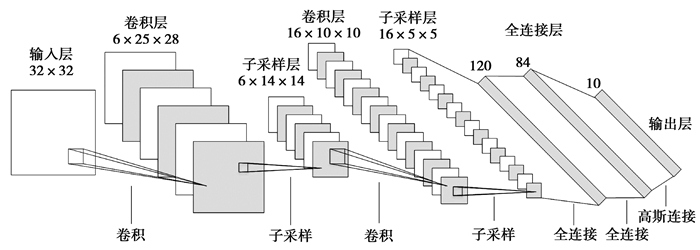
1 关键技术 1.1 CNN基本原理典型的卷积神经网络LeNet-5的结构如图 1所示。网络分为输入层、卷积层、子采样层、全连接层和输出层。
|
图 1 LeNet-5结构 Fig. 1 The structure of LeNet-5 |
卷积层也称为特征提取层,卷积层通过不同的卷积核卷积前一层,每个卷积核对应一个提取特征,与前一层的感受连接。卷积核共享网络权重,每个卷积核提取有限的信息,因此通常使用多个卷积核来获取更多特征。
卷积运算的输出是
| $ x=f(\sum{x}*{{w}_{ij}}+b), $ | (1) |
其中:wij是卷积核,b是偏置,x是输入特征图,*是卷积算子,f(·)是激活函数。
子采样层也称为特征映射层,对从卷积层提取的特征进行操作。通过下采样操作,大大减少节点数量、网络连接数量和网络计算的复杂性。
下采样的输出是
| $ x=f(\beta \text{down} (x)+b), $ | (2) |
其中:β是权值,b是偏置,down(·)是下采样函数,f(·)是激活函数。
全连接层中的所有神经元节点都与前一层节点互连。它的输出是
| $ h(x)=f(wx+b), $ | (3) |
其中:x是全连接层的输入,w是权重,b是偏置,f(·)是激活函数。
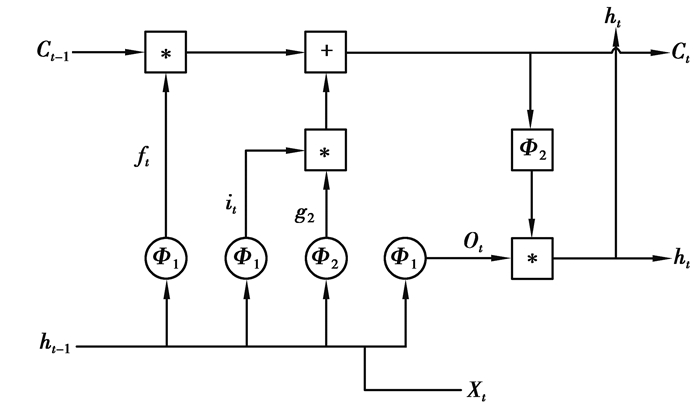
1.2 LSTM基本原理LSTM是循环神经网络(RNN, recurrent neural network)的一个变种,它解决了梯度反向传播过程中的梯度消失和爆炸问题。LSTM的关键是LSTM单元,它可以决定是否维护状态信息。LSTM单元结构如图 2所示。
|
图 2 LSTM单元结构 Fig. 2 The structure of LSTM Cell |
LSTM单元包含输入门、遗忘门和输出门。输入门用来决定输入信息,以保存单元的状态。遗忘门用于最后一次确定单元的状态。输出门决定LSTM单元的输出。输出的ct和ht反复输入到LSTM单元。具有正向传播的LSTM单元计算如下
| $ {{f}_{t}}=\sigma ({{W}_{f}}*[{{h}_{t-1}}, {{x}_{t}}]+{{b}_{f}}), $ | (4) |
| $ {{i}_{t}}=\sigma ({{W}_{i}}*[{{h}_{t-1}}, {{x}_{t}}]+{{b}_{i}}), $ | (5) |
| $ {{g}_{2}}=\text{tan}h({{W}_{c}}*[{{h}_{t-1}}, {{x}_{t}}]+{{b}_{c}}), $ | (6) |
| $ {{c}_{t}}={{f}_{t}}*{{c}_{t-1}}+{{i}_{t}}*{{g}_{2}}, $ | (7) |
| $ {{o}_{t}}=\sigma (W_{o}^{*}[{{h}_{t-1}}, {{x}_{t}}]+{{b}_{o}}), $ | (8) |
| $ {{h}_{t}}={{o}_{t}}*\text{tan}h({{c}_{t}}), $ | (9) |
公式(4),(5)和(6)分别是遗忘门、输入门和输出门。Wf、Wi和Wc分别是遗忘门、输入门和输出门的权重。σ(·)和tan h(·)是sigmoid函数和双曲正切函数。
1.3 FCM基本原理FCM算法由Dunn提出并由Bezdek进一步发展,是一种常用的聚类分析方法。FCM将一组s维向量X =(X1, ….Xn)划分为c个组,其中Xj=(Xj1, …, Xjn)′表示j=1, …, n的第j个样本。第i组有中心向量vi=(vi1, …, vis),FCM的目的是确定聚类中心vi,其中“1ic”。对于第j个样本Xj和第i个聚类中心vi,uij(∈[0, 1])表示样本Xj属于聚类中心vi的隶属度,形成模糊隶属度矩阵U =(uij)n×c。目标函数J的定义如下
| $ {\mathit{\boldsymbol{v}}_i} = \frac{{\sum\limits_{j = 1}^n {u_{ij}^m} {\mathit{\boldsymbol{x}}_j}}}{{\sum\limits_{j = 1}^n {u_{ij}^m} }}, $ | (10) |
| $ {d_{ij}} = {\left( {\sum\limits_{k = 1}^s {{{({v_{ik}} - {x_{jk}})}^2}} } \right)^{\frac{1}{2}}}, $ | (11) |
| $ {u_{ij}} = \frac{1}{{\sum\limits_{k = 1}^c {{{\left( {\frac{{{d_{ij}}}}{{{d_{kj}}}}} \right)}^{2/(m - 1)}}} }}, i = 1, \cdots , c;j = 1, \cdots , n, $ | (12) |
| $ {\rm{min}}(J(\mathit{\boldsymbol{U}}, \mathit{\boldsymbol{V}})) = \sum\limits_{i = 1}^c {\sum\limits_j^n {u_{ij}^m} } d_{ij}^2, $ | (13) |
对于
FCM算法可描述如下:
1) 选择一个整数c和一个判别精度ε,在区间[0, 1]内用c×n个随机数初始化模糊隶属度矩阵U。
2) 根据式(10)计算vi(i=1, …, c)。
3) 分别根据式(11)和式(12)计算dij和uij,用新计算出的uij更新模糊隶属度矩阵U。
4) 用式(13)计算目标函数J。如果J2个相邻值之间的差小于判别精度ε,则停止计算。否则转到步骤2)。
1.4 CNN-LSTM-FCM基本原理CNN-LSTM-FCM模型如图 3所示

|
图 3 CNN-LSTM-FCM模型结构 Fig. 3 The structure of CNN-LSTM-FCM model |
模型通过CNN进行特征提取,利用LSTM预测信号标签,将二者组装为一个网络,通过组合2个网络中的图层来直接对信号进行分类,模型的输出为属于每一个类别的概率。
序列折叠层用于将输入的序列构建成测量数据帧。
卷积层对每组信号进行卷积,实现特征提取。根据输入数据的维数,卷积运算可分为一维卷积和二维卷积,二维卷积通常用于处理图像。由于模型的输入是多个传感器信号,一个传感器就是一维度信号,多组传感器信号构成了一个矩阵,因此使用的是一维卷积。
序列展开层和扁平化层用于恢复序列结构、输出矢量序列。
LSTM层和输出层用于对输出的矢量序列进行分类。LSTM层的输入信号中,既包含特征信号,又包含原始信号,通过信号融合,使输入信号中包含更多信息,提高了诊断准确率。在LSTM层后设置了FCM层,作为整个模型优化参数设计的一部分,进一步提高了诊断精度。
对于任何分类模型来说,只能对训练过的信号进行分类,把未知信号归为已知类别。笔者构建的模型,是用回归的思想解决含未知信号的分类问题。例如:训练集包含五种类别,在测试集中加入一种未知类别。测试时,若输入1类信号,那么输出在1左右;若输入未知信号,则输出在0.5左右,不接近任何一类,从而识别出未知信号。若输入信号中含有多种未知信号,不能对它们进一步分类,只能统一划归为未知信号。
传统CNN只能输出某一特定类的概率,而CNN-LSTM-FCM模型可以分别输出每一类的概率,实现复合故障的解耦。例如:有5组传感器信号,1和3为故障信号,其余正常,将这组数据输入传统CNN模型,输出可能是故障1,也可能是故障3,但只能输出其中一种故障。若输入CNN-LSTM-FCM模型,则模型的概率输出为[1 0 1 0 0],从而诊断出同时具有故障1和3。
模型的损失函数如下
| $ J(\theta ) = - \frac{1}{m}\left[ {\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^k 1 } \{ {y_i} = j\} {\rm{lg}}\frac{{{e^{\mathit{\boldsymbol{\theta }}_j^{\rm{T}}{x_i}}}}}{{\sum\limits_{l = 1}^k {{e^{{\mathit{\boldsymbol{\theta }}_j}^{\rm{T}}{x_i}}}} }}} \right], $ | (14) |
其中:xi为输入数据,yi为所属类别,m为样本数,θ为参数集,用于使损失函数最小化。
利用CNN-LSTM-FCM模型进行故障诊断的过程如下:
1) 按照文献[5]提出的方法构建测量数据帧并将其归一化。
2) 将数据集的80%构建为训练集,20%为测试集,在测试集中加入未知故障信号。
3) 利用训练集对CNN-LSTM-FCM模型进行预训练。
4) 利用测试集测试模型故障诊断效果。
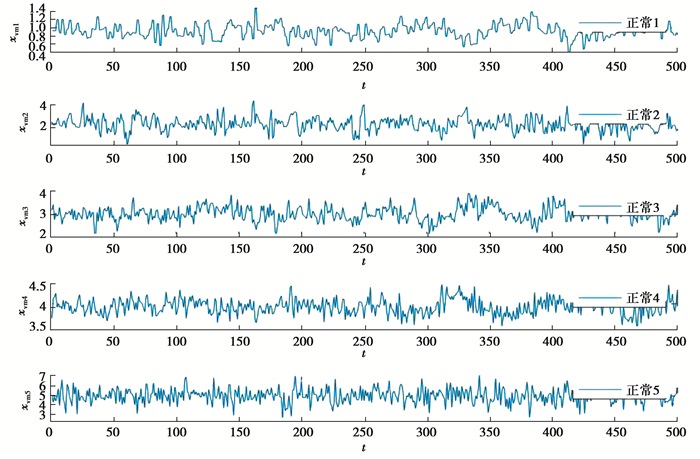
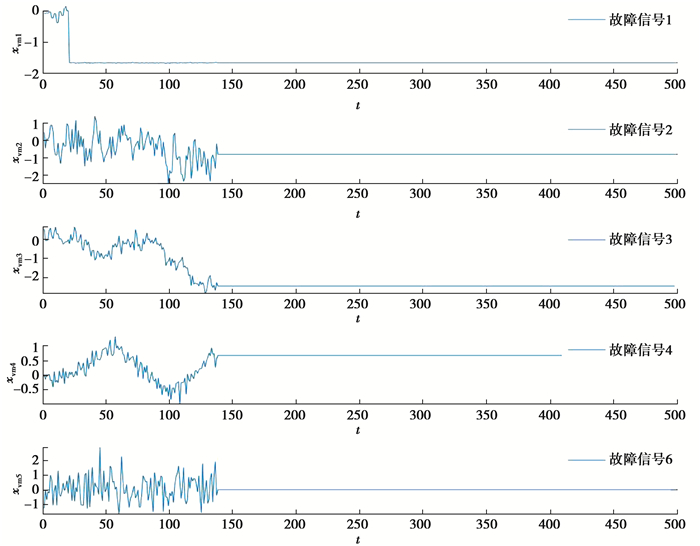
2 实验及分析 2.1 构建数据集选用mathworks官网上发布的化学过程故障测量数据,共有5个传感器采集数据,每个传感器信号中均有正常信号和故障信号。对于同时段的5个传感器信号,每个信号截取500个采样点,按照图 4和图 5的方式构建52*500的测量数据帧并归一化。图中的1~5行分别表示传感器1~5的信号,每个传感器信号有20%的概率为故障信号,实现了数据的随机选择,不同传感器信号的故障是否相互独立,使得最终构建的测量数据帧包含各种故障类型的随机组合。将80%的数据集用作训练集,20%为测试集。在训练集中,传感器1~4均包含正常信号和故障信号,传感器5个包含正常信号。在测试集中,加入传感器5的故障信号,作为未知故障。每个传感器信号的部分正常状态、故障状态分别如图 4、5所示。
|
图 4 正常信号 Fig. 4 Normal signal |
|
图 5 故障信号 Fig. 5 Fault signal |
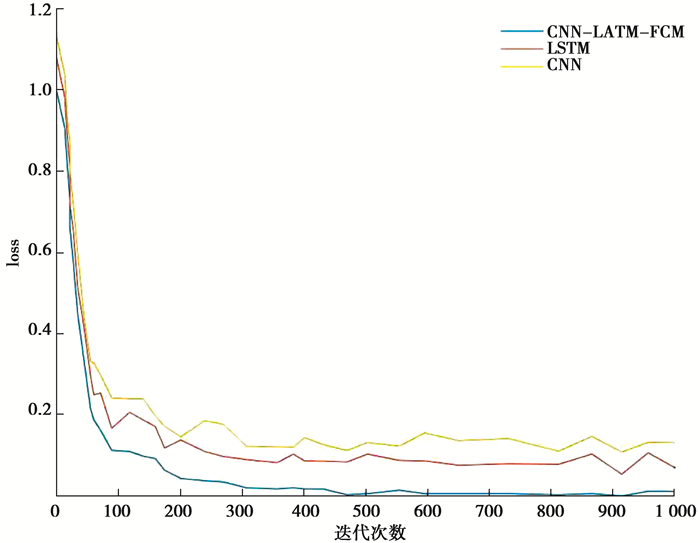
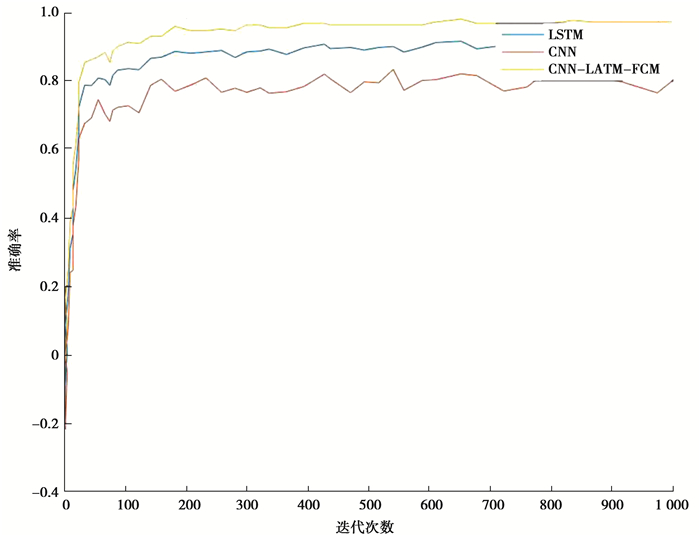
先用训练集对模型进行预训练,然后用测试集检测故障诊断效果。将提出的模型与CNN、LSTM进行比较,不同模型对应的损失值如图 6所示,准确率如图 7所示,数值如表 1所示。从图、表所示的信息来看,CNN-LSTM-FCM模型的损失值最低、准确率最高、收敛速度最快,其次是LSTM模型,CNN模型诊断效果最不理想。实验结果表明,对于含未知复合故障的多传感器信号故障诊断,CNN-LSTM-FCM模型具有更好的诊断效果,解决传统故障诊断模型只能诊断出已知、单一类别故障的问题。
|
图 6 损失值 Fig. 6 Loss value |
|
图 7 准确率 Fig. 7 Accuracy |
| 表 1 各模型损失值、准确率 Table 1 Loss value and accuracy of each model |
随着装备功能不断完善,装备结构愈发复杂,往往需要用到多个传感器采集信号,其故障具有未知性、复合性,传统故障诊断模型只能诊断已知、单一类别故障,迫切需要其他方式解决这一问题。将LSTM和FCM与CNN进行组合,解决含未知复合故障的多传感器信号故障诊断问题,并通过与CNN、LSTM模型对比验证了其优越性。
提出的CNN-LSTM-FCM模型主要有以下优势:1)用回归的思想解决了含未知信号的分类问题。2)能够实现概率分类输出,解耦复合故障。3)通过优化参数设计提高了诊断准确率。
模型还有以下问题有待改进:1)层数和参数设置主要凭借经验,需要多次尝试才能达到较好诊断效果。2)使用传感器测量的数据,有时会因为传感器本身原因,造成测量数据存在问题,如何处理这种nan类型数据也有待研究。可以通过差值法、剔除法等方式解决这个问题,本实验选择的是剔除法。
| [1] |
Guo L, Lei Y G, Xing S B, et al. Deep convolutional transfer learning network:a new method for intelligent fault diagnosis of machines with unlabeled data[J]. IEEE Transactions on Industrial Electronics, 2019, 66(9): 7316-7325. DOI:10.1109/TIE.2018.2877090 |
| [2] |
Gao D W, Zhu Y S, Wang X, et al. A fault diagnosis method of rolling bearing based on complex morlet CWT and CNN[C/OL]. 2018 Prognostics and System Health Management Conference (PHM-Chongqing). Piscataway, NJ: IEEE, 2018(2018-01-19)[2020-05-25]. https://doi.org/10.1109/PHM-Chongqing.2018.00194
|
| [3] |
Zhuang Z L, Qin W. Intelligent fault diagnosis of rolling bearing using one-dimensional multi-scale deep convolutional neural network based health state classification[C/OL]. 2018 IEEE 15th International Conference on Networking, Sensing and Control (ICNSC). Piscataway, NJ: IEEE, 2018(2018-05-21)[2020-05-25]. https://doi.org/10.1109/ICNSC.2018.8361296
|
| [4] |
Huang R Y, Liao Y X, Zhang S H, et al. Deep decoupling convolutional neural network for intelligent compound fault diagnosis[J]. IEEE Access, 2019, 7: 1848-1858. DOI:10.1109/ACCESS.2018.2886343 |
| [5] |
吴魁, 王仙勇, 孙洁, 等. 基于深度卷积网络的多传感器信号故障诊断方法研究[J]. 计算机测量与控制, 2018, 26(1): 18-21. WU Kui, WANG Xianyong, SUN Jie, et al. Study of multi-sensor fault diagnose method based on convolutional neural networks[J]. Computer Measurement & Control, 2018, 26(1): 18-21. (in Chinese) |
| [6] |
Li P H, Zhang Z J, Xiong Q Y, et al. State-of-health estimation and remaining useful life prediction for the lithium-ion battery based on a variant long short term memory neural network[J]. Journal of Power Sources, 2020, 459: 228069. DOI:10.1016/j.jpowsour.2020.228069 |
| [7] |
Gao L, Li D H, Li D, et al. An improved LSTM based sensor fault diagnosis strategy for the air-cooled chiller system[C/OL]. 2019 Chinese Control Conference (CCC). Piscataway, NJ: IEEE, 2019(2019-10-17)[2020-05-25]. https://doi.org/10.23919/ChiCC.2019.8866339
|
| [8] |
Sun Z H, Zheng H Y, Shi B H. Faults prediction and diagnoses of shield machine based on LSTM[C/OL]. 2019 Chinese Control And Decision Conference (CCDC). Piscataway, NJ: IEEE, 2019(2019-09-12)[2020-05-25]. https://doi.org/10.1109/CCDC.2019.8832341
|
| [9] |
Zhang Z Q, Zhou F N, Chen D M. Application of improved parallel LSTM in bearing fault diagnosis[C/OL]. 2019 Chinese Automation Congress (CAC). Piscataway, NJ: IEEE, 2019(2020-04-13)[2020-05-25]. https://doi.org/10.1109/CAC48633.2019.8997417
|
| [10] |
Fu J, Sun C, Yu Z, et al. A hybrid CNN-LSTM model based actuator fault diagnosis for six-rotor UAVs[C/OL]. 2019 Chinese Control And Decision Conference (CCDC). Piscataway, NJ: IEEE, 2019(2019-09-12)[2020-05-25]. https://doi.org/10.1109/CCDC.2019.88327062019.
|
| [11] |
Tan Z L, Pan P S. Network fault prediction based on CNN-LSTM hybrid neural network[C/OL]. 2019 International Conference on Communications, Information System and Computer Engineering (CISCE). Piscataway, NJ: IEEE, 2019(2019-08-22)[2020-05-25]. https://doi.org/10.1109/CISCE.2019.00113
|
| [12] |
Zheng L, Xue W H, Chen F, et al. A fault prediction of equipment based on CNN-LSTM network[C/OL]. 2019 IEEE International Conference on Energy Internet (ICEI). Piscataway, NJ: IEEE, 2019(2019-08-08)[2020-05-25]. https://doi.org/10.1109/ICEI.2019.00101
|
| [13] |
Gao Y, Gong P, Li L X. An end-to-end model based on CNN-LSTM for industrial fault diagnosis and prognosis[C/OL]. 2018 International Conference on Network Infrastructure and Digital Content (IC-NIDC). Piscataway, NJ: IEEE, 2018(2018-11-08)[2020-05-25]. https://doi.org/10.1109/ICNIDC.2018.8525759
|
| [14] |
Du W, Wang Y X. Stacked convolutional LSTM models for prognosis of bearing performance degradation[C/OL]. 2019 Prognostics and System Health Management Conference (PHM-Qingdao). Piscataway, NJ: IEEE, 2019(2019-12-26)[2020-05-25]. https://ieeexplore.ieee.org/document/8943063
|
| [15] |
Qiao M Y, Yan S H, Tang X X, et al. Deep convolutional and LSTM recurrent neural networks for rolling bearing fault diagnosis under strong noises and variable loads[J]. IEEE Access, 2020, 8: 66257-66269. DOI:10.1109/ACCESS.2020.2985617 |
 2020, Vol. 43
2020, Vol. 43

