b. 河北工程大学 土木工程学院, 河北 邯郸 056038
b. College of Civil Engineering, Hebei University of Engineering, Handan 056038, Hebei, P. R. China
受果蝇觅食过程的启发,台湾学者Pan[1]于2012年提出了较为高效的群智能优化算法——果蝇算法(FOA, fruit fly optimization algorithm)。由于该算法原理清晰、参数较少、操作简单,受到广泛关注。学者通过深入研究将其运用到预测、物流、调度、结构设计等领域,得到了较高的认可度。该算法同样存在不足[2-3]:1)标准果蝇算法无法求解最优值为负的问题;2)解决复杂、高维和非线性优化问题的能力较弱;3)易陷入局部极值点等。
针对上述典型问题,不少学者对标准果蝇算法进行了改进。在候选解产生方面:Pan[4]在味道浓度判定值中加入可以为负的逃逸参数,使得候选解能够取到负值。在搜索半径方面:Pan等[5]引入自适应参数来调节果蝇的搜索半径,使之能够较好地平衡全局搜索能力及局部搜索能力。在飞行策略方面:Wang[6]、Li[7]、张前图等[8]加入了群体协作和随机摄动的操作,进而解决算法的早熟问题。在种群多样性方面:刘志雄等[9]将果蝇群体分成多个相同规模的子种群、韩俊英等[10]提出了一种动态双子群协同进化FOA,提升搜索精度。
研究通过设计混合算法:融合免疫反应[11-13]的混合果蝇算法(IAFOA, fruit fly optimization algorithm based on immune algorithm)对标准果蝇算法进行性能改进。充分利用免疫算法来改善果蝇算法后期易陷入局部极值的不足,即当进化停滞步数t大于进化停滞步数阈值T时,执行免疫操作[14-15]来克服基本果蝇算法的缺陷。通过标准函数及求解0~1背包问题的测试验证改进算法具有较好的鲁棒性及智能性[16]。最后,将其应用于桁架结构优化问题,通过对比其他算法验证IAFOA的可行性。
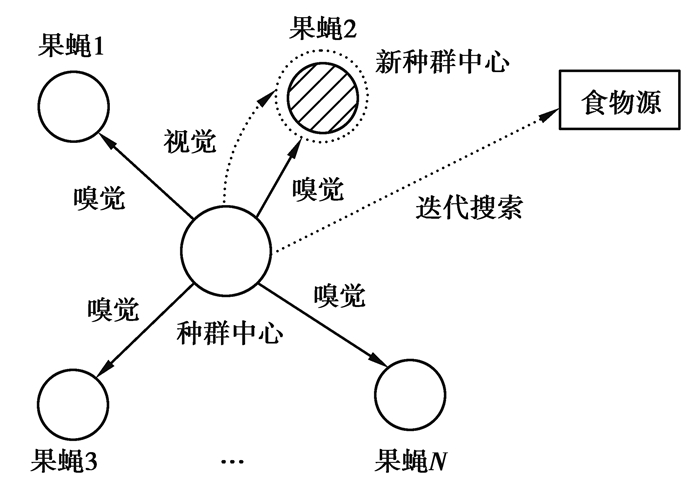
1 基本果蝇算法果蝇算法(FOA, fruit fly optimization algorithm)是一种新兴启发式算法,模拟自然界果蝇的觅食活动寻求目标函数的最优解,果蝇觅食示意图,如图 1所示。其基本步骤如下[17-19]
|
图 1 果蝇觅食示意图 Fig. 1 Schematic diagram of fruit fly foraging |
步骤1:初始化参数。设置种群规模SSizepop和最大迭代次数MMaxgen,初始化种群位置
| $ ({X_{{\rm{\_axis }}}}, Y{{\rm{ }}_{{\rm{\_axis }}}})。$ | (1) |
步骤2:赋予果蝇个体觅食的随机方向及距离
| $ \left\{ \begin{array}{l} {X_i} = {X_{{\rm{\_axis}}}}{\rm{ + }}{R_{{\rm{ Value }}}}, \\ {Y_i} = {Y_{{\rm{ \_axis }}}}{\rm{ + }}{R_{{\rm{ Value }}}}。\end{array} \right. $ | (2) |
步骤3:起初不能获知食物源位置,先计算果蝇个体与原点之间的距离Di,再计算味道浓度判定值Si,
| $ {{D_i} = \sqrt {X_i^2 + Y_i^2} , } $ | (3) |
| $ {{S_i} = 1/{D_i}}。$ | (4) |
步骤4:将Si带入味道浓度判定函数(fitness function)求出果蝇个体位置的味道浓度Ti,
| $ {T_i} = {\rm{ Fitness }}({S_i})。$ | (5) |
步骤5:找出果蝇群体中味道浓度最高的个体为
| $ [{B_{{\rm{ BestTaste }}}}, {B_{{\rm{ BestIndex }}}}, ] = {\rm{min}}({T_i})。$ | (6) |
步骤6:保留最佳味道浓度值与坐标,种群中其他个体向该位置飞去,
| $ {T_{{\rm{ Best }}}} = {B_{{\rm{ Best Taste }}}}, $ | (7) |
| $ \left\{ \begin{array}{l} {X_{{\rm{\_axis}}}} = {X_{{\rm{ bestIndex }}}}, \\ {Y_{{\rm{\_axis}}}} = {Y_{{\rm{ bestIndex }}}}。\end{array} \right. $ | (8) |
步骤7:终止条件,判断最佳位置浓度是否优于前一代,并且达到最大迭代次数,否则跳转步骤2进入迭代寻优。
2 融合免疫反应的混合果蝇算法果蝇具有较发达的嗅觉和视觉系统,在觅食过程中先通过嗅觉进行大范围搜索,并向周围的果蝇发出食物气味信息。当果蝇通过比较发现具有较高浓度的位置时,果蝇个体将依靠视觉功能飞向该位置。正是由于这样的种群特性,降低了种群多样性,使模拟其特性的果蝇算法同其他仿生智能算法一样具有容易陷入局部最优的缺陷,带来早熟问题。
免疫算法从体细胞理论和网络理论中得到启发,实现了与免疫系统类似的自我调节和生成不同抗体的功能。该算法具有很强的局部搜索能力,将其引入果蝇算法执行过程后期,提出融合免疫反应的混合果蝇算法IAFOA,新算法IAFOA可以用来平衡果蝇算法易陷入局部最优的不足,提高搜索效率。2种标准算法对应关系如表 1所示。
| 表 1 IA和FOA在求解组合优化问题时的对应关系 Table 1 The correspondence between IA and FOA in solving combinatorial optimization problems |
免疫算法(IA, immune algorithm)是一种仿生优化类算法,该研究最初是从20世纪80年代中期的免疫学研究发展而来。1990年,Bersini[20]首次使用免疫算法来解决问题。IA算法通过模拟生物免疫系统功能进行抗原(目标函数)的识别,对免疫系统中的存储记忆原理的模拟,抗原和抗体(优化解)的结合,以及免疫系统自身多样性的模仿,实现了类似于免疫系统的抗原识别、细胞分化、记忆和自我调节的功能[21]。其基本步骤如下:
步骤1:抗原识别。输入目标函数和约束条件作为免疫算法的抗原。
步骤2:产生初始抗体。在解空间范围内随机产生初始抗体。
步骤3:计算亲和性(适应度评价)。按给定的适应度评价函数判定各个抗体与抗原的亲和性及抗体和抗体之间的亲和性。
抗原与抗体V之间的亲和性Av定义为
| $ {A_{\rm{v}}} = 1/[1 + {O_{\rm{P}}}{t_{\rm{v}}}], $ | (9) |
式中:OPtv表示抗原和抗体的匹配程度;Av的值介于0~1之间。当OPtv=0时,Av=1,这表明抗体和抗原非常匹配, 即该抗体为最优的解。
步骤4:记忆单元的更新。将步骤3计算出的与抗原亲和性最高的抗体加入记忆单元,并取代原有抗体。
步骤5:促进和抑制节的产生。计算抗体i的期望值Exi,期望值低的抗体将被抑制。
| $ {E_{xi}} = {A_i}/{C_i}, $ | (10) |
式中:Ai是抗原与抗体i的亲和性;Ci是抗体i的数目。
步骤6:产生新抗体。父代通过遗传、变异、交叉产生下一代抗体。
步骤7:是否满足终止条件。是,终止算法;否,跳转步骤3。
2.2 IAFOA种群多样性改进免疫系统是通过阻拦细菌入侵维持生物正常代谢的基本防御系统。该系统通过识别基因类型以产生不同的抗体,通过调节机制促进新个体的出现、抑制个体的过多产生,从而实现生物的多样性[22]。
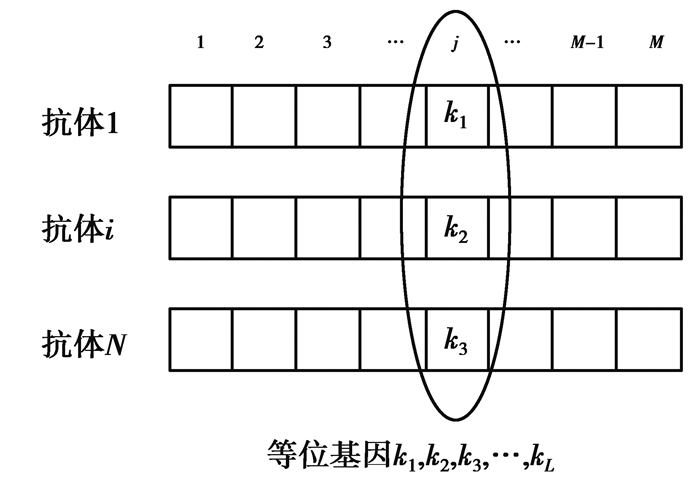
设免疫系统有N个抗体,每个抗体有M个基因,如图 2所示。第j个基因的信息熵Hj(N)为
| $ {H_j}(N) = \sum\limits_{i = 1}^N {( - {P_{ij}} \times {\rm{log}}{P_{ij}})} 。$ | (11) |
|
图 2 基因的信息熵 Fig. 2 Information entropy of genes |
如果在位置j上所有抗体的等位基因都相同,那么Hj(N)等于0。
故,系统的平均信息熵H(N)为
| $ H(N) = \sum\limits_{j = 1}^M {{H_j}} (N)/M。$ | (12) |
算法以标准果蝇算法为基本框架,调用FOA算法,构造各次迭代的可行解集,然后采用进化停滞步数t作为触发条件,当t>T(进化停滞步数阈值)时,调用IA搜索过程,将免疫算法中免疫因子(对应果蝇个体)寻求抗原(对应果蝇算法中的食物源)产生抗体(优化解)的过程用于扩大搜索的空间。对经过IA搜索后获得的可行解集执行精英保留策略,得到的优化解与原可行解集共同用于更新搜索空间中气味信息的浓度,以指导其他果蝇的路径寻找机制。
其中,进化停滞步数阈值T为进入IA算法的指标,过早引入IA算法,不利于IA的搜索能力,甚至无法收敛可行解;过晚进入IA算法,不利于提高计算效率。通过多次独立试验取值,研究采用T=3作为进入IA算法的触发条件值。
如满足触发条件,则以某一固定概率p将果蝇重新分配到寻优空间中,并对不同个体根据其适应度值赋予不同的自适应免疫概率P(i),通过P(i)选出需进行免疫操作的果蝇个体,执行免疫操作,进而迭代搜索得优化解放入原优化解集进行比较。
| $ P(i) = \frac{{({T_{{\rm{ Best }}}} - {T_i})}}{{({T_{{\rm{ Best }}}} - {T_{{\rm{ Worst }}}})p}}, $ | (13) |
其中,为避免算法陷入局部最优解,给定IA算法中免疫因子一定的初始概率p=0.25使其随机分配,增加解的多样性。
IAFOA的流程如下
步骤1:初始化参数。设置种群规模SSizepop和最大迭代次数MMaxgen,初始化种群位置X_axis和Y_axis,进化停滞步数t=0。
步骤2:根据式(3)随机产生果蝇群体。
步骤3:采用式(4)~式(7)对种群进行操作。
步骤4:根据式(14)记录并保留最佳味道浓度值,更新进化迭代步数t。
| $ \left\{ {\begin{array}{*{20}{l}} {if({B_{{\rm{ Best Taste }}}} < {T_{{\rm{ Best }}}})}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {T_{{\rm{ Best }}}} = {B_{{\rm{ Best Tastel }}}}}\\ {{\rm{ }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{else }}(t = t + 1)}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {T_{{\rm{ Best }}}} = {B_{{\rm{ BestTaste2}}}}}\\ {{\rm{ }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{end }}} \end{array}} \right. $ | (14) |
步骤5:判断t<T是否成立,若是直接转步骤7;否则,根据式(13)计算果蝇个体自适应免疫概率,按照免疫算法进行免疫操作,未执行免疫操作的个体转步骤7。
步骤6:对执行免疫操作所得的新种群重复执行步骤2~步骤4进行迭代搜索。
步骤7:令ggen=ggen+1,若ggen<MMaxgen则转步骤2,否则终止迭代。
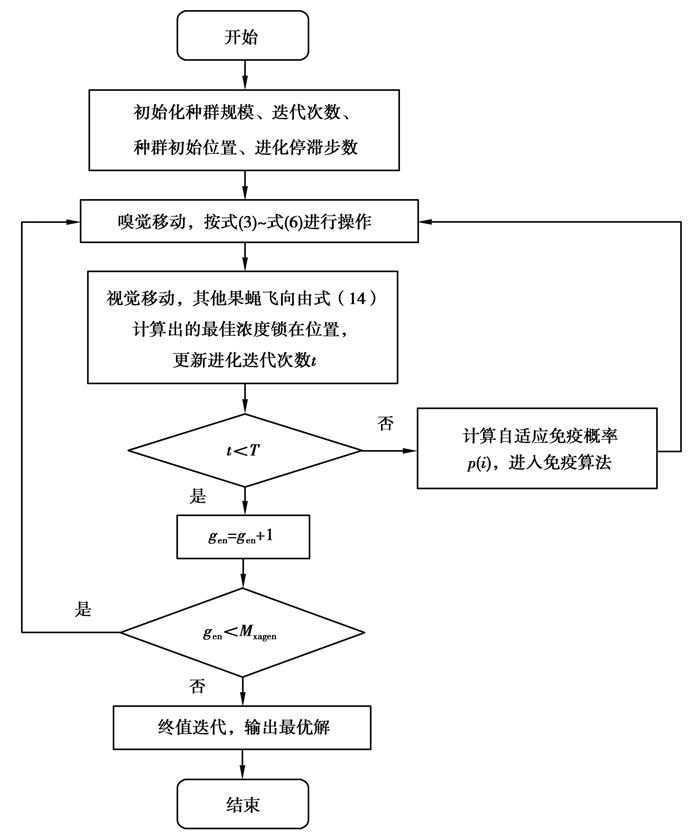
IAFOA流程图,如图 3所示。
|
图 3 改进果蝇算法算法迭代图 Fig. 3 Iteration diagram of IAFOA algorithm |
为验证文中算法的有效性,选取4个标准测试函数进行数值仿真试验来测试IAFOA算法的性能[23]。另外,选取0~1背包问题进行仿真实验,将结果与其他算法进行比较。初始化参数:种群规模SSizepop=200,最大迭代次数MMaxgen=1 000,维度D=30,初始概率p=0.25,进化停滞步数阈值T=3。
3.1 标准函数测试第1个标准函数:Rosenbrock函数
| $ {f_1}(x){\rm{ }} = \mathop \sum \limits_{i = 1}^{d - 1} [100{({x_{i + 1}} - x_i^2)^2} + {({x_i} - 1)^2}]。$ |
第2个标准函数:Ackley函数
| $ {f_2}(x) = - a{\rm{exp}}( - b\sqrt {\frac{1}{d}\sum\limits_{i = 1}^d {x_i^2} } ) - {\rm{exp}}(\frac{1}{d}\sum\limits_{i = 1}^d {{\rm{cos}}} (c{x_i})) + a + {\rm{exp}}(1)。$ |
第3个标准函数:Griewank函数
| $ {f_3}(x) = \frac{1}{{4{\kern 1pt} {\kern 1pt} {\kern 1pt} 000}}\sum\limits_{i = 1}^D {x_i^2} - \prod\limits_{i = 1}^D {{\rm{cos}}} \left( {\frac{{{x_i}}}{{\sqrt i }}} \right) + 1。$ |
第4个标准函数:Schaffer函数
| $ {f_4}(x) = {\rm{sin}}\left( {\frac{{\sqrt {\sum\limits_{i = 1}^D {(x_i^2)} } - 0.5}}{{1 + 0.001 * {{\left( {\sum\limits_{i = 1}^D {(x_i^2)} } \right)}^2}}}} \right) + 0.5, $ |
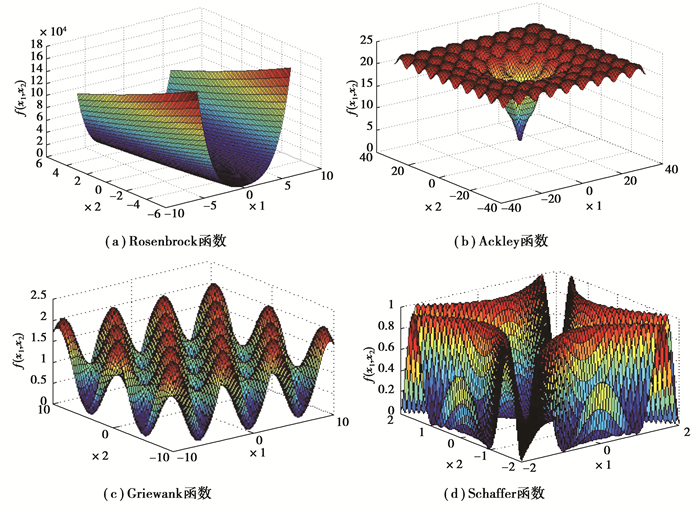
式中:Rosenbrock函数为单峰值函数,主要用来测试文中改进算法在运算过程中的收敛性能;Ackley函数和Griewank函数均为较复杂的多峰值函数,易使算法陷入局部最优,从而得不到真正的最优值,用来测试改进算法处理易陷入“早熟”的能力;Schaffer函数具有复杂的空间性,用来测试改进算法的计算精度、收敛稳定性和算法时间复杂度。4种标准函数如图 4所示。
|
图 4 标准函数图像 Fig. 4 Standard function image |
通过运用4种不同标准函数分别对文中改进算法的收敛性能、运行效率、处理“局部最优”以及“早熟”问题进行测试,寻优测试中的最优值、平均值,反映出解的质量。标准差反映了算法的鲁棒性。运行时间则反映算法收敛速度及精度。由表 2可以看出,融合免疫反应的混合果蝇算法在标准函数上的表现优于标准果蝇算法。该改进算法是可行且有效的。
| 表 2 标准函数优化性能对比 Table 2 Comparison of optimization performance for benchmark functions |
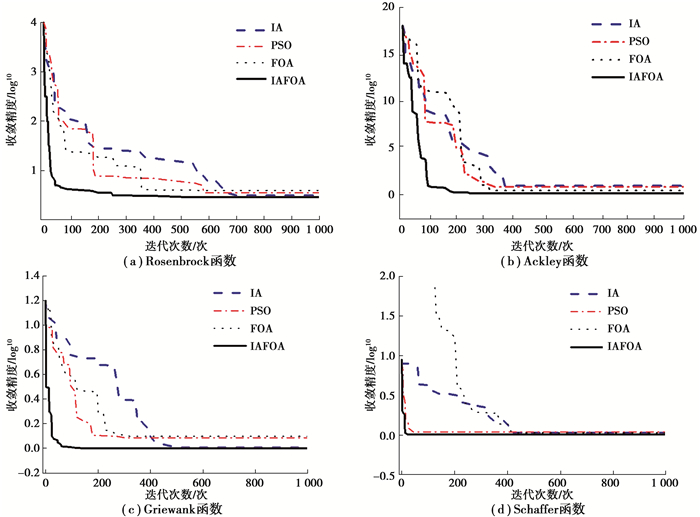
为了更加直观地看出改进算法性能的有效性,图 5是免疫算法(IA, immune algorithm)、粒子群算法(PSO,particle swarm optimization)、标准果蝇算法(FOA, fruit fly optimization algorithm)及融合免疫反应的混合果蝇算法(IAFOA, fruit fly optimization algorithm based on immune algorithm)在上述4种标准函数下的收敛曲线图。采用多次运行结果的平均值作为最终结果以避免偶然误差。
|
图 5 算法在4种函数下的迭代曲线 Fig. 5 The iterative curve of the algorithm under four functions |
0~1背包问题是组合优化领域常见问题之一,该问题的描述为:设物品总数为D,第i个物品的体积和价格分别为wi和pi,一个背包的最大容量为V,怎样选择物品使得背包的总价值最大,即为0~1背包问题。其数学模型为
| $ { {\rm{max}} f = \mathit{\boldsymbol{RX}} = \sum\limits_{i = 1}^D {{R_i}} {x_i}, } $ | (15) |
| $ {\rm{s}}.{\rm{t}}.\;{\bf{WX}} = \sum\limits_{i = 1}^D {{w_i}} {x_i} \le V, $ | (16) |
式中:R =(R1, R2, …, RD)、W =(w1, w2, …, wD)、X =(x1, x2, …, xD)分别表示物品的价值向量、体积向量、解向量;xi为决策向量,xi=0表示未放入包,xi=1表示放入包。
算例的基本参数设置,如表 3所示。
| 表 3 0~1背包问题基本参数对照表 Table 3 Comparison table of basic parameters of 0~1 knapsack problem |
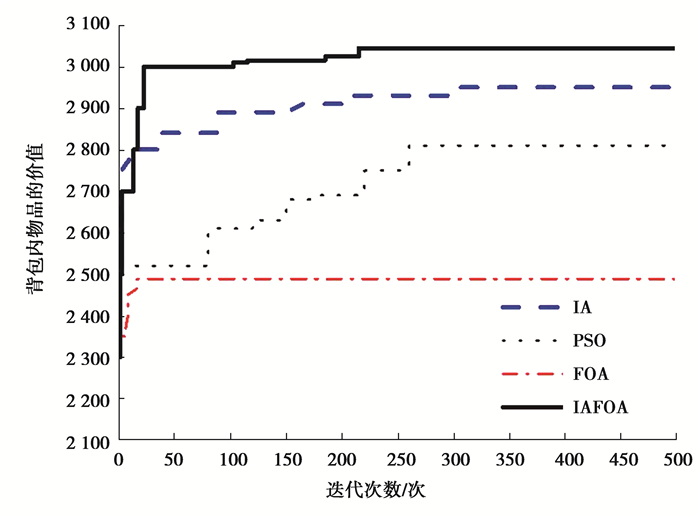
改进算法及其他3种标准算法的优化对比,如表 4和图 6所示。结果表明,改进算法在求解0~1背包问题时的优化性能较优。
| 表 4 0~1背包问题结果对照表 Table 4 Result comparison table of 0~1 knapsack problem |
|
图 6 算例优化过程曲线 Fig. 6 Optimization process curve of the example |
以截面积为设计变量的桁架优化模型问题描述为
| $ {{\rm{min}}F = W(x), } $ | (17) |
| $ {{\rm{ s}}{\rm{.t}}{\rm{. }}{g_i}(x) \le 0, i = 1, 2, \cdots , m, } $ | (18) |
式中:gi(x)为约束函数;m为约束个数。
4.1.2 目标函数| $ W(A) = \sum\limits_{i = 1}^n \rho {A_i}{L_i}, $ | (19) |
式中:W(A)为结构的重量;Ai、Li分别为第i根杆件的截面积和长度;ρ为材料密度;n为设计变量个数。
4.1.3 约束条件结构中各个杆件需满足强度、刚度、稳定性及截面尺寸的要求
| $ {\frac{{{\sigma _i}}}{{[\sigma ]}} - 1 \le 0, } $ | (20) |
| $ {\frac{{{\mu _j}}}{{{\mu _{{\rm{max}}}}}} - 1 \le 0, } $ | (21) |
| $ {{A_{{\rm{min}}}} \le {A_i} \le {A_{{\rm{max}}}}, } $ | (22) |
式中:σi为第i根杆件的正应力;[σ]为材料的许用应力;μj为节点j的位移;μmax节点j的许用位移;Amin、Amax分别为杆件截面的上、下限。
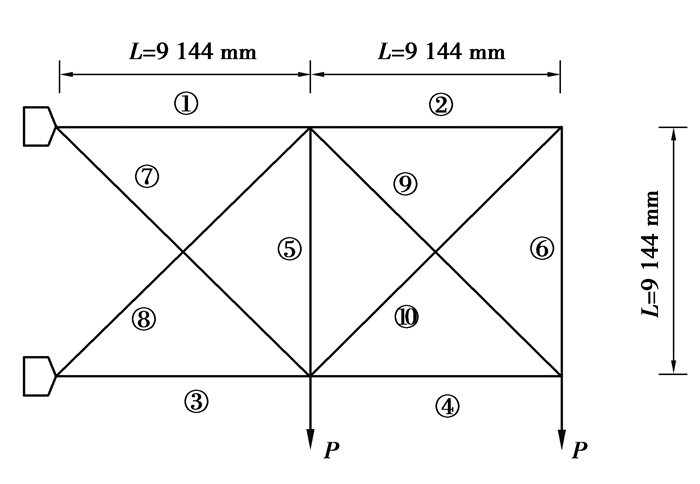
4.2 算例1建立10杆桁架结构模型,如图 7所示,其包含节点数6个,设计变量10个,为求得结构的最小总重量,现对其进行优化。E=68 950 MPa,ρ=2 768/m3,σ=±172.4 MPa,规定杆件截面面积的浮动范围为[0.645, 258]cm2,该结构体系中图示节点受到大小为P=444.5 kN且方向向下的集中荷载,优化结果如表 5所示。
|
图 7 平面桁架结构图 Fig. 7 Plane truss structure diagram |
| 表 5 平面桁架结构优化结果 Table 5 Results of plane truss structure optimization |
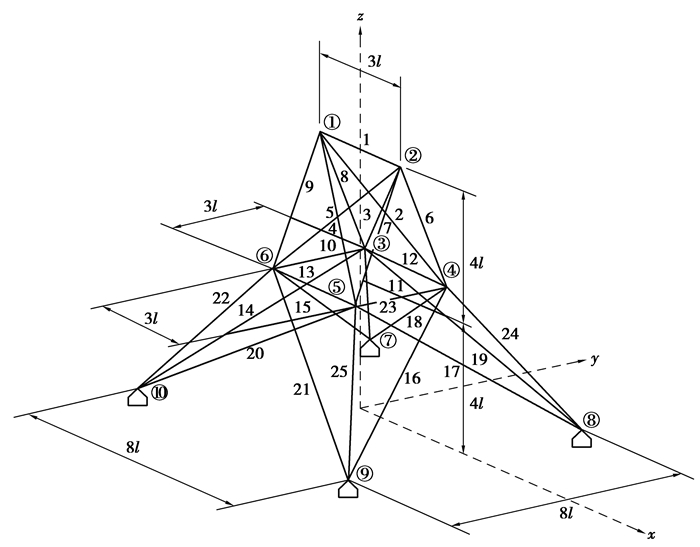
选取25杆件空间桁架结构[22],如图 8所示。桁架结构的基本参数:杆件长度l=0.635 m,弹性模量E=6.895×104MPa,材料密度ρ=2.678×103 kg/m3,许用应力范围:[-275.8, 275.8],结构受荷载情况如表 6所示,节点1和节点2的最大竖向位移y=8.889 mm。优化结果如表 7所示。
|
图 8 空间桁架结构图 Fig. 8 Space truss structure |
| 表 6 25杆桁架结构荷载工况 Table 6 Load conditions of 25-bar truss structure |
| 表 7 25杆桁架结构优化结果对比 Table 7 Comparison of optimization results of 25-bar truss structure |
通过该经典算例模型进行优化对比,由表 5及表 7优化结果可以看出,新算法IAFOA在求解速度和优化程度上的表现更良好,能够达到预想结果。通过图 9迭代曲线可以看出,IAFOA算法具有较好的全局搜索能力,在收敛速度及精度上比其他3种标准算法有较大的提高。
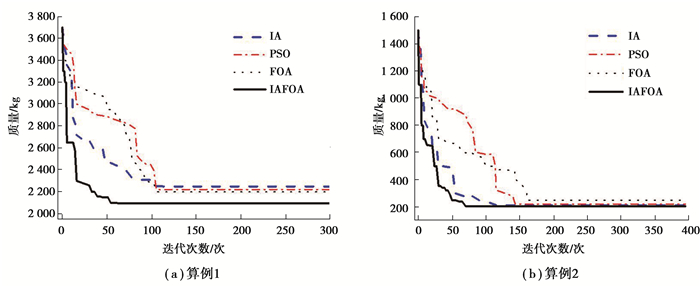
|
图 9 2个算例的寻优迭代曲线 Fig. 9 The optimization iteration curve of two examples |
研究将IA引入到FOA中构建IAFOA算法。IAFOA同时结合了原有标准FOA算法的全局搜索能力和IA算法自身较强的局部搜索能力,在数值模拟、求解优化问题以及算例分析中IAFOA在收敛性、运行效率、跳出“局部最优”上均取得了较好的结果。文中虽然改进了算法的一些不足,但缺乏对参数停滞步数阔值T、固定概率p的调节,还需要更加详细的改进以求IAFOA算法收敛得更快更精准。另外,文中实例较为简单,算法应用于复杂结构优化中的相关研究仍需进一步深入。
| [1] |
Pan W T. A new fruit fly optimization algorithm:taking the financial distress model as an example[J]. Knowledge-Based Systems, 2012, 26: 69-74. DOI:10.1016/j.knosys.2011.07.001 |
| [2] |
Shan D, Cao G H, Dong H J. LGMS-FOA:An improved fruit fly optimization algorithm for solving optimization problems[J]. Mathematical Problems in Engineering, 2013, 2013(7): 1256-1271. |
| [3] |
Zhang Y, Cui G, Wu J, et al. A novel multi-scale cooperative mutation fruit fly optimization algorithm[J]. Knowledge-Based Systems, 2016, 114: 24-35. DOI:10.1016/j.knosys.2016.09.027 |
| [4] |
Pan W T. Using modified fruit fly optimisation algorithm to perform the function test and case studies[J]. Connection Science, 2013, 25(2/3): 151-160. |
| [5] |
Pan Q K, Sang H Y, Duan J H, et al. An improved fruit fly optimization algorithm for continuous function optimization problems[J]. Knowledge-Based Systems, 2014, 62: 69-83. DOI:10.1016/j.knosys.2014.02.021 |
| [6] |
Wang L, Shi Y, Liu S. An improved fruit fly optimization algorithm and its application to joint replenishment problems[J]. Expert Systems with Applications, 2015, 42(9): 4310-4323. DOI:10.1016/j.eswa.2015.01.048 |
| [7] |
Li J, Pan Q, Mao K, et al. Solving the steelmaking casting problem using an effective fruit fly optimization algorithm[J]. Knowledge-Based Systems, 2014, 72: 28-36. DOI:10.1016/j.knosys.2014.08.022 |
| [8] |
张前图, 房立清, 赵玉龙. 具有Levy飞行特征的双子群果蝇优化算法[J]. 计算机应用, 2015, 35(5): 1348-1352. ZHANG Qiantu, FANG Liqing, ZHAO Yulong. Gemini fly optimization algorithm with Levy flight characteristics[J]. Computer Applications, 2015, 35(5): 1348-1352. (in Chinese) |
| [9] |
刘志雄, 王雅芬, 张煜. 多种群果蝇优化算法求解自动化仓库拣选作业调度问题[J]. 武汉理工大学学报, 2014, 36(3): 71-77. LIU Zhixiong, WANG Yafen, ZHANG Yu. Multi-population fruit fly optimization algorithm for automated warehouse selection scheduling[J]. Journal of Wuhan University of Technology, 2014, 36(3): 71-77. (in Chinese) |
| [10] |
韩俊英, 刘成忠, 王联国. 动态双子群协同进化果蝇优化算法[J]. 模式识别与人工智能, 2013, 26(11): 1057-1067. HAN Junying, LIU Chengzhong, WANG Lianguo. Dynamic twin group coevolution drosophila optimization algorithm[J]. Pattern Recognition and Artificial Intelligence, 2013, 26(11): 1057-1067. (in Chinese) |
| [11] |
蔡自兴, 龚涛. 免疫算法研究的进展[J]. 控制与决策, 2004, 19(8): 841-846. CAI Zixing, GONG Tao. Progress of immune algorithm research[J]. Control and Decision, 2004, 19(8): 841-846. (in Chinese) |
| [12] |
Chen D, Li S, Wang J, et al. A multi-objective trajectory planning method based on the improved immune clonal selection algorithm[J]. Robotics and Computer-Integrated Manufacturing, 2019, 59: 59, 431-442. |
| [13] |
Zhen Y, Ding Y, Hao K, et al. An adaptive immune algorithm for service-oriented agricultural internet of things[J]. Neurocomputing, 2019, 3-12. |
| [14] |
Corus D, Oliveto P S, Yazdani D. When hypermutations and ageing enable artificial immune systems to outperform evolutionary algorithms[J]. Theoretical Computer Science, 2019, 3: 1-34. |
| [15] |
胡东方, 雷若楠. 基于实例推理与人工免疫系统的工程产品设计方法[J]. 计算机集成制造系统, 2018, 24(1): 146-153. HU Dongfang, LEI Ruonan. Engineering product design method based on case reasoning and artificial immune system[J]. Computer Integrated Manufacturing System, 2018, 24(1): 146-153. (in Chinese) |
| [16] |
徐小平, 师喜婷, 钱富才. 基于猴群算法求解0-1背包问题[J]. 计算机系统应用, 2018, 27(5): 133-138. XU Xiaoping, SHI Xiting, QIAN Fucai. Solving 0-1 knapsack problem based on monkey swarm algorithm[J]. Application of Computer System, 2018, 27(5): 133-138. (in Chinese) |
| [17] |
Hassan Z, Bahman N, Mohammad M. The economic lot scheduling problem in limited-buffer flexible flow shops:Mathematical models and a discrete fruit fly algorithm[J]. Applied Soft Computing Journal, 2019, 6: 904-919. |
| [18] |
王凌, 郑晓龙. 果蝇优化算法研究进展[J]. 控制理论与应用, 2017, 34(5): 557-563. WANG Ling, ZHENG Xiaolong. Research progress of fruit fly optimization algorithm[J]. Control Theory and Application, 2017, 34(5): 557-563. (in Chinese) |
| [19] |
Hu J, Chen P, Yang Y, et al. The fruit fly optimization algorithms for patient-centered care based on interval trapezoidal type-2 fuzzy numbers[J]. International Journal of Fuzzy Systems, 2019, 5: 1270-1287. |
| [20] |
Bersini H, Varela F. Hints for adaptive problem solving gleaned from immune network[A]. Berlin Heidelberg: Springer-Verlag, 1991: 343-354.
|
| [21] |
张金梦, 刘慧君. 遗传算法优化BP神经网络的泊车位数量预测[J]. 重庆大学学报, 2018, 41(3): 76-81. ZHANG Jinmeng, LIU Huijun. Prediction of parking space based on BP neural network optimized by genetic algorithm[J]. Journal of Chongqing University, 2018, 41(3): 76-81. (in Chinese) |
| [22] |
谢开贵, 曾晓晖, 李春燕, 等. 免疫算法与其他随机优化算法的比较分析[J]. 重庆大学学报, 2003, 26(11): 43-47. XIE Kaigui, ZENG Xiaohui, LIU Chunyan, et al. Comparative analysis of immune algorithm and other stochastic optimization algorithms[J]. Journal of Chongqing University, 2003, 26(11): 43-47. (in Chinese) |
| [23] |
李彦苍, 王旭. 基于信息熵的改进海豚群算法及其桁架优化[J]. 重庆大学学报, 2019, 42(5): 76-85. LI Yancang, WANG Xu. Improved dolphin swarm algorithm based on information entropy and its truss optimization[J]. Journal of Chongqing University, 2019, 42(5): 76-85. (in Chinese) |
 2020, Vol. 43
2020, Vol. 43

