2. 招商局重庆交通科研设计院有限公司 自动驾驶技术交通运输行业研发中心, 重庆 400067;
3. 重庆大学 自动化学院, 重庆 400044
2. Research and Development Center of Transport Industry of Self-driving Technology, China Merchants Chongqing Communications Technology Research & Design Institute Co., Ltd., Chongqing 400067, P. R. China;
3. College of Automation, Chongqing University, Chongqing 400044, P. R. China
环道是一个城市的交通枢纽,也是车流量强度最大的地区,从各地不同方向到达的车流非常集中,是一个路网密集、交叉口关联性极强的复杂系统,交叉口上游交通流的持续汇入和下游交通流不能及时疏散是造成环道拥堵的根本原因,在交通高峰期甚至会导致环道出现“死锁”现象。城市环道交通控制系统中广泛使用的仍是单点定时控制方法,这种方法是基于进出单点交叉口的交通流呈规律性分布,在稳定情况下有比较好的控制效果,但在交通流分布不稳定,随机性较强情况下,单点定时控制难以满足实时控制效果,产生较大的延误和信号周期的损失[1]。
环道交通是一个多交叉口组成的环形交通路网,多交叉口之间有较强关联性,如何从整体角度出发,将环道整体视为一个研究对象,环道内所有交叉口作为研究对象,在达到单个交叉口配时最优的情况下,对所有交叉口进行信号协调,是解决问题的关键[2]。近年来,多智能体系统研究是人工智能领域的一个研究热点,由于多智能体具备学习性、自调节性、以及交互性等优良特性。考虑交通系统是时间和空间上非线性、时变的随机系统, 对交通系统的实时优化控制非常适合采用多智能体系统。在研究和分析各种多智能体在交通控制领域的基础上,将城市环道这一抽象模型引入研究范围,对城市环道进行模型的建立,并进行特性分析,尝试将多智能体技术引入到城市环道的交通控制中,实现不同的时段对城市环道交通的最优控制,研究背景选为重庆市两路口环道,该环道共有5个交叉口,高峰时段的交通流量较大,交通流负载过大,在环道模型中具有代表性,构建一套合理的智能控制系统,针对交通评价指标进行分析,选择具有代表性的交通评价指标,对该控制系统的控制效果与现有控制效果进行对比分析,证明该智能控制系统的合理性和有效性。
1 城市环道多交叉口信号协同控制算法交通系统是一个在物理上分散、功能上紧密相连的大型复杂系统,对于交通路网中的各个子系统,各自处于不同的时间和空间上动态变化的环境中,这些特性非常适合使用多智能体的思想进行求解。多智能体系统比较符合交通系统中各个元素的特征[3]。因此,基于多智能体所形成的交通模型比较符合实际交通环境。此外,多智能体的开放性使得它自身可以与其他的控制方法结合,使得问题的求解更加便捷和简单[4]。
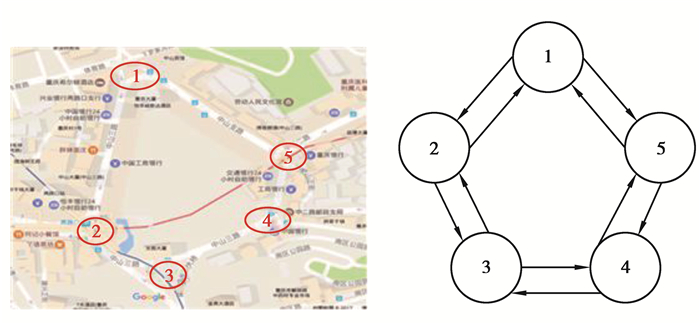
如图 1所示,以重庆市两路口环道为例,构件抽象的交互性多智能体系统模型,说明5个交叉口所构成的交叉口系统与多智能体系统对比,5个智能体之间彼此互相关联,左右图两者的拓扑结构非常相似,因此考虑可以将多智能体理论应用到环道交叉口的协调控制中[5]。
|
图 1 两路口环道与多智能体系统模型对比示意图 Fig. 1 The schemativ diagram of two intersection loop and multi-agent system model comparison |
对于一个城市交通路网,主干道往往承受着比较大的交通负载,对干道的各个交叉口进行协调控制,从而保证主干道上车流的畅通运行和减轻路网的负载已成为缓解城市交通拥堵改善城市交通运行状况的关键所在。对于干道协调控制,往往根据2个指标进行优化:停车延误和绿波带,根据这2项指标,有两种干道协调设计思路:
1) 绿波协调控制设计;
2) 停车延误协调控制设计。绿波协调控制设计是以车辆在干道上行驶时绿波带最大化为设计目标;停车延误协调控制设计是车辆的停车延误最小化为设计目标。
1.1 干道协调绿波控制干道绿波协调控制是基于绿波带的设计思想,对干道上多个交叉口进行协调相位设计,绿波带设计,从而使得车流能够不停车地直行通过各个交叉口。进行干道绿波协调设计一般只适用于交通状况较小或者未饱和的状态,滤波协调控制的核心在于绿波带的设计,通过求得最大绿波带,使得绿波时间在整个公共信号周期时间内的比值达到最大,使得车辆可以尽可能不停车地驶离干道。绿波带的宽度往往是衡量滤波协调控制的评价指标。
下面对绿波协调控制的几个基本概念做解释:
1) 协调相位:是指干道上的多个信号交叉口为了达到协调控制而设计的相位,一般为直行相位。
2) 绿波带:是指在同一绿灯时间内,经过车道的车辆相距最远的2条连续行驶轨迹线的空间。表征绿波带的2个属性是绿波带宽度以及绿波带速度。其中,绿波带宽度是指车辆在2个交叉口之间连续获得通行的最小绿灯时间;绿波带速度是指车辆在获得绿波时的平均速度。如果车辆能以绿波带速度在干道上行驶,理想情况下,可以不停顿地通过各个交叉口。
笔者提出基于多智能体的环道内交叉口绿波协调算法,算法的基本思路是:将环道上的每一个交叉口都看做是一个智能体,并且环道上的相邻交叉口之间可以建立信息沟通,两者之间的信息可以共享,两者之间的通信忽略时延,那么环道上多个交叉口的协调控制就是多智能体的协调控制[6]。
1.2 算法模型与参数定义环道交叉口多智能体的模型如下式所示
| $\left\{\right. \mathrm{Agent} \left., S_{t}(i, j), C_{k}, T_{k}(i, j), P_{\text {next }}^{i}\right\}, i=1, 2, \cdots, n ; j=1, 2, \cdots, m ; t, k 均为正整 , $ | (1) |
式中:Agent为交叉口多智能体的集合;St(i, j)为交叉口多智能体i的状态;Ck为交叉口多智能体的周期长度;Tk(i, j)为交叉口多智能体i的每个相位的最大相位时间;Pnexti为交叉口多智能体i的下一个相位[7]。
| $\mathrm{Agent}=\left[\mathrm{Agent}_{1}, \mathrm{Agent}_{2}, \cdots, \mathrm{Agent}_{n}\right] ;$ | (2) |
| $S_{t}(i, j)=\left[s_{t}(i, 1), s_{t}(i, 2), \cdots s_{t}(i, m)\right] ;$ | (3) |
| $C_{k=}\left[C_{k}(1), C_{k}(2), \cdots, C_{k}(m)\right] ; $ | (4) |
| $T_{k}(i, j)=\left[t_{k}(i, 1), t_{k}(i, 2), \cdots, t_{k}(i, m)\right] 。$ | (5) |
其中:st(i, j)指的是在t时刻第i个交叉口智能体的第j个相位的状态值;Ck(i)为第i个智能体在第k个周期的周期值;tk(i, j)为第i个智能体在第k个周期的第j个相位的最大相位时间。
在定义完环道交叉口智能体的模型之后,求解各个交叉口智能体的交通参数是非常核心的部分,主要的交通参数有3个:周期、各个相位绿灯时间、和相位选择策略[8]。以下对这3个参数的求解进行阐述
周期:周期的求解如下
| $C_{k}(i)=\left\{\begin{array}{cl}\frac{1.5 L_{i}+5}{1-Y_{i}} & , Y<0.9 ; \\ \text { 预案 } & , Y \geqslant 0.9 。\end{array}\right.$ | (6) |
当满足最优周期条件时,根据韦伯斯特算法求得最佳周期,若不满足,则启用预案中的周期时长。
相位绿灯时间:基于行驶安全考虑,每个相位应设有最小的通行时间tmin,通常取10 s,这里定义第i个交叉口智能体的第j个相位的流量为q(i, j),且在t时刻,第i个交叉口的总的通行车流为Qi(t),t(i, j)为第i个交叉口智能体的第j个相位应该获取的绿灯时长。那么,根据流量分配原则
| $t_{(i, j)}=\frac{q_{(i, j)}}{Q_{i}(t)} C_{k}(i), $ | (7) |
相位选择策略:此时,利用多智能体系统的通信与信息共享的特点进行设计。设计思路:假设交叉口智能体agenti此时正在对车流Tf进行放行,此时,交叉口智能体agenti给相邻的交叉口智能体agenti+1发送一个通知Notification,这里agenti+1表示下游交叉口智能体。智能体agenti+1根据发来的通知,得到放行时刻,计算出绿波车流到达的时刻,从而对自身进行自适应调整,使得道路的通行能力最优化[9]。
为进一步说明协调相位的选择策略,这里,对相邻交叉口的时距图进行分析,对立面的一些参数进行解释,如下图 2所示,为2个交叉口智能体的时距图。

|
图 2 交叉口相位时距图 Fig. 2 The intersection phase time distance diagram |
图中,Ii、Ii-1为相邻的交叉口,Ck(i)为交叉口Ii的第k个信号周期时长,tk1为信号周期的开始时刻,tk6为结束时刻,tk2为下行绿波时间开始时刻,tk3为下行绿波时间结束时刻,下行绿波时间是指车流从交叉口Ii到Ii-1的绿波时间,同理,tk4、tk5为上行绿波时间开始结束时刻。Δtki是2个绿波带的时间间隔,也就是tk4和tk3的差值。这里定义时间间隔集合Δtk=[tk2-tk1, Δtki, tk6-tk5],时间间隔Δtk的选择直接影响到相邻智能体交叉口的协调绿波控制效果[10]。
交叉口智能体的相位选择基于2方面的考虑:1)一是智能体自身当前的状态,单个交叉口是自适应的控制策略,将单个交叉口视为智能体,如果做当前相位的选择,必然会影响到自适应控制的控制效果。2)需要考虑协调车流(也就是绿波车流)到达此交叉口的时刻与当前时刻的时间间隔。在2个相邻交叉口智能体满足绿波条件的基础上,待协调车流到达时间与交叉口智能体的剩余可选择的相位时间时长的大小之差,也就是两者的匹配程度会影响智能体的控制效果:如果两者之间相等,那么协调车流可以不停车地连续经过2个相邻交叉口,如果不相等,肯定对绿波效果有影响[11]。
经过上面的分析,可以得到当前智能体的相位选择策略主要由2个因素决定,即:智能体的当前状态以及时间匹配度。分别用st(i, j)表示当前智能体的状态参数,以及TimeMatch表示时间匹配度。其中时间匹配度定义如下
| $\mathrm{TimeMatch} =\left\{\begin{array}{cl}1, & \Delta t=t_{(i, j)}, \Delta t \in \Delta t_{k} ;\\ \frac{\Delta t-t_{\min }}{\Delta t-t_{(i, j)}} & \Delta t \neq t_{(i, j)}, \Delta t \in \Delta t_{k}, \end{array}\right.$ | (8) |
其中tmin为提到的最小相位时间,Δt为时间间隔集合Δtk中的取值。
因为相位选择策略主要由上面2个参数决定,因此定义当前智能体的协调适应度变量
| $A \mathrm{~d} a p t=s_{t}(i, j) \times \mathrm{TimeMatch}, $ | (9) |
相位选择算法流程如表 1所示。
| 表 1 相位选择算法 Table 1 Phase selection algorithm |
经过分析,基于多智能体的绿波协调算法利用智能体之间的通信能力,将所需传递的有用信息传递给相邻智能体,经过智能体的推理计算,得到协调控制参数以及智能体的下一步执行策略[12]。
这里定义相邻智能体之间的发送信息交流表达式为
| $ {\rm{Send\_Info}} =\left\{t_{s}^{u}(i), t_{e}^{u}(i), t_{s}^{d}(i), t_{e}^{d}(i)\right\}, $ | (10) |
其中:tsu(i)为上行方向协调绿灯开始时刻;teu(i)为上行方向协调绿灯结束时刻。同理tsd(i)、ted(i)为下行方向协调绿灯的开始以及结束时刻[13-15]。
此外,定义相邻智能体之间接受信息交流表达式为
| $ {\rm{Receive\_Info}} =\left\{t_{s}^{u}(i-1), t_{e}^{u}(i-1), t_{s}^{d}(i+1), t_{e}^{d}(i+1)\right\} 。$ | (11) |
基于智能体周期、相位绿灯时间、以及信号选择策略的研究,多智能体的绿波协调算法如表 2所示:
| 表 2 绿波协调算法 Table 2 Green wave coordination algorithm |
结合单点自适应配时算法和基于多智能体的滤波协调算法,提出算法描述如下:
1) 获取各个路口不同方向的实时车流量。
2) 根据自适应控制配时算法得到各个路口的周期与各个相位的绿灯时间。
3) 基于多智能体信息互通的思想,不同路口将自己的周期与各相位绿灯时间发给相邻路口。
4) 判断各个路口之间的周期是否相同或成整数倍,若是,则可以进行滤波协调控制,各个路口智能体根据相邻路口的周期与协调相位绿灯时长,调整自己的协调相位绿灯时间;若不是,则不满足绿波协调的条件,各个路口智能体执行自己的配时方案即可。
5) 实时车流量数据的更新频率为5 min,所以,每个路口信号灯的配时方案执行次数:
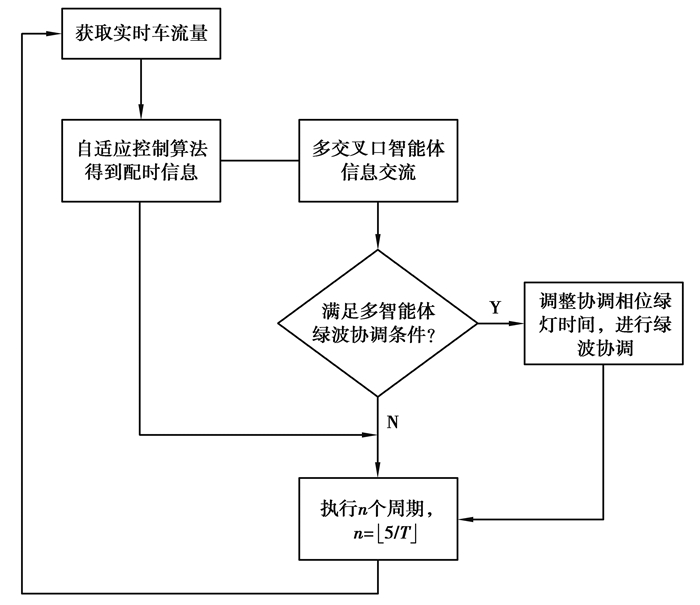
算法总的流程图如下图 3所示。
|
图 3 算法总流程图 Fig. 3 Algorithm folw chart |
以重庆市两路口环道为实验仿真对象,分别选取其5个交叉口在低峰、平峰、高峰3个时段下的车流量进行实验仿真,表 3为5个交叉口的各时段车流量分布。
| 表 3 各时段车流量分布 Table 3 Traffic flow distribution in different periods |
使用vissim交通仿真软件进行仿真,为体现出所提算法的有效性,分别在两路口环道原有配时、韦伯斯特定时配时以及所提配时算法3种情况下,进行对比实验,实验结果如图 4—图 9所示。
1) 低峰时段
|
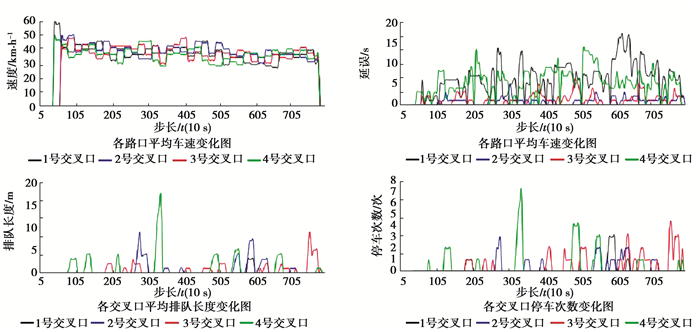
图 4 低峰时控制效果仿真曲线 Fig. 4 The simulation curve of low peak time control effect |
|
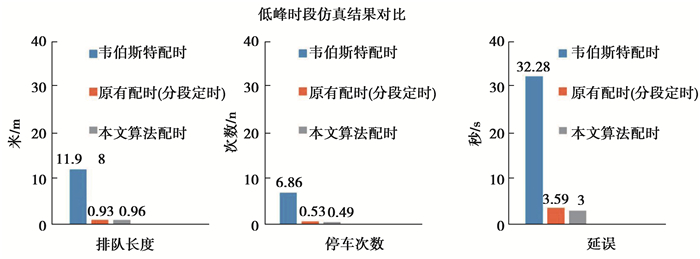
图 5 低峰时控制效果对比 Fig. 5 Comparison of low peak time control effect |
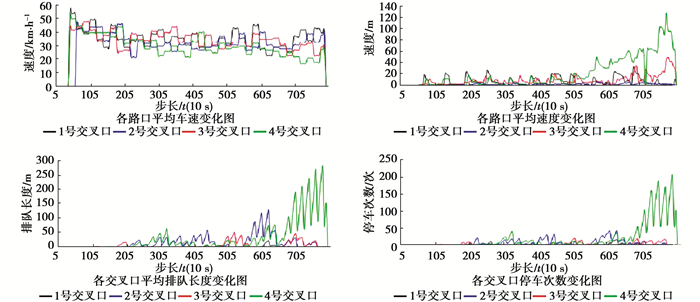
2) 平峰时段
|
图 6 平峰时控制效果仿真曲线 Fig. 6 The simulation vurve of mid peak time control effect |
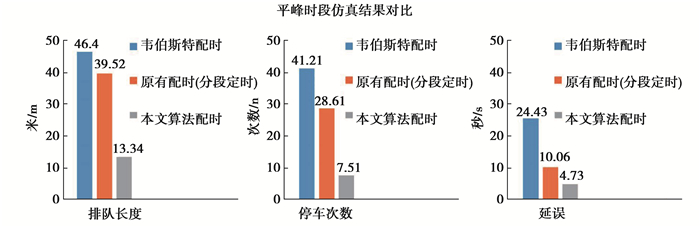
|
图 7 平峰时段控制效果对比 Fig. 7 Comparison of mid peak time control effect |
3) 高峰时段
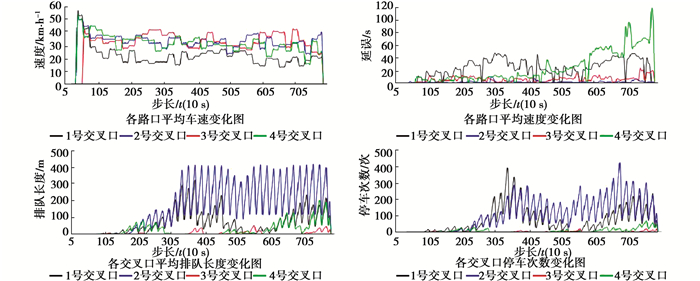
|
图 8 高峰时控制效果仿真曲线 Fig. 8 The simulation curve of high peak tim control effect |
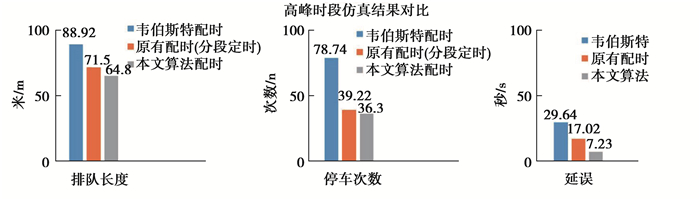
|
图 9 高峰时段控制效果对比 Fig. 9 Comparison of high peak time control effect |
由上面的实验仿真结果可以看到,在低车流量下,环道路网使用的自适应多智能体控制配时方案和原有的配时方案相比,两者的参数对比基本相差不大;在车流量不大的交通环境下,使用自适应多智能体控制配时方案相比原有的配时方案有着比价明显的优势,排队长度、停车次数、延误3项指标均有明显的降低;在车流量较大,环道交通处于近乎堵塞的情况下,使用自适应多智能体控制配时方案和原有的配时方案在排队长度和平均停车次数这2项指标表现上基本相差不大,因为此时的交通负载处于过载状态,但由于自适应多智能体控制算法是根据实时车流计算出的配时信息而且还考虑了相邻交叉口的绿波协调,因此在延误这项指标上,有着明显的减小。
3 结论本文以城市作为多智能体应用抽象模型,进行了城市环道交通信号控制模型构建与特性分析,提出了基于多智能体的城市环道多交叉口信号协同控制算法,实现了城市环道交通不同时段的最优控制,希望为城市环道交通信号提供参考。
| [1] |
左岩岩, 李金娜, 张雨. 现代城市交通问题与对策研究[J]. 长江丛刊, 2017(32): 136-136. Zuo Y Y, Li J N, Zhang Y. Research on modern urban traffic problems and countermeasures[J]. Journal of Yangtze River, 2017(32): 136-136. (in Chinese) |
| [2] |
何延玲. 大城市环状道路的成因与功能分析[J]. 公路交通技术, 2003, 19(5): 1-3. He Y L. Analysis of causes and functions of circular road in big cities[J]. Technology of Highway and Transport, 2003, 19(5): 1-3. (in Chinese) DOI:10.3969/j.issn.1009-6477.2003.05.001 |
| [3] |
刘金琨, 尔联洁. 多智能体技术应用综述[J]. 控制与决策, 2001, 16(2): 133-140. Liu J X, Er L J. Review of the application of multi-agent technology[J]. Control and Decision, 2001, 16(2): 133-140. (in Chinese) |
| [4] |
Salkham A, Cunningh R, Garg A, et al. A collaborative reinforcement learning approach to urban traffic control optimization[C]//2008 IEEE/WIC/ACM International Conference on Web Intelligence and Intelligent Agent Technology, December 9-12, 2008. Sydney, Australia. IEEE, 2008: 560-566.
|
| [5] |
杨文臣, 张轮, 施弈骋, 等. 智能体技术在城市交通信号控制系统中应用综述[J]. 武汉理工大学学报:交通科学与工程版, 2014(4): 709-718. Yang W C, Zhang L, Shi Y Z, et al. Overview of application of agent technology in urban traffic signal control system[J]. Journal of Wuhan University of Technology:Transportation Science and Engineering, 2014(4): 709-718. (in Chinese) DOI:10.3963/j.issn.2095-3844.2014.04.003 |
| [6] |
李杨, 徐峰, 谢光强, 等. 多智能体技术发展及其应用综述[J]. 计算机工程与应用, 2018(9). Li Y, Xu F, Xie G Q, et al. Overview of the development and application of multi-agent technology[J]. Computer Engineering and Applications, 2018(9). (in Chinese) |
| [7] |
Töröj J, KertéSz J. The green wave model of two-dimensional traffic:transitions in the flow properties and in the geometry of the traffic jam[J]. Physica A:Statistical Mechanics and Its Applications, 1996, 231(4): 515-533. DOI:10.1016/0378-4371(96)00144-6 |
| [8] |
Corman F, D'Ariano A, Pacciarelli D, et al. Evaluation of green wave policy in real-time railway traffic management[J]. Transportation Research Part C:Emerging Technologies, 2009, 17(6): 607-616. |
| [9] |
Shen G J. Urban traffic trunk two-direction green waveintelligent control strategy and its application[C]//Proceedings of the 6th World Congress on IntelligentControl and Automation, Dalian: Dalian University of Technology, 2006: 8563-8567.
|
| [10] |
马亚锋, 刘澜. 干线局部拥堵的绿波带与红波带协调控制策略[J]. 城市交通, 2017(01): 70-75+101. Ma Y F, Liu L. Coordinated control strategy of green wave band and red wave band in local congestion of main line[J]. Urban Transport, 2017(01): 70-75+101. (in Chinese) |
| [11] |
鄢小文, 徐建闽, 荆彬彬. 不同周期信号交叉口间的相位差优化模型[J]. 华南理工大学学报(自然科学版), 2017(6). Yan X W, Xu J B, Jing B B. Optimization model of phase difference between different periodic signal intersections[J]. Journal of South China University of Technology(Natural Science Edition), 2017(6). (in Chinese) |
| [12] |
卢凯, 徐建闽, 李林. 过饱和交通状态下的停车延误协调控制模型[J]. 控制理论与应用, 2010, 27(12): 1623-1630. Lu K, Xu J Z, Li L. Coordination control model of parking delay under supersaturated traffic conditions[J]. Control Theory and Applications, 2010, 27(12): 1623-1630. (in Chinese) |
| [13] |
Yang Z Y, Ding Z Y. Actuated green wave control for grid-like network traffic signal coordination[C]//2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), October 9-12, 2016. Budapest, Hungary. IEEE, 2016: 953-958.
|
| [14] |
王玉鹏. 基于VISSIM的感应信号控制交通仿真研究[J]. 交通与运输, 2009(1): 43-46. Wang Y P. Research on traffic simulation of inductive signal control based on VISSIM[J]. Journal of Transportation and Transportation, 2009(1): 43-46. (in Chinese) |
| [15] |
刘宜恩, 刘易家, 尹世德, 等. 基于Vissim的交叉口信号优化配时仿真评价[J]. 自动化与仪表, 2018, 33(4): 1-4. Liu Y E, Liu Y J, Yin S D, et al. Estimation of timing simulation of intersection signals based on vissim[J]. Journal of Automation & Instrumentation, 2018, 33(4): 1-4. (in Chinese) |
| [16] |
Sun D Z. Using micro-simulation vissim to study the effectiveness of left-turn waiting area implementation[C]//Applied Mechanics and Materials.[s.L.]: Troms Teah Publications Ltd, 2018: 187-191.
|
 2021, Vol. 44
2021, Vol. 44

