随着互联网时代的来临,网络资源数量呈爆炸式增长,个性化推荐系统建立在大量用户数据的基础上,能够为每位用户推荐出最感兴趣或者最需要的信息。近年来,个性化推荐算法已经成为学术界的研究热点之一。推荐系统中应用最广泛的是协同过滤推荐算法(CF, Collaborative Filtering),其概念最早由1992年Goldberg等[1]在开发Tapestry邮件过滤系统时首次提出,其核心思想是通过算法对用户的历史行为数据进行分析,并挖掘出用户的兴趣偏好,根据不同的兴趣偏好对用户进行类别划分并推荐偏好相似的物品。目前,在推荐算法中还存在数据稀疏性、可扩展性、冷启动等问题。数据的稀疏性是造成推荐系统精确度不高的主要原因之一。广泛应用的推荐系统中,用户项目(user-item)评分矩阵提供了反映用户对项目喜好程度的重要信息。当项目数量巨大时,评分矩阵往往具有高度的稀疏性,缺失率甚至会达到90%以上。极度稀疏的用户评分矩阵会使得利用经典的协同过滤算法计算的相似性精度不高,无法准确找出目标用户的最近邻居。为解决评分矩阵的稀疏性问题,常用的方法有两类,一类是基于预测项目评分的协同过滤算法,例如,韩亚楠等[3]和Liji等[4]分别利用用户属性偏好和用户的属性来对评分矩阵进行填充。另一类解决稀疏性的方法是利用奇异值分解(SVD, Singular Value Decomposition)对评分矩阵进行降维[5-7]。但在维数很高的情形中,降维将会导致信息损失,影响模型预测效果。Bokde等[8-9]指出将多种传统推荐算法相结合可以有效提高推荐精确度。当用户与项目数量巨大时,计算量较大,推荐算法很难在短时间内作出响应。在推荐算法中融合聚类方法可以有效提高推荐系统的响应速度[9-11]。
除了上述基于协同过滤算法建立的个性化推荐系统,也有很多基于机器学习方法建立的推荐系统,例如,胡思才等[12]建立了基于深度神经网络和概率矩阵分解的混合推荐算法;Wei等[13]结合协同过滤与深度学习方法解决冷启动问题。Wang等[14]提出的树增强嵌入方法并结合树模型和嵌入模型的优点,使得推荐模型同时具有可泛化性和可解释性。Chen[15]提出了XGBoost (eXtreme Gradient Boosting)算法,它是一种集成树模型,能在梯度提升(Gradient Boosting)框架下实现大规模集成学习,其特点是计算高效,能够解决实际问题。分析结果显示,XGBoost算法有助于提升推荐问题中的精确度[17-18]。这归功于XGBoost算法能从大规模数据集中学习到数据之间复杂的相关性。
为了解决评分矩阵的稀疏性问题,提高推荐精确度,文中提出基于矩阵分解与XGBoost集成学习方法构建的个性化推荐算法MFXGB(Matrix Factorization XGBoost algorithm)。该推荐算法实质为一个监督模型,可以充分利用用户项目评分矩阵中的信息和用户及项目自身的特征,利用聚类方法降低计算时间,并且能够有效提高推荐的准确度。
1 融合矩阵分解与XGBoost的推荐算法 1.1 填充评分矩阵(SVD++算法)MFXGB推荐算法可分为3个阶段,第一阶段就是采用矩阵分解的方法来填充用户项目评分矩阵。假设用户项目评分矩阵R=(rui)n×m,它包含了n个用户对m个项目的评分,其中,元素rui表示用户u对项目i的评分。经典的矩阵分解方法为SVD算法[18],是将含有缺失值的用户项目评分矩阵R,用
| $ {\hat r_{ui}} = \mu + {b_i} + {b_u} + \mathit{\boldsymbol{q}}_i^{\rm{T}}{\kern 1pt} {\mathit{\boldsymbol{p}}_u}, $ | (1) |
其中:μ为基准评分;bi为项目i的个体偏差;bu为用户u的个体偏差。
SVD++算法[18]在SVD算法的基础上进一步引入了用户对有过评分行为的项目的“隐式反馈”信息。假设用户u对项目i有评分,代表该用户u对项目i有偏好,在式(1)中进一步增加用户u的已有偏好信息。定义
| $ {\hat r_{ui}} = \mu + {b_i} + {b_u} + \mathit{\boldsymbol{q}}_i^{\rm{T}}\left( {{\mathit{\boldsymbol{p}}_u} + \frac{1}{{\sqrt {|N(u)} |}}\sum\limits_{j \in N(u)} {{\mathit{\boldsymbol{x}}_j}} } \right), $ | (2) |
其中:N(u)表示用户u评价过的项目集合;|N(u)|表示用户u给出评价的项目数。式(2)相较于式(1)增加了已有评分的所有隐含信息项
| $ \begin{array}{l} \mathop {\min }\limits_{{b_i},{b_u},{\mathit{\boldsymbol{q}}_i},{\mathit{\boldsymbol{p}}_u},{x_j}} \sum\limits_{{r_{ui}} \in \mathit{\boldsymbol{R}}} {{{\left( {{r_{ui}} - \mu - {b_i} - {b_u} - \mathit{\boldsymbol{q}}_i^{\rm{T}}\left( {{\mathit{\boldsymbol{p}}_u} + \frac{1}{{\sqrt {\mid N(u)\mid } }}\sum\limits_{j \in N(u)} {{\mathit{\boldsymbol{x}}_j}} } \right)} \right)}^2}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \lambda \left\{ {\sum\limits_u {\left( {b_u^2 + {{\left\| {{\mathit{\boldsymbol{p}}_u}} \right\|}^2}} \right)} + \sum\limits_i {\left( {b_i^2 + {{\left\| {{\mathit{\boldsymbol{q}}_i}} \right\|}^2}} \right)} } \right\}。\end{array} $ | (3) |
MFXGB推荐算法采用SVD++算法填充用户项目评分矩阵,将最优化式(3)得到的特征矩阵估计
MFXGB算法的第二阶段就是利用聚类算法构造用户和项目的特征。第一阶段已经利用矩阵分解的方法得到了填充完整的用户评分矩阵,即预测得到了用户项目的“评分”特征,可以用作模型的自变量。但在实际应用中,用户和项目的个数都可能巨大,将其作为自变量直接利用XGBoost算法进行训练的计算成本过高,对处理大数据时产生的计算量巨大的问题尤为突出。为此,采用聚类方法将用户和项目按相似度分门别类,再计算每个用户和项目的“类别”特征,以节约计算时间。
具体来说,用户评分矩阵的行向量代表用户的评分向量。基于n个用户的评分向量,将这n个用户分成K1个类别,每个类别代表用户的评分偏好属性。例如,有些用户比较挑剔,总是给予很低的评分,可以将其归入一个类别;有些用户总是给予较高的评分,则将其归入另一个类别。文中采用K-均值方法进行聚类,类别数K1可根据实际问题自行设定。特别地,若K1=n,则代表不对用户进行聚类,以每个用户的评分向量作为其“评分”特征。同理,将m个项目分成K2个类别,每个类别代表项目的类别评分属性。例如,有些小众的文艺电影总是评分不高,而有些动作大片受到很多人的关注和欢迎,可以分别将它们归入不同的类别。同理,若K2=m,则代表不对项目进行聚类。
进行聚类后,可分别计算得到每类用户和项目的中心向量,再通过计算每个用户的评分向量与K1类用户的中心向量之间的相似度,这就是用户的“评分”特征。这里采用Pearson相关系数来计算评分向量与中心向量之间的相似度。相似度越高,表明该用户与某个类别用户的评分偏好越相似。例如,将用户聚为三类,计算得到用户1的评分向量与三类的中心向量的相似度分别为0.7、0.5和0.4,这表明用户1和第一类用户的评分偏好最为相似。将(0.7, 0.5, 0.4)这个向量作为用户1的“评分”特征,在下一步中放入XGBoost模型进行训练。同理,可以计算得到每个项目的评分向量与K2类项目的中心向量之间的相似度,作为项目的“评分”特征。
除此之外,每个用户和每个项目还有其自身的特征,例如,基于电影的数据集中,用户的年龄、性别、职业、电影的类别等。假设共有K3个这样的特征,称为基础特征。那么,将K1个用户“评分”特征、K2个项目“评分”特征和K3个用户与项目的基础特征结合在一起,构成(nm)×(K1+K2+K3)维的特征矩阵,用于训练预测模型。
1.3 建立XGBoost预测模型MFXGB算法的第三阶段就是利用XGBoost算法训练推荐模型。XGBoost算法[15]利用集成树模型预测响应变量,并用梯度提升树算法优化求解。假设数据集中有n个样本,p个特征,记为
| $ {\hat y_i} = \sum\limits_{m = 1}^M {{f_m}} ({\mathit{\boldsymbol{X}}_i}), $ | (4) |
其中,fm为第m棵回归树的函数表达式。常用的回归树为加法形式,即
| $ L = \sum\limits_i l \left( {{{\hat y}_i},{y_i}} \right) + \sum\limits_k \varOmega \left( {{f_k}} \right), $ | (5) |
其中,l(·, ·)为损失函数,
| $ {L^{(t)}} = \sum\limits_{i = 1}^n l \left( {{y_i},\hat y_i^{(t - 1)} + {f_t}\left( {{\mathit{\boldsymbol{X}}_i}} \right)} \right) + \varOmega \left( {{f_t}} \right)。$ | (6) |
将上述目标函数在
| $ L(t) \cong \sum\limits_{i = 1}^n {\left[ {{g_i}{f_t}\left( {{\mathit{\boldsymbol{X}}_i}} \right) + \frac{1}{2}{h_i}f_t^2\left( {{\mathit{\boldsymbol{X}}_i}} \right)} \right]} + \varOmega \left( {{f_t}} \right), $ | (7) |
其中,gi和hi分别为损失函数在
| $ \omega _j^* = - \frac{{\sum\limits_{i \in {I_j}} {{g_i}} }}{{\sum\limits_{i \in {I_j}} {{h_i}} + \lambda }},{\rm{ }}{\tilde L^{(t)}}(q) = - \frac{1}{2}\sum\limits_{j = 1}^T {\frac{{{{\left( {\sum\limits_{i \in {I_j}} {{g_i}} } \right)}^2}}}{{\sum\limits_{i \in {I_j}} {{h_i}} + \lambda }}} + \gamma T。$ | (8) |
然后采用贪婪算法(Exact Greedy Algorithm)寻找最优的q(·),使得
MFXGB算法第三阶段将第二阶段中构建的特征矩阵中用户和项目特征作为自变量
基于矩阵分解的XGBoost个性化推荐算法(MFXGB)主要包括以下3个步骤,其算法步骤如图 1所示。

|
图 1 MFXGB算法步骤结构图 Fig. 1 The flowcharts of the MFXGB algorithm |
步骤1.使用SVD++的矩阵分解方法填充用户项目评分矩阵中缺失的元素;
步骤2.利用填充完整的矩阵通过聚类算法构造用户和项目的特征,即分别将用户和项目进行聚类,计算每个用户和项目的“类别”特征,再加入用户和项目的基础信息,最终将数据集处理成一个适用于有监督训练的数据集。
步骤3.使用XGBoost算法对目标项目进行评分预测,根据预测结果生成推荐列表。
2 实验结果与分析 2.1 数据来源与数据描述实验采用Minnesota大学GroupLens研究小组提供的MovieLens实验数据集(http://grouplens.org/datasets/movielens/),其中包括2组不同规模的数据集,如表 1所示。数据集的记录格式为用户ID、项目ID、评分值、评分时间,其中每个用户至少对15部电影进行评分,评分范围为1~5的正整数,值越高表示用户对该电影的喜爱程度越高。
| 表 1 MovieLens数据集描述 Table 1 Data description of the MovieLens datasets |
除了用户评分数据集外,还有用户和电影的信息记录维表。在用户信息维表中,记录了每个用户的年龄、性别、职业与邮政编码等信息。在电影信息维表中,记录了电影的名称、发布时间、链接以及所属的类别等信息,原数据集中将所有电影共分为19个类别,每一部电影可能会属于几个不同的类别。
实验环境配置如下:PC Inter(R)Core(TM)i5-8300H CPU @2.30GHz64位操作系统,虚拟内存24 G,编程语言:python3.7。
2.2 评价指标为了衡量算法的预测准确度,采用平均绝对误差(MAE, mean absolute error)和均方根误差(RMSE, root mean square error)对算法进行评价,其定义如下:
| $ {\rm{MAE}} = \frac{1}{m}\sum\limits_{i = 1}^m {\left| {{{\hat y}_i} - {y_i}} \right|} $ |
| $ {\rm{RMSE}} = \frac{1}{m}\sqrt {\sum\limits_{i = 1}^m {{{\left( {{{\hat y}_i} - {y_i}} \right)}^2}} } $ |
其中,
为了避免偶然性对实验结果的影响,文中利用五折交叉验证的方法对推荐算法的效果进行评估,即将原始数据集等分为5个子集,每次选择其中的4个子集作为训练集,剩下的1个子集作为测试集。最终将5次实验中得到的预测误差取平均值,来衡量算法的推荐精确度。将文中MFXGB推荐算法的结果与传统的协同过滤推荐算法进行对比。
2.3 结果分析 2.3.1 算法的效果展示将MFXGB算法与矩阵分解(SVD++)推荐算法、基于项目的协同过滤推荐算法(Item-CF)和基于用户的协同过滤推荐算法(User-CF)进行比较,以验证MFXGB算法的有效性。取聚类数为60,在MFXGB算法中取K1=K2=60,基于数据集MovieLens_100k计算得到的实验结果,如图 2所示。
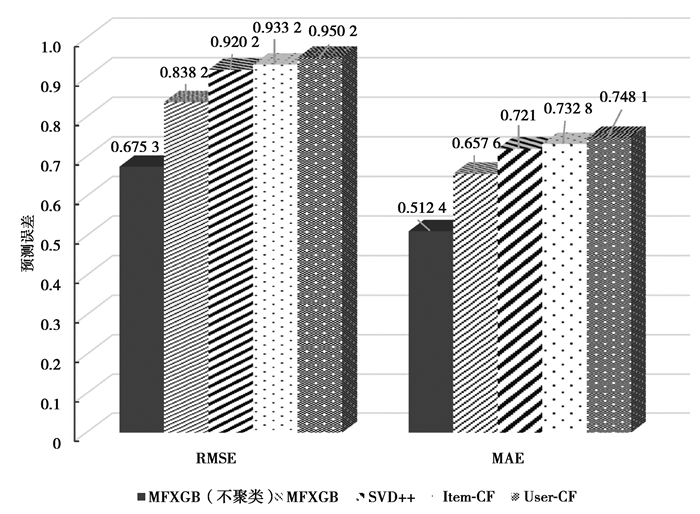
|
注:MFXGB、Item-CF和User-CF算法都取聚类数为60。 图 2 基于MovieLens_100k数据集的各算法结果对比图 Fig. 2 RMSE and MAE comparison of MFXGB algorithm, SVD++ algorithm, Item-based CF algorithm and User-based CF algorithm using the MovieLens_100 k dataset |
可以看出,MFXGB推荐算法的RMSE和MAE明显小于传统的协同过滤推荐算法和矩阵分解算法。特别地,不进行聚类的MFXGB模型的预测效果最好,RMSE比SVD++算法提升了26.61%,比Item-CF和User-CF算法分别提升了27.64%和28.93%,MAE相比于SVD++算法、Item-CF和User-CF算法分别提升了28.93%、30.08%和31.51%。当聚类数K1=K2=60时,MFXGB算法的RMSE比SVD++、和Item-CF和User-CF算法分别提升了8.91%、10.18%和11.79%,MAE分别提升了8.79%、10.26%和12.10%,推荐精确度也有明显提高。但是,不进行聚类的MFXGB算法计算成本非常高,它的计算时间是MFXGB算法(K1=K2=60)的14.96倍。可见利用聚类方法构造特征将有效提升计算速度。
为了避免小数据集带来的偶然性,采用数据量更大的MovieLens_1M数据集验证算法的普适性,仍取聚类数为60,实验结果如图 3所示。不聚类的MFXGB算法计算量较大,计算时间将超过30 h,因此未记录不聚类的MFXGB算法结果。同样可以看出,针对MovieLens_1M数据集,MFXGB推荐算法的精确度都明显好于其他3种算法。
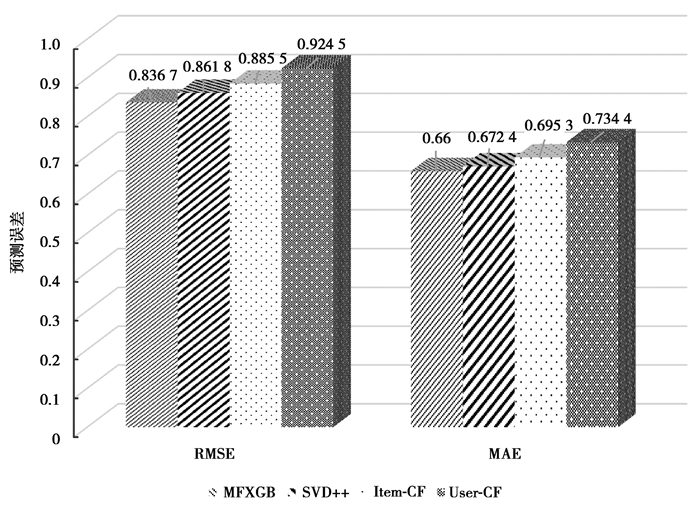
|
注: MFXGB、Item-CF和User-CF算法都取聚类数为60。 图 3 基于MovieLens_1M数据集的各算法结果对比图 Fig. 3 RMSE and MAE comparison of MFXGB algorithm, SVD++ algorithm, Item-based CF algorithm and User-based CF algorithm using the MovieLens_1M dataset |
MFXGB算法的稳健性主要从聚类数、矩阵填充和加入用户与项目的基础特征这3个方面进行分析,实验结果均基于MovieLens_100k数据集。
1) 聚类数对计算时间和推荐算法效果的影响。
选取聚类数K1=K2分别为10、20、30、40、50、60、70、80、90、100、200,K1=n, K2=m(不聚类),将MFXGB算法的预测误差和计算时间绘制成折线图,如图 4所示。可见随聚类数量的增加,算法的RMSE和MAE均呈下降趋势;当不进行聚类时,算法预测精度明显提升,但计算时间成本较高。因此,在实际应用中,应兼顾计算时间成本与预测效果来选择聚类数。
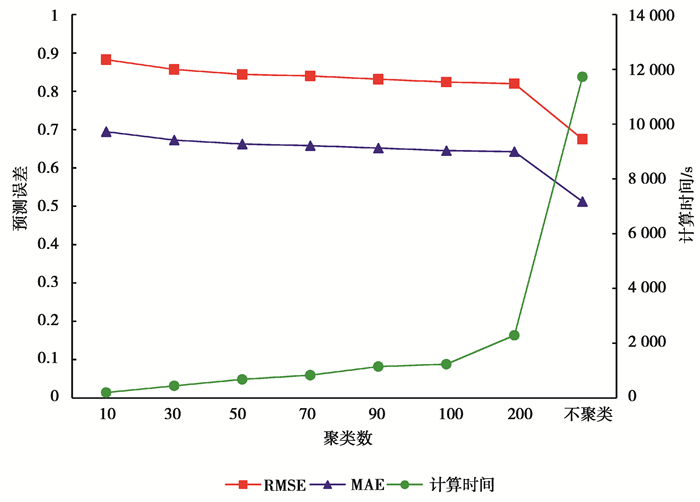
|
注:RMSE和MAE对应左侧的主纵坐标轴,计算时间对应右侧的次纵坐标轴。 图 4 MFXGB模型的预测误差和训练时间与聚类数的折线图 Fig. 4 RMSE and MAE and computation time comparison of different clustering numbers in the MFXGB algorithm |
2) 矩阵填充对算法效果的影响。
MFXGB推荐算法的特点之一就是事先对用户评分矩阵进行填充。将MFXGB算法与未进行缺失值填充的XGBoost算法进行效果对比,实验结果如图 5所示。使用未填充用户评分矩阵的XGBoost算法时,先将评分矩阵中的缺失值填充为零,再进行聚类。可以看出,随聚类数量k的增加,填充矩阵对模型的效果提升显著。当取聚类数为60时,MFXGB算法比XGBoost算法的RMSE和MAE均减小了4.5%,结果表明,矩阵分解对用户评分矩阵进行填充,能够提高算法的精确度。
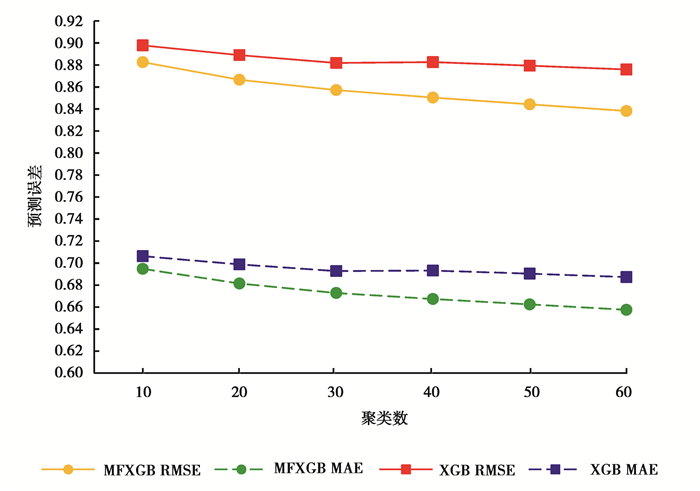
|
图 5 MFXGB算法与XGBoost算法的预测误差RMSE和MAE对比图 Fig. 5 RMSE and MAE comparison between the MFXGB algorithm and the XGBoost algorithm |
3) 加入用户和项目的基础特征对模型的影响。
MFXGB推荐算法的另一大特点是建立了基于XGBoost算法的有监督模型,在聚类后产生的用户和项目特征基础上再加入年龄、性别、职业作为用户的基础特征,加入电影类型作为项目的基础特征。
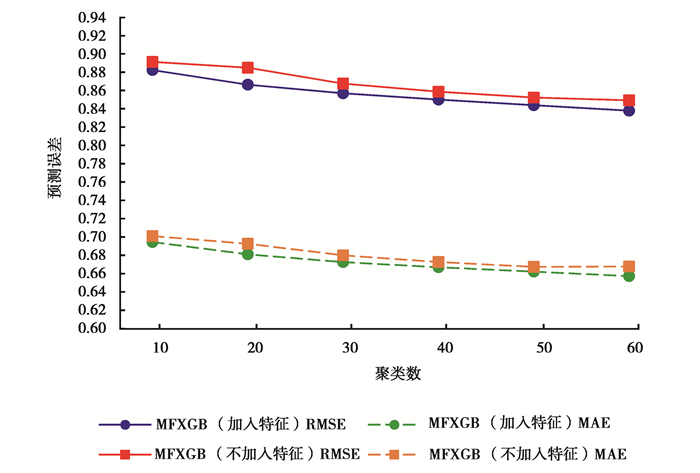
图 6绘制了MFXGB算法加入基础特征与不含加入基础特征的预测误差RMSE和MAE并随聚类数变化的折线图。实验结果表明,加入用户和项目基础特征对算法有一定的提升效果。无论聚类数为多少,加入用户和项目的基础特征的MFXGB算法的预测误差始终小于不加入基础特征的算法。进一步说明增加基础信息会提升推荐精确度。
|
图 6 加入基础特征的MFXGB模型与不加入基础特征的MFXGB模型的预测误差的对比图 Fig. 6 RMSE and MAE comparison between the MFXGB algorithm with user and item's attributes and the MFXGB algorithm without user and item's attributes |
运用MFXGB算法训练的模型,生成所选取的用户的推荐列表。表 2展示了2个用户的Top10推荐列表。
| 表 2 基于MFXGB推荐算法产生的用户1和2的推荐列表 Table 2 The recommendation lists generated by the MFXGB algorithm for users 1 and 2 |
以用户1为例,在Top10的推荐列表中,有6部电影都有用户1的5分评分,表明该用户非常喜爱这6部电影。考虑到只挑选了预测评分排名前10的电影进行推荐,而这些电影的推荐评分大多都在4.5分以上,基于数据集MovieLens_100k,计算所有用户产生的Top10推荐列表中,用户评价为5分的电影数量占MFXGB算法推荐的10部电影的平均比例为28.57%。说明MFXGB算法对用户评价为5分的电影的推荐精确率(precision)达到28.57%。考虑到各个用户评为5分的电影数量可能各不相同,针对这一情况,计算Top10推荐列表对用户评为5分电影的召回率,即Top10列表中所推荐的电影中用户真实评价为5分的电影所占比例。基于数据集MovieLens_100k,计算得到用户评价为5分的电影召回率为19.18%。除此之外,在Top10推荐列表中,推荐给用户的未评分电影平均数为6.63,表明MFXGB算法能推荐大约6部给用户未看过但可能感兴趣的电影,可以为商家带来盈利。
3 结论随着网络资源数量的快速增加,传统推荐算法受限于高度稀疏的用户项目的评分矩阵,推荐效果不佳。针对评分矩阵高度稀疏性问题,文中提出的融合矩阵分解和XGBoost的推荐算法MFXGB,能够有效解决用户项目评分矩阵的稀疏性问题并提升推荐精确度。MFXGB算法具有三大特点:一是事先对用户项目评分矩阵进行填充,避免过多的缺失值对模型预测结果产生影响;二是对用户和项目进行K-均值聚类,对用户和项目进行特征提取,克服计算成本过高的困难;三是利用XGBoost算法训练一个有监督模型用于预测用户评分,该模型还允许加入用户和电影的自身属性作为自变量,使信息量更加丰富,有利于提升模型预测效果。实证结果表明,MFXGB的推荐效果明显优于传统的推荐算法。MFXGB算法可以广泛应用于各个领域,如旅游景点、商品、音乐、新闻、图书等推荐问题中,帮助消费者找到自己感兴趣的东西,同时也能够为商家创造不菲的收益。
| [1] |
Goldberg D, Nichols D, Oki B M, et al. Using collaborative filtering to weave an information tapestry[J]. Communications of the ACM, 1992, 35(12): 61-70. DOI:10.1145/138859.138867 |
| [2] |
Desrosiers C, Karypis G. A comprehensive survey of neighborhood-based recommendation methods[M]//Ricci F, Rokach L, Shapira B, Kantor P B. Recommender Systems Handbook. New York: Springer, 2011: 107-144.
|
| [3] |
韩亚楠, 曹菡, 刘亮亮. 基于评分矩阵填充与用户兴趣的协同过滤推荐算法[J]. 计算机工程, 2016, 42(01): 36-40. Han Y N, Cao H, Liu L L. Collaborative filtering recommendation algorithm based on score matrix filling and user interest[J]. Computer Engineering, 2016, 42(01): 36-40. (in Chinese) DOI:10.3969/j.issn.1000-3428.2016.01.007 |
| [4] |
Li J U, Chai Y H, Chen J R. Improved personalized recommendation based on user attributes clustering and score matrix filling[J]. Computer Standards & Interfaces, 2017, 57: 59-67. |
| [5] |
Guan X, Li C T, Guan Y. Matrix factorization with rating completion:an enhanced SVD model for collaborative filtering recommender systems[J]. IEEE Access, 2017, 5: 27668-27678. DOI:10.1109/ACCESS.2017.2772226 |
| [6] |
王娟, 熊巍. 基于矩阵分解的最近邻推荐系统及其应用[J]. 统计与决策, 2019(6): 17-20. Wang J, Xiong W. Collaborative filtering recommender system based on matrix factorization and its application[J]. Statistics & Decision, 2019(6): 17-20. (in Chinese) |
| [7] |
石鸿瑗, 孙天昊, 李双庆, 等. 融合时间和类型特征加权的矩阵分解推荐算法[J]. 重庆大学学报, 2019, 42(1): 79-87. Shi H Y, Sun T H, Li S Q, et al. A matrix factorization recommendation algorithm with time and type weight[J]. Journal of Chongqing University, 2019, 42(1): 79-87. (in Chinese) |
| [8] |
Bokde D, Girase S, Mukhopadhyay D. Matrix factorization model in collaborative filtering algorithms:a survey[J]. Procedia Computer Science, 2015, 49(1): 136-146. |
| [9] |
Wu Y, Liu X, Xie M, et al. CCCF: Improving collaborative filtering via scalable user-item co-clustering[C]//WSDM'16: Proceedings of the Ninth ACM International Conference on Web Search and Data Mining. New York: ACM Press, 2016: 73-82.
|
| [10] |
Liao C L, Lee S J. A clustering based approach to improving the efficiency of collaborative filtering recommendation[J]. Electronic Commerce Research and Applications, 2016, 18: 1-9. DOI:10.1016/j.elerap.2016.05.001 |
| [11] |
Najafabadi M K, Mahrin M N, Chuprat S, et al. Improving the accuracy of collaborative filtering recommendations using clustering and association rules mining on implicit data[J]. Computers in Human Behavior, 2017, 67: 113-128. DOI:10.1016/j.chb.2016.11.010 |
| [12] |
胡思才, 孙界平, 琚生根, 等. 基于深度神经网络和概率矩阵分解的混合推荐算法[J]. 四川大学学报(自然科学版), 2019, 56(6): 1033-1041. Hu S C, Sun J P, Ju S G, et al. Hybrid recommendation algorithm based on deep neural network and probabilistic matrix factorization[J]. Journal of Sichuan University(Natural Science Edition), 2019, 56(6): 1033-1041. (in Chinese) DOI:10.3969/j.issn.0490-6756.2019.06.008 |
| [13] |
Wei J, He J H, Chen K, et al. Collaborative filtering and deep learning based recommendation system for cold start items[J]. Expert Systems With Applications, 2017, 69: 29-39. DOI:10.1016/j.eswa.2016.09.040 |
| [14] |
Wang X, He X, Feng F, et al. TEM: Tree-enhanced embedding model for explainable recommendation[C]//WWW'18: Proceedings of the 2018 World Wide Web Conference. 2018: 1543-1552.
|
| [15] |
Chen T Q, Guestrin C. XGBoost: A scalable tree boosting system[C]//Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco California USA. New York, NY, USA: ACM, 2016: 785-794.
|
| [16] |
张昊, 纪宏超, 张红宇. XGBoost算法在电子商务商品推荐中的应用[J]. 物联网技术, 2017(2): 102-104. Zhang H, Ji H C, Zhang H Y. Application of the XGBoost algorithm in the e-commerce recommendation system[J]. Internet of Things Technologies, 2017(2): 102-104. (in Chinese) |
| [17] |
齐德法, 徐连诚, 朱振方. 融合协同过滤的XGBoost推荐算法[J]. 计算机应用研究, 2020, 37(5): 1317-1320. Qi D F, Xu L C, Zhu Z F. XGBoost recommendation algorithm with collaborative filtering[J]. Application Research of Computers, 2020, 37(5): 1317-1320. (in Chinese) |
| [18] |
Koren Y, Bell R. Advances in collaborative filtering[M]//Ricci F, Rokach L, Shapira B, Kantor P B. Recommender Systems Handbook. New York: Springer, 2011: 145-186
|
 2021, Vol. 44
2021, Vol. 44

