Web服务是一种平台独立、低耦合、可编程的Web应用程序，具有良好的互操作性，广泛用于开发大规模的分布式应用程序。随着信息技术的迅猛发展，特别是云计算等新型服务计算的兴起，软件应用、计算能力、数据等许多资源都被打包成服务，Web服务的数量呈指数级增长，大量功能相同或相似的Web服务不断涌现^[1]。用户因为缺乏相应的专业知识而无法作出选择，及时准确地为用户发现和选择高质量的服务成为服务计算领域亟待解决的问题^[2]。

个性化推荐技术作为缓解信息过量产生和有效信息发现不平衡的有效方法之一^[3]，被引入到Web服务领域，可以及时高效地为用户提供满足需求的Web服务，提高用户的满意度^[4]。个性化服务推荐技术的一个重要问题是如何获得Web服务的质量(Quality of Service，QoS)。QoS作为描述Web服务的主要非功能性特征，包括Web服务的响应时间、吞吐量、价格和可靠性等^[5]。精确的QoS可以有效地提高Web服务推荐的性能^[6]。尽管用户可以通过亲自调用Web服务来评估QoS，但是要在短时间对大量候选服务的QoS进行准确评估是不太可能的^[7]。与此同时，网络环境的不确定性以及恶意的用户反馈可能导致用户调用Web服务时的QoS是虚假的，包含噪声的^[8]。实际应用中，用户对Web服务的QoS矩阵通常是稀疏的，包含噪声的，对Web服务推荐影响较大。由于Web服务的QoS属性受到用户和Web服务所在的位置、访问时间以及网络环境等因素的影响，当前的研究多在已有的基于用户或服务协同过滤推荐^{[5, 9-10]}的基础上，利用时间和位置的特征^{[2, 11-14]}，对QoS的预测结果进行优化，以更好地进行协同过滤推荐。

笔者在上述工作的基础上，总结Web服务的时空特征为：短时间内，相似用户通常具有相似的网络环境和网络性能，进而有较大可能在相同的Web服务上观察到相似的性能。因此，得出用户服务的QoS矩阵具有结构相似性。

1) 全局结构相似性。考虑到用户的网络行为在短时间(如s、min、h)内通常变化不明显(在2 h内用户一直使用视频类软件看电影)，即存在用户在较短时间内使用相同的或者类似的Web服务的现象，相邻两个时间段(s、min、h)内的用户服务QoS矩阵的全局结构是相似的^[14]。这种全局结构相似性是时间相似性的一种体现。

2) 局部结构相似性。相邻用户通常处于同一自治系统，或者处于相邻自治系统内，其在相邻时间段内具有相同或相似网络环境的可能性较大，有可能对相同服务的QoS反馈是相似的^[15]。QoS矩阵在相邻用户上具有局部的结构相似性，这种局部结构相似性本质上反映了用户位置的相似性。

文中将上述特征融入到对QoS的预测上，提出了基于全局和局部结构相似性的稀疏矩阵分解模型(Global and Local Structure Similarity based Sparse Matrix Factorization Machine, GLMF)，以达到提升QoS预测精度的目标。①将QoS矩阵的时空特征与矩阵分解相结合，提出了一种基于全局和局部结构相似性的稀疏矩阵分解模型。在矩阵分解时，通过保留其与前一时刻QoS值的全局相似性信息，以及当前时刻用户的局部相似性信息，可以显著提高QoS的预测性能。②使用真实的Web服务QoS数据集对提出的方法进行了实验评估。结果验证了所提方法具有较高的预测性能，表明了该方法可以很好地处理数据稀疏和噪声的问题。

基于协同过滤方法的Web服务推荐得到广泛的研究和应用，并取得较好的效果。协同过滤推荐技术主要分为基于记忆的协同过滤推荐^[16]、基于模型的协同过滤推荐。基于记忆的方法又可分为基于用户的^[17]和基于物品的^[18]两种方法。基于记忆的协同过滤推荐需要根据历史数据得到相似用户或服务，基于相似用户或服务，实现对Web服务的QoS值的预测。基于模型的方法^[19]通过历史数据的学习，建立一个全局模型，确定用户物品间的隐含关系，实现对QoS值的预测。Zheng等^[20]将基于用户和基于物品的方法进行混合，实现Web服务的可靠性预测。Wang等^[10]基于用户相似性和基站相似度实现移动网络环境下Web服务的个性化推荐，并在此基础上对QoS值进行预测。卢凤等^[9]基于用户和服务的时空相似性特征，对相似性计算方法进行了改进，构建了Web服务推荐系统的框架，提高了对QoS协同预测的精确度。王磊等^[5]为避免协同过滤推荐精度受数据稀疏的影响，提出基于K-means聚类的Slope One算法，能够有效地提升QoS预测的精度。基于模型的方法能发现用户服务之间隐含的关系，具有更高的预测精度^[21]。为进一步提高QoS的预测精度，Zhang等^[14]基于Web服务的时间感知属性对用户服务时间矩阵进行分解，有效地填充了未知的QoS值。Chen等^[14]将用户或服务聚为一类，认为同类的用户或服务共享某种隐含特征，并基于此实现对QoS值的预测。Yang等^[11]基于用户和服务的位置信息对用户服务矩阵进行分解，有效地解决数据稀疏和冷启动的问题，Liu等^[13]也利用位置属性对协同过滤推荐的结果进行优化。Ryu等^[15]则在位置信息的基础上，基于偏好可传播性对用户服务矩阵进行分解，有效地解决了冷启动的问题。唐明董等^[12]在位置信息的基础上，采用因子分解方法进行矩阵分解，有效地解决了数据稀疏和冷启动的问题。

目前，解决数据稀疏等问题取得了较多成果，然而其主要工作均建立在用户和服务的地理位置相似性上，对其时间属性的应用并不充分。文中将充分应用用户或服务的时间空间属性，挖掘用户、服务之间的隐含关系，提升QoS的预测性能。

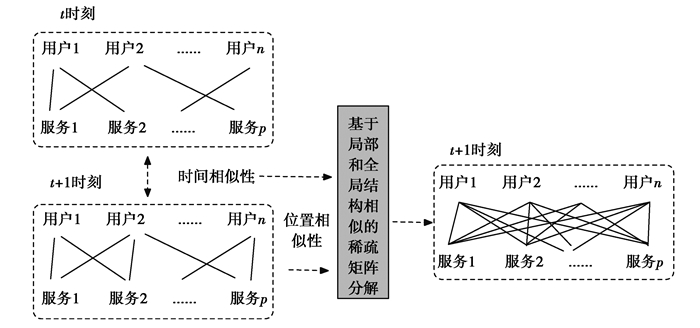
1 基于全局和局部结构相似性的稀疏矩阵分解模型(GLMF)

先介绍GLMF方法的总体流程，然后对GLMF的实现细节进行描述，包括模型和算法步骤。GLMF方法的总体流程，如图 1所示，GLMF通过记录t+1时刻用户服务QoS矩阵的位置相似性和相邻时间QoS矩阵的时间相似性，采用稀疏矩阵分解的方法对t+1时刻未知的QoS值进行预测。

1.1 QoS矩阵的构建

对未知QoS值的预测需要获得历史Web服务调用所产生的QoS数据，主要通过服务用户的反馈以及QoS的监测系统产生。前者收集用户对Web服务的反馈，如响应时间、可用性及信誉等；后者通过部署在服务器上的监测系统收集Web服务的QoS属性。所有服务调用产生的QoS记录可以用一个矩阵来表示，即用户服务的QoS矩阵，每个QoS记录可能包含多个QoS参数。下面给出各个时刻t下的用户服务QoS矩阵的形式化表示。

1) S代表Web服务集合，S={s₁, s₂, …, s_p}；U用于代表调用Web服务的所有用户的集合，U={u₁, u₂, …, u_n}。这里假设所有时刻的用户和服务不变。

2) R^t代表t时刻用户调用服务产生QoS记录的矩阵，即用户服务QoS矩阵，$ \boldsymbol{R}^{t}=\left\{r_{i j}^{t} \mid u_{i} \in U, s_{j} \in S\right\}$。其中，$ {r_{ij}^t}$代表t时刻用户u_i调用服务s_j产生的QoS记录，该记录可以是响应时间、吞吐量、反馈等。若用户未调用过该服务，则QoS记录为空。真实场景中，每个时刻用户通常仅使用部分Web服务，产生的用户服务QoS矩阵应当十分稀疏。文中要解决的问题可以形式化表示为基于稀疏矩阵R^t和R^t+1，实现对矩阵R^t+1的低秩填充。

1.2 模型简介

对t+1时刻的矩阵R^t+1进行典型的低秩矩阵分解，其损失函数为

$ F=\underset{A^{t+1}, B^{ t+1}}{\operatorname{argmin}}\left(\left\|\boldsymbol{R}^{t+1}-\boldsymbol{A}^{t+1}\left(\boldsymbol{B}^{t+1}\right)^{\mathrm{T}}\right\|_{F}^{2}+\lambda_{1}\left(\left\|\boldsymbol{A}^{t+1}\right\|_{F}^{2}+\left\|\boldsymbol{B}^{t+1}\right\|_{F}^{2}\right)\right), $

(1)

其中，R^t+1(N×P)，$\parallel \cdot \parallel _F^2 $表示矩阵的F范数，$\left\|A^{t+1}\right\|_{F}^{2}+\left\|B^{t+1}\right\|_{F}^{2} $是正则项，用于避免过拟合，A^t+1和B^t+1又可称之为用户和服务的隐特征矩阵。假设共有M个隐式特征，则A^t+1(N×M)，B^t+1(P×M)。

由于相邻时刻网络环境相差不大，相似用户调用服务的QoS属性可能具有相似性，且相邻时刻的QoS矩阵也具有相似性。上述特征反映在QoS矩阵上分别是局部结构相似性(位置相似性)和全局结构相似性(时间相似性)。将其融入到式(1)中得到修正后的损失函数为

$\begin{array}{c} F=\underset{A^{t+1}, B ^{t+1}}{\operatorname{argmin}}\left(\left\|\boldsymbol{R}^{t+1}-\boldsymbol{A}^{t+1}\left(\boldsymbol{B}^{t+1}\right)^{\mathrm{T}}\right\|_{F}^{2}+\lambda_{1}\left(\left\|\boldsymbol{A}^{t+1}\right\|_{F}^{2}+\left\|\boldsymbol{B}^{t+1}\right\|_{F}^{2}\right)+\lambda_{2}\left(\left\|\boldsymbol{A}^{t+1}\left(\boldsymbol{B}^{t+1}\right)^{\mathrm{T}}-\boldsymbol{R}^{t}\right\|_{F}^{2}\right)+\right. \\ \left.\lambda_{3}\left(\left\|\boldsymbol{L}\left(\boldsymbol{A}^{t+1}\left(\boldsymbol{B}^{t+1}\right)^{\mathrm{T}}\right)\right\|_{F}^{2}\right)\right)。\end{array} $

(2)

其中，第3项通过最小化t+1时刻与t时刻QoS矩阵差异性的方式保留t时刻QoS矩阵的全局结构特征；第4项通过拉普拉斯矩阵L保留t+1时刻的局部结构特征，L=D-W。W是R^t+1的相似度矩阵(采用欧氏距离进行表示，距离越大，相似度越小)，D是对角矩阵(其对角线上的元素来自于对W各行的求和)。

基于式(2)计算梯度为

$ \begin{aligned} \frac{\partial F}{\partial \boldsymbol{A}^{t+1}}=-\boldsymbol{R}^{t+1} \boldsymbol{B}^{t+1}+\boldsymbol{A}^{t+1}\left(\boldsymbol{B}^{t+1}\right)^{\mathrm{T}} \boldsymbol{B}^{t+1}+\lambda_{1} \boldsymbol{A}^{t+1}+\\ \lambda_{2}\left(\boldsymbol{A}^{t+1}\left(\boldsymbol{B}^{t+1}\right)^{\mathrm{T}}-\boldsymbol{R}^{t}\right) \boldsymbol{B}^{t+1}+\lambda_{3} \boldsymbol{L}^{\mathrm{T}} \boldsymbol{L} \boldsymbol{A}^{t+1}\left(\boldsymbol{B}^{t+1}\right)^{\mathrm{T}} B^{t+1}, \end{aligned} $

$ \begin{array}{c} \frac{\partial F}{\partial \boldsymbol{B}^{t+1}}=-\left(\boldsymbol{R}^{t+1}\right)^{\mathrm{T}} \boldsymbol{A}^{t+1}+\boldsymbol{B}^{t+1}\left(\boldsymbol{A}^{t+1}\right)^{\mathrm{T}} \boldsymbol{A}^{t+1}+\lambda_{1} \boldsymbol{B}^{t+1}+ \\ \left.\lambda_{2}\left(\boldsymbol{A}^{t+1}\left(\boldsymbol{B}^{t+1}\right)^{\mathrm{T}}-\boldsymbol{R}^{t}\right)\right)^{\mathrm{T}} \boldsymbol{A}^{t+1}+\lambda_{3} \boldsymbol{B}^{t+1}\left(\boldsymbol{A}^{t+1}\right)^{\mathrm{T}} \boldsymbol{L}^{\mathrm{T}} \boldsymbol{L} \boldsymbol{A}^{t+1}。\end{array} $

采用乘性迭代法则对A^t+1和B^t+1进行寻优：

$ \begin{aligned} \boldsymbol{A}^{t+1} =\boldsymbol{A}^{t+1} \frac{\boldsymbol{C}}{\boldsymbol{D}} , \end{aligned} $

(3)

$ \boldsymbol{B}^{t+1} =\boldsymbol{B}^{t+1} \frac{\boldsymbol{E}}{F}, $

(4)

其中，$ \boldsymbol{C}=\boldsymbol{R}^{t}+1 \boldsymbol{B}^{t+1}+\lambda_{2} \boldsymbol{R}^{t} \boldsymbol{B}^{t+1}$；

$ \boldsymbol{D}=\boldsymbol{A}^{t+1}\left(\boldsymbol{B}^{t+1}\right)^{\mathrm{T}} \boldsymbol{B}^{t+1}+\lambda_{1} \boldsymbol{A}^{t+1}+\lambda_{2} \boldsymbol{A}^{t+1}\left(\boldsymbol{B}^{t+1}\right)^{\mathrm{T}} \boldsymbol{B}^{t+1}+\lambda_{3} \boldsymbol{L}^{\mathrm{T}} \boldsymbol{L} \boldsymbol{A}^{t+1}\left(\boldsymbol{B}^{t+1}\right)^{\mathrm{T}} \boldsymbol{B}^{t+1};$

$E=\left(\boldsymbol{R}^{t+1}\right)^{\mathrm{T}} A^{t+1}+\lambda_{2}\left(R^{t}\right)^{\mathrm{T}} A^{t+1}; $

$F=\boldsymbol{B}^{t+1}\left(\boldsymbol{A}^{t+1}\right)^{\mathrm{T}} \boldsymbol{A}^{t+1}+\lambda_{1} \boldsymbol{B}^{t+1}+\lambda_{2} \boldsymbol{B}^{t+1}\left(\boldsymbol{A}^{t+1}\right)^{\mathrm{T}} A^{t+1} \lambda_{3} \boldsymbol{B}^{t+1}\left(\boldsymbol{A}^{t+1}\right)^{\mathrm{T}} \boldsymbol{L}^{\mathrm{T}} \boldsymbol{L} \boldsymbol{A}^{t+1}。$

1.3 基于全局和局部结构相似性的稀疏矩阵分解算法

算法1.基于时空感知的稀疏矩阵分解算法。

输入：用户服务QoS矩阵R^t+1和R^t；隐式特征数M；误差标准ε和δ；迭代次数count。

输出：QoS预测值填充后的QoS矩阵$\widetilde {{\mathit{\boldsymbol{R}}^{t + 1}}} $。

① 随机初始化分解因子A^t+1(N×M)和B^t+1(P×M)；

② cnt=0；

③ 按照式(5)和式(6)计算误差度量指标MAE和RMSE；

④ while cnt < count || MAE < ε||RMSE < δ

⑤ 按照式(3)和式(4)对A^t+1和B^t+1更新；

⑥ 按照式(5)和式(6)计算误差度量指标MAE和RMSE；

⑦ end while

⑧ $ \widetilde {{R^{t + 1}}} = {A^{t + 1}}{\left( {{B^{t + 1}}} \right)^{\rm{T}}}$。

2 实验验证与分析

为了验证方法的有效性，采用真实的Web服务QoS数据进行实验评估^[14]。该数据集采集自wsdream.com网站，包含4 532个Web服务在64个相邻时间段内被142个用户调用的QoS记录，主要是吞吐量(throughput)和响应时间(response time，或round trip time，RTT)两方面。值得注意的是，QoS有多种属性，包括响应时间、吞吐量等客观属性，也包括用户对服务质量的反馈等主观属性。对于客观属性数据，需要对其归一化以消除不同量纲的影响；对于主观属性数据，可以利用用户平均值与整体平均值进行纠偏(这里假定整体均值是中立的)。

文中使用服务的RTT数据来评估所提出的方法。实验采用的数据集是用户端的轻量级中间件自动收集用户调用服务时产生的真实QoS记录，由于所处网络环境、设备的不同，其QoS记录必然是包含噪声的。此外，真实环境下的RTT矩阵是稀疏的，在实验时为了模拟实际的Web服务应用场景，通过随机移除RTT矩阵的一部分数据实现对矩阵的稀疏化。采用稀疏度(移除数据的大小/总矩阵的大小)来衡量矩阵的稀疏程度。稀疏化后的矩阵是可看做训练数据，而被移除的数据可看做测试数据。

2.1 评估指标

通过计算预测的RTT值与实际RTT值之间的偏差来评估文中方法在预测Web服务RTT的准确性。常用的误差度量指标：平均绝对误差MAE(mean absolute error)和均方根误差RMSE(root mean squared error)。二者的计算公式如下：

$ {{\rm{MAE}} = \frac{1}{{|{\rm{SP}}|}}\sum\limits_{r_{i, j}^{t + 1} \in {\rm{SP}}} {\left| {r_{i, j}^{t + 1} - {r^{\tilde t + 1}}_{i, j}} \right|} , } $

(5)

$ {{\rm{RMSE}} = \sqrt {{{\left| {r_{i, j}^{t + 1} - r_{i, j}^{\tau + 1}} \right|}^2}} , } $

(6)

其中, SP是被移除的数据，即用于测试的数据集，|SP|是数据集的大小。MAE和RMSE的值越小，代表预测的精度越高。

2.2 对比方法的选择

为了比较GLMF方法与其他方法在预测性能上的优劣，实验中将其与以下2个经典的预测方法进行了对比：

1) 非负矩阵分解(non-negative matrix factorization，NMF)。NMF约束分解后的矩阵分量为非负的。在QoS预测中，这种假设是合理的。

2) 奇异值分解(single value decomposition，SVD)。SVD是实现矩阵低秩近似的典型方式之一。基于历史数据的潜在信息寻找一个属性空间，用户调用服务的QoS值由用户和服务在此属性空间的点集求得。

3) Kmeans+Slope One算法。基于项目(服务)的协同过滤推荐中，Slope One算法可以有效地实现缺值预测。然而，Slope One算法在实现时未考虑到项目与项目之间的相似性。因此，在空缺值预测之前，使用K-means算法对项目进行聚类以提高QoS预测精度。

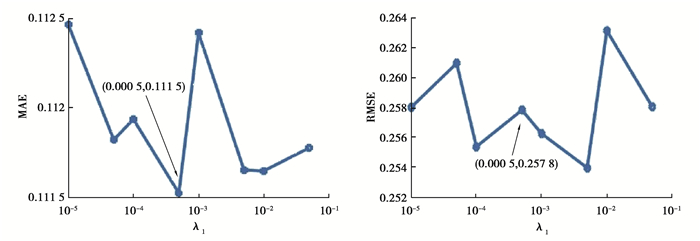
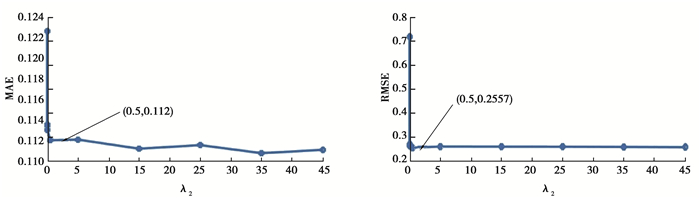
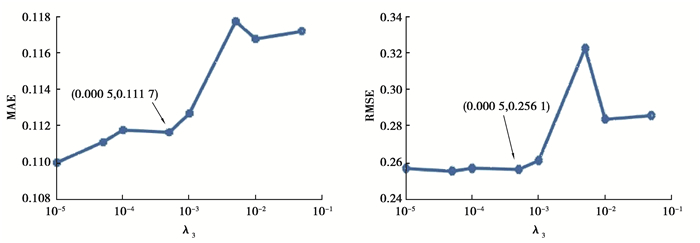
2.3 参数λ₁、λ₂、λ₃对预测性能的影响

参数λ₁所在项是为了防止过拟合而设置的，参数λ₂和λ₃分别用于保留QoS矩阵的全局结构相似性和局部结构相似性。文中矩阵的稀疏度均设置为0.9，隐式特征数目设置为30。从图 2、图 3和图 4可以发现，参数λ₁、λ₂、λ₃的取值在一定程度上会影响到预测的精度。图 2中MAE和RMSE起初随着参数λ₁的增加快速下降，当λ₁大于0.000 5时，整体反而上升。图 3中MAE和RMSE起初随着参数λ₂的增加快速下降，当λ₂大于0.5时，基本保持平稳或者缓慢下降。图 4中MAE和RMSE起初随着λ₃的增加基本保持不变，当λ₃大于0.000 5时，反而快速上升。由此，参数λ₁的值可固定为0.000 5；参数λ₂和λ₃可分别设置为0.5，0.000 5。

2.4 QoS矩阵的稀疏度对预测性能的影响

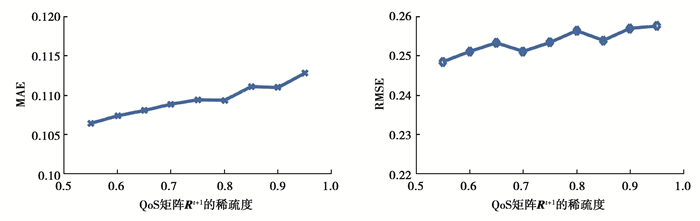
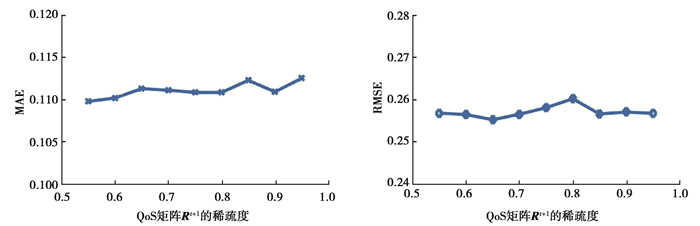
在真实场景中，各个时刻的QoS矩阵均是稀疏的，其稀疏程度不同，预测性能是不同的。文中模型对时刻t和t+1的QoS矩阵(R^t和R^t+1)进行处理，矩阵R^t和R^t+1的稀疏度均会对预测性能有影响。具体结果如图 5和图 6所示。图 5中固定矩阵R^t的稀疏度为0.9，矩阵R^t+1的稀疏度范围为[0.55, 0.95]，每步增长0.05。由图 5可知，MAE和RMSE的值随着稀疏度的增加整体上不断增加，且整体增加幅度不大。这意味着适当的收集QoS记录，减小数据稀疏度可以提高预测的精度。图 6中固定矩阵R^t+1的稀疏度为0.9，矩阵R^t的稀疏度范围为[0.55, 0.95]，每步增长为0.05。由图 6可知，随着稀疏度的增加，MAE值出现缓慢的增长，RMSE值基本保持不变。这意味着前一时刻矩阵的稀疏度对预测的性能有影响，但影响效果十分有限，表明文中方法具有良好的可扩展性，少量的全局结构信息可以达到较好的预测性能。

2.5 隐特征数目对预测性能的影响

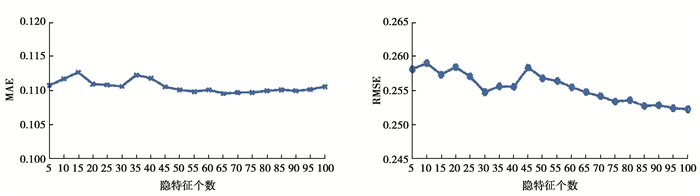
隐特征个数体现了对QoS矩阵认知的程度。隐特征个数越高意味着对QoS矩阵的认知越高，增加了计算的复杂度；隐特征个数越少，虽然降低了计算的复杂度，但是减少了对QoS矩阵的认知。图 7展示了隐特征数目对预测性能的影响，其中QoS矩阵R^t和R^t+1的稀疏度均设置为0.9，隐特征数目的范围为[5, 100]，每步增长5。随着隐特征数目的增加，RMSE整体上呈现显著的降低，MAE整体上变化不大。这表明隐特征数目的增加，一定程度上加强了对QoS矩阵的认知，导致预测性能总体变好。然而，在[20, 40]范围内，MAE和RMSE值均出现一定的波动。因为并不是所有增加的隐特征都能有效加强对QoS矩阵的认知。文中均衡计算性能和预测性能，最终在实验中设置隐特征数目为30。

2.6 不同方法预测性能的对比

表 1显示了GLMF与各种对比方法的预测结果。其中，Kmeans+Slope One算法是基于记忆的协同过滤方法，这种方法在数据稠密时能取得较好的效果，却并不适用于数据稀疏的环境，因此预测性能最低。NMF、SVD和GLMF均利用矩阵分解理论对用户服务QoS矩阵进行建模，发现用户服务的隐含特征，提高了预测的性能。由表 1可知，随着矩阵稀疏度的增加，无论何种方法，其MAE和RMSE值均增加，预测性能均下降。值得一提的是，GLMF方法在高稀疏度情境下，其MAE和RMSE值均小于其他方法，具有更优的预测性能。相比于NMF，GLMF的MAE值最大下降了3.25%，RMSE值最大下降了6.65%；相比于SVD，GLMF的MAE值最大下降了3.67%，RMSE值最大下降了7.01%。与NMF和SVD相比，GLMF充分利用了用户服务QoS矩阵的全局和局部结构特征，进一步提高了预测精度。

3 结论

文中针对用户服务间的QoS预测问题，充分利用时空特征，即相邻时间段内，相似用户具有相似的网络环境，更大可能具有相似的QoS属性，提出了一种基于全局和局部结构相似性的稀疏矩阵分解算法。该算法将QoS预测问题归结为矩阵的低秩近似问题，通过乘性迭代的方式寻找矩阵的因子，最终实现对QoS矩阵的低秩填充。实验结果表明，基于全局和局部结构相似性的稀疏矩阵分解模型(GLMF)与经典的矩阵分解方法、基于记忆的协同过滤方法相比，QoS预测性能有一定的提高，能有效解决数据稀疏、噪声等问题。未来拟将文中方法进一步应用于更多场景下，如为基于情景的Web服务推荐(主要包括基于QoS的服务聚集、服务组合优化和服务的异常检测等)提供支撑。