基于性能的抗震设计和评估程序需要精确的非线性有限元模型,要求能够捕捉到与各级性能目标相关的结构响应。地震灾害报告和试验数据表明,强烈的地震动会使结构产生非线性变形,在梁柱端部形成塑性铰。损伤累积会使塑性铰区域强度和刚度退化,影响结构抗力和动力特性,造成局部和整体倒塌[1]。实际有限元模型不仅要稳定可靠,计算效率高,而且能体现出构件在往复荷载作用下,塑性铰区域强度和刚度退化的现象。
为了精确地预测结构在地震作用下倒塌,Ibarra[2]提出了一种包含强度和刚度退化的IMK(Ibarra-Medina-Krawinkler)滞回规则,该模型描述力和变形的关系,能对钢构件、胶合板和RC(钢筋混凝土)构件进行模拟。结果表明,该模型能较好地模拟包含退化在内的构件受力特征。Lignos[3]根据大量钢构件试验结果在OpenSees中提出了ModIMK(Modified IMK)弯矩转角模型,并成功预测了四层钢框架的倒塌。Haselton[4]对ModIMK弯矩转角模型应用于混凝土构件进行了研究,提出了各参数的计算方法,模拟结果和试验结果吻合较好。国内外对ModIMK弯矩转角模型已经进行了大量研究和广泛的应用,但是ModIMK弯矩转角模型明显的不足是该模型描述的是构件宏观的整体变形,对截面层次上的参数,如截面曲率等无法提取,这不利于结构性能评估。
OpenSees中基于力的单元(Force-Based Element)能对构件从截面层次上进行定义,赋予材料本构模型,对构件力变形关系进行模拟。Scott[1]进一步开发了塑性铰(Beam With Hinges)单元,可以实现构件塑性区域集中在某一确定的长度范围内,其余部分处于弹性状态,该模型和常用的等效塑性铰模型原理非常接近。目前,在OpenSees中已经开发了大量的钢筋和混凝土材料的本构模型,可以在塑性铰单元中应用。根据Scott另一项研究[5],可以把弯矩曲率关系赋予塑性铰区截面,计算效率将更高,但目前能直接应用的钢筋混凝土截面弯矩曲率滞回规则比较少。近来,Barbosa等[6]对ModIMK弯矩转角模型用于定义截面弯矩曲率关系进行了研究,因为这一模型本质上是力和变形的本构关系,变形可以是转角也可以是曲率。文献[6]通过把转角除以塑性铰长度转化为弯矩曲率关系,来定义塑性铰单元的截面,但这一做法存在一定的不足,因为通过转换得到的弯矩曲率关系没有真实的物理意义,例如,屈服转角除以塑性铰长度得到的屈服曲率并不是截面真实的屈服曲率,从本质上看,得到的曲率并不能用来评估构件的状态。
文中通过理论推导和试验数据验证,提出了基于试验结果的RC矩形柱弯矩曲率骨架曲线计算方法,滞回规律选用ModIMK滞回规则,在OpenSees中应用塑性铰单元,对RC柱进行模拟,计算结果和试验结果吻合非常好。所提出的弯矩曲率塑性铰模型计算效率高,降低了模型复杂度,为RC构件在截面层次上进行评估提供了一种简便的方法。
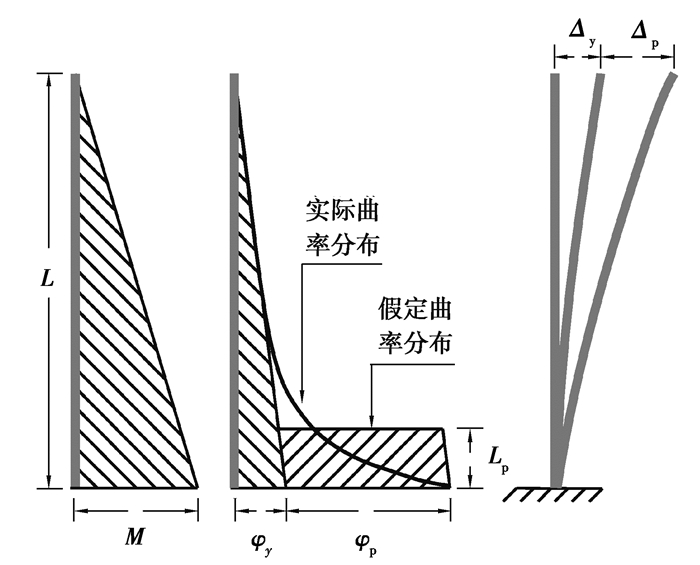
1 集中塑性铰模型基本理论 1.1 Priestley等效塑性铰模型RC柱顶位移主要由弯曲变形、滑移变形和剪切变形三分量组成,剪跨比大于2的RC柱剪切变形一般可以忽略不计[7-8]。Priestley[9]提出的等效塑性铰计算方法,如图 1所示,柱顶总位移Δ由屈服位移Δy和塑性位移Δp组成。在等效塑性铰长度Lp范围内,假定曲率为恒定的常数,则柱顶位移Δ可为:
| $ {\varDelta = {\varDelta _{\rm{y}}} + {\varDelta _p} = {\varDelta _{\rm{y}}} + {\varphi _{\rm{p}}}{L_{\rm{p}}}\left( {L - \frac{1}{2}{L_{\rm{p}}}} \right),} $ | (1) |
| $ {{L_{\rm{p}}} = 0.08L + 0.022{f_{\rm{y}}}{d_{\rm{b}}} \ge 0.044{f_{\rm{y}}}{d_{\rm{b}}},} $ | (2) |
|
图 1 等效塑性铰分析方法 Fig. 1 Equivalent plastic hinge analysis method |
式中:fy为纵筋屈服强度,db为纵筋直径。等效塑性铰长度Lp的第一项考虑RC柱弯曲效应,第二项考虑柱底纵筋粘结滑移效应(bond-slip),相当于纵筋拔出效应(pull out)或纵筋应变渗透效应(strain penetration)[8]。
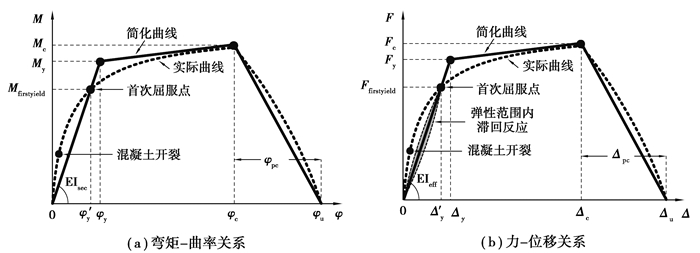
1.2 RC柱屈服状态定义RC柱在侧向荷载反复作用下,变形是一个非线性的过程,随着侧向荷载的增加,经历混凝土开裂和钢筋屈服等过程,侧向荷载达到一定的最大值后开始下降,柱子逐渐破坏。这一过程可以简化为三折线模型,如图 2所示,分为弹性段、强化段和软化段。对于RC悬臂柱,柱底截面曲率达到屈服曲率φy时,顶部位移为屈服位移Δy,屈服曲率φy由式(3)定义[9-10]。
| $ {\varphi _{\rm{y}}} = \frac{{{M_{\rm{y}}}}}{{{M_{{\rm{firstyield}}}}}}\varphi _{\rm{y}}^\prime , $ | (3) |
|
图 2 RC柱骨架曲线定义 Fig. 2 Definition of RC column skeleton curve |
式中:My为屈服弯矩,取最外边缘混凝土压应变达到0.004时的截面弯矩;Mfirstyield为首次屈服点弯矩,取最外边缘混凝土压应变达到0.00 2时弯矩和最外侧纵筋拉应变达到屈服时弯矩中的较小值[9],此时对应的截面曲率为φ′y,对应的柱顶侧向力是图 2(b)中的Ffirstyield。截面割线刚度EIsec,如图 2(a)所示,由式(4)计算[11-13]:
| $ {\rm{E}}{{\rm{I}}_{{\rm{sec}}}} = \frac{{{M_{\rm{y}}}}}{{{\varphi _{\rm{y}}}}}。$ | (4) |
Priestley基于大量研究提出了RC截面屈服曲率φy计算方法[9]:
| $ {\varphi _{\rm{y}}} = \lambda \frac{{{\varepsilon _{\rm{y}}}}}{D}, $ | (5) |
式中:RC圆柱λ=2.45,矩形柱λ=2.14;εy为纵筋屈服应变;D为截面高度。
RC柱在侧向荷载作用下,底部纵筋从基础中滑移会引起端部附加转动,增加柱顶位移,计算屈服位移Δy应考虑纵筋滑移效应[8, 12-14]。根据弹性理论,RC悬臂柱顶屈服位移Δy表示为
| $ {\varDelta _{\rm{y}}} = \frac{{{F_{\rm{y}}}{L^3}}}{{3{\rm{E}}{{\rm{I}}_{{\rm{eff}}}}}}。$ | (6) |
则截面有效刚度EIeff为
| $ {\rm{E}}{{\rm{I}}_{{\rm{eff}}}} = \frac{{{F_{\rm{y}}}{L^3}}}{{3{\varDelta _{\rm{y}}}}} = \frac{{{M_{\rm{y}}}{L^2}}}{{3{\varDelta _{\rm{y}}}}}。$ | (7) |
由于纵筋滑移效应增加了柱顶位移,所以截面有效刚度EIeff小于截面割线刚度EIsec。
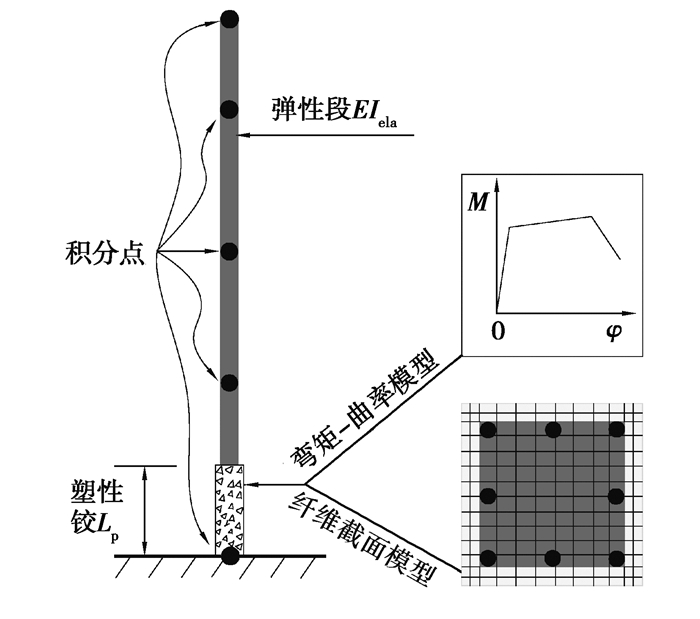
2 Beam With Hinges单元弹性段刚度确定 2.1 Beam With Hinges单元基本理论Scott在OpenSees平台上开发了基于力法的Beam With Hinges单元[1],该单元将塑性变形集中在端部一定长度范围内,其余部分处于弹性状态。应用时需要定义单元端部的塑性铰长度Lp和截面特性以及弹性段截面刚度EIela。在定义塑性铰区截面时,一般做法是用纤维截面来定义[15],再根据平截面假定,通过积分过程,将纤维应力应变关系变为截面弯矩曲率关系。Scott提出可以将截面弯矩曲率关系直接赋予塑性铰区截面上[5],如图 3所示,这样既能获得截面层次上响应,又避免了由材料性能到截面性能的积分过程,在高应变状态下,数值收敛性也有改善。
|
图 3 Beam With Hinges单元 Fig. 3 Beam With Hinges Element |
对于悬臂柱而言,在地震荷载作用下,塑性铰通常在柱底区段范围内产生,而柱顶不易进入非线性状态[16],在实际应用中,将柱顶的塑性铰长度假定为零,只令柱底端部具有塑性铰,模型如图 3所示,根据单元基本理论,柱顶位移Δ表达式为[8]
| $ \varDelta = \frac{{{M_{{\rm{base }}}}}}{{{\rm{E}}{{\rm{I}}_{{\rm{ela }}}}}}\left( {\frac{{{L^2}}}{3} - L{L_{\rm{p}}}} \right) + {\varphi _{{\rm{base }}}}L{L_{\rm{p}}}, $ | (8) |
式中:Mbase和φbase分别为柱底弯矩和曲率。当塑性铰区的截面屈服时,柱顶屈服位移Δy为
| $ {\varDelta _{\rm{y}}} = \frac{{{M_{\rm{y}}}}}{{{\rm{E}}{{\rm{I}}_{{\rm{ela}}}}}}\left( {\frac{{{L^2}}}{3} - L{L_{\rm{p}}}} \right) + {\varphi _{\rm{y}}}L{L_{\rm{p}}}。$ | (9) |
根据Scott建议[5],RC截面弯矩曲率关系可以用等效线性简化模型来定义,如图 2(a)所示。对于屈服状态,令式(6)和式(9)相等,可求解出弹性段截面刚度EIela[8]:
| $ {\rm{E}}{{\rm{I}}_{{\rm{ela}}}} = {\rm{E}}{{\rm{I}}_{{\rm{eff}}}}\frac{{\frac{{{L^2}}}{3} - L{L_{\rm{p}}}}}{{\frac{{{L^2}}}{3} - {\varphi _{\rm{y}}}\frac{{{\rm{E}}{{\rm{I}}_{{\rm{eff}}}}}}{{{M_{\rm{y}}}}}L{L_{\rm{p}}}}}, $ | (10) |
结合式(4)和式(10),可改写为
| $ {\rm{E}}{{\rm{I}}_{{\rm{ela}}}} = {\rm{E}}{{\rm{I}}_{{\rm{eff}}}}\frac{{\frac{{{L^2}}}{3} - L{L_{\rm{p}}}}}{{\frac{{{L^2}}}{3} - \frac{{{\rm{E}}{{\rm{I}}_{{\rm{eff}}}}}}{{{\rm{E}}{{\rm{I}}_{{\rm{sec}}}}}}L{L_{\rm{p}}}}} = {\rm{E}}{{\rm{I}}_{{\rm{eff}}}}\frac{{\frac{1}{3} - \frac{{{L_{\rm{p}}}}}{L}}}{{\frac{1}{3} - {\alpha _{{\rm{sec}}}}\frac{{{L_{\rm{p}}}}}{L}}}。$ | (11) |
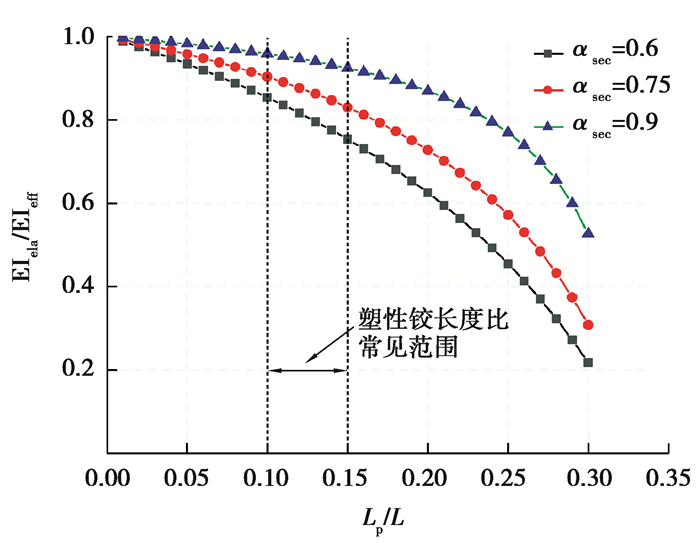
Berry[8]基于试验结果提出截面有效刚度EIeff与截面割线刚度EIsec的比值关系αsec只跟剪跨比有关,且小于1.0,当剪跨比为2.0~4.0,αsec比值约为0.6~0.9。由式(11)可知,EIela与EIeff的比值与Lp/L和αsec的关系如图 4所示,可以看出,当αsec不变时,EIela与EIeff的比值随Lp/L的增加而减小。在常见塑性铰长度比范围时,EIela与EIeff比值大约为0.7~0.9。EIela比EIeff小的原因是塑性铰区弯矩曲率关系用的是截面真实的弯矩曲率关系,只能模拟柱子弯曲变形,底部钢筋粘结滑移造成的顶部附加位移只能通过减小上部弹性段的刚度来模拟。当塑性铰长度越长时,构件中只考虑弯曲变形的部分就越长,弹性段截面刚度就越小,这样计算的顶部位移才能和试验结果吻合。
|
图 4 弹性段截面刚度与设计参数关系 Fig. 4 Elastic segment section stiffness versus design parameters |
为验证塑性铰单元对屈服位移计算结果的准确性,计算的屈服位移需与试验数据对比。对比数据选用文献[17]中的数据库,该数据库共包括62根RC矩形柱的试验数据,每一个试验结果都详细报道了钢筋屈曲时的位移,这在下文计算中是一个重要的对比数据。试件主要参数、实测数据和计算值及比值关系列于表 1中,屈服弯矩My也列于表中。
| 表 1 试件主要参数及结果 Table 1 Main parameters and results of specimens |
由式(9)计算屈服位移时,弹性段截面刚度EIela由式(10)确定,其中EIeff采用应用较为广泛的Elwood模型[13],如式(12)所示。
| $ \frac{{{\rm{E}}{{\rm{I}}_{{\rm{eff }}}}}}{{{\rm{E}}{{\rm{I}}_{\rm{g}}}}} = \frac{{0.45 + 2.5n}}{{1 + 110\left( {\frac{{{d_b}}}{D}} \right)\left( {\frac{D}{L}} \right)}} \le 1.0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{and}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \ge 0.2, $ | (12) |
式中:n为轴压比;EIg为毛截面刚度。
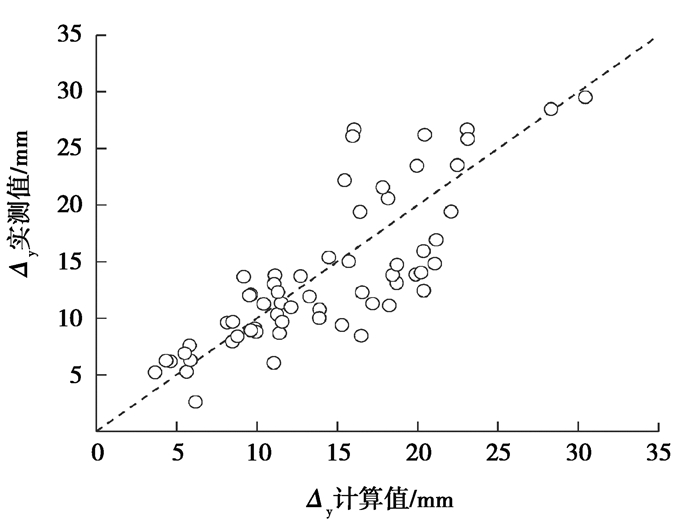
屈服位移Δy计算结果列于表 1,试验值与式(9)计算值比值的均值为0.99,变异系数(COV)为0.28,精度较高,离散性小。图 5是计算值与试验值关系,表明计算结果与试验实测数据吻合较好。
|
图 5 屈服位移计算值与试验值比较 Fig. 5 Comparison between calculated and experimental yield displacement |
图 2(a)给出了弯矩曲率曲线及其线性骨架曲线,对于屈服点弯矩和曲率已有介绍。屈服后,截面受弯承载力会有一定提高,达到一定峰值后逐渐下降,进入破坏状态。RC柱的破坏通常与核心混凝土压碎、箍筋断裂、纵筋屈曲等状态密切相关,当纵筋发生屈曲后,约束箍筋很快会断裂,约束混凝土被压碎,柱子也逐渐失去侧向承载力[4, 17-18]。Fardis基于试验数据提出了RC矩形柱截面承载力出现显著下降时核心混凝土极限压应变εcu, c表达式[14]:
| $ {{\varepsilon _{{\rm{cu}},{\rm{c}}}} = {\varepsilon _{{\rm{cu}}}} + 0.04\sqrt {a{\rho _{{\rm{eff}}}}} ,} $ | (13) |
| $ {0.003{\kern 1pt} {\kern 1pt} {\kern 1pt} 5 \le {\varepsilon _{{\rm{cu}}}} = {{(18.5/D)}^2} \le 0.01,} $ | (14) |
| $ {a = \left( {1 - \frac{{{s_{\rm{h}}}}}{{2{b_o}}}} \right)\left( {1 - \frac{{{s_{\rm{h}}}}}{{2{h_o}}}} \right)\left[ {1 - \frac{{\sum {b_i^2} }}{{6{b_o}{h_o}}}} \right],} $ | (15) |
式中:εcu为未约束混凝土极限应变;a为约束系数;ρeff为配箍特征值;sh为箍筋间距;b0和h0分别为箍筋中心线为边界所约束的截面核心宽度和高度,bi为受箍筋约束的纵向钢筋间距。
截面受压区高度c采用Priestley的计算式[9]:
| $ c = (0.25 + 0.85n)D \le D。$ | (16) |
根据平截面假定,则截面曲率φc的表达式为
| $ {\varphi _{\rm{c}}} = \frac{{{\varepsilon _{{\rm{cu,c}}}}}}{{c - {c_o}}}。$ | (17) |
因为受弯承载力出现下降时混凝土保护层已经剥离,计算截面曲率φc时,受压区高度需扣除混凝土保护层厚度co。
骨架曲线上的峰值点弯矩Mc由式(18)计算[4]:
| $ {M_{\rm{c}}}/{M_{\rm{y}}} = (1.25){(0.89)^n}{(0.91)^{0.01{f_{\rm{c}}}}}。$ | (18) |
根据统计,这一比值平均值大约在1.13左右,随着轴压比的增加有所提高。
对于图 2(a)中峰值荷载后的软化段,Haselton[4, 19-20]指出峰值弯矩后的变形由于缺乏可靠的试验数据,对于约束良好的RC柱,建议当侧向承载力从峰值点下降到零时对应的位移增量Δpc=0.1L(见图 2(b)),根据式(8)可得:
| $ {\varDelta _{{\rm{pc}}}} = {\varphi _{{\rm{pc}}}}L{L_{\rm{p}}} - \frac{{{M_{\rm{c}}}}}{{{\rm{E}}{{\rm{I}}_{{\rm{ela}}}}}}\left( {\frac{{{L^2}}}{3} - L{L_{\rm{p}}}} \right)。$ | (19) |
根据试验结果统计,式(19)右侧第二项均值在0.006L左右,相对Δpc来说比较小,可以忽略,得φpc=0.1/Lp。
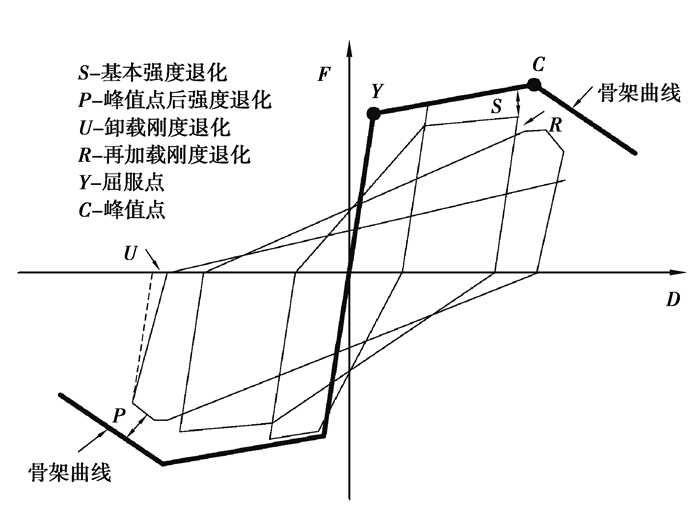
3.2 滞回规则RC柱在往复荷载作用下,塑性铰区域出现强度和刚度退化,采用能考虑退化的ModIMK滞回规则[4]定义弯矩曲率滞回曲线,如图 6所示,由弹性段、硬化段和软化段构成。在反复加载强度和刚度退化方面,一般需要定义4个退化系数,分别为基本强度退化系数、峰值点后强度退化系数、卸载刚度退化系数和再加载刚度退化系数,当变形超过屈服点时,即可激活4种循环退化模式。根据文献[4]的研究,对于混凝土结构这4个系数可以取相同值。
|
图 6 ModIMK滞回规则 Fig. 6 ModIMK hysteretic rules |
退化是基于能量耗散规则控制,构件能量耗散能力Et,是θcap, pl(峰值弯矩对应的转角与屈服转角差值)与屈服弯矩My的倍数,即Et=γθcap, plMy。由于文中把ModIMK模型应用于弯矩曲率关系,故能量耗散能力Et变为Et=γ(φc-φy)My。对于RC矩形柱的能量耗散系数γ可由经验式(20)计算[4]:
| $ \gamma = (30){0.3^n}。$ | (20) |
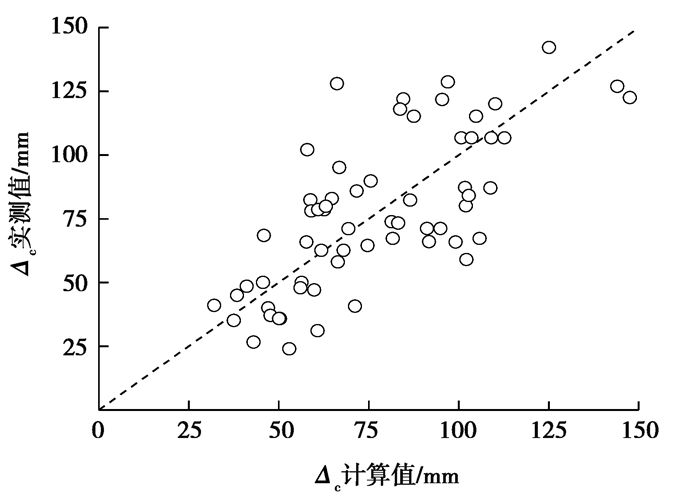
文中方法计算了表 1中62个试件的弯矩曲率滞回曲线,赋予OpenSees中塑性铰单元,对这些试件进行模拟加载分析。根据Berry的研究[17],截面承载力出现显著下降和纵筋屈曲密切相关,所以计算中曲率达到φc时的位移与纵筋屈曲位移具有比较价值。实测纵筋屈曲位移Δc和计算曲率达到φc时位移Δc分别列于表 1中,其关系如图 7所示。由表 1可知,其比值均值为1.01,离散系数(COV)为0.29,两者比值均值接近1,离散性较小,表明纵筋屈曲是承载力下降的重要原因,此后柱子破坏会进一步加快,直至失去承载力。
|
图 7 Δc位移计算值与试验值比较 Fig. 7 Comparison between calculated and experimental displacement |
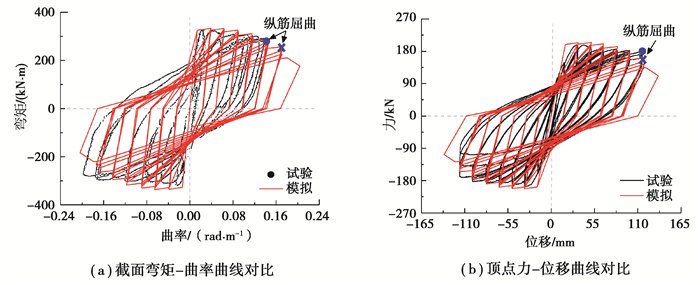
选取表 1中Saatcioglu[21]的拟静力试验结果和计算结果进行比较,文献中提供了详细的试件参数和完整的力位移曲线试验结果。此外,还提供了测量的底部350 mm长度范围内的弯曲变形角和弯矩的滞回曲线,把转角测量结果除以350 mm就可以得到底部的平均曲率数据。限于篇幅,这里仅给出试件BG8的模拟结果,如图 8所示。从图 8(a)的截面弯矩曲率曲线对比可以看出,试件在往复荷载作用下,承载力和刚度及其退化都得到了很好的模拟,图 8(b)所示为顶点的力位移曲线,试验中在侧向位移110 mm左右时纵筋出现屈曲,侧向力出现比较明显的下降,在计算中侧向位移达到110 mm时,承载力也出现显著下降,进一步加载,侧向力出现明显的下降。计算结果表明,文中提出的弯矩曲率骨架曲线,配合ModIMK滞回规则,可以比较准确地对承载力和刚度进行预测,对反复荷载作用下强度和刚度的退化也能计算,无论是弯矩曲率曲线还是力位移曲线均能有较好的模拟。
|
图 8 BG8试验与模拟曲线对比 Fig. 8 Comparison of BG8 test and simulation curve |
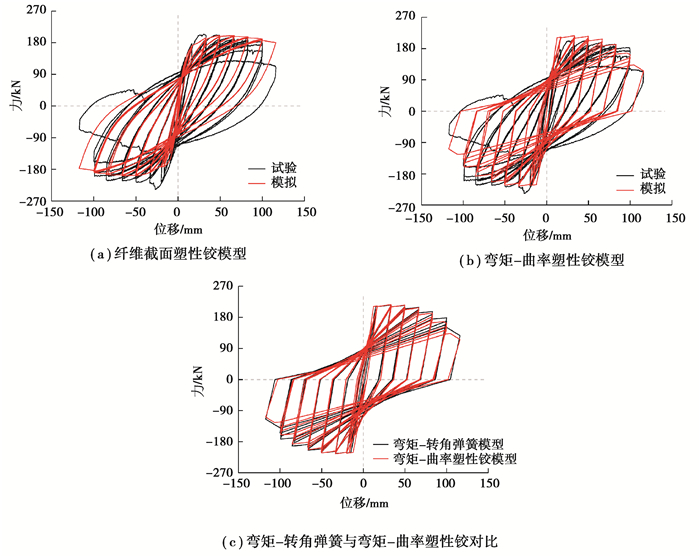
OpenSees中有丰富的单元和建模方法可以对RC柱抗震性能进行模拟,这里主要用塑性铰单元和ModIMK弯矩转角弹簧模型[2]进行对比研究,前者塑性铰区截面分别用纤维截面和文中提出的弯矩曲率模型进行定义。用这3种方法对表 1中Saatcioglu[21]试验中的试件BG5进行模拟。在用纤维模型定义截面时,用Concrete02模拟混凝土,约束混凝土本构选择Mander模型计算,用Steel02模拟钢筋,塑性铰长度取相同值。模型模拟结果如图 9所示,可以看出,3种模型计算的承载力与试验结果均吻合较好。但是,随着位移加大,试验结果显示构件的强度和刚度开始逐渐退化,考虑了这一效果的ModIMK弯矩转角弹簧模型和弯矩曲率塑性铰模型对此可以进行比较准确地模拟,纤维截面塑性铰模型在这方面模拟相对较差。弯矩转角弹簧模型和弯矩曲率塑性铰模型,由于都采用ModIMK滞回规律,由图 9(c)可以看出,两者的滞回曲线基本吻合,只是在试件破坏的最后一级加载有所不同。
|
图 9 BG5试验与不同建模方法结果比较 Fig. 9 Comparison of BG5 test and different simulation results |
ModIMK弯矩转角弹簧模型是由端部零长度弹簧单元和上部弹性单元串联形成,共计3个节点和2个单元,模型的节点、自由度和单元比塑性铰单元多;此外,不能获得截面层次上曲率响应。弯矩曲率塑性铰模型避免了由材料性能到截面性能的积分过程,计算成本降低,在高应变状态下,数值收敛性有所改善,优于纤维截面塑性铰模型。通过对比分析表明,文中弯矩曲率模型用于塑性铰单元可较准确地模拟RC柱在低周往复荷载作用下的响应,在计算上占有优势。
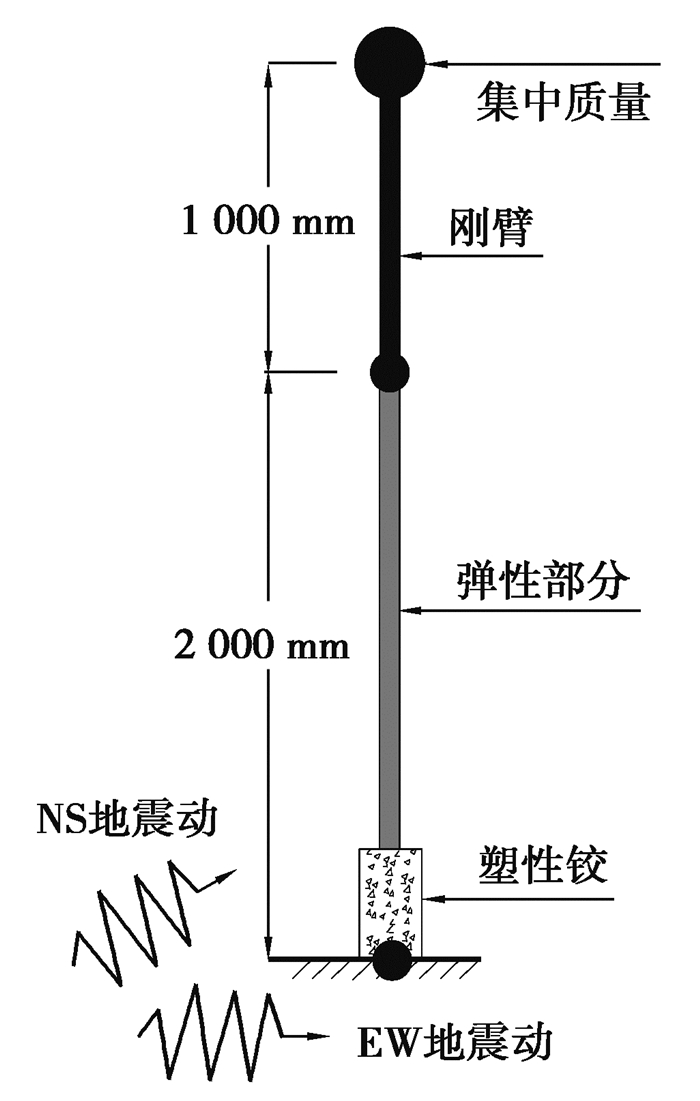
4.3 时程分析数值模拟为了进一步验证弯矩曲率塑性铰模型在时程分析上精度和稳定性,选取Hideaki的RC方柱双向振动台试验进行模拟[22]。该试件柱高2 000 mm;截面高度、宽度均为600 mm;保护层厚度为40 mm;圆柱体混凝土抗压强度为34.1 MPa;配有48根直径为10 mm的纵筋,其屈服强度为384 MPa;箍筋间距75 mm,直径为6 mm,屈服强度为350 MPa;轴向荷载360 kN;集中质量为36 t,质心在柱顶1 000 mm处。地震波为Takatori台站记录的1995年Kobe波东西向和南北向地震动,最大峰值分别是0.67 g和0.62 g,试验时对原记录时间压缩0.5倍,进行了2次序列试验,地震波峰值按0.2倍和1.0倍进行缩放。
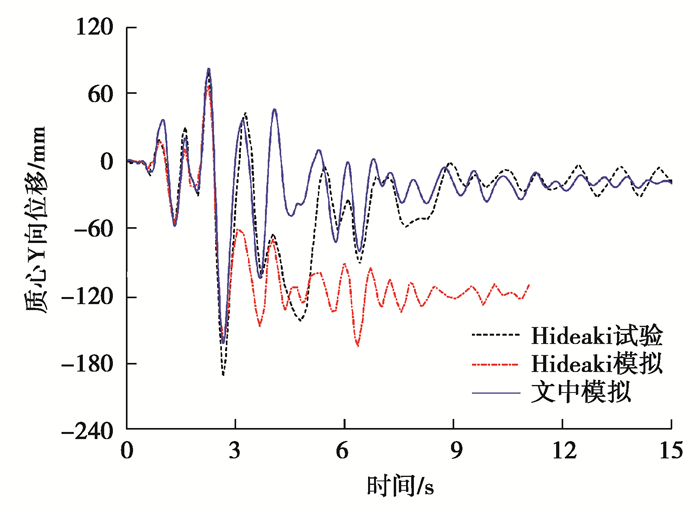
根据Hideaki建议[22],柱顶位置到集中质量质心处用刚臂连接,rayleigh阻尼比取2%,考虑P-Δ效应,分析时间步为0.000 5 s,模型如图 10所示。文中模拟曲线与试验曲线以及Hideaki[22]模拟曲线对比如图 11所示,可以看出,文中方法与Hideaki的模拟结果均能较准确地预测出最大位移,但在强烈的非线性阶段后,Hideaki的模拟曲线偏离了试验曲线,在残余位移上出现了明显的偏差[23]。文中模拟曲线与试验曲线较为吻合,残余位移相对Hideaki的模拟结果有较好的改善。文中弯矩曲率塑性铰模型可较准确地模拟RC柱在强震作用下的动力响应。
|
图 10 时程分析模型 Fig. 10 Time history analysis model |
|
图 11 质心Y方向时程响应曲线 Fig. 11 Centroid Y-direction time-history response curve |
在理论分析和数据验证基础上,提出RC柱弯矩曲率骨架曲线,用考虑强度和刚度退化的ModIMK滞回规则定义其滞回规律,将该弯矩曲率模型用于OpenSees塑性铰单元,以此模拟RC柱抗震性能,得出以下结论:
1) 确定了塑性铰单元弹性段截面刚度计算方法,发现其在截面有效刚度基础上需要进行修正。
2) 提出了RC矩形截面弯矩曲率骨架曲线计算方法,采用ModIMK滞回规律定义其强度和刚度的退化,计算的截面弯矩曲率曲线和试验曲线吻合较好,也能很好地模拟柱顶的力和位移关系。
3) 弯矩曲率塑性铰模型相比ModIMK弯矩转角弹簧模型,节点、自由度和单元减少,模型复杂度降低,并且可以获得截面层次上的曲率响应。
4) 数值模拟结果表明,弯矩曲率塑性铰模型在静力分析和动力分析方面均能对试验结果进行较好地预测,验证了模型的有效性和稳定性。
| [1] |
Scott M, Fenves G. Plastic hinge integration methods for force-based beam-column elements[J]. Journal of Structural Engineering, 2006, 132(2): 244-252. |
| [2] |
Ibarra L F, Medina R A, Krawinkler H. Hysteretic models that incorporate strength and stiffness deterioration[J]. Earthquake Engineering Structural Dynamics, 2005, 34(12): 1489-1511. DOI:10.1002/eqe.495 |
| [3] |
Lignos D, Krawinkler H. Deterioration modeling of steel components in support of collapse prediction of steel moment frames under earthquake loading[J]. Journal of Structural Engineering, 2011, 137(11): 1291-1302. DOI:10.1061/(ASCE)ST.1943-541X.0000376 |
| [4] |
Haselton C, Liel A, Lange S C, et al. Beam-column element model calibrated for predicting flexural response leading to global collapse of RC frame buildings[J]. Berkeley: Pacific Earthquake Engineering Research Center, 2008.
|
| [5] |
Scott M, Ryan K L. Moment-rotation behavior of force-based plastic hinge elements[J]. Earthquake Spectra, 2013, 29(2): 597-607. DOI:10.1193/1.4000136 |
| [6] |
Ribeiro F L A, Barbosa A R, Scott M, et al. Deterioration modeling of steel moment resisting frames using finite-length plastic hinge force-based beam-column elements[J]. Journal of Structural Engineering, 2015, 141(2): 04014112. |
| [7] |
Lehman, D E, Moehle, J P. Seismic performance of well-confined concrete bridge columns[R]. Berkeley: Pacific Earthquake Engineering Research Center, 2000.
|
| [8] |
Berry M, Lehman D E, Lowes L. Lumped-plasticity model for performance simulation of bridge columns[J]. Aci Structural Journal, 2008, 105(3): 270-279. |
| [9] |
Priestley M, Seible F, Calvi G M. Seismic design and retrofit of bridges[M]. New York: Wiley, 199.
|
| [10] |
顾冬生, 吴刚. 地震荷载作用下FRP加固钢筋混凝土圆柱变形能力计算方法研究[J]. 工程力学, 2013, 30(1): 261-270. Gu D H, Wu G. Deformation capacity of frp retrofitted circular concrete columns under simulated seismic loading[J]. Engineering Mechanics, 2013, 30(1): 261-270. (in Chinese) |
| [11] |
郭磊, 李建中, 范立础. 桥梁结构抗震设计中截面刚度的取值分析[J]. 同济大学学报(自然科学版), 2004, 32(11): 1423-1427. Guo L, Li J Z, Fan L C. Analysis of section stiffness adopted in seismic design for bridge structures[J]. Journal of Tongji University (Natural Science), 2004, 32(11): 1423-1427. (in Chinese) DOI:10.3321/j.issn:0253-374X.2004.11.003 |
| [12] |
郑罡, 李贵乾. 钢筋混凝土桥墩有效刚度[J]. 土木工程学报, 2013, 46(6): 44-52. Zheng G, Li G Q. Effective stiffness of reinforced concrete bridge piers[J]. China Civil Engineering Journal, 2013, 46(6): 44-52. (in Chinese) |
| [13] |
Elwood K J, Eberhard M O. Effective stiffness of reinforced concrete columns[J]. ACI Structural Journal, 2009, 106(4): 476-484. |
| [14] |
Grammatikou S, Biskinis D, Fardis M. Ultimate strain criteria for RC members in monotonic or cyclic flexure[J]. Journal of Structural Engineering, 2016, 142(9): 04016046. |
| [15] |
张永兵, 周明军, 郑磊. 基于改进IMK恢复力模型的填充墙RC框架结构地震易损性分析[J]. 重庆大学学报, 2018, 41(3): 67-75. Zhang Y B, Zhou M J, Zheng L. Seismic fragility analysis of infilled reinforced concrete frame building based on modified ibarra-medina-krawinkler model[J]. Journal of Chongqing University, 2018, 41(3): 67-75. (in Chinese) |
| [16] |
李忠献, 李杨, 李宁. RC桥墩抗震性能分析模型与验证[J]. 地震工程与工程振动, 2014, 34(1): 71-80. Li Z X, Li Y, Li N. Seismic analysis model of RC bridge piers:simulation and verification[J]. Earthquake Engineering and Engineering Dynamics, 2014, 34(1): 71-80. (in Chinese) |
| [17] |
Berry M P, Eberhard M O. Practical performance model for bar buckling[J]. Journal of Structural Engineering, 2005, 131(7): 1060-1070. |
| [18] |
Goodnight J C, Kowalsky M J, Nau J M. Strain limit states for circular RC bridge columns[J]. Earthquake Spectra, 2016, 32(3): 1627-1652. |
| [19] |
Haselton C B, Liel A B, Taylor-Lange S C, et al. Calibration of model to simulate response of reinforced concrete beam-columns to collapse[J]. ACI Structural Journal, 2016, 113(6): 1141-1152. |
| [20] |
Haselton C B, Liel A B, Deierlein G G, et al. Seismic collapse safety of reinforced concrete buildings:Ⅰ. Assessment of ductile moment frames[J]. Journal of Structural Engineering, 2011, 137(4): 481-491. |
| [21] |
Saatcioglu M, Grira M. Confinement of reinforced concrete columns with welded reinforced grids[J]. ACI Structural Journal, 1999, 96(1): 29-39. |
| [22] |
Nishida H, Unjoh S. Dynamic response characteristic of reinforced concrete column subjected to bilateral earthquake ground motions[C]//Proceedings of the 13th World Conference on Earthquake Engineering. Vancouver, Canada: 2004.
|
| [23] |
丁阳, 伍敏, 徐龙河, 等. 钢筋混凝土柱基于易损性曲线的地震损伤评估[J]. 工程力学, 2012, 29(1): 81-86. Ding Y, Wu M, Xu L H, et al. Vulnerability curves-based seismic damage assessment of RC columns[J]. Engineering Mechanics, 2012, 29(1): 81-86. (in Chinese) |
 2021, Vol. 44
2021, Vol. 44



