2. 浙江中科依泰斯卡岩石 工程研发有限公司, 杭州 310000
2. HydroChina ITASCA Research and Development Center, Hangzhou 310000, P. R. China
随着中国工程建设的迅猛发展,地下洞室空间的建设和结构使用要求越来越高,对超大规模(跨度超过50 m)的地下空间的需求开始上升。我国地下工程跨度一般较小,对大跨度的勘察设计、建设等方面还缺乏成套的技术。地下工程除要求满足特定的使用功能外,还特别强调施工过程中的安全以及在长期运营过程中的安全稳定。同时,大跨度地下工程具有结构受力复杂、安全风险高的特点,且受岩体质量、结构面特征、初始地应力场等众多因素影响,是一项非常复杂的地下工程活动。
目前,国内外对于大跨度洞室的研究较少,尤其对跨度大于50 m以上洞室的研究更少。例如,向欣[1]通过3DEC离散元软件结合金沙江某水电站调压井工程,对大跨度洞室(50 m筒径)拱顶的稳定性和支护措施进行了研究,结果表明,采用系统支护与混凝土置换加强支护可以有效控制顶拱错动带的变形;徐干成等[2]对60 m跨度的扁平地下洞室开挖方案进行了研究;Broch等[3]通过挪威大跨度地下洞室的工程案例,研究了61 m大跨度洞室的开挖和支护;Barton[4]通过离散元软件UDEC对挪威62 m大跨度洞室的变形进行预测,并对实际变形值进行了监测。
洞室的设计中,矢跨比(洞室中矢高S与洞室跨度L之比S/L)的设计对洞室稳定性的影响至关重要,过小的矢跨比可能会造成顶拱无法形成应力拱,无拱效应,导致洞室稳定性差,而较大的矢跨比会有利于拱效应的形成,能够提高洞室的稳定性,但较大的矢跨比同时会增加建造成本,如何设计大跨度洞室的矢跨比是大跨度设计中的一项重要内容。一般认为岩体强度、埋深、地应力、结构面等因素对洞室稳定有直接影响,在洞室矢跨比设计中应该重点考虑。
能满足洞室变形、稳定等一系列条件下的最小矢跨比,称为洞室最小矢跨比。在最小矢跨比研究中,洞室的变形标准是最为关键的,洞室的矢跨比、岩体强度、埋深等因素,究竟以什么标准来判断洞室稳定是个非常关键的问题。Sakurai[5]提出了极限应变的概念,即洞室变形小于或等于极限应变时,洞室无需特殊支护便能够稳定。在国内规范中也都提及了一般洞室变形收敛的控制值,如, 水工隧道设计规范和公路隧洞设计规范等,但这些规范所针对的都是小跨度洞室,并不适用于跨度大于50 m的大跨度洞室。极限应变已有较多研究,例如, Sakurai[5]、Barton[6]、Hoek[7-8]、Singh等[9]都对极限应变的标准进行了研究。目前,国内外对大跨度洞室的最小矢跨比鲜有研究,而最小矢跨比的确定对大跨度洞室的设计有着重要的参考价值。笔者提出适用于大跨度洞室的应变标准,再采用能够考虑岩体软化、剪胀、体胀、密度变化等开挖响应特征的Cavehoek本构模型[10],研究埋深、地应力、地质强度指标GSI和结构面对60 m大跨度洞室最小矢跨比的影响。
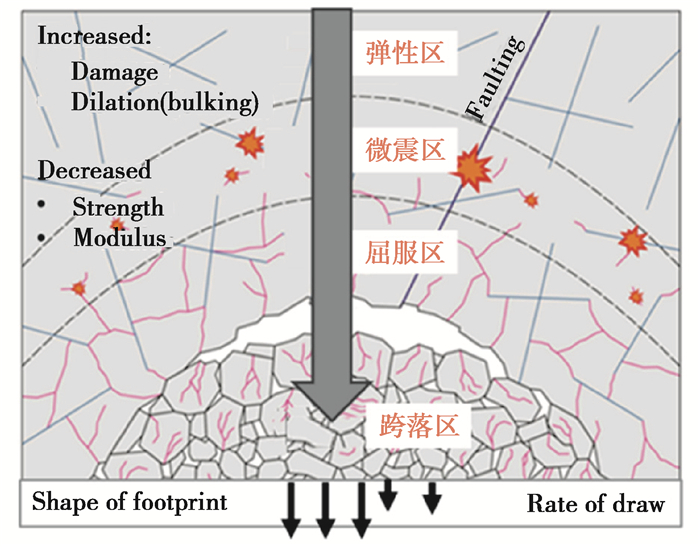
1 Cavehoek本构模型理论Cavehoek本构模型是美国Itasca公司于2010年开发的[10],主要应用于煤矿长壁开采和采空区发展的三维计算[11-13]。Duplancic[14]通过波速法对帕克斯的矿区围岩进行了调查,发现煤层开挖后围岩的应力状态主要可分为4个区域:垮落区、屈服区、微震区、弹性区,如图 1所示。
|
图 1 开挖过程中围岩的力学响应示意 Fig. 1 Mechanical response diagram of surrounding rock during excavation |
弹性区:并未扰动的区域,岩体仍处于弹性状态;微震区:由于旧裂纹的滑动或新裂纹的产生,微震行为在该区域的发育较为集中;屈服区:该区域岩体的应力状态有着显著的降低,且裂隙较为发育,破坏特征明显。同时,该区域岩体强度损失较多,仅能够为上覆岩体提供较小的支护压力;垮落区:由于开挖导致岩体垮落的区域。
开采过程计算分析的本构需要能够反映出岩体从无扰动状态到崩塌的过程,而在大跨度洞室最小矢跨比计算中,围岩的响应与煤层开采时上部围岩的响应机制基本一致:当洞室矢跨比非常小时,无法形成应力拱,上部岩层垮塌,当洞室矢跨比达到一定要求时,上部岩层可以稳定,在整个过程中,围岩的响应包括:围岩变形和应力的重分布;岩体破坏后,岩体强度由峰值强度降到残余强度的水平;岩体的剪胀行为;岩体的体胀行为;变形参数的软化、密度变化等围岩响应特征。
Cavehoek本构主要包括:岩体密度、岩体质量评分GSI、岩块材料常数mi、岩块单轴抗压强度UCS、岩块弹性模量Ei、岩体残余强度等参数,若需要考虑结构面,还需考虑结构面的参数:粘聚力、摩擦角、抗拉强度、剪胀角等。Cavehoek本构遵循的是Hoek Brown准则[15]:
| $ {\sigma _1} = {\sigma _3} + {\rm{UCS}}\left( {{m_b}\frac{{{\sigma _3}}}{{{\rm{UCS}}}} + s} \right)a, $ | (1) |
| $ \left\{ {\begin{array}{*{20}{c}} {{m_b} = {m_i}\exp \left( {\frac{{{\rm{GSI}} - 100}}{{28}}} \right),}\\ {s = \exp \left( {\frac{{{\rm{GSI}} - 100}}{9}} \right),}\\ {a = \frac{1}{2} + \frac{1}{6}\left( {{{\rm{e}}^{ - {\rm{GSI}}/15}} - {{\rm{e}}^{ - 20/3}}} \right)}。\end{array}} \right. $ | (2) |
式中:σ1为最大主应力;σ3为最小主应力;UCS为岩块单轴抗压强度;mi为岩块材料常数;GSI为岩体质量评分。
本构模型中岩体的弹性模量主要根据Hoek和Diederichs[16]提出的等式进行计算:
| $ {E_{{\rm{rm}}}} = {E_i}\left( {0.02 + \frac{1}{{1 + {{\rm{e}}^{(60 - {\rm{GSI}})/11)}}}}} \right), $ | (3) |
式中:Ei为岩块弹性模量;Erm为岩体弹性模量。
岩体的体积和密度的变化等,可根据岩体的膨胀系数来确定,膨胀系数定义为
| $ B = \frac{{\Delta V}}{{{V_i}}} = \frac{n}{{(1 - n)}}, $ | (4) |
式中:B为膨胀系数;ΔV为体积变化量;Vi为初始体积;n为孔隙率。
计算中,岩体的剪胀角是随岩体塑性剪切应变的变化而变化:
| $ {\psi _{\gamma {\rm{p}}}} = 2[{\tan ^{ - 1}}\sqrt {{N_\psi }} ] - \frac{{\rm{ \mathsf{ π} }}}{2}, $ | (5) |
| $ \left\{ {\begin{array}{*{20}{c}} {{\psi _{{\rm{peak }}}} = \frac{{{\varphi _c}}}{{1 + {{\log }_{10}}{\rm{UCS}}}}{{\log }_{10}}\frac{{{\rm{UCS}}}}{{{\sigma _3} + 0.1}},}\\ {{N_{\psi {\rm{ peak }}}} = \frac{{1 + \sin {\psi _{{\rm{peak }}}}}}{{1 - \sin {\psi _{{\rm{peak }}}}}},}\\ {{N_\psi } = 1 + \left( {{N_\psi } - 1} \right){{\rm{e}}^{ - {\gamma ^p}}}/{\gamma ^{p,*}},} \end{array}} \right. $ | (6) |
式中:ψγp为岩体当前剪胀角;ψpeak为峰值强度时岩体剪胀角;φc为内摩擦角;γp为塑性剪应变;γp, *为实验室所得塑性剪切应变实验值。
因此,Cavehoek本构模型能够考虑大跨度洞室开挖中围岩的种种响应特征,文中采用Cavehoek模型计算大跨度洞室矢跨比由小到大的开挖过程,求得满足一定应变标准时,当前矢跨比即为最小矢跨比。
2 极限应变计算方法极限应变εcr主要是指洞室在小于等于该应变时,洞室在无特殊支护下能够稳定,即洞室应变小于等于该值,则洞室处于稳定状态;若大于该值,则洞室稳定存在一定的风险,需要注意的是极限应变总是小于破坏时的应变。对于大跨度洞室的极限应变εcr的判断标准,目前没有明确的规定,但国内外对一般洞室的极限应变均有研究和规定,如《水工隧道设计规范2004》和《公路隧道设计规范》,都对洞室的应变标准进行了相关规定。其中,明确说明该规范主要是针对矢跨比在0.8~20 m的洞室。对于大跨度洞室的极限应变求解方法,需要追溯到极限应变的最初求解原理,文中将介绍几种极限应变的求解方法,提出适合于大跨度洞室的极限应变计算方法。
2.1 Sukurai法[5]较早时期Sakurai曾提出极限应变的概念,计算思路为
| $ {\varepsilon _{{\rm{ci}}}} = \frac{{{\sigma _{{\rm{ci}}}}}}{{{E_i}}}({\rm{ percent }}), $ | (7) |
式中:εci为岩块的极限应变;Ei为岩体弹性模量;σci为岩体单轴抗压强度(UCS)。需要注意的是该公式求出来的极限应变是岩块的极限应变εci,如何将岩块计算出的结果应用到实际尺度的洞室中呢?Sakurai认为岩块与实际的岩体相比,岩块中不含结构面、裂隙等,而岩体中包含结构面和裂隙等。如果依据式(7)的思路,实际岩体的应变可以表示为
| $ {\varepsilon _{{\rm{cr}}}} = \frac{{{\sigma _{{\rm{cr}}}}}}{{{E_r}}} = \frac{{m{\sigma _{\rm{c}}}}}{{nE}} = \left( {\frac{m}{n}} \right){\varepsilon _{{\rm{ci}}}}, $ | (8) |
式中:m和n分别为岩块的单轴抗压强度σci和弹性模量Ei的折减系数,;Er为岩体弹性模量;σcr为岩体单轴抗压强度。其中m和n值的区间为0~1.0,对于土而言m和n的比值基本为1,因此,土体实验的结果可以直接应用到工程实践中。对于岩石,通过实验发现m和n的比值在1~3,证明了岩块极限应变与岩体的极限应变在一个数量级,其原因主要是因为岩体中的裂隙等对单轴抗压强度和弹性模量的影响是同时的,而并非只对某个值影响。岩块的极限应变εci是岩体的极限应变的1~3倍,如果采用岩块的极限应变εci作为预警值,那么这个值已经包括了一个安全系数1~3。
2.2 Singh法[9]Singh[17]通过对洞室的反馈分析,得到:
| $ \begin{array}{*{20}{c}} {{\sigma _{{\rm{cr}}}} = 7{\gamma ^{{\rm{Q}}1/3}}{\rm{MPa}},Q < 10,{J_{\rm{w}}} = 1.0,}\\ {{\sigma _{{\rm{ci}}}} < 100{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{MPa,}}} \end{array} $ | (9) |
式中:γ为岩体的密度,gm/cc;σcr为岩体的单轴抗压强度;Q为岩体质量的分值;JW是水对Q分值的折减系数;σci为岩体的单轴抗压强度。
极限应变可以通过岩块的参数和Q值来得到:
| $ {\frac{1}{{{\varepsilon _{{\rm{cr}}}}}} = \frac{{{E_{{\rm{tr}}}}}}{{{\sigma _{{\rm{cr}}}}}} = \frac{{{E_i}}}{{{\sigma _{{\rm{cr}}}}}}{{\left( {\frac{{{\sigma _{{\rm{cr}}}}}}{{{\sigma _{{\rm{ci}}}}}}} \right)}^{ - 1.6}} = {E_i}\left( {7{\gamma ^{Q1/3}}} \right)0.6{{\left( {{\sigma _{{\rm{ci}}}}} \right)}^{ - 1.6}},} $ | (10) |
| $ {{\varepsilon _{{\rm{cr}}}} = 31.1\frac{{\sigma _{{\rm{ci}}}^{1.6}}}{{{E_i}{\gamma ^{0.6}}Q0.2}}({\rm{ percent }}),} $ | (11) |
式中:εci为岩块的极限应变;Ei为岩体弹性模量;σci为岩体单轴抗压强度(UCS)。
Singh还基于Barton[6]提出的关系式对极限应变进行了研究,Barton建议:
| $ {E_{\rm{r}}} = 10{\left[ {\frac{{Q{\sigma _{{\rm{ci}}}}}}{{100}}} \right]^{1/3}} \times {10^3}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{MPa,}} $ | (12) |
式中:σci为岩体单轴抗压强度;Er为岩体弹性模量;Q为岩体质量的分值。
最终得到极限应变为
| $ {\varepsilon _{{\rm{cr}}}} = 5.84\frac{{\sigma _{{\rm{ci}}}^{0.88}}}{{{Q^{0.12}}E_i^{0.63}}}({\rm{ percent }})。$ | (13) |
Hoek通过对众多工程的统计,发现:
| $ {\varepsilon _{{\rm{cr}}}} = 1.073\sigma _{{\rm{cr}}}^{ - 0.318}, $ | (14) |
式中:εci为岩块的极限应变;σcr为岩体单轴抗压强度(UCS)。
3 计算方案 3.1 模拟工况文中主要从GSI、埋深、侧压力系数K0、结构面几个方面进行研究。对于大跨度洞室,成洞的前提条件对岩体质量是有要求的,这一点从Q系统中也可以看出,对于跨度大于50~60 m的大跨度洞室,在无特殊支护下,GSI一般大于40。因此,GSI共考虑40、45、50...80共9种情况。埋深考虑100、200、300、400、500 m共5种情况。侧压力系数考虑0.7、0.9、1.1、1.3、1.5、1.7共6种情况,结构面倾角考虑0°~90°,每10°为一种工况,共10种情况。具体计算工况如表 1所示。
| 表 1 计算工况 Table 1 Calculated condition |
岩块的参数按某实验中得到的弱风化晶屑凝灰岩的上、中、下3种值来考虑,具体如表 2所示。
| 表 2 cavehoek本构岩体计算参数 Table 2 arameters of cavehoek constitutive |
结构面的参数按胶结结构面的参数来考虑,取一般胶结结构面参数的上限值和下限值进行计算,具体参数如表 3所示。
| 表 3 胶结结构面计算参数 Table 3 Calculation parameters of cementing structure surface |
由分析可知,岩体的极限应变εcr一般可以根据围岩岩体条件来获得,例如, 岩体的弹性模量,如果缺少实验资料,Q值同样可以用来求解临界应变。对于洞室来说,洞室开挖后围岩的应力会重新分布,洞室的环向应力会逐渐增大,接着达到岩体单轴抗压强度,如果环向应力再增大,环向岩体将会屈服破坏,洞室的稳定取决于围岩的应力状态,因此, 岩体的极限应变εcr被用来作为洞室的极限应变,评估洞室的稳定性。
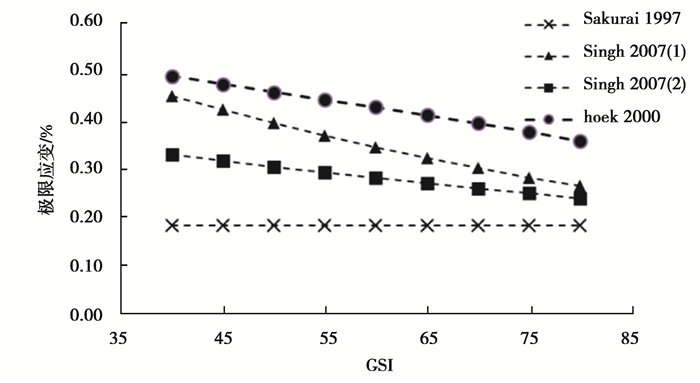
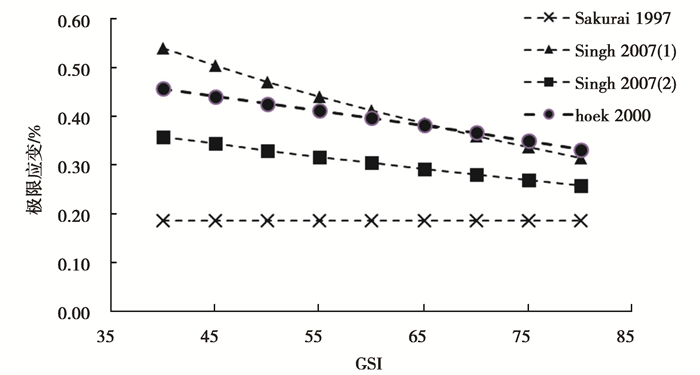
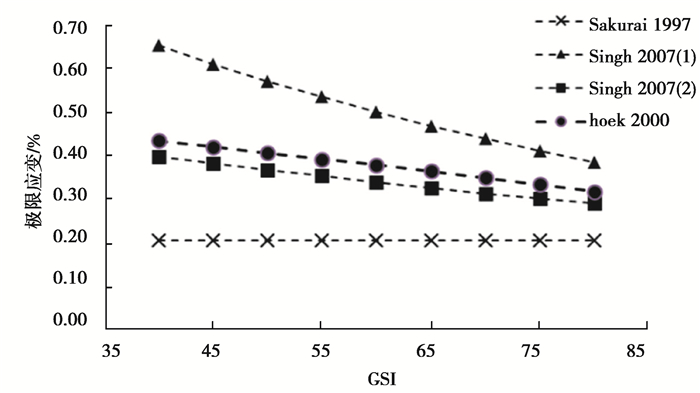
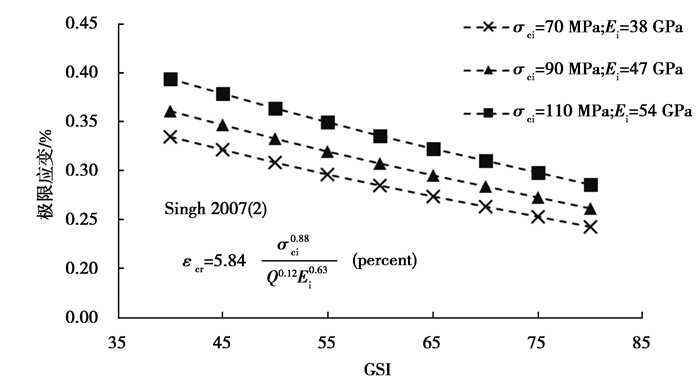
在极限应变求取中有Sakurai法、Singh法、Hoek法,其中,Singh根据他自己以及Barton提出的岩体参数关系分别提出了2种极限应变求取法,考虑了岩体质量以及岩块本身力学性质。图 2~图 4为不同强度弱风化晶屑凝灰岩通过以上4种方法计算出的在各GSI下的极限应变值εcr。GSI与Q值得换算如式(15)所示。其中,Sakurai法由于按岩块极限变形来考虑的,偏于保守。Singh提出的方法一与Hoek提出的方法在不同岩石强度下,所求得的岩体极限应变εcr值大于或小于前2种方法,而Singh基于Barton关系式提出的方法二在各条件下均小于前2种方法,考虑大跨度工程的安全问题,文中采用Singh的方法二计算出的岩体极限应变作为洞室变形的极限应变εcr,结果如图 5所示。
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{RMR}} = {\rm{GSI}} - 5,}\\ {Q \approx {{10}^{\frac{{({\rm{RMR}} - 50)}}{{15}}}}}。\end{array}} \right. $ | (15) |
|
图 2 UCS=70 MPa,Ei=37.0 GPa时各GSI下的极限应变 Fig. 2 When UCS=70 MPa, Ei=37.0 GPa, the limit strain under each GSI |
|
图 3 UCS=90 MPa,Ei=47.0 GPa时各GSI下的极限应变 Fig. 3 When UCS=90 MPa, Ei=47.0 GPa, the limit strain under each GSI |
|
图 4 UCS=110 MPa,Ei=54.0 GPa时各GSI下的极限应变 Fig. 4 When UCS=110 MPa, Ei=54.0 GPa, the limit strain under each GSI |
|
图 5 各GSI下计算采用的极限应变标准值 Fig. 5 The standard value of ultimate strain used under each GSI is calculated |
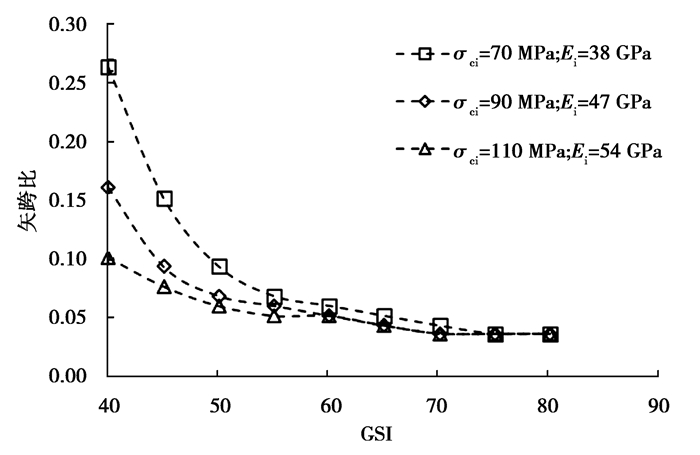
图 6为不同强度弱风化晶屑凝灰岩在不同GSI下60 m大跨度洞室最小矢跨比计算结果,由图可知,在不同岩石强度下,GSI对60 m大跨度洞室最小矢跨比的影响是不同的,岩石强度越低,GSI的影响越大,岩石强度越高,GSI的影响越小;GSI对60 m大跨度洞室最小矢跨比的影响主要在GSI取40~55之间,当GSI大于或等于60时,GSI的改变对最小矢跨比的影响较小;当前岩体条件下,60 m大跨度洞室的矢跨比为0.04~0.26。
|
图 6 不同强度晶屑凝灰岩在不同GSI时的最小矢跨比 Fig. 6 The minimum sagittal span ratio of crystal tuff with different strength at different GSI |
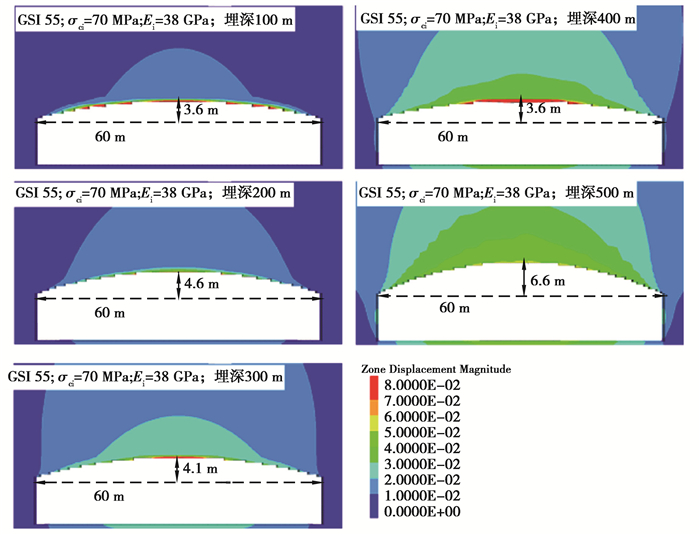
图 7给出了弱风化晶屑凝灰岩下限值时不同GSI下洞室最小矢跨比计算结果,由图可知,虽然GSI大于或等于60时,对60 m大跨度洞室的最小矢跨比的影响较小,但对洞室整体的变形仍然有影响,GSI越大,洞室变形越小。

|
图 7 弱风化晶屑凝灰岩下限值时不同GSI下洞室最小矢跨比计算结果 Fig. 7 The calculation results of the minimum sagittal span ratio of different GSI in the lower limit value of weakly weathered crystal tuff |
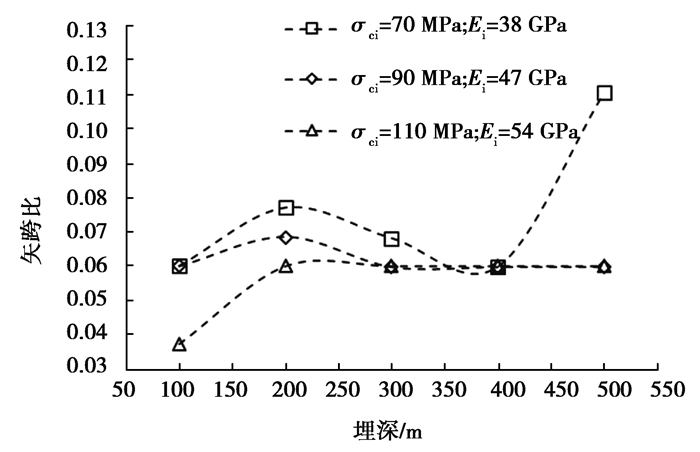
图 8为不同强度弱风化晶屑凝灰岩在不同埋深下洞室最小矢跨比计算结果,由图可知,在100~500 m埋深内,埋深对60 m大跨度洞室的最小矢跨比的影响比GSI的影响小;不同岩石强度下,在埋深小于200 m时,矢跨比随埋深的增大呈增大趋势;对于岩石强度取下限值时,当埋深超过200 m时,最小矢跨比有增大的趋势;对于岩石强度取上限值和中值时,当埋深超过200 m时,最小矢跨比基本不变;在当前岩体条件下,埋深从100~200 m,60 m大跨度洞室最小矢跨比分布范围为0.04~0.11。
|
图 8 不同强度弱风化晶屑凝灰岩在不同埋深时的最小矢跨比 Fig. 8 The minimum sagittal span ratio of slightly weathered crystal tuff with different strength at different burial depths |
图 9给出了弱风化晶屑凝灰岩下限值时不同埋深下洞室最小矢跨比计算结果,由图可知,虽然100~500 m埋深内,埋深对60 m大跨度洞室的最小矢跨比的影响较小,但对洞室整体的变形仍然是有影响的,埋深越大,洞室整体变形越大。
|
图 9 弱风化晶屑凝灰岩下限值时不同埋深下洞室最小矢跨比计算结果 Fig. 9 Calculation results of the minimum sagittal span ratio of the lower limit value of weakly weathered crystal tuff with different buried depths |
图 10为不同强度弱风化晶屑凝灰岩在不同侧压力系数下60 m大跨度洞室最小矢跨比计算结果,由图可知,侧压力系数从0.7~1.7对60 m洞室最小矢跨比影响较小,岩石强度不同,最小矢跨比在不同侧压力系数下所表现出的规律也不一样;在岩石强度为高值时,最小矢跨比随着侧压力系数的增大而减小;当岩石强度为中值时,最小矢跨比随着侧压力系数的增大先减小后增大;当岩石强度取低值时,最小矢跨比随着侧压力系数的增大表现为以增长为主的趋势;对于当下的埋深和岩石条件,侧压力系数为0.7~1.7时,60 m大跨度洞室最小矢跨比的范围为0.04~0.1。主要原因是不同岩石条件和不同应力状态下,所达到的拱效应不一样,侧压力系数越高,岩体条件越好,越有利于拱效应的形成,但岩体条件越差,较高的侧压力系数反而不利于拱效应的形成。
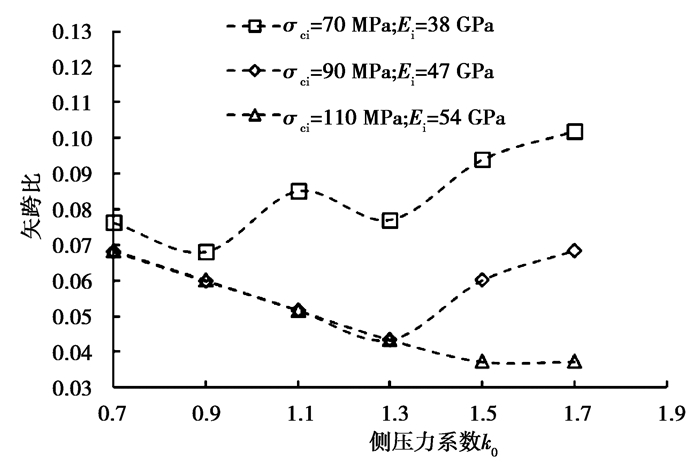
|
图 10 不同强度弱风化晶屑凝灰岩在不同GSI时的最小矢跨比 Fig. 10 Minimum sagittal span ratio of slightly weathered crystal tuff with different strength at different GSI |
图 11给出了弱风化晶屑凝灰岩下限值时不同侧压力系数下洞室最小矢跨比计算结果,由图可知,侧压力系数从0.7~1.7时,对60 m大跨度洞室的最小矢跨比的影响较小,但对洞室整体的变形仍然是有影响的,基本表现为侧压力系数越大,洞室整体变形越大。
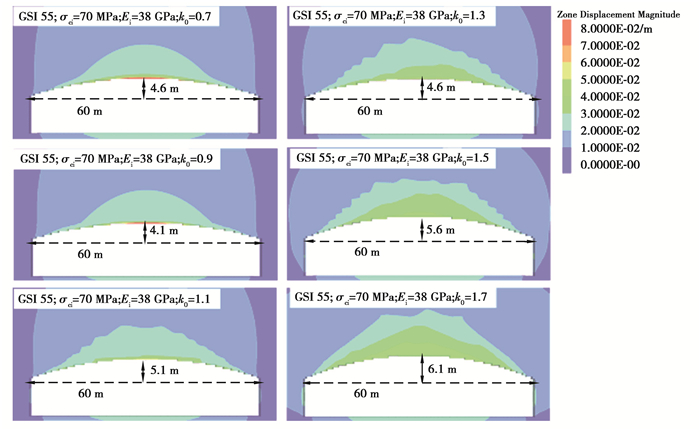
|
图 11 弱风化晶屑凝灰岩下限值时不同侧压力系数下洞室最小矢跨比计算结果 Fig. 11 Calculation results of the minimum sagittal span ratio of the cavity under different lateral pressure coefficients under the lower limit value of weakly weathered crystal tuff |
在结构面对矢跨比的影响分析中发现,某些情况下即使应变小于极限应变标准值,但洞室整体变形范围较大,即扰动范围较大,这种现象不利于大跨度洞室的稳。如图 12所示,图中几种情况的应变均未超过极限应变标准值,但扰动范围大,这种情况是不能安全成拱的,因此在结构面对最小矢跨比研究中,大跨度洞室的安全不能仅仅从极限应变标准来,还应当根据具体计算结果来判断是否是结构面主导的问题。
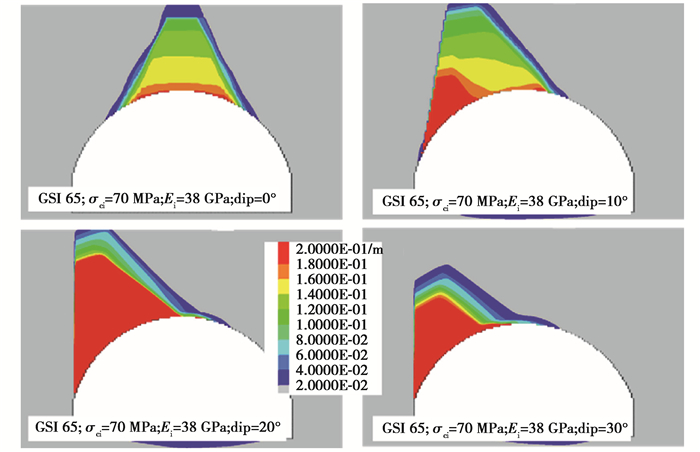
|
图 12 应变满足要求但变形范围较大的情况 Fig. 12 When the strain meets the requirement but the deformation range is large |
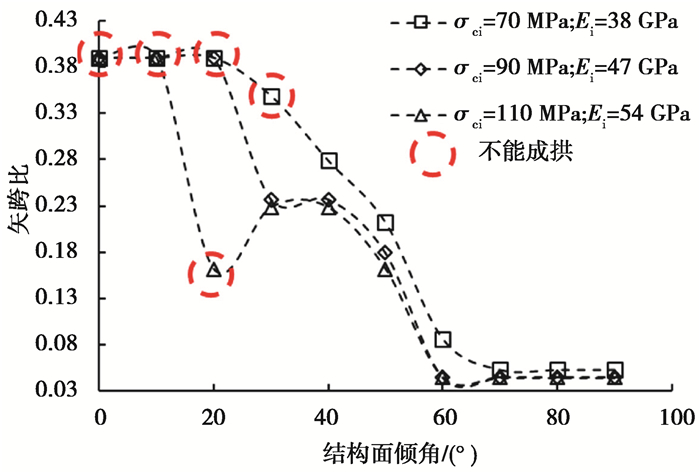
|
图 13 不同强度弱风化晶屑凝灰岩在不同倾角结构面时的最小矢跨比(结构面参数取低值) Fig. 13 Minimum Sagittal span Ratio of slightly weathered crystal tuff with Different Strength at different Dip Angle structural Planes (structural plane parameters are taken as low values) |
根据上述原则,对两种强度的结构面在不同倾角下的60 m大跨度洞室最小矢跨比进行了统计(图中红色圆圈标记表示不能成拱),如图 14和图 15所示。从图中可知,结构面参数取低值时,结构面的倾角对大跨度洞室成拱起关键作用,倾角为0°~30°时,虽然应变满足条件,但仍然安全裕度较低,不能成拱;结构面参数取高值时,结构面的影响相对减小,在岩石强度较小时,缓倾结构面对洞室稳定性影响较大;缓倾结构面对大跨度洞室稳定影响非常大,结构面的倾角越大,越有利于大跨度洞室的稳定,最小矢跨比随着倾角的增大呈减小趋势。
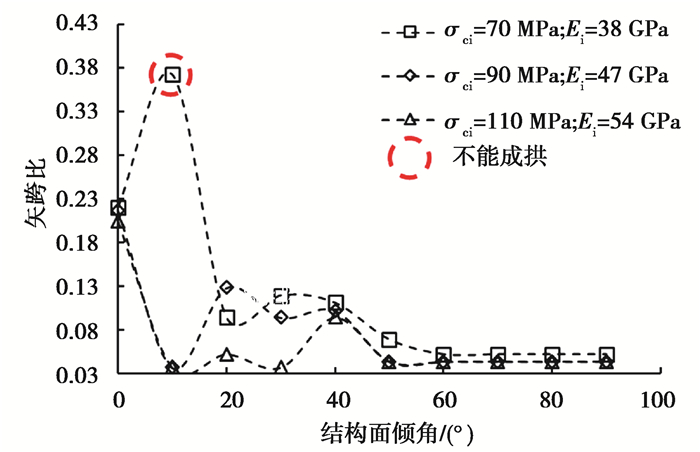
|
图 14 不同强度弱风化晶屑凝灰岩在不同倾角结构面时的最小矢跨比(结构面参数取高值) Fig. 14 Minimum sagittal span Ratio of crystal tuff with different strength and weak weathering at different dip Angle structural Planes (structural plane parameters are taken as high values) |
基于能反应岩体开挖多种响应特征的Cavehoek本构,对60m大跨度洞室的最小矢跨比进行了研究,主要得到以下结论:
1) GSI对60 m大跨度洞室最小矢跨比影响较大,GSI值越高,最小矢跨比越小,其中GSI在40~55间对最小矢跨比影响最大;
2) 埋深对60 m大跨度洞室最小矢跨比的影响相对GSI的影响来说,埋深的影响较小,最小矢跨比与埋深的关系并非为线性关系;
3) 侧压力系数对60 m大跨度洞室最小矢跨比的影响相对GSI的影响来说,侧压力系数的影响较小,同时不同岩石强度下,所表现出的规律也是不同的;
4) 结构面对60 m大跨度洞室的影响非常复杂,结构面的倾角对大跨度洞室能否安全成拱起关键性作用,缓倾结构面不利于大跨度洞室的成拱,结构面的倾角越大,越有利于大跨度洞室的稳定,最小矢跨比随着倾角的增大呈减小趋势。
另外,研究中未能考虑埋深对极限应变标准值的影响,同时跨度的变化对最小矢跨比的影响也未能进行分析,在后续工作中将针对这两点进行研究。
| [1] |
向欣, 王义锋, 孟国涛, 等. 大跨度地下洞室拱顶稳定性及支护措施研究[J]. 岩石力学与工程学报, 2012, 31(2): 3643-3649. Xiang X, Wang Y F, Meng G T, et al. Study of stability and supporting measures of chamber arch crown for large span underground caverns[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(2): 3643-3649. (in Chinese) |
| [2] |
徐干成, 袁伟泽, 徐景茂, 等. 大跨度扁平地下洞室开挖方案研究[J]. 地下空间与工程学报, 2018, 14(S2): 275-280. Xu G C, Yuan W Z, Xu J M, et al. Study on excavation scheme of large span flat underground cavern[J]. Chinese Journal of Underground Space and Engineering, 2018, 14(S2): 275-280. (in Chinese) |
| [3] |
Broch E, Myrvang A M, Stjern G. Support of large rock caverns in norway[J]. Tunnelling and Underground Space Technology, 1996, 11(1): 11-19. DOI:10.1016/0886-7798(96)00046-6 |
| [4] |
Barton N, By T L, Chryssanthakis P, et al. Predicted and measured performance of the 62 m span norwegian olympic ice hockey cavern at gjøvik[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1994, 31(6): 617-641. |
| [5] |
Sakurai S. Lessons learned from field measurements in tunnelling[J]. Tunnelling and Underground Space Technology, 1997, 12(4): 453-460. DOI:10.1016/S0886-7798(98)00004-2 |
| [6] |
Barton N. Some new Q-value correlations to assist in site characterisation and tunnel design[J]. International Journal of Rock Mechanics and Mining Sciences, 2002, 39(2): 185-216. DOI:10.1016/S1365-1609(02)00011-4 |
| [7] |
Hoek E, Marinos P. Predicting tunnel squeezing problems in weak heterogeneous rock masses[J]. Tunnels and Tunnelling international, 2000, 32(11): 45-51. |
| [8] |
Hoek E. Tunnel support in weak rock[C]//Keynote address, Symposium of Sedimentary Rock Engineering, Taipei, Taiwan, 1998, 12.
|
| [9] |
Singh M, Singh B, Choudhari J. Critical strain and squeezing of rock mass in tunnels[J]. Tunnelling and Underground Space Technology, 2007, 22(3): 343-350. DOI:10.1016/j.tust.2006.06.005 |
| [10] |
Pierce M. CaveHoek constitutive model: theory and implementation[M]. Itasca technical memorandum, 2010.
|
| [11] |
SjöBerg J, Perman F, Lope A A D, et al. Deep sublevel cave mining and surface influence[C]//Proceedings of the Eighth International Conference on Deep and High Stress Mining, Australian Centre for Geomechanics, Perth, 2017: 357-372.
|
| [12] |
Hebert Y, Sharrock G. Three-dimensional simulation of cave initiation, propagation and surface subsidence using a coupled finite difference-cellular automata solution[C]//Proceedings of the Fourth International Symposium on Block and Sublevel Caving, Australian Centre for Geomechanics, Perth, 2018.
|
| [13] |
Pierce M. Numerical modeling of rock mass weakening, bulking and softening associated with cave mining[J]. ARMA e-Newsletter Spring, 2013(9). |
| [14] |
Duplancic P, Brady B H. Characterisation of caving mechanisms by analysis of seismicity and rock stress[C]//9th ISRM Congress. International Society for Rock Mechanics and Rock Engineering, 1999.
|
| [15] |
Hoek E, Carranza-Torres C, Corkum B. Hoek-Brown failure criterion-2002 edition[J]. Proceedings of NARMS-Tac, 2002, 1: 267-273. |
| [16] |
Hoek E, Diederichs M S. Empirical estimation of rock mass modulus[J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(2): 203-215. DOI:10.1016/j.ijrmms.2005.06.005 |
| [17] |
Singh B, Villadkar M N, Samadhiya N K, et al. Rock mass strength parameters mobilised in tunnels[J]. Tunnelling and Underground Space Technology, 1997, 12(1): 47-54. DOI:10.1016/S0886-7798(96)00060-0 |
 2021, Vol. 44
2021, Vol. 44

