b. 重庆大学 汽车工程学院, 重庆 400044;
c. 重庆大学 机械工程学院, 重庆 400044
b. School of Vehicle Engineering, Chongqing University, Chongqing 400044, P. R. China;
c. School of Mechanical Engineering, Chongqing University, Chongqing 400044, P. R. China
近几年来汽车电动化、智能化的飞速发展,使具有真空助力器的传统液压制动系统难以满足实际功能上的需求。对于真空助力制动系统,在新能源汽车上需安装电子真空泵及空气压缩机等部件,增加了整车质量与能源消耗。而电子机械制动系统(electro mechanical braking, EMB)研发不够完善,控制算法集成度高及簧下质量增加等问题有待解决[1-2]。电动液压助力器不需要额外的真空源,可以准确、快速地控制制动压力,在自适应续航系统和自动紧急制动系统中具有很强的适应性[3],成了目前的研究热点。
为解决驾驶员在紧急制动中踏板力不足问题,真空助力器通过制动踏板速度或制动压力阈值来识别驾驶员的意图,执行相应的控制策略[4]。以制动踏板速度作为识别依据时,会出现制动位移较小,踏板速度很大的情况,识别不准确。以制动压力阈值作为识别依据时,制动压力是制动踏板位移及速度的结果量,无法保证识别的实时性[5]。
针对制动意图识别问题,国内外学者提出了多种制动意图识别的方法:以制动踏板位移和速度作为识别参数,结合操纵和控制经验,应用模糊推理方法、人工神经网络方法、结合模糊推理与神经网络方法和隐马尔可夫模型方法来识别驾驶员制动意图等[6-8]。在模糊推理方法中,模糊规则和隶属函数的设置依靠经验,不具有学习和自适应能力。在人工神经网络方法中,计算时间长,计算量大。同时驾驶员的制动行为是一个动态过程,而模糊推理与神经网络处理时间序列的能力不强,主要用于静态识别[9-10]。针对上述存在的问题,研究中以电动液压助力制动系统为研究对象,选取助力电机的转角、转速和整车车速作为制动意图识别参数,采用具有较强时间序列处理能力的隐式马尔可夫模型对制动意图进行识别来控制助力电机执行不同的助力模式。在紧急制动工况下,解决驾驶员因踏板力不足而导致制动距离过长的问题,提高驾驶安全性。
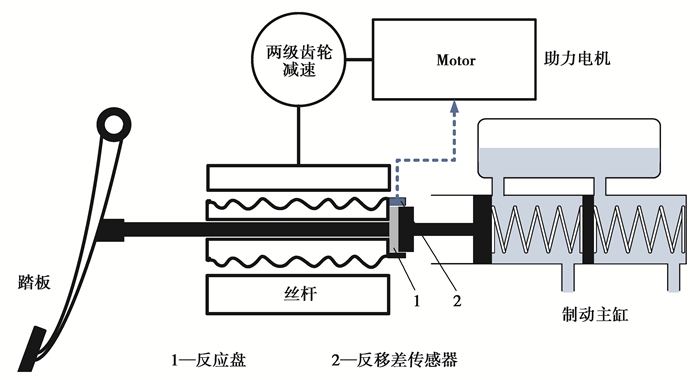
1 电动液压助力制动系统电动液压助力制动系统主要由制动踏板、电动液压助力器、ABS泵和制动器组成,其结构简图如图 1所示。
|
图 1 电动液压助力器结构简图 Fig. 1 The structure diagram of Electric Power Hydraulic booster |
当驾驶员踩下制动踏板时,位移传感器检测到踏板推杆与助力推板间的位移差,助力电机启动,经过减速机构推动助力推板,与踏板推杆保持一定位移差。同时,踏板推杆力与电机助力通过反应盘共同作用在主缸推杆上,产生制动压力。根据电动液压助力器的工作原理,在踏板推杆位移和助力推板间的位移差设计中,设计了正常制动和紧急制动电机助力模式,根据驾驶员的制动意图识别对两种助力模式进行执行控制,具有助力模式控制的电动液压助力制动系统如图 2所示。

|
图 2 电动液压助力制动系统 Fig. 2 Electric Power Hydraulic booster Braking System |
在路面附着系数一定的情况下,不考虑整车阻力,驾驶员进行制动时,期望的制动强度与制动主缸压强具有相对确定关系, 即
| $ z=\frac{{\pi {d_1^2}{f_1}{r_1}P + \pi {d_2^2}{f_2}{r_2}P\beta }}{{mgR}}, $ | (1) |
式中:m为整车质量,kg;d1, d2分别为前、后制动轮缸直径,mm;f1, f2分别为前、后制动器摩擦片系数;r1,r2分别为前、后制动器制动半径, mm;R为车轮滚动半径, mm;P为制动主缸压强, MPa;β为前后轴压强分配系数。
本文研究对象为中心阀式串联主缸,当主缸参数及制动液确定时,制动压强仅与主缸推杆位移及其速度有关[11-12],即
| $ {x_{_{\rm{h}}}}={\rm{ }}\frac{{p\cdot \theta }}{{2\pi \cdot i}}{\rm{ - }}\alpha , $ | (2) |
式中:xh为踏板推杆位移, mm;p为丝杆导程, mm;i为两级齿轮减速比;θ为电机转角,rad;α为位移差,mm。因此,可将制动压强看作为助力电机转角、转速的函数,即
电动液压助力器动力源采用永磁同步电机,其参数如表 1所示。在电机控制中采用位置环、速度环、电流环三环控制方法与速度补偿和摩擦补偿控制策略,对踏板推杆位移与负载跟随如图 3所示,在进程与回程中,位移的跟踪误差为±0.12 mm,负载跟踪误差为±0.09 N·m,最大位移误差和负载发生在电机启动和结束阶段,而在电机助力阶段,电机位移与负载跟随具有良好效果。
| 表 1 助力电机参数 Table 1 The parameters of booster motor |

|
图 3 踏板推杆位移、负载跟踪结果图 Fig. 3 The following result of pedal push rod displacement and load |
制动过程中,驾驶员的踏板力可反映出驾驶员的意图。但在克服踏板空行程后,踏板力与踏板位移有相对确定关系,并受到踏板速度的影响。同时,踏板力的传感器安装不便,安装间隙较大,受制制动系统间隙和制动盘磨损状态影响,准确性和实时性不高,所以一般不作为驾驶员制动意图的识别参数[13]。
整车的制动强度是汽车减速度与重力加速度的比值,反映汽车制动能力的大小,部分整车参数如表 2所示,取路面附着系数为0.8。在不同速度下,相同的制动主缸压强会有不同的制动强度,如图 4所示,在制动强度一定时,车速越大所需的制动液压强度会有所减小。因此,在研究中将整车速度作为驾驶员制动意图识别参数。
| 表 2 某SUV部分整车参数 Table 2 The vehicle parameters of a SUV |

|
图 4 制动主缸压强与制动强度关系 Fig. 4 The relationship between brake master cylinder pressure and brake strength |
HMM模型通常用λ=(A, B, ψ)来表示。其中:
| $ \mathit{\boldsymbol{A}}{\rm{ }} = {\rm{ }}\left\{ {{a_{ij}}} \right\}{_{N \times N}}\;\;1 \le i, j \le N{\rm{ , }} $ | (3) |
| $ \mathit{\boldsymbol{B}}{\rm{ }} = {\rm{ }}\left\{ {{b_{jk}}} \right\}{_{N \times Q}}\;\;\;\;1 \le k \le Q, $ | (4) |
式中:aij表示从状态i到状态j的概率;bjk表示在状态j时观测状态k发生的概率;A为状态转移概率矩阵;B为观测概率矩阵;ψ为初始状态概率矩阵;N, Q分别为隐藏状态数和观测状态数。
研究中选取助力电机转角与转速作为观测特征量时,转角与速度为连续信号,在观测序列时间长度为T内,将观测特征量矢量化,拟合成混合高斯密度函数,可以描述为
| $ \left\{ \begin{array}{l} {b_j}\left( O \right){\rm{ }} = \sum\limits_{m = 1}^G {\mathit{\boldsymbol{\omega }}{_{jm}}N\left( {O, {\rm{ }}\mathit{\boldsymbol{\mu }}{_{jm}}, {\rm{ }}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}{_{jm}}} \right), } \\ N{\rm{ }}\left( {O, {\rm{ }}\mathit{\boldsymbol{\mu }}{_{jm}}, {\rm{ }}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}{_{jm}}} \right) = {\rm{ }}\frac{1}{{\left( {2\pi } \right){^{d/2}}\left| {{\rm{ }}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}{_{jm}}} \right|{^{1/2}}}}{\rm{exp}}\left[ {{\rm{ - }}\frac{1}{2}\left( {O - \mathit{\boldsymbol{\mu }}{_{jm}}} \right){^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{jm}^{{\rm{ - }}1}\left( {O - {\rm{ }}\mathit{\boldsymbol{\mu }}{_{jm}}} \right)} \right], \end{array} \right. $ | (5) |
式中:O为要拟合的观测特征量序列;ωjm,μjm,Σjm分别为状态为j数量为G的混合高斯函数的混合权重、均值和协方差矩阵;d为观测状态的维度。其中ωjm有以下约束:
| $ \left\{ \begin{array}{l} \sum\limits_{m = 1}^G {\mathit{\boldsymbol{\omega }}{_{jm}} = 1} , \\ {\mathit{\boldsymbol{\omega }}_{jm}} \ge 0。\end{array} \right. $ | (6) |
因此,对HMM参数进行重估,更新bj(O),定义ξt(i, j)表示在t时刻为i状态,在t+1时刻为j状态的概率,则
| $ {\xi _t}\left( {i, j} \right) = {\rm{ }}\frac{{{\alpha _t}\left( i \right){\beta _t}\left( i \right)}}{{\sum\limits_{i = 1}^N {{\alpha _t}\left( i \right){\beta _t}\left( i \right)} }}{\rm{ }} \times \frac{{\mathit{\boldsymbol{\omega }}{_{jm}}P{\rm{ }}\left[ {O, {\rm{ }}\mathit{\boldsymbol{\mu }}{_{jm}}, {\rm{ }}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}{_{jm}}} \right]}}{{\sum\limits_{m = 1}^G {{\omega _{jm}}P{\rm{ }}\left[ {O, {\rm{ }}\mathit{\boldsymbol{\mu }}{_{jm}}, {\rm{ }}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}{_{jm}}} \right]} }}, $ | (7) |
则ωjm,μjm,Σjm重估为
| $ {\mathit{\boldsymbol{\bar \omega }}_{jm}} = \frac{{\sum\limits_{t = 1}^K {{\xi _t}\left( {i, j} \right)} }}{{\sum\limits_{t = 1}^K {\sum\limits_{m = 1}^G {{\xi _t}\left( {i, j} \right)} } }}, $ | (8) |
| $ {{\mathit{\boldsymbol{\bar \mu }}}_{jm}} = \frac{{\sum\limits_{t = 1}^K {{\xi _t}\left( {i, j} \right){O_t}} }}{{\sum\limits_{t = 1}^K {{\xi _t}\left( {i, j} \right)} }}, $ | (9) |
| $ {{\mathit{\boldsymbol{ \boldsymbol{\bar \varSigma} }}}_{jm}} = \frac{{\sum\limits_{t = 1}^K {{\xi _t}\left( {i, j} \right)({O_t}{\rm{ - }}{\mu _{jm}})({O_t}{\rm{ - }}{\mu _{jm}})'} }}{{\sum\limits_{t = 1}^K {{\xi _t}\left( {i, j} \right)} }}。$ | (10) |
目前区分紧急制动大部分利用制动踏板位移与速度大小来区分[14-15],但是制动系统的区别导致结果不具有代表性。因此,研究中以驾驶员的期望制动强度区分紧急制动,定义制动强度大于0.4属于紧急制动,HMM模型观测序列表示为
| $ O\left( t \right) = \left\{ {\theta \left( t \right), n\left( t \right), k\left( t \right)} \right\}, $ | (11) |
式中:θ(t),n(t),k(t)分别表示助力电机转角、转速和整车速度标记的时间序列。其中,利用K-mean算法对整车速度进行标记
| $ k = \left\{ \begin{array}{l} 1\;\;v \in \left[ {0, 30} \right), \\ 2\;\;v \in [30, 60), \\ 3\;\;v \in [60, 90), \\ 4\;\;v \in [90, 120)。\end{array} \right. $ | (12) |
式中v为整车车速, km/h。
3.2 意图识别HMM模型训练为了使制动意图识别的参数数据不受到驾驶员习惯的影响,在Matlab/Simulink与AMESim环境下搭建电动液压助力制动系统联合仿真模型,如图 5所示。该模型中,以制动踏板力为输入起始信号,通过制动踏板模型将踏板力转换为踏板推杆力,将踏板推杆力与助力推板位移通过联合仿真接口输入至液压系统中。通过AMESim模型中各器件的作用,在Matlab/Simulink联合仿真接口接收助力负载力、踏板推杆与助力推板间的位移差和制动主缸压强。通过助力电机的位移跟随控制,输出踏板推杆位移和助力推板位移。

|
图 5 电动液压助力制动系统联合仿真模型 Fig. 5 The co-simulation model of Electric Power Hydraulic booster Braking System |
不同整车速度下,对电动液压助力制动系统输入不同形式、不同大小的踏板力,如图 6所示,分为线性输入、sin类输入和cos类输入。根据QC/T 307—2016《汽车用真空助力器性能要求及台架试验方法》,选取观测状态时间序列的时间长度为制动系统的反应时间0.3 s。对应每个制动踏板力输入,采集电机转角、转速及制动压强数据,形成观测数据集和制动压强数据集,计算不同工况下整车的阻力,与制动压强数据集计算得到制动强度数据集。最后以制动强度为特征值,对转角、转速和车速数据集进行划分,得到了正常制动和紧急制动的数据集。

|
图 6 制动踏板力输入形式 Fig. 6 The input shape of brake pedal force |
意图识别HMM模型离线训练流程如图 7所示,对每个意图识别HMM模型,首先对HMM模型的初始矩阵和状态转移矩阵初始化。输入观测序列数据,取高斯混合数量M的值,然后将权重矩阵、均值矩阵和协方差矩阵初始化。接着利用EM(expectation maximum)算法对这些参数进行迭代重估,并计算对数似然估计。判断对数似然估计是否收敛,分别得到两种制动意图的HMM模型参数。

|
图 7 离线训练流程 Fig. 7 Offline training process |
以紧急制动意图的HMM模型训练为例,选取总体观测样本2/3的数据,利用上述离线训练方法对紧急制动模型参数进行训练。高斯函数的混合度越高,对观测序列的拟合度就越高,但训练和识别中的计算量也会增大许多,取高斯混合数M=2。设置最大迭代次数为500,收敛条件为前后参数的对数似然估计差值的绝对值小于10-5。对HMM模型进行训练,得到对数似然估计值的迭代变化如图 8所示,在迭代169次后达到收敛条件,结束迭代过程,输出紧急制动意图HMM参数。

|
图 8 对数似然估计迭代值 Fig. 8 Log-likelihood Iterative value |
将训练好的紧急制动与正常制动的HMM参数保存至模型库,建立了HMM识别模型。制动意图识别流程如图 9所示,传感器采集到电机转角、转速和车速的初始信号,从初始信号中提出观测序列,将该观测序列分别输入到训练好的识别模型中,利用前向-后向算法计算该观测序列在此模型下的对数似然估计,选取对数似然估计最大的模型为当前的制动意图识别结果。

|
图 9 制动意图识别流程图 Fig. 9 The identification of braking intention |
为了验证训练的HMM参数对制动意图识别的准确性,从采集到的观测序列总体样本中选取总体1/3的数据,其中紧急制动操作250次,正常制动80次。为保证具有较好的实时性,截取时间长度为0.1 s的观测数据长度,对制动意图进行识别,制动意图识别结果如图 10所示。

|
图 10 制动意图识别验证结果 Fig. 10 The verification results of braking intention identification |
在图 10右纵坐标中,制动意图标识号为1表示处于正常制动状态,标识号为2表示处于紧急制动状态。在紧急制动样本中,紧急制动HMM模型计算的对数似然估计大于正常制动HMM模型,其制动意图识别的准确度达到96.4%。而在正常制动样本中,正常制动HMM模型计算的对数似然估计较大,制动意图识别的准确度达到100%。
4.2 整车试验将训练好HMM参数写入到电动液压助力器的控制器中,在不同车速及制动踏板力输入下进行仿真。仿真条件为:初始车速分别为50和100 km/h,制动踏板力最大值为200 N,变化率分别为300,400和500 N/s。
制动意图识别结果如图 11所示,在300和500 N/s的踏板力输入中,在两种速度条件下制动意图的识别一致,分别为正常制动和紧急制动意图。在400 N/s的踏板力输入中,制动意图的识别在车速为50 km/h为正常制动,在100 km/h中为紧急制动。仿真结果如图 12所示,根据电动液压助力制动系统中控制器识别的驾驶员制动意图,助力电机执行两种助力模式。在紧急制动模式中,电机助力的范围增加,使制动踏板位移和速度均有增加,制动主缸压强从原来的4.9 MPa增加到6.7 MPa,以提供更大的制动力。另外,从踏板力400 N/s的结果中可以看出整车速度对制动意图识别结果的影响。

|
图 11 制动意图识别结果 Fig. 11 The identification results of braking intention |

|
图 12 各工况仿真结果图 Fig. 12 The simulation results of various working condition |
图 13是在车速为100,60和30 km/h,对应的踏板力变化率分别为400,450和500 N/s,最大踏板力为200 N的工况下,是否采用制动意图识别的制动距离和车速的结果。通过结果可以发现,在采用制动意图识别紧急制动后,车辆的制动距离和制动时间有明显的减小,提高了驾驶安全性。并且从结果中可以看出,在车速越大的情况下,采用制动意图识别的制动效果更好,在100 km/h车速,400 N/s踏板力变化率的情况下,车辆的制动距离从原来的72.3 m缩短到57.2 m,制动时间从原来5.5 s减小到4.3 s。

|
图 13 制动距离和车速仿真结果图 Fig. 13 The simulation results of braking distance and vehicle speed |
为了解决驾驶员在紧急状况下踏板力不足而导致制动距离过长问题,笔者采用隐马尔科夫模型对驾驶员制动意图进行识别来控制助力电机的助力模式,并进行了各种工况下的仿真试验,得到了以下结论:
1) 选取助力电机转角、转速和车速作为制动意图识别参数,根据隐马尔可夫模型的制动意图识别方法在330次制动操纵中,正常制动意图准确率达到100%,紧急制动意图达到96.4%,可准确、实时地识别出驾驶员的制动意图。
2) 具有制动意图识别的电动液压助力制动系统在最大踏板力一定的情况下,可有效提高制动主缸的液压压强,减小制动距离,提高驾驶安全性。在车速较大的情况下,具有制动意图识别的制动效果更好,在车速为100 km/h,踏板变化率为400 N/s,踏板力最大为200 N的情况下,制动主缸液压压强增加了1.8 MPa,制动距离减小了15.1 m。
| [1] |
Kim S, Huh K. Fault-tolerant braking control with integerated EMBs and regenerative in-wheel motors[J]. International Journal of Automotive Technology, 2016, 17(5): 923-936. DOI:10.1007/s12239-016-0090-1 |
| [2] |
Jo C, Cheon J, Kim J, et al. A study on design for noise reduction of hEMB[C]//SAE Technical Paper Series. 400 Commonwealth Drive, Warrendale, PA, United States: SAE International, 2015: 2015-01-2702.
|
| [3] |
Yu Z P, Xu S Y, Xiong L, et al. An integrated-electro-hydraulic brake system for active safety[C]//SAE Technical Paper Series. 400 Commonwealth Drive, Warrendale, PA, United States: SAE International, 2016: 2016-01-1640.
|
| [4] |
张德兆, 秦立峰, 王建强, 等. 基于电子真空助力器的汽车驾驶辅助系统制动压力控制[J]. 汽车工程, 2011, 33(12): 1067-1072. Zhang D Z, Qin L F, Wang J Q, et al. Brake pressure control for vehicle driver assistance system base on electronic vacuum booster[J]. Automotive Engineering, 2011, 33(12): 1067-1072. (in Chinese) |
| [5] |
张文波. 基于隐马尔可夫模型的EHB系统制动意图识别方法研究[D]. 长春: 长春工业大学, 2014. Zhang W B. Braking intention recognition for EHB system based on hidden Markov model[D]. Changchun: Changchun University of Technology, 2014. (in Chinese) http://cdmd.cnki.com.cn/article/cdmd-10190-1014318442.htm |
| [6] |
崔高健, 曲代丽, 李绍松, 等. 驾驶员制动意图辨识技术研究现状[J]. 机械工程与自动化, 2016(4): 219-221, 226. Cui G J, Qu D L, Li S S, et al. Research status of driver braking intention recognition technology[J]. Mechanical Engineering & Automation, 2016(4): 219-221, 226. (in Chinese) DOI:10.3969/j.issn.1672-6413.2016.04.094 |
| [7] |
Li S T, Guo L S, Xu H, et al. Research on the EHB system control method base on identification of drivers' braking intentions[C]//2009 7th Asian Control Conference. August 27-29, 2009, Hong Kong, China. IEEE, 2009: 1439-1443.
|
| [8] |
Zheng H Y, Ma S N, Fang L X, et al. Braking intention recognition algorithm based on electronic braking system in commercial vehicles[J]. International Journal of Heavy Vehicle Systems, 2019, 26(3/4): 268. DOI:10.1504/IJHVS.2019.101464 |
| [9] |
宗长富, 王畅, 何磊, 等. 基于双层隐式马尔科夫模型的驾驶意图辨识[J]. 汽车工程, 2011, 33(8): 701-706. Zong C F, Wang C, He L, et al. Driving intention recognition based on double-layer HMM[J]. Automotive Engineering, 2011, 33(8): 701-706. (in Chinese) |
| [10] |
Zhao X, Wang S, Ma J, et al. Identification of driver's braking intention based on a hybrid model of GHMM and GGAP-RBFNN[J]. Neural Computing and Applications, 2019, 31(1): 161-174. |
| [11] |
Meng D J, Zhang L J, Yu Z P. A dynamic model for brake pedal feel analysis in passenger cars[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2016, 230(7): 955-968. DOI:10.1177/0954407015598030 |
| [12] |
Chen P C, Wu J, Zhao J, et al. Design and position control of a novel electric brake booster[J]. SAE International Journal of Passenger Cars-Mechanical Systems, 2018, 11(5): 389-400. DOI:10.4271/2018-01-0812 |
| [13] |
王英范, 宁国宝, 余卓平. 乘用车驾驶员制动意图识别参数的选择[J]. 汽车工程, 2011, 33(3): 213-216, 230. Wang Y F, Ning G B, Yu Z P. Parameter selection for the identification of driver's braking intention for passenger car[J]. Automotive Engineering, 2011, 33(3): 213-216, 230. (in Chinese) |
| [14] |
王庆年, 孙磊, 唐先智, 等. HEV制动意图识别的研究[J]. 汽车工程, 2013, 35(9): 769-774, 831. Wang Q N, Sun L, Tang X Z, et al. A study on braking intention identification for HEV[J]. Automotive Engineering, 2013, 35(9): 769-774, 831. (in Chinese) DOI:10.3969/j.issn.1000-680X.2013.09.003 |
| [15] |
Suzuki H. Prediction of driver's brake pedal operation in vehicle platoon system: model development and proposal[C]//2016 7th International Conference on Intelligent Systems, Modelling and Simulation (ISMS). January 25-27, 2016, Bangkok, Thailand. IEEE, 2016: 289-294.
|
 2021, Vol. 44
2021, Vol. 44

