b. 重庆大学 汽车工程学院, 重庆 400044
b. School of Automotive Engineering, Chongqing University, Chongqing 400044, P. R. China
双离合自动变速器(DCT)具有传动效率高、无间断换挡及行驶舒适性好等优点,目前在汽车领域已取得广泛关注[1-3]。起步控制一直是DCT车辆研究中的重点和难点之一[4]。起步过程中要求严格控制冲击和摩擦损失,而这两者之间存在一定的矛盾。此外,驾驶员的起步意图也是必须考虑的因素[5]。因此,设计一种有效的起步控制策略是至关重要的。
目前对于DCT起步控制的研究很多,主要包括基于模型的优化控制[6-8]和以模糊控制为主的智能控制[9-10]。文献[11]将驾驶员意图、主从动盘转速差及发动机转速状态作为输入,利用模糊规则确定了离合器结合速度。文献[12]基于驾驶意图与离合器结合状态设计模糊控制器,并利用蚁群算法优化控制参数,实现了更为精确的离合器压力控制。文献[13]利用神经网络与模糊推理的原理,提出了以车辆载重、路面坡度及驾驶员起步意图为神经网络输入,以离合器主从动盘转速差与主动盘转速的比值和离合器接合速度为控制量的双离合器协同智能起步控制策略。
对于基于动力学模型的起步控制,文献[14]考虑了发动机最低转速与离合器最大转矩,利用极小值原理实现了起步优化控制。文献[15]采用线性二次型最优控制方法,将冲击度转换为最优控制的约束,以滑摩功最小为控制目标,得到了离合器结合压力的最优值。文献[16]针对双离合器联合起步提出了模型预测控制,并与单离合器PID控制进行了对比。文献[17]基于极小值原理,以起步时间与冲击度为评价指标,得到不同油门开度下优化后的离合器转矩。此外,文献[18]提出了考虑扰动与建模误差观测器的线性二次型输出调节器,可以在一定程度上减少建模精度与扰动的影响。
目前的智能控制方法可以很好地体现驾驶员的起步意图,且具有较好的鲁棒性,但其控制效果完全依赖于模糊规则的制定,无法实现离合器结合过程的动态优化控制。基于模型的优化控制可以实现起步过程的全局或局部优化,然而DCT起步过程具有复杂性和耦合性,建立精准高效的物理模型是很困难且费时的,此外,随着驱动条件的变化和长期服役后老化,物理模型也会产生一定建模误差,从而影响控制效果[19]。
基于上述分析,笔者提出了基于输入输出数据的数据驱动预测控制策略(简称DDPC)。主要工作包括:1)将DCT车辆起步过程等效为自回归移动平均外生模型(ARMAX),基于输入输出数据获得起步过程的数据驱动模型;2)将ARMAX模型与预测控制原理相结合,提出了数据驱动预测控制策略,用于起步过程的优化控制;3)基于MATLAB/Simulink仿真平台搭建5速DCT起步模型,验证所提控制策略的有效性和优越性。
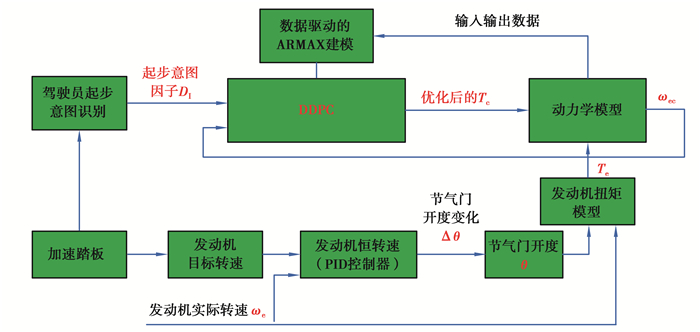
1 起步控制策略DCT起步过程实质是发动机和离合器协调控制的过程,如果将Te作为控制变量,求解过程将十分复杂[17],而如果将Te当作恒定值则不符合实际情况,考虑将发动机和离合器单独控制。DCT起步控制策略如图 1所示,包含发动机恒转速控制及离合器的DDPC控制策略。对于发动机控制部分:由加速踏板开度确定发动机的目标转速,采用PID控制节气门开度变化率,之后根据发动机动态转矩模型确定发动机输出转矩Te。对于离合器控制部分:首先可根据LSTM神经网络模型得到驾驶员起步意图(定义为起步意图因子DI)[20],经代数变化可得到权重系数β的大小,以确定参考轨迹Rref;将数据驱动建模与预测控制原理相结合,从而实现在线的滚动优化控制。
|
图 1 基于ARMAX模型的起步控制策略 Fig. 1 Starting control strategy based on ARMAX model |
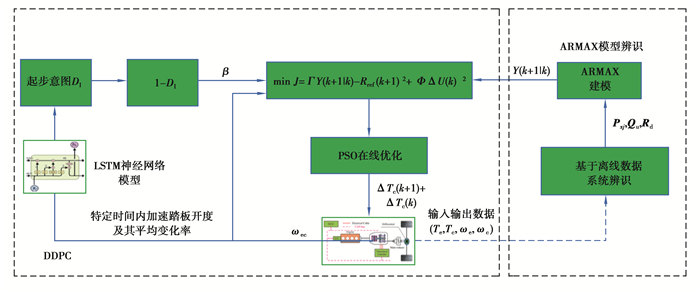
预测控制的要点包括:1)根据获得的测量值,预测系统的未来动态;2)在给定约束条件下优化性能指标,计算未来控制信号序列;3)将优化求解得到的第一个控制输入应用于控制系统;4)在下一次采样时,重复上述步骤,找到一个新的输入函数,其中包含测量的新信息。因此,对于“将来”系统状态的准确预测是预测控制的基础。利用系统输入输出数据,将ARMAX建模与预测控制原理相结合,实现体现驾驶员意图的DCT车辆起步优化控制;求解算法采用改进的粒子群算法(PSO)。具体流程如图 2所示。
|
图 2 基于ARMAX建模的DDPC流程图 Fig. 2 DDPC controller schematic flow based on ARMAX modeling |
基于ARMAX进行数据驱动建模的方法可以解决难以建立精准物理模型的问题,并已在汽车工业取得一些应用[21-22]。该方法只需要系统的输入输出数据,利用系统辨识的思想就可以获得代替系统特征的数据驱动模型[23]。
将起步过程考虑为与时间序列相关的线性ARMAX模型,基于大量起步过程的输入输出数据,利用最小二乘法(LSM)可以实现ARMAX结构参数的辨识。ARMAX模型的结构如式(1)所示。
| $ \left\{\begin{array}{l} \boldsymbol{\alpha}(z) x(k)=\boldsymbol{\beta}(z) u(k)+\boldsymbol{\gamma}(z) \boldsymbol{d}(k), \\ y_{\mathrm{c}}(k)=[0,1] \boldsymbol{x}(k), \\ y_{\mathrm{e}}(k)=[1,0] \boldsymbol{x}(k)。\end{array}\right. $ | (1) |
式中:x表示ωe和ωec组成的向量;ye表示ωe,yc表示ωec;u表示离合器扭矩Tc;d表示发动机转矩Te与阻力矩Tv组成的向量,表示可测扰动。笔者并未对ωe采用预测控制,其预测结果有助于验证辨识的效果。在ARMAX模型中,输入输出数据包含发动机转矩Te、离合器转矩Tc、阻力矩Tv、发动机角速度ωe及从动盘角速度ωc。考虑到实际应用,这些数据均可直接或间接从实车传感器获得,其中ωe,ωc可由转速传感器直接得到;Te可由发动机动态转矩模型得到;Tc可由油压及离合器摩擦系数换算得到,即Tc=f(μ, p),在实车控制过程中,可以通过f-1反推控制油压p;Tv则可通过设计力矩观测器计算得到[24]。
α(z),β(z),γ(z)分别表示自回归多项式矩阵、外生多项式矩阵及移动平均值矩阵,z是转换符号。
| $ \left\{\begin{array}{l} \boldsymbol{\alpha}(z)=I+\boldsymbol{\alpha}^{1} \times z^{-1}+\cdots+\boldsymbol{\alpha}^{n_{\boldsymbol{\alpha}}} \times z^{-n_{\boldsymbol{\alpha}}}, \\ \boldsymbol{\beta}(z)=\boldsymbol{\beta}^{1} \times z^{-1}+\cdots+\boldsymbol{\beta}^{n_{\boldsymbol{\beta}}} \times z^{-n_{\boldsymbol{\beta}}} ,\\ \boldsymbol{\gamma}(z)=\boldsymbol{\gamma}^{1} \times z^{-1}+\cdots+\boldsymbol{\gamma}^{n_{\boldsymbol{\gamma}}} \times z^{-n_{\boldsymbol{\gamma}}}。\end{array}\right. $ | (2) |
式中矩阵α(z),β(z),γ(z)可以展开为如下形式:
| $ \boldsymbol{\alpha}(z)=\left[\begin{array}{ccc} 1 & \cdots & 0 \\ \vdots & & \vdots \\ 0 & \cdots & 1 \end{array}\right]+\left[\begin{array}{ccc} \alpha_{11}^{(1)} & \cdots & \alpha_{1 m}^{(1)} \\ \vdots & & \vdots \\ \alpha_{m 1}^{(1)} & \cdots & \alpha_{m m}^{(1)} \end{array}\right] \times z^{-1}+\cdots+\left[\begin{array}{ccc} \alpha_{11}^{\left(n_{\boldsymbol{\alpha}}\right)} & \cdots & \alpha_{1 m}^{\left(n_{\boldsymbol{\alpha}}\right)} \\ \vdots & & \vdots \\ \alpha_{m 1}^{\left(n_{\boldsymbol{\alpha}}\right)} & \cdots & \alpha_{m m}^{\left(n_{\boldsymbol{\alpha}}\right)} \end{array}\right] \times z^{-n_{\boldsymbol{\alpha}}}, $ |
| $ \boldsymbol{\beta}(z)=\left[\begin{array}{ccc} \beta_{11}^{(1)} & \cdots & \beta_{1 n}^{(1)} \\ \vdots & & \vdots \\ \beta_{n 1}^{(1)} & \cdots & \beta_{n n}^{(1)} \end{array}\right] \times z^{-1}+\cdots+\left[\begin{array}{ccc} \beta_{11}^{\left(n_{\boldsymbol{\beta}}\right)} & \cdots & \beta_{1 n}^{\left(n_{\boldsymbol{\beta}}\right)} \\ \vdots & & \vdots \\ \beta_{n 1}^{\left(n_{\boldsymbol{\beta}}\right)} & \cdots & \beta_{n n}^{\left(n_{\boldsymbol{\beta}}\right)} \end{array}\right] \times z^{-n_{\boldsymbol{\beta}}}, $ |
| $ \boldsymbol{\gamma}(z)=\left[\begin{array}{ccc} \gamma_{11}^{(1)} & \cdots & \gamma_{1 r}^{(1)} \\ \vdots & & \vdots \\ \gamma_{r 1}^{(1)} & \cdots & \gamma_{r r}^{(1)} \end{array}\right] \times z^{-1}+\cdots+\left[\begin{array}{ccc} \gamma_{11}^{\left(n_{\boldsymbol{\gamma}}\right)} & \cdots & \gamma_{1 m}^{\left(n_{\boldsymbol{\gamma}}\right)} \\ \vdots & & \vdots \\ \gamma_{m 1}^{\left(n_{\boldsymbol{\gamma}}\right)} & \cdots & \gamma_{m m}^{\left(n_{\boldsymbol{\gamma}}\right)} \end{array}\right] \times z^{-n_{\boldsymbol{\gamma}}}。$ |
其中nα,nβ,nγ分别表示输出、外生输入及可测扰动的阶次。m,n,r分别表示x,u,d的个数,其中m=r=2,n=1。α(z)是m×m的矩阵,β(z)是m×n的矩阵,γ(z)是m×r的矩阵。这些矩阵代表着所研究物理系统的动态特性。一般这些矩阵系数可以利用最小二乘法进行计算[25]。
为了更清晰地观察ARMAX模型在起步过程中的使用并简化相关计算,式(1)可以转化为以下形式:
| $ \left\{\begin{array}{l} \boldsymbol{x}(k)=\sum\limits_{j_{1}=1}^{n_{\boldsymbol{\alpha}}} \boldsymbol{P}_{x j_{1}} x(k-j)+\sum\limits_{j_{2}=1}^{n_{\boldsymbol{\beta}}} \boldsymbol{Q}_{u j_{2}} u(k-j)+\sum\limits_{j_{3}=1}^{n_{\boldsymbol{\gamma}}} \boldsymbol{R}_{\boldsymbol{d} j_{3}} \boldsymbol{d}(k-j), \\ y_{c}(k)=[0,1] \boldsymbol{x}(k), \\ y_{e}(k)=[1,0] \boldsymbol{x}(k)。\end{array}\right. $ | (3) |
其中:
| $ \boldsymbol{P}_{x_{j_{1}}}=-\left[\begin{array}{ccc} \alpha_{11}^{(j)} & \cdots & \alpha_{1 m}^{(j)} \\ \vdots & & \vdots \\ \alpha_{m 1}^{(j)} & \cdots & \alpha_{m m}^{(j)} \end{array}\right] \times z^{-j}, j_{1}=1,2, \cdots, n_{\boldsymbol{\alpha}}, $ |
| $ \boldsymbol{Q}_{u j_{2}}=\left[\begin{array}{ccc} \beta_{11}^{(j)} & \cdots & \beta_{1 n}^{(j)} \\ \vdots & & \vdots \\ \beta_{n 1}^{(j)} & \cdots & \beta_{n n}^{(j)} \end{array}\right] \times z^{-j}, j_{2}=1,2, \cdots, n_{\boldsymbol{\beta}}, $ |
| $ \boldsymbol{R}_{d j_{3}}=\left[\begin{array}{ccc} \gamma_{11}^{(j)} & \cdots & \gamma_{1 r}^{(j)} \\ \vdots & & \vdots \\ \gamma_{r 1}^{(j)} & \cdots & \gamma_{r r}^{(j)} \end{array}\right] \times z^{-j}, j_{3}=1,2, \cdots, n_{\boldsymbol{\gamma}}。$ |
式中:Pxj1是m×m矩阵;Quj2是m×n矩阵;Rdj3是m×r矩阵,它们代表DCT车辆起步过程的系统特性。
基于上述ARMAX结构,为了获得精确的ARMAX模型,需要确定其模型阶次。通常,模型的阶次(nα,nβ,nγ) 可以通过Akaike信息准则(定义为VAIC)来确定[26],即
| $ V_{\mathrm{AIC}}=2 k+n^{*} \ln \left(S / n^{*}\right)。$ | (4) |
式中:S代表真实值与辨识值误差的平方和;k表示ARMAX结构中辨识参数的总个数;n*代表用于辨识的样本总数。一般,VAIC的值应尽可能小,同时需要保证其结构不至于很复杂。
1.1.2 基于ARMAX建模的DDPC通常,DCT起步控制的目标包括:1)避免发动机熄火;2)充分反映驾驶员的起步意图;3)尽量避免振动和冲击;4)尽可能延长离合器的使用寿命。为了实现平稳快速的起步过程,目标函数可设为
| $ \min J=\| \boldsymbol{\varGamma}\left(\boldsymbol{Y}(k+1 \mid k)-\boldsymbol{R}_{\mathrm{ref}}(k+1)\left\|^{2}+\right\| \boldsymbol{\varPhi} \Delta \boldsymbol{U}(k) \|^{2}\right., $ | (5) |
式中Rref(k+1)=βiωec(k), i=1, 2, …, Np,表示跟踪轨迹,β∈[0, 1],由驾驶员起步意图DI决定,即β=1-DI。将起步意图分为3类,即DI对应3个不同的数值,慢、中、急3类起步意图因子大小分别取为0.20,0.45,0.70;Y(k+1|k) 表示预测输出,预测时域为Np,计算公式为
| $ \boldsymbol{Y}(k+1 \mid k)=\boldsymbol{I} y(k)+\boldsymbol{S}_{x 1} \Delta \boldsymbol{x}(k)+\boldsymbol{S}_{x 2} \Delta \boldsymbol{x}(k-1)+\boldsymbol{S}_{u} \Delta \boldsymbol{U}(k)+\boldsymbol{S}_{d} \Delta \boldsymbol{d}(k), $ | (6) |
| $ \boldsymbol{S}_{x j_{1}}=\left[\begin{array}{l} \boldsymbol{C}_{\mathrm{c}} \boldsymbol{P}_{x j_{1}} \\ \boldsymbol{C}_{\mathrm{c}} \boldsymbol{P}_{x j_{1}}^{2} +\boldsymbol{C}_{\mathrm{c}} \boldsymbol{P}_{x j_{1}} \\ \ \ \ \ \ \ \ \ \ \ \ \ \vdots \\ \sum\limits_{i=1}^{N_{\mathrm{p}}} \boldsymbol{C}_{\mathrm{c}} \boldsymbol{P}_{x j_1}^{i} \end{array}\right],\boldsymbol{S}_{\mathrm{d}}=\left[\begin{array}{l} \boldsymbol{C}_{\mathrm{c}} \boldsymbol{R}_{\mathrm{d}} \\ \boldsymbol{C}_{\mathrm{c}} \boldsymbol{P}_{x} \boldsymbol{R}_{\mathrm{d}}+\boldsymbol{C}_{\mathrm{c}} \boldsymbol{R}_{\mathrm{d}} \\ \ \ \ \ \ \ \ \ \ \ \ \ \vdots \\ \sum\limits_{i=1}^{N_{\mathrm{p}}} \boldsymbol{C}_{\mathrm{c}} \boldsymbol{P}_{x}^{i-1} \boldsymbol{R}_{\mathrm{d}} \end{array}\right], $ |
| $ \boldsymbol{S}_{\mathrm{u}}=\left[\begin{array}{cccccc} \boldsymbol{C}_{\mathrm{c}} \boldsymbol{Q}_{\mathrm{u}} & 0 & 0 & \cdots & 0 \\ \sum\limits_{i=1}^{2} \boldsymbol{C}_{\mathrm{c}} \boldsymbol{P}_{x} \boldsymbol{Q}_{\mathrm{u}} & \boldsymbol{C}_{\mathrm{c}} \boldsymbol{Q}_{\mathrm{u}} & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & & \vdots \\ \sum\limits_{i=1}^{N_{\mathrm{u}}} \boldsymbol{C}_{\mathrm{c}} \boldsymbol{P}_{x}^{i-1} \boldsymbol{Q}_{\mathrm{u}} & \sum\limits_{i=1}^{{N}_{\mathrm{u}}-1} \boldsymbol{C}_{\mathrm{c}} \boldsymbol{P}_{x}^{i-1} \boldsymbol{Q}_{\mathrm{u}} & \cdots & \cdots & \boldsymbol{C}_{\mathrm{c}} \boldsymbol{Q}_{\mathrm{u}} \\ \vdots & \vdots & \vdots & & \vdots \\ \sum\limits_{i=1}^{N_{\mathrm{p}}} \boldsymbol{C}_{\mathrm{c}} \boldsymbol{P}_{x}^{i-1} \boldsymbol{Q}_{\mathrm{u}} & \sum\limits_{i=1}^{N_{\mathrm{p}}-1} \boldsymbol{C}_{\mathrm{c}} \boldsymbol{P}_{x}^{i-1} \boldsymbol{Q}_{\mathrm{u}} & \cdots & \cdots & \sum\limits_{i=1}^{N_{\mathrm{p}}-{N}_{\mathrm{u}}-1} \boldsymbol{C}_{\mathrm{c}} \boldsymbol{P}_{x}^{i-1} \boldsymbol{Q}_{\mathrm{u}} \end{array}\right]。$ |
ΔU(k)表示控制变量的变化率,即离合器传递转矩的变化率,这样可以更好限制其大小,防止冲击度过大,控制时域为Nu,本文中,令Nu=Np=4;Δd(k)表示系统可测扰动,假设在预测时域内其值保持不变;Γ表示对于ωc跟随ωe快慢的要求,也即是反映对起步时间的要求,并在一定程度上体现滑摩功的大小;Φ表示对转矩变化率的限制,即对冲击度大小的限制,其值越大表示对转矩变化率的惩罚越大,即减小冲击度。
经过相应矩阵运算,式(5)可转化为
| $ \min J(\Delta u(k))=\Delta \boldsymbol{U}(k)^{\mathrm{T}} \boldsymbol{H} \Delta \boldsymbol{U}(k)+\boldsymbol{G}(k+1 \mid k)^{\mathrm{T}} \Delta \boldsymbol{U}(k)+\boldsymbol{E}_{\mathrm{p}}(k+1)^{\mathrm{T}} \boldsymbol{\varGamma} \boldsymbol{E}_{\mathrm{p}}(k+1), $ | (7) |
其中:
| $ \boldsymbol{H}=2\left(\boldsymbol{S}_{\mathrm{u}}^{\mathrm{T}} \boldsymbol{\varGamma}^{\mathrm{T}} \boldsymbol{\varGamma} \boldsymbol{S}_{\mathrm{u}}+\boldsymbol{\varPhi}^{\mathrm{T}} \boldsymbol{\varPhi}\right), $ |
| $ \boldsymbol{G}(k+1)=2 \boldsymbol{S}_{\mathrm{u}}^{\mathrm{T}} \boldsymbol{Q}^{\mathrm{T}} \boldsymbol{Q} \boldsymbol{E}_{\mathrm{p}}(k+1), $ |
| $ \boldsymbol{E}_{\mathrm{p}}(k+1)=\boldsymbol{R}_{\mathrm{ref}}(k+1)-\boldsymbol{I}_{N_{\mathrm{p}}, 1} y(k)-\boldsymbol{S}_{x 1} \Delta \boldsymbol{x}(k)-\boldsymbol{S}_{x 2} \Delta \boldsymbol{x}(k-1)-\boldsymbol{S}_{\mathrm{d}} \Delta \boldsymbol{d}(k)。$ |
MPC的显著特征就是可以显式地对控制量与状态量添加约束,这意味着控制器允许输入约束,并且从不生成试图违反这些约束的控制变量和状态变量[27]。相关约束条件包括:Te∈[Temin, Temax],Tc∈[Tcmin, Tcmax],
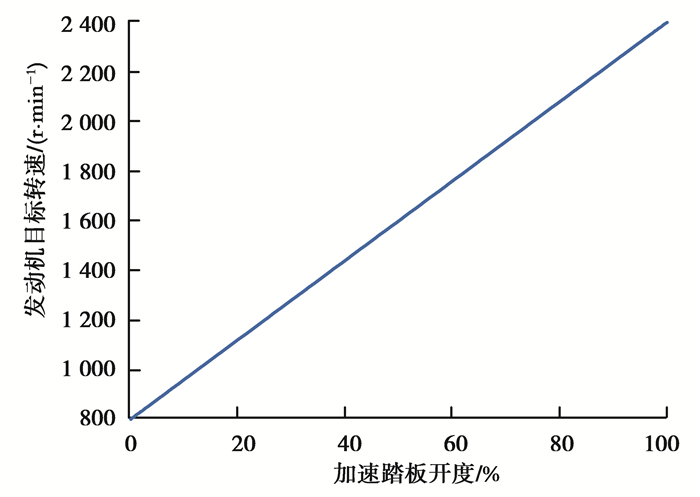
为了减少滑摩功的产生并减少起步时间,发动机目标转速应该维持在较低值。当行驶阻力较小时,加速踏板的开度可在一定程度上反映驾驶员的需求转速[17]及起步完成时(主从动盘同步)的车速大小,因此设定发动机目标转速与加速踏板开度成正比例关系,如图 3所示。
|
图 3 发动机目标转速 Fig. 3 Engine target speed |
为了验证所提控制策略的有效性,利用MATLAB /Simulink仿真平台搭建了5速DCT整车模型。首先基于仿真车辆实现ARMAX模型的辨识,并验证其有效性,然后基于该数据模型验证控制策略的有效性。
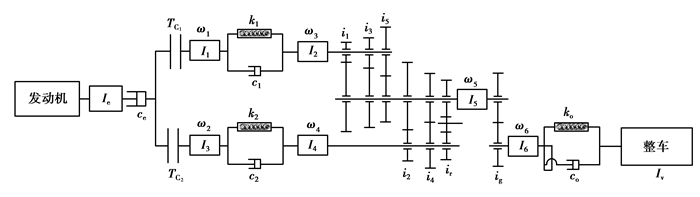
2.1 DCT起步系统描述所建仿真模型主要包含发动机、湿式双离合器、5速变速器、传动轴及整车模型,结构如图 4所示,模型相关参数见表 1。为了建立DCT起步系统的物理模型,提出如下假设:1)系统由无惯性弹性环节和无弹性惯性环节组成,各相关部件以集中质量形式存在;2)忽略传动系统中扭振影响及离合器热衰退;3)忽略轴的横向振动、轴承和轴承座的弹性及齿轮啮合弹性;4)忽略系统间隙和同步器啮合过程。
|
图 4 DCT整车传动系统简图 Fig. 4 Structural diagram of DCT driveline system |
| 表 1 DCT车辆参数 Table 1 Parameter values of DCT vehicle |
图 4中,TC1,TC2分别表示离合器C1,C2传递转矩,ko是车辆半轴与轮胎的当量扭转刚度,co是车辆半轴与轮胎的旋转黏性阻尼系数,Ie是发动机曲轴(包括飞轮)和离合器主动盘的等效转动惯量,ωc是离合器C1从动盘的角速度,I1,I2分别表示离合器C1,C2从动盘减振器主动部分当量转动惯量,I3是离合器C1减振器从动部分、输入轴1(实心轴)及关联奇数齿轮当量转动惯量,ω3是输入轴1实心轴的角速度,I4是离合器C2减振器从动部分、输入轴2(空心轴)及关联偶数齿轮当量转动惯量,ω4是输入轴2实心轴的角速度,I5是中间轴及其关联齿轮、主减速器主动部分当量转动惯量,ω5是中间轴的角速度,I6是主减速器从动部分、差动器、半轴以及车轮当量转动惯量,ω6是车辆半轴的角速度,Iv是整车等效到输出轴的当量转动惯量,ωv是车轮的角速度,k1,k2分别表示离合器C1,C2减振器的扭转刚度,c1,c2是离合器C1、C2减振器的结构阻尼系数,ko是车辆半轴与轮胎的当量扭转刚度,co表示车辆半轴与轮胎的旋转黏性阻尼系数,i1~i5分别表示1~5挡传动比,ig是主减速器传动比。
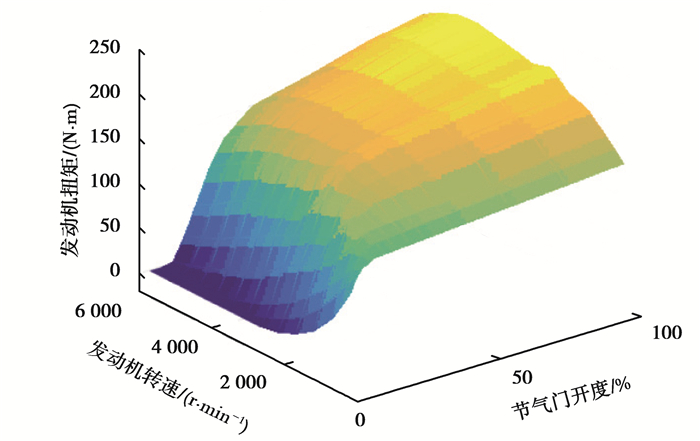
2.1.1 发动机模型发动机稳态转矩模型如图 5,由于发动机大部分时间处于非稳态工况,采用修正系数的方法来对发动机稳态工况下的输出扭矩进行修正并作为非稳态工况下的输出扭矩,即发动机的动态输出扭矩为
| $ T_{\mathrm{e}}=T_{\mathrm{e}}^{\prime}-\lambda \dot{\omega}_{\mathrm{e}}。$ | (8) |
|
图 5 发动机稳态转矩模型 Fig. 5 Steady torque model of engine |
式中:Te表示发动机动态输出转矩;T′e表示发动机稳态转矩; λ是非稳态工况下发动机输出扭矩下降系数,对不同的发动机λ大小不等,该发动机λ取0.03。
2.1.2 起步动力学模型DCT起步过程分为两个阶段,即滑摩阶段和同步阶段。接下来,针对不同阶段进行建模。
采用1挡单离合起步,在滑摩阶段,离合器C1逐渐结合,TC1则相应增加;而离合器C2保持分离状态并不传递转矩。该阶段起步动力学模型可简化为式(9)中的四自由度模型,即
| $ \left\{\begin{array}{l} T_{\mathrm{e}}-T_{\mathrm{c} 1}-c_{\mathrm{e}} \omega_{\mathrm{e}}=I_{\mathrm{e}} \dot{\omega}_{\mathrm{e}}, \\ T_{\mathrm{c}_{1}} i_{\mathrm{g}} i_{1}-I_{\mathrm{v}} \dot{\omega}_{\mathrm{w}}-T_{\mathrm{v}}=i_{\mathrm{a}_{1}} i_{1} \dot{\omega}_{1}+\left(I_{6}+i_{\mathrm{g}}^{2} i_{1}^{2} I_{\mathrm{eq}}^{1}\right) \dot{\omega}_{6} ,\\ T_{\mathrm{c}_{1}}-I_{1} \dot{\omega}_{1}=k_{1}\left(\theta_{1}-\theta_{3}\right)+c_{1}\left(\omega_{1}-\omega_{3}\right) ,\\ I_{\mathrm{v}} \dot{\omega}_{\mathrm{w}}+T_{\mathrm{v}}=k_{\mathrm{o}}\left(\theta_{6}-\theta_{\mathrm{v}}\right)+c_{\mathrm{o}}\left(\omega_{6}-\omega_{\mathrm{v}}\right)。\end{array}\right. $ | (9) |
式中:θ1,θ3分别表示ω1,ω3对应的角位移,rad;θ6,θv分别为ω6,ωv对应的角位移,rad;Tv表示等效到变速器输出轴的行驶阻力矩。
主从动盘同步后,此时ωe=ωc,起步过程进入稳定运行阶段,该阶段动力学模型转化为
| $ \left\{\begin{array}{l} T_{\mathrm{e}}-T_{1}=\left(I_{\mathrm{e}}+I_{1}\right) \dot{\omega}_{\mathrm{e}}, \\ T_{1} i_{\mathrm{g}} i_{1}-T_{\mathrm{o}}=\left(I_{6}+i_{\mathrm{g}}^{2} i_{1}^{2} I_{\mathrm{eq}}^{1}\right) \dot{\omega}_{6} ,\\ T_{\mathrm{o}}-T_{\mathrm{v}}=I \dot{\omega}_{\mathrm{v}}。\end{array}\right. $ | (10) |
起步阻力是由重力、滚动阻力、风阻以及加速阻力决定的函数,即
| $ T_{\mathrm{v}}=\left(m g \sin \alpha+f m g \cos \alpha+\frac{1}{2} C_{\mathrm{D}} A \rho v^{2}+\delta m a\right) r_{\mathrm{v}}。$ | (11) |
1) 冲击度。其值大小反映了驾驶员乘坐的舒适性,冲击度一般定义为车速的二阶导数,如式(12)。按照德国标准,一般j应当小于10 m/s3。
| $ j=\frac{\mathrm{d}(\mathrm{d} v / \mathrm{d} t)}{\mathrm{d} t}。$ | (12) |
2) 滑摩功。滑摩功大小直接影响离合器的使用寿命及整车驾驶性能,DCT车辆起步过程产生的滑摩功可描述为
| $ W=\int_{t_{0}}^{t_{1}} T_{\mathrm{c}} \omega_{\mathrm{e}} \mathrm{d} t+\int_{t_{1}}^{t_{2}} T_{\mathrm{c}}\left[\omega_{\mathrm{e}}-\omega_{\mathrm{c}}\right] \mathrm{d} t。$ | (13) |
式中:t0为离合器摩擦面开始接触时刻;t1表示车辆开始运动的时刻;t2表示离合器主从动盘同步的时刻。
3) 起步时间。起步时间直接反映驾驶员起步意图的快慢,一般表示从起步开始到主从动盘同步的时间,即t2的大小。
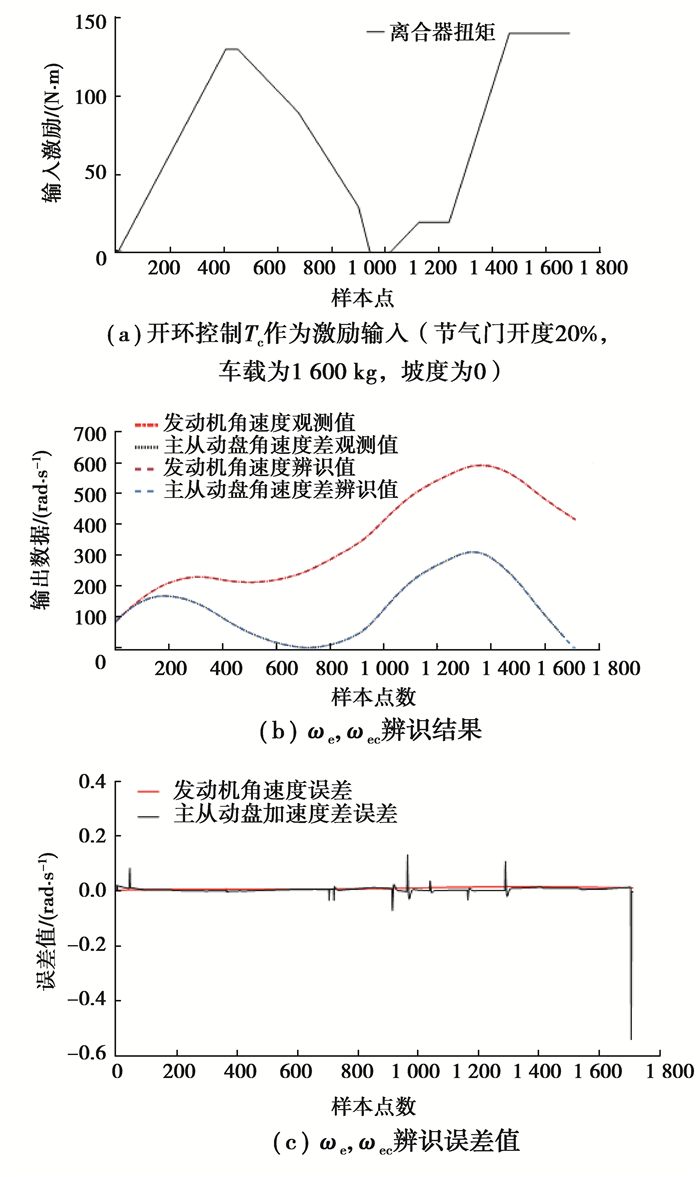
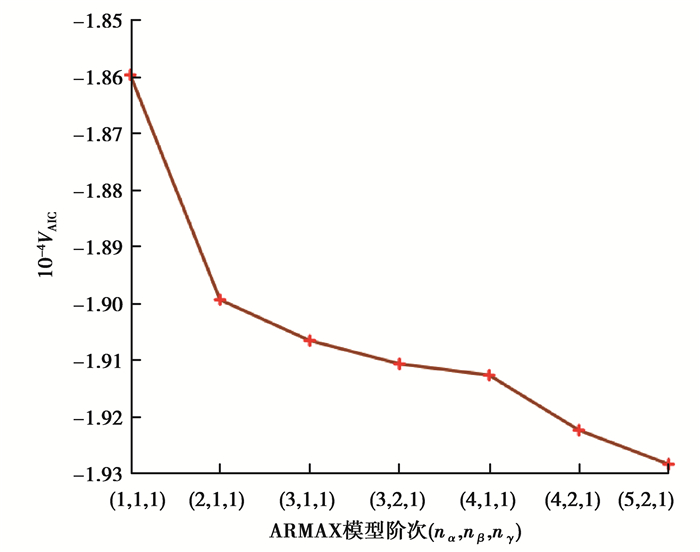
2.2 基于仿真数据的ARMAX建模为了获得ARMAX数据驱动模型,首先基于仿真数据进行系统辨识,得到有效的ARMAX模型,然后针对此模型进行验证,其中采样频率为100 Hz。为了获得足够数据样本,设计如图 6(a)的开环控制输入激励,将所得输入输出数据作为训练样本,辨识ARMAX模型参数。辨识效果如图 6(b)(c)所示,其中ωe, ωec的辨识误差均在±1 (rad/s)以内。经过多次离线辨识,得到不同阶次下的AIC值,如图 7所示。随着阶次增加,AIC值呈下降趋势,当阶次大于(2, 1, 1)时,VAIC下降趋势放缓。根据AIC准则,将ARMAX的阶次确定为(2, 1, 1),并得到辨识矩阵Pxj, Qu, Rd,如表 2所示。
|
图 6 VAIC随着ARMAX模型阶次增加的变化 Fig. 6 VAIC for increasing orders of ARMAX model |
|
图 7 训练组数据 Fig. 7 Training data |
| 表 2 ARMAX模型参数矩阵 Table 2 Matrix Value of ARMAX modeling |
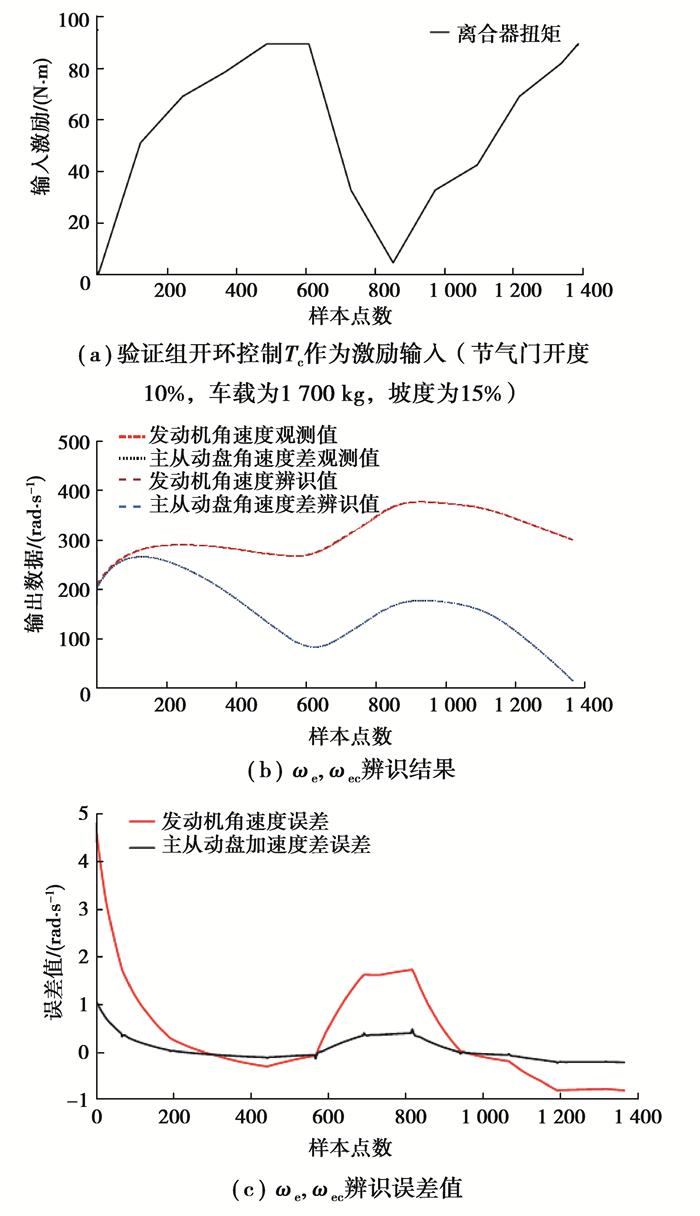
为了验证所获得ARMAX模型的效果,改变工况条件,并设计如图 8(a)的开环输入,获得起步过程的输入输出数据,利用这些数据对ARMAX数据模型进行验证,辨识效果如图 8(b)(c)。图 8(c)是验证组的辨识误差,其中ωe的辨识误差在±5 rad/s以内,ωec的辨识误差在±2.5 rad/s以内,表明所获得ARMAX模型可以有效表征DCT车辆起步过程的系统特性,为后面验证基于此数据模型的控制策略奠定了基础。
|
图 8 验证组数据 Fig. 8 Validation data |
基于以上仿真获得的ARMAX数据驱动模型,将分3步对所提出的控制策略进行验证:1)针对不同起步意图进行仿真分析,验证DDPC在不同起步条件下的稳定性以及对于不同起步意图的适应性;2)与传统的发动机恒转速控制相对比,验证DDPC控制方法的优越性;3)以正常起步意图为例,改变起步工况(车载和坡度),验证DDPC控制方法的鲁棒性。
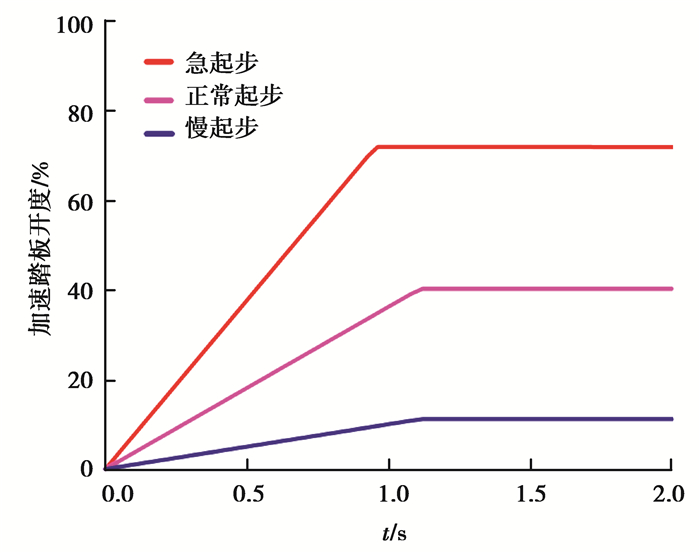
2.3.1 不同起步意图下的DDPC控制效果基于仿真模型,制定了较有代表性的3组加速踏板开度变化,即慢起步、正常起步和急起步,如图 9所示。基于此,实现控制策略在不同起步意图下的优化控制。
|
图 9 不同起步意图下的加速踏板开度 Fig. 9 Accelerator pedal in different intentions |
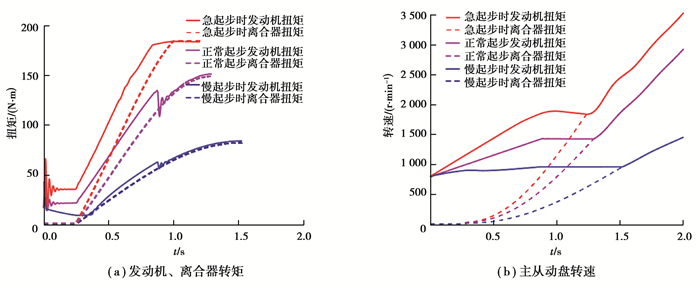
由图 10(a)(b)可以看出,刚开始起步时,由于发动机转速增加,发动机转矩比离合器转矩大很多,而当发动机转速达到目标转速后,为了维持发动机转速恒定,发动机转矩先减至与离合器传递转矩大致相等而后随之平稳增加。针对不同起步意图下的转矩变化,当急起步时,离合器传递转矩变化率最大,这是实现快速起步所需要的;而慢起步时离合器传递转矩变化率最小,这更有利于实现平稳的起步过程;正常起步时的离合器转矩变化率则介于急起步与慢起步之间。由图 10(b)可以看出,在慢起步下,起步时间最长,且同步时转速最低;急起步时所需时间最少,且同步时转速最高;正常起步下起步时间和同步时转速均介于急起步与慢起步之间。
|
图 10 不同起步意图下各控制量与状态量 Fig. 10 Control and status variables in different intentions |
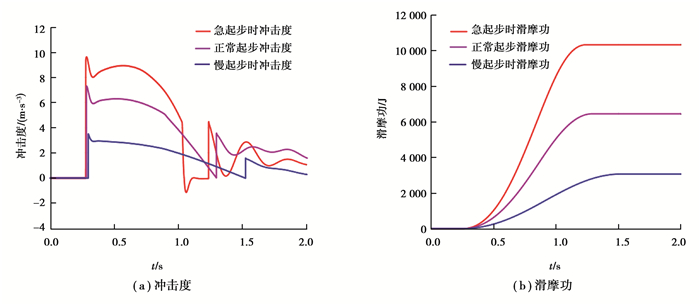
图 11是不同起步意图下的各评价指标,由(a)图可以看出,3种起步意图下,冲击度均小于10 m/s3,可以满足对于起步舒适性的要求。其中慢起步冲击度最小,这可以很好地满足驾驶员对于平稳起步的需求。急起步时冲击度是3种意图中最大的,此时舒适性有所降低,但满足了驾驶员快速起步的意图。如(b)图所示,在急起步时产生的滑摩功大于在正常起步和慢起步时产生的滑摩功,这主要是因为在急起步时离合器接合时间的减少很有限,而发动机转速提高很多,这导致主从动盘间的转速差较大。根据式(13),在车辆起步过程中产生的滑摩功也相应变大。因此,在3种起步意图中,慢起步时的滑摩功最小。对于起步时间,急起步时为1.23 s,正常起步为1.29 s,慢起步时为1.52 s。具体的评价指标如表 3所示。由此可见,所制定的控制策略可以很好地反映驾驶员起步意图的要求。
|
图 11 不同起步意图下各评价指标 Fig. 11 Evaluation indexes in different intentions |
| 表 3 评价指标对比 Table 3 Comparison of evaluation indexes |
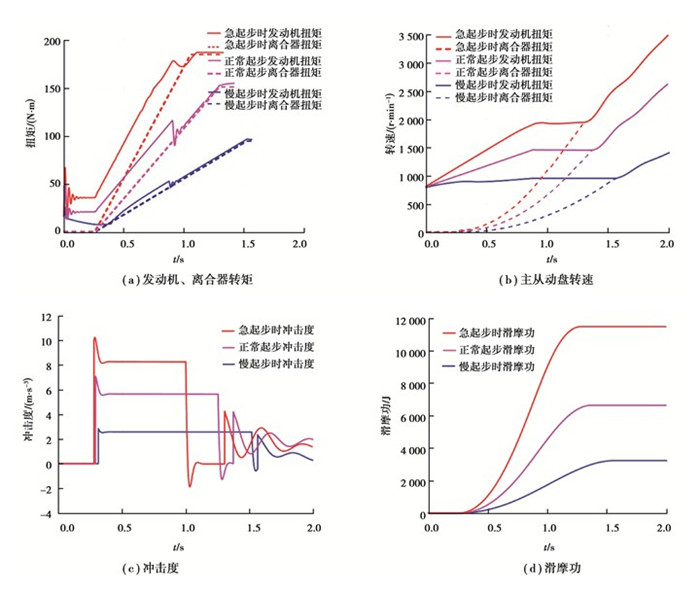
为了验证基于ARMAX模型的DDPC的优越性,将其与传统的基于PID的发动机恒转速控制方法进行了比较。其原理如下:根据发动机转矩模型,通过目标油门踏板开度和目标发动机转速确定目标发动机转矩,从而得到目标离合器转矩,其值约等于目标发动机转矩,以保持发动机恒转速运行;根据不同目标油门踏板开度下的冲击度限制,可以计算出最大离合器扭矩变化率,因为其值可近似看作与冲击度成正比。同时,通过PID控制器控制节气门开度变化率来尽可能使实际发动机转速维持在目标发动机转速。仿真结果如图 12所示,具体评价指标见表 3。与PID控制器相比,DDPC控制下慢起步时的冲击度略有增加(0.2 m/s3),但滑摩功和起步时间都有所改善,其中滑摩功减少了130 J (4.0%),起步时间减少了0.04 s (2.6%);正常起步时,冲击度无明显变化,滑摩功和起步时间分别减少了145 J (2.2%)和0.08 s (6.1%);急起步时,冲击度、滑摩功和起步时间分别改善了0.6 m/s3(5.8%)、1 100 J (9.7%)和0.08 s (6.1%)。总之,与传统的控制方法相比,所提出的DDPC可有效改善DCT车辆的起步性能。
|
图 12 PID控制下仿真结果 Fig. 12 Simulation results under PID controller |
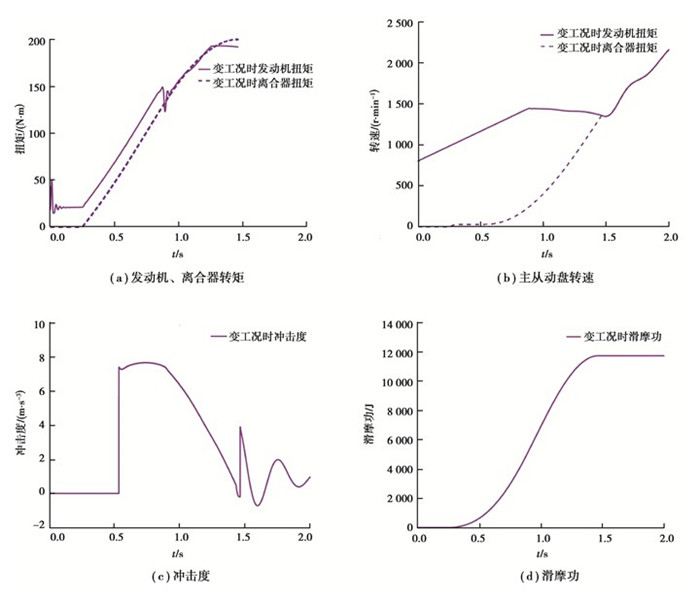
为了验证DDPC控制策略的鲁棒性,以正常起步意图为例,改变车辆起步工况及车载质量,实现不同工况下的起步过程。其中车辆负载由1 600 kg改为1 900 kg,道路坡度由0改为20%。由图 13所示,此时起步需要更多时间(1.46 s)和更大的离合器扭矩,所产生的冲击度和滑摩功分别为7.6 m/s3和11 720 J。显然,在改变工况和车载后,DDPC依然可以很好地实现起步过程的优化控制,这说明所提控制方法具有一定的鲁棒性。
|
图 13 正常起步意图下变工况时DDPC控制效果 Fig. 13 Control effects of DDPC controller in normal intention under changed condition |
针对DCT车辆起步过程难以建立精确物理模型等问题,笔者提出了基于数据驱动建模的预测控制策略。首先,基于数据驱动建模方法获得DCT车辆起步过程的ARMAX模型,并利用MATLAB/Simulink平台对该方法进行了验证,其次,针对所提出的数据驱动预测控制方法进行多组仿真分析,结果表明:
1) 基于ARMAX建立的数据驱动模型可以有效地表征DCT车辆起步过程。
2) 提出的DDPC可以很好地控制DCT起步过程,并有效体现驾驶员的起步意图。
3) 与传统的发动机恒转速控制相对比,DDPC可有效改善起步控制的性能。
4) 以正常起步意图为例,DDPC在起步工况(车载和坡度)变化时依然可以很好地控制起步过程,在一定程度上证明其具有鲁棒性。
下阶段的工作将着重于提高ARMAX模型辨识的精度以及控制策略的实车验证。随着处理芯片计算速度的提高及控制策略的适当简化,所提控制方法可用于改善实际DCT车辆的起步性能。
| [1] |
Kim S, Oh J, Choi S. Gear shift control of a dual-clutch transmission using optimal control allocation[J]. Mechanism and Machine Theory, 2017, 113: 109-125. DOI:10.1016/j.mechmachtheory.2017.02.013 |
| [2] |
Liu Y G, Qin D T, Jiang H, et al. Shift control strategy and experimental validation for dry dual clutch transmissions[J]. Mechanism and Machine Theory, 2014, 75: 41-53. DOI:10.1016/j.mechmachtheory.2014.01.013 |
| [3] |
马彪, 关万俊, 陈漫, 等. 联合油压控制的DCT升挡控制策略研究[J]. 重庆大学学报, 2015, 38(4): 24-30, 37. Ma B, Guan W J, Chen M, et al. Study on DCT up-shift control strategy with united control[J]. Journal of Chongqing University, 2015, 38(4): 24-30, 37. (in Chinese) |
| [4] |
秦大同, 刘永刚, 胡建军, 等. 双离合器式自动变速器两离合器起步控制与仿真[J]. 机械工程学报, 2010, 46(18): 121-127. Qin D T, Liu Y G, Hu J J, et al. Control and simulation of launch with two clutches for dual clutch transmissions[J]. Journal of Mechanical Engineering, 2010, 46(18): 121-127. (in Chinese) |
| [5] |
Han L, Liu H X, Wang J W, et al. Optimization control of CVT clutch engagement based on MPC[J]. International Journal of Automotive Technology, 2019, 20(6): 1161-1171. DOI:10.1007/s12239-019-0109-5 |
| [6] |
Zhang H, Wang J M. Vehicle lateral dynamics control through AFS/DYC and robust gain-scheduling approach[J]. IEEE Transactions on Vehicular Technology, 2016, 65(1): 489-494. DOI:10.1109/TVT.2015.2391184 |
| [7] |
Zhang H, Huang X Y, Wang J M, et al. Robust energy-to-peak sideslip angle estimation with applications to ground vehicles[J]. Mechatronics, 2015, 30: 338-347. |
| [8] |
Meng F, Tao G, Zhang T, et al. Optimal shifting control strategy in inertia phase of an automatic transmission for automotive applications[J]. Mechanical Systems and Signal Processing, 2015, 60/61: 742-752. |
| [9] |
Hou R, Lin C, Zhang L L. An automatic clutch engagement strategy for electric vehicle based on fuzzy control[C]//Mechatronics and Automatic Control Systems, 2014: 153-160. DOI: 10.1007/978-3-319-01273-5_16.
|
| [10] |
Qu J Y, Zhang Y R. Control of clutch engagement for AMT based on fuzzy logic[C]//2010 Third International Symposium on Information Science and Engineering. December 24-26, 2010, Shanghai, China. IEEE, 2010: 47-50.
|
| [11] |
Kong H F, Yan G. Study on fuzzy control technology for starting process of AMT clutch[C]//2009 International Forum on Information Technology and Applications. May 15-17, 2009, Chengdu, China. IEEE, 2009: 103-106.
|
| [12] |
Miao L Y, Cheng X S, Li X S. Start-up control of automated mechanical transmission with wet clutch[C]//2017 IEEE 2nd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC). March 25-26, 2017, Chongqing, China. IEEE, 2017: 2603-2606.
|
| [13] |
吴光强, 司建玉. 双离合器自动变速器起步的智能控制策略[J]. 同济大学学报(自然科学版), 2012, 40(1): 81-87. Wu G Q, Si J Y. Launching intelligent control strategy for dual clutch transmission[J]. Journal of Tongji University (Natural Science), 2012, 40(1): 81-87. (in Chinese) DOI:10.3969/j.issn.0253-374x.2012.01.015 |
| [14] |
Wu M X, Zhang J W, Lu T L, et al. Research on optimal control for dry dual-clutch engagement during launch[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2010, 224(6): 749-763. |
| [15] |
秦大同, 陈清洪. 基于最优控制的AMT/DCT离合器通用起步控制[J]. 机械工程学报, 2011, 47(12): 85-91. Qin D T, Chen Q H. Universal clutch starting control of AMT/DCT automatic transmission based on optimal control[J]. Journal of Mechanical Engineering, 2011, 47(12): 85-91. (in Chinese) |
| [16] |
Jiang Z J, Liu Q F, Dong S Y, et al. Launch coordination control based on twin-clutch torque distribution for DCT vehicle[J]. IFAC-PapersOnLine, 2018, 51(31): 904-909. |
| [17] |
Zhao Z G, He L, Zheng Z X, et al. Self-adaptive optimal control of dry dual clutch transmission (DCT) during starting process[J]. Mechanical Systems and Signal Processing, 2016, 68/69: 504-522. |
| [18] |
Gao B Z, Hong J L, Qu T, et al. Linear-quadratic output regulator for systems with disturbance: Application to vehicle launch control[C]//2016 31st Youth Academic Annual Conference of Chinese Association of Automation (YAC). November 11-13, 2016, Wuhan, China. IEEE, 2016: 135-140.
|
| [19] |
Lu X H, Chen H, Wang P, et al. Design of a data-driven predictive controller for start-up process of AMT vehicles[J]. IEEE Transactions on Neural Networks, 2011, 22(12): 2201-2212. |
| [20] |
Liu Y G, Zhao P, Qin D T, et al. Driving intention identification based on long short-term memory and A case study in shifting strategy optimization[J]. IEEE Access, 2019, 7: 128593-128605. |
| [21] |
BEN MRAD R. Non-linear systems representation using armax models with time-dependent coefficients[J]. Mechanical Systems and Signal Processing, 2002, 16(5): 803-815. |
| [22] |
Petridis A P, Shenton A T. Inverse-NARMA: a robust control method applied to SI engine idle-speed regulation[J]. Control Engineering Practice, 2003, 11(3): 279-290. |
| [23] |
Pawlus W, Karimi H R, Robbersmyr K G. Data-based modeling of vehicle collisions by nonlinear autoregressive model and feedforward neural network[J]. Information Sciences, 2013, 235: 65-79. |
| [24] |
Zhao Z G, Li X Y, He L, et al. Estimation of torques transmitted by twin-clutch of dry dual-clutch transmission during vehicle's launching process[J]. IEEE Transactions on Vehicular Technology, 2017, 66(6): 4727-4741. |
| [25] |
Liu H S, Zhu L, Pan Z H, et al. ARMAX-based transfer function model identification using wide-area measurement for adaptive and coordinated damping control[J]. IEEE Transactions on Smart Grid, 2017, 8(3): 1105-1115. |
| [26] |
Kapsalas C N, Sakellariou J S, Koustoumpardis P N, et al. An ARX-based method for the vibration control of flexible beams manipulated by industrial robots[J]. Robotics and Computer-Integrated Manufacturing, 2018, 52: 76-91. |
| [27] |
Pisaturo M, Cirrincione M, Senatore A. Multiple constrained MPC design for automotive dry clutch engagement[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(1): 469-480. |
 2021, Vol. 44
2021, Vol. 44

