2. 中国石油西南油气田分公司重庆气矿, 重庆 400021
2. China Petroleum Xinan Oil & Gas Field Company Chongqing Gas Mine, Chongqing 400021, P. R. China
工业机器人是智能制造系统的关键装备,也是数字化车间的重要构成部分。中国工业机器人量大面广,其负载远远小于工业机器人本体质量,且在运行过程中由于频繁进行加减速,导致工业机器人能效较低。而随着近年来能源成本的上升,如何提升工业机器人能效,降低工业机器人能耗成本,逐渐成为各界关注的焦点。
许多学者通过优化机器人运动轨迹的方式降低机器人能耗。文献[1-2]使用比例因子对机器人的运动时间进行缩放,调整机器人的运动速度。Pellicciari等[3]在重要的2个轨迹节点之间插入多个虚拟控制点,使用3次样条或5次样条曲线对这些点进行插值构成运动轨迹。文献[4-5]使用B样条曲线在机器人的关节空间进行轨迹规划,通过粒子群算法优化B样条曲线的控制点,使得机器人的整体能耗最低,并展示了良好的实验效果。文献[6-7]也使用B样条曲线规划机器人轨迹,不过优化参数为轨迹中间节点之间的时间间隔。
以上方法均基于工业机器人功率模型进行能耗优化,但功率模型较为复杂,其中大量电机参数难以直接获取,实验辨识结果准确性较低。文献[8]使用扭矩的平方作为目标函数衡量机器人的功率,Riazi等[9]使用伪功率代替机器人的实际功率。此外,Hong等[10]对比了几种不同的目标函数,包括摩擦损耗、电机能耗和扭矩的平方等。以上众多的目标函数中,加速度的平方和、伪功率、扭矩的平方和及机械能都不能正确、全面地反映机器人系统的总功率,因而最终的优化结果并不一定理想。
针对以上问题,笔者在对机器人系统永磁同步电机、伺服驱动器功能部件的能耗分析的基础上,提出了工业机器人功率等效模型。该模型通过高阶多项式建立起机器人损耗功率与电机扭矩、电机角速度的映射关系。在获取机器人运动过程中的扭矩和关节角等数据后,通过最小二乘法求解功率损耗模型中的系数。
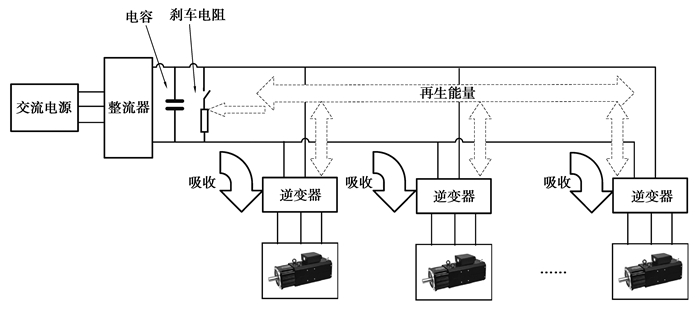
1 工业机器人系统建模工业机器人是典型的机电一体化系统,由机械元件、伺服电机、驱动系统和外围部件组成。为了准确估计机器人的实时功率,有必要对每个元件的功耗特性进行详细分析。如图 1所示,整流器把电网供来的三相交流电转化为直流电,直流电通过直流总线供给逆变器,逆变器再根据控制规律把直流电转化为特定幅值和特定频率的交流电,用于驱动伺服电机,伺服电机通过减速器后带动机器人关节做旋转运动。在直流总线上,接了一个电容和制动电阻,其作用是让直流总线的电压保持在一定范围内,防止电压过高危及电路的安全。下面将详细介绍各部分的功耗特性。
|
图 1 机器人电气系统 Fig. 1 Robot electrical system |
典型的工业机器人是由多个连杆串联而成,连杆之间用旋转副或移动副连接。在已知末端轨迹的情况下,机器人每个关节的位移、角速度和角加速度可以通过逆运动学求解得到。如果已知负载,便可通过拉格朗日方程或牛顿-欧拉迭代法求取关节扭矩[11],其表达式为
| $ \boldsymbol{\tau}=\boldsymbol{B}(\boldsymbol{q}) \ddot{\boldsymbol{q}}+\boldsymbol{C}(\boldsymbol{q}, \dot{\boldsymbol{q}}) \dot{\boldsymbol{q}}+\boldsymbol{g}(\boldsymbol{q})+\boldsymbol{J}^{\mathrm{T}}(\boldsymbol{q}) \boldsymbol{h}_{\mathrm{e}}+\boldsymbol{\tau}_{\mathrm{f}},$ | (1) |
式中:q,
关节摩擦力可以用简单的线性模型来计算,由库伦摩擦和黏滞摩擦两项组成,表达式为
| $ \boldsymbol{\tau}_{\mathrm{f}}=\boldsymbol{F}_{\mathrm{V}} \dot{\boldsymbol{q}}+\boldsymbol{F}_{\mathrm{S}} \operatorname{sign}(\dot{\boldsymbol{q}}),$ | (2) |
式中:FV是黏滞系数;FS是库伦摩擦系数。
由于电机的输出轴转速较高、力矩较小,通常需要减速器来匹配实际的工况需求。因此,电机扭矩和转速可以表示为
| $ \boldsymbol{\tau}_{\mathrm{m}}=\boldsymbol{k}_{\mathrm{r}}^{-1} \boldsymbol{\tau},$ | (3) |
| $ \dot{\boldsymbol{q}}_{\mathrm{m}}=\boldsymbol{k}_{\mathrm{r}} \dot{\boldsymbol{q}},$ | (4) |
式中:τm是关节电机的扭矩;kr是减速器的减速比;
电机输出的有效功率可以表示为
| $ \boldsymbol{P}_{\mathrm{mec}}=\boldsymbol{\tau}_{\mathrm{m}} \dot{\boldsymbol{q}}_{\mathrm{m}},$ | (5) |
式中Pmec代表电机输出端的有效功率,它包括了在机器人关节由减速器引起的摩擦损失和传递到连杆端的机械能。
使用式(1)计算机器人关节扭矩,会涉及连杆的动力学参数,如连杆质量、质心和转动惯量,这些参数可以通过文献[12-15]的方法来获取。
1.2 伺服电机工业机器人轨迹复杂多变,关节电机处于频繁启动和制动中,伴随着机器人不停地加速和减速。永磁同步电机拥有优越的调速性能,且结构简单、效率高、转动惯量小,广泛应用于工业机器人中[16]。
为了对永磁同步伺服电机的工作原理进行有效描述,通常把电机放在静止的三相(a/b/c轴)坐标系、静止的两相(α/β轴)坐标系或动态的两相(d/q轴)坐标系中进行分析。根据Park的理论,把永磁同步电机的三相电路分解到d/q两轴上,若分解过程按照幅值不变的原则,永磁同步电机的输出扭矩可以表示为[17]
| $ \tau_{\mathrm{m}}=\frac{3}{2} p\left[\psi_{\mathrm{f}} i_{\mathrm{q}}+\left(L_{\mathrm{d}}-L_{\mathrm{q}}\right) i_{\mathrm{d}} i_{\mathrm{q}}\right],$ | (6) |
式中:τm为电机扭矩;p为电机的极对数;ψf为转子永磁体磁链;iq为q轴电流;id为d轴电流;Ld为定子绕组直轴电感;Lq为定子绕组交轴电感。
永磁同步伺服电机矢量控制的策略主要有4种[18],d轴电枢电流id=0的控制、功率因数等于1的控制、恒定磁链的控制和最大力矩电流比的控制。其中,直轴电流为0的控制称为磁场定向控制,控制方法简单、计算量小,广泛应用于工业场合。当d轴电流为0时,电机扭矩的表达式为
| $ \tau_{\mathrm{m}}=k_{\mathrm{t}} i,$ | (7) |
式中:i=iq;
永磁同步电机消耗的总功率为有效功率和损耗两部分之和
| $ P_{\mathrm{m}}=P_{\mathrm{mec}}+P_{\mathrm{m}, \text { loss }},$ | (8) |
式中:Pm代表电机总功率;Pm, loss代表电机损耗功率。
电机的损耗可以分为以下几个部分[5]:
1) 定子绕组的铜损。这是电流通过绕组时产生的损耗,转化为焦耳热的形式散发出去,与绕组中电流的平方成正比。
2) 铁损。这是因为交变电流的作用,磁路中的磁通在铁磁材料中交变产生的损耗,包括磁滞损耗和涡流损耗两部分,假设与电机角速度成正比。
3) 附加损耗。代表了多方面的损耗,难以及精确计算且占比很小,忽略不计。
综上所述,只考虑的铜损和铁损,电机的损耗为
| $ P_{\mathrm{m}, \mathrm{loss}}=P_{\mathrm{Cu}}+P_{\mathrm{Fe}}=i^{2} R+k_{\mathrm{Fe}}\left|\dot{q}_{\mathrm{m}}\right|,$ | (9) |
式中:R表示定子绕组的电阻;kFe代表铁损系数。
电机总功率可以表示为
| $ P_{\mathrm{m}}=\tau_{\mathrm{m}} \dot{q}_{\mathrm{m}}+i^{2} R+k_{\mathrm{Fe}}\left|\dot{q}_{\mathrm{m}}\right|。$ | (10) |
驱动系统由3部分组成,分别是整理器、直流总线和逆变器,如图 1所示。驱动系统存在两种工作状态,分别对应工业机器人加速和减速两种工况。
当机器人加速运动时,关节电机处于电动机工作模式,需要从外界吸收电能。电网中的电能依次通过整流器、直流总线及逆变器输送到电机。
当机器人减速运动时,关节电机处于发电机的工作模式,向外界反馈能量。一般情况下,由于整流器的电路结构不允许电流反向流动,电机产生的能量不能反向输送到电网。这时,再生电能经过逆变器,到达直流总线后存储在电容上,导致总线电压升高。如果直流总线电压达到上限值,就会触发制动电阻的开关导通,电流通过电阻产生焦耳热,散失在空气中,使得总线上的电压保持在一定范围内。
1) 逆变器。永磁同步电机的运行效率非常高,一般在90%以上,其损耗和逆变器处于同一个数量级,因此对逆变器的损耗进行建模就显得非常必要。逆变器的损耗分为以下几个部分[3]:
a.恒定损耗。这部分损耗与负载无关,其大小是一个恒定的常数。
b.导通损耗。这是功率开关导通时的损耗,其大小与导通压降、器件电流有关,假设正比于电流的平方。
c.开关损耗。在逆变器的工作过程中,开关管在不断地打开与关闭,假设这部分的损耗正比于电流。
因此,逆变器的总损耗为
| $ P_{\text {inv, loss }}=P_{\text {inv }, \text { const }}+k_{\text {sw }} i+k_{\text {con }} i^{2}, $ | (11) |
式中:Pinv, loss为逆变器的损耗总功率;Pinv, const为逆变器的恒定损耗功率;ksw为逆变器的开关损耗系数;kcon为导通损耗系数。
逆变器总功率为电机的功率与逆变器损耗之和
| $ P_{\text {inv }}=P_{\mathrm{m}}+P_{\text {inv }, \text { loss }}=P_{\mathrm{m}}+P_{\text {inv }, \text { const }}+k_{\mathrm{sw}} i+k_{\text {con }} i^{2}。$ | (12) |
2) 直流总线。如图 1所示,所有逆变器都连接在直流总线上,因此逆变器之间可以进行能量交换。若某个轴的电机处于减速状态并向直流总线反馈能量,恰好另一个轴处于加速状态且从总线吸收能量,则处于减速状态的电机反馈的电能直接流向正在加速的电机。
一般情况下,直流总线上的电容都非常小,存储的电能非常有限,可以忽略不计[5]。假设处于加速状态的电机的功率为正,处于减速状态的电机功率为负。若所有电机的功率之和大于0,直流总线从整流器吸收电能,此时总线功率为所有逆变器功率之和。若所有电机的功率之和小于0,则认为这些再生电能全部被直流总线上的制动电阻消耗了,此时总线从整流器吸收电能的功率为0。
| $ P_{\mathrm{DC}}=\left\{\begin{array}{cl} P_{\text {inv }, \text { all }} & P_{\text {inv, all }}>0, \\ 0 & P_{\text {inv, all }}<0。\end{array}\right. $ | (13) |
式中:PDC为直流总线的从整流器吸收电能的功率;Pinv, all是所有逆变器的功率之和。
3) 整流器。假设整流器是理想的三相全波整流,其损耗非常小,可忽略不计[4]。因此,整流器的总功率为
| $ P_{\text {rec }}=P_{\mathrm{DC}}。$ | (14) |
工业机器人系统中,除了考虑电机与伺服驱动器消耗的电能外,示教器、散热风扇等也需要供电,这部分功率是固定的。综上所述,机器人的总功率和总能耗表示为
| $ P_{\text {robot }}=P_{\text {rec }}+P_{\text {const }}, $ | (15) |
| $ E_{\text {robot }}=\int_{0}^{T} P_{\text {robot }}(t) \mathrm{d} t, $ | (16) |
式中:Probot为工业机器人的总功率;Pconst为外围设备的恒定功率;Erobot为机器人一个运动周期的总能耗。机器人外围设备的功率可通过待机测试获取。
2 工业机器人损耗分析 2.1 工业机器人损耗模型工业机器人系统中的每种元件都有自己的功耗特性,文中第1部分已经把所有元件的损耗和电机电流、电机角速度联系起来,阐述了机器人系统总功率的计算方法。结合式(10)(12),机器人每个轴的逆变器功率可以表示为
| $ P_{\mathrm{inv}}=\tau_{\mathrm{m}} \dot{q}_{\mathrm{m}}+i^{2} R+k_{\mathrm{Fe}} \dot{q}_{\mathrm{m}}+P_{\mathrm{inv}, \mathrm{const}}+k_{\mathrm{sw}} i+k_{\mathrm{con}} i^{2} 。$ | (17) |
把式(7)代入可得
| $ P_{\mathrm{inv}}=P_{\mathrm{inv} , \text { const }}+\frac{k_{\mathrm{sw}}}{k_{\mathrm{t}}} \tau_{\mathrm{m}}+\frac{R+k_{\text {con }}}{k_{\mathrm{t}}^{2}} \tau_{\mathrm{m}}^{2}+k_{\mathrm{Fe}}\left|\dot{q}_{\mathrm{m}}\right|+\tau_{\mathrm{m}} \dot{q}_{\mathrm{m}} 。$ | (18) |
把式(18)中的最后一项移到左边可以得到
| $ P_{\text {inv }}-\tau_{\mathrm{m}} \dot{q}_{\mathrm{m}}=P_{\text {inv }, \text { const }}+\frac{k_{\mathrm{sw}}}{k_{\mathrm{t}}} \tau_{\mathrm{m}}+\frac{R+k_{\text {con }}}{k_{\mathrm{t}}^{2}} \tau_{\mathrm{m}}^{2}+k_{\mathrm{Fe}} \dot{q}_{\mathrm{m}}, $ | (19) |
或者表示为
| $ P_{0}=k_{1}+k_{2} \tau_{\mathrm{m}}+k_{3} \tau_{m}^{2}+k_{4}\left|\dot{q}_{\mathrm{m}}\right|, $ | (20) |
式中:P0=Pinv-
若对驱动系统中所有逆变器的总损耗进行计算,其表达式为
| $ P_{\text {loss }}=\sum\nolimits_{i=1}^{n} P_{0, i}=k+\sum\nolimits_{i=1}^{n}\left(k_{i, 2} \tau_{\mathrm{m}, i}+k_{i, 3} \tau_{\mathrm{m}, i}^{2}+k_{i, 4}\left|\dot{q}_{\mathrm{m}, i}\right|\right), $ | (21) |
式中:k代表所有逆变器的恒定损耗之和;ki, j表示关节i的第j个损耗系数;τm, i是关节i的电机扭矩;
由此,机器人的总功率可以表示为
| $ P_{\text {robot }}=\sum\limits_{i=1}^{n} \tau_{\mathrm{m}, i} q_{\mathrm{m}, i}+P_{\text {loss }}+P_{\text {const }}。$ | (22) |
式(21)计算了伺服驱动的总损耗,是估计工业机器人总功率必不可少的环节,式中系数繁多,需要通过实验对未知参数进行辨识,这里采用最小二乘法作为式(21)中系数的辨识算法。
由式(22)可知,当已知机器人的关节运动和总功率时,其总损耗可以表示为
| $ P_{\text {loss }}=P_{\text {robot }}-\sum\limits_{i=1}^{n} \tau_{\mathrm{m}, i} q_{\mathrm{m}, i}-P_{\text {const }}。$ | (23) |
式(21)可以改写为
| $ \boldsymbol{A} \boldsymbol{b}=\boldsymbol{c}, $ | (24) |
式中:
| $ \boldsymbol{A}=\left[\begin{array}{cccccccc} 1 & \tau_{\mathrm{m}, 1}\left(t_{1}\right) & \tau_{\mathrm{m}, 1}^{2}\left(t_{1}\right) & \left|\dot{q}_{\mathrm{m}, 1}\left(t_{1}\right)\right| & \cdots & \tau_{\mathrm{m}, \mathrm{n}}\left(t_{1}\right) & \tau_{\mathrm{m}, \mathrm{n}}^{2}\left(t_{1}\right) & \left|\dot{q}_{\mathrm{m}, \mathrm{n}}\left(t_{1}\right)\right| \\ 1 & \tau_{\mathrm{m}, 1}\left(t_{2}\right) & \tau_{\mathrm{m}, 1}^{2}\left(t_{2}\right) & \left|\dot{q}_{\mathrm{m}, 1}\left(t_{2}\right)\right| & \cdots & \tau_{\mathrm{m}, \mathrm{n}}\left(t_{2}\right) & \tau_{\mathrm{m}, \mathrm{n}}^{2}\left(t_{2}\right) & \left|\dot{q}_{\mathrm{m}, \mathrm{n}}\left(t_{2}\right)\right| \\ \vdots & \vdots & \vdots & \vdots & & \vdots & \vdots & \vdots \\ 1 & \tau_{\mathrm{m}, 1}\left(t_{u}\right) & \tau_{\mathrm{m}, 1}^{2}\left(t_{u}\right) & \left|\dot{q}_{\mathrm{m}, 1}\left(t_{u}\right)\right| & \cdots & \tau_{\mathrm{m}, \mathrm{n}}\left(t_{u}\right) & \tau_{\mathrm{m}, \mathrm{n}}^{2}\left(t_{u}\right) & \left|\dot{q}_{\mathrm{m}, \mathrm{n}}\left(t_{u}\right)\right| \end{array}\right], $ |
| $ \boldsymbol{b}=\left[\begin{array}{llllllll} k & k_{1,2} & k_{1,3} & k_{1,4} & \cdots & k_{n, 2} & k_{n, 3} & k_{n, 4} \end{array}\right]^{\mathrm{T}}, $ |
| $ \boldsymbol{c}=\left[P\left(t_{1}\right), P\left(t_{2}\right), \cdots, P\left(t_{u}\right)\right]^{\mathrm{T}}。$ |
若机器人运动过程中采集的数据组数远远大于损耗系数的个数,矩阵A是满秩矩阵,满足最小二乘法的使用条件,损耗系数的解为
| $ \boldsymbol{b}=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}\right)^{-1} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{c}。$ | (25) |
本节中主要描述工业机器人损耗参数辨识的实验过程,包括机器人实验轨迹设计、数据采集及使用最小二乘法辨识参数,并开展相应的验证实验(基于辨识结果预测机器人的实时功率和总能耗)。实验设备是KUKA KR60-3机器人。
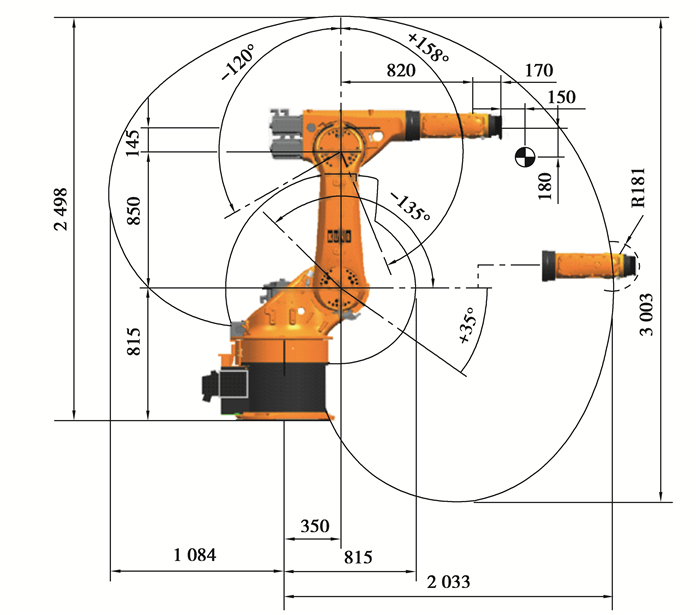
3.1 实验设计KUKA KR60-3工业机器人,如图 2所示(图中单位为mm),是一个负载60 kg的六自由度工业机器人。表 1给出了该机器人的DH参数,表 2给出了相关的运动限制条件。
|
图 2 KUKA KR60-3机器人 Fig. 2 KUKA KR60-3 robot |
| 表 1 KUKA KR60-3 DH参数 Table 1 KUKA KR60-3 DH parameters |
| 表 2 KUKA KR60-3运动限制条件 Table 2 KUKA KR60-3 movement restriction |
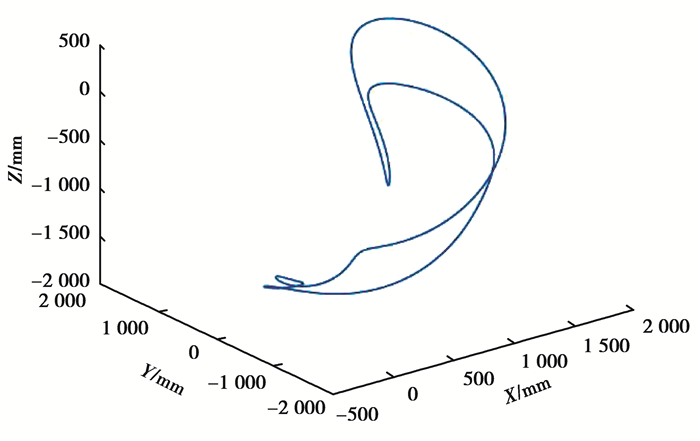
激励轨迹采用有限项傅里叶级数函数,如式(26),基频选用0.041 7 Hz,周期是24 s。这种轨迹有以下几种好处:末端轨迹封闭,可以方便地进行多次重复试验,并通过解析法求解关节角速度和角加速度,如式(27)(28),有效地降低噪声带来的影响。图 3展示了该轨迹的三维图形。
| $ q_{i}(t)=q_{i, 0}+\sum\limits_{k=1}^{N}\left(a_{i, k} \sin \left(k w_{\rm{f}} t\right)+b_{i, k} \cos \left(k w_{\rm{f}} t\right)\right), i=1,2, \cdots, n, $ | (26) |
| $ \dot{q}_{i}(t)=\sum\limits_{k=1}^{N}\left(a_{i, k} k w_{\rm{f}} \cos \left(k w_{f} t\right)-b_{i, k} k w_{\rm{f}} \sin \left(k w_{\rm{f}} t\right)\right) , $ | (27) |
| $ \ddot{q}_{i}(t)=-\sum\limits_{k=1}^{N}\left(a_{i, k} k^{2} w_{\rm{f}}^{2} \sin \left(k w_{\rm{f}} t\right)+b_{i, k} k_{2} w_{\rm{f}}^{2} \cos \left(k w_{\rm{f}} t\right)\right) 。$ | (28) |
|
图 3 机器人轨迹 Fig. 3 Robot trajectory |
为了辨识相关的能耗参数,设计了6个关节的傅里叶级数轨迹,并在关节空间对KUKA机器人编程。KUKA机器人的控制器提供关节扭矩和关节位置的数据接口,使得采集数据变得相当方便。
信号采集设备的采样周期是12 ms,采样数据包括所有关节位置和关节扭矩。最后采用最小二乘法求解机器人损耗表达式中的相关系数。
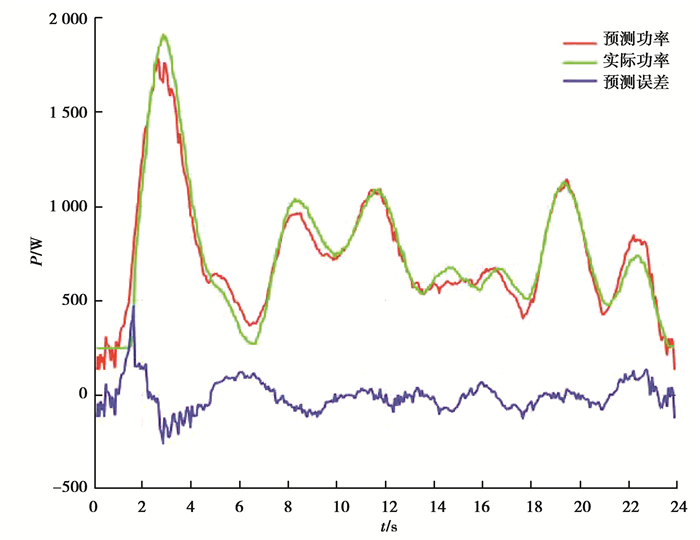
表 3给出了参数辨识的结果(包括外围设备的恒定功率),图 4对比了机器人的测量功率和基于辨识结果的预测功率。绿线代表实际测量功率,红线代表预测功率,蓝线代表两者之差,表 4展示了相关的预测误差项。从图 4可以看出,除了机器人刚开始运动的部分,测量功率和预测功率的差值很小。
| 表 3 参数辨识结果 Table 3 Parameter identification results |
|
图 4 机器人功率图 Fig. 4 Robot power diagram |
| 表 4 辨识轨迹功率相关误差 Table 4 Power-related errors of identification trajectory |
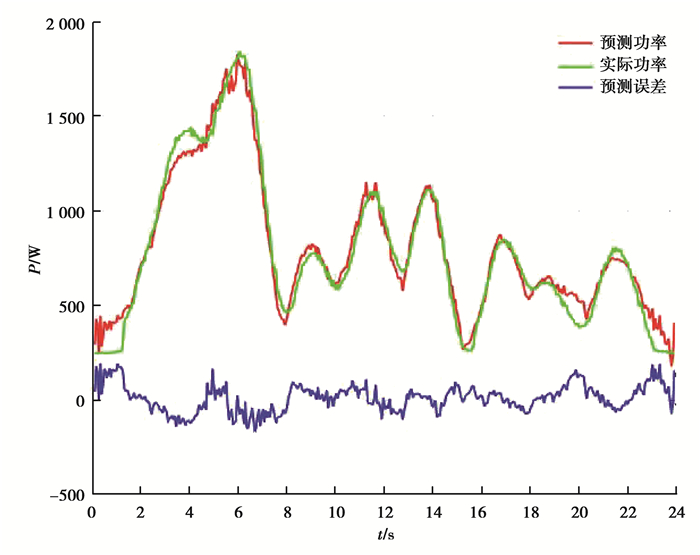
为了验证能耗模型和参数辨识结果的有效性,设计了不同于辨识实验的轨迹。该轨迹的实际测量功率和预测功率及两者的差值如图 5所示。功率和能耗的相关误差项如表 5所示。
|
图 5 机器人验证轨迹功率图 Fig. 5 Robot power diagram of verification trajectory |
| 表 5 验证轨迹功率相关误差 Table 5 Power-related errors of the verification trajectory |
图 5表明,预测功率和实际功率的误差很小,说明了辨识结果的正确性,该方法可以有效预测机器人的功率。
在图 4和图 5中,轨迹起始部分的功率预测误差都比较大,这是机器人的瞬态效应引起的。
总体来说,不管是参数辨识轨迹还是实验验证轨迹,功率的预测误差相对于测量值都是很小的。从表 4和表 5中可以看出,预测功率的均方根相对误差在10%以内,而预测能耗的相对误差则在1%左右,这是功率预测误差正负相抵消的结果。
4 结语笔者详细分析了工业机器人电气系统的工作原理和功耗特性,并整合各元件的损耗,将机器人的总损耗表示为电机扭矩和角速度的函数。在此基础上,设计机器人的有限项傅里叶级数轨迹,使用最小二乘法辨识损耗系数。为了验证方法的有效性,在KUKA KR60-3机器人上开展了验证实验。研究结果表明,在未知机器人电气参数的情况下,该方法可以有效预测机器人的实时功率和总能耗。
| [1] |
Pellicciari M, Berselli G, Leali F, et al. A method for reducing the energy consumption of pick-and-place industrial robots[J]. Mechatronics, 2013, 23(3): 326-334. DOI:10.1016/j.mechatronics.2013.01.013 |
| [2] |
Wigstrom O, Lennartson B, Vergnano A, et al. High-level scheduling of energy optimal trajectories[J]. IEEE Transactions on Automation Science and Engineering, 2013, 10(1): 57-64. DOI:10.1109/TASE.2012.2198816 |
| [3] |
Pellicciari M, Berselli G, Balugani F. On designing optimal trajectories for servo-actuated mechanisms: detailed virtual prototyping and experimental evaluation[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(5): 2039-2052. DOI:10.1109/TMECH.2014.2361759 |
| [4] |
Hansen C, Kotlarski J, Ortmaier T. Experimental validation of advanced minimum energy robot trajectory optimization[J]. 2013 16th International Conference on Advanced Robotics (ICAR), 2013, 1-8. |
| [5] |
Hansen C, Öltjen J, Meike D, et al. Enhanced approach for energy-efficient trajectory generation of industrial robots[J]. 2012 IEEE International Conference on Automation Science and Engineering (CASE), 2012, 1-7. |
| [6] |
Huang J S, Hu P F, Wu K Y, et al. Optimal time-jerk trajectory planning for industrial robots[J]. Mechanism and Machine Theory, 2018, 121: 530-544. DOI:10.1016/j.mechmachtheory.2017.11.006 |
| [7] |
Gasparetto A, Zanotto V. A new method for smooth trajectory planning of robot manipulators[J]. Mechanism and Machine Theory, 2007, 42(4): 455-471. DOI:10.1016/j.mechmachtheory.2006.04.002 |
| [8] |
Liu Y J, Liang L, Han H J, et al. A method of energy-optimal trajectory planning for palletizing robot[J]. Mathematical Problems in Engineering, 2017, 2017: 1-10. |
| [9] |
Riazi S, Wigström O, Bengtsson K, et al. Energy and peak power optimization of time-bounded robot trajectories[J]. IEEE Transactions on Automation Science and Engineering, 2017, 14(2): 646-657. DOI:10.1109/TASE.2016.2641743 |
| [10] |
Hong Y, Kim J, Park F C. Comparative analysis of energy-based criteria for dynamics-based robot motion optimization[C]//2017 IEEE Conference on Control Technology and Applications (CCTA). August 27-30, 2017, Maui, HI, USA. IEEE, 2017: 175-180.
|
| [11] |
Siciliano B, Khatib O. Robotics and the handbook[M]//Springer Handbook of Robotics. Cham: Springer International Publishing, 2016: 1-6.
|
| [12] |
Swevers J, Verdonck W, De Schutter J. Dynamic model identification for industrial robots[J]. IEEE Control Systems Magazine, 2007, 27(5): 58-71. DOI:10.1109/MCS.2007.904659 |
| [13] |
Jiang S R, Jiang M, Cao Y F, et al. A typical dynamic parameter identification method of 6-degree-of-freedom industrial robot[J]. Proceedings of the Institution of Mechanical Engineers, Part Ⅰ: Journal of Systems and Control Engineering, 2017, 231(9): 740-752. |
| [14] |
Khalil W, Gautier M, Lemoine P. Identification of the payload inertial parameters of industrial manipulators[C]//Proceedings 2007 IEEE International Conference on Robotics and Automation. April 10-14, 2007, Rome, Italy. IEEE, 2007: 4943-4948.
|
| [15] |
Khalil W, Dombre E. Trajectory generation[M]//Modeling, Identification and Control of Robots. Amsterdam: Elsevier, 2002: 313-345.
|
| [16] |
Gadaleta M, Berselli G, Pellicciari M, et al. A simulation tool for computing energy optimal motion parameters of industrial robots[J]. Procedia Manufacturing, 2017, 11: 319-328. DOI:10.1016/j.promfg.2017.07.114 |
| [17] |
杨国良. 永磁同步电机控制技术[M]. 北京: 知识产权出版社, 2015. Yang G L. Permanent magnet synchronous motor control technology[M]. Beijing: Intellectual Property Press, 2015: 153. (in Chinese) |
| [18] |
Monajemy R, Krishnan R. Comparison of torque control strategies based on the constant power loss control system for PMSM[M]//Control in Power Electronics. Amsterdam: Elsevier, 2002: 225-249.
|
 2021, Vol. 44
2021, Vol. 44


