以有限单元法为代表的基于偏微分方程的相关数值方法已经得到了广泛的运用,但在模拟裂纹扩展等不连续问题时,基于连续性假设的有限单元法无法自发模拟裂纹扩展,国内外学者通过设置界面单元或采用网格重划分技术来处理,但仍存在网格依赖性的问题[1]。
2000年,美国Sandia国家实验室的Silling博士提出了基于非局部作用思想的近场动力学方法[2-3],在国际上引起了广泛关注,从根本上解决了连续介质力学在模拟裂纹路径等不连续问题时偏导数不存在的问题,逐渐成为计算力学与工程仿真及相关领域研究热点[4],在断裂破坏问题中得到了广泛应用[5-8]。然而,近场动力学计算效率相较有限元而言过低。为此,国内外学者尝试将近场动力学与有限元结合起来,充分发挥两者优势。Macek和Silling[9]将研究对象划分为PD子域与FE子域以及重叠域,重叠域采用有限元实体模型,将重叠域中的PD模型以及PD子域视作杆单元,通过镶嵌单元技术,实现了对PD与FEM的混合建模;Liu和Hong[10]在近场动力学子域与有限元子域设置界面单元,在界面单元内加入一定的物质点,计算耦合力并将耦合力通过两种方式分配到界面单元的结点上,以此来实现两种方法的混合建模;Seleson等[11-12]通过在[0, 1]区间内变化的混合函数将局部作用区域的应变能密度与PD应变能密度混合实现了两区域的平滑过渡;Ren等[13]利用不连续的Galerkin法建立了经典近场动力学控制方程,并给出了相关算例。上述混合模型均在显式体系下求解,处理静力问题时需引入人工阻尼,阻尼的大小影响迭代收敛速度,进而导致计算效率不足。此外,上述文章均局限于通过低阶单元与近场动力学方法实现混合建模,缺乏对高阶单元与近场动力学混合建模研究。
在此基础上,本文所建立的模型将研究对象划分为PD子域与FE子域,在裂纹出现的区域,采用近场动力学模型,其他区域采用等参元模型。通过杆单元连接PD物质点与等参元结点来实现混合建模。该模型无需引入人工阻尼,提高了计算效率。同时,该混合模型在FE子域采用八结点等参元,提高了计算精度,最后,通过对悬臂梁弹性变形及含裂纹正方形板破坏过程的模拟,证明了该混合模型的有效性。
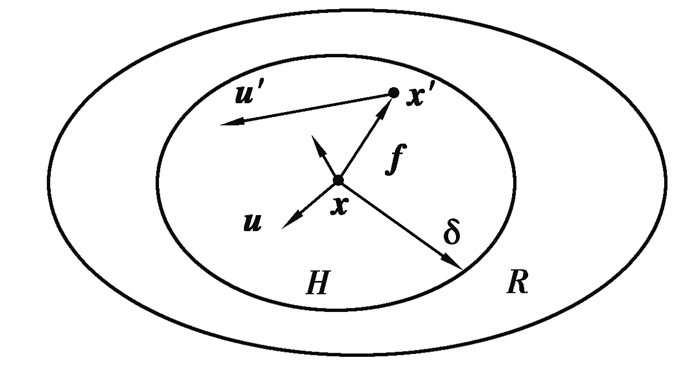
1 近场动力学简介 1.1 近场动力学方法如图 1所示,设在任意时刻t, 任意空间R内任一物质点x与其邻域一定范围δ内的其他物质点(x′∈R: ‖x′-x‖≤δ)存在单位相互作用力f,根据牛顿第二定律,可得[14]:
| $ \rho \ddot{\boldsymbol{u}}(\boldsymbol{x}, t)=\int_{H_{\boldsymbol{x}}} \boldsymbol{f}\left(\boldsymbol{u}\left(\boldsymbol{x}^{\prime}, t\right)-\boldsymbol{u}(\boldsymbol{x}, t), \boldsymbol{x}^{\prime}-\boldsymbol{x}\right) \mathrm{d} V_{\boldsymbol{x}^{\prime}}+\boldsymbol{b}(\boldsymbol{x}, t) \text { 。} $ | (1) |
|
图 1 物质点间的相互作用 Fig. 1 Interaction of material points |
令式(1)中x′-x=ξ,u′-u=η,ξ为物质点间相对位置,η为物质点间相对位移。
式中:Hx为物质点x的邻域范围,δ为邻域范围尺寸,ρ为物质点材料密度,u为物质点的位移,b为外力密度。
基于保守场的定义和性质,一定存在一个标量函数w(η, ξ)(物质点对势能密度),使得:
| $ \boldsymbol{f}(\boldsymbol{\eta}, \boldsymbol{\xi})=\frac{\partial w(\boldsymbol{\eta}, \boldsymbol{\xi})}{\partial \boldsymbol{\eta}}。$ | (2) |
物质点间的作用类似一个中心弹簧,则
| $ w(\boldsymbol{\eta}, \boldsymbol{\xi})=\frac{c(\boldsymbol{\xi}) s^{2} \boldsymbol{\xi}}{2},$ | (3) |
式中:c(ξ)为微模量函数,
| $ \boldsymbol{f}(\boldsymbol{\eta}, \boldsymbol{\xi})=\frac{\boldsymbol{\eta}+\boldsymbol{\xi}}{|\boldsymbol{\eta}+\boldsymbol{\xi}|} s c(\boldsymbol{\xi}) \mu(t, \boldsymbol{\xi}),$ | (4) |
μ为一标量函数,用来表征键的断裂:
| $ \mu(t, \boldsymbol{\xi})=\left\{\begin{array}{l} 1, s\left(t^{\prime}, \boldsymbol{\xi}\right)<s_{0}, 0 \leqslant t^{\prime} \leqslant t;\\ 0, \text { 其他。} \end{array}\right. $ | (5) |
式中: s0为临界伸长率。当伸长率小于临界伸长率s0时,μ(t, ξ)=1,键未发生断裂,否则,μ(t, ξ)=0,键断裂。这里考虑材料的拉压异性,可以通过材料的抗拉强度、抗压强度和弹性模量E去表征:
| $ s_{0}= \begin{cases}f_{\mathrm{t}} / E, & s(\boldsymbol{\xi})>0, \\ f_{\mathrm{c}} / E, & s(\boldsymbol{\xi})<0 。\end{cases} $ | (6) |
在近场动力学理论中,统一定义局部损伤
| $ \varphi(\boldsymbol{x}, t)=1-\frac{\int_{H} \mu(\boldsymbol{x}, t, \boldsymbol{\xi}) \mathrm{d} V_{\boldsymbol{\xi}}}{\int_{H} \mathrm{~d} V_{\boldsymbol{\xi}}}, $ | (7) |
式中:0≤φ≤1,φ=0表示材料未损伤,φ=1表示该点完全损伤。
1.2 改进的PMB模型式(3)中的微观模量函数c(ξ)可表示为:
| $ c(\boldsymbol{\xi})=c(0, \delta) g(\boldsymbol{\xi}, \delta),$ | (8) |
式中:c(0, δ)为集中函数,g(ξ, δ)为核函数,表示远程力大小随物质点间距变化的规律。在改进的PMB模型中,考虑远程力对微观模量的影响,取核函数[16-17]为:
| $ g(\boldsymbol{\xi}, \delta)=\left\{\begin{array}{cl} {\left[1-\left(\frac{\|\boldsymbol{\xi}\|}{\delta}\right)^{2}\right]^{2},} & \|\boldsymbol{\xi}\| \leqslant \delta; \\ 0, & \|\boldsymbol{\xi}\| \geqslant \delta。\end{array}\right. $ | (9) |
根据近场动力学应变能密度与连续介质力学应变能密度相等的原则,可以得到平面应力状态下的集中函数为:
| $ c(0, \delta)=\frac{315 E}{8 {\rm{ \mathsf{ π} }} \delta^{3}}。$ | (10) |
有限单元法静力问题求解方程为
| $ \boldsymbol{K} \boldsymbol{U}=\boldsymbol{R}, $ | (11) |
式中:K为整体刚度矩阵,U为整体位移列阵,R为整体等效结点荷载列阵。K和R可由式(12)得出
| $ \left.\begin{array}{l} \boldsymbol{K} =\sum \boldsymbol{C}_{\mathrm{e}}^{\mathrm{T}} \boldsymbol{k} \boldsymbol{C}_{\mathrm{e}} \\ \boldsymbol{R} =\sum \boldsymbol{C}_{\mathrm{e}}^{\mathrm{T}} \boldsymbol{R}^{\mathrm{e}} \\ \boldsymbol{k} =\int_{\Omega \mathrm{e}} \boldsymbol{B}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{B} t \mathrm{~d} x \mathrm{~d} y \end{array}\right\}, $ | (12) |
式中:Ce为选择矩阵,k为单元刚度矩阵,Re为等效荷载列阵,B为应变转换矩阵,D为弹性矩阵。
2.2 八结点等参元相较于矩形单元,等参元精度高,且适用于复杂的曲线边界与曲面边界,因此得到了广泛的应用。这里在有限元子域采用八结点等参元。
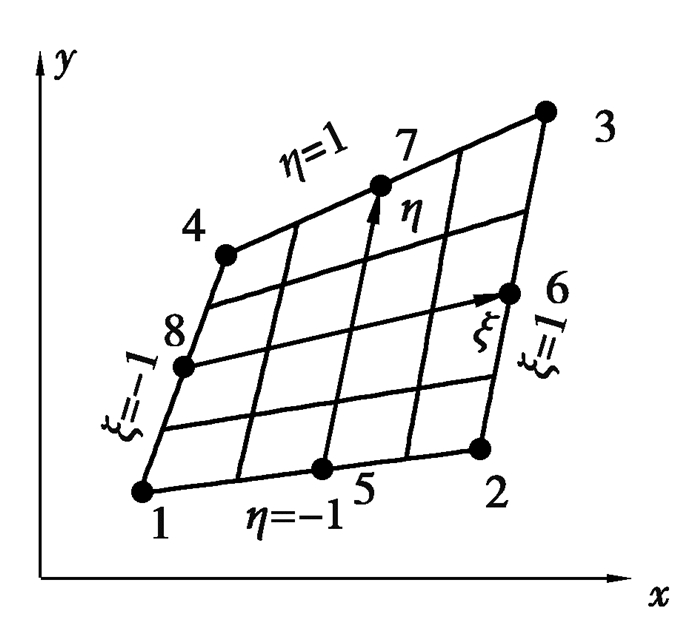
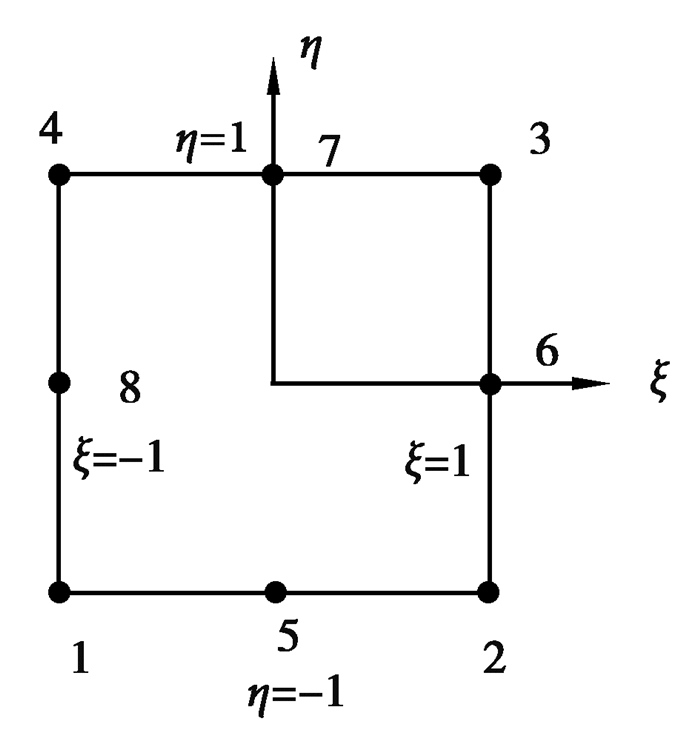
图 2为四边形单元在整体坐标系xy下的单元结点分布,在每个四边形单元上建立局部坐标系ξη,如图 3所示,通过坐标变换,将每个四边形单元映射到标准正方形单元,建立了两种单元的对应关系。
|
图 2 四边形单元 Fig. 2 Quadrilateral element |
|
图 3 正方形单元 Fig. 3 Square element |
设单元中任意一点的位移是u,v,单元结点位移为ui,vi(i=1,8),其位移模式为
| $ u=\sum\limits_{i=1}^{8} N_{i} u_{i}, v=\sum\limits_{i=1}^{8} N_{i} v_{i} 。$ | (13) |
坐标变换为:
| $ x=\sum\limits_{i=1}^{8} N_{i} x_{i}, y=\sum\limits_{i=1}^{8} N_{i} y_{i} 。$ | (14) |
式中,Ni=(i=1, 8)为八结点等参元形函数,其表达式为:
| $ \begin{array}{c} N_{i}=\frac{1}{4}\left(1+\xi_{i} \xi\right)\left(1+\eta_{i} \eta\right)\left(\xi_{i} \xi+\eta_{i} \eta-1\right), \quad(i=1,2,3,4), \\ \left.\begin{array}{c} N_{5}=\frac{1}{2}\left(1-\xi^{2}\right)(1-\eta) \\ N_{6}=\frac{1}{2}\left(1-\eta^{2}\right)(1+\xi) \\ N_{7}=\frac{1}{2}\left(1-\xi^{2}\right)(1+\eta) \\ N_{8}=\frac{1}{2}\left(1-\eta^{2}\right)(1-\xi) \end{array}\right\}, \end{array} $ | (15) |
式中,ξ, η是定义在标准单元上的局部坐标,ξi,ηi(i=1, 2, 3, 4)分别代表标准单元4个结点的局部坐标值。
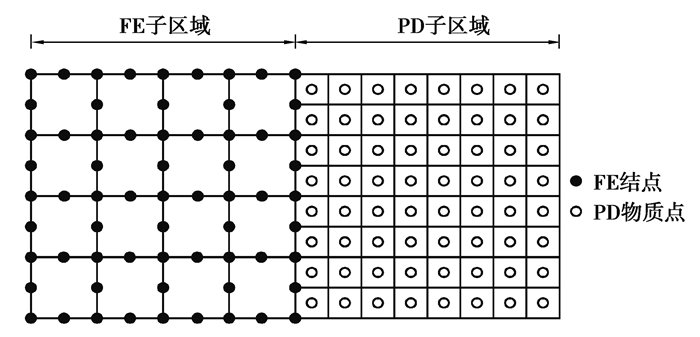
3 近场动力学与有限元耦合方案如图 4所示,将几何模型划分为PD子域与FE子域,在PD子域采用近场动力学建模,在FE子域采用八结点等参元建模。在两类子域的交界面上,如图 5所示,交界面上的每个有限元结点通过杆单元与其近场范围内的物质点相连接[18-19],其中,PD子域物质点对间相互作用可视为杆单元。为求解近场动力学方程,将研究对象离散为一系列带有物性信息的物质点,近场动力学积分方程转化为对有限个物质点的求和,即:
| $ \rho \ddot{\boldsymbol{u}}=\sum\limits_{j} \boldsymbol{f}\left(\boldsymbol{u}_{j}^{n}-\boldsymbol{u}_{i}^{n}, \boldsymbol{x}_{j}-\boldsymbol{x}_{i}\right) V_{j}+\boldsymbol{b}_{i}^{n}。$ | (16) |
|
图 4 有限元(FE)与近场动力学(PD)子域 Fig. 4 FE and PD region |

|
图 5 FE结点与PD物质点连接示意图 Fig. 5 Interactions between FE nodes and PD nodes through trusses |
对于静力问题,令加速度为0,可得近场动力学的平衡方程:
| $ \sum\limits_{j} \boldsymbol{f}\left(\boldsymbol{u}_{j}^{n}-\boldsymbol{u}_{i}^{n}, \boldsymbol{x}_{j}-\boldsymbol{x}_{i}\right) V_{j}+\boldsymbol{b}_{i}^{n}=0。$ | (17) |
根据公式(1),可将PD方程改写成矩阵形式
| $ \boldsymbol{K}_{i j}^{\mathrm{PD}} \boldsymbol{u} \cdot \mu(s)=\boldsymbol{f}, $ | (18) |
式中KijPD为任意物质点i,j的刚度贡献矩阵
| $ \boldsymbol{K}_{i j}^{\mathrm{PD}}=\frac{c(\boldsymbol{\xi})}{|\boldsymbol{\xi}|^{3}}\left[\begin{array}{cccc} \xi_{x}^{2} & & \\ \xi_{x} \xi_{y} & \xi_{y}^{2} & \mathrm{sym} \\ -\boldsymbol{\xi}_{x}^{2} & -\xi_{x} \xi_{y} & \xi_{x}^{2} \\ -\xi_{x} \xi_{y} & -\xi_{y}^{2} & \xi_{x} \xi_{y} & \xi_{y}^{2} \end{array}\right], $ | (19) |
式中:c(ξ)为微模量函数,|ξ|=|xi-xj|,ξx=xix-xjx,ξy=xiy-xjy,上标x,y分别为坐标在x,y轴的坐标分量。
杆单元的刚度贡献矩阵为:
| $ \boldsymbol{K}^{\mathrm{t}}=\frac{k\left(\boldsymbol{\xi}^{\prime}, \delta\right)}{\left|\boldsymbol{\xi}^{\prime}\right|^{3}}\left[\begin{array}{cccc} \xi_{x}^{\prime 2} & & \\ \xi_{x}^{\prime} \xi_{y}^{\prime} & \xi_{y}^{\prime 2} & \mathrm{sym} & \\ -\xi_{x}^{\prime 2} & -\xi_{x}^{\prime} \xi_{y}^{\prime} & \xi_{x}^{\prime 2} & \\ -\xi_{x}^{\prime} \xi_{y}^{\prime} & -\xi_{y}^{\prime 2} & \xi_{x}^{\prime} \xi_{y} & \xi_{y}^{\prime 2} \end{array}\right], $ | (20) |
式中:
通过求解式(12)、式(19)、式(20),分别得到了等参元、物质点对间、杆单元的刚度贡献矩阵,其中,物质点对间相互作用视为杆单元,通过对刚度贡献矩阵的集成,形成整体刚度矩阵。最后根据有限元静力方程求解位移,实现了近场动力学与有限元的混合建模。
4 数值算例 4.1 悬臂梁的弹性变形悬臂梁几何尺寸及子域划分如图 6所示[19],跨长1 000 mm,截面高为200 mm,弹性模量E为100 GPa,泊松比ν=1/3,物质点间距取为2.5 mm,近场范围尺寸取δ=4Δx,有限元网格为10 mm×10 mm的八结点等参单元,右端受大小为1 050 kN/m的均布荷载,探讨不同数值方法对精度的影响。
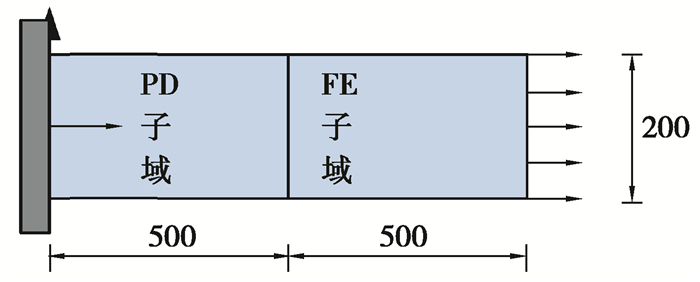
|
图 6 悬臂梁几何模型 Fig. 6 Geometric model of cantilever beam |
表 1给出了采用不同数值方法得到的最大水平位移计算结果。由表 1可得,采用近场动力学方法计算的最大水平位移与解析解的相对误差为2.19%,采用四结点混合模型时相对误差为0.67%,采用八结点混合模型的误差为0.28%,混合模型的精度比近场动力学的计算精度高,且本文中建立的八结点混合模型高于四结点混合模型的计算精度。证明了本文中提出的混合模型的精确性。其中,当不设置FE子域时,可根据有限元静力求解方程,得到近场动力学计算结果。
| 表 1 最大水平位移计算结果 Table 1 Calculation results of maximum horizontal displacement |
考虑如图 7所示含I型裂纹正方形板,模型尺寸及材料参数如下,边长为50 mm,在板中间预制一条长为10 mm的裂纹,弹性模量为30 GPa,ft为2.01 MPa,fc为20.1 MPa,泊松比为1/3。将正方形板划分为两个有限元子域与一个近场动力学子域,物质点间距取为0.5 mm,近场范围尺寸取δ=4Δx,有限元网格为2 mm×2 mm八结点等参元,采用位移加载,每一步位移增量为1.0×10-8 m。
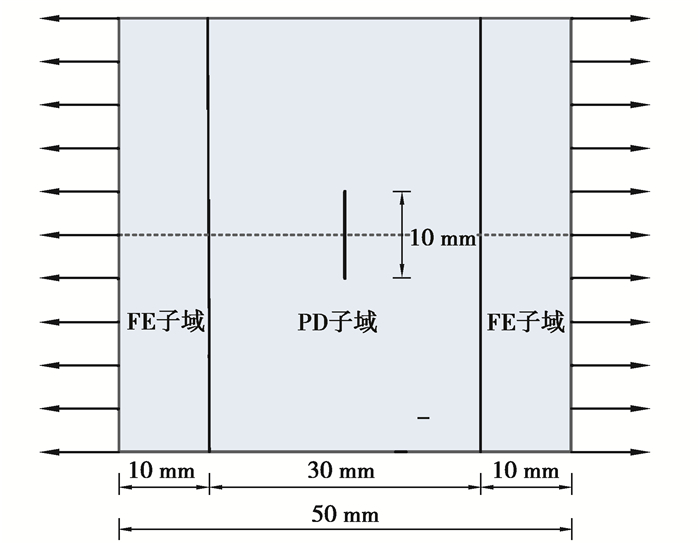
|
图 7 正方形板几何模型 Fig. 7 Geometric model of square plate |
混合模型计算得到的正方形板裂纹扩展过程如图 8所示,当加载到57步时(此时位移荷载为5.7×10-7 m), 预制裂纹的裂尖出现损伤;随着荷载的进一步增大,裂纹发生扩展,如图 8(b)(c)所示;当加载至92步时,(此时位移荷载为9.2×10-7 m),裂纹贯穿整个正方形板,构件发生破坏。
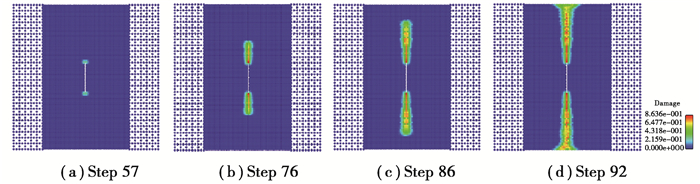
|
图 8 裂纹扩展示意图 Fig. 8 Crack propagation process |
考虑如图 9所示的含两条斜裂纹的正方形板,模型尺寸及材料参数如下,板的边长为50 mm,初始裂纹长度为10 mm,b为10 mm,弹性模量为30 GPa,ft为2.01 MPa,fc为20.1 MPa,泊松比为1/3。将正方形板划分为两个有限元子域与一个近场动力学子域,物质点间距取为0.5 mm, 近场范围尺寸取δ=4Δx,有限元网格为2 mm×2 mm的八结点等参单元,采用位移加载,每一步位移增量为1.5×10-8 m。
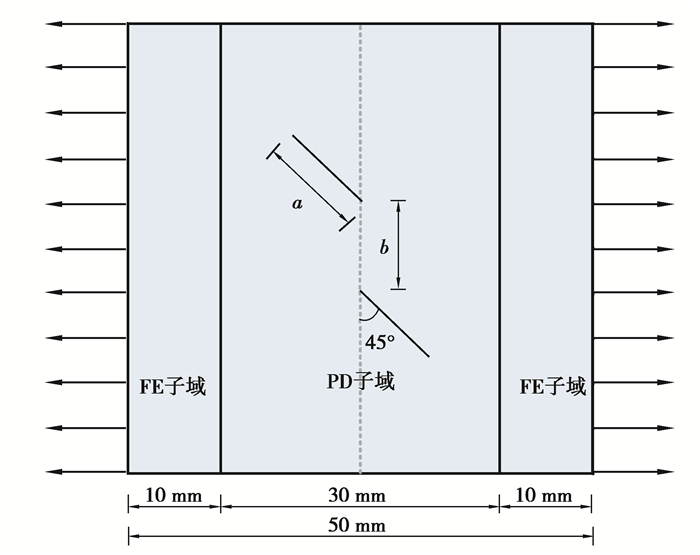
|
图 9 正方形板几何模型 Fig. 9 Geometric model of square plate |
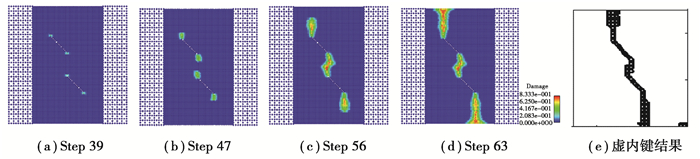
混合模型计算得到的正方形板裂纹扩展过程如图 10所示,加载到39步时(此时位移荷载为5.85×10-7 m),裂纹裂尖出现损伤;随着荷载的进一步增大,裂纹发生扩展并交汇,如图 10(b)(c)所示;当加载至63步时,(此时位移荷载为9.45×10-7 m),裂纹贯穿整个正方形板,构件发生破坏。图 10(e)为多维虚内键计算结果[20]。对比可得,混合模型与虚内键计算结果基本吻合。
|
图 10 裂纹扩展示意图 Fig. 10 Crack propagation process |
PD理论通过求解积分方程模拟材料断裂破坏行为,在分析裂纹扩展等不连续问题时具有显著优势,然而,PD理论计算效率相较FEM而言过低。为兼顾两者优势,采用近场动力学与有限元混合建模的方法,建立了新的混合模型,该模型将研究对象划分为PD子域与FE子域,在PD子域采用近场动力学建模型,FE子域采用等参元模型,通过杆单元连接PD物质点与等参单元结点来实现混合建模。此混合模型在求解处理静力问题时无需引入人工阻尼,采取类似有限元的方法,对刚度集成,形成整体刚度矩阵,然后根据有限元支配方程求解静力问题,提高了计算效率。同时在FE子域采用八结点等参元建模,提高了混合模型的计算精度。最后,采用所建立的混合模型计算分析了悬臂梁的弹性变形和含裂纹正方形板的破坏过程,取得了较好的结果,为断裂破坏问题的解决提供了一种新思路。
| [1] |
Murotani K, Yagawa G, Choi J B. Adaptive finite elements using hierarchical mesh and its application to crack propagation analysis[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 253: 1-14. DOI:10.1016/j.cma.2012.07.024 |
| [2] |
Silling S A, Epton M, Weckner O, et al. Peridynamic states and constitutive modeling[J]. Journal of Elasticity, 2007, 88(2): 151-184. DOI:10.1007/s10659-007-9125-1 |
| [3] |
Silling S A. Linearized theory of peridynamic states[J]. Journal of Elasticity, 2010, 99(1): 85-111. DOI:10.1007/s10659-009-9234-0 |
| [4] |
黄丹, 章青, 乔丕忠, 等. 近场动力学方法及其应用[J]. 力学进展, 2010, 40(4): 448-459. Huang D, Zhang Q, Qiao P Z, et al. A review on peridynamics(PD) method and its applications[J]. Advances in Mechanics, 2010, 40(4): 448-459. (in Chinese) |
| [5] |
顾鑫, 章青, 黄丹. 基于近场动力学方法的混凝土板侵彻问题研究[J]. 振动与冲击, 2016, 35(6): 52-58. Gu X, Zhang Q, Huang D. Peridynamics used in solving penetration problem of concrete slabs[J]. Journal of Vibration and Shock, 2016, 35(6): 52-58. (in Chinese) |
| [6] |
郁杨天, 章青, 顾鑫. 含单边缺口混凝土梁冲击破坏的近场动力学模拟[J]. 工程力学, 2016, 33(12): 80-85. Yü Y T, Zhang Q, Gu X. Impact failure simulation of a single-edged notched concrete beam based on peridynamics[J]. Engineering Mechanics, 2016, 33(12): 80-85. (in Chinese) DOI:10.6052/j.issn.1000-4750.2015.05.0396 |
| [7] |
沈峰, 章青, 顾鑫. 弹丸侵彻混凝土靶板破坏过程的近场动力学模拟[J]. 重庆大学学报, 2019, 42(1): 64-69. Shen F, Zhang Q, Gu X. Peridynamics modeling for projectile penetrating into concrete[J]. Journal of Chongqing University, 2019, 42(1): 64-69. (in Chinese) |
| [8] |
沈峰, 章青, 黄丹, 等. 基于近场动力学方法的结构准静态变形的定量计算[J]. 重庆大学学报, 2016, 39(5): 49-55. Shen F, Zhang Q, Huang D, et al. Quatitative calculation of quasi-static deformation of structure based on peridynamics theory[J]. Journal of Chongqing University, 2016, 39(5): 49-55. (in Chinese) |
| [9] |
Macek R W, Silling S A. Peridynamics via finite element analysis[J]. Finite Elements in Analysis and Design, 2007, 43(15): 1169-1178. DOI:10.1016/j.finel.2007.08.012 |
| [10] |
Liu W Y, Hong J W. A coupling approach of discretized peridynamics with finite element method[J]. Computer Methods in Applied Mechanics and Engineering, 2012, 245/246: 163-175. DOI:10.1016/j.cma.2012.07.006 |
| [11] |
Seleson P, Beneddine S, Prudhomme S. A force-based coupling scheme for peridynamics and classical elasticity[J]. Computational Materials Science, 2013, 66: 34-49. DOI:10.1016/j.commatsci.2012.05.016 |
| [12] |
Seleson P, Ha Y D, Beneddine S. Concurrent coupling of bond-based peridynamics and the navier equation of classical elasticity by blending[J]. International Journal for Multiscale Computational Engineering, 2015, 13(2): 91-113. DOI:10.1615/IntJMultCompEng.2014011338 |
| [13] |
Ren B, Wu C T, Askari E. A 3D discontinuous Galerkin finite element method with the bond-based peridynamics model for dynamic brittle failure analysis[J]. International Journal of Impact Engineering, 2017, 99: 14-25. DOI:10.1016/j.ijimpeng.2016.09.003 |
| [14] |
Silling S A. Reformulation of elasticity theory for discontinuities and long-range forces[J]. Journal of the Mechanics and Physics of Solids, 2000, 48(1): 175-209. DOI:10.1016/S0022-5096(99)00029-0 |
| [15] |
Silling S A, Askari E. A meshfree method based on the peridynamic model of solid mechanics[J]. Computers & Structures, 2005, 83(17/18): 1526-1535. |
| [16] |
Huang D, Lu G D, Wang C W, et al. An extended peridynamic approach for deformation and fracture analysis[J]. Engineering Fracture Mechanics, 2015, 141: 196-211. DOI:10.1016/j.engfracmech.2015.04.036 |
| [17] |
Huang D, Lu G D, Qiao P Z. An improved peridynamic approach for quasi-static elastic deformation and brittle fracture analysis[J]. International Journal of Mechanical Sciences, 2015, 94/95: 111-122. DOI:10.1016/j.ijmecsci.2015.02.018 |
| [18] |
郁杨天, 章青, 顾鑫. 近场动力学与有限单元法的混合模型与隐式求解格式[J]. 浙江大学学报(工学版), 2017, 51(7): 1324-1330. Yu Y T, Zhang Q, Gu X. Hybrid model of peridynamics and finite element method under implicit schemes[J]. Journal of Zhejiang University(Engineering Science), 2017, 51(7): 1324-1330. (in Chinese) |
| [19] |
章青, 郁杨天, 顾鑫. 近场动力学与有限元的混合建模方法[J]. 计算力学学报, 2016, 33(4): 441-448, 450. Zhang Q, Yu Y T, Gu X. Hybrid modeling methods of peridynamics and finite element method[J]. Chinese Journal of Computational Mechanics, 2016, 33(4): 441-448, 450. (in Chinese) |
| [20] |
张振南, 陈永泉. 基于VMIB多裂纹岩石材料拉伸破坏数值模拟[J]. 岩土工程学报, 2008, 30(10): 1490-1495. Zhang Z N, Chen Y Q. Numerical simulation for fracture propagation of multi-cracked rock materials using virtual multidimensional internal bonds[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(10): 1490-1495. (in Chinese) DOI:10.3321/j.issn:1000-4548.2008.10.012 |
 2021, Vol. 44
2021, Vol. 44



