2. 重庆大学 航空航天学院, 重庆 400044
2. College of Aerospace Engineering, Chongqing University, Chongqing 400044, P. R. China
现代先进航空发动机工作状态下轴承腔中处于空气、油滴和壁面油膜共存的润滑与换热状态[1]。通常,润滑油自轴承滚动体等旋转元件以油滴的形式甩入轴承腔,与干燥腔壁发生碰撞,在腔壁上形成初始的壁面油膜,其后的工作过程中油滴与附着于腔壁的油膜碰撞。油滴与壁面油膜碰撞后部分附着于油膜而剩余部分随之发生飞溅并形成尺寸更小的二次油滴悬浮于腔内的空气中。油滴与壁面油膜的作用过程以及二次油滴的初始特性,不仅直接影响着分布于轴承腔壁面的油膜厚度和流动速度等重要流体动力学特征,更为重要的是进而影响着轴承腔的润滑与换热功能。因此,开展油滴与油膜的碰撞及其后油膜的动力学特性分析,为轴承腔的润滑与换热研究提供参考依据是十分重要的工作。
液滴(包括油滴)与液膜(油膜)碰撞后的动力学现象非常复杂,且与液膜的深度有很大的关联。液滴与较薄液膜碰撞后出现黏附/沉积、反弹、铺展以及飞溅四种典型的现象,与较厚液膜碰撞后则表现为附着、形成空腔和飞溅三种现象[2, 3]。根据无量纲液膜厚度H*(H* = h/d0,其中,h为液膜的厚度,d0为液滴的直径),液膜可以分为薄液膜(H* < 0.1)、浅液膜(0.1≤H* < 1)、厚液膜(1≤H* < 4), 以及深液膜(H*≥4.0)四种类型[4-6]。迄今对于液滴与液膜碰撞的研究仍多集中于与浅液膜的正碰撞,Rioboo等[7]和Okawa等[8]试验研究了水、水-甘油混合物,以及十六烷等液滴与浅液膜的正碰撞过程,探讨了碰撞速度、液滴直径以及液膜厚度对碰撞结果的影响。研究发现,低速液滴与浅液膜碰撞后直接附着于液膜表面形成表面液膜;随着碰撞速度的增加,碰撞结果由液滴附着演变为形成冠状液膜;当碰撞速度较大时,形成的冠状液膜将发生破碎并生成二次液滴。Vander Wal等[9]采用高速相机拍摄了水、水-甘油混合物,以及庚烷等液滴与液膜的正碰撞过程。研究表明,随着液膜厚度的变化,液滴与液膜正碰撞后出现瞬时飞溅和延迟飞溅两种典型碰撞现象。Josserand等[10]基于质量守恒和能量守恒原理建立了液滴与浅液膜正碰撞后飞溅/沉积的临界状态理论分析模型,通过与简化的二维数值分析模型计算结果对比,验证了理论分析模型的有效性。Che等[11]采用高速相机拍摄了水、硅油和水-甘油混合物三种液滴与浅液膜的正碰撞过程,分别探讨了水滴与硅油和水-甘油混合物浅液膜正碰撞后形成的冠状液膜和中心射流形态演化过程,以及硅油和水-甘油混合物两种液滴与浅水膜正碰撞后的扩散过程。Michon等[12]采用高速相机拍摄了水滴与深水膜正碰撞后形成的空腔坍塌过程以及坍塌形成的射流,探讨了水滴直径、碰撞速度等对射流形状与速度的影响。梁刚涛等[13]采用CLSVOF(coupled level set and volume of fluid)方法建立了水滴与浅水膜正碰撞的简化二维数值分析模型,分析和探讨了碰撞初期冠状水膜的流动形态以及形态演化过程。
已有关于液滴与液膜碰撞的研究工作多集中于液滴与浅液膜或薄液膜的正碰撞,研究成果对于理解和诠释油滴与深油膜正碰撞的动力学特性贡献极为有限。此外,数值计算中广泛采用的简化二维数值分析模型,难以描述液滴与液膜的实际碰撞情况,以及碰撞后液滴和液膜的复杂流体动力学行为。因此,开展油滴与深油膜碰撞的三维数值分析,揭示更接近于实际情况的油滴与深油膜碰撞过程动力学特性,为轴承腔中典型工作状态下精确的油气两相流动润滑与换热分析提供技术支持具有显著的学术和工程意义。
基于VOF方法建立了油滴与深油膜正碰撞的三维数值分析模型,通过数值计算,分析了冠状油膜和空腔的形成及其形貌演化与流动铺展过程,探讨了油滴直径和碰撞速度对冠状油膜和空腔特性,以及二次油滴直径分布的影响;借助相关试验结果,验证了提出的三维数值模拟方法的正确性,研究工作有助于揭示轴承腔中油滴与壁面油膜碰撞的物理本质。
1 数值分析模型 1.1 控制方程假设油滴与深油膜正碰撞过程为瞬态不可压缩层流流动,采用VOF方法对其界面进行动态追踪计算。此外,假设碰撞过程中润滑油与空气之间没有热量和能量的传递,也没有质量转移。因此,润滑油与空气各相的连续性方程和动量方程可表示为
| $ \nabla \cdot \boldsymbol{u}=0, $ | (1) |
| $ \frac{\partial(\rho \boldsymbol{u})}{\partial t}+\nabla \cdot(\rho \boldsymbol{uu})=-\nabla p+\nabla \cdot\left[\mu\left(\nabla \boldsymbol{u}+\nabla \boldsymbol{u}^{\mathrm{T}}\right)\right]+\rho g+\boldsymbol{F}_{\sigma}, $ | (2) |
式中:u为流体速度矢量;p为压力;g为重力加速度;ρ和μ分别为流体的加权平均密度和动力黏度;Fσ为动量源项;上标T为矩阵转置符号。
VOF方法是通过求解网格单元中流体体积分数实现网格不变情况下的界面重构的,根据其追踪界面的基本思想,润滑油的体积分数αL方程可表示为[14]
| $ \frac{\partial \alpha_{\mathrm{L}}}{\partial t}+\nabla \cdot\left(\boldsymbol{u}_{L} \alpha_{L}\right)=0, $ | (3) |
式中uL为润滑油的速度矢量。体积分数αL = 0和αL = 1,分别表示网格单元中全部为空气和润滑油;0 < αL < 1,表示网格单元为润滑油与空气分界面网格[15, 16]。
对于任意计算网格,流体的加权平均密度和动力黏度分别为
| $ \rho=\alpha_{\mathrm{L}} \rho_{\mathrm{L}}+\left(1-\alpha_{\mathrm{L}}\right) \rho_{\mathrm{G}}, $ | (4) |
| $ \mu=\alpha_{\mathrm{L}} \mu_{\mathrm{L}}+\left(1-\alpha_{\mathrm{L}}\right) \mu_{\mathrm{G}}, $ | (5) |
式中下标L和G分别表示润滑油和空气。
由连续性表面张力模型(CSF),方程(2)中的动量源项Fσ计算公式为[15-17]
| $ \boldsymbol{F}_{\sigma}=2 \sigma \kappa \frac{\rho \nabla \alpha}{\rho_{\mathrm{L}}+\rho_{\mathrm{G}}}, $ | (6) |
式中,σ为润滑油的表面张力系数;κ为润滑油与空气的界面表面曲率,其计算方法见文献[17]。
1.2 数值计算模型油滴与深油膜正碰撞后的油膜流动状态发展过程呈现近似循环对称性[9],为简化数值计算,提高计算效率,采用1/4计算模型,计算域与网格如图 1所示。定义计算域的大小为x×y×z=5d0×5d0×12d0 (d0为油滴直径),以消除计算边界对空气流动和油膜状态发展的影响,采用六面体均匀网格对计算域进行网格划分,如图 1(a)所示。油滴与油膜的初始位置如图 1(b)所示,油膜的厚度为4d0,油滴的初始位置位于油膜液面之上。为提高VOF方法对界面追踪的精度,经大量的试算与分析后,数值计算过程中采用最大等级为4级的自适应网格加密技术对润滑油与空气界面附近区域的网格进行局部加密处理(如图 1(b)~(d)),以单元密度梯度作为标定变量控制加密区域范围[16, 18]。
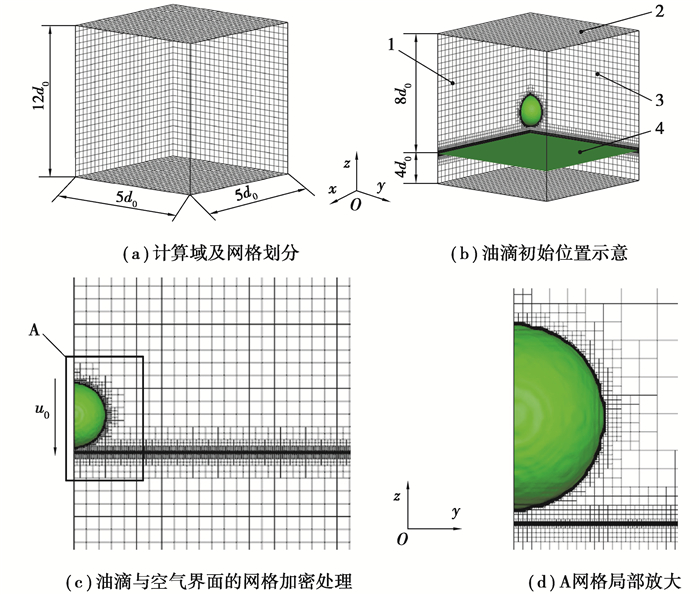
|
图 1 数值分析的计算域与网格模型 Fig. 1 Computational domain and grid model in the numerical calculation |
计算边界条件设置为:边界1和3设置为对称边界条件;边界2设置为相对压力为0的压力出口边界条件;其余边界均设置为无滑移的静止壁面条件;平面4为油膜表面,油膜表面之下为润滑油,以上为空气。初始条件设置为:油滴的初始速度为u0,方向为z轴负方向(如图 1(c));油膜区域中润滑油体积分数αL=1,空气域(除油滴)中润滑油体积分数αL=0;计算中考虑重力的影响,重力方向为z轴负方向。
计算中取润滑油密度为ρL=980 kg/m3,动力黏度为μL=2.254×10-2 Pa·s,表面张力系数为σ=0.032 N/m;空气密度为ρG=1.225 kg/m3,动力黏度为μG=1.789×10-5 Pa·s。除特殊说明,油滴的直径为3.46 mm,油膜的厚度为4d0(13.84 mm),即油膜的无量纲厚度为4。
采用二阶迎风格式离散动量方程,其中压力项采用PRESTO!算法求解;压力-速度方程的耦合采用PISO格式;体积分数方程采用Geo-Reconstruct方法离散;时间采用一阶隐式差分格式离散,计算的最大时间步长为1.0×10-6 s,每个时间步长内的最大迭代步数为25,收敛标准为各变量的平均残差小于1.0×10-5。
1.3 结果分析中的物理参数定义为便于定量表达数值计算结果,定义如图 2所示的若干物理特征参数:油冠直径Dcr为冠状油膜顶部颈缩区内表面所在圆平面的直径;油冠高度Hcr为冠状油膜顶部颈缩区至油膜液面的距离;空腔直径Dca为油滴与油膜碰撞后形成的近似半球形空腔的直径;空腔深度Hca为油膜液面至空腔底部的距离。
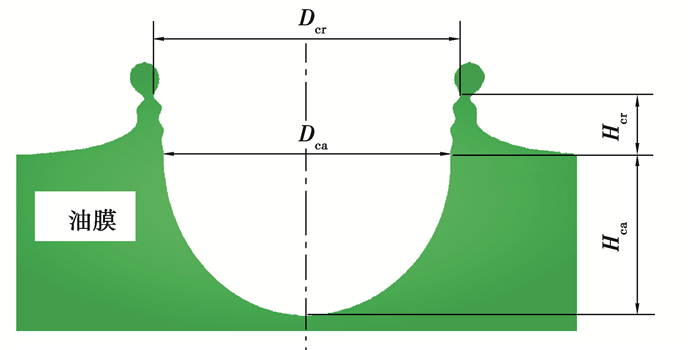
|
图 2 结果分析中相关物理参数的定义示意 Fig. 2 Definition of physical parameters in result analysis |
采用文献[19]中的水滴与水膜正碰撞试验工作对提出的数值分析模型进行验证。试验使用的水滴直径为4.2 mm,碰撞速度为3.7 m/s,水膜厚度为100 mm。采用本文中提出的数值分析模型对其进行数值计算,水膜形态发展以及二次液滴的直径分布数值计算结果与试验结果的对比如图 3(左侧为数值计算结果;右侧为试验结果,括号内的时间为其对应的铺展时刻)和图 4所示。考虑到计算效率,数值计算时水膜厚度取4倍水滴直径16.8 mm。水膜厚度的进一步增加对计算结果的影响非常小,可以忽略不计。
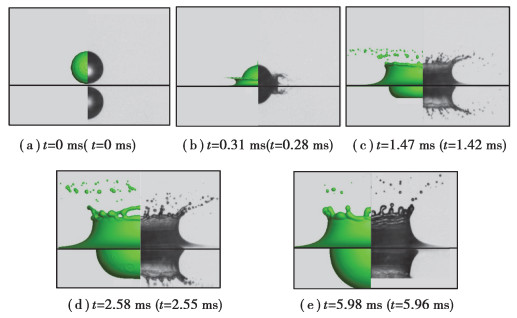
|
图 3 水膜形态的数值计算结果与试验结果对比 Fig. 3 Comparison of water film morphology between numerical calculation and test results |
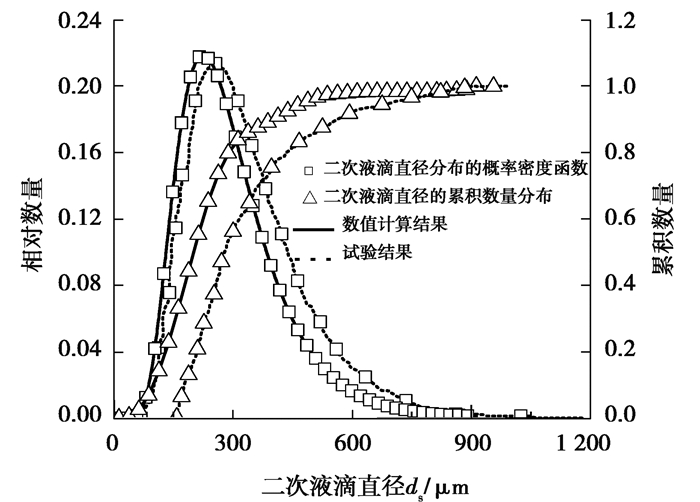
|
图 4 二次液滴直径分布的数值计算结果与试验结果对比 Fig. 4 Comparison of secondary droplet diameter distribution between numerical calculation and test results |
由图 3可以看出,采用本文数值计算方法获得的5个时刻的水膜形态结果与试验结果有较好的一致性。图中数值计算结果和试验结果在时间上的差异,主要是由两者的初始时刻差异造成的。
由图 4可以看出,二次液滴直径分布的概率密度函数和累积数量分布数值计算结果与试验结果在数值上有一定的误差,但在变化趋势上具有较好的吻合性。造成误差的主要原因可能在于,第一是试验中采用高速摄影技术难以捕捉到尺寸非常小的二次液滴,其二是基于图像处理的试验数据分析方法引入了一定的测量误差,故而出现了较为明显的试验结果相对于数值计算结果整体右移的趋势。上述工作一定程度上证明了本文提出的数值计算模型的正确性和可靠性。
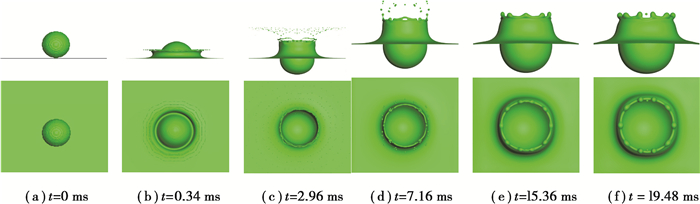
3 结果与讨论图 5给出了油滴直径为3.46 mm、碰撞速度为5.0 m/s、油膜厚度为13.84 mm条件下,油滴与油膜正碰撞后形成的冠状油膜状态发展过程以及二次油滴的飞溅情况。图 5中油膜铺展视图的第一行为主视图,第二行为对应的俯视图。由图 5可以看出,油滴与油膜接触后,在惯性力的作用下挤压并排开接触区域油膜,接触区域的油膜以碰撞点为中心向四周扩展,同时在油滴周围形成厚度较薄的环形空间铺展油膜,其间受空气扰动影响,油膜边缘出现润滑油分离,生成大量尺寸较小、飞溅速度较大的二次油滴(如图 5(a)~(c)),即发生瞬时飞溅[9]。随着时间的推移,油滴不断下沉并融入油膜,油滴的质量和碰撞能量持续转移给油膜,油液不断进入到向外铺展的空间油膜中,空间油膜的直径和高度不断增大,继而发展为冠状油膜;受扰动的空气作用,冠状油膜边缘出现Rayleigh-Plateau不稳定现象,破碎生成尺寸较大、飞溅速度较小的二次油滴,但其间没有明显的指状射流形成(如图 5(d))。其后,冠状油膜继续向外发展,同时因表面张力而出现轻微的收缩,达到最大高度后,因重力作用缓慢向油膜液面回落(如图 5(e)和(f)),此阶段没有二次油滴生成,但原来的二次油滴由于惯性作用继续向空气中离散,进而逸出计算域,以至于图 5(e)和(f)中没有观察到二次油滴。
|
图 5 碰撞速度为5.0 m/s条件下油滴与深油膜正碰撞后的油膜状态发展过程 Fig. 5 Film development process of oil droplet impacting normally onto a deep pool at impact velocity 5.0 m/s |
图 5中还可以看出,在冠状油膜形成和发展期间,油膜内部也形成了一个以碰撞点为球心的近似半球形空腔,且空腔的直径随着时间的推移而增大。其原因可以归因于,持续与油膜融入的油滴转移给油膜的碰撞能量驱使油膜沿空腔径向运动的结果。
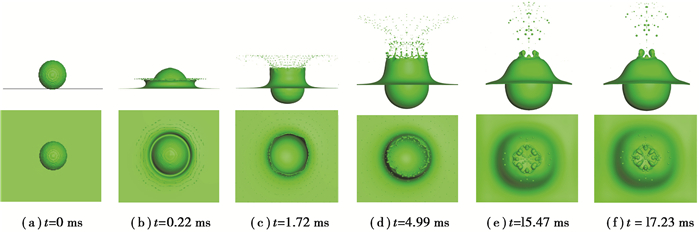
图 6给出了油滴直径为3.46 mm、碰撞速度为7.0 m/s、油膜厚度为13.84 mm条件下,油滴与油膜正碰撞后形成的冠状油膜状态发展过程以及二次油滴的飞溅情况。由图 6可以看出,与碰撞速度为5.0 m/s条件下的碰撞结果相比较,不同的是冠状油膜状态发展的中后期,油膜边缘出现了指状射流,顶部区域呈现出了明显的向中心的聚合和回缩,形成了“钟鼎形”油膜冠顶(如图 6(d)~(f)), 与文献[20, 21]的试验结果吻合。其原因在于,较高碰撞速度的油滴碰撞能量更大,与油膜碰撞后转移给冠状油膜的铺展能量也更大,油膜铺展的更快,形成的油膜厚度更薄,致使于在表面张力的作用下顶部区域聚合和回缩的趋势更为明显,故而呈现出“钟鼎形”冠顶。另外,相比于碰撞速度为5.0 m/s的情况,二次油滴的数量更大,持续产生二次油滴的时间也更长,这均与液滴的碰撞能量较大有关。
|
图 6 碰撞速度为7.0 m/s条件下油滴与深油膜正碰撞后的油膜状态发展过程 Fig. 6 Film development process of oil droplet impacting normally onto a deep pool at impact velocity 7.0 m/s |
图 7给出了油滴直径为3.46 mm,碰撞速度为5.0 m/s、油膜厚度为13.84 mm条件下,油滴与油膜正碰撞后的冠状油膜状态发展过程中生成的二次油滴的直径ds分布直方图及其概率密度函数。图 7中纵坐标二次油滴相对数量为直径区间内二次油滴的数量与其总数量之比值。由图 7可以看出,碰撞生成的小直径二次油滴数量很大,其直径主要集中在小于300 μm的范围内,是二次油滴的主要组成部分;而大直径的二次油滴数量非常少。其原因可能在于,二次油滴主要由碰撞初期铺展能量较大而厚度较薄的环形油膜瞬时飞溅产生,较大的铺展能量使得油膜被雾化为直径较小的油滴,故而大部分二次油滴的直径较小。此外,通过对二次油滴直径计算结果的数据拟合,得到其直径分布的概率密度函数基本服从对数正态分布。计算得到的二次油滴直径分布特性与文献[19]中的试验研究结论一致。
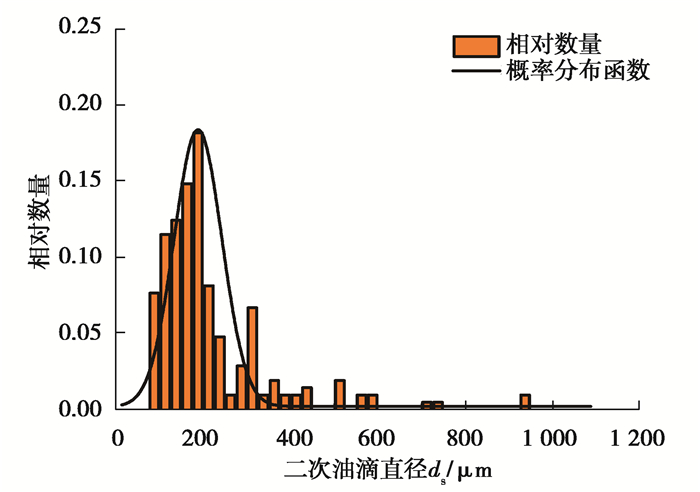
|
图 7 二次油滴直径分布的直方图及其概率密度函数 Fig. 7 Histogram of secondary oil droplet diameter distribution and its probability density function |
图 8给出了同一计算条件下二次油滴初始速度us分布的散点图。从图 8中可以看出,小直径二次油滴的初始速度较为分散,而大直径二次油滴的初始速度较为集中且速度值较小。前者的原因在于,小直径二次油滴在冠状油膜形成与状态发展过程中均有产生,而决定其初始速度的油膜铺展能量随着油膜状态发展而逐渐减小,从而造成生成的二次油滴初始速度也随之变小的结果。后者出现的原因是,大直径油滴产生于冠状油膜状态发展的中后期,较小的铺展能量使得二次油滴的初始速度也比较小且较为集中。
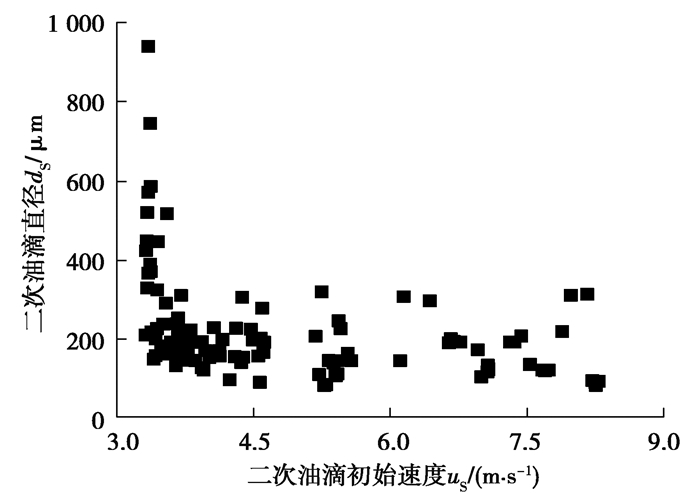
|
图 8 二次油滴初始速度分布散点图 Fig. 8 Scatter diagram of initial velocity distribution of secondary oil droplets |
图 9给出了碰撞速度为5.0 m/s条件下油滴直径对冠状油膜油冠高度和直径的影响。从图 9(a)中可以看出,随着油滴直径的增大冠状油膜油冠高度是增大的。显然这与大直径油滴具有较高的动量有关,大直径油滴在与油膜碰撞后转移给冠状油膜的动量也较大,加速了油膜向上(z轴正向)铺展。此外,图 9中铺展时间t < 1.5 ms时,油冠高度几乎不受油滴直径影响,表明环形油膜形成与铺展初始阶段由油滴转移给油膜的动量而产生的铺展加速度差异很小。图中冠状油膜达到最大高度的时间随着油滴直径的增大而增大,表明大直径油滴形成的油膜铺展的更高更远。
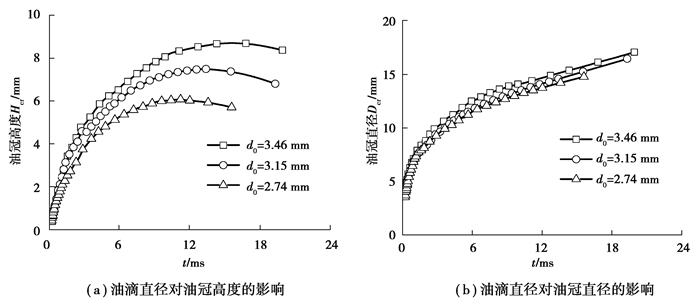
|
图 9 油滴直径对冠状油膜油冠高度和直径的影响 Fig. 9 Effects of oil droplet diameter on the crown height and diameter |
图 9(a)中还可以看出,同一油滴直径下,冠状油膜油冠高度随着铺展时间先增大,达到最大高度后逐渐减小,变化过程近似抛物线,这是冠状油膜流动铺展过程中受重力作用的结果。
由图 9(b)可以看出,油冠直径受油滴直径的影响不明显。显然是,冠状油膜状态发展变化过程中润滑油表面张力抑制了油膜在径向(xy平面)的扩展所致。
图 10给出了碰撞速度对冠状油膜油冠高度和直径的影响。从图 10(a)中可以看出,冠状油膜达到最大高度之前,油冠高度随着碰撞速度的增大而增大;而且油滴碰撞速度越大,油冠的最大高度也越大,达到最大高度的时间越短。显然这是由于高速度的油滴具有更大的碰撞能量,进而转移给油膜的铺展能量更大,形成的环形油膜厚度更薄,故而加速了油膜铺展进程,缩短了铺展时间。
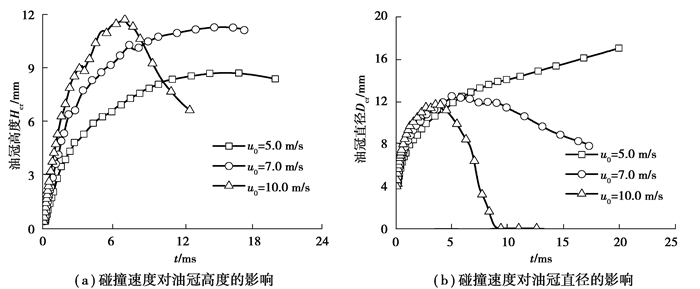
|
图 10 碰撞速度对冠状油膜油冠高度和直径的影响 Fig. 10 Effects of impact velocity on the crown height and diameter |
另外,图 10中碰撞速度为10.0 m/s情况下的油冠高度在达到最大值后突然减小,表明厚度较薄的冠状油膜已经从克服重力向上铺展阶段转捩为在重力作用下加速向油膜液面回落阶段。
图 10(b)中油冠直径的变化分为两个阶段:第一个阶段为环形油膜形成与铺展阶段(铺展时间t < 5.0 ms),油冠直径几乎不受碰撞速度的影响,其原因显然是表面张力抑制了油膜沿径向铺展的结果;第二个阶段为冠状油膜状态发展的中后期(铺展时间t > 5.0 ms),油冠直径随着碰撞速度的增加而减小,这是因为碰撞速度较大的油滴形成的冠状油膜高度较大、平均厚度较薄,随着油膜状态的发展,表面张力使得顶部区域的油膜加速向中心聚集和回缩所致。值得注意的是,碰撞速度为10.0 m/s时,油冠直径在达到最大值后减小至0并保持恒定,是油冠顶部在表面张力作用下完全闭合,形成“钟鼎形”冠顶的结果。
图 11给出了碰撞速度为5.0 m/s条件下油滴直径对空腔深度和直径的影响。图中的铺展时间范围内空腔虽然还没有达到最大深度但已接近深度的最大值。此外,为了便于对比表达,图中深度值采用了负数表示。可以看出,空腔深度和直径均随着油滴直径增大而增大。这一现象的产生是由于在碰撞速度恒定的情况下,大直径油滴具有的碰撞能量更大,碰撞后转移给油膜的扩展能量也较大,使得油滴完全融入油膜前在其内部运动的距离更大,排开的油液更多。
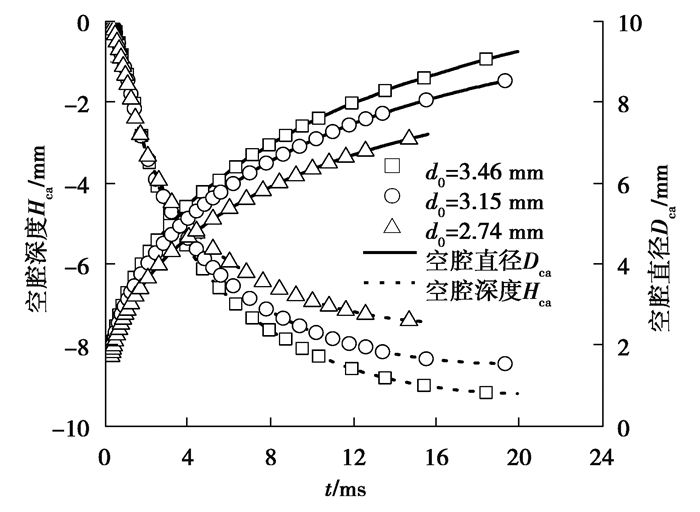
|
图 11 油滴直径对空腔深度和直径的影响 Fig. 11 Effects of droplet diameter on the cavity height and diameter |
图 11中还可以看出,同一油滴直径下,空腔深度和直径随着铺展时间的变化近似对数函数曲线关系,即空腔深度和直径的增加速度随着油膜铺展时间是逐渐减小的,表明空腔的发展受与油膜深度成正比的液体压力、润滑油黏滞力,以及表面张力的抑制作用,排开油液的阻力不断增大。
图 12所示为碰撞速度对空腔深度和直径的影响规律。可以看到,空腔深度和直径均随着碰撞速度增大而增大。这显然也是由于高碰撞速度油滴具有的高碰撞能量对于油滴和油膜运动贡献的结果。
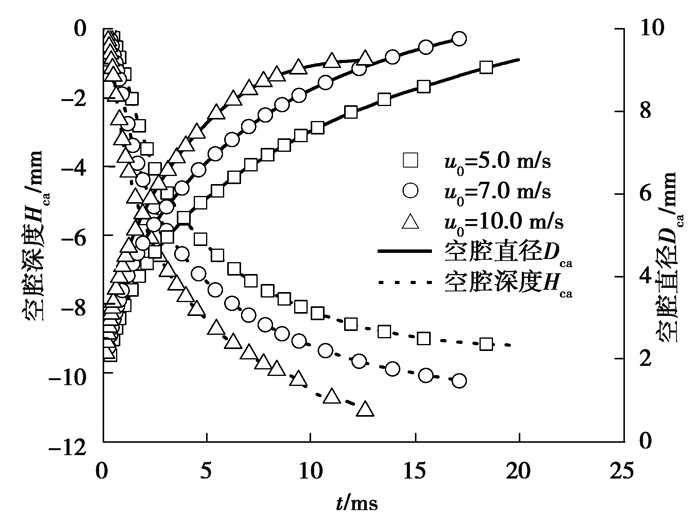
|
图 12 碰撞速度对空腔深度和直径的影响 Fig. 12 Effects of impingement velocity on the cavity height and diameter |
图 13给出了碰撞速度为5.0 m/s条件下油滴直径对二次油滴直径分布的影响。可以看出,随着油滴直径的增大,二次油滴直径分布越加分散,大直径油滴数量增多,小直径油滴数量减少。其原因可以理解为,一是大直径油滴碰撞能量较大,转移给环形油膜的空间铺展能量也较大,二是大直径油滴与油膜碰撞后转移给环形油膜质量要大一些,两者共同作用使得形成的冠状油膜的厚度和达到的空间高度均更大一些,铺展时间更长,增加了产生大直径二次油滴的概率,故而油滴直径区间增大、直径分布更为分散。图 13中二次油滴相对数量的最大值随着油滴直径的增大而减小,表明小直径油滴更易于形成直径较小的二次油滴,反应出惯性力、润滑油黏度和表面张力对二次油滴生成的复杂作用机制[22]。
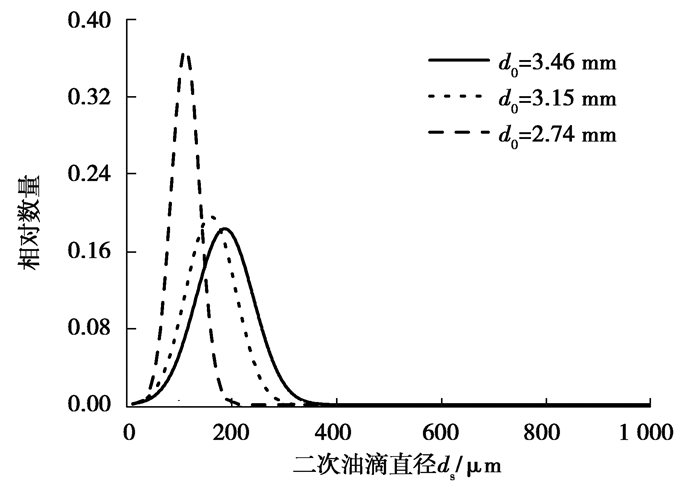
|
图 13 油滴直径对二次油滴直径分布的影响 Fig. 13 Effects of droplet diameter on the secondary droplet diameter distribution |
图 14所示为碰撞速度对二次油滴直径分布的影响。可以看出,随着碰撞速度的增大,二次油滴直径分布的更加集中,小直径油滴数量增多,大直径油滴数量减小。其原因可以理解为,较高碰撞速度下油滴转移给环形油膜的空间铺展能量较大,致使形成的冠状油膜厚度更薄一些,受空气扰动后边缘破碎生成的二次油滴更为细小且数量更大[9]。
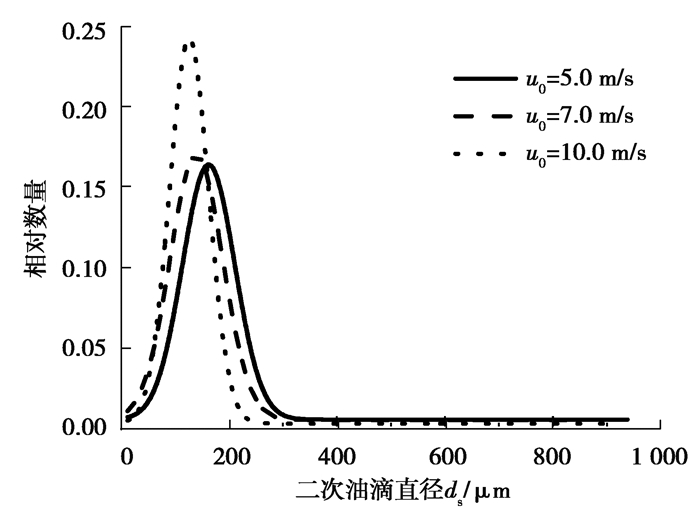
|
图 14 碰撞速度对二次油滴直径分布的影响 Fig. 14 Effects of impact velocity on the secondary droplet diameter distribution |
1) 油滴与深油膜正碰撞后以接触点为中心排开润滑油,形成环形溅射油膜,在油滴的冲击作用下,油膜中的润滑油持续进入环形溅射油膜,溅射油膜最终发展为冠状油膜。与此同时,油膜液面以下形成以接触点为球心的近似半球形空腔。碰撞速度较大时,形成的冠状油膜厚度较薄,在表面张力的作用下,油膜顶部区域的润滑油向其中心聚合和回缩,形成“钟鼎形”冠顶。
2) 冠状油膜形成和发展过程中油膜边缘破碎生成溅射的二次油滴,二次油滴直径呈对数正态分布;小直径二次油滴的初始速度较为分散,大直径油滴的初始速度较为集中且其值较小。
3) 随着油滴直径的增大,油冠高度、空腔深度和直径是增加的;二次油滴直径分布更加分散,大直径油滴数量增多;油冠直径受油滴直径的影响不显著。
4) 随着碰撞速度的增大,油冠高度、油冠直径、空腔深度和直径都是增加的;二次油滴以小直径油滴为主,直径分布较为集中。
| [1] |
王莉娜, 陈国定, 孙恒超. 轴承腔油滴沉积特性及油膜流动特征分析[J]. 航空学报, 2016, 37(10): 3159-3169. Wang L N, Chen G D, Sun H C. Characteristics analysis of oil droplet deposition and oil film flow in a bearing chamber[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(10): 3159-3169. (in Chinese) |
| [2] |
Bai C X, Gosman A D. Development of methodology for spray impingement simulation[C]//SAE Technical Paper Series, 400 Commonwealth Drive, Warrendale, PA, United States: SAE International, 1995: 69-87.
|
| [3] |
Bisighini A, Cossali G E. High-speed visualization of interface phenomena: single and double drop impacts onto a deep liquid layer[J]. Journal of Visualization, 2011, 14(2): 103-110. DOI:10.1007/s12650-011-0072-3 |
| [4] |
MacKlin W C, Metaxas G J. Splashing of drops on liquid layers[J]. Journal of Applied Physics, 1976, 47(9): 3963-3970. DOI:10.1063/1.323218 |
| [5] |
Tropea C, Marengo M. The impact of drops on walls and films[J]. Multiphase Science and Technology, 1999, 11(1): 19-36. DOI:10.1615/MultScienTechn.v11.i1.20 |
| [6] |
Wang A B, Chen C C, Hwang W C. On some new aspects of splashing impact of drop-liquid surface interactions[M]. Vienna: Springer Vienna, 2002: 303-306.
|
| [7] |
Rioboo R, Bauthier C, Conti J, et al. Experimental investigation of splash and crown formation during single drop impact on wetted surfaces[J]. Experiments in Fluids, 2003, 35(6): 648-652. DOI:10.1007/s00348-003-0719-5 |
| [8] |
Okawa T, Shiraishi T, Mori T. Production of secondary drops during the single water drop impact onto a plane water surface[J]. Experiments in Fluids, 2006, 41(6): 965-974. DOI:10.1007/s00348-006-0214-x |
| [9] |
Vander Wal R L, Berger G M, Mozes S D. Droplets splashing upon films of the same fluid of various depths[J]. Experiments in Fluids, 2006, 40(1): 33-52. DOI:10.1007/s00348-005-0044-2 |
| [10] |
Josserand C, Zaleski S. Droplet splashing on a thin liquid film[J]. Physics of Fluids, 2003, 15(6): 1650. DOI:10.1063/1.1572815 |
| [11] |
Che Z Z, Matar O K. Impact of droplets on immiscible liquid films[J]. Soft Matter, 2018, 14(9): 1540-1551. DOI:10.1039/C7SM02089A |
| [12] |
Michon G J, Josserand C, Séon T. Jet dynamics post drop impact on a deep pool[J]. Physical Review Fluids, 2017, 2(2): 023601. DOI:10.1103/PhysRevFluids.2.023601 |
| [13] |
梁刚涛, 沈胜强, 杨勇. 单液滴撞击平面液膜飞溅过程的CLSVOF模拟[J]. 热科学与技术, 2012, 11(1): 8-12. Liang G T, Shen S Q, Yang Y. CLSVOF simulation for splashing of single drop impact on flat liquid film[J]. Journal of Thermal Science and Technology, 2012, 11(1): 8-12. (in Chinese) DOI:10.3969/j.issn.1671-8097.2012.01.002 |
| [14] |
Hirt C, Nichols B. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39(1): 201-225. DOI:10.1016/0021-9991(81)90145-5 |
| [15] |
王鼎铭, 陈薄, 古忠涛, 等. 旋转圆盘表面油膜流动特性分析[J]. 推进技术, 2019, 40(1): 53-60. Wang D M, Chen B, Gu Z T, et al. Flow characteristics of oil film on surface of a rotating disk[J]. Journal of Propulsion Technology, 2019, 40(1): 53-60. (in Chinese) |
| [16] |
周超, 古忠涛, 陈薄, 等. 油滴/金属壁面正碰撞的油膜动力学特性[J]. 航空动力学报, 2019, 34(7): 1607-1614. Zhou C, Gu Z T, Chen B, et al. Oil film dynamic characteristics during oil droplet's normal impact onto metallic surface[J]. Journal of Aerospace Power, 2019, 34(7): 1607-1614. (in Chinese) |
| [17] |
Brackbill J, Kothe D, Zemach C. A continuum method for modeling surface tension[J]. Journal of Computational Physics, 1992, 100(2): 335-354. DOI:10.1016/0021-9991(92)90240-Y |
| [18] |
Theodorakakos A, Bergeles G. Simulation of sharp gas-liquid interface using VOF method and adaptive grid local refinement around the interface[J]. International Journal for Numerical Methods in Fluids, 2004, 45(4): 421-439. DOI:10.1002/fld.706 |
| [19] |
Peduto D D. Oil droplet impact dynamics in aero-engine bearing chambers: correlations derived from direct numerical simulations[D]. Nottingham: University of Nottingham, 2015.
|
| [20] |
Rein M. Phenomena of liquid drop impact on solid and liquid surfaces[J]. Fluid Dynamics Research, 1993, 12(2): 61-93. DOI:10.1016/0169-5983(93)90106-K |
| [21] |
Pan K L, Cheng K R, Chou P C, et al. Collision dynamics of high-speed droplets upon layers of variable thickness[J]. Experiments in Fluids, 2008, 45(3): 435-446. DOI:10.1007/s00348-008-0486-4 |
| [22] |
Samenfink W, Elsäßer A, Dullenkopf K, et al. Droplet interaction with shear-driven liquid films: analysis of deposition and secondary droplet characteristics[J]. International Journal of Heat and Fluid Flow, 1999, 20(5): 462-469. DOI:10.1016/S0142-727X(99)00035-1 |
 2021, Vol. 44
2021, Vol. 44


