1b. 重庆交通大学 土木工程学院, 重庆 400074;
2. 中铁大桥 科学研究院有限公司, 武汉 430034;
3. 桥梁结构健康与安全国家重点实验室, 武汉 430034
1b. School of Civil Engineering, Chongqing Jiaotong University, Chongqing 400074, P. R. China;
2. China Railway Bridge Science Research Institute Ltd., Wuhan 430034, P. R. China;
3. State Key Laboratory for Health and Safety of Bridge Structures, Wuhan 430034, P. R. China
近年来,随着中国经济的迅速发展,各行各业对交通运输的要求日益增大,车辆荷载存在明显的递增趋势。在大流量、高负载车辆的长期作用下,桥梁的使用寿命大幅降低,甚至引起桥梁坍塌事故屡屡发生[1-2],即实际运营车辆荷载与设计荷载存在明显差距,且规范的更新速度远不及车辆荷载等级提升的速度[3],因此在桥梁设计和评估工作中,准确把握车辆荷载未来发展情况十分重要。开展卡车荷载预测及桥梁结构受力分析,可以准确把握车辆荷载发展变化规律,及时了解桥梁的服役状况,这既是进行运营车辆管制、治理超限运输的基础工作,也是在役桥梁安全运营、检测评估、加固改造的前提。
针对车辆荷载的预测,前人做过不少研究,Yu等[4]采用Monte Carlo和影响线方法模拟了长期交通荷载,并基于非平稳贝叶斯方法预测了桥梁寿命期间的最大交通荷载;鲁乃唯等[5]采用交通量的区间增长模型模拟日极值,并由Rice公式外推预测了车辆荷载最大值;阮欣等[6]及周军勇等[7]提出合成车流方法模拟交通流并实现荷载效应预测,并采用广义极值分布外推车辆荷载极值;Fu等[8]基于渐进极值理论对不同交通状态下汽车荷载进行了极值预测;李植淮等[9]以及冯海月等[10]基于GPD模型的拟合方法,实现了基准期内车辆荷载效应的极值估计;Mazas等[11]针对超越阈值法的阈值选择问题提出了一种双阈值方法,并进行了不同评估期荷载值的预测;Zhou等[12]在广义Pareto分布的超阈值峰值法的基础上提出一种基于混合峰值超阈值法的桥梁交通荷载效应特征值和最大值分布预测方法;余志武等[13]利用灰色系统和马尔科夫链建立了公路交通量增长随机过程预测模型,预测了某一车辆荷载总质量范围内的车辆数。OBrien等[14-15]基于动态称重(WIM)数据,采用蒙特卡罗方法对桥梁的荷载效应进行了模拟。然而,既有研究大多基于年平均日交通量(ADTT),忽略了交通量本身的周期性和季节性问题。事实上,1天24小时内的交通量有峰值和谷值,不同时间段的交通量存在极大差异,其产生的作用效应等也将显著不同。在以往的研究中,对交通荷载进行外推时,大多假设交通是一个平稳随机过程,但实测数据表明,车辆荷载存在着明显的递增趋势,且其增长趋势并非趋于常数或是线性函数,即车辆荷载呈现出非平稳增长。
为此,笔者基于年平均每小时交通量(AAHT),考虑交通量周期性问题和季节性变化,建立季节性差分自回归移动平均(SARIMA)模型分解长期趋势和季节模式,通过识别过去的详细交通模式预测未来卡车交通荷载,并在考虑车辆非平稳增长和不考虑车辆非平稳增长两种条件下,分别计算其产生的梁桥疲劳损伤。
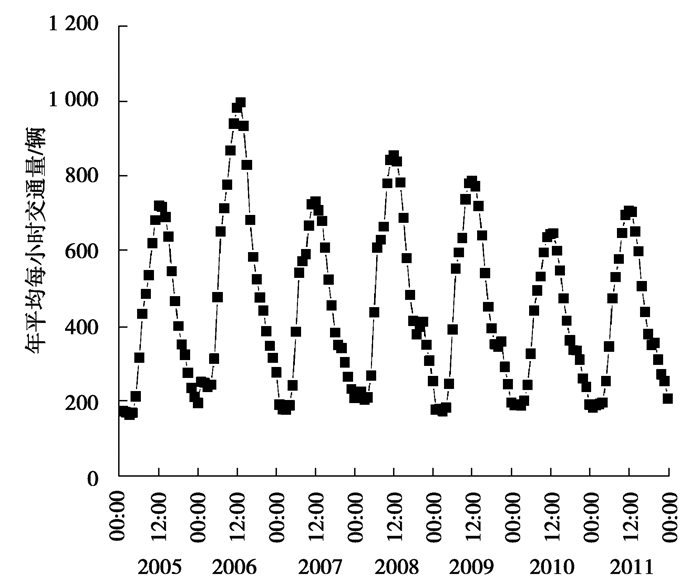
1 监测数据概况文中数据来自安徽省某公路桥梁长期健康监测系统,该桥梁为双向6车道,安装的监测系统记录了所有通行卡车信息。笔者整理了2005—2011年的监测数据,考虑同向行驶3条车道情况,共计23 043 208辆车。对原始数据进行预处理,剔除存在问题的记录后共有16 680 757辆有效车辆数据,每条数据包含了车道、时间、重量等信息。现定义各年份1天24小时内每小时的交通总量除以实际统计天数为年平均每小时交通量(AAHT),其计算结果如图 1所示。
|
图 1 年平均每小时交通量 Fig. 1 Annual average hourly traffic |
由图 1可知,各年份的AAHT具有明显的周期性,以24 h为一个周期计,则各年份的AAHT都有明显的高峰(12:00左右)和低谷(00:00左右),且交通量大小差距明显。其中,2006年的AAHT峰值明显高于其他年份。
2 卡车荷载预测模型与检验时间序列模型非常适合具有不确定性和不易建立精确数学模型的系统建模,例如自回归求和移动平均(ARIMA)模型及其变形形式就被广泛应用于交通流的预测,其中SARIMA模型就是ARIMA模型的一种变形形式。SARIMA模型能够充分考虑交通流数据中的周期性特征,有效解决交通流数据不平稳的问题。此外,SARIMA模型能够根据所研究交通系统不断变化的特征自动调整自身,易实现车辆数据的实时调整[16]。因此,笔者将构建SARIMA模型来实现未来卡车荷载预测。
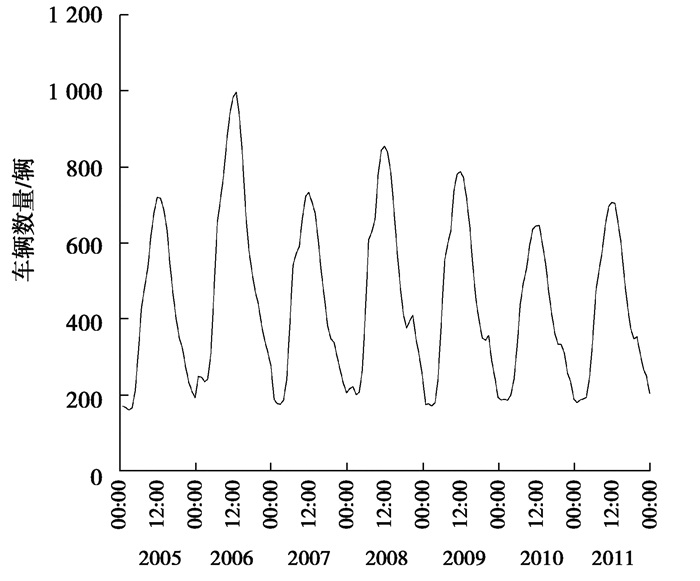
2.1 预测模型的构建 2.1.1 模型平稳性检验绘制出7年卡车数据AAHT的时间序列如图 2所示,对其进行ADF(augmented Dickey-Fuller)单位根检验以判断序列的稳定性,具体检验结果如表 1所示。
|
图 2 年平均每小时交通量时序 Fig. 2 The time series of the AAHTs |
| 表 1 原始数据ADF检验表 Table 1 The ADF test for the original data |
由表 1可知,ADF统计量为-2.382 719,其值小于对应于5%统计水平的临界值-1.942 781,表明所研究的AAHT时间序列不具有单位根,即该时间序列本身是一种平稳过程。
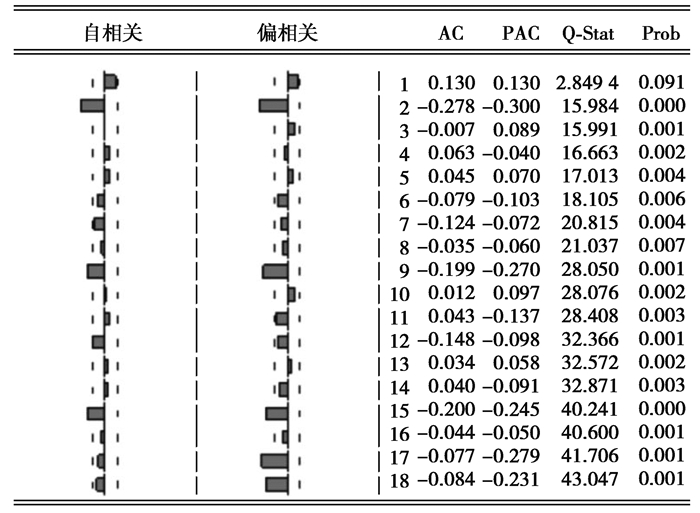
2.1.2 模型定阶与识别由交通量样本序列的平稳性检验结果可知,所观察的交通数据本身是平稳的,因此不需要再对其时间序列进行普通差分或季节差分处理,故差分阶数d和季节差分阶数D均取为0,年平均每小时交通量时间序列自带周期s为24。绘出样本数据的自相关和偏自相关图如图 3所示。由图 3可知,样本的自相关系数和偏相关系数都不显著为0,所以P=Q=1(P为模型中SAR项的滞后阶数,Q为模型中SMA项的滞后阶数),年平均每小时交通量时间序列的自相关系数和偏相关系数均在2阶截尾。于是,(p,q)的选择范围有(1,1)(1,2)(2,1)(2,2),p表示交通流序列的滞后阶数,q表示误差序列滞后阶数。
|
图 3 样本数据自相关图及偏相关图 Fig. 3 Autocorrelation diagram and partial correlation diagram of the data |
对上述几种模型进行分析比较,根据修正的拟合优度R2最大、AIC值和SC值最小的原则来选择最佳的模型。分别将p、q值代入模型中,计算得到各个模型的相关参数,如表 2所示,最终模型确定为SARIMA(2,0,2)(1,0,1)24。
| 表 2 模型判别 Table 2 Model discrimination |
为了检验模型的准确性与有效性,首先利用2005—2008年这4年的车辆数据计算AAHT,通过建立的SARIMA模型对2009年、2010年和2011年的交通量进行预测,并将预测结果与实测数据进行对比如图 4所示。从图 4中看出,预测结果与实际数据吻合较好,充分说明本模型能够正确预测未来车辆交通流量。

|
图 4 预测交通量与实际交通量结果对比图 Fig. 4 The comparison between the predicted and actual traffic volume |
现利用收集的7年的桥梁健康监测数据,通过建立的SARIMA模型进一步预测后十年间(2012—2021年)的AAHT,结果如图 5所示。从图 5可知,交通量呈现明显的非平稳增长趋势,到2021年,AAHT预测量峰值达到850辆左右,最小值为350辆左右,其ADTT如图 6所示,可见ADTT呈明显的增长趋势。
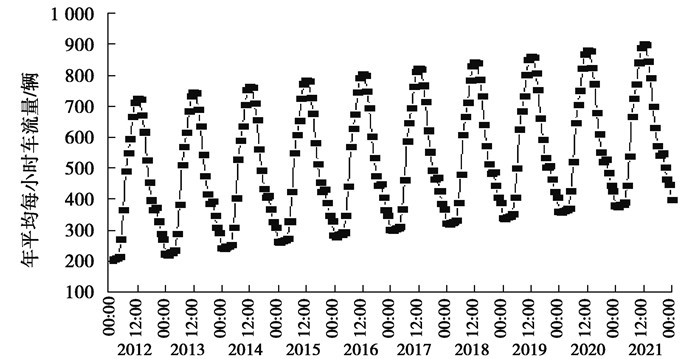
|
图 5 2012—2021年平均每小时交通预测量 Fig. 5 The forecasted AAHTs from 2012 to 2021 |
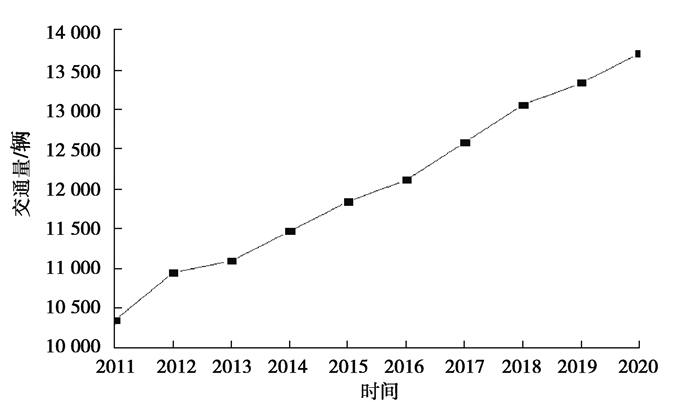
|
图 6 2012—2021年平均日交通预测量 Fig. 6 The forecasted ADTTs from 2012 to 2021 |
为计算车辆通行产生的荷载效应,现对各类型车辆的轴重(AL)、轴距(AD)、车辆总重(GVW)等参数进行统计分析。将车辆按轴数分类,其中7轴、8轴和9轴车样本量极少可以忽略,仅考虑2~6轴的车辆。限于篇幅,下文以数量最多的5轴车为例,第一轴的轴重概率分布拟合结果如图 7~9所示,其余参数和车型的统计分析方法相同。

|
图 7 1车道上5轴车第一轴重AL1 Fig. 7 The first axle load of 5-axle vehicles in lane 1 |
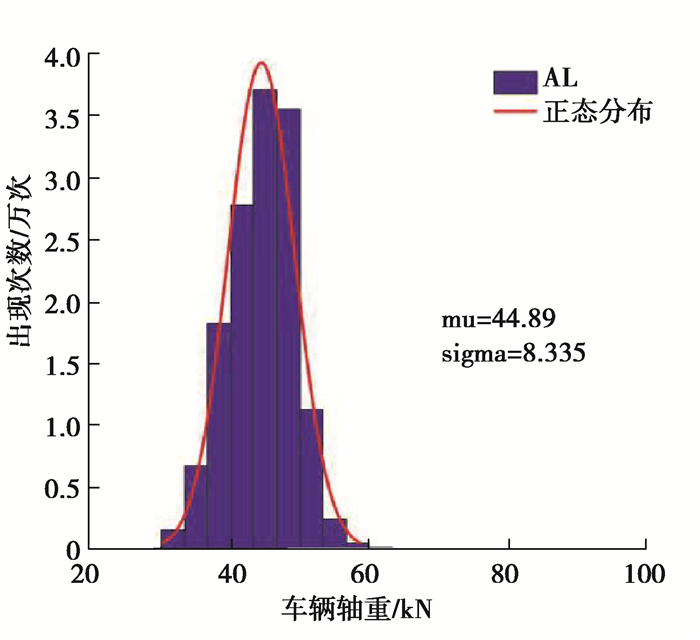
|
图 8 2车道上5轴车第一轴重AL1 Fig. 8 The first axle load of 5-axle vehicles in lane 2 |

|
图 9 3车道上五轴车第一轴重AL1 Fig. 9 The first axle load of 5-axle vehicles in lane 3 |
为更详细地阐述卡车荷载预测问题,现以预测的2021年交通流量为例,对不同车道的年平均每小时交通量进行分析。
3.2.1 2021年年平均每小时交通预测量根据所建立SARIMA模型的预测结果,2021年AAHT预测值的具体结果如表 3所示。
| 表 3 2021年年平均每小时交通预测量 Table 3 The annual average hourly traffic forecast in 2021 |
对卡车数据进行统计分析,计算得到各车道交通量占总交通量的百分比(Pvt(Lk)),结果如表 4所示。
| 表 4 各车道交通量及占比 Table 4 The traffic volume and the percentage of each lane |
基于2021年的AAHT预测值,根据式(1)即可计算出2021年桥梁每条车道上的AAHT,如图 10所示。可见,3条车道的交通量差异明显,其中2车道为主车道,交通量最大值约为500辆/h。
| $ U_{\mathrm{t}}\left(L_{k}\right)=P_{\mathrm{vt}}\left(L_{k}\right) \times V_{\mathrm{t}}, $ | (1) |
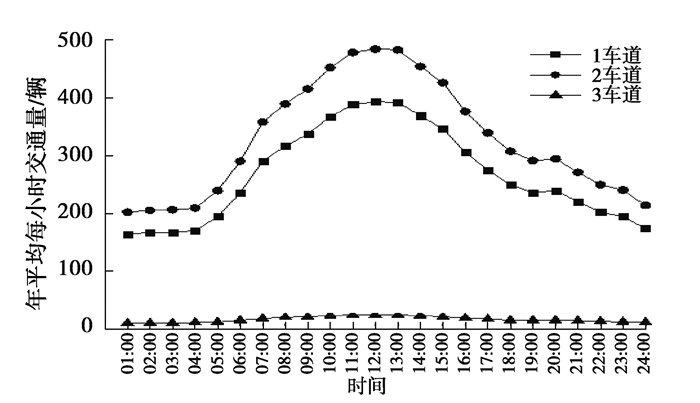
|
图 10 2021年不同车道上年平均每小时交通量(辆) Fig. 10 The AAHTs of three lanes in 2021 |
式中:Ut(Lk)为第k车道上每小时的交通量;Pvt(Lk)为第k车道交通量占比;Vt为2021年的AAHT。
3.3 各车道上不同车型交通量计算为进一步研究车辆通行时所施加荷载的大小,现对3条车道上不同车型的交通流量进行计算,在此基础上计算桥梁所承受的卡车荷载。各车道上各车型的交通量和其占比Pi,以及总交通量如表 5~7所示。
| 表 5 1车道上不同类型车的比例 Table 5 The proportion of each vehicle type in lane 1 |
| 表 6 2车道上不同类型车的比例 Table 6 The proportion of each vehicle type in lane 2 |
| 表 7 3车道上不同类型车的比例 Table 7 The proportion of each vehicle type in Lane 3 |
于是,可根据各车道交通量及各车型占比计算出每种车型的AAHT如表 8所示。
| 表 8 各车道上各车型交通量 Table 8 The traffic volume of each vehicle type in each lane |
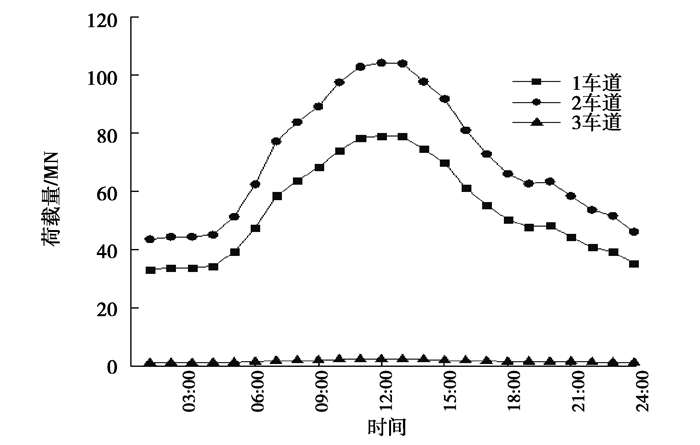
据此,结合前文各车型的车辆总重概率分布情况,即可计算出不同时段桥梁承受的车辆总重如图 11所示。从图 11可以看出,2车道在各时段承受的荷载量最大,3车道则最小,其最大值仅约为前者的1/46,1车道的荷载最大值约为2车道的3/4。
|
图 11 桥梁各车道上不同时段的荷载量 Fig. 11 The total weights of vehicles at each interval for each lane |
文中的卡车荷载预测以及卡车荷载参数模拟,主要是为了研究卡车荷载的非平稳增长对在役桥梁结构疲劳损伤的影响。为此,选择某简支T型梁桥为例,通过有限元模型加载进行相应的计算分析。
4.1 结构的疲劳损伤由疲劳累积损伤模型,结构的疲劳性能可用S-N曲线描述,其曲线方程为[17]
| $ N S^{m}=C, $ | (2) |
式中:N为应力幅值用总次数;S为应力幅值;C为材料疲劳细节参数;m为疲劳强度曲线参数,一般取3.0[18]。由Miner线性累积损伤理论:
| $ D=\sum\limits_{i=1}^{n} \frac{n_{i}}{N_{i}}, $ | (3) |
式中:D为疲劳损伤度;ni为对应第i级应力水平的应力循环数;Ni为对应第i级应力水平的疲劳寿命。
由式(2)和(3)可得结构疲劳损伤的计算式为:
| $ D=\frac{1}{C} \sum\limits_{i=1}^{n} n_{i} S_{i}^{m}。$ | (4) |
式(4)为结构疲劳损伤计算式,其中Si为第i级应力幅值。若以结构的内力幅Mi作为统计参量替代Si,暂不考虑C的影响,则可定义相对疲劳损伤Dc描述外荷载对结构造成的损伤程度,即
| $ D_{\mathrm{c}}=\sum\limits_{i=1}^{n}\left(n_{i} M_{i}^{m}\right)=N M_{\mathrm{e}}^{m}, $ | (5) |
式中:Dc为结构相对疲劳损伤度;Mi为第i个内力幅,梁桥结构可取为弯矩幅;Me为等效内力幅。
| $ M_{\mathrm{e}}=\sum\limits_{i=1}^{n} \gamma_{i} M_{\mathrm{e}i}, $ | (6) |
| $ M_{\mathrm{e} i}=\left(\sum \frac{n_{i} M_{i}^{m}}{N}\right)^{\frac{1}{m}}, $ | (7) |
式中:Mei为第i级应力水平下的等效内力幅;λi为第i级应力水平下等效内力幅折减系数;由参考文献[19]可知,3车道桥梁可取折减系数γ1=0.40,γ2=1.0,γ3=0.15。
于是第i级应力水平下的相对疲劳损伤度为
| $ \frac{D_{i}}{D_{\mathrm{c}}}=\frac{n_{i} M_{\mathrm{e} i}^{m}}{N M_{\mathrm{e}}^{m}}。$ | (8) |
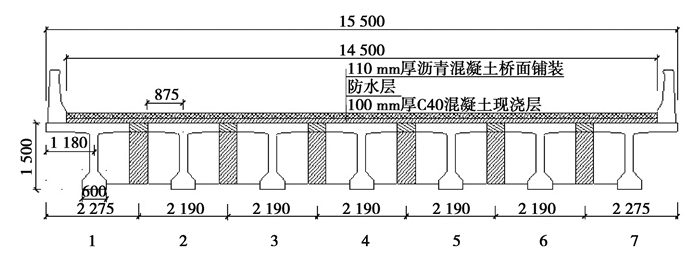
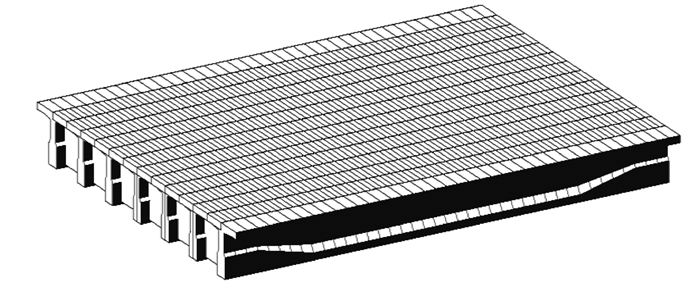
文中的实桥模型为一简支T型梁桥,跨径20 m,桥面宽度为15.5 m,其上部结构由7片预应力混凝土T型梁组成,其跨中横断面如图 12所示,依次对T型梁编号为1~7号梁,梁间距为2.190 m。预制梁长、高分别为19.92 m和1.5 m。采用C50混凝土;普通钢筋采用热轧HRB400号钢筋,预应力筋采用低松弛高强度钢绞线。利用有限元分析软件建立桥梁模型如图 13所示,全桥共生成个301个节点,526个单元。根据本文3.1节的统计分析结果建立车辆模型如表 9所示,依次加载到桥梁模型上,得到不同车辆产生的跨中最大弯矩值(Mmaxi),如表 10所示(限于篇幅,仅展示1车道计算结果)。
|
图 12 跨中截面横断面图 Fig. 12 Cross-sectional view of mid-span section |
|
图 13 桥梁有限元模型 Fig. 13 The finite element model of bridge |
| 表 9 1车道车辆模型及交通量 Table 9 Models and traffic volumes of vehicles in lane 1 |
| 表 10 1车道跨中最大弯矩值 Table 10 Maximum bending moment in lane 1 |
由式(7)可计算出各车道的等效应力幅分别为:1车道Me1=178.033 1 kN·m;2车道Me2=124.158 5 kN·m;3车道Me3=133.503 0 kN·m;
由式(6)可计算出3条车道叠加的总等效应力幅为:
| $ M_{\mathrm{e}}=0.40 \times M_{\mathrm{e1}}+1.0 \times M_{\mathrm{e} 2}+0.15 \times M_{\mathrm{e} 3}=215.39719 \mathrm{kN} \cdot \mathrm{m}。$ | (9) |
利用偏心压力法计算桥梁荷载横向分布系数:各主梁横截面相同,梁数n=7,梁间距为2.19 m,得到各主梁横向分布系数m如表 10所示。
| 表 10 各主梁横向分布系数 Table 10 Transverse distribution coefficient of each beam |
根据3条车道总弯矩效应及主梁横向分布系数,将弯矩分配到7片主梁,计算得到各主梁跨中最大弯矩值Mi的值如表 11所示。
| 表 11 各梁跨中最大弯矩值 Table 11 Maximum bending moment of each beam |
由式(8)可计算出各梁的相对疲劳损伤分别为:
| $ \frac{D_{1}}{D_{\mathrm{c}}} \approx 0.2316 ; \frac{D_{2}}{D_{\mathrm{c}}} \approx 0.0549 ; \frac{D_{3}}{D_{\mathrm{c}}} \approx 0.0127 ; \frac{D_{4}}{D_{\mathrm{c}}} \approx 0.0054 ; \frac{D_{5}}{D_{\mathrm{c}}} \approx 0.0127 ; \frac{D_{6}}{D_{\mathrm{c}}} \approx 0.0549 ; \frac{D_{7}}{D_{\mathrm{c}}} \approx 0.2316 。$ |
运用同样的方法,对不考虑交通量非平稳增长时的车辆数据进行计算,得到不考虑交通量非平稳增长时各梁的相对疲劳损伤分别为:
| $ \frac{D_{1}}{D_{\mathrm{c}}} \approx 0.2316 ; \frac{D_{2}}{D_{\mathrm{c}}} \approx 0.0549 ; \frac{D_{3}}{D_{\mathrm{c}}} \approx 0.0127 ; \frac{D_{4}}{D_{\mathrm{c}}} \approx 0.0054 ; \frac{D_{5}}{D_{\mathrm{c}}} \approx 0.0127 ; \frac{D_{6}}{D_{\mathrm{c}}} \approx 0.0549 ; \frac{D_{7}}{D_{\mathrm{c}}} \approx 0.2316 。$ |
经对比不难发现,考虑车辆非平稳增长时各主梁的疲劳损伤度较不考虑非平稳增长时要大, 前者的疲劳损伤度约为后者的1.7倍,表明车辆的非平稳增长对桥梁的疲劳损伤影响显著,在桥梁的荷载分析以及安全性评估中应给予考虑。
5 结论利用安徽省某公路桥梁长期健康监测数据,计算了年平均每小时交通量AAHT,构建了SARIMA模型进行非平稳卡车荷载预测。在此基础上,对比分析了考虑车辆非平稳增长和不考虑车辆非平稳增长2种情况下桥梁的疲劳损伤度。主要得到以下结论:
1) 年平均小时交通量AAHT能够描述交通荷载的季节性特征,基于AAHT的SARIMA模型能够较准确地预测未来车辆交通流情况。
2) 桥梁各车道上分布的卡车荷载存在明显差异,以2021年预测结果为例,2车道在各时段分布的荷载量最大,其值为104 163.26 kN,3车道分布的荷载量则最小,其值为2 275.2 kN,仅约为2车道的1/46,1车道上卡车荷载最大值为79 075.7 kN,约为2车道的3/4。
3) 考虑卡车荷载非平稳增长时各主梁的疲劳损伤度约为不考虑车辆非平稳增长时的1.7倍,表明车辆非平稳增长对桥梁结构的疲劳损伤影响显著。
致谢
全体作者衷心感谢中铁大桥局桥梁科学研究院为本研究提供了相关的桥梁健康监测数据。
| [1] |
赵少杰, 唐细彪, 任伟新. 桥梁事故的统计特征分析及安全风险防控原则[J]. 铁道工程学报, 2017, 5(59): 59-64. Zhao S J, Tang X B, Ren W X. The statistical characteristics analysis of bridge accidents and prevention principle of security risk[J]. Journal of Railway Engineering Society, 2017, 5(59): 59-64. (in Chinese) |
| [2] |
吉伯海, 傅中秋. 近年国内桥梁倒塌事故原因分析[J]. 土木工程学报, 2010, 43(S1): 495-498. Ji B H, Fu Z Q. Analysis of Chinese bridge collapse accident causes in recent years[J]. China Civil Engineering Journal, 2010, 43(S1): 495-498. (in Chinese) |
| [3] |
韩万水, 闫君媛, 武隽, 等. 基于长期监测的特重车交通荷载特性及动态过桥分析[J]. 中国公路学报, 2014, 7(2): 222-232. Han W S, Yan J Y, WU J, et al. Extra-heavy truck load features and bridge dynamic response based on long-term traffic monitoring record[J]. China Journal of Highway and Transport, 2014, 7(2): 222-232. (in Chinese) |
| [4] |
Yu Y, Cai C S, He W, et al. Prediction of bridge maximum load effects under growing traffic using non-stationary Bayesian method[J]. Engineering Structures, 2019, 185: 171-183. DOI:10.1016/j.engstruct.2019.01.085 |
| [5] |
鲁乃唯, 刘扬, NOORI Mohammad. 交通量持续增长下大跨桥梁时变极值外推分析[J]. 工程力学, 2018, 35(7): 159-166. Lu N W, Liu Y, Noori M. Extrapolation of time-variant extreme effect on long-span bridge considering steadily growing traffic volume[J]. Engineering Mechanics, 2018, 35(7): 159-166. (in Chinese) |
| [6] |
阮欣, 周小燚, 郭济. 基于合成车流的桥梁车辆荷载效应极值预测[J]. 同济大学学报(自然科学版), 2012, 40(10): 1458-1462, 1485. Ruan X, Zhou X Y, Guo J. Extreme value vehichle load vehicle flow extrapolation for bridge effect based on synthetic[J]. Journal of Tongji University(Natural Science), 2012, 40(10): 1458-1462, 1485. (in Chinese) DOI:10.3969/j.issn.0253-374x.2012.10.004 |
| [7] |
周军勇, 石雪飞, 阮欣, 等. 高速公路分车道荷载差异及其响应特性[J]. 同济大学学报: 自然科学版, 2018, 46(4): 458-464. Zhou J Y, Shi X F, Ruan X, et al. Lane load disparities and their loading effect characteristics of freeway[J]. Journal of Tongji University: Natural Science, 2018, 46(4): 458-464. (in Chinese) |
| [8] |
Fu G K, You J. Extrapolation for future maximum load statistics[J]. Journal of Bridge Engineering, 2011, 16(4): 527-535. DOI:10.1061/(ASCE)BE.1943-5592.0000175 |
| [9] |
李植淮, 李春前, 孙健康, 等. 基于GPD模型的车辆荷载效应极值估计[J]. 工程力学, 2012, 29(S1): 166-171. Li Z H, Li C Q, Sun J K, et al. Estimation of extreme vehicle load effect based on GPD model[J]. Engineering Mechanics, 2012, 29(S1): 166-171. (in Chinese) |
| [10] |
冯海月, 伊廷华, 陈斌. 采用广义Pareto分布进行车辆荷载效应极值估计的研究[J]. 振动与冲击, 2015, 34(15): 7-11, 22. Feng H Y, Yi T H, Chen B. Extreme estimation for vehicle load effect based on generalized Pareto distribution[J]. Journal of Vibration and Shock, 2015, 34(15): 7-11, 22. (in Chinese) |
| [11] |
Mazas F, Hamm L. A multi-distribution approach to POT methods for determining extreme wave heights[J]. Coastal Engineering, 2011, 58(5): 385-394. DOI:10.1016/j.coastaleng.2010.12.003 |
| [12] |
Zhou X Y, Schmidt F, Toutlemonde F, et al. A mixture peaks over threshold approach for predicting extreme bridge traffic load effects[J]. Probabilistic Engineering Mechanics, 2016, 43: 121-131. DOI:10.1016/j.probengmech.2015.12.004 |
| [13] |
余志武, 朱红兵, 蒋丽忠, 等. 公路桥梁车辆荷载随机过程模型[J]. 中南大学学报(自然科学版), 2011, 42(10): 3131-3135. Yu Z W, Zhu H B, Jiang L Z, et al. Vehicles load stochastic process model of highway bridges[J]. Journal of Central South University(Science and Technology), 2011, 42(10): 3131-3135. (in Chinese) |
| [14] |
OBrien E J, Bordallo-Ruiz A, Enright B. Lifetime maximum load effects on short-span bridges subject to growing traffic volumes[J]. Structural Safety, 2014, 50: 113-122. DOI:10.1016/j.strusafe.2014.05.005 |
| [15] |
OBrien E J, Enright B. Modeling same-direction two-lane traffic for bridge loading[J]. Structural Safety, 2011, 33(4/5): 296-304. |
| [16] |
Wang F Y, Xu Y L. Traffic load simulation for long-span suspension bridges[J]. Journal of Bridge Engineering, 2019, 24(5): 05019005. DOI:10.1061/(ASCE)BE.1943-5592.0001381 |
| [17] |
赵少杰, 任伟新. 超限超载交通对桥梁疲劳损伤及可靠度的影响[J]. 中南大学学报(自然科学版), 2017, 48(11): 3045-3051. Zhao S J, Ren W X. Effect of overrun and overloaded vehicles on fatigue damage and reliability of highway bridges[J]. Journal of Central South University(Science and Technology), 2017, 48(11): 3045-3051. (in Chinese) |
| [18] |
AASHTO. AASHTO LRFD bridge design specifications[S]. 6th ed. Washington, DC: 2017.
|
| [19] |
Fu G K, Liu L, Bowman M D. Multiple presence factor for truck load on highway bridges[J]. Journal of Bridge Engineering, 2013, 18(3): 240-249. DOI:10.1061/(ASCE)BE.1943-5592.0000330 |
 2021, Vol. 44
2021, Vol. 44