2. 上海维宏电子科技股份有限公司, 上海 200241
2. Shanghai Weihong Electronic Technology Co., Ltd., Shanghai 200241, P. R. China
电容式位移传感器是一种基于电容极板效应的间接测距装置。由于其具有结构简单、检测精度高、灵敏度高、非接触式等优点[1], 广泛应用于激光随动控制系统测量切割头与加工工件距离。加工过程中, 由于喷渣、极板接地不良、气体扰动、工件表面不平整、电容边缘效应等原因, 导致电容传感器获取的位置信息中存在较大随机扰动。为获得良好控制品质, 在进行控制系统设计过程中, 需要对位置微分信号进行有效提取[2-3]。采用直接微分(差分) 方法进行微分信号提取, 由于噪声扰动导致不能有效提取微分信号[4], 严重情况下引发震颤, 机械异响等问题。因此获取高质量原始信号逼近和准确的微分信号对于控制品质的提高有重要意义。
跟踪微分器(DT, differentialtracker), 由韩京清提出一种从不连续或者带有随机噪声信号中提取连续信号以及微分信号技术[5]。通过对其频域分析, 表明其在含有随机噪声、不连续原始信号逼近、微分信号提取具有较好性能[6], 相较于广泛应用的卡尔曼滤波器[7]计算复杂度更小。跟踪微分器应用于自抗扰控制[2]、信号处理[8]、模式识别等领域。
跟踪微分器中的作用函数对滤波特性、跟踪相位滞后、微分信号估计准确度起决定性作用, 因此作用函数被作为重点研究内容。现有文献中, 在解决相位滞后, 微分信号提取方面许多学者提出了不同形式跟踪函数。文献[9]中提出非线性幂次项形式跟踪函数, 在平衡点附近为线性, 远离平衡点为非线性, 避免抖振现象发生。文献[10]在非线性滑模跟踪微分器分析基础上, 提出一种结构简单、易于实现的非线性微分器。文献[11]在综合分析综合控制器属性基础上提出双曲正切形式的跟踪微分器, 文献[12]对采用此形式的跟踪微分器进行相位分析。此外不乏基于sigmoid函数[13], 反正切[14]等其他形式的跟踪微分器。文献[15]提出一种通过使用原始信号进行补偿方式改进跟踪微分器, 该方法中将通过低通滤波器滤波的原始信号作为补偿量, 但由于低通滤波器本质是一阶惯性环节, 自身存在响应及时性和噪声抑制的矛盾, 导致在输入信号噪声较大情况下, 不能兼顾相位补偿和输出噪声问题。实践中发现, 虽然基于不同形式作用函数的跟踪微分器都能有较好效果, 但存在参数调试繁琐, 不能很好平衡跟踪相位滞后和微分信号噪声放大问题。将前馈补偿思路引进跟踪微分器, 针对跟踪微分器由于二阶串联积分系统导致跟踪相位滞后以及降低噪声影响提出复合跟踪微分器。在不增大微分信号噪声情况下, 通过前馈补偿作用降低跟踪信号相位滞后。在等效线性分析基础上[16], 跟踪微分器等效于二阶环节, 可以将二阶环节固有频率和阻尼比对系统性能影响作为参考。最后将复合跟踪微分器应用于电容式位移传感器中, 通过仿真及实测结果表明, 复合跟踪微分器在相位滞后、微分信号提取方面具有更好效果, 且方便调试。
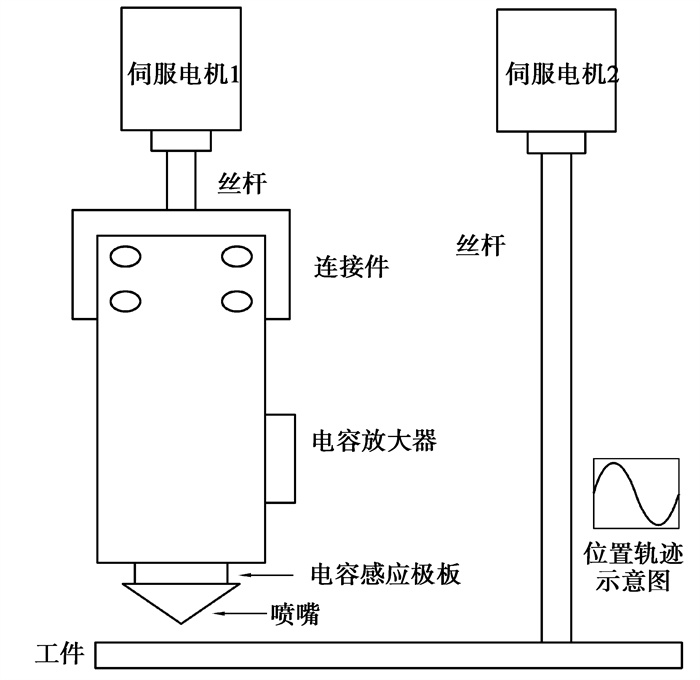
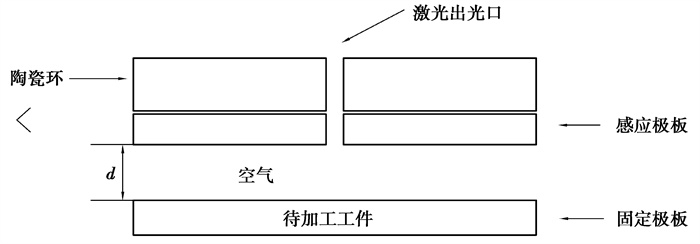
1 电容式位移传感器原理分析实验平台所采用的传感器类型为变间隙式平行板电容传感器, 电容极板由感应极板和固定极板2部分构成, 感应极板安装于电容传感器下端, 待加工工件作为固定极板。感应极板形状为激光切割系统中普遍使用的圆形极板。加工过程中, 安装在切割头底部的电容极板随着切割头运动, 通过检测固定极板和感应极板间电容信号, 并由电容放大电路对信号进行初步处理, 实现切割头相对于加工工件位置的实时测量。电容式位移传感器激光切割头示意图如图 1所示, 变间隙式平行板感应极板端截面如图 2所示。
|
图 1 切割头示意 Fig. 1 Schematic of cutting head |
|
图 2 电容极板截面图 Fig. 2 Sectional view of capacitor plate |
测距原理
| $ C = \frac{{{\varepsilon _0} \times {\varepsilon _1} \times S}}{d}, $ | (1) |
其中: C为极板电容; S为极板面积; d为极板间距; ε1, ε0为真空介电常数、相对介电常数。
由于极板之间为空气, 一般情况下ε1 =1, 上式可表述为
| $ C = \frac{{{\varepsilon _0}S}}{d}, $ | (2) |
极板间距变化量Δd与电容变化量ΔC对应关系
| $ C + \Delta C = \frac{{{\varepsilon _0}S}}{{d + \Delta d}}。$ | (3) |
从式(2) 可以看出, 电容传感器位置和电容值对应关系和介电常数有关, 介电常数通常不是固定值, 且非线性和灵敏度之间存在矛盾。因此, 实验中采用离线查表的方式实现位置检测。在进行查表前, 需完成标定动作以生成电容—位置高度对应表。加工过程中根据实时电容查表获取对应高度。上述根据电容查表获取高度的方法相较于通过电容值计算得到高度方法具有计算机资源消耗低、精度高等优势。
2 复合跟踪微分器 2.1 经典跟踪微分器跟踪微分器具有较好的滤波特性, 不仅能在含有噪声的测量信号中获取良好的原始信号逼近, 还兼具微分信号的估计作用[17]。研究限于二阶跟踪微分器在原始信号滤波, 及一阶微分信号提取中的使用。
经典跟踪微分器的基本原理如下
二阶系统
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1}\left( t \right) = {x_2}\left( t \right)}\\ {{{\dot x}_2}\left( t \right) = f\left( {{x_1}\left( t \right), {x_2}\left( t \right)} \right)} \end{array}} \right., $ | (4) |
其中: x1, x2是系统的状态变量; f (.) 是系统的作用函数。
定理1:
对上述二阶系统, 按菲利波夫意义所有解x1 (t), x2 (t) 有界且满足
| $ \mathop {\lim {x_1}}\limits_{t \to \infty } \left( t \right) = 0;\mathop {\lim {x_2}}\limits_{t \to \infty } \left( t \right) = 0。$ | (5) |
则对于任意有界可积信号v (t), t ∈ [0, + ∞] 及任意常数T >0。式(6) 将满足
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1}\left( t \right) = {x_2}\left( t \right)}\\ {{{\dot x}_2}\left( t \right) = {R^2}.f\left( {{x_1}\left( t \right), {x_2}\left( t \right), \frac{{{x_2}\left( t \right)}}{R}} \right)} \end{array}} \right., $ | (6) |
结论表明, 构造适当的作用函数f (.), 使得式(4) 渐进稳定, x1 (t) 将平均收敛于v (t), x2 (t) 收敛于x1(t) 的广义导数, 式(6) 称为跟踪微分器, 文献[18]从收敛性角度对跟踪微分器给出完整的理论证明。
2.2 复合跟踪微分器1) 等效线性分析
针对由不同形式跟踪函数构成的跟踪微分器在分析以及参数调试等方面存在难点, 浙江大学的劳立明[19]等人对跟踪微分器在平衡点附近和远离平衡点进行系统性分析并得出结论: 跟踪微分器性能主要由平衡点附近动态特性决定。在忽略高阶项时, 给出不同形式跟踪函数的统一形式, 并从频域角度给出理论分析证明。
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1}\left( t \right) = {x_2}\left( t \right), }\\ {{{\dot x}_2}\left( t \right) = - {a_1}|{x_1}\left( t \right){|^{{\beta _1}}}{\mathop{\rm sgn}} \left( {{x_1}\left( t \right)} \right) - {a_2}|{x_2}\left( t \right){|^{\beta 2}}{\mathop{\rm sgn}} \left( {{x_2}\left( t \right)} \right), } \end{array}} \right. $ | (7) |
α1, α2, β1, β2的参数在设计过程中, 需要保证式(4) 的收敛性[18]。通过在平衡点附近线性化之后, 可进一步将不同形式跟踪函数写成如下形式,
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1}\left( t \right) = {x_2}\left( t \right), }\\ {{{\dot x}_2}\left( t \right) = - {R^2}\left[ { - {k_1}\left( {{x_1}\left( t \right) - v\left( t \right)} \right) - {k_2}\frac{{{x_2}\left( t \right)}}{R}} \right]} \end{array}} \right.。$ | (8) |
2) 复合跟踪微分器原理
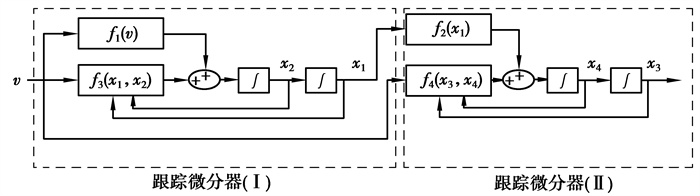
复合跟踪微分器由2个跟踪微分器通过串级形式构成, 复合跟踪微分器系统框图如图 3所示。
|
图 3 复合跟踪微分器系统框图 Fig. 3 Block diagram of compound tracking differentiator system |
复合跟踪微分器的微分表达式如下, 其中: v是输入信号; x1, x2为跟踪微分器(I) 的跟踪输出和一阶微分输出; R1, k1, k2为跟踪微分器(I) 的系统参数; x3, x4为跟踪微分器(II) 的跟踪输出和一阶微分输出; R2, k3, k4为跟踪微分器(II) 的系统参数。
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1}\left( t \right) = {x_2}\left( t \right), }\\ {{{\dot x}_2}\left( t \right) = R_1^2\left[ { - {k_1}\left( {{x_1}\left( t \right) - v\left( t \right)} \right) - {k_2}\frac{{{x_2}\left( t \right)}}{{{R_1}}}} \right] + {a_1}\dot v\left( t \right), }\\ {{{\dot x}_3}\left( t \right) = {x_4}\left( t \right), }\\ {{{\dot x}_4}\left( t \right) = R_2^2\left[ { - {k_3}\left( {{x_3}\left( t \right) - v\left( t \right)} \right) - {k_4}\frac{{{x_4}\left( t \right)}}{{{R_2}}}} \right] + {a_2}{{\dot x}_1}\left( t \right), } \end{array}} \right. $ | (9) |
对上述复合跟踪微分器在零初始条件下进行拉斯变换, 可以得到复合跟踪微分器中参考信号和跟踪输出传递函数分别为
| $ \frac{{{X_1}\left( s \right)}}{{V\left( s \right)}} = \frac{{{a_1}s + {k_1}R_1^2}}{{{s^2} + {k_2}{R_1}s + {k_1}R_1^2}}, $ | (10) |
| $ \frac{{{X_2}\left( s \right)}}{{V\left( s \right)}} = \frac{{{a_2}s + {k_3}R_2^2}}{{{s^2} + {k_4}{R_2}s + {k_3}R_2^2}}, $ | (11) |
从传递函数可知, 使用前馈补偿的方式给系统引入了零点, 并且可以通过修改系数补偿系数α对零点进行配置, 修改补偿系数就是对零点进行配置的过程, 当补偿系数为零则为一般形式的跟踪微分器。对系统而言, 零点的配置一方面提升系统的稳定性, 另一方面系统的响应速度也相应提高, 有利于降低跟踪信号的相位滞后。
设补偿系数α =0, 则跟踪微分器传递函数变为二阶环节形式,
| $ \frac{{{X_1}\left( s \right)}}{{V\left( s \right)}} = \frac{{{a_1}s + {k_1}R_1^2}}{{{s^2} + {k_2}{R_1}s + {k_1}R_1^2}} = \frac{{\omega _{n1}^2}}{{{s^2} + 2{\xi _1}{\omega _{n1}}s + \omega _{n1}^2}}, $ | (12) |
| $ \frac{{{X_2}\left( s \right)}}{{V\left( s \right)}} = \frac{{{a_2}s + {k_3}R_2^2}}{{{s^2} + {k_4}{R_2}s + {k_3}R_2^2}} = \frac{{\omega _{n2}^2}}{{{s^2} + 2\xi {\omega _{n2}}s + \omega _{n2}^2}}, $ | (13) |
从参数调试的角度看,
对复合跟踪微分器而言, 2个跟踪器的作用不相同。跟踪微分器(I) 主要作用是从原始信号中提取光滑跟踪信号作为跟踪微分器(II) 的补偿量, 跟踪微分器(II) 在复合跟踪微分器中起主导作用, 在设计过程中, 需要根据原始信号特性分别调整相应跟踪微分器(I) 和跟踪微分器(II) 的参数。满足滤波和微分信号提取要求。
3 仿真及实验结果分析为验证复合跟踪微分器在原始信号逼近, 以及微分信号提取的有效性, 搭建Simulink仿真模型, 仿真模型框图如图 4所示, 复合跟踪微分器使用跟踪微分器(I) 和跟踪微分器(II) 串联形式, 跟踪微分器输入带高斯白噪声(均值: 0, 方差0.001) 频率1 Hz, 幅值1的正弦信号。实验平台通过控制工件进行正弦(频率1 Hz, 幅值1 mm) 运动, 模拟实际加工过程。

|
图 4 Simulink仿真图 Fig. 4 Simulink simulation diagram |
分别对上述跟踪微分器在MATLAB/SIMULINK平台上进行仿真, 并在测试平台上进行实际测试, 从仿真和实验平台上的结果看, 复合跟踪微分器在电容式位移传感器中, 提取原始位置信号以及速度信号估计中优异性能, 图 5、图 6分别为仿真和实际测试结果。

|
图 5 仿真结果 Fig. 5 Simulation results |

|
图 6 实验平台测试 Fig. 6 Experimental platform test |
从仿真和实测结果可以看出, 在相同原始信号输入的条件下, 复合跟踪器在相位滞后和微分信号提取准确性上有更好效果。复合跟踪微分器是由2个等效线性形式跟踪微分器组成, 2个跟踪微分器的作用不同, 决定其在参数上的差异。通过跟踪微分器在零点附近进行等效线性变换可知, 跟踪微分器为二阶环节, 二阶环节的性能由系统的固有频率和阻尼系数决定。降低系统的阻尼系数、增大固有频率, 可减小跟踪信号相位滞后, 但阻尼系数过小会降低抑制噪声能力导致振荡。为保证复合跟踪微分器既能以较小相位滞后跟踪原始信号, 又能很好抑制噪声保证微分估计信号的品质。通过跟踪器(I) 对原始信号进行滤波, 并将经过滤波之后的跟踪输出作为跟踪微分器(II) 补偿量。将跟踪微分器(I) 阻尼系数设置小于0.5, 以实现光滑跟踪输出。跟踪微分器(II) 在复合跟踪微分器中起主导作用, 其阻尼系数和固有频率设置比跟踪微分器(I) 大, 具有较好滤波性能, 在跟踪微分器(I) 的光滑补偿作用下, 保证复合跟踪微分器跟踪输出相位滞后小的同时能对噪声有很好的抑制作用。因此, 与经典跟踪微分器比较, 复合跟踪微分器具有更灵活结构, 更好兼顾跟踪输出相位滞后和微分信号的提取。
4 结语主要讨论了跟踪微分器的等效线性形式, 以及复合跟踪微分器原理, 将复合跟踪微分器使用在电容式位移传感器中, 通过MATLAB/SIMULINK仿真以及实际测试, 验证了复合跟踪微分器相较于经典跟踪微分器在原始信号逼近及微分信号提取相位滞后更小。通过输入幅值1、频率1 Hz的含噪正弦测试信号, 结果表明复合跟踪微分器和经典跟踪微分器均能光滑逼近原始信号、提取微分信号, 复合跟踪微分器相比于经典微分跟踪器, 相位滞后小0.03 rad, 兼顾了相位滞后和噪声放大。跟踪微分器作为自抗扰控制的重要组成部分, 在对含噪原始信号处理过程中, 保证光滑逼近的同时降低相位滞后, 对于提高激光随动控制系统性能具有重要意义。
| [1] |
王海. 电容式激光切割头高度跟随控制系统的研究与实现[D]. 武汉: 华中科技大学, 2016. Wang H. Research and implementation of height following control system for capacitor laser cutting head[D]. Wuhan: Huazhong University of Science and Technology, 2016. (in Chinese) |
| [2] |
Bu X W, Wu X Y, Chen Y X, et al. Design of a class of new nonlinear disturbance observers based on tracking differentiators for uncertain dynamic systems[J]. International Journal of Control, Automation and Systems, 2015, 13(3): 595-602. DOI:10.1007/s12555-014-0173-6 |
| [3] |
Zhao B, Li Y C. Decentralized differential tracker based control of reconfigurable manipulators without velocity sensor[C]//Proceedings of the 33rd Chinese Control Conference. July 28-30, 2014, Nanjing, China: IEEE, 2014: 8370-8374.
|
| [4] |
Wang X H, Chen Z Q, Yang G. Finite-time-convergent differentiator based on singular perturbation technique[J]. IEEE Transactions on Automatic Control, 2007, 52(9): 1731-1737. DOI:10.1109/TAC.2007.904290 |
| [5] |
韩京清, 黄远灿. 二阶跟踪—微分器的频率特性[J]. 数学的实践与认识, 2003, 33(3): 71-74. Han J Q, Huang Y C. Frequency characteristic of second-order tracking-differentiator[J]. Mathematics in Practice and Theory, 2003, 33(3): 71-74. (in Chinese) DOI:10.3969/j.issn.1000-0984.2003.03.014 |
| [6] |
Wang H W, Wang H P. A comparison study of advanced tracking differentiator design techniques[J]. Procedia Engineering, 2015, 99: 1005-1013. DOI:10.1016/j.proeng.2014.12.634 |
| [7] |
Dulgar O, Gezer R B, Kutay A T. Extended Kalman filter based robust altitude controller for sea skimming missiles[C]//AIAA Guidance, Navigation, and Control Conference. 4-8 January 2016, San Diego, California, USA. Reston, Virginia: AIAA, 2016.
|
| [8] |
董存会, 练星, 武晓辉. 线性跟踪微分器跟踪干扰信号的研究[J]. 纺织高校基础科学学报, 2014, 27(4): 439-442, 458. Dong C H, Lian X, Wu X H. Research on linear tracking-differentiator to track interference signal[J]. Basic Sciences Journal of Textile Universities, 2014, 27(4): 439-442, 458. (in Chinese) DOI:10.3969/j.issn.1006-8341.2014.04.009 |
| [9] |
王新华, 陈增强, 袁著祉. 全程快速非线性跟踪-微分器[J]. 控制理论与应用, 2003, 20(6): 875-878. Wang X H, Chen Z Q, Yuan Z Z. Nonlinear tracking-differentiator with high speed in whole course[J]. Control Theory & Applications, 2003, 20(6): 875-878. (in Chinese) DOI:10.3969/j.issn.1000-8152.2003.06.012 |
| [10] |
葛连正, 陈健, 李瑞峰. 改进的跟踪微分器设计[J]. 吉林大学学报(工学版), 2011, 41(5): 1439-1443. Ge L Z, Chen J, Li R F. Design of an improved tracking differentiator[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(5): 1439-1443. (in Chinese) |
| [11] |
毛海杰, 李炜, 冯小林. 基于双曲正切的非线性跟踪微分器设计[J]. 计算机应用, 2016, 36(S1): 305-309. Mao H J, Li W, Feng X L. Design of nonlinear tracking differentiator based on hyperbolic tangent function[J]. Journal of Computer Applications, 2016, 36(S1): 305-309. (in Chinese) |
| [12] |
刘延泉, 郭佳颖. 双曲正切跟踪微分器设计及相平面分析[J]. 电力科学与工程, 2017, 33(10): 74-78. Liu Y Q, Guojia Y. Design and phase plane analysis of a hyperbolic tangent tracking differentiator[J]. Electric Power Science and Engineering, 2017, 33(10): 74-78. (in Chinese) DOI:10.3969/j.ISSN.1672-0792.2017.10.013 |
| [13] |
邵星灵, 王宏伦. 基于改进sigmoid函数的非线性跟踪微分器[J]. 控制理论与应用, 2014, 31(8): 1116-1122. Shao X L, Wang H L. Nonlinear tracking differentiator based on improved sigmoid function[J]. Control Theory & Applications, 2014, 31(8): 1116-1122. (in Chinese) |
| [14] |
卜祥伟, 吴晓燕, 马震, 等. 改进的反正切跟踪微分器设计[J]. 上海交通大学学报, 2015, 49(2): 164-168. Bu X W, Wu X Y, Ma Z, et al. Design of a modified arctangent-based tracking differentiator[J]. Journal of Shanghai Jiao Tong University, 2015, 49(2): 164-168. (in Chinese) |
| [15] |
Tian D P, Shen H H, Dai M. Improving the rapidity of nonlinear tracking differentiator via feedforward[J]. IEEE Transactions on Industrial Electronics, 2014, 61(7): 3736-3743. DOI:10.1109/TIE.2013.2262754 |
| [16] |
Feng H, Li S J. A tracking differentiator based on Taylor expansion[J]. Applied Mathematics Letters, 2013, 26(7): 735-740. DOI:10.1016/j.aml.2013.02.003 |
| [17] |
Guo B Z, Zhao Z L. On convergence of tracking differentiator and application to frequency estimation of sin usoidal signals[C]//2011 8th Asian Control Conference (ASCC). China: IEEE, 2011: 1470-1475.
|
| [18] |
Guo B Z, Zhao Z L. On convergence of tracking differentiator[J]. International Journal of Control, 2011, 84(4): 693-701. DOI:10.1080/00207179.2011.569954 |
| [19] |
劳立明, 陈英龙, 赵玉刚, 等. 跟踪微分器的等效线性分析及优化[J]. 浙江大学学报(工学版), 2018, 52(2): 224-232. Lao L M, Chen Y L, Zhao Y G, et al. Equivalent linear analysis and optimization of tracking differentiator[J]. Journal of Zhejiang University (Engineering Science), 2018, 52(2): 224-232. (in Chinese) |
 2021, Vol. 44
2021, Vol. 44


