地震信号可用于勘察地下结构,是进行油气资源获取的重要前期工作之一[1]。但在野外进行地震勘探时受地表环境复杂性影响或仪器性能限制导致采集到的地震信号往往存在噪声,信噪比较低。如果不对这些信号去噪势必会影响后续的处理,不利于真实反映地质结构信息[2-3]。针对地震信号去噪,国内外学者提出了不同的去噪方法,按处理领域大致可分为两大类:一是空间域基于滤波的去噪算法,包括均值滤波、中值滤波、维纳滤波等。二是变换域的去噪算法,包括傅里叶变换、小波变换[4]、Radon变换等。
当前地震信号去噪算法中多尺度几何分析受到广泛关注,常用的多尺度几何分析方法包括Curvelet变换[5]、Contourlet变换[6]和Ridgelet变换[7],均已成功应用于地震信号去噪并取得良好的效果。2007年,Guo等[8]根据紧支撑框架构造理论,经过严密的数学逻辑推导得到了Shearlet变换,它克服了小波变换的局限性,有更好的方向灵敏度,更稀疏的表示性能,并且能够捕捉地震信号的内在几何特征。但传统的Shearlet变换不具有平移不变性,导致去噪后会出现伪吉布斯现象。为解决这一问题,非下采样Shearlet变换(NSST,nonsubsampled shearlet transform)应运而生,取消了传统Shearlet变换的下采样操作,使其不仅有更好的方向敏感性和最优稀疏表示性能,还具有平移不变性,克服了伪吉布斯现象,极大地推动了多尺度几何分析工具的发展。
近年来,基于Shearlet变换的地震数据处理方法相继提出,传统的阈值处理方法是对变换域所有系数使用统一阈值,但基于传统阈值处理方法的Shearlet变换在地震信号去噪中存在局限性,因此童思友等[9]对阈值处理的方法进行了改进,提出了随尺度和方向变化的自适应阈值。赵海涛[10]从变换的角度对其进行了改进,根据信号的方向和空间相关性提出了基于循环平移的Shearlet变换自适应阈值降噪算法。但由于Shearlet变换不具有平移不变性,而且对地震信号进行稀疏表示亦不是最优的,随后提出的非下采样Shearlet变换则解决了传统Shearlet变换存在的问题,因此刘昕等[11]采用非下采样Shearlet变换对地震信号进行噪声压制,结果表明该方法比小波变换的去噪能力更强。
非局部均值算法最初是用于数字图像处理,能很大程度上减小振铃效应,但传统的NLM(non-local means)不能够很好地衡量图像细节和边缘信息,会导致图像失真,因此郭晨龙等[12]提出了带有梯度信息的GSSIM(gradient structural similarity)算法,能较好地保存图像边缘和细节信息。王思涛等[13]则直接将边缘检测算法和NLM算法相结合,同样可达到保存图像边缘信息的目的。但以上处理都是在时空域进行,Souidene等[14]根据小波系数服从广义高斯分布,提出了基于广义高斯模型的非局部均值算法,成功将NLM应用于小波域,直接对小波系数进行处理,去噪效果良好,但该算法只适用于小波变换一级分解,具有局限性。
考虑到Shearlet变换在高维空间比小波变换有更好的稀疏表示,且Shearlet系数也服从广义高斯分布,因此文中考虑在Shearlet域使用NLM算法,并将之用于地震信号去噪。已知Shearlet变换之后的细节参数近似为广义高斯分布[15],在此基础上对变换之后的细节系数进行NLM去噪,经过反变换得到去噪之后的地震信号。实验表明去噪效果良好。
1 非下采样Shearlet变换 1.1 传统的Shearlet变换Shearlet变换是复小波理论和多尺度几何分析通过特殊形式的具有合成膨胀的仿射系统构成[16],通过对基函数的缩放、剪切和平移等仿射变换来生成具有不同特征的Shearlet函数。当维数n=2时,Shearlet函数的具有合成膨胀的仿射系统定义为:
| $ S_{A B}(\psi)=\left\{\psi_{l, m, n}(x)=|\operatorname{det} \boldsymbol{A}|^{l / 2} \psi\left(\boldsymbol{B}^{m} \boldsymbol{A}^{l} x-n\right): l, m \in Z, n \in Z^{2}\right\}, $ | (1) |
式中:ψ∈L2(R2);l是尺度参数;m是剪切参数;n是平移参数。A和B都是2×2的可逆矩阵,且|detB|=1。A是各向异性膨胀矩阵,控制Shearlet变换的尺度,又称为尺度矩阵,B是剪切矩阵,控制Shearlet变换的方向。对∀a>0,b∈R,可得尺度矩阵A和剪切矩阵B为:
| $ \boldsymbol{A}=\left[\begin{array}{cc} a & 0 \\ 0 & \sqrt{a} \end{array}\right], \boldsymbol{B}=\left[\begin{array}{ll} 1 & b \\ 0 & 1 \end{array}\right]。$ | (2) |
当a=4, b=1时,即A=A0=
对任意的(ξ1, ξ2)∈D0,令Q1=Ŝ0(ξA0-lB0-m), Q2=Ŝ1(2-2lξ1)2, Q3=Ŝ2(2lξ2/ξ1-1),都有:
| $ \sum\limits_{l \geqslant 0}\sum\limits_{ m=-2 l}^{2 l-1}\left|Q_{1}\right|^{2}=\sum\limits_{l \geqslant 0}\sum\limits_{ m=-2 l}^{2 l-1}\left|Q_{2}\right|\left|Q_{3}\right|^{2}, $ | (3) |
| $ S_{i, m, n}^{(0)}=2^{\frac{3l}{2}} S^{(0)}\left(B_{0}^{m} A_{0}^{l} x-n\right): l \geqslant 0,-2^{l} \leqslant m \leqslant 2^{l}-1, n \in Z^{2}, $ | (4) |
| $ L^{2}\left(D_{0}\right)^{V}=\left\{f \in L^{2}\left(R^{2}\right): \sup p \hat{f} \subset D_{0}\right\}, $ | (5) |
式中:D0={(ξ1, ξ2)∈
| $ {\rm{sup}}\;pS_{l,m,n}^{(0)} \subset \left\{ {\left( {{\xi _1},{\xi _2}} \right):{\xi _1} \in \left[ { - {2^{2l - 1}}, - {2^{2l - 4}}} \right] \cup \left[ {{2^{2l - 4}},{2^{2l - 1}}} \right],\left| {l{2^{ - l}} + {\xi _2}/{\xi _1}} \right| \le {2^{ - l}}} \right\}。$ | (6) |
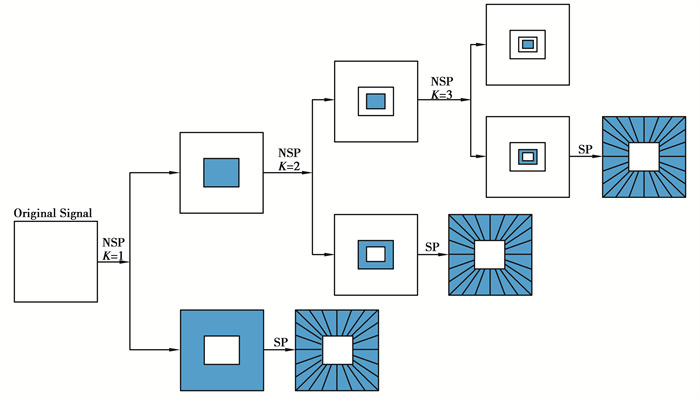
这意味着每个元素Ŝl, m, n由尺寸为22j×2j的梯形支撑,且方向沿着斜率为l2-j的直线。Shearlet变换的剪切分解如图 1所示。
|
图 1 NSST的多尺度和多方向分解 Fig. 1 The multi-scale and multi-directional decompositions of NSST |
如果F={ψl, m, n(x): l, m∈Z, n∈Z2}表示Shearlet基函数,那么每个地震信号都可以用F表示出来,FN是最大Shearlet系数的近似值为:
NSST是剪切变换的移位不变版本。NSST与剪切变换的不同之处在于NSST取消了下采样器和上采样器,是一种完全移位不变的多尺度和多向扩展。NSST是由非下采样拉普拉斯金字塔变换(NSLP)与剪切滤波器组合而成[18]。其中NSLP的分析可以通过迭代处理完成,为
| $ R_{\mathrm{NSLP} j+1}=A_{j} f=\left(A h_{j}^{1} \prod\limits_{k=1}^{j-1} A h_{k}^{0}\right) f, $ | (7) |
式中:f是一幅图像;RNSLPj+1是NSLP变换后在j+1尺度下的细节参数;Ahk0和Ahj1分别是尺度为k和j的NSLP的低通和高通滤波器。给定N×N图像fa0和方向Dj的数量,以固定分辨率尺度j描述的NSST的过程可以总结如下:
1) 使用NSLP将faj-1分解为大小为N×N的低通图像faj和高通图像fdj;
2) 在伪极坐标网格中计算
3) 对Pfdj应用带通滤波以获得
4) 应用逆FFT以在伪极坐标网格中获得NSST系数{fd, kj}Dj k=1。
2 非局部均值算法NLM算法在2005年由Baudes等[19]提出,该算法主要利用自然图像中普遍存在的冗余信息进行去噪,利用了整幅图像进行去噪,以图像块或者像素为单位在搜索框中寻找相似区域,再求平均,能够较好地去除高斯噪声[20-21]。若给定一个离散的噪声图像υ=υ(i)|i∈I,估计值N[υ](i)可由图像中所有像素的加权平均值计算得出:
| $ N[\upsilon](i)=\sum\limits_{j \in I} \omega(i, j) \upsilon(j), $ | (8) |
其中权重ω(i, j)取决于像素i和j相似度:
| $ \omega(i, j)=\sum\limits_{j \in S_{i}} \frac{1}{Z(i)} \mathrm{e}^{-\|y(i)-y(j)\| 2 / h^{2}} \upsilon(j), $ | (9) |
Z(i)是归一化系数:
| $ Z(i)=\sum\limits_{j \in S_{i}} \mathrm{e}^{-\|y(i)-y(j)\| 2} / h^{2}, $ | (10) |
式中:h是平滑核宽度参数,控制平均范围;y(i), y(j)表示的是邻域窗口,大小通常为5×5, 7×7, 9×9,i, j表示的是邻域窗口的中心像素点;Si是搜索窗口,其大小通常选为21×21。
文中提出的算法和经典NLM算法采用的邻域窗口均为7×7,搜索窗口均为21×21。为保证有足够多的相似度高的点,邻域窗口选择应遵循一定规律,过小会影响去噪效果,过大会增加算法时间复杂度,因此文中邻域窗口大小设为7×7;搜索窗口同理,选取过小会导致失去地震信号的整体联系,无法处理小范围内随机变化的点[22],过大则会增加时间成本,因此,综合考虑选择搜索窗口的大小为21×21。
3 基于非下采样Shearlet变换和非局部均值的地震信号去噪近年来,多尺度几何分析方法在地震信号去噪中受到广泛关注,Shearlet变换作为多尺度几何分析方法中的一种,已经成功应用于地震信号去噪与重建,并取得良好的效果[23]。NLM算法应用于地震信号去噪取得了良好的效果,但该算法经常直接用在时空域,而不能直接在变换域使用。针对这一问题,Souidene等[14]提出了基于广义高斯模型的非局部均值算法,首次将非局部均值算法应用于小波变换域,但是这种方法有较大的局限性。因为小波变换只能反映信号的点奇异性,不能有效表示二维信号中具有多方向性的边缘和纹理等几何特性,即在高维情况下小波变换不是最优的表示方法,而随后发展起来的Shearlet变换在高维情况有最优的稀疏表示,且Shearlet变换之后的系数亦满足广义高斯分布,因此考虑将Souidene提出的方法应用于Shearlet域,提出了Shearlet域基于广义高斯模型的非局部均值算法。
该方法将广义高斯分布和主成分分析(PCA, principal component analysis)引入Shearlet域的NLM算法中,首先将地震信号进行NSST分解,得到几组Shearlet系数,由于Shearlet变换后的细节子带系数近似为广义高斯分布,可使用Souidene提出的方法估计尺度参数α和形状参数β,然后将主成分分析方法应用于NLM的邻域窗口和搜索窗口,得到其主成分进行下一步计算,提高运算速度。最后进行Shearlet逆变换得到去噪之后的地震信号。提出方法为:
| $ \omega(i, j)=\sum\limits_{j \in S_{i}} \frac{1}{Z(i)} \mathrm{e}^{-\|{g(i)-g(j) \| \beta /(h \alpha) \beta}} \upsilon(j), $ | (11) |
其中:
| $ Z(i)=\sum\limits_{j \in S_{i}} \mathrm{e}^{-\|g(i)-g(j)\| \beta /(h \alpha) \beta}, $ | (12) |
式中:g(i)和g(j)是NLM中邻域窗口的主成分,是式(9)和式(10)中y(i)和y(j)进行主成分分析之后的主成分,即g(i)和g(j)是y(i)和y(j)降维之后的表示[24]。当计算完成之后,根据式(8)来计算结果,即完成了对Shearlet系数的处理,并进行Shearlet逆变换即可得到去噪之后的地震信号。
3.1 参数估计关于广义高斯分布的参数估计方法有很多,通常采用标准差σ和绝对值的平均值E[|X|]的比值[25]:
| $ \frac{\sigma}{E[|X|]}=\frac{\sqrt{\varGamma(1 / \beta) \varGamma(3 / \beta)}}{\varGamma(2 / \beta)}, $ | (13) |
式中:σ是Shearlet系数的标准差;E[|X|]代表Shearlet系数绝对值的平均值,可根据先验信息设定形状参数β的取值范围,然后在范围之内遍历得到最优β值。代入式(14)即可得到尺度参数α,为
| $ \alpha=\left(\frac{\beta}{L} \sum\limits_{i=1} L\left|x_{i}\right|^{\beta}\right) \frac{1}{\beta} \text { 。} $ | (14) |
主成分分析是由Pearson提出,Hotelling加以发展的一种多变量统计方法,主要用于“降维”。所谓的“降维”,就是减少相关性的变量数目,用较少的变量(主成分)来取代原先的变量。通过主成分分析可以从复杂的关系中找到一些主成分,从而能更直观地找到各变量的内在关系。一般来说,提取到的主成分与原始变量之间应满足4个基本关系,即每一个主成分都是各原始变量的线性组合;主成分的数目远远小于原始变量的数目;主成分保留了原始变量绝大部分信息;各主成分之间互不相关。
主成分分析以方差最大理论为基础,所谓的方差最大理论,是指从二维空间向一维空间转换时需要找一个方向使得投影在该方向上的方差最大,即在此方向上关于原始变量的差异是最大的,差异越大,方差也就越大。
在文中,使用R表示地震信号中的所有点,r表示从R中随机选取的点,即样本,以y(i)为例,采用基于特征值分解协方差矩阵对其进行降维处理。具体步骤如下:
1) 去平均值(即中心化),即每位特征减去各自的平均值y;
2) 计算协方差矩阵:
3) 用特征值分解法求协方差矩阵
4) 将特征值按照从大到小的顺序排列,选其中非零的k个,将其对应的特征向量组成矩阵P,那么原矩阵转换到新空间中,即g(i)=P×y(i)。
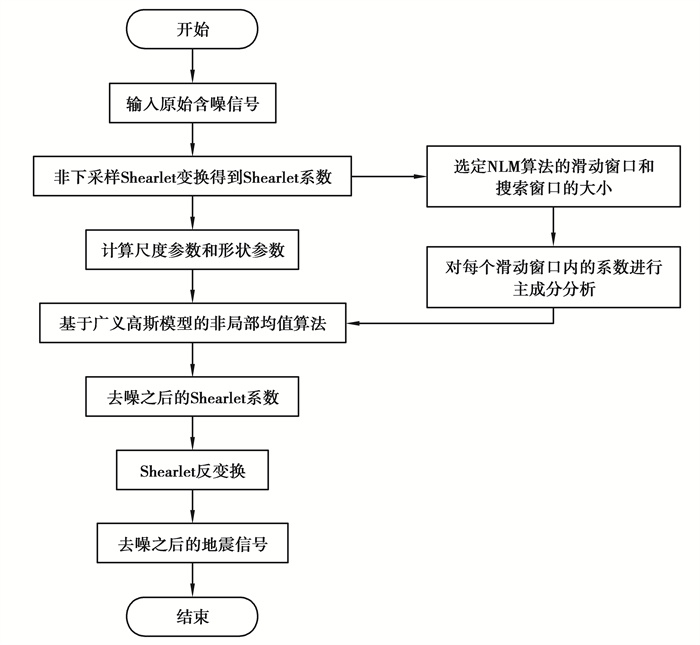
3.3 非下采样Shearlet变换和非局部均值结合后用于地震信号去噪Shearlet域基于非局部均值的地震信号去噪算法,首先将原始含噪信号进行非下采样Shearlet变换得到Shearlet系数,然后对每个子带计算其尺度参数α和形状参数β,使用Souidene提出的基于广义高斯模型的非局部均值算法对系数进行处理,得到去噪之后的系数,使用过程中对NLM算法用到的滑动窗口进行主成分分析以降低空间复杂度,最后通过Shearlet反变换得到去噪之后的地震信号。具体流程如图 2所示。
|
图 2 Shearlet域基于非局部均值的地震信号去噪算法流程图 Fig. 2 Flow chart of seismic signal denoising algorithm based on non-local mean in Shearlet domain |
去噪实验在一台戴尔笔记本上运行,处理器为i5-4200U,CPU为1.60 GHZ,内存为4 GB,64位操作系统,安装有MATLAB-R2014b,地震信号去噪实验中使用的算法都是通过多组实验,反复调整参数,以去噪效果最优的参数组合进行对比实验。通过峰值信噪比(peak signal-to-noise ratio,PSNR)、去噪均方误差(mean squared error,LMSE)及结构相似度(structural similarity index,SSIM)等量化指标,比较Shearlet和NLM结合算法、Shearlet和硬阈值法结合、NLM算法以及Wiener滤波算法的性能。其中PSNR是使用最广,最普遍的评价指标,在保证去噪之后视觉效果的前提下,希望越大越好;LMSE是反应估计量和被估计量之间差异程度的度量,希望越小越好;SSIM中c1=(0.01×L)2,c2=(0.03×L)2,L是采样值的动态范围,常用来衡量两种图像相似度,取值越接近1越好。
| $ P_{\mathrm{SNR}}=10 \log _{10}\left(\frac{\max \left(y^{2}\right)}{L_{\mathrm{MSE}}}\right), $ | (15) |
| $ L_{\mathrm{MSE}}=\frac{1}{m n} \sum\limits_{i=1}^{m} \sum\limits_{j=1}^{n}\left(\left(y_{d}-y\right)_{i, j}\right)^{2}, $ | (16) |
| $ S_{\mathrm{SIM}}=\frac{\left(2 \bar{x} \times \bar{y}+c_{1}\right)\left(2 \sigma_{x y}+c_{2}\right)}{\left(\bar{x}^{2}+\bar{y}^{2}+c_{1}\right)\left(\sigma_{x}^{2}+\sigma_{y}^{2}+c_{2}\right)}。$ | (17) |
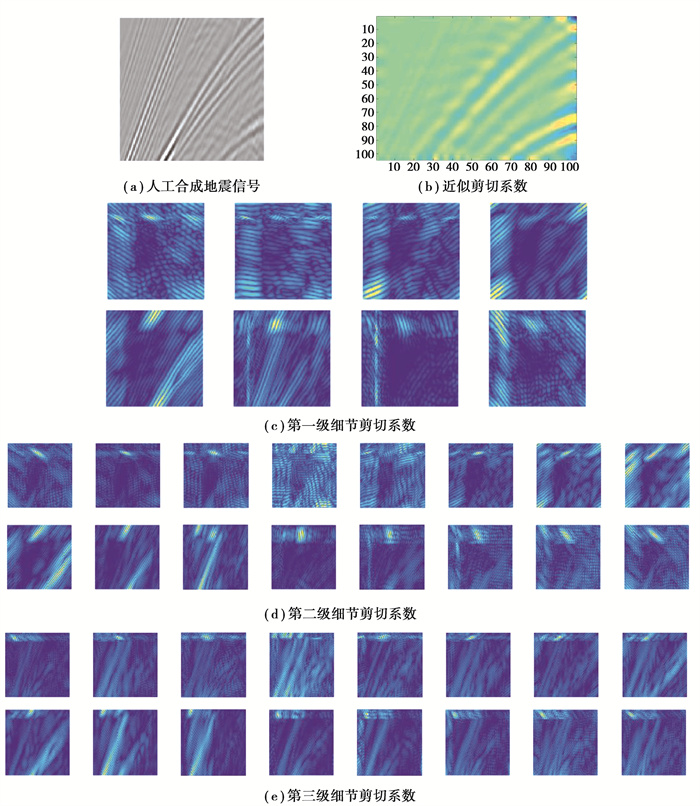
在实验中,使用三级Shearlet分解,每一级分别包含3,4和4的剪切方向,每个级别内方向子带数Ns=2s,因此,每一级分别包含的方向子带数为8,16和16。图 3展示了人工合成地震信号近似系数和三级剪切变换细节系数。图 3(a)为人工合成地震信号,图 3(b)是原始地震信号的近似剪切系数,图 3(c)为第一级细节剪切系数,图 3(d)为第二级细节剪切系数,图 3(e)为第三级细节剪切系数。
|
图 3 剪切分解的示意图 Fig. 3 An illustration of shearlet decomposition |
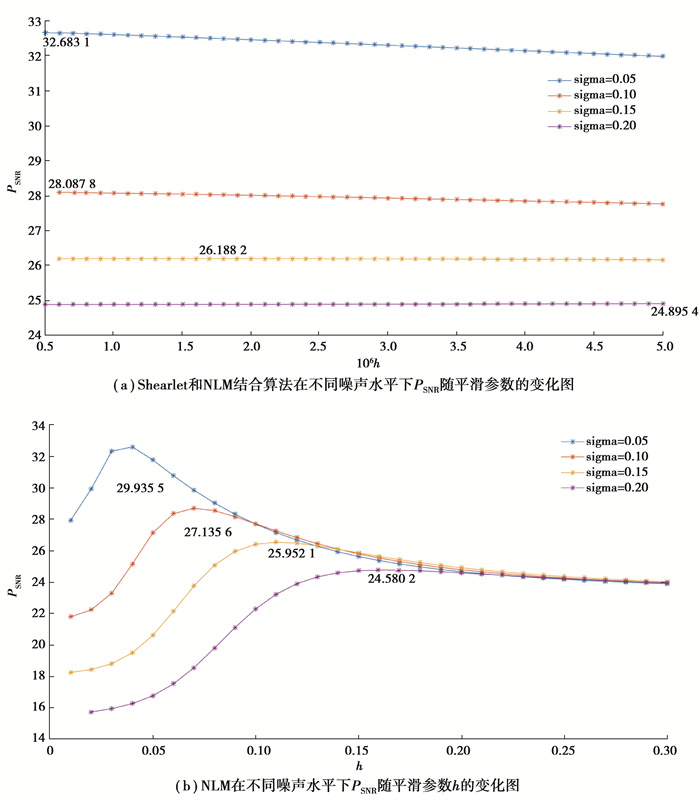
该人工合成信号共计104道,每道104个均匀采样点,分别对该信号加方差为5%、10%、15%、20%的高斯白噪声。为了使得文中算法和NLM算法都达到最优的去噪效果,需选取最优的平滑参数h,由于没有严格的公式计算平滑参数h,因此需进行多次试验,找到最优的平滑参数h之后,即可对人工合成地震信号进行去噪。图 4展示了文中算法和NLM算法在不同噪声水平下PSNR随平滑参数h的变化图,其中图 4(a)是Shearlet和NLM结合算法在不同噪声水平下PSNR随平滑参数的变化图,图 4(b)是NLM算法在不同噪声水平下PSNR随平滑参数h的变化图。
|
图 4 文中算法和NLM算法在不同噪声水平下PSNR随平滑参数h的变化图 Fig. 4 The variation of PSNR with smoothing parameters under different noiselevels by proposed algorithm and NLM |
对该地震信号添加噪声方差为10%的高斯噪声,原始人工合成地震信号如图 5(a)所示,图 5(b)是含噪地震信号,图 5(c)是NLM算法去噪结果,图 5(d)是硬阈值(hard threshold)法去噪结果,图 5(e)是Wiener滤波去噪结果,图 5(f)是文中算法去噪结果。

|
图 5 人工合成地震信号去噪 Fig. 5 Synthetic seismic signal denoising |
如图 5所示,4种去噪算法基本都能实现去噪任务,从去噪效果上来看,NLM算法的去噪结果还存在一些噪点,对细节部分的处理不如文中算法。硬阈值算法的PSNR虽然很高,但是由于硬阈值算法本身在进行去噪时过于绝对,不能够自适应,所以硬阈值去噪算法丢失了大量的细节信息,导致效果图过于平滑。Wiener滤波去噪结果还存在较大的噪声,各方面都不如另外3种算法。综合各方面考虑,文中算法去噪效果最佳。4种去噪算法的量化数据由表 1给出。
| 表 1 各算法对人工合成地震信号去噪的性能(高斯噪声) Table 1 Performance ofeach algorithm for denoising artificially synthesized seismic signals (Gaussian noise) |
从表 1可以看出,对人工合成地震信号在噪声水平为10%的时候NLM算法和硬阈值算法的去噪效果相差不大,但都比文中算法略差,Wiener滤波算法效果最差。从量化结果看,文中算法的PSNR的比NLM算法的PSNR高0.929,即提高了3.3%。因为NLM算法和硬阈值算法并不注重对细节部分的处理,导致去噪效果不理想,而文中算法对细节的处理更好,去噪效果更好。
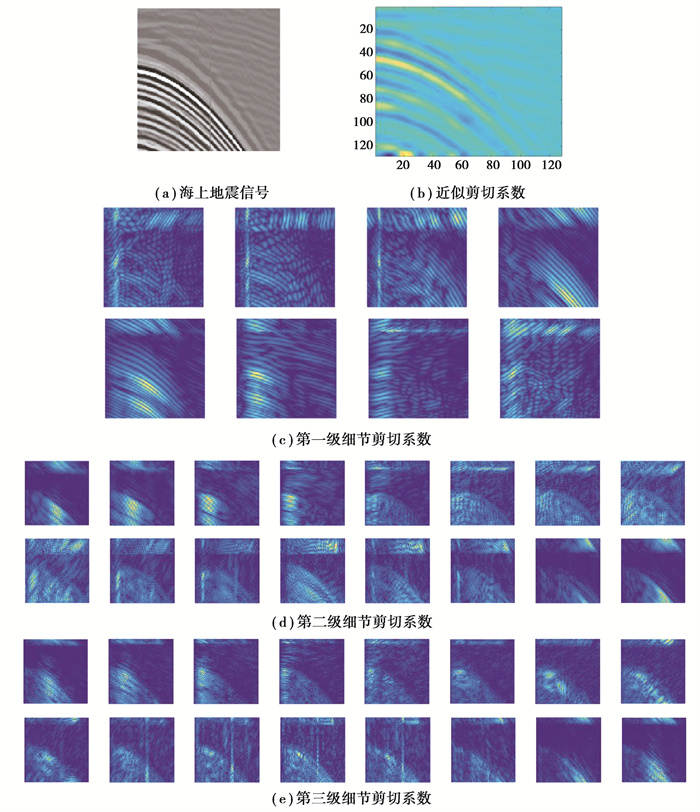
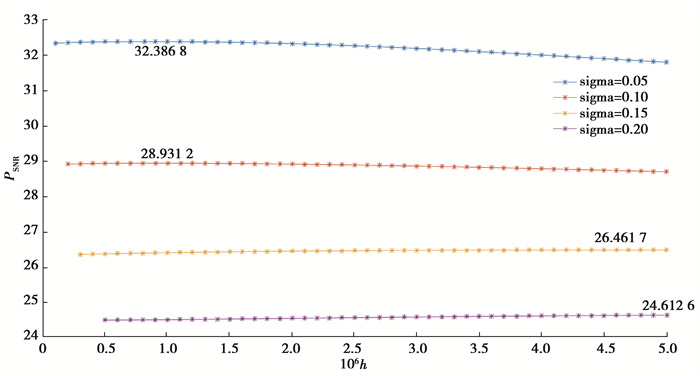
4.2 海上地震信号去噪该地震信号是野外海洋单炮数据Marshot3400.DAT中分割出的数据,共128道,每道128个采样点。图 6展示了海洋地震信号近似系数和三级剪切变换细节系数的图示。图 6(a)为海上地震信号,图 6(b)为海上地震信号近似剪切系数,图 6(c)为第一级细节剪切系数,图 6(d)为第二级细节剪切系数,图 6(e)为第三级细节剪切系数。分别对该信号加方差为5%、10%、15%、20%的高斯白噪声,文中提出的算法中涉及一个平滑参数h,该参数没有严格的计算公式,只能根据经验选取,文中在一定范围内进行实验,选取最优的平滑参数h。图 7展示了Shearlet和NLM结合算法在不同噪声水平下PSNR随平滑参数h的变化图。
|
图 6 剪切分解的示意图 Fig. 6 An illustration of shearlet decomposition |
|
图 7 文中算法的PSNR随平滑参数变化曲线图 Fig. 7 The variation of PSNR with smoothing parameters at different noise levels by proposed algorithm |
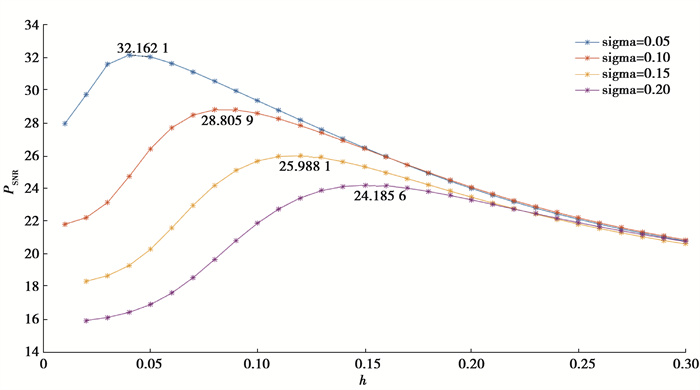
NLM算法中平滑参数h按同样方法选取其最优值,图 8展示了NLM算法在不同噪声水平下PSNR随平滑参数h的变化图。
|
图 8 NLM算法的PSNR随平滑参数变化曲线图 Fig. 8 The variation of PSNR with smoothing parameters at different noise levels by NLM algorithm |
文中算法和对比算法平滑参数h均选择使其去噪效果最优的值,通过对比图 7和图 8可以看到,以加方差为15%的高斯白噪声为例,文中算法去噪效果最优的平滑参数h=0.51×10-5,NLM去噪效果最优的平滑参数h=0.12。
图 9展示了噪声方差为15%,平滑参数均取最优值的情况下的去噪结果,图 9(a)是原始地震信号,图 9(b)是含噪地震信号,图 9(c)是NLM算法去噪结果,图 9(d)是硬阈值法去噪结果,图 9(e)是Wiener滤波去噪结果,图 9(f)是文中算法去噪结果。

|
图 9 海洋地震信号去噪 Fig. 9 Marine seismic signals denoising |
如图 9所示,4种去噪算法基本都能实现去噪任务,比较4种去噪算法的性能,发现文中算法和NLM算法的PSNR比硬阈值算法更高,4种去噪算法的具体差异已量化比较,表 2展示了4种去噪算法的去噪性能。
| 表 2 各算法对海上地震信号去噪的性能(高斯噪声) Table 2 Performance of each algorithm for denoising marine seismic signals (Gaussian noise) |
表 2可看出,在噪声水平5%的情况下,文中算法和NLM算法的去噪性能相差不大,但比硬阈值法和Wiener滤波算法好,从具体量化结果来看,文中算法的PSNR为32.336 1,比NLM算法的PSNR多出0.721 6,即提高了2.23%。随着噪声水平的增加,文中算法更注重于细节处理所以仍能保持性能最佳,而NLM算法在噪声水平逐渐增大的情况下,去噪效果逐渐不理想。硬阈值法去噪时会由于阈值设定问题导致去噪结果更平滑,丢失一些细节信息,从而导致去噪效果不理想。Wiener滤波算法对高斯噪声有较强的抑制效果,但代价是容易失去地震信号的边缘信息,导致去噪效果较差。
5 结论文中提出的算法利用非下采样Shearlet变换后的细节系数近似为广义高斯分布,结合NLM算法以及PCA对细节系数进行处理,再进行Shearlet逆变换得到去噪结果。将该算法应用于海洋地震信号和人工合成地震信号,与传统的NLM算法、硬阈值法、Wiener滤波算法相比,文中算法对细节部分的处理更出色,NLM算法对含有更多相似块的地震信号去噪效果更好,硬阈值算法对信号和噪声区别较大的地震信号去噪效果更好,Wiener滤波算法对含有高斯噪声的地震信号处理效果较好。就文中涉及的2种地震信号,文中算法能综合考虑到细节部分和整体部分且无关噪声种类,从而达到更好的去噪效果,因此采用Shearlet变换和NLM算法相结合对地震信号进行去噪更具优势。
| [1] |
金朝娣, 能昌信, 刘玉强, 等. 小波域相关算法在随钻地震信号处理中的应用[J]. 煤炭学报, 2012, 37(4): 621-626. Jin Z D, Nai C X, Liu Y Q, et al. SWD signal processing based on wavelet domain correlation algorithm[J]. Journal of China Coal Society, 2012, 37(4): 621-626. (in Chinese) |
| [2] |
解吉高, 刘春成, 刘志斌, 等. 下刚果盆地北部中新统深水浊积岩储层及含油性地震预测[J]. 石油学报, 2015, 36(1): 33-40. Xie J G, Liu C C, Liu Z B, et al. Seismic prediction of the reservoir and oil-bearing property of Miocene deep-water turbidite in northern Lower Congo Basin[J]. Acta Petrolei Sinica, 2015, 36(1): 33-40. (in Chinese) |
| [3] |
宋维琪, 张宇. 基于压缩感知理论的微地震资料噪声压制[J]. 地球物理学进展, 2017, 32(4): 1636-1642. Song W Q, Zhang Y. Noise suppression of the microseismic data based on the compressive sampling theory[J]. Progress in Geophysics, 2017, 32(4): 1636-1642. (in Chinese) |
| [4] |
Cao S Y, Chen X P. The second-generation wavelet transform and its application in denoising of seismic data[J]. Applied Geophysics, 2005, 2(2): 70-74. DOI:10.1007/s11770-005-0034-4 |
| [5] |
E J Candès, D L Donoho. Curvelets[R]. USA: Department of Statistics, Stanford University, 1999.
|
| [6] |
Do M N, Vetterli M. Contourlets[M]. Studies in Computational Mathematics. Amsterdam, The Netherlands: Elsevier, 2003: 83-105.
|
| [7] |
Donoho D L. Orthonormal ridgelets and linear singularities[J]. SIAM Journal on Mathematical Analysis, 2000, 31(5): 1062-1099. DOI:10.1137/S0036141098344403 |
| [8] |
Guo K H, Labate D. Optimally sparse multidimensional representation using shearlets[J]. SIAM Journal on Mathematical Analysis, 2007, 39(1): 298-318. DOI:10.1137/060649781 |
| [9] |
童思友, 高航, 刘锐, 等. 基于Shearlet变换的自适应地震资料随机噪声压制[J]. 石油地球物理勘探, 2019, 54(4): 744-750. Tong S Y, Gao H, Liu R, et al. Seismic random noise adaptive suppression based on the Shearlet transform[J]. Oil Geophysical Prospecting, 2019, 54(4): 744-750. (in Chinese) |
| [10] |
赵海涛. 基于循环平移Shearlet变换自适应阈值消减微震勘探随机噪声[D]. 长春: 吉林大学, 2017. Zhao H T. Adaptive threshold based on cycle spinning shearlet transform for microseismic random noise attenuation[D]. Changchun: Jilin University, 2017. (in Chinese) |
| [11] |
刘昕, 陈祖斌, 王东鹤, 等. 基于非下采样shearlet变换的微地震随机噪声压制[J]. 煤炭技术, 2016, 35(1): 128-129. Liu X, Chen Z B, Wang D H, et al. Microseismic random noise attenuation based on non-subsampled shearlet transform[J]. Coal Technology, 2016, 35(1): 128-129. (in Chinese) |
| [12] |
郭晨龙, 赵旭阳, 郑海燕, 等. 一种基于改进非局部均值滤波算法的红外图像去噪[J]. 红外技术, 2018, 40(7): 638-641. Guo C L, Zhao X Y, Zheng H Y, et al. Infrared image denoising method based on improved non-local means filter[J]. Infrared Technology, 2018, 40(7): 638-641. (in Chinese) |
| [13] |
王思涛, 金聪. 基于边缘提取的非局部均值图像去噪[J]. 电子测量技术, 2018, 41(11): 99-102. Wang S T, Jin C. Non-local mean image denoising based on edge extraction[J]. Electronic Measurement Technology, 2018, 41(11): 99-102. (in Chinese) |
| [14] |
Souidene W, Beghdadi A, Abed-Meraim K. Image denoising in the transformed domain using non local neighborhoods[C]//2006 IEEE International Conference on Acoustics Speech and Signal Processing Proceedings. New York, USA: IEEE, 2006.
|
| [15] |
Zhang X H, Zhang Q, Jiao L C. Image denoising with non-local means in the shearlet domain[C]// 2011 International Workshop on Multi-Platform/Multi-Sensor Remote Sensing and Mapping. New York, USA: IEEE, 2011.
|
| [16] |
Anju T S, Nelwin Raj N R. Shearlet transform based image denoising using histogram thresholding[C]// 2016 International Conference on Communication Systems and Networks (ComNet). New York, USA: IEEE, 2017.
|
| [17] |
Sun Z G, Shi R. GF-3 SAR image despeckling based on non-subsampled shearlet transform[C]// 2017 SAR in Big Data Era: Models, Methods and Applications (BIGSARDATA). New York, USA: IEEE, 2017.
|
| [18] |
Yang H Y, Wang X Y, Niu P P, et al. Image denoising using nonsubsampled shearlet transform and twin support vector machines[J]. Neural Networks, 2014, 57: 152-165. DOI:10.1016/j.neunet.2014.06.007 |
| [19] |
Buades A, Coll B, Morel J M. A non-local algorithm for image denoising[C] // 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. New York, USA: IEEE, 2005.
|
| [20] |
王倩, 彭海云, 秦杰, 等. NSCT域分类预处理的改进非局部均值去噪算法[J]. 计算机辅助设计与图形学学报, 2018, 30(3): 436-446. Wang Q, Peng H Y, Qin J, et al. Improved NLM denoising algorithm based on classification preprocess in NSCT Domain[J]. Journal of Computer-Aided Design & Computer Graphics, 2018, 30(3): 436-446. (in Chinese) |
| [21] |
李玲. 基于非局部均值的图像去噪方法研究[D]. 淮南: 安徽理工大学, 2018. Li L. Research on image denoising based on non-local means[D]. Huainan: Anhui University of Science and Technology, 2018. (in Chinese) |
| [22] |
王银杰. 基于非局部均值滤波的图像去噪算法[D]. 哈尔滨: 哈尔滨理工大学, 2019. Wang Y J. The study of image denoising methods based on the non-local means[D]. Harbin: Harbin University of Science and Technology, 2019. (in Chinese) |
| [23] |
Hou W L, Jia R S, Sun H M, et al. Random noise reduction in seismic data by using bidimensional empirical mode decomposition and shearlet transform[J]. IEEE Access, 2019, 7: 71374-71386. DOI:10.1109/ACCESS.2019.2920021 |
| [24] |
杨欣程. 主成分分析方法在遥感数字图像处理中的应用综述[J]. 中国水运.航道科技, 2017, 3: 67-71. Yang X C. Application of principal component analysis in remote sensing digital image processing[J]. China Water Transportation (Science & Technology for Waterway), 2017, 3(3): 67-71. (in Chinese) |
| [25] |
郭一民. 基于非下采样Shearlet变换的图像去噪算法研究[D]. 西安: 西安电子科技大学, 2013. Guo Y M. Image noise reduction based on non-subsampled shearlet transform[D]. Xi'an: Xidian University, 2013. (in Chinese) |
 2021, Vol. 44
2021, Vol. 44


