2. 中国航发湖南动力机械研究所, 湖南 株洲 412002
2. Hunan Aviation Powerplant Research Institute, Zhuzhou 412002, Hunan, P. R. China
行星传动系统具备结构紧凑、传递功率大、承载能力高、抗冲击和振动的能力强以及传动平稳等优点,故而有十分广泛的用途。内齿圈作为行星传动系统的重要构件之一,其动态啮合特性直接影响传动系统的均载和动载性能,分析内齿圈的振动机理,提出相应的减振、降噪措施,对于设计动力学性能优良的行星齿轮传动装置有十分重要的现实意义。
理论分析和实验研究都表明,内齿圈的柔度对系统动态特性的影响是不容忽视的[1-4]。增加行星轮系中内齿圈的柔性将使行星齿轮之间的载荷分配更加均匀。Hidaka等[3]对传统的内齿圈结构进行了深入的研究,得出了轮缘厚度对变形、应力和载荷分担系数的影响。结果表明,当轮缘厚度较小时,内齿圈的弯曲变形起主导作用。随着齿厚的增加,内齿圈上的最大应力逐渐从齿槽向齿根转移,但对其载荷分担性能的影响不显著。Kahraman等[5]还利用有限元法建立了行星轮系的准静态模型,以分析传统内齿圈的柔度对齿轮应力和载荷分布的影响。此外,Kahraman等[6]利用类似的方法,进一步研究了传统内齿圈的柔度对系统动态特性的影响,研究表明减小内齿圈的厚度有助于补偿齿轮制造安装误差造成的不均匀载荷效应。然而由于传统内齿圈结构轮缘较厚并呈现刚度高的特点,从而影响传动系统的均载和动载性能。为获取更加优良的系统动态性能,学者们对传统内齿圈的结构进行优化后获得了可以降低传动系统振动和不均载的柔性内齿圈结构。例如:薄壁柔性内齿圈结构[7]、新材料和弹性支撑的内齿圈结构等。
然而,目前对于传统内齿圈结构与柔性内齿圈结构的结构特点与柔性差异及对系统均载和动载的影响甚少有文献报道。笔者对此进行详细分析,以期为系统传动构件的设计选用提供帮助。
1 内齿圈类型及柔性分析对常见的3种内齿圈结构[8](传统内齿圈、薄壁柔性内齿圈及弹性销内齿圈)展开对比分析,以了解各内齿圈结构的特性以及其对行星传动系统动态特性的影响,为设计行星传动系统结构设计提供理论基础。
为准确对比分析3种结构的特点,笔者将采用完全相同模数、齿数、外径、变位系数、轮缘厚度、压力角及相同齿宽参数的内齿圈,参数见表 1。
| 表 1 内齿圈部分参数 Table 1 Parameters of ring gear |
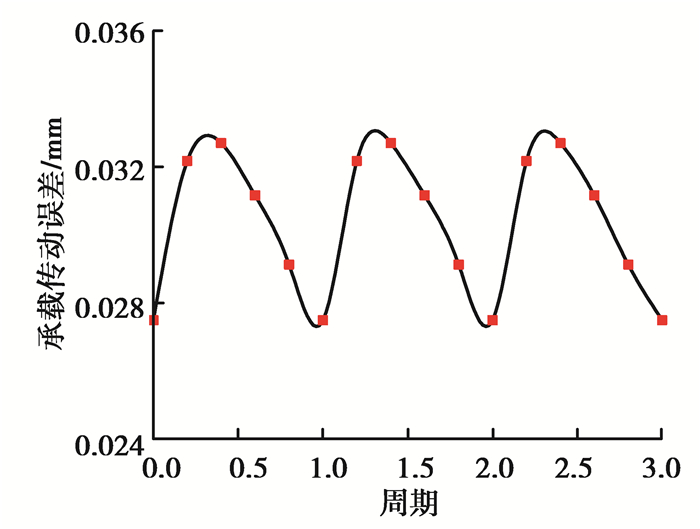
传统内齿圈结构具备轮缘厚度大并且采用轮缘外侧固定支承的方式(见图 1),致使诸多学者在分析轮齿啮合过程时忽略不计轮缘变形,仅考虑轮齿的承载变形。通过构建传统内齿圈与外啮合齿轮的有限元模型,按照中心距装配,设置材料属性,采用“static, general”静态分析步,并设置齿轮中心参考点与轮齿网格耦合。采用“surface-to-surface contact”面面接触分析类型及“small sliding”微小滑移算法,并设置接触属性为切向无摩擦且法向硬接触。从而获取了含轮缘柔性的单个啮合周期下的轮齿承载传动误差曲线,如图 2所示。

|
图 1 传统内齿圈有限元模型 Fig. 1 Finite element model of traditional ring |
|
图 2 传统内齿圈承载传动误差曲线 Fig. 2 Loaded transmission errors of traditional ring |
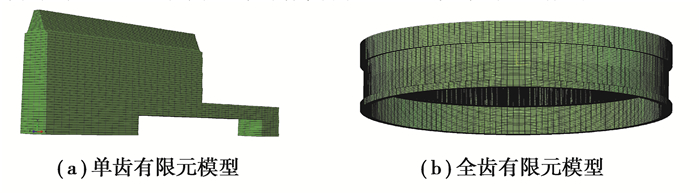
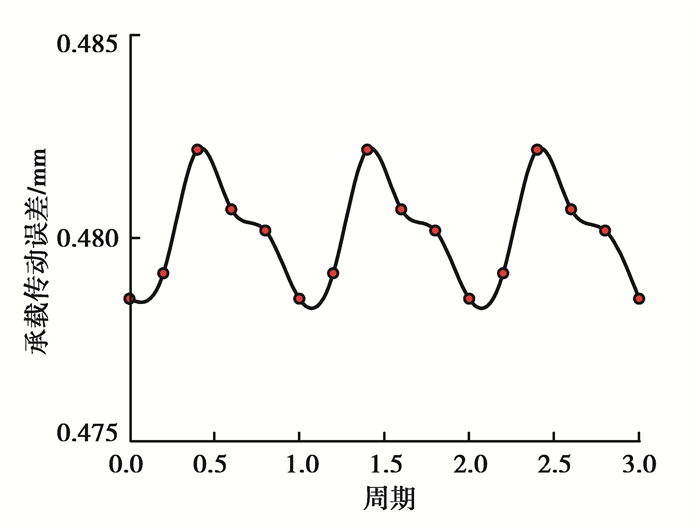
薄壁柔性内齿圈通过依靠齿轮本身弹性变形使各行星轮载荷均匀减少振动,该结构采用下端面固定且延伸轮缘长度形成悬臂的特点。通过构建新型柔性内齿圈的单齿有限元模型并环形阵列合并形成全齿模型,见图 3。设定材料属性(弹性模量206 000 MPa,泊松比0.3,密度7.85 g/cm3)、采用静力通用分析步并设置相关接触面及接触特性后施加扭矩于太阳轮中心点位置,准确获得单个啮合周期内的承载传动误差曲线,如图 4所示。
|
图 3 薄壁柔性内齿圈有限元模型 Fig. 3 Finite element model of thin-walled ring |
|
图 4 承载传动误差曲线 Fig. 4 Loaded transmission errors of thin-walled ring |
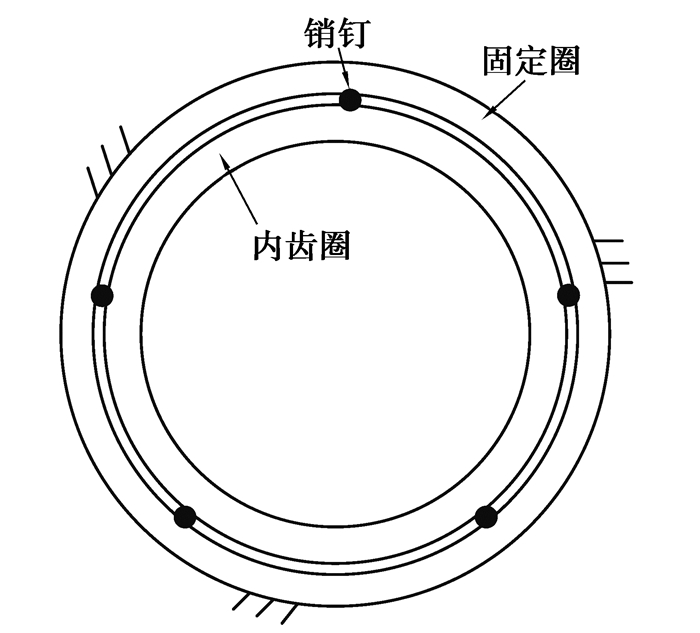
弹性销内齿圈则通过将内齿圈轮缘与外接基体部分间添加销连接,通过控制销的柔性以降低整体刚度提升系统的均载性能。由于该结构的有限元模型计算时存在收敛困难且计算时间过长的问题,因此在结合其结构和支撑特点的情况下给出了一种数值解法,提高效率的同时保证了准确度,具体方程可见作者已发表文献[9],此处仅做简要阐述。假设内齿圈有n个支座(以5支座为例,见图 5),内齿圈可分为至少n段均匀弯曲的弯曲梁[10]。通过分析可得内齿圈的周向位移ω、径向位移μ和弯曲角θ所造成的啮合线上总体变形。
|
图 5 内齿圈销支承原理图 Fig. 5 Schematic diagram of pin |
1) 固定支撑的内齿圈通常采用螺栓连接。在支承位置的平移位移完全受约束,仅保留转动自由度,即u=0;ω=0;θ1=θ2。
2) 采用销钉支承内齿圈时存在两种边界条件。当梁沿径向远离圆心时,它将与销钉接触。梁在支承位置的周向位移和径向位移受到完全约束。此时边界条件与固定相同,即u=0;ω=0;θ1=θ2。当梁沿着接近圆心的径向移动时,它将通过与销钉分离。梁在支承位置的周向位移和径向位移可以同时进行。此时,边界条件为u1=u2;ω1=ω2;θ1=θ2。
基于上述分析,通过对任意截面曲线梁的任意边界约束位置设置不同的边界条件,可以得到相应的变形、内力和转矩。
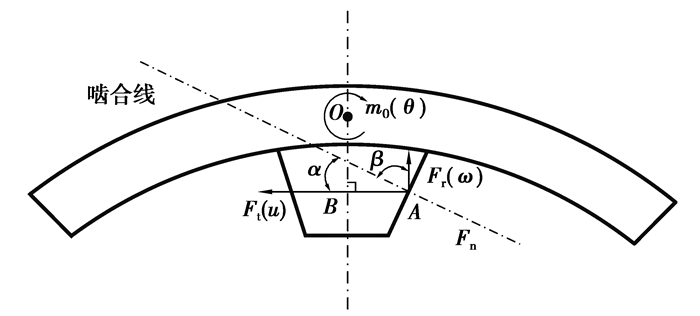
将内齿轮轮齿部分作为刚体,啮合力以周向力、径向力和转矩的形式作用于内齿轮的关系见图 6。
| $ \left\{\begin{array}{l} F_{\mathrm{r}}=F_{\mathrm{n}} \sin \alpha, \\ F_{\mathrm{t}}=F_{\mathrm{n}} \cos \alpha, \\ m_{0}=F_{\mathrm{t}}|O B|-F_{\mathrm{r}}|A B| 。\end{array}\right. $ | (1) |
|
图 6 内齿圈变形沿啮合线线的位移(含力分解) Fig. 6 Displacement of ring gear deformation along the meshing line (including force decomposition) |
周向位移ω、径向位移μ和弯曲角θ所造成的啮合线上总体变形,
| $ \sigma=\omega \cos \alpha+\mu \sin \alpha+\theta|O A| \sin \beta。$ | (2) |
根据支撑边界条件,通过对均匀曲线梁的分析,得到了梁的周向位移ω、径向位移μ和弯曲角θ等表达式。根据一般弹性体材料力学原理,将截面内力与变形联系起来,可以建立以下基本微分方程:
| $ \left\{\begin{array}{l} M_{x}=-E I_{x}\left(\frac{\mathrm{d}^{2} \omega}{\mathrm{d} z^{2}}-\frac{\phi}{r}\right), \\ T=-E I_{\omega}\left(\frac{\mathrm{d}^{3} \phi}{\mathrm{d} z^{3}}+\frac{1}{r} \frac{\mathrm{d}^{3} \omega}{\mathrm{d} z^{3}}\right)+G I_{\mathrm{d}}\left(\frac{\mathrm{d} \phi}{\mathrm{d} z}+\frac{1}{r} \frac{\mathrm{d} \omega}{\mathrm{d} z}\right), \\ \frac{\mathrm{d} M}{\mathrm{~d} \phi_{z}}=-T-r Q, \end{array}\right. $ | (3) |
式中:A是梁的横截面积;E是弹性模量;G是剪切模量;Ix和Iy对应x和y轴的弯曲惯性矩;Id是关于z轴的扭转惯性矩;Iω是梁的变形常数;Q是剪切力。
通过对上述公式的推导和变换,得到了弯曲的微分方程及相应的扭转角和弯曲角的表达式。
| $ \left\{\begin{array}{l} \frac{\mathrm{d}^{3} \omega}{\mathrm{d} \phi_{z}^{3}}+\frac{\mathrm{d} \omega}{\mathrm{d} \phi_{z}}=\frac{r^{3}}{E I}[(1+k) T+r Q], \\ \phi=\frac{1}{r} \frac{\mathrm{d}^{2} \omega}{\mathrm{d} \phi_{z}^{2}}+\frac{r}{E I} M, \\ \theta=\frac{\mathrm{d} \omega}{\mathrm{d} z}=\frac{1}{r} \frac{\mathrm{d} \omega}{\mathrm{d} \phi_{z}}, \end{array}\right. $ | (4) |
式中:
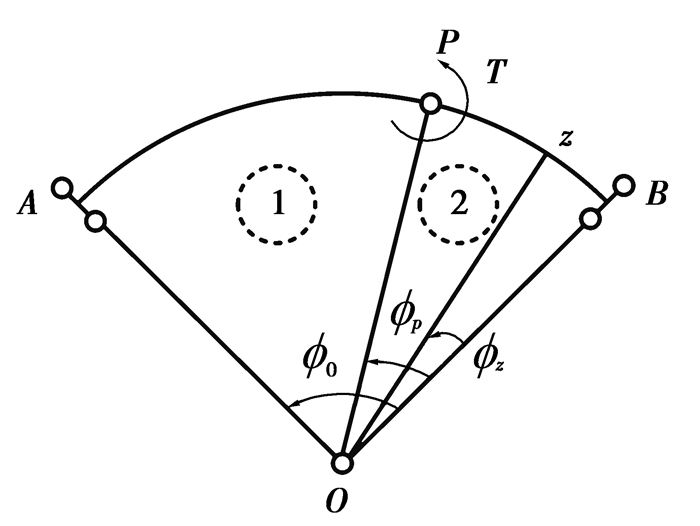
当集中荷载和扭矩作用于梁的任意位置时,梁的各截面内力被分成两部分,如图 7所示。
|
图 7 集中荷载和集中扭矩下的变形计算 Fig. 7 Deformation calculation under concentrated load and concentrated torque |
如图 7所示,当集中载荷P和集中扭矩T作用于梁的任何位置ϕp,每个部分的梁的内力方程为:当0≤ϕz≤ϕp,
| $ \left\{\begin{array}{l} M_{z p}=(p r+T) \frac{\sin \left(\phi_{0}-\phi_{p}\right)}{\sin \phi_{0}} \sin \phi_{z}, \\ T_{z p}=p r\left[1-\frac{\phi_{p}}{\phi_{0}}-\frac{\sin \left(\phi_{0}-\phi_{p}\right)}{\sin \phi_{0}} \cos \phi_{z}\right]-T \frac{\sin \left(\phi_{0}-\phi_{p}\right)}{\sin \phi_{0}} \cos \phi_{z}, \\ Q_{z p}=-p\left(1-\frac{\phi_{p}}{\phi_{0}}\right)。\end{array}\right. $ | (5) |
当ϕp≤ϕz≤ϕ0,
| $ \left\{\begin{array}{l} M_{z p}=(p r+T) \frac{\sin \phi_{p}}{\sin \phi_{0}} \sin \left(\phi_{0}-\phi_{z}\right), \\ T_{z p}=p r\left[\frac{\sin \phi_{p}}{\sin \phi_{0}} \sin \left(\phi_{0}-\phi_{z}\right)-\frac{\phi_{p}}{\phi_{0}}\right]+T \frac{\sin \phi_{p}}{\sin \phi_{0}} \sin \left(\phi_{0}-\phi_{z}\right), \\ Q_{z p}=p \frac{\phi_{p}}{\phi_{0}}。\end{array}\right. $ | (6) |
由上式得到挠度微分方程为:
| $ \frac{\mathrm{d}^{3} \omega_{1}}{\mathrm{~d} \phi_{z}^{3}}+\frac{\mathrm{d} \omega_{1}}{\mathrm{~d} \phi_{z}}=\frac{p r^{3}}{E I}\left\{\left[\left(1-\frac{\phi_{p}}{\phi_{0}}\right)-\frac{\sin \left(\phi_{0}-\phi_{p}\right)}{\sin \phi_{p}} \cos \phi_{z}\right]-\left(1-\frac{\phi_{p}}{\phi_{0}}\right)\right\}-\frac{{Tr}^{2}}{E I}(1+k) \frac{\sin \left(\phi_{0}-\phi_{p}\right)}{\sin \phi_{p}} \cos \phi_{z}, $ |
| $ \frac{\mathrm{d}^{3} \omega_{2}}{\mathrm{~d} \phi_{z}^{3}}+\frac{\mathrm{d} \omega_{2}}{\mathrm{~d} \phi_{z}}=\frac{p r^{3}}{E I}\left\{(1+k) \frac{\sin \phi_{p}}{\sin \phi_{0}} \cos \left(\phi_{0}-\phi_{z}\right)-k \frac{\phi_{p}}{\phi_{0}}\right\}+\frac{{Tr}^{2}}{E I}(1+k) \frac{\sin \phi_{p}}{\sin \phi_{0}} \cos \left(\phi_{0}-\phi_{z}\right) $ |
并得通解为:
| $ \left\{\begin{array}{l} \omega_{1}=A+B \sin \phi_{z}+C \cos \phi_{z}+\frac{p r^{3}+T r^{2}}{E I} \cdot \frac{(1+k)}{2} \frac{\sin \left(\phi_{0}-\phi_{p}\right)}{\sin \phi_{0}} \phi_{z} \cos \phi_{z}+\frac{p r^{3}}{E I} k\left(1-\frac{\phi_{p}}{\phi_{0}}\right) \phi_{z}, \\ \omega_{2}=D+E \sin \phi_{z}+F \cos \phi_{z}-\frac{p r^{3}+T r^{2}}{E I} \cdot \frac{(1+k)}{2} \frac{\sin \phi_{p}}{\sin \phi_{0}} \phi_{z} \cos \left(\phi_{0}-\phi_{z}\right)-\frac{p r^{3}}{E I} k \frac{\phi_{p}}{\phi_{0}} \phi_{z}。\end{array}\right. $ | (7) |
基于边界条件和连续条件,
1) ϕz=0:ω1=0或ω″1=0。
2) ϕz=ϕp: ω1=ω2, ω′1=ω′2和ω″1=ω″2。
3) ϕz=ϕp: ω2=0和ω″2=0。
得到相关系数:
| $ \left\{\begin{aligned} A=& 0 ; C=0, \\ B=& \frac{p r^{3}+\operatorname{Tr}^{2}}{2 E I}(1+k) \frac{\phi_{0} \sin \phi_{p}-\phi_{p} \cos \left(\phi_{0}-\phi_{p}\right) \sin \phi_{p}}{\sin ^{2} \phi_{p}}-\frac{p r^{3}}{2 E I}(1+3 k) \frac{\sin \left(\phi_{0}-\phi_{p}\right)}{\sin \phi_{0}} -\\ & \frac{{Tr}^{2}}{2 E I}(1+k) \frac{\sin \left(\phi_{0}-\phi_{p}\right)}{\sin \phi_{0}}, \\ D=& \frac{p r^{3}}{E I} k \phi_{p}, \\ E=& \frac{p r^{3}}{2 E I}\left[(1+k) \frac{\phi_{0} \sin \phi_{p}}{\sin ^{2} \phi_{0}}-(1+k) \phi_{p} \cos \phi_{p} \cot \phi_{0}+(1+3 k) \sin \phi_{p} \cot \phi_{0}\right]+\\ & \frac{{Tr}^{2}}{2 E I}\left[\frac{(1+k)}{\tan \phi_{0}}\left(\frac{\phi_{0} \sin \phi_{p}}{\sin \phi_{0} \cos \phi_{0}}-\phi_{p}+\sin \phi_{p}\right)\right], \\ F=& \frac{p r^{3}}{2 E I}\left[(1+k) \phi_{p} \cos \phi_{p}-(1+3 k) \sin \phi_{p}\right]+\frac{{Tr}^{2}}{2 E I}(1+k)\left(\phi_{p} \cos \phi_{p}-\sin \phi_{p}\right) 。\end{aligned}\right. $ | (8) |
将得到的常数代入公式,得到集中荷载和集中扭矩作用下弯曲梁的弯曲度及弯扭角的计算公式为:当0≤ϕz≤ϕp,
| $ \begin{aligned} \omega_{1}=& \frac{p r^{3}}{2 E I}\left\{\frac{(1+k)}{\sin \phi_{0}}\left[\frac{\phi_{0} \sin \phi_{p}}{\sin \phi_{0}} \sin \phi_{z}-\phi_{p} \cos \left(\phi_{0}-\phi_{p}\right) \sin \phi_{z}+\phi_{z} \sin \left(\phi_{0}-\phi_{p}\right) \cos \phi_{z}\right]-\right.\\ &\left(1+3 k \frac{\sin \left(\phi_{0}-\phi_{p}\right)}{\sin \phi_{0}} \sin \phi_{z}+2 k\left(1-\frac{\phi_{p}}{\phi_{0}}\right) \phi_{z}\right\}+\frac{{Tr}^{2}}{2 E I}\left\{\frac { ( 1 + k ) } { \operatorname { sin } \phi _ { 0 } } \left[\frac{\phi_{0} \sin \phi_{p}}{\sin \phi_{0}} \sin \phi_{z}-\right.\right.\\ &\left.\left.\left.\phi_{p} \cos \left(\phi_{0}-\phi_{p}\right) \sin \phi_{z}+\phi_{z} \sin \left(\phi_{0}-\phi_{p}\right) \cos \phi_{z}\right]-\sin \left(\phi_{0}-\phi_{p}\right) \cos \phi_{z}\right]\right\}。\end{aligned} $ | (9) |
| $ \begin{gathered} \theta_{1}=\frac{1}{r} \frac{\mathrm{d} \omega_{1}}{\mathrm{~d} \phi_{z}}= \\ \begin{aligned} &\frac{p r^{2}}{2 E I}\left\{\frac{(1+k)}{\sin \phi_{0}}\left[\frac{\phi_{0} \sin \phi_{p}}{\sin \phi_{0}} \cos \phi_{z}-\phi_{p} \cos \left(\phi_{0}-\phi_{p}\right) \cos \phi_{z}-\phi_{z} \sin \left(\phi_{0}-\phi_{p}\right) \sin \phi_{z}\right]-\right. \\ &\left.2 k\left[\frac{\sin \left(\phi_{0}-\phi_{p}\right)}{\sin \phi_{0}} \cos \phi_{z}-1+\frac{\phi_{p}}{\phi_{0}}\right]\right\}+\frac{\operatorname{Tr}}{E I}\left\{\frac { ( 1 + k ) } { 2 \operatorname { sin } \phi _ { 0 } } \left[\frac{\phi_{0} \sin \phi_{p}}{\sin \phi_{0}} \cos \phi_{z}-\phi_{p} \cos \left(\phi_{0}-\right.\right.\right. \\ &\left.\left.\left.\phi_{p}\right) \cos \phi_{z}-\phi_{z} \sin \left(\phi_{0}-\phi_{p}\right) \sin \phi_{z}\right]\right\}, \end{aligned} \end{gathered} $ | (10) |
| $ \begin{gathered} \phi_{1}=\frac{1}{r} \frac{\mathrm{d}^{2} \omega_{1}}{\mathrm{~d} \phi_{z}^{2}}+r \frac{M}{E I}= \\ \begin{aligned} &\frac{p r^{2}}{2 E I}\left\{\frac{(1+k)}{\sin \phi_{0}}\left[\phi_{p} \cos \left(\phi_{0}-\phi_{p}\right) \sin \phi_{z}-\phi_{0} \frac{\sin \phi_{p}}{\sin \phi_{0}} \sin \phi_{z}\right]-\sin \left(\phi_{0}-\phi_{p}\right)\left(\phi_{z} \cos \phi_{z}-\right.\right. \\ &\left.\left.\sin \phi_{z}\right)\right\}+\frac{{Tr}}{E I}\left\{\frac { ( 1 + k ) } { 2 \operatorname { sin } \phi _ { 0 } } \left[\phi_{p} \cos \left(\phi_{0}-\phi_{p}\right) \sin \phi_{z}-\phi_{0} \frac{\sin \phi_{p}}{\sin \phi_{0}} \sin \phi_{z}-\sin \left(\phi_{0}-\right.\right.\right. \\ &\left.\left.\left.\phi_{p}\right)\left(\phi_{z} \cos \phi_{z}-\sin \phi_{z}\right)\right]-k \frac{\sin \phi_{p}}{\sin \phi_{0}} \sin \left(\phi_{0}-\phi_{p}\right)\right\}。\end{aligned} \end{gathered} $ | (11) |
当ϕp≤ϕz≤ϕ0,
| $ \begin{aligned} \omega_{2}=& \frac{p r^{3}}{2 E I}\left\{\frac{(1+k)}{\sin \phi_{0}}\left[\frac{\phi_{0} \sin \phi_{p}}{\sin \phi_{0}} \sin \phi_{z}+\phi_{p} \sin \left(\phi_{0}-\phi_{p}\right) \cos \phi_{p}-\phi_{z} \cos \left(\phi_{0}-\phi_{p}\right) \cos \phi_{p}\right]-\right.\\ &\left.(1+3 k) \frac{\sin \left(\phi_{0}-\phi_{z}\right)}{\sin \phi_{0}} \sin \phi_{p}+2 k \phi_{p}\left(1-\frac{\phi_{z}}{\phi_{0}}\right)\right\}+\frac{{Tr}^{2}}{E I}\left\{\frac { ( 1 + k ) } { 2 \operatorname { sin } \phi _ { 0 } } \left[\frac{\phi_{0} \sin \phi_{p}}{\sin \phi_{0}} \sin \phi_{z}+\right.\right.\\ &\left.\left.\phi_{p} \sin \left(\phi_{0}-\phi_{p}\right) \cos \phi_{p}-\phi_{z} \cos \left(\phi_{0}-\phi_{p}\right) \sin \phi_{p}-\sin \phi_{p} \sin \left(\phi_{0}-\phi_{z}\right)\right]\right\} 。\end{aligned} $ | (12) |
| $ \begin{gathered} {\theta_{2}}=\frac{1}{r} \frac{\mathrm{d} \omega_{2}}{\mathrm{~d} \phi_{z}}= \\ \begin{aligned} &\frac{p r^{2}}{\sin \phi_{0}}\left[\frac{\phi_{0} \sin \phi_{p}}{\sin \phi_{0}} \cos \phi_{z}-\phi_{p} \cos \left(\phi_{0}-\phi_{z}\right) \cos \phi_{p}-\phi_{z} \sin \left(\phi_{0}-\phi_{z}\right) \sin \phi_{p}\right]+ \\ &\left.2 k\left[\frac{\cos \left(\phi_{0}-\phi_{z}\right)}{\sin \phi_{0}} \sin \phi_{p}-\frac{\phi_{p}}{\phi_{0}}\right]\right\}+\frac{{Tr}}{E I}\left\{\frac { ( 1 + k ) } { 2 \operatorname { sin } \phi _ { 0 } } \left[\frac{\phi_{0} \sin \phi_{p}}{\sin \phi_{0}} \cos \phi_{z}-\phi_{p} \cos \left(\phi_{0}-\right.\right.\right. \\ &\left.\left.\left.\phi_{z}\right) \cos \phi_{p}-\phi_{z} \sin \left(\phi_{0}-\phi_{z}\right) \sin \phi_{p}\right]\right\}。\end{aligned} \end{gathered} $ | (13) |
| $ \begin{gathered} \phi_{2}=\frac{1}{r} \frac{\mathrm{d}^{2} \omega_{2}}{\mathrm{~d} \phi_{z}^{2}}+r \frac{M}{E I}= \\ \begin{aligned} &\frac{p r^{2}}{2 E I}\left\{\frac{(1+k)}{\sin \phi_{0}}\left[\phi_{z} \cos \left(\phi_{0}-\phi_{z}\right) \sin \phi_{p}-\phi_{0} \frac{\sin \phi_{p}}{\sin \phi_{0}} \sin \phi_{z}\right]-\sin \left(\phi_{0}-\phi_{z}\right)\left(\phi_{p} \cos \phi_{p}-\right.\right. \\ &\left.\left.\sin \phi_{p}\right)\right\}+\frac{p r^{2}}{2 E I}\left\{\frac{(1+k)}{\sin \phi_{0}}\left[\phi_{z} \cos \left(\phi_{0}-\phi_{z}\right) \sin \phi_{p}-\phi_{0} \frac{\sin \phi_{p}}{\sin \phi_{0}} \sin \phi_{z}\right]-\sin \left(\phi_{0}-\right.\right. \\ &\left.\left.\phi_{z}\right)\left(\phi_{p} \cos \phi_{p}-\sin \phi_{p}\right)\right\}+\frac{{Tr}}{E I}\left\{\frac { ( 1 + k ) } { 2 \operatorname { sin } \phi _ { 0 } } \left[\phi_{z} \cos \left(\phi_{0}-\phi_{z}\right) \sin \phi_{p}-\phi_{0} \frac{\sin \phi_{p}}{\sin \phi_{0}} \sin \phi_{z}-\right.\right. \\ &\left.\left.\sin \left(\phi_{0}-\phi_{z}\right)\left(\phi_{p} \cos \phi_{p}-\sin \phi_{p}\right)\right]-k \frac{\sin \left(\phi_{0}-\phi_{z}\right)}{\sin \phi_{0}} \sin \phi_{p}\right\}。\end{aligned} \end{gathered} $ | (14) |
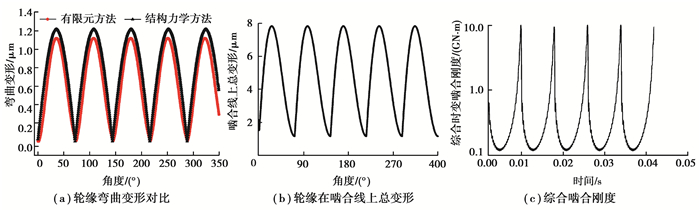
至此,获取了弹性销内齿圈结构的轮缘的变形以及综合时变啮合刚度(轮齿时变啮合刚度采用有限元方法),并给出了固定支承下该方法计算结果与有限元进行了对比,见图 8。
|
图 8 轮缘变形对比与综合啮合刚度 Fig. 8 Deformation comparison and comprehensive meshing stiffness |
通过分析3种内齿圈结构的柔性,可获知传统刚性内齿圈结构的柔性最小,刚度最大。薄壁内齿圈结构的柔性最好,且波动幅值较小。弹性销内齿圈结构的柔性介于以上两者之间,但存在柔性波动过大的问题,该缺点将导致时变啮合刚度的波动剧烈,从而影响系统的均载和动载特性。为更加准确定量地获知3种内齿圈结构对行星传动系统的动态特性影响的区别,下文将通过构建行星传动系统的动力学模型,进一步对比3种内齿圈结构的动力学特性的差异。
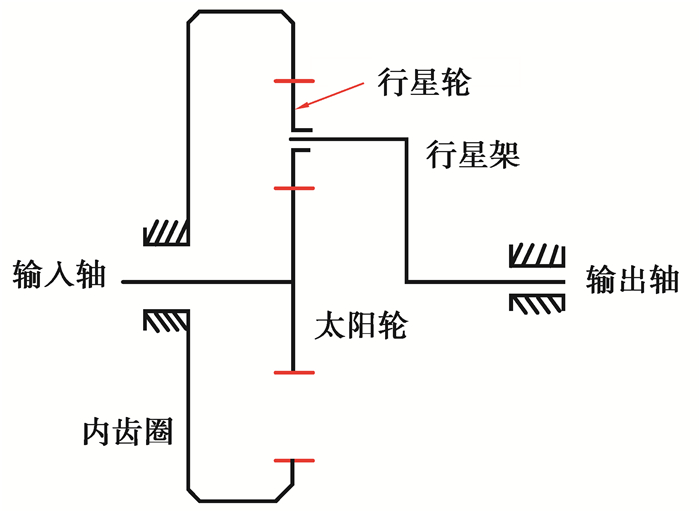
2 动力学特性分析为进一步了各内齿圈结构对行星传动系统的动态特性的影响对比,采用集中质量法[9]构建了行星传动系统的动力学方程。图 9为行星齿轮传动简图。整个系统由太阳轮、5个行星轮和内齿圈组成。输入的功率由太阳轮分流经过行星轮后再汇流到行星架上输出。
|
图 9 行星齿轮传动简图 Fig. 9 Schematic diagram of planetary gear transmission |
建模时采用集中质量模型,将齿轮视为集中质量传统圆盘,啮合副的弹性变形简化为沿啮合线的时变弹簧刚度,支承处的弹性变形则用等效弹簧刚度表示,齿轮均为直齿轮,且各行星轮的物理和几何参数相同,不计齿轮啮合时摩擦力的影响,考虑齿轮的安装误差、制造误差,则系统的动力学模型如图 10所示[11]。
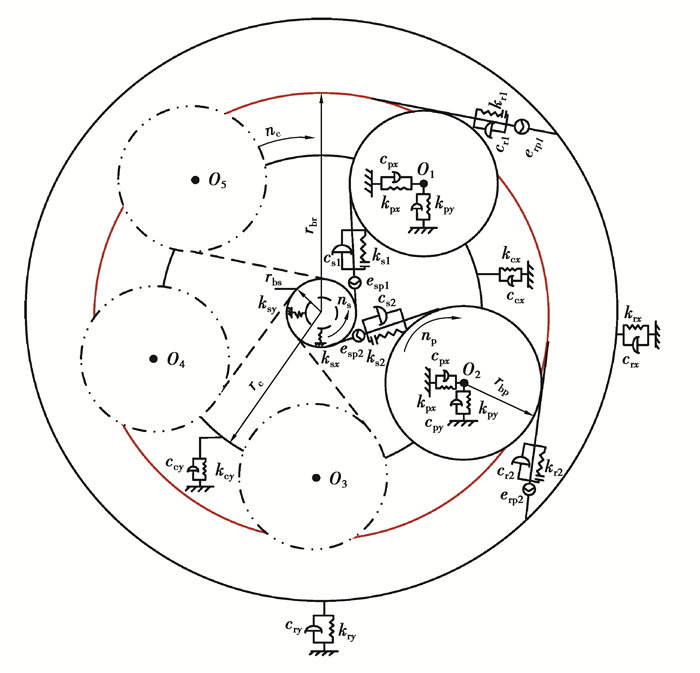
|
图 10 行星传动系统动力学模型 Fig. 10 Dynamic model of the system |
所构建行星传动系统的动力学模型的广义坐标为X={xs, ys, us, xpi, ypi, xr, yr, ur, xc, yc, uc}, 其中i=1, 2, …, 5。
图 10中,kspi表示太阳轮与行星轮啮合副间的轮齿时变啮合刚度;kspi表示太阳轮与行星轮啮合副间的啮合阻尼;krpi表示行星轮与内齿圈啮合副间的轮齿时变啮合刚度;crpi表示行星轮与内齿圈啮合副间的啮合阻尼;ksx表示太阳轮的支承处在x方向上的等效弹簧刚度;ksy表示太阳轮的支承处在y方向上的等效弹簧刚度;csx表示太阳轮的支承处在x方向上的等效阻尼;csy表示太阳轮的支承处在y方向上的等效阻尼;kpix表示行星轮的支承处在x方向上的等效弹簧刚度;kpiy表示行星轮的支承处在y方向上的等效弹簧刚度;cpix表示行星轮的支承处在x方向上的等效阻尼;cpiy表示行星轮的支承处在y方向上的等效阻尼;krx表示内齿圈的支承处在x方向上的等效弹簧刚度;kry表示内齿圈的支承处在y方向上的等效弹簧刚度;crx表示内齿圈的支承处在x方向上的等效阻尼;cry表示内齿圈的支承处在y方向上的等效阻尼;kcx表示行星架的支承处在x方向上的等效弹簧刚度;kcy表示行星架的支承处在y方向上的等效弹簧刚度;ccx表示行星架的支承处在x方向上的等效阻尼;ccy表示行星架的支承处在y方向上的等效阻尼。
按照行星轮系工况(见表 2),传递功率2 958.8 kW、输出转速1 128 r/min,采用Runge-Kutta算法对系统动力学方程进行求解。
| 表 2 行星轮系构件参数 Table 2 Parameters of planetary gear transmission components |
目前对于行星传动系统各构件间相对位置关系的分析已经较为完善,故本节对各构件间相对位置关系的分析过程不再赘述。结合相关文献获知各构件相对位置关系在端面啮合线上的相对位移关系转化公式见下文1)至4),图 11与图 12为各构件间相对位置关系图(图中忽略综合误差)。
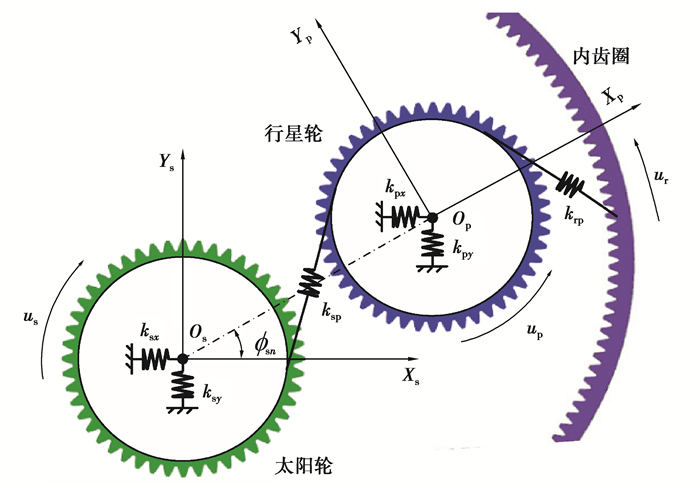
|
图 11 太阳轮与行星轮间相对位移关系 Fig. 11 Relative displacement relationship between sun and planetary wheel |
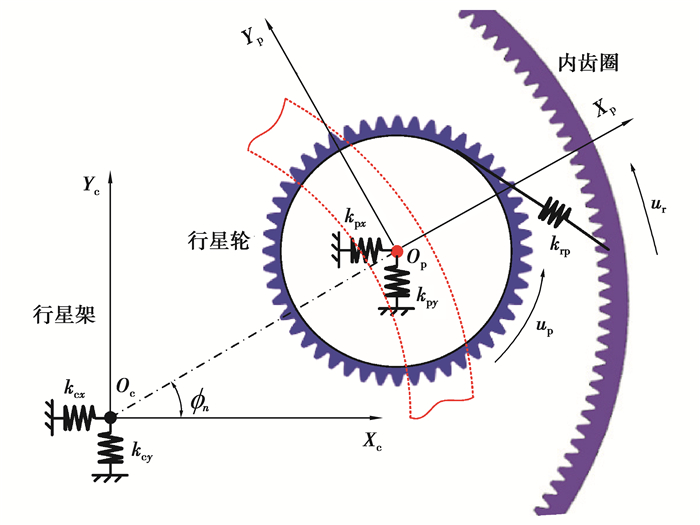
|
图 12 行星架与行星轮间相对位移关系 Fig. 12 Relative displacement relationship between carrier and planetary wheel |
1) 太阳轮中心和行星轮中心在端面啮合线上的相对位移:
| $ \delta_{{\rm{s}} n}=\left(u_{s}-x_{s} \sin \phi_{{\rm{s}} n}+y_{\rm{s}} \cos \phi_{{\rm{s}} n}\right)-\left(-u_{n}+x_{n} \sin \alpha+y_{n} \cos \alpha\right)-e_{{\rm{s}} n}(t) 。$ | (15) |
2) 行星轮中心和内齿圈中心在端面啮合线上的相对位移:
| $ \delta_{\mathrm{r} n}=\left(u_{\mathrm{r}}-x_{\mathrm{r}} \sin \phi_{\mathrm{r}n}+y_{\mathrm{r}} \cos \phi_{\mathrm{r}n}\right)-\left(u_{n}-x_{n} \sin \alpha+y_{n} \cos \alpha\right)-e_{\mathrm{r} n}(t) \text { 。} $ | (16) |
3) 行星轮中心和行星架中心在xc、yc、uc方向上的相对位移:
| $ \delta_{{\rm{c}} n x}=x_{{\rm{c}}}-u_{{\rm{c}}} \sin \phi_{n}-x_{n} \cos \phi_{n}+y_{n} \sin \phi_{n}, $ | (17) |
| $ \delta_{{\rm{c}} n y}=y_{{\rm{c}}}+u_{{\rm{c}}} \cos \phi_{n}-x_{n} \cos \phi_{n}-y_{n} \sin \phi_{n}, $ | (18) |
| $ \delta_{{\rm{c}} n u}=u_{{\rm{c}}}-y_{n}-x_{{\rm{c}}} \sin \phi_{n}+y_{{\rm{c}}} \cos \phi_{n}。$ | (19) |
4) 行星轮中心和行星架中心在xn、yn方向上的相对位移:
| $ \delta_{\mathrm{p}n x}=x_{n}-x_{\mathrm{c}} \cos \phi_{n}-y_{\mathrm{c}} \sin \phi_{n}, $ | (20) |
| $ \delta_{\mathrm{p} n y}=y_{n}-u_{\mathrm{c}}+x_{\mathrm{c}} \sin \phi_{n}-y_{\mathrm{c}} \cos \phi_{n} \text { 。} $ | (21) |
式中:x、y、u分别代表各构件直角坐标轴的x方向、y方向以及转动方向。下标s、c、r、n则分别代表太阳轮、行星架、内齿圈以及第n个行星轮。α为齿轮啮合角;ϕsn=ϕn-α表示δsn与ys之间夹角;ϕrn=ϕn+α表示δrn与yr之间夹角;ϕn表示第n个行星轮的分布角;ern(t)、esn(t)分别为第n个外、内啮合副端面啮合线上的当量累积啮合误差。
2.2 误差分析本文中考虑的系统误差包括太阳轮、行星轮、内齿圈的偏心误差Es、Epi、Er及安装误差As、Api、Ar,各构件的偏心误差的相位角为θEs、θEpi、θEr,各构件的安装误差的相位角为θAs、θApi、θAr,i=1, 2, …, 5。各误差的相位角的起始位置为各构件坐标系中x轴,逆时针方向为正。
为便于读者的阅读,于图 13给出了行星轮的偏心误差、安装误差以及相应相位角的示意图,其他构件的误差定义与其相同。具体含义如下:在O上装配该构件时将不存在安装误差,为理论装配位置。O1为构件理想制造中心,O2为构件实际安装位置。
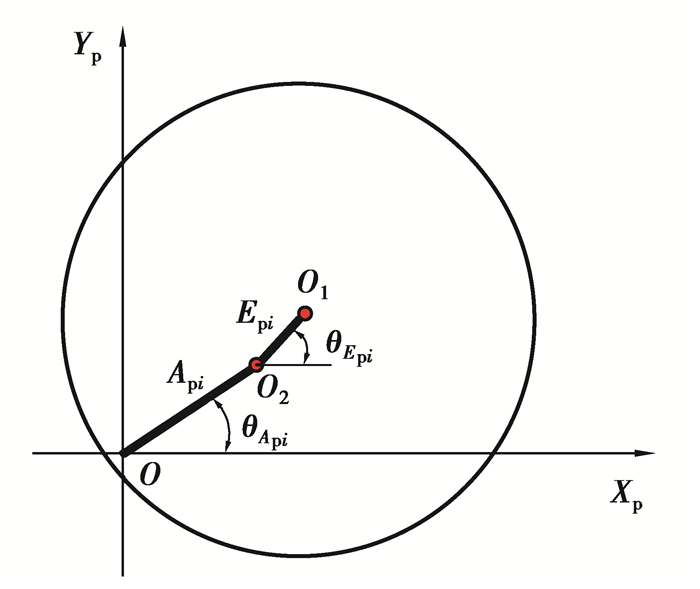
|
图 13 行星轮偏心误差与安装误差示意图 Fig. 13 Schematic diagram of eccentric error and installation error of planetwheel |
依据对于构件偏心误差与安装误差的位置关系定义,可将各构件的偏心误差和安装误差分别向相对应的端面啮合线方向上投影得到各构件的当量啮合误差,并将内、外啮合线上的当量啮合误差进行累加即可得到相应的啮合线上的累积啮合误差。这里规定啮合线方向为被动轮指向主动轮,太阳轮旋转方向为正,行星轮、内齿圈的旋转方向为负。至此获得了行星轮、太阳轮、内齿圈以及行星架在啮合线上的啮合误差关系式,具体见下文。
1) 行星轮偏心误差Epi向第i个外啮合副端面啮合线方向投影得到当量啮合误差:
| $ e_{E_{{\rm{p}} i {\rm{w}}}}=-E_{{\rm{p}} i} \sin \left[\left(\omega_{{\rm{p}} i}-\omega_{\rm{c}}\right) t+\theta_{E_{{\rm{p}} i}}+\alpha_{{\rm{w}}}\right] ; $ | (22) |
偏心误差Epi向第i个内啮合副端面啮合线方向投影得到当量啮合误差:
| $ e_{E_{{\rm{p}} i {\rm{n}}}}=E_{{\rm{p}} i} \sin \left[\left(\omega_{{\rm{p}} i}-\omega_{\rm{c}}\right) t+\theta_{E_{{\rm{p}} i}}-\alpha_{{\rm{w}}}\right] ; $ | (23) |
安装误差Api向第i个外啮合副端面啮合线方向投影得到当量啮合误差:
| $ e_{A_{{\rm{p}} i {\rm{w}}}}=A_{{\rm{p}} i} \sin \left(\theta_{A \mathrm{p} i}+\alpha_{{\rm{w}}}-\phi_{{\rm{p}} i}\right) ; $ | (24) |
安装误差Api向第i个内啮合副端面啮合线方向投影得到当量啮合误差:
| $ e_{A_{\mathrm{p} i {\rm{n}}}}=A_{\mathrm{p}i} \sin \left(\theta_{A \mathrm{p}i}-\alpha_{\mathrm{w}}-\phi_{\mathrm{p}i}\right) 。$ | (25) |
2) 太阳轮偏心误差Es向第i个外啮合副端面啮合线方向投影得到当量啮合误差:
| $ e_{E_{\rm{s}}}=-E_{\rm{s}} \sin \left(\left(\omega_{\rm{s}}-\omega_{\rm{c}}\right) t+\theta_{E_{\rm{s}}}+\alpha_{\rm{w}}-\phi_{{\rm{p}} i}\right) \text {; } $ | (26) |
安装误差As向第i个外啮合副端面啮合线方向投影得到当量啮合误差:
| $ e_{A_{\rm{s}}}=-A_{\rm{s}} \sin \left(-\omega_{\rm{c}} t+\theta_{A_{\rm{s}}}+\alpha_{\rm{w}}-\phi_{{\rm{p}} i}\right) \text { 。} $ | (27) |
3) 内齿圈偏心误差Er向第i个内啮合副端面啮合线方向投影得到当量啮合误差:
| $ e_{E_{\mathrm{r}}}=E_{\mathrm{r}} \sin \left(-\omega_{\mathrm{c}} t+\theta_{E_{\mathrm{r}}}-\alpha_{\mathrm{n}}-\phi_{{\rm{p}} i}\right) ; $ | (28) |
安装误差Api向第i个内啮合副端面啮合线方向投影得到当量啮合误差:
| $ e_{A_{\mathrm{r}}}=A_{\mathrm{r}} \sin \left(-\omega_{\mathrm{c}} t+\theta_{A_{\mathrm{r}}}-\alpha_{\mathrm{n}}-\phi_{{\rm{p}} i}\right) \text { 。} $ | (29) |
式中:Epi、Api分别为行星轮偏心误差和安装误差;Es、As分别为太阳轮偏心误差和安装误差;Er、Ar分别为内齿圈偏心误差和安装误差;θEpi、θApi分别为行星轮偏心误差角和安装误差角;θAs、θEs分别为太阳轮偏心误差角和安装误差角;θEr、θAr分别为内齿圈偏心误差角和安装误差角;ωs、ωp、ωc分别为太阳轮、行星轮和行星架的角速度;αw、αn分别为外、内啮合副端面啮合角;ϕpi第i个行星轮相对于x轴的位置角,ϕpi=2π·i-1/5。
假设齿轮副的齿侧间隙为b,在计入时变啮合刚度、齿侧间隙及系统阻尼的条件下,获得了行星轮与太阳轮、行星轮与内齿圈间的啮合力表达式。
行星轮与太阳轮间啮合力:
| $ F_{\mathrm{s} n}=k_{\mathrm{s} n} f\left(\delta_{\mathrm{s} n}, b\right)+c_{\mathrm{s} n} \dot{\delta}_{\mathrm{s} n}, $ | (30) |
| $ c_{\mathrm{s} n}=2 \zeta \sqrt{\frac{k_{\mathrm{sp}i} I_{\mathrm{s}} I_{\mathrm{p}}}{I_{\mathrm{s}} r_{\mathrm{bp}}^{2}+I_{\mathrm{p}} r_{\mathrm{bs}}^{2}},} $ | (31) |
| $ f\left(\delta_{\mathrm{s} n}, b\right)=\left\{\begin{array}{l} \delta_{\mathrm{s} n}-b, \delta_{\mathrm{s} n}>b, \\ 0,-b \leqslant \delta_{\mathrm{s} n} \leqslant b, \\ \delta_{\mathrm{s} n}+b, \delta_{\mathrm{s} n}<-b 。\end{array}\right. $ | (32) |
行星轮与内齿圈间啮合力:
| $ F_{\mathrm{r} n}=k_{\mathrm{r} n} f\left(\delta_{\mathrm{r} n}, b\right)+c_{\mathrm{r} n} \dot{\delta}_{\mathrm{r} n}, $ | (33) |
| $ c_{\mathrm{r} n}=2 \zeta \sqrt{\frac{k_{\mathrm{rp}i} I_{\mathrm{r}} I_{\mathrm{p}}}{I_{\mathrm{r}} r_{\mathrm{bp}}^{2}+I_{\mathrm{p}} r_{\mathrm{br}}^{2}},} $ | (34) |
| $ f\left(\delta_{\mathrm{r} n}, b\right)=\left\{\begin{array}{l} \delta_{\mathrm{r} n}-b, \delta_{\mathrm{r} n}>b, \\ 0,-b \leqslant \delta_{\mathrm{r} n} \leqslant b, \\ \delta_{\mathrm{r} n}+b, \delta_{\mathrm{r} n}<-b。\end{array}\right. $ | (35) |
式中:f(δsn, b)为行星轮与太阳轮间齿侧间隙非线性函数;f(δrn, b)为行星轮与内齿圈间齿侧间隙非线性函数。
至此,根据牛顿第二运动定律,结合前文分析建立了考虑时变啮合刚度、偏心误差、安装误差等特性的行星齿轮传动系统非线性动力学方程。
1) 太阳轮运动微分方程。
| $ \left\{\begin{array}{l} m_{\mathrm{s}}\left(\ddot{x}_{\mathrm{s}}-2 \omega_{\mathrm{c}} \dot{y}_{\mathrm{s}}-\omega_{\mathrm{c}}^{2} x_{\mathrm{s}}\right)-\sum F_{\mathrm{s} n} \sin \phi_{\mathrm{s} n}+c_{\mathrm{s} x} \dot{x}_{\mathrm{s}}+k_{\mathrm{s} x} x_{\mathrm{s}}=0, \\ m_{\mathrm{s}}\left(\ddot{y}_{\mathrm{s}}+2 \omega_{\mathrm{c}} \dot{x}_{\mathrm{s}}-\omega_{\mathrm{c}}^{2} y_{\mathrm{s}}\right)+\sum F_{\mathrm{s} n} \cos \phi_{\mathrm{s} n}+c_{\mathrm{s} y} \dot{y}_{\mathrm{s}}+k_{\mathrm{s} y} y_{\mathrm{s}}=0, \\ \left(I_{\mathrm{s}} / r_{\mathrm{s}}^{2}\right) \ddot{u}_{\mathrm{s}}+\sum F_{\mathrm{s} n}+c_{\mathrm{su}} \dot{u}_{\mathrm{s}}+k_{\mathrm{s}u} u_{\mathrm{s}}=T_{\mathrm{s}} / r_{\mathrm{s}}。\end{array}\right. $ | (36) |
式中:ms、Is分别表示太阳轮的质量与转动惯量;ksx、csx分别表示太阳轮的横向支承刚度及横向支承阻尼;ksy、csy分别表示太阳轮的纵向支承刚度及纵向支承阻尼;ksu、csu分别表示太阳轮的扭转方向的支承刚度及扭转阻尼;Ts为输入扭矩;rs为太阳轮基圆半径,Is为太阳轮的转动惯量,αsp为太阳轮与行星轮的啮合角。
2) 行星轮运动微分方程。
| $ \left\{\begin{array}{l} m_{\mathrm{p}}\left(\ddot{x}_{n}-2 \omega_{\mathrm{c}} \dot{y}_{n}-\omega_{\mathrm{c}}^{2} x_{n}\right)-F_{\mathrm{s}n} \sin \alpha_{\mathrm{sp}}+F_{\mathrm{r}n} \sin \alpha_{\mathrm{rp}}+c_{\mathrm{p} x} \dot{\delta}_{\mathrm{p}nx}+k_{\mathrm{p}x} \delta_{\mathrm{p}nx}=0, \\ m_{n}\left(\ddot{y}_{n}+2 \omega_{\mathrm{c}} \dot{x}_{n}-\omega_{\mathrm{c}}^{2} y_{n}\right)-F_{\mathrm{s}n} \cos \alpha_{\mathrm{sp}}-F_{\mathrm{r}n} \cos \alpha_{\mathrm{rp}}+c_{\mathrm{p}y} \dot{\delta}_{\mathrm{p}ny}+k_{\mathrm{p}y} \delta_{\mathrm{p}ny}=0, \\ \left(I_{n} / r_{n}^{2}\right) \ddot{u}_{n}+F_{\mathrm{s}n}-F_{\mathrm{r} n}=0, n=1,2, \cdots, N 。\end{array}\right. $ | (37) |
式中:mp、Ip分别表示行星轮的质量与转动惯量;kpx、cpx分别表示行星轮的横向支承刚度及横向支承阻尼;kpy、cpy分别表示行星轮的纵向支承刚度及纵向支承阻尼;rn为行星轮基圆半径,In为行星轮的转动惯量。
3) 内齿圈运动微分方程。
| $ \left\{\begin{array}{l} m_{\mathrm{r}}\left(\ddot{x}_{\mathrm{r}}-2 \omega_{\mathrm{c}} \dot{y}_{\mathrm{r}}-\omega_{\mathrm{c}}^{2} x_{\mathrm{r}}\right)-\sum F_{\mathrm{r} n} \sin \psi_{\mathrm{r} n}+c_{\mathrm{r} x} \dot{x}_{\mathrm{r}}+k_{\mathrm{r} x} x_{\mathrm{r}}=0, \\ m_{\mathrm{r}}\left(\ddot{y}_{\mathrm{r}}+2 \omega_{\mathrm{c}} \dot{x}_{\mathrm{r}}-\omega_{\mathrm{c}}^{2} y_{\mathrm{r}}\right)+\sum F_{\mathrm{r} n} \cos \psi_{\mathrm{r} n}+c_{\mathrm{r} y} \dot{y}_{\mathrm{r}}+k_{\mathrm{r} y} y_{\mathrm{r}}=0, \\ \left(I_{\mathrm{r}} / r_{\mathrm{r}}^{2}\right) \ddot{u}_{\mathrm{r}}+\sum F_{\mathrm{r} n}+c_{\mathrm{r} u} \dot{u}_{\mathrm{r}}+k_{\mathrm{r}u} u_{\mathrm{r}}=0。\end{array}\right. $ | (38) |
式中:mr、Ir分别表示内齿圈的质量与转动惯量;krx、crx分别表示内齿圈的横向支承刚度及横向支承阻尼;kry、cry分别表示内齿圈的纵向支承刚度及纵向支承阻尼;kru、cru分别表示内齿圈的扭转方向的支承刚度及扭转阻尼;rr为内齿圈基圆半径,Ir为内齿圈的转动惯量,αrp为内齿圈与行星轮的啮合角。
4) 行星架运动微分方程。
| $ \left\{\begin{array}{l} m_{\mathrm{c}}\left(\ddot{x}_{\mathrm{c}}-2 \omega_{\mathrm{c}} \dot{y}_{\mathrm{c}}-\omega_{\mathrm{c}}^{2} x_{\mathrm{c}}\right)-\sum c_{\mathrm{p} x} \dot{\delta}_{\mathrm{c} n x}+\sum k_{\mathrm{p}x} \delta_{\mathrm{c} n x}+c_{\mathrm{c}x} \dot{x}_{\mathrm{c}}+k_{\mathrm{c}x} x_{\mathrm{c}}=0, \\ m_{\mathrm{c}}\left(\ddot{y}_{\mathrm{c}}+2 \omega_{\mathrm{c}} \dot{x}_{\mathrm{c}}-\omega_{\mathrm{c}}^{2} y_{\mathrm{c}}\right)+\sum c_{\mathrm{p} x} \dot{\delta}_{\mathrm{c}nx}+\sum k_{\mathrm{p}x} \delta_{\mathrm{c}nx}+c_{\mathrm{s} y} \dot{y}_{\mathrm{c}}+k_{\mathrm{c} y} y_{\mathrm{c}}=0, \\ \left(I_{\mathrm{c}} / r_{\mathrm{c}}^{2}\right) \ddot{u}_{\mathrm{c}}+\sum c_{\mathrm{p}u} \dot{\delta}_{\mathrm{c}nu}+\sum_{\mathrm{p}u} \delta_{\mathrm{c} u}+c_{\mathrm{c}nu} \dot{u}_{\mathrm{c}}+k_{\mathrm{c}u} u_{\mathrm{c}}=-T_{\mathrm{c}} / r_{\mathrm{c}}。\end{array}\right. $ | (39) |
式中:mc分别表示行星架的质量;kcx、ccx分别表示行星架的横向支承刚度及横向支承阻尼;kcy、ccy分别表示行星架的纵向支承刚度及纵向支承阻尼;kcu、ccu分别表示行星架的扭转方向的支承刚度及扭转阻尼,Ic为行星架的转动惯量,Tc为行星架的输出扭矩。
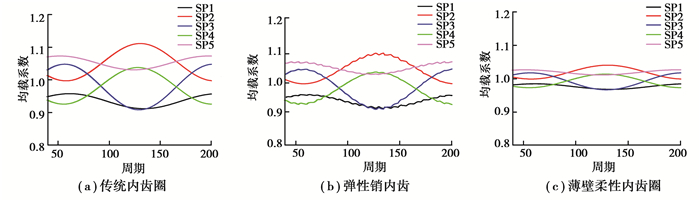
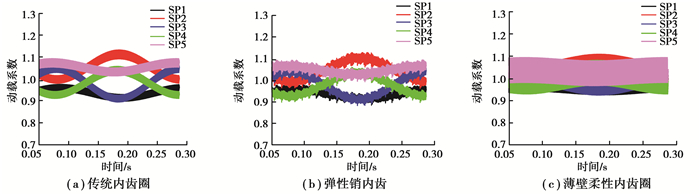
通过构建的行星传动系统的动力学模型,将所获各内齿圈的承载传动误差转化为时变啮合刚度引入模型,设置误差类型如表 3所示(考虑实际工况下,系统的误差是无法避免的,并且当系统不存在误差时,系统将完全均载,亦将无法对比齿圈结构类型的差异。),进而准确获取并对比了传统内齿圈、薄壁柔性内齿圈以及弹性销内齿圈3种结构下的系统的均载系数和动载系数状况。具体如图 14、15所示。
| 表 3 误差设置 Table 3 Error setting |
|
图 14 均载系数对比 Fig. 14 Comparison of load sharing coefficient |
|
图 15 动载系数对比 Fig. 15 Comparison of dynamic load factorcoefficients |
由图 14和图 15可知以下结论:1)传统内齿圈的柔性最差,系统的均载系数为1.12,系统的均载系数和动载系数均较另外两种内齿圈结构明显偏大。2)弹性销内齿圈结构由于结构的特点,导致轮齿接触的时变啮合刚度不断变换,且当处于销钉位置时刚度会明显增大。其系统的均载系数为1.098,虽然较传统内齿圈结构有所降低,但明显振动较多,且在动载系数上振动更是表现明显。3)薄壁柔性内齿圈结构的均载效果最好且无多余振动,系统的均载系数仅为1.048,但由于其支撑方式的原因导致系统的各支路的动载系数波动增大,但整体趋向于均匀,波动变缓。
3 结论柔性内齿圈的提出是对传统内齿圈机构的全新改革,然而目前对于该类结构的分析甚少。在本文中,通过构建各内齿圈结构类型的柔性分析模型以及系统的动力学模型,从静力学特性和动态特性两方面对比分析各结构的优缺点。结论如下:
1) 传统内齿圈由于轮缘厚度大且支承方式的特点导致其刚性最强柔性最差,往往仅分析受载时轮齿部分的承载变形。由于柔度差导致采用该结构会较其他的柔性内齿圈结构在系统的均载系数和动载系数上明显偏大。
2) 弹性销内齿圈结构在轮齿啮合过程中存在内齿圈偏离圆心和靠近圆心的两种姿态,且由于销钉的存在会导致在相邻两个销钉之间内齿圈的变形不均匀呈拱形的特点,这将导致轮齿接触的时变啮合刚度波动剧烈,且当处于销钉位置时刚度会明显增大。该结构在降低系统的均载系数的同时存在振动明显增多的缺陷,并且导致系统的动载系数波动剧烈且杂乱无章。
3) 薄壁柔性内齿圈结构由于支撑位置位于下端面,靠内齿圈自身的柔性实现均载,因此其均载效果最好且无多余振动,并且在啮合过程中亦不会出现时变啮合刚度的剧烈波动。但亦因为其支撑方式的原因会造成齿面载荷的偏载出现,因此在设计时可考虑在轮缘的上端面设计加强环以降低齿面偏载的弊端。此外薄壁内齿圈结构会导致系统的各支路的动载系数波动增大,但各支路的波动趋向于均匀变缓。
| [1] |
许华超, 秦大同. 内激励下弹性边界柔性直齿内齿圈振动响应研究[J]. 机械工程学报, 2018, 54(9): 161-167. Xu H C, Qin D T. Vibration response of flexible spur ring gear with elastic foundation under internal excitation[J]. Journal of Mechanical Engineering, 2018, 54(9): 161-167. (in Chinese) |
| [2] |
秦大同. 国际齿轮传动研究现状[J]. 重庆大学学报, 2014, 37(8): 1-10. Qin D T. Review of research on international gear transmissions[J]. Journal of Chongqing University, 2014, 37(8): 1-10. (in Chinese) |
| [3] |
Hidaka T, Terauchi Y, Nagamura K. Dynamic behavior of planetary gear: 7th report, influence of the thickness of the ring gear[J]. Bulletin of JSME, 1979, 22(170): 1142-1149. DOI:10.1299/jsme1958.22.1142 |
| [4] |
Kahraman A, Ligata H, Singh A. Influence of ring gear rim thickness on planetary gear set behavior[J]. Journal of Mechanical Design, 2010, 132(2): 021002. DOI:10.1115/1.4000699 |
| [5] |
Kahraman A, Vijayakar S. Effect of internal gear flexibility on the quasi-static behavior of a planetary gear set[J]. Journal of Mechanical Design, 2001, 123(3): 408-415. DOI:10.1115/1.1371477 |
| [6] |
Kahraman A, Kharazi A A, Umrani M. A deformable body dynamic analysis of planetary gears with thin rims[J]. Journal of Sound and Vibration, 2003, 262(3): 752-768. DOI:10.1016/S0022-460X(03)00122-6 |
| [7] |
Gevarter W B. NASA technical memorandum[M]. Ohio: Lewis Research Center, 1998.
|
| [8] |
张展. 实用齿轮设计计算手册[M]. 北京: 机械工业出版社, 2011: 680-685. Zhang Z. Practical gear design calculation manual[M]. Beijing: China Machine Press, 2011: 680-685. (in Chinese) |
| [9] |
Hu S Y, Fang Z D. The analysis and modeling of the synthetical meshing stiffness of inner gearing considering the flexible inner ring gear[J]. Shock and Vibration, 2019, 2019: 1-10. |
| [10] |
姚玲森. 曲线梁[M]. 北京: 人民交通出版社, 1989: 67-80. Yao L S. Curved beam[M]. Beijing: China Communications Press, 1989: 67-80. (in Chinese) |
| [11] |
胡升阳, 方宗德. 行星传动均载及动载系数定义改进与分析[J]. 西安交通大学学报, 2019, 53(8): 40-46, 113. Hu S Y, Fang Z D. Improvement and analysis of the definitions of load sharing and dynamic load factors of planetary transmission[J]. Journal of Xi'an Jiaotong University, 2019, 53(8): 40-46, 113. (in Chinese) |
 2021, Vol. 44
2021, Vol. 44


