b. 重庆大学 机械传动国家重点实验室, 重庆 400044
b. State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, P. R. China
路径规划作为智能汽车的决策层,对于提高驾驶人出行效率、缓解城市拥堵具有重要作用。起讫点行程时间是人们出行普遍较为关心之处,因此也成为了路径规划的首要需求[1],其评价指标是路段行程时间的累加值。根据路段行程时间是否变化,可以将路径规划划分为静态路径规划(static path planning,SPP)和滚动路径规划(rolling path planning,RPP)。
SPP主要研究起讫点的累积最小权值,如最短路程或最短静态行程时间,较经典的研究方法有Dijkstra算法、A*算法、蚁群算法等[2],但都各有缺陷。近年来,国内外学者针对上述算法提出了对应的改进策略,以提高算法的运行效率和规划精度。如针对A*算法易陷入局部最优、搜索速度较慢的缺陷,顾青等[3]设计了新的启发式估计能源成本函数以改善A*算法;Fu等[4]通过改进当前节点与目标节点的搜索策略提高了A*算法的搜索成功率;王维等[5]对估计路径代价进行指数衰减的方式加权,使得A*算法自适应地搜索目标点。蚁群算法同样存在收敛速度慢、容易陷入局部最优的缺点,王志中等[6]提出了蚂蚁相遇和蚂蚁回退策略,并改进了信息素残留方法。此外,文献[7-8]也都对蚁群算法进行了相应的改进。A*算法、蚁群算法等都属于智能启发式算法,无论如何改进算法,其包含的随机因子总有可能使路径搜索陷入局部最优,因而也就无法保证所得路径是全局最优解。尽管经典的Dijkstra算法冗余度较高,但当前计算机技术和网络通信技术的巨大发展有效地弥补了这一不足,考虑到该算法能保证找到全局最优解,仍不失为一种较好的方法。
RPP伴随着城市交通的发展而受到广泛关注,主要研究交通信息的获取及改进路径搜索算法的性能。在获取交通信息方面,Chai等[9]提出了自适应信号控制网络中的动态交通路径规划策略;El-Wakeel等[10]提出了一种基于人群感知的动态路线规划系统;李军[11]提出通过预测道路未来时刻交通信息,不断调用内嵌算法,从而实现了多阶段的RPP;Zhao等[12]通过信息中心网络中的大数据获取和分析架构,不断滚动规划智能车的行驶路线。在改进路径搜索算法随机性方面,Tilk等[13]在有界双向动态规划约束的最短路径问题求解变量加速技术的基础上,引入动态中途点来减少最短路径问题求解整体计算量。随裕猛等[14]在分析A*和D* Lite算法的不足之后,提出了D* Lite Label算法。刘琳等[15]依托车联网平台,通过查找车辆当前位置节点实时获取路网权值并进行动态路径规划。上述RPP的核心思想可以归纳为通过反复调用路径规划算法,不断更新汽车行驶路线,因此汽车实际行驶路线是由多阶段规划的局部最优路径拼接而成,而局部最优的叠加并不能推导出全局最优。另外,文献[16]详细阐述了城市交通流具有周期相似性,文献[17]研究了交通流与路段权值的定量关系,路段行程时间作为路段权值的一种评价指标,也顺理成章地体现了周期相似性特征,这一研究成果为时变权值路网的全局最优路径规划开辟了新颖的研究思路。
随着人们对准时到达目的地、缩短出行时间的需求的日益增加,传统的SPP和RPP方法已不再适用。基于此,首先系统分析了现有路径规划方法的不足之处,随后推导了时变权值路网的临界周期路段的实际权值,并基于Dijkstra算法提出了GOPP方法。在验证经典Dijkstra算法能实现全局最优解和运算时间低的基础上,分别利用SPP、RPP和GOPP三种方法规划路径。结果表明,GOPP可以实现时变权值路网的累积行程时间最小,该方法对于有效缩短交通出行时间和智能交通系统的发展具有一定的理论指导意义。
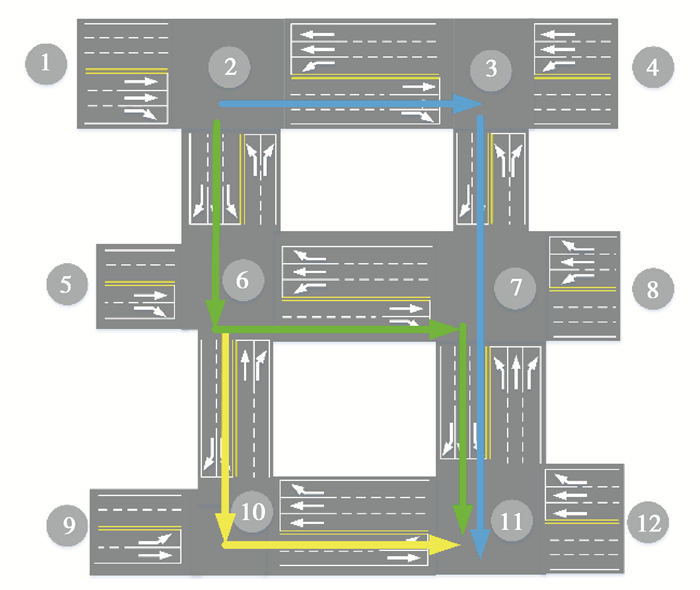
1 传统路径规划的缺陷为了引出GOPP算法,首先探讨当前最常见的两种路径规划方法的缺陷。如图 1所示是一个路段行程时间动态更新的示例路网,在时段1和时段2的路段行程时间如表 1所示,两个时段相邻。假设当前车辆位于交叉口2,当前时刻t0处于时段1,目标交叉口为11,现探讨起讫点为(2,11)的传统路径规划方法。
|
图 1 示例路网及3种路径规划方法比较 Fig. 1 Example road network and comparison of three path planning methods |
| 表 1 示例路网的时变路段行程时间 Table 1 Time-varying travel time of road sections in the example road network |
SPP只考虑路网当前时刻的权值,根据时段1的权值分布计算得到的最优路径为2→6→7→11,如图 1绿色路径所示。现假设车辆到达交叉口6的时刻恰好是时段1和时段2的临界时刻,路网权值随即更新为时段2的权值。则车辆在经过6→7→11时所耗费的行程时间应当参考时段2的权值分布,那么在时段1规划的所谓“最优路径”也就无法证明在时段2是否继续保持最优。因此,SPP的路径是特定时域(时段1)的最优路径,无法证明在全时域保持最优。
考虑到SPP的缺陷,研究人员提出了RPP方法。参考SPP在交叉口2规划的绿色路径,当车辆到达交叉口6时,路网权值发生更新。此时RPP根据时段2的权值立即重新规划剩余的道路网络的路径,计算发现黄色路线的累积权值小于绿色路线的累积权值,因此将行驶路线更改为黄色路线。RPP的两次路径规划起点分别为交叉口1和交叉口6,对应的路径分别为2→6和6→10→11,路径规划的空域显然不同。因此,RPP的实际行驶路径是由特定空域中的局部最优路径拼接而成的,局部最优的叠加并非全局最优,故RPP无法证明在全空域保持最优。
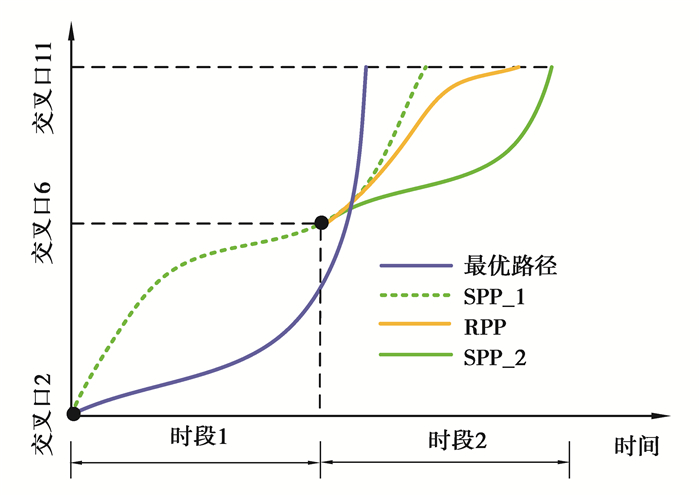
实际上,根据表 1的权值变化通过计算证明图 1的蓝色路径才是最优路径。为更加直观地展示3种路径规划方式的区别,绘制了如图 2所示的起讫点直线距离变化示意图。图 2中交叉口2和交叉口11的纵坐标之差表示两个交叉口间的空间直线距离,车辆从交叉口2出发,随时间推移到达交叉口11。其中,SPP_1表示车辆在交叉口2利用SPP方法规划路径计算得到的理想直线距离变化曲线,但由于车辆在交叉口6时路网权值更新,车辆继续按照SPP路径行驶的实际直线距离变化曲线如SPP_2所示。值得注意的是,蓝色最优路径在时段1并未体现其优势,进入时段2却率先到达了目标点。
|
图 2 起讫点直线距离变化示意图 Fig. 2 Schematic diagram of linear distance change between starting and ending points |
以上示例展示了当前两种常见路径规划方式的核心思想,由于其均无法实现全局最优,因此有必要深刻分析图 1蓝色最优路径的生成原理,探索一种新的求解复杂城市路网全局最优路径的方法。在此之前,首先介绍城市路网的拓扑结构及交通仿真数据的存储,将其作为路径规划的数据基础。
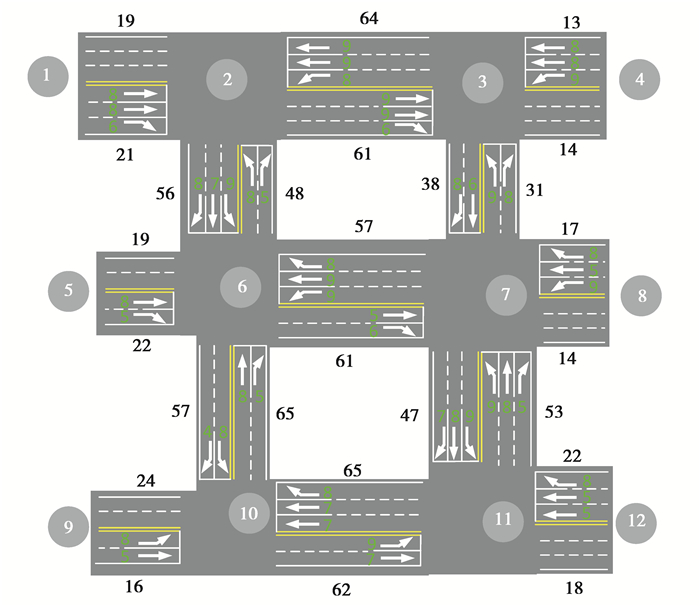
2 路网的拓扑结构与交通仿真 2.1 路网拓扑结构与数据存储城市路网是一个权值时变且包含转向限制的有向图[18],如图 3所示。这里的时变性是指因交通流具有一定的周期相似性,导致路网权值(如路段行程时间)也呈现周期相似性规律的特性,权值更新的周期应当视具体路网和交通情况而定。
|
图 3 路网拓扑结构示意图 Fig. 3 Schematic diagram of road network topology |
路网拓扑结构要素释义如下:1)圆标数字是节点编号,表示路网中的交叉路口(仅考虑十字形和丁字形交叉路口);2)路段是指两个相邻节点之间的道路,且具有方向性,如6→7表示由节点6指向节点7的路段,并定义节点6为父节点,节点7为子节点;3)黑色数字表示路段权值,用来描述车辆行驶该路段所花费的代价,选取路段行程时间作为权值。4)绿色数字表示转向延误权值,描述车辆在交叉口转向所耗费的时间,如车辆的路径规划为1→2→6,车辆从节点1到达节点2须右转,则右转的延误权值为9,若节点有转向限制,则用无穷大代表转向延误权值。
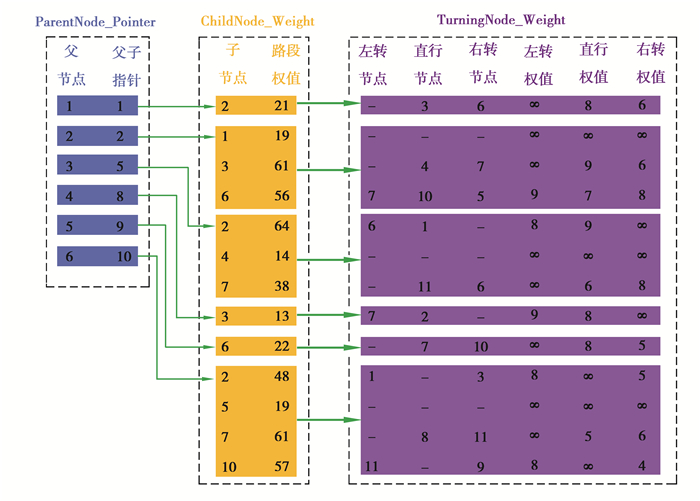
城市路网的数据存储需要考虑交叉口、转向限制以及路段之间的联通性等,目前关于路网数据存储方面的研究有邻接矩阵、邻接表、十字链表等多种建模存储方法[19]。笔者参考文献[20]提出的前向关联边数据存储结构(后文简称数据存储结构),并针对路径规划算法的需要做适当改进,以快速方便地访问路网数据,基于图 3路网的数据存储结构如图 4所示(部分节点数据)。
|
图 4 路网的数据储存结构 Fig. 4 Data storage structure of road network |
数据存储结构主要由3个矩阵构成:1)路网共有12个节点,构造12×2矩阵ParentNode_Pointer。矩阵的第一列存放路网所有节点(视为父节点),并按升序排列,第二列存放父子节点指针;2)再分析路网节点之间的联通关系,构造n×2矩阵ChildNode_Weight(n视具体路网而定)。该矩阵的第一列依次存放矩阵ParentNode_Pointer的每一个父节点的所有邻节点(视为子节点),每一个父节点的若干子节点仍升序排列,第二列存放父节点指向子节点的路段权值。当矩阵ChildNode_Weight唯一确定后,记录每一个父节点的最小子节点所在的行编号,并存放在矩阵ParentNode_Pointer对应的父子节点指针。3)最后分析路网节点间的转向限制及对应权值,构造n×6矩阵TurningNode_Weight。第1至3列存放由父节点指向子节点并转向后的节点编号(只考虑左转、直行及右转),第4至6列存放对应的转向权值。
2.2 路网建模及交通仿真车联网、智能交通系统以及云大数据的蓬勃发展促成了车路云信息交互与协同运作,但路网交通历史统计数据与实时数据当前较难获取,在此利用交通仿真软件Vissim获取路网相关交通数据。
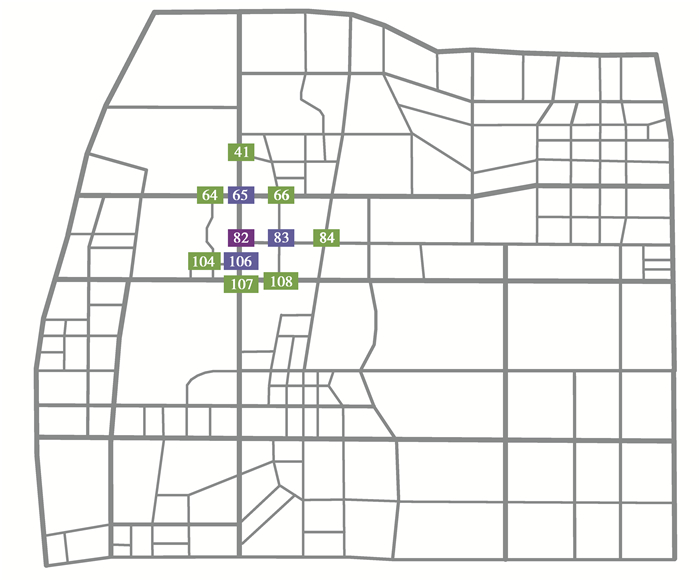
环境建模方面,基于Vissim建立重庆大学城局部路网,主要工作包括路段的建立、红绿灯及交通配时的设置、路口交通分流策略的设置等。该路网共有230个节点,778条路段,总面积近70 km2,如图 5所示。图中,节点82周围的蓝色节点表示子节点,绿色数字表示子节点的邻近节点。
|
图 5 基于Vissim软件的重庆大学城路网建模 Fig. 5 Road network modeling of Chongqing University Town based on Vissim software |
交通仿真方面,结合重庆大学城实际交通情况和路网建模环境,在路网边沿若干重要节点设置两组车流量,分别模拟早高峰期间8:17—8:30与8:30—8:43(以下分别称为时段1和时段2,并设路网权值时变周期为780 s)两个时段的车流输入。同时为每个路段设置行程时间采集器,采集结果作为路段权值。另外为了让车流充分融入路网内部以体现不同路段的交通特性,在1 800 s后再开始记录行程时间。最后对仿真所得数据做统计分析,得到大学城路网行程时间数据库,以此作为路径规划的数据来源。以节点82作为父节点的部分仿真行程时间数据如表 2所示。
| 表 2 部分仿真行程时间数据 Table 2 Partial simulation travel time data |
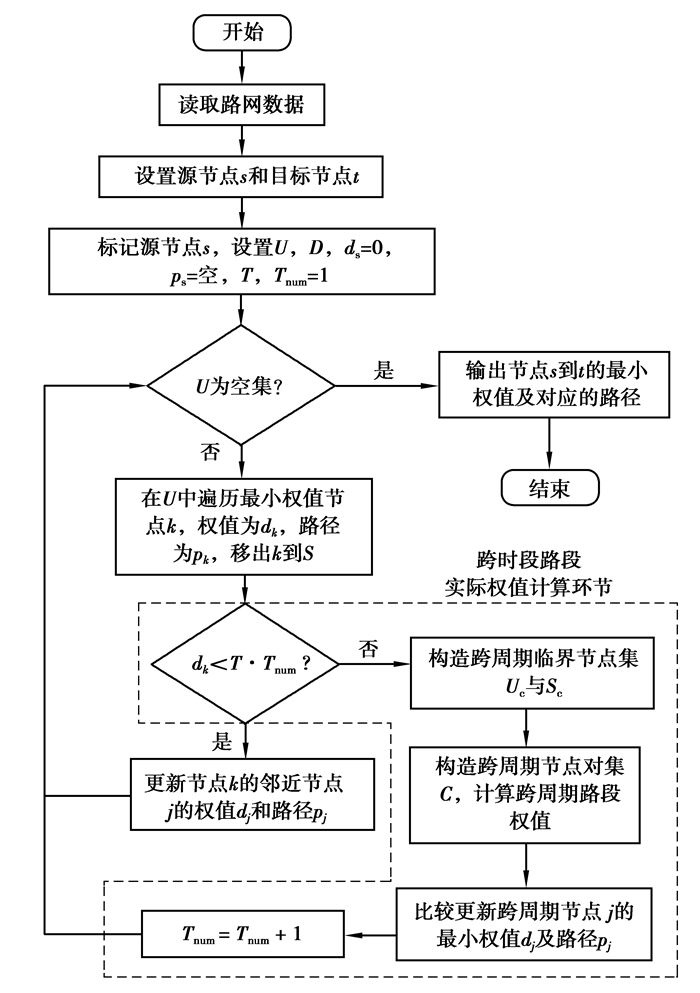
路径规划算法笔者在经典Dijkstra算法基础上,新增跨时段路段实际权值计算环节,提出了GOPP算法,如图 6所示。
|
图 6 GOPP算法流程 Fig. 6 Flow chart of GOPP algorithm |
以图 1示例路网为例,介绍GOPP算法的5个步骤:
1) 初始化。设源节点为s,目标节点为t,di表示源节点s到节点i的最小累计权值,pi是到节点i所经过的路径节点集合。S表示最小累计权值已知的节点的集合,U为最小累计权值未知的点的集合。初始时刻,节点s的邻近子节点的权值di和路径pi可以读取路网数据直接得到,不相邻的节点最小累计权值设为∞。在图 1中,设源节点为1,目标节点为11,路网权值时变周期为T,时段编号为Tnum=1,车辆在源节点1的时刻为t0,则t0+Tnum·T为权值更新时刻。初始时刻S={1},U={2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}。节点2与节点1相邻,故d2可以获知,其余节点累积权值均为∞。
2) 遍历未知节点集。进入循环,在U中搜索距源点s权值最小的节点k,将该点从U移到S中,同时将该点k的权值和对应的路径分别存放到dk和pk中。在第1)步基础上,设集合U中节点2具有最小累计权值d2,故S={1, 2},U={3, 4, 5, 6, 7, 8, 9, 10, 11, 12}。
3) 比较更新邻近节点权值。设节点k至邻近子节点j的路段权值与转向权值之和为w(k, j),判断dk+w(k, j)与dj的大小,更新s至j的最小权值dj和对应路径pj。在第2)步基础上,节点2的邻近节点包括3和6,由于节点3和6的累积权值为无穷大,故此时应当更新d3和d6。传统Dijkstra算法从第1)步至第3)步不断循环,直至U=
4) 判断路网权值是否更新。若至节点k的最小权值dk>T·Tnum,表明在到达节点k的路段将经历路网权值更新。在前三步基础上,设当前S={1, 2, 3, 6},U={4, 5, 7, 8, 9, 10, 11, 12},集合U中节点10具有最小累计权值d10,且d10>T·Tnum,表明按照路径1→2→6→10经历了权值更新,且发生在路段6→10。我们定义节点6为临界父节点,节点10为临界子节点,节点6与10共同构成临界节点对。
5) 计算临界节点对的实际累计权值。在第4)步基础上,设临界路段6→10在时段1和时段2的权值分别为ω6_10_1和ω6_10_2,车辆在路段6→10于时段1的行驶路程比例r为:
| $ r=\frac{T \cdot T_{\text {num }}-d_{6}}{\omega_{6\_ 10\_ 1}}。$ | (1) |
则路径1→2→6→10的实际累计权值为:
| $ {d_{10}} = {d_6} + r \cdot {\omega _{6\_10\_1}} + (1 - r) \cdot {\omega _{6\_10\_2}}。$ | (2) |
据此将集合S中的所有临界父节点构成集合Sc,将集合U中的所有临界子节点构成集合Uc,进而组成临界节点对集C。参照式(1)与式(2),可以计算临界节点对集的所有跨时段路段实际权值。之后更新时段编号Tnum,然后循环第2)步到第5)步,直到U=
仿真实验所用的硬件平台是Win10 @64 bit + Intel Core i5-4590 @3.3 GHz +RAM @ 8G,软件平台是MATLAB 2018a。
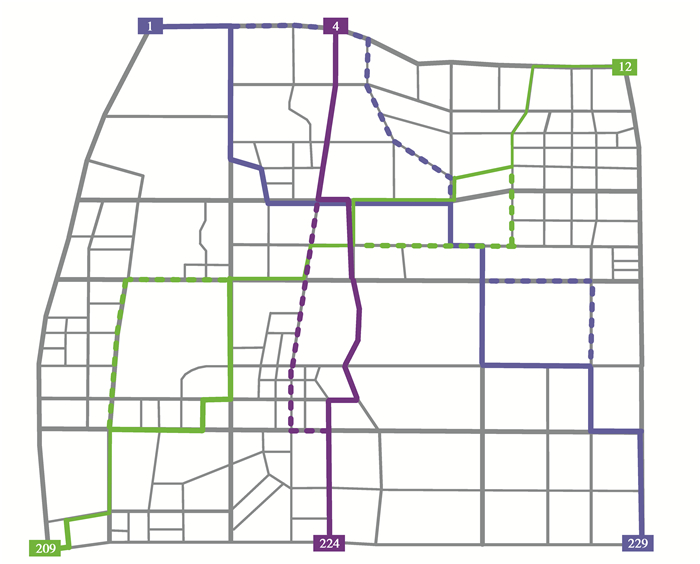
4.1 经典Dijkstra算法与蚁群算法的比较首先,为了体现经典Dijkstra算法在静态权值路网中的全局最优计算能力,基于预先建立的重庆大学城局部路网和时段1(8:17—8:30)的路段行程时间数据库,将智能启发式算法代表之一的蚁群算法作为对照[6],不失一般性地设定了3组起讫点进行仿真实验。路径规划结果及累积路段行程时间如图 7和表 3所示,图 7中的蓝色、紫色、绿色分别代表起讫点(1,229)(4,224)(12,209),实线与虚线分别代表Dijkstra算法和蚁群算法。
|
图 7 Dijkstra算法与蚁群算法的3组路径规划结果 Fig. 7 Three groups of path planning results of Dijkstra algorithm and ant colony algorithm |
| 表 3 Dijkstra算法与蚁群算法的3组路径规划的累计行程时间 Table 3 Cumulative travel time of three groups of path planning based on Dijkstra algorithm and ant colony algorithm |
由表 3可知,Dijkstra算法的累积行程时间均小于蚁群算法。以图 7的起讫点(12, 209)为例,蚁群算法所规划的路径与Dijkstra算法部分重合,表明具有一定的路径寻优能力,但中途有两次与Dijkstra算法路径分离,这是由于蚁群算法本身自带随机因子,在从源节点至目标节点的搜索过程中受随机因素影响较大,尽管在蚂蚁信息素的引导下可以加快收敛,但同时也增大了陷入局部最优的概率。
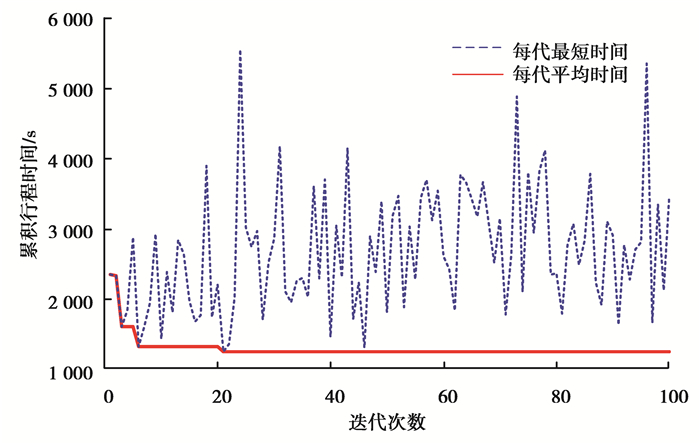
图 8为蚁群算法的行程时间随迭代次数的变化图,由图可知当迭代次数达到22次后,蚁群算法便已陷入了局部最优,极不利于对全局最优路径的求解,而作为广度优先搜索算法的Dijkstra算法则避免了局部最优的缺陷。另外,蚁群算法和Dijkstra算法的运行时间大约分别在1 s和1.5 s左右,Dijkstra算法以额外较小的运行时间成本获得了更满意的最优路径。综上所述,选择Dijkstra算法作为静态权值路网的全局最优路径规划方法是可行且有效的,在时变权值路网中则采用改进之后的GOPP算法。
|
图 8 蚁群算法行程时间随迭代次数的变化 Fig. 8 The change of the travel time of ant colony algorithm with the number of iterations |
为了验证所提出的GOPP算法在时变权值路网求解全局最优路径的优越性,需要合理设定起讫点及路径规划时刻,否则可能因累积行程时间小于本时段周期,或者部分路段的行程时间在相邻时段变化不大,而出现GOPP和RPP、SPP的路径规划结果相同的情况。基于此,笔者在细致分析所建路网及行程时间特点基础上,选取了起讫点(12, 209)作为仿真实验节点。设车辆位于源节点12的时刻为早上8:17(即时段1起始时刻),路网的权值将在8:30更新,利用Dijkstra算法分别采用SPP、RPP和GOPP 3种思想进行路径规划,3种路径规划结果见表 4和图 9。
| 表 4 3种路径规划结果累计权值比较 Table 4 Comparison of cumulative travel time of three path planning methods |
|
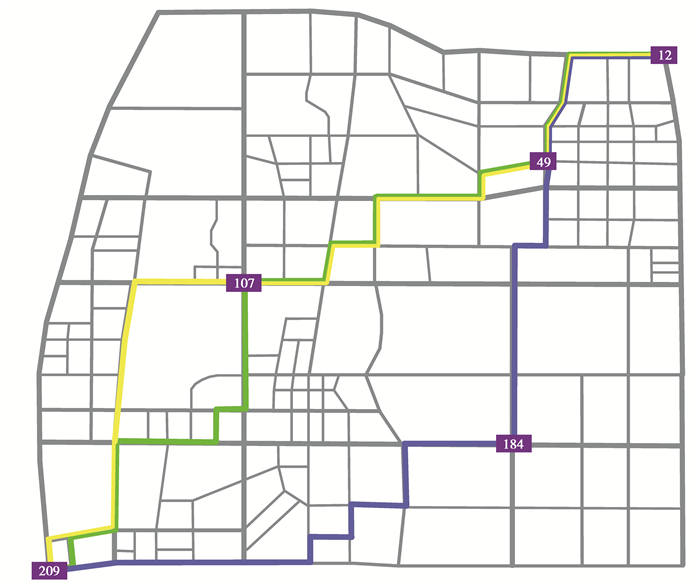
图 9 3种路径规划仿真结果比较 Fig. 9 Comparison of simulation results of three path planning methods |
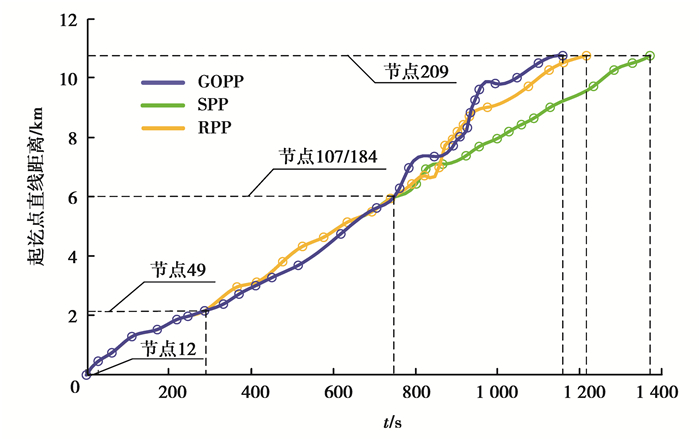
3种路径规划方式的起讫点直线距离变化曲线如图 10所示。
|
图 10 3种路径规划方式的起讫点直线距离变化曲线 Fig. 10 Straight line distance curves of starting and ending points of three path planning methods |
综合分析图 9和图 10,并结合重庆大学城实际交通情况,可以看出:
1) 3种算法制定的3条路径在节点12至节点49重合,然后GOPP方法出现分离;算法SPP和RPP沿路段49→48朝西延伸至节点107,之后再次出现分离;而算法GOPP沿49→72朝南延伸直至目标节点;
2) 节点107南向路段(大学城中路)分布有重庆大学、重庆一中等学校,北向路段分布有重庆师范大学、大学城地铁站,仿真结果表明算法SPP和RPP到达节点107的时刻为8:30:11,此时正是早高峰拥堵时段,路网权值已经更新。因此,RPP在节点107基于时段2的路网权值重新规划剩余路径,规划结果表明节点107沿西(大学城南路)行驶可以有效避免拥堵;
3) 节点184东西路段(大学城南路)是大学城路网的骨干路段,南北路段分布有华润微电园、固废流转中心等企业,在时段1交通较为拥堵,进入时段2逐渐缓解,因此图 10蓝色曲线在经过了节点184后便较快到达了终点。故GOPP规划路径累计权值为仅为1 158.7 s,相比SPP和RPP分别减少了212.7 s和57.6 s,证明了GOPP在缩短出行规划时间上的优越性。
5 结论首先分析了现有路径规划方法的不足,随后推导了跨时段路段的实际权值,界定了路径规划领域的局部最优叠加值与全局最优值的区别,并基于Dijkstra算法提出了一种全局最优路径规划方法。仿真结果表明,GOPP相比SPP和RPP具有最小的累积权值,有效地验证了GOPP在面向时变权值路网求解全局最优路径的优越性。有如下结论:
1) SPP和RPP两类常见路径规划方式在面对具有权值时变特性的交通路网时,无法求解全局最优路径;
2) 经典的Dijkstra算法尽管算法冗余度较高,却以广度优先比智能启发式算法更能求得全局最优解;
3) 基于Dijkstra算法的GOPP路径规划方法能够实现权值时变路网的时间最短全局最优路径的求解,可以有效缩短驾驶员的交通出行时间,对今后智能网联汽车和智能交通系统的发展具有一定的理论指导意义。
| [1] |
盛强, 郑鹏飞, 孙军艳. 动态路网下带时间窗车辆路径规划问题研究[J]. 物流技术, 2018, 37(10): 36-39, 47. Sheng Q, Zheng P F, Sun J Y. Research on vehicle routing problem with time windows under dynamic road network[J]. Logistics Technology, 2018, 37(10): 36-39, 47. (in Chinese) DOI:10.3969/j.issn.1005-152X.2018.10.008 |
| [2] |
Liu Y K, Zhang Q Y, Yu L J. Picking robot path planning based on improved ant colony algorithm[C]//201934rd Youth Academic Annual Conference of Chinese Association of Automation (YAC). June 6-8, 2019, Jinzhou, China. IEEE, 2019: 473-478.
|
| [3] |
顾青, 豆风铅, 马飞. 基于改进A*算法的电动车能耗最优路径规划[J]. 农业机械学报, 2015, 46(12): 316-322. Gu Q, Dou F Q, Ma F. Energy optimal path planning of electric vehicle based on improved A* algorithm[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(12): 316-322. (in Chinese) DOI:10.6041/j.issn.1000-1298.2015.12.043 |
| [4] |
Fu B, Chen L, Zhou Y T, et al. An improved A* algorithm for the industrial robot path planning with high success rate and short length[J]. Robotics and Autonomous Systems, 2018, 106: 26-37. DOI:10.1016/j.robot.2018.04.007 |
| [5] |
王维, 裴东, 冯璋. 改进A*算法的移动机器人最短路径规划[J]. 计算机应用, 2018, 38(5): 1523-1526. Wang W, Pei D, Feng Z. The shortest path planning for mobile robots using improved A* algorithm[J]. Journal of Computer Applications, 2018, 38(5): 1523-1526. (in Chinese) |
| [6] |
王志中. 基于改进蚁群算法的移动机器人路径规划研究[J]. 机械设计与制造, 2018(1): 242-244. Wang Z Z. Path planning for molile robot based on improved ant colony algorithm[J]. Machinery Design & Manufacture, 2018(1): 242-244. (in Chinese) DOI:10.3969/j.issn.1001-3997.2018.01.069 |
| [7] |
Song Q, Zhao Q L, Wang S X, et al. Dynamic path planning for unmanned vehicles based on fuzzy logic and improved ant colony optimization[J]. IEEE Access, 2020, 8: 62107-62115. DOI:10.1109/ACCESS.2020.2984695 |
| [8] |
He F M, Xu Y N, Wang X R, et al. An improved ant colony algorithm for solving time-dependent road network path planning problem[C]//2019 6th International Conference on Information Science and Control Engineering (ICISCE). December 20-22, 2019, Shanghai, China. IEEE, 2019: 126-130.
|
| [9] |
Chai H J, Zhang H M, Ghosal D, et al. Dynamic traffic routing in a network with adaptive signal control[J]. Transportation Research Part C: Emerging Technologies, 2017, 85: 64-85. DOI:10.1016/j.trc.2017.08.017 |
| [10] |
El-Wakeel A S, Noureldin A, Hassanein H S, et al. iDriveSense: dynamic route planning involving roads quality information[C]//2018 IEEE Global Communications Conference (GLOBECOM). December 9-13, 2018, Abu Dhabi, United Arab Emirates. IEEE, 2018: 1-6.
|
| [11] |
李军. 城市智能交通中的动态路径规划研究[D]. 杭州: 杭州电子科技大学, 2016. Li J. Dynamic path planning research in intelligent transportation of cities[D]. Hangzhou: Hangzhou Dianzi University, 2016. (in Chinese) |
| [12] |
Zhao C C, Dong M X, Ota K, et al. Edge-MapReduce-based intelligent information-centric IoV: cognitive route planning[J]. IEEE Access, 2019, 7: 50549-50560. DOI:10.1109/ACCESS.2019.2911343 |
| [13] |
Tilk C, Rothenbächer A K, Gschwind T, et al. Asymmetry matters: Dynamic half-way points in bidirectional labeling for solving shortest path problems with resource constraints faster[J]. European Journal of Operational Research, 2017, 261(2): 530-539. DOI:10.1016/j.ejor.2017.03.017 |
| [14] |
随裕猛, 陈贤富, 刘斌. D-star Lite算法及其动态路径规划实验研究[J]. 微型机与应用, 2015, 34(7): 16-19. Sui Y M, Chen X F, Liu B. D-star Lite algorithm and its experimental study on dynamic path planning[J]. Microcomputer & Its Applications, 2015, 34(7): 16-19. (in Chinese) DOI:10.3969/j.issn.1674-7720.2015.07.006 |
| [15] |
刘琳, 李春媛, 陈彦虎, 等. 基于路由节点的最优油耗路径规划模型[J]. 重庆大学学报, 2018, 41(7): 73-81. Liu L, Li C Y, Chen Y H, et al. Research on path planning model of optimal fuel consumption based on routing nodes[J]. Journal of Chongqing University, 2018, 41(7): 73-81. (in Chinese) |
| [16] |
汪振. 快速路交通流相似性研究[D]. 北京: 北京交通大学, 2008. Wang Z. Research on the similarity of freeway traffic flow[D]. Beijing: Beijing Jiaotong University, 2008. (in Chinese) |
| [17] |
温惠英, 卢德佑, 汤左淦. 考虑行程时间波动性的城市道路阻抗函数模型[J]. 公路工程, 2019, 44(3): 27-32. Wen H Y, Lu D Y, Tang Z G. Urban road impedance function model considering the volatility of travel time[J]. Highway Engineering, 2019, 44(3): 27-32. (in Chinese) |
| [18] |
王东炜, 李辉, 李岩, 等. 城市道路网络路段状态相关性与道路间距分析[J]. 交通运输工程学报, 2017, 17(1): 101-108. Wang D W, Li H, Li Y, et al. Analysis of road section state correlation and road distance in urban road network[J]. Journal of Traffic and Transportation Engineering, 2017, 17(1): 101-108. (in Chinese) DOI:10.3969/j.issn.1671-1637.2017.01.012 |
| [19] |
Li Y, Gao Y. A high-efficient data model of road network in vehicle navigation system[J]. Applied Mechanics and Materials, 2011, 135/136: 37-42. DOI:10.4028/www.scientific.net/AMM.135-136.37 |
| [20] |
Dial R, Glover F, Karney D, et al. A computational analysis of alternative algorithms and labeling techniques for finding shortest path trees[J]. Networks, 1979, 9(3): 215-248. DOI:10.1002/net.3230090304 |
 2021, Vol. 44
2021, Vol. 44


