随着消费水平的升级,各大车企加快了推出新车的节奏,单一车型的开发流程已经不能满足快速出车的要求,平台架构概念开始广泛出现在车企设计生产的过程中。目前,借助传统汽车的设计和制造经验,各大车企已陆续推出了自己的平台架构。
杨宏等[1]对某纯电动专属车身平台架构的开发进行了介绍,采用拓扑优化定义了全新的载荷传递路径,并对车身进行了碰撞性能的分析和优化,但使用的是单位载荷模拟碰撞工况,并非实际的碰撞载荷;赵永宏等[2]利用拓扑优化技术,在刚度和碰撞综合工况下对某平台车身进行了传力路径优化,并探讨了逐级施加约束控制后车身结构内的最优载荷传递路径,但在两种工况下,使用的是同一个拓扑优化模型,造成优化结果的工程可实施性不好;麻桂艳等[3]利用参数化建模软件SFE CONCEPT,提出将车身进行模块化分类,在项目开发早期,可快速实现车身结构的性能验证及优化,快速实现平台不同车型的参数化车身模型搭建,进行平台车身的结构设计和优化,但其研究的是单一动力类型下的平台车身结构优化,并未考虑多动力的平台架构车身结构的优化策略;王磊等[4]借助隐式参数化建模技术,建立了某平台三厢车和两厢车的SFE参数化车身模型,考虑车身刚度和模态性能,通过经验结构优化、形状参数化优化和料厚优化3种手段,对平台上的两款车型进行了车身结构优化,但在车身结构进行优化的过程中,没有考虑碰撞工况,其优化方案的实际应用价值不高。
当前很多工程人员和研究学者,做了很多关于平台架构车身结构优化的研究,提出了一些具体的方法和手段,但很少有系统研究在概念设计阶段如何针对平台架构车身结构进行优化设计的文章。为此提出了一种新的车身结构优化设计方法,考虑平台架构的不同车型和动力,使得平台架构上的车身结构达到一个较为理想的性能带宽水平。
1 全局拓扑优化该平台架构轴距范围2 780~2 860 mm,涵盖纯电和增程两种动力配置,车型包括高低两种姿态。对于平台架构设计,带宽越大,问题越复杂,不能按传统单一车型的开发思维逐一设计,总体优化策略为选取代表车型进行重点优化的同时兼顾验证其他车型。在综合考虑了各方面因素后,选取了平台架构上轴距最大的7座SUV作为主优对象,考虑车身刚度、模态以及碰撞工况作为优化工况,对平台架构下的车体进行结构优化。同时通过将优化方案代入不同车型不同动力下进行验证及优化,保证整个平台架构下的车身结构处于目标性能带宽下。
在平台架构概念设计阶段的早期,通过全局拓扑优化,尝试寻找不同的车身传力路径。目前,行业内关于拓扑优化已经有了很多的研究。在介绍拓扑优化的文献[5-7]中,对于碰撞工况的加载,采用的是简化均布载荷,这种加载方法过于简单,会导致拓扑优化分析出来的结果工程可实施性不高。相较均布载荷法,非线性等效静态载荷法具有以下优点:
1) 优化结果离散性更好,更容易解读路径;
2) 优化结果更接近于实际情况,工程应用程度较高;
3) 材料分布更合理,解读出来的结构轻量化效果更好。
在全局拓扑优化阶段,综合考虑了弯曲刚度、扭转刚度、正碰、25%小偏置碰和侧碰工况,优化过程如下所述。
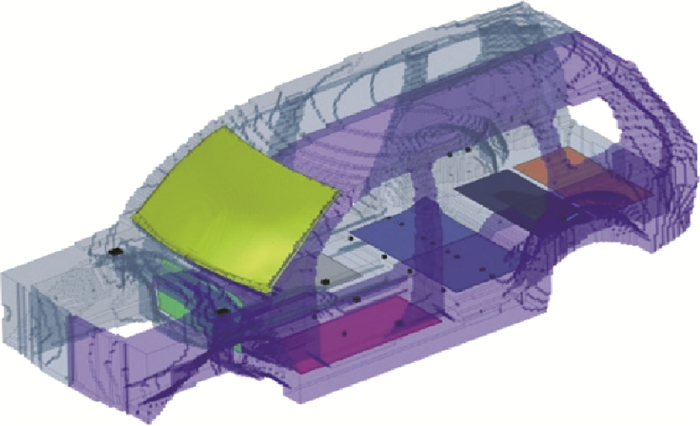
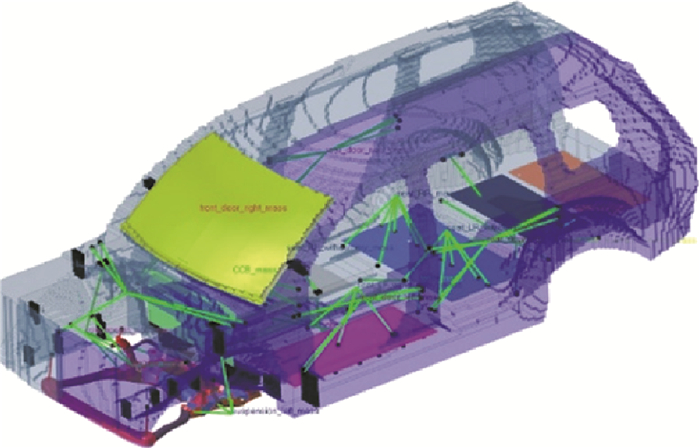
1.1 模型设置刚度工况采用的是白车身模型,同时考虑前围板、风挡玻璃、地板等对拓扑优化结果的影响,拓扑优化模型如图 1所示。碰撞工况采用的是整车模型,在白车身模型基础之上,增加前副车架、车门、前罩、IP、座椅、动力总成、前后悬架等系统,这些子系统,在概念设计阶段,如果没有参考模型,可以用集中质量单元代替,通过RBE2或RBE3单元与设计空间的实体单元连接起来,拓扑优化模型如图 2所示。
|
图 1 白车身拓扑优化模型 Fig. 1 Topology optimization model of BIW |
|
图 2 整车拓扑优化模型 Fig. 2 Topology optimization model of whole vehicle |
对弯曲刚度工况,在前排及后排4个乘员位置各施加z向500 N集中力,共2 000 N。约束前悬减震器支座y向和z向平动自由度以及后悬减震器全部方向平动自由度。
对扭转刚度工况,在左右前悬减震器支座z向上建立MPC约束,约束后悬减震器支座全部方向的平动自由度。
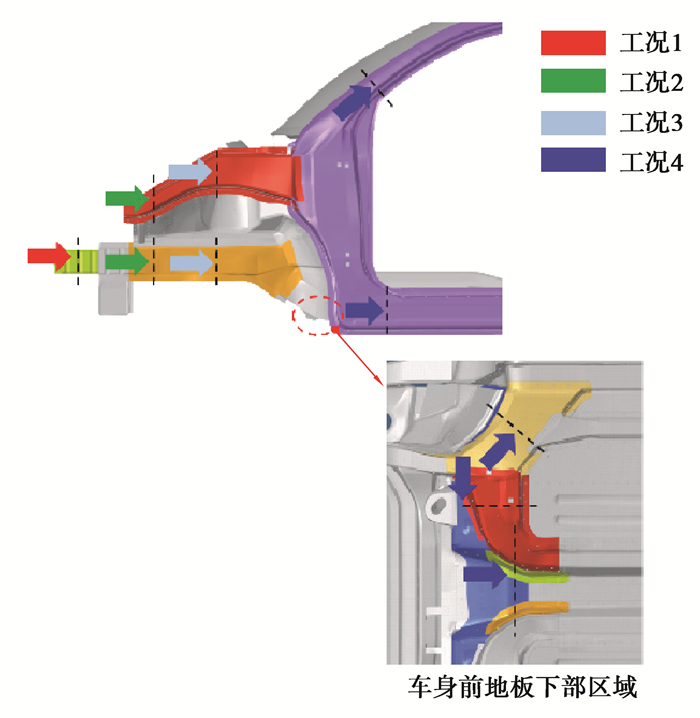
对碰撞工况,整车承受的是高速非线性动态载荷,拓扑优化需要将高速非线性动态载荷等效为线性静态载荷。主要等效方法是根据车身碰撞形态,将关键时刻车身结构压溃处的最大载荷作为等效静态载荷。对于正碰和25%小偏置碰工况,线性化等效为4个静力工况,对应工况的加载位置如图 3所示,分别是:
|
图 3 FRB及SOB工况线性化载荷 Fig. 3 FRB and SOB condition linearized load |
1) 工况1:加载在吸能盒中部;
2) 工况2:加载在前纵梁和SHOTGUN的前端;
3) 工况3:加载在前纵梁和SHOTGUN中部;
4) 工况4:加载在门槛梁、A柱、中央通道、前纵梁根部。
其中,对于正碰工况,整车左右对称加载,对于25%小偏置碰工况,只在整车左侧加载。
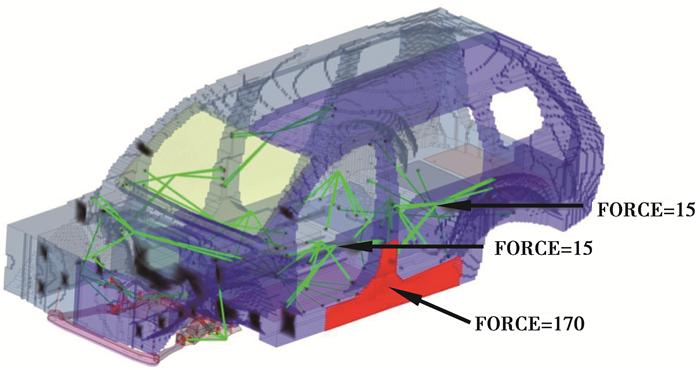
对于侧碰工况,提取壁障与前后门、门槛梁以及B柱的接触力,分别施加在前后门的质心位置处,以及壁障与门槛和B柱的接触面积内抓取的RBE2单元上,如图 4所示。
|
图 4 MDB工况线性化载荷 Fig. 4 MDB condition linearized load |
多模型优化(multi-model optimization,MMO),可以在一次优化计算中同时考虑多个计算模型,这些模型共享某些共同的设计变量,共享的设计变量会得到相同的优化结果。其优势在于:
1) 模型可以是完全不同,或者部分相同;
2) 载荷可以不同,参数可以不同,目标函数、约束及响应可以单独定义,也可以组合定义;
3) 多模型优化主要考虑性能和扩展性,非常适合于平台架构开发上使用。
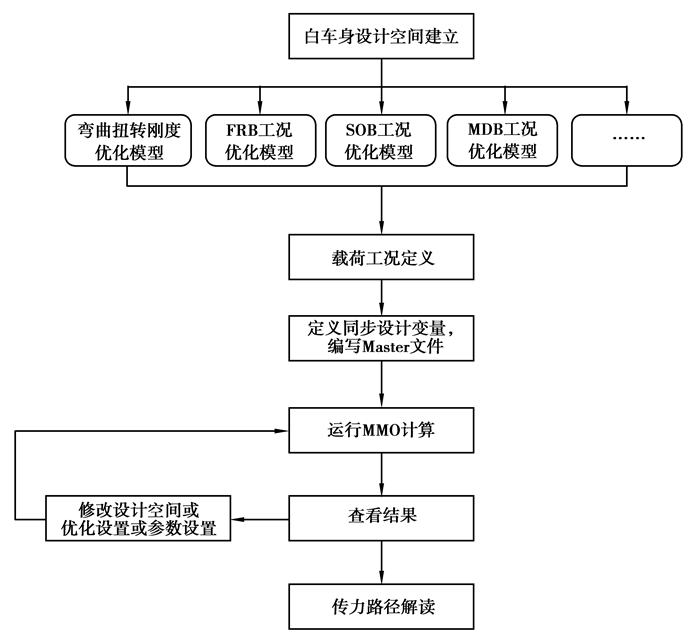
MMO优化流程如图 5所示。
|
图 5 MMO优化流程 Fig. 5 MMO optimization process |
本次平台架构的拓扑优化的数学模型为:
| $ \left. \begin{array}{l} {\rm{Object}}:f(x) = \min f(M)\\ {\rm{Design}}\;\;{\rm{Variables}}:{\rho _i}\\ \begin{array}{*{20}{c}} {{\rm{ Constrains: }}}&{f\left( {{C_{{\rm{bend }}}}} \right) \le {f_{\rm{o}}}\left( {{C_{{\rm{bend }}}}} \right)}\\ {}&{f\left( {{C_{{\rm{torsion }}}}} \right) \le {f_{\rm{o}}}\left( {{C_{{\rm{torsion }}}}} \right)}\\ {}&{f\left( {{C_{{\rm{FRB}}}}} \right) \le {f_{\rm{o}}}\left( {{C_{{\rm{FRB}}}}} \right)}\\ {}&{f\left( {{C_{{\rm{SOB}}}}} \right) \le {f_{\rm{o}}}\left( {{C_{{\rm{SOB}}}}} \right)}\\ {}&{f\left( {{C_{{\rm{MDB}}}}} \right) \le {f_{\rm{o}}}\left( {{C_{{\rm{MDB}}}}} \right)} \end{array} \end{array} \right\}。$ | (1) |
式中:f(M)为设计空间的质量,ρi为设计空间材料的相对密度,f(Cbend)、f(Ctorsion)、f(CFRB)、f(CSOB)、f(CMDB)分别为优化模型的弯曲刚度工况、扭转刚度工况、FRB工况、SOB工况和MDB工况对应下的全局柔度,fo(Cbend)、fo(Ctorsion)、fo(CFRB)、fo(CSOB)、fo(CMDB)分别为弯曲刚度工况、扭转刚度工况、FRB工况、SOB工况和MDB工况对应下的全局柔度目标值。其中,碰撞工况全局柔度目标值是根据柔度与质量的Pareto曲线来确定的。
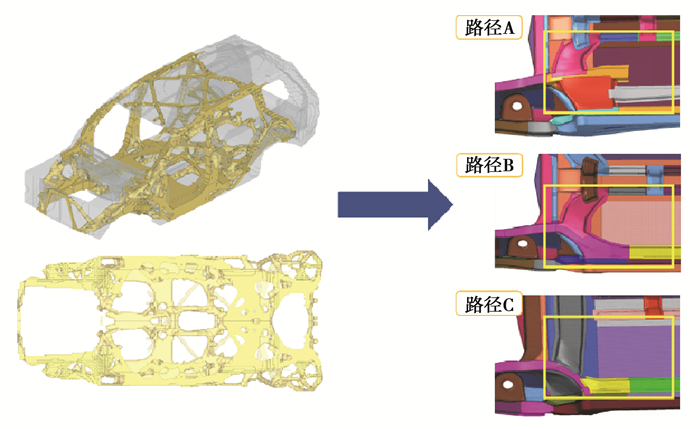
通过MMO多模型拓扑优化,联合设计部门,共同对拓扑结果进行解读,得到3种不同的传力路径形式,如图 6所示。
|
图 6 拓扑优化方案解读 Fig. 6 Interpretation of topology optimization scheme |
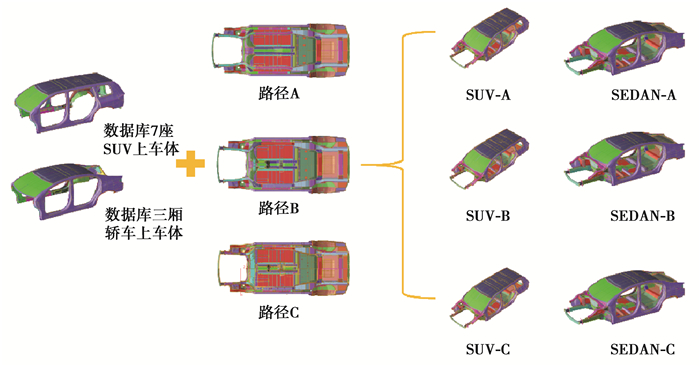
利用隐式参数化建模软件SFE CONCEPT,同时考虑到上车身通常不在平台架构的范围内,结合拓扑优化解读出来的3种不同传力路径,选取了高低两款成熟的上车身与平台架构下车身进行模型耦合,搭建高低车分析模型共6个,如图 7所示。
|
图 7 不同传力路径的平台架构高低车分析模型 Fig. 7 High and low vehicle analysis model of platform architecture with different transmission paths |
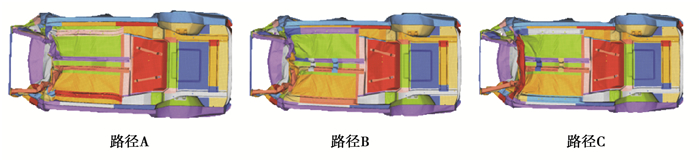
平台架构包含EVR和EV两种动力类型,相较于EV动力,因增加了增程器以及排气系统,EVR动力类型的前舱空间布置非常紧凑,占用了大部分的碰撞吸能空间,碰撞工况更为恶劣一些,故主优车型的动力选择EVR。对3种不同传力路径的车身结构进行了FRB工况分析,各路径结构下的初始车身变形模式如图 8所示。
|
图 8 不同传力路径下的7座SUV初始FRB工况车身变形模式 Fig. 8 Initial body deformation of 7-seat SUV under FRB condition with different force transmission paths |
从初始结果可以看出,3种不同传力路径下都没有产生正常的变形模式。为了确定平台架构的传力路径形式,需对3种不同传力路径进行优化,其优化策略主要为:对于3种传力路径的共有结构,采用同一种优化方案;对于不同传力路径的特有结构,采用对应路径下的特有优化方案。
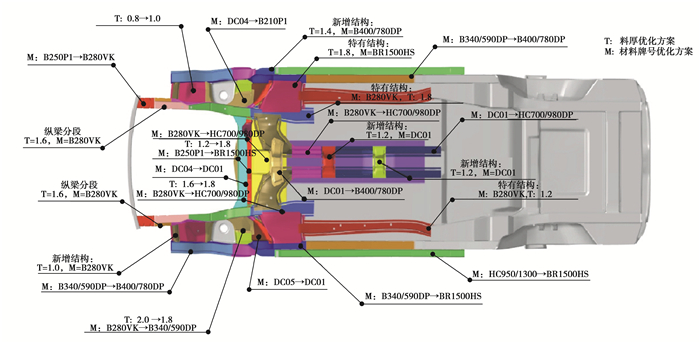
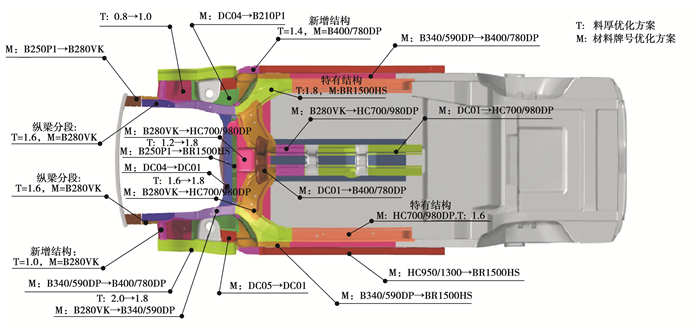
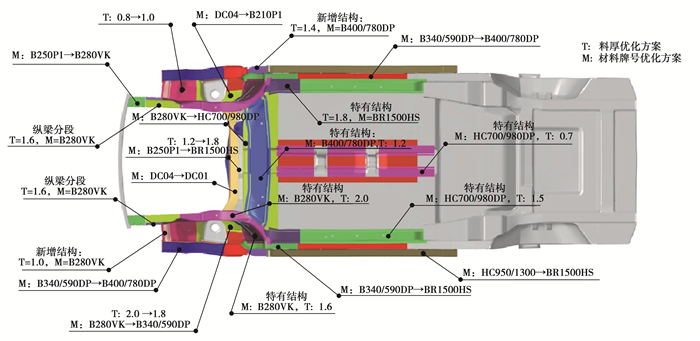
通过对初始分析结果的解读,从料厚、材料牌号、结构3个方向对3种不同传力路径的共有结构和特有结构进行了优化,3种不同传力路径的优化方案如图 9~11所示。
|
图 9 路径A优化方案 Fig. 9 Path A optimization scheme |
|
图 10 路径B优化方案 Fig. 10 Path B optimization scheme |
|
图 11 路径C优化方案 Fig. 11 Path C optimization scheme |
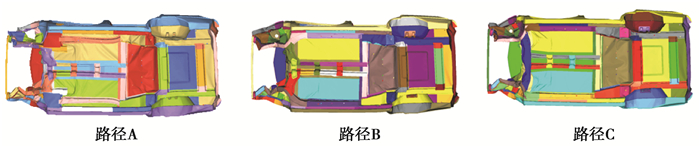
优化后的3种不同传力路径下的FRB工况车身变形模式如图 12所示。从图中可以看出:路径B的前纵梁变形模式最好,吸能盒和纵梁前段溃缩变形,纵梁中段发生Z形的折弯变形,纵梁后段有些许的溃缩。
|
图 12 不同传力路径下的7座SUV优化后FRB工况车身变形模式 Fig. 12 Optimized FRB deformation mode of 7-seat SUV under different transmission paths |
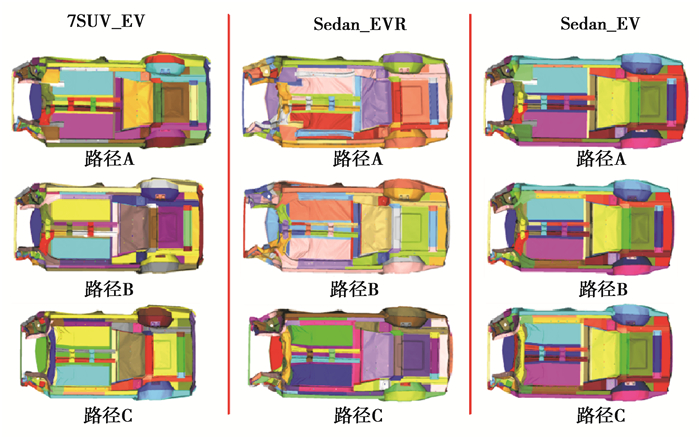
对于平台架构传力路径的确定,需拉通考虑平台架构不同车型和不同动力。将2.2节中的优化方案代入到三厢轿车的EVR和EV动力,以及7座SUV的EV动力下进行验证,结果如图 13所示。从图中可以看出:优化方案在平台架构不同车型不同动力下进行验证,得到的结论与主优车型是一样的。
|
图 13 优化后的不同传力路径下的不同车型不同动力的FRB工况车身变形模式 Fig. 13 Optimized FRB body deformation modes of different power and vehicle types under different transmission paths |
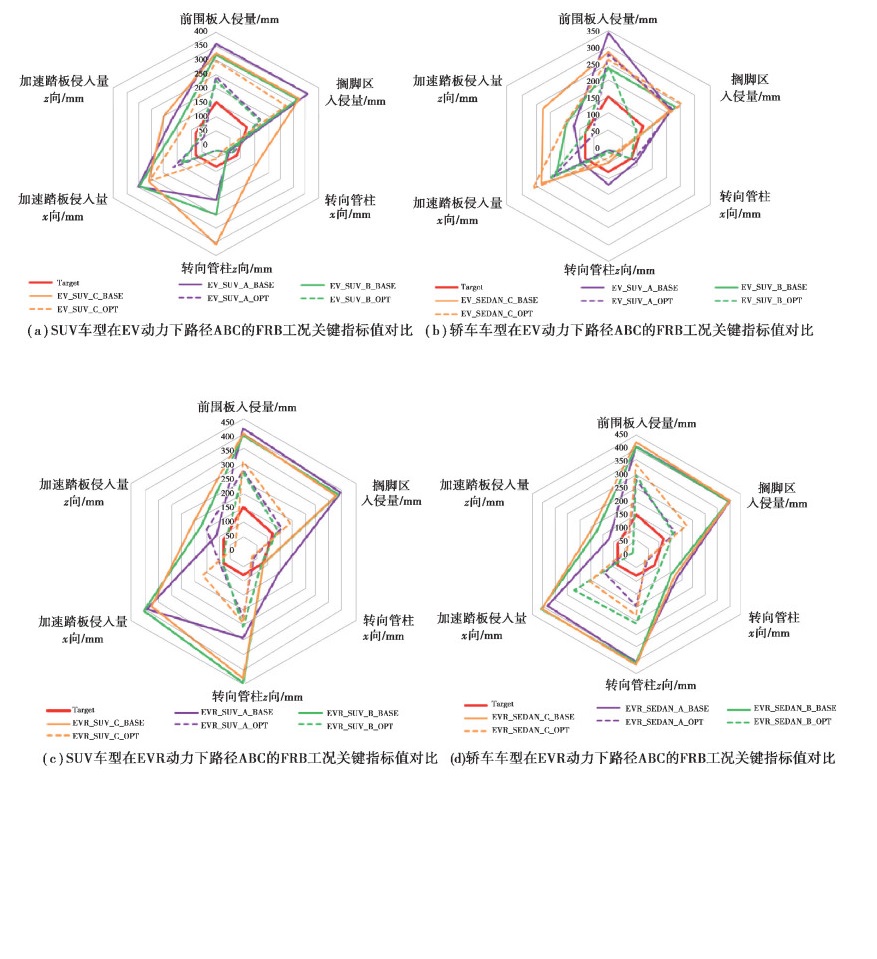
高低车不同动力下FRB工况的重要指标对比情况如图 14所示。从图中可以看出:优化后的3种不同传力路径的FRB工况性能指标都有较大提升,且A、B路径的性能情况要优于路径C。考虑到平台架构要兼顾EV和EVR两种动力类型,且路径B下的车身质量要减少9 kg,最终平台架构的车身传力路径确定为路径B的形式。
|
图 14 不同车型不同动力下的3种传力路径FRB工况关键指标优化前后对比 Fig. 14 Comparison before and after optimization of key indexes of FRB condition of three force transmission paths under different vehicles and power types |
在确定了平台的传力路径形式后,接下来需要对具体传力路径下的车身截面以及车身料厚进行优化,在保证性能最优的前提下尽量实现轻量化设计。
3.1 截面优化利用参数化优化的手段,联合SFE CONCEPT软件,提取梁截面大小参数作为变量,考虑刚度工况进行参数化优化,得到各个参数的最佳匹配效果。
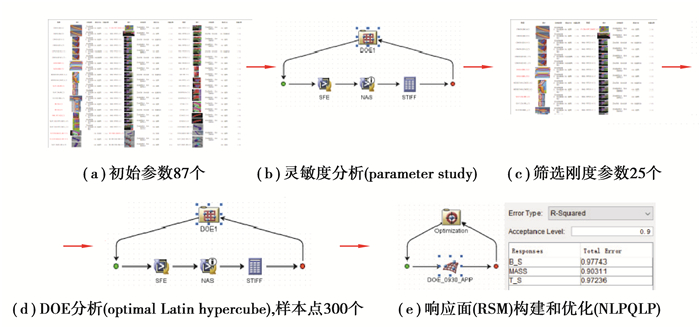
在SFE CONCEPT软件中录制87个截面几何变量,每个位置的局部形状改变均可以由一个参数来控制,通过ISIGHT软件调用变量表来驱动SFE对模型的几何形状进行更改,参数化优化的流程如图 15所示:首先考虑弯曲扭转刚度,对这些变量进行灵敏度分析(parameter study)筛选出敏感变量31个;以筛选出的变量为设计变量,选用合适的算法来生成样本点进行DOE分析,构建响应面;以白车身的质量最轻、弯曲和扭转刚度性能最佳为目标,利用合适的算法进行优化。
|
图 15 参数化优化流程图 Fig. 15 Parametric optimization flow chart |
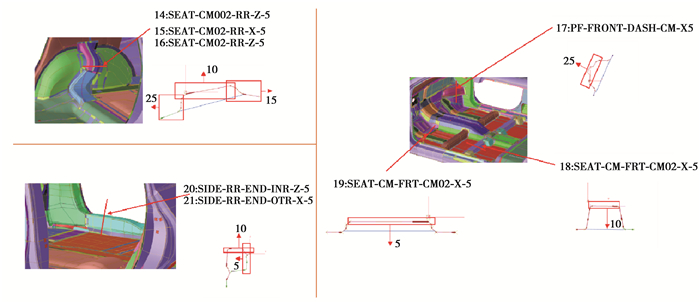
优化后的部分参数变化情况如图 16所示,性能优化情况如表 1所示,从表中可以看出:通过优化,虽然车身质量略有增加,但车身的弯曲和扭转刚度性能大幅增加,为后续通过料厚优化进行减质量奠定了基础。
|
图 16 部分设计变量优化结果 Fig. 16 Partial optimization results of design variables |
| 表 1 参数化优化前后结果对比 Table 1 Comparison of results before and after parametric optimization |
对于车身钣金件的料厚优化,目前主要有2种思路:第1种是文献[8-9]中所述的基于Optistruct软件,考虑刚度模态性能进行料厚优化;第2种是文献[10-12]中所述的以料厚为变量,通过DOE建立其近似模型,基于近似模型进行料厚优化。上述两种不同的车身钣金件料厚优化方法,都有其各自的不足:对于基于Optistruct的料厚灵敏度优化,其不能考虑非线性工况,只能基于刚度模态等线性工况进行优化,且只能进行单优化目标设置,导致其优化考虑工况较少,优化结果工程可实施率不高;而对于车身钣金件料厚的近似模型优化,虽然其可以考虑包括线性工况和非线性工况在内的多种工况,但因其需要进行大量的样本点DOE分析,需大量计算资源与时间,且如果考虑了碰撞这种非线性极强的工况,除了计算资源与时间耗费较大以外,不容易搭出精度可靠的近似模型,优化效果不可控制。
针对正碰工况,采用等效静态载荷法(ESL),以车身钣金件料厚为优化变量,考虑车身刚度、模态和正碰性能,进行了料厚减质量优化,相较于上述两种优化思路,ESL法具有如下优势[13-15]:
1) ESL法可以利用成熟的线性优化方法求解,一般运行5次非线性分析和25轮线性优化便可达到收敛,优化效率和算法可靠性大大优于灵敏度优化和近似模型优化;
2) ESL法可以选择不同的性能指标,如:质量、位移和应变能等作为目标函数,而不仅限于内能密度均匀化一个目标,因而更符合工程实际的要求。
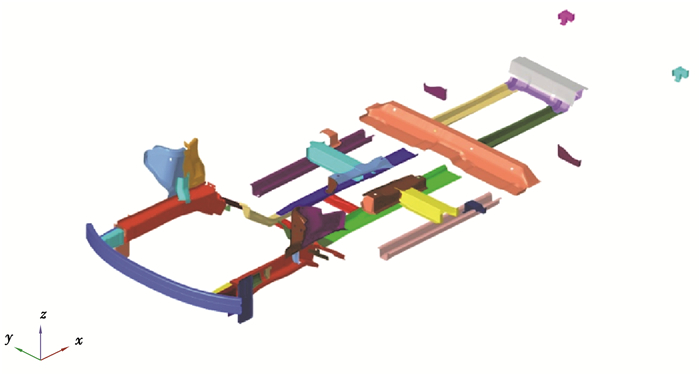
基于ESL法,利用GENESIS软件对平台架构的下车身钣金件进行料厚优化,设计变量如图 17所示,对称件设为一个变量,共29个变量。
|
图 17 料厚优化设计变量 Fig. 17 Material thickness optimization design variables |
本次优化的数学模型为:
| $ \left. \begin{array}{l} {\rm{Object: }}f(x) = \left\{ {\min f(M), \min {f_i}(I)} \right\}\\ {\rm{ DesignVariables: }}{t_i}{\rm{ }}\\ {\rm{Constrains: }}{f_i}(I) \le {f_{\rm{o}}}(I)\\ f\left( {{S_{{\rm{bend }}}}} \right) \le {f_{\rm{o}}}\left( {{S_{{\rm{bend }}}}} \right)\\ f\left( {{S_{{\rm{torsion }}}}} \right) \le {f_{\rm{o}}}\left( {{S_{{\rm{torsion }}}}} \right)\\ f\left( {{M_{{\rm{bend }}}}} \right) \le {f_{\rm{o}}}\left( {{M_{{\rm{bend }}}}} \right)\\ f\left( {{M_{{\rm{torsion }}}}} \right) \le {f_{\rm{o}}}\left( {{M_{{\rm{torsion }}}}} \right) \end{array} \right\}, $ | (2) |
式中:f(M),fi(I)为车身质量和正碰过程中的前围板6个关键点位置侵入量(i=1, 2, …, 6),ti为平台架构车身下车体钣金件料厚变量,fo(I)为车身优化前前围板正碰过程中的6个关键点位置初始侵入量,f(Sbend)、f(Storsion)、f(Mbend)、f(Mtorsion)为优化模型的车身弯曲刚度、扭转刚度、弯曲模态、扭转模态,fo(Sbend)、fo(Storsion)、fo(Mbend)、fo(Mtorsion)为初始模型的车身弯曲刚度、扭转刚度、弯曲模态、扭转模态。
通过优化,白车身质量减少15.7 kg,部分料厚变化情况如表 2所示。
| 表 2 料厚变化情况 Table 2 Change of material thickness |
对减质量后的模型进行相关性能验证,其刚度模态变化情况如表 3所示,从表中可以看出:料厚优化后的车身刚度和模态值变化不大,减质量效果十分明显。
| 表 3 料厚优化前后性能对比 Table 3 Performance comparison before and after material thickness optimization |
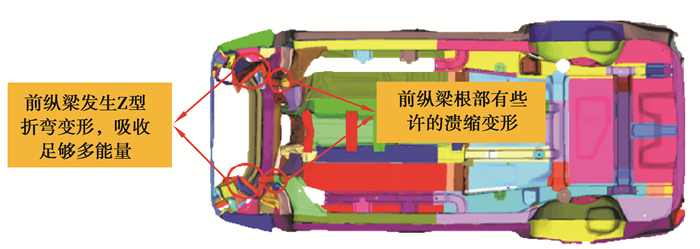
料厚优化后的车身FRB工况变形模式如图 18所示,从图中可以看出:优化后的前纵梁变形模式良好,吸能盒和纵梁前段溃缩变形,纵梁中段发生Z形的折弯变形,纵梁后段有些许的溃缩。
|
图 18 减质量后的FRB工况车身变形 Fig. 18 Body deformation in FRB condition after weight reduction |
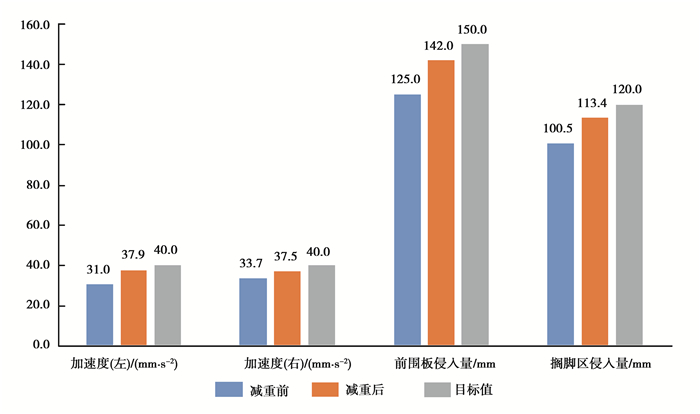
料厚优化前后的FRB工况关键性能指标值及目标值对比如图 19所示,从图中可以看出:优化后的FRB工况指标值相较优化前略有降低,但仍满足目标值要求。
|
图 19 减质量前后FRB工况关键指标对比 Fig. 19 Comparison of key indicators of FRB before and after weight reduction |
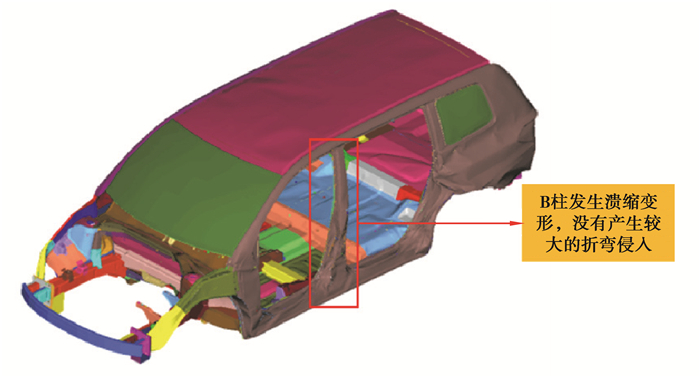
料厚优化后的车身MDB工况变形模式如图 20所示,从图中可以看出:优化后的车身B柱没有产生溃缩变形,没有产生较大的折弯侵入。
|
图 20 减质量后的MDB工况车身变形 Fig. 20 Body deformation of MDB condition after weight reduction |
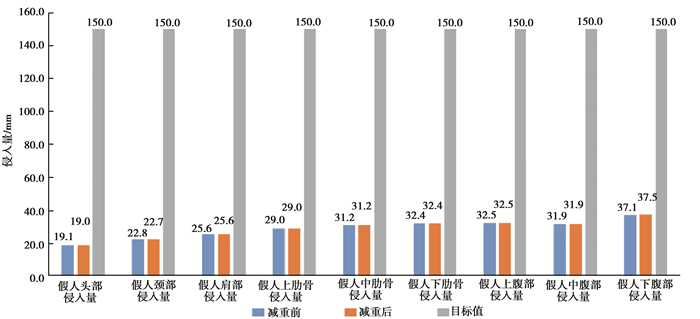
料厚优化前后的MDB工况关键性能指标值及目标值对比如图 21所示,从图中可以看出:优化后的MDB工况指标值相较优化前基本不变,满足目标值要求。
|
图 21 减质量前后MDB工况关键指标对比 Fig. 21 Comparison of key indicators of MDB condition before and after weight reduction |
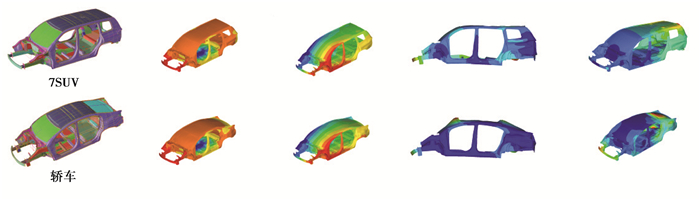
利用SFE CONCEPT快速建立平台架构不同车型的参数化车身模型,将截面优化方案和料厚优化方案代入到平台架构的不同车型不同动力下进行验证,刚度模态性能如图 22和表 4所示。
|
图 22 平台架构高低车车身刚度模态性能验证 Fig. 22 Modal and stiffness performance verification of high and low vehicle body of platform architecture |
| 表 4 高低车刚度和模态值 Table 4 Stiffness and modal value of high and low vehicle |
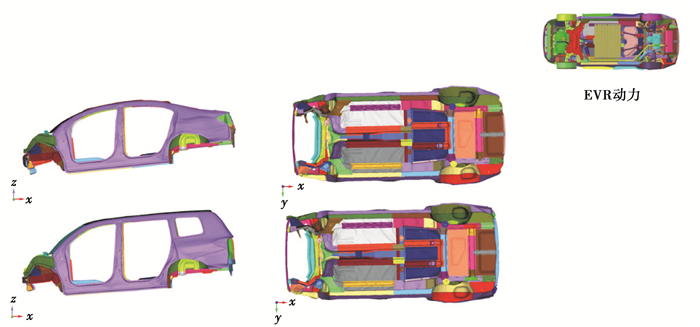
将优化方案代入到EVR动力下的高低车进行FRB工况分析,结果如图 23所示。从图中可以看出:在EVR动力下,架构高低车车身在FRB工况下,都具有较好的车身变形模式。
|
图 23 高低车EVR动力FRB工况验证分析结果 Fig. 23 FRB condition verification results under high and low vehicle with EVR power |
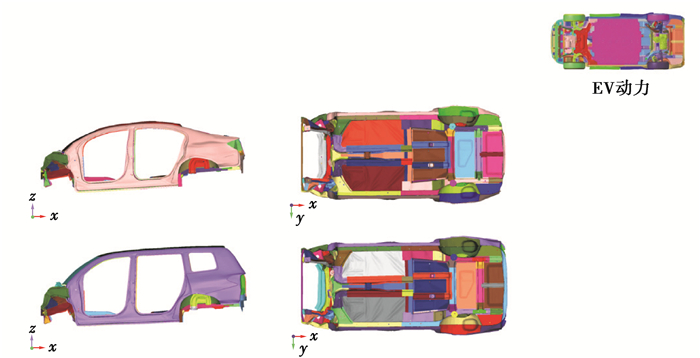
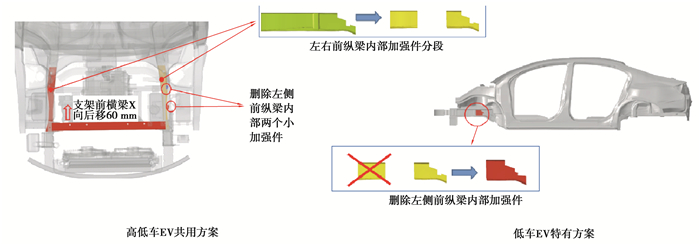
将优化方案代入到EV动力下的高低车进行FRB工况分析,结果如图 24所示。从图中可以看出:在EV动力下,高低车车身变形模式不理想,且大多数性能指标不满足目标值,针对这个问题,对于平台架构的EV动力,提出了如图 25所示的高低车车身结构优化方案。
|
图 24 高低车EV动力FRB工况验证分析结果 Fig. 24 FRB condition verification results under high and low vehicle with EV power |
|
图 25 EV动力下的高低车结构优化方案 Fig. 25 High and low vehicle structure optimization scheme with EV power |
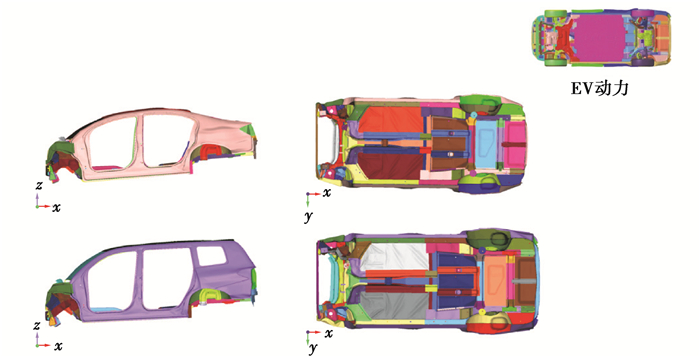
优化后的EV动力下的高低车FRB工况的分析结果如图 26所示。从图中可以看出:优化后的前纵梁变形模式良好,吸能盒和纵梁前段溃缩变形,纵梁中段发生Z形的折弯变形,纵梁后段有些许的溃缩。
|
图 26 高低车EV动力FRB工况优化结果 Fig. 26 Optimization results of high and low vehicle under FRB condition with EV power |
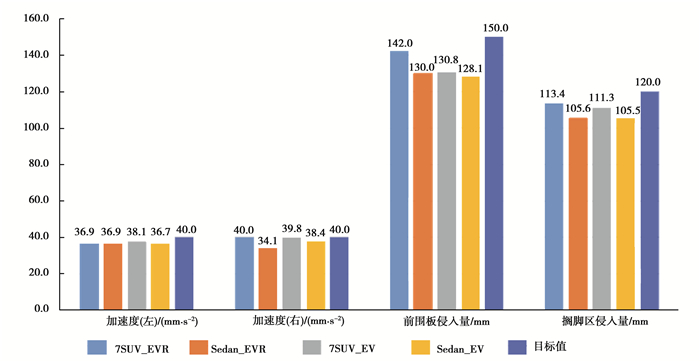
经过优化,平台架构不同车型、不同动力的FRB工况关键指标项与目标值的对比如图 27所示,从图中可以看出:优化后的FRB工况指标值均满足目标值要求。
|
图 27 平台架构不同车型、不同动力FRB工况关键指标项验证值 Fig. 27 Validation values of key indicators of FRB condition under different vehicle and power types |
1) 利用MMO法进行综合工况拓扑优化,采用碰撞等效载荷法进行加载,解读出来的车身传力路径结果工程可实施性更高。后续的研究重点是如何在拓扑优化结果解读中减少人为因素的影响,将拓扑优化结果转化为更精确的分析模型。
2) 采用近似模型法对车身截面进行优化的时候,考虑的是刚度工况。后续的研究重点是如何在考虑车身模态和碰撞工况的前提下,搭建精准的近似模型进行截面优化。
3) 考虑碰撞、刚度和模态工况,基于ESL法进行了车身的料厚优化。后续的研究重点是基于该技术路线,如何开展车身的形貌优化、形状优化等。
4) 对平台架构的车身结构优化,是基于尺寸最大的车型进行的,这种技术路线势必会造成较小尺寸车型性能过剩的情况,若考虑将优化方案代入到其他小尺寸车型中进行验证并开展轻量化设计的工作,将使文中的研究结论更加合理。
| [1] |
杨宏, 黄兴, 陈东, 等. 纯电动专属车身平台架构开发与应用[J]. 汽车工程师, 2020(2): 48-54, 58. Yang H, Huang X, Chen D, et al. Development and application of exclusive platform architecture of pure electric body[J]. Auto Engineer, 2020(2): 48-54, 58. (in Chinese) DOI:10.3969/j.issn.1674-6546.2020.02.013 |
| [2] |
赵永宏, 袁焕泉, 陈东, 等. 平台化车身架构拓扑优化方法研究[J]. 汽车实用技术, 2018(4): 83-87. Zhao Y H, Yuan H Q, Chen D, et al. Study of the topology optimization method for platform vehicle-body structures[J]. Automobile Applied Technology, 2018(4): 83-87. (in Chinese) |
| [3] |
麻桂艳, 李成鑫, 汤湧. 轻量化车身平台架构设计方法研究[J]. 汽车实用技术, 2019(22): 138-139, 142. Ma G Y, Li C X, Tang Y. The study on architectural design method of lightweight car body[J]. Automobile Applied Technology, 2019(22): 138-139, 142. (in Chinese) |
| [4] |
王磊, 王峻峰, 鲁永建, 等. 基于平台化开发的白车身轻量化设计[C]//2015中国汽车工程学会年会论文集(Volume3). 北京: 中国汽车工程学会, 2015: 27-29. Wang L. Wang J F, Lu Y J, et al. Lightweight design of BIW based on platform development[C]//2015 China Society of Automotive Engineering Annual Conference Proceedings (Volume 3). Beijing: China Society of Automotive Engineering, 2015: 27-29. (in Chinese) |
| [5] |
徐中明, 陶能发, 赖诗洋, 等. 基于折衷规划法的转向节多目标拓扑优化设计[J]. 重庆大学学报, 2017, 40(12): 1-7. Xu Z M, Tao N F, Lai S Y, et al. Multi-objective topology optimization for vehicle steering knucklebased on the compromise programming method[J]. Journal of Chongqing University, 2017, 40(12): 1-7. (in Chinese) DOI:10.11835/j.issn.1000-582X.2017.12.001 |
| [6] |
张伟, 侯文彬, 胡平. 基于拓扑优化的电动汽车白车身优化设计[J]. 湖南大学学报(自然科学版), 2014, 41(10): 42-48. Zhang W, Hou W B, Hu P. The body in white optimization of an electric vehicle using topology optimization[J]. Journal of Hunan University (Natural Sciences), 2014, 41(10): 42-48. (in Chinese) |
| [7] |
武敬伟, 胡朝辉, 丁晓明, 等. 电动车车身正向概念轻量化设计[J]. 机械设计与制造, 2017(3): 246-249. Wu J W, Hu Z H, Ding X M, et al. Lightweight forward conceptual design of electric vehicle body[J]. Machinery Design & Manufacture, 2017(3): 246-249. (in Chinese) DOI:10.3969/j.issn.1001-3997.2017.03.066 |
| [8] |
李胜琴, 刘轩龄, 冯新园. 白车身灵敏度分析及轻量化设计[J]. 武汉理工大学学报(交通科学与工程版), 2019, 43(5): 832-836. Li S Q, Liu X L, Feng X Y. Sensitivity analysis and lightweight design on body-in-white[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2019, 43(5): 832-836. (in Chinese) DOI:10.3963/j.issn.2095-3844.2019.05.009 |
| [9] |
陈旭, 钱益明, 田云强, 等. 全地形车车架结构灵敏度分析及轻量化设计[J]. 重庆大学学报, 2013, 36(6): 91-97. Chen X, Qian Y M, Tian Y Q, et al. Sensitivity analysis and lightweight design for the frame of all-terrain vehicles[J]. Journal of Chongqing University, 2013, 36(6): 91-97. (in Chinese) |
| [10] |
张帅, 郭志军, 王传青. 基于分析驱动设计的参数化白车身前端结构轻量化多目标优化[J]. 汽车工程, 2019, 41(9): 1102-1107. Zhang S, Guo Z J, Wang C Q. Multi-objective lightweight optimization of parametric frontend BIW structure based on analysis-driven design[J]. Automotive Engineering, 2019, 41(9): 1102-1107. (in Chinese) |
| [11] |
Costas M, Díaz J, Romera L, et al. A multi-objective surrogate-based optimization of the crashworthiness of a hybrid impact absorber[J]. International Journal of Mechanical Sciences, 2014, 88: 46-54. DOI:10.1016/j.ijmecsci.2014.07.002 |
| [12] |
Yang S, Qi C, Guo D M, et al. Topology optimization of a parallel hybrid electric vehicle body in white[J]. Applied Mechanics and Materials, 2011, 148/149: 668-671. DOI:10.4028/www.scientific.net/AMM.148-149.668 |
| [13] |
Lee H A, Park G J. Nonlinear dynamic response topology optimization using the equivalent static loads method[J]. Computer Methods in Applied Mechanics and Engineering, 2015, 283: 956-970. DOI:10.1016/j.cma.2014.10.015 |
| [14] |
Kohar C P, Zhumagulov A, Brahme A, et al. Development of high crush efficient, extrudablealuminium frontrails for vehicle lightweighting[J]. International Journal of Impact Engineering, 2016, 95: 17-34. DOI:10.1016/j.ijimpeng.2016.04.004 |
| [15] |
Duddeck F, Hunkeler S, Lozano P, et al. Topology optimization for crashworthiness of thin-walled structures under axial impact using hybrid cellular automata[J]. Structural and Multidisciplinary Optimization, 2016, 54(3): 415-428. DOI:10.1007/s00158-016-1445-y |
 2021, Vol. 44
2021, Vol. 44















