在现代制造业生产中,多品种小批量、多样化个性化定制的生产模式已成为发展趋势,这必将会对柔性制造系统(flexible manufacturing system, FMS)提出更高的要求。生产调度是柔性制造系统的基础,制定科学合理的调度方案,对柔性制造系统的性能具有重要影响。其中,柔性作业车间调度问题(flexible job shop scheduling problem,FJSP)是非常复杂的NP难题。在以往的FJSP研究中,为了简化数学模型解决问题,大多忽略了工件在不同机器之间的运输时间,或将其包含在工件加工时间内,这都是不合理的,特别是当工件的移动完全依赖于自动导引小车(automated guided vehicle,AGV)并且运输时间与加工时间相当时[1]。因此,有必要对FMS中的机器与AGV同时调度问题进行研究。
针对机器与AGV同时调度问题,国内外学者进行了很多研究。早期,Bilge等[2]将问题表述为一个非线性混合整数规划模型,采用带滑动时间窗的迭代启发式方法进行求解。这种精确求解算法能够在简单小规模问题上取得全局最优解,但随着问题复杂度的增加,无法在合理时间内搜索到满意解。近年来,智能优化算法如遗传算法[3-8]、差分进化算法[9]、粒子群算法[10-11]、蚁群算法[12]、花授粉算法[13]等,在求解具有复杂约束的同时调度问题上,取得了较好的进步。Abdelmaguid等[3]提出一种新的启发式编码方案,采用混合遗传算法同时调度机器与AGV。Kumar等[9]提出机器选择和车辆分配两种启发式算法,并与差分进化算法相结合,为工件分配合适的机器与AGV,但没有对算法进行改进,仅对工序操作进行了基本差分变换。Zhang等[10]结合主粒子和嵌套粒子的特点,设计了一种改进粒子群优化算法来求解同时调度问题。
差分进化(differential evolution,DE)算法是一种基于种群进化的智能优化算法,具有全局搜索能力强,操作简单,鲁棒性好的优点。为了增强算法性能,通常需要对算法进行改进。Pan等[14]提出一种求解车间调度问题的离散DE算法,并结合局部搜索算法以改善算法性能。杨锋英等[15]提出一种改进DE算法求解AGV调度问题,设计了基于个体生存时间的种群更新机制以增强种群多样性,提高算法的搜索能力。吴秀丽等[16]针对分布式柔性作业车间调度问题,为离散DE算法设计了新的变异和交叉方式,并引入模拟退火方法以提高算法的局部搜索能力。
从现有文献来看,DE算法在求解复杂组合优化问题上能有较好的表现,但在机器与AGV同时调度问题上应用还较少。并且,大多文献把集成调度问题分解为了机器调度和AGV调度两个子问题,忽视了机器调度与AGV调度的紧密联系,以及忽略了可变工艺路线对AGV搬运的影响。因此,针对FMS中机器与AGV同时调度问题,在完善集成调度数学模型和改进算法性能方面有进一步研究价值。另外,当AGV数量大于1时,可能会发生冲突,对机器与AGV调度造成影响。但文中主要围绕零件加工尺寸较小的车间,其运输的AGV载重和尺寸也较小,虽然可能发生冲突,但是在车间区域内能并行通过,冲突问题产生的概率较小。
笔者针对FMS中机器与AGV同时调度问题,建立了以最大完工时间最小为优化目标的调度数学模型,提出了基于工序、机器、AGV的3层编码结构,以解决机器分配和AGV分配。针对DE算法易陷入局部最优的问题,设计了一种混合变邻域搜索的改进离散差分进化算法,以每次迭代的最优解作为局部搜索的初始解,设计了3种不同的邻域结构进行变邻域搜索,并采用种群更新策略以增强种群多样性,进而提升算法搜索到更好解的可能性。最后,通过对比实验,验证了所提算法求解FMS中机器与AGV同时调度问题的有效性和优越性。
1 问题描述及建模 1.1 问题描述假设柔性作业车间有n个待加工工件在m台机器上加工,若干辆相同的AGV负责工件在机器之间运送。每个工件有ni道不同的工序,每道工序可选择的加工机器不唯一,每台AGV可以在任意两台机器之间运送工件。已知每个工件加工所需的工序,每道工序在对应加工机器上的加工时间,以及小车在不同机器间的运输时间,要求在满足一定约束条件下,为每道工序选择最合适的加工机器和搬运小车,确定每个工件的每道工序在各机器上的最佳加工顺序和开工、完工时间,以及在各AGV上的最佳搬运顺序和开始搬运、完成搬运时间,最终满足优化目标。
为了简化FMS中机器和AGV同时调度问题,假设条件如下:
1) 零时刻,所有机器与AGV都可用,机器与AGV连续工作。
2) 任意时刻,每台机器一次只能加工一个工件,每辆小车一次只能搬运一个工件。
3) 同工件的工序有先后约束,不同工件之间无约束。
4) AGV数量提前确定。
5) AGV行驶速度恒定,其负重不影响小车行驶速度。
6) AGV在任意两台机器之间的运输路线是固定的,运输时间仅与机器之间的距离有关。
7) 每台机器前设置有缓冲区,缓冲区无限大,以避免死锁。
8) 所有待加工工件在开始加工前都放在装载台M0,完成所有工序加工的工件放入卸载台Mm+1。
9) 小车每次执行完任务后停靠在加工机器旁,不返回起点。
10) 小车没有装载工件的行驶过程称为空载,装载工件的运送过程称为负载。
11) 不考虑AGV可能发生冲突、故障、电量不足等问题。
1.2 数学模型为了建立问题的模型,引入如下符号和变量:
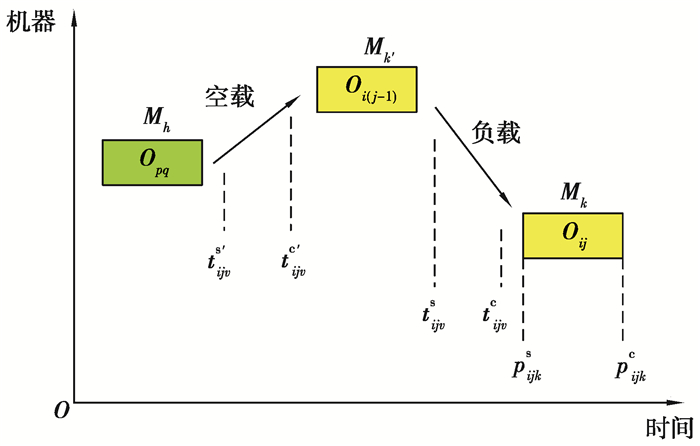
Ji表示工件i,i∈{1, 2, …, n};Mk表示机器k,k∈(1, 2, …, m);Rv表示小车v,v∈(1, 2, …, w);Oij表示工件Ji的第j道工序,j∈{1, 2, …, ni};Ci表示工件Ji的完工时间;pijks表示工序Oij在机器k上开始加工的时间;pijk表示工序Oij在机器k上的加工时间;pijkc表示工序Oij在机器k上完成加工的时间;Tij表示小车运送工序Oij的搬运任务;tijvs'表示小车Rv搬运任务Tij的空载开始时间;tijvc'表示小车Rv搬运任务Tij的空载完成时间;tijvs表示小车Rv搬运任务Tij的负载开始时间;tijvc表示小车Rv搬运任务Tij的负载完成时间;thk表示小车从机器Mh到Mk的运输时间;t'表示小车的空载运输时间;t表示小车的负载运输时间;M表示一个无穷大的正数。
为了便于理解,变量的表示含义如图 1所示。假设工序Oij在机器Mk上加工,工件i的前一道工序Oi(j-1)在机器Mk'上加工,工序Opq在机器Mh上加工。若小车Rv有一搬运任务Tij,需从当前位置Mh空载行驶至Mk'领取工件i,再从Mk'搬运工件i至Mk进行加工。
|
图 1 变量含义示意图 Fig. 1 Schematic diagram of variable meaning |
以最大完工时间最小为优化目标,针对FMS中机器与AGV同时调度问题,建立数学模型如下。
目标函数:
| $ f=\min \left(\max \limits_{1 \leqslant i \leqslant n} C_{i}\right) 。$ | (1) |
约束条件:
1) 每道工序一次只能分配给一台机器加工。
| $ \sum\limits_{k=1}^{m} x_{i j k}=1 \text { 。} $ | (2) |
2) 每道搬运任务一次只能分配给一辆小车运送。
| $ \sum\limits_{v=1}^{w} z_{i j v}=1 \text { 。} $ | (3) |
3) 同一辆小车,只有前一道任务Tpq搬运完后,才能开始下一道任务Tij的搬运。
| $ t_{p q v}^{\mathrm{c}} \leqslant t_{i j v}^{\mathrm{s'}}+M\left(1-\beta_{T p q i j v}\right), $ | (4) |
式中,tpqvc表示小车Rv搬运任务Tpq的负载完成时间,∀p∈{1, 2, …, n},q∈{1, 2, …, ni}。
4) 小车从当前的机器位置Mh行驶至该工件前一道工序的加工机器Mk'处领取工件。
| $ t_{i j v}^{\mathrm{s}^{\prime}}+\sum\limits_{h=1}^{m} \sum\limits_{k^{\prime}=1}^{m} x_{p q h} \cdot x_{i(j-1) k^{\prime}} \cdot t_{h k^{\prime}}=t_{i j v}^{\mathrm{c}^{\prime}}。$ | (5) |
5) 小车空载到达机器Mk'并且工序Oi(j-1)加工完成,才能开始搬运。
| $ \max \left(t_{i j v}^{\mathrm{c}^{\prime}}, p_{i(j-1) k^{\prime}}^{\mathrm{c}}\right) \leqslant t_{i j v}^{\mathrm{s}}。$ | (6) |
6) 小车从机器Mk'搬运工件到工序Oij的加工机器Mk处进行加工。
| $ t_{i j v}^{\mathrm{s}}+\sum\limits_{k^{\prime}=1}^{m} \sum\limits_{k=1}^{m} x_{i(j-1) k^{\prime}} \cdot x_{i j k} \cdot t_{k^{\prime} k}=t_{i j v}^{\mathrm{c}} \text { 。} $ | (7) |
7) 小车负载到达机器Mk并且机器空闲,才能开始加工。
| $ \max \left(t_{i j v}^{\mathrm{c}}, p_{i' j' k}^{\mathrm{c}}\right) \leqslant p_{i j k}^{\mathrm{s}}+M\left(1-\alpha_{i' j'{i j k}}\right) \text {, } $ | (8) |
式中,pi'j'kc表示机器Mk前一道工序Oi'j'的加工完成时间,∀i'∈{1, 2, …, n},j'∈{1, 2, …, ni}。
8) 工序Oij在机器Mk上加工。
| $ p_{i j k}^{\mathrm{s}}+\sum\limits_{k=1}^{m} x_{i j k} \cdot p_{i j k}=p_{i j k}^{\mathrm{c}}。$ | (9) |
基本DE算法是基于实数编码的,主要作用于连续域的优化问题。而柔性作业车间的调度问题是离散的组合优化问题,所以需要改进DE算法的变异、交叉操作,以适应算法的离散搜索过程。同时,变邻域搜索(variable neighborhood search,VNS)算法能够有效避免算法陷入局部最优,提高算法的局部搜索能力。因此,提出混合变邻域搜索的改进离散差分进化(improved discrete differential evolutionVNS,IDDE-VNS)算法求解FMS中机器与AGV同时调度问题。
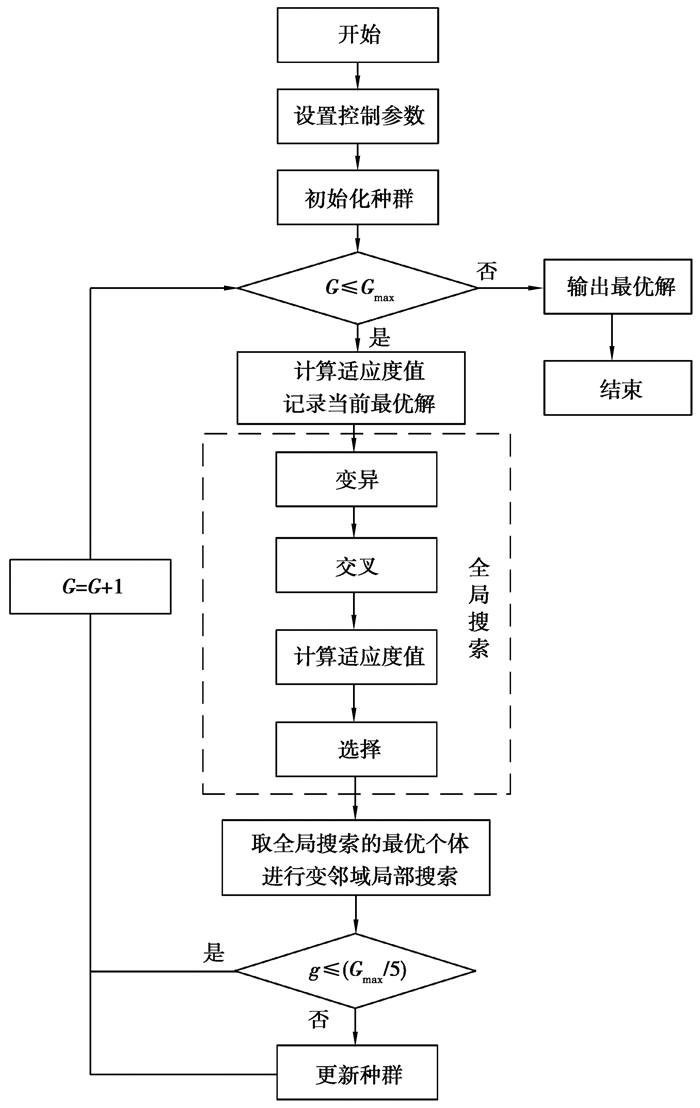
2.1 总体流程设计IDDE-VNS算法的总体流程设计如图 2所示。
|
图 2 IDDE-VNS算法流程图 Fig. 2 Flow chart of IDDE-VNS algorithm |
具体步骤如下。
步骤1:输入调度信息,工件加工信息和小车运输时间。设置DE算法控制参数,初始种群规模P,最大迭代次数Gmax,变异概率F,交叉概率Cr,小车数量Nagv,初始温度T0。
步骤2:根据编码方式和初始种群规模,随机生成初始种群。
步骤3:判断终止迭代条件,即当前迭代次数G是否达到最大迭代次数Gmax,若是,输出最优解,结束迭代;若否,计算种群适应度值,记录当前最优解xbest。
步骤4:全局搜索。
1) 根据变异概率F,选择初始目标种群X执行变异操作得到变异种群V。
2) 根据交叉概率Cr,对目标种群X与变异种群V进行交叉操作得到试验种群U。
3) 重新计算试验种群U的适应度值。
4) 引入模拟退火思想,比较目标种群X与试验种群U,按退火概率选择相应的个体进入下一代。
步骤5:局部搜索。对全局搜索得到的最优个体进行变邻域搜索,获得新的最优个体x'best。
步骤6:更新种群。判断当前最优解x'best与前一代最优解xbest是否相等,若相等,g=g+1;若不相等,g=0。当g=Gmax/5时,即最优解连续代Gmax/5不变,则新产生一部分个体替换原种群中的较差个体[17]。否则,跳转步骤3,经过步骤4、5、6操作后的种群作为下一代目标种群X,继续迭代。
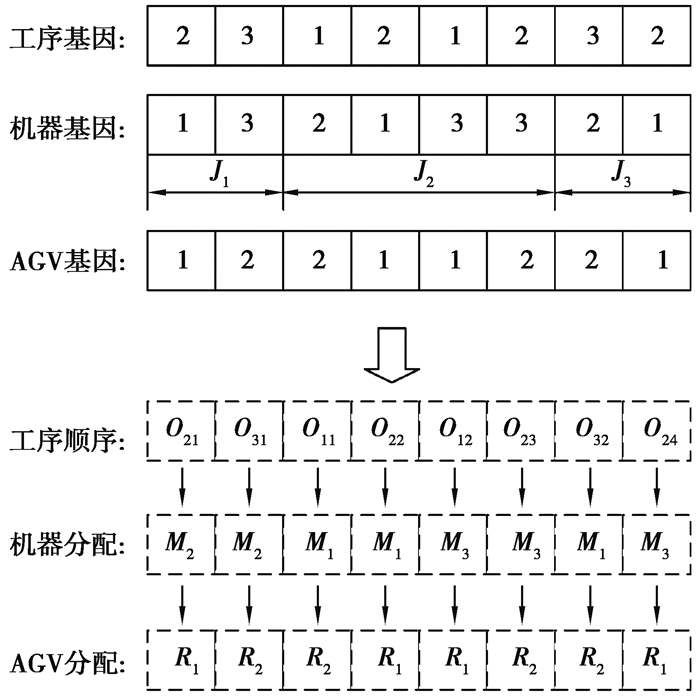
2.2 详细设计 2.2.1 编码和解码方法为了表示问题的解,首先需要设计编码。算法的性能和效率很大程度上取决于染色体的编码,需要考虑染色体的可行性、完备性、健全性和非冗余性。对于FMS中机器与AGV同时调度问题,不光要安排工序的加工顺序,还要确定每道工序的加工机器和每次负责搬运的小车。因此,编码分为3个部分。第1行表示基于工序的编码,第2行表示基于机器的编码,第3行表示基于AGV的编码。为了便于解释编码过程,采用一个3×3FJSP算例来描述,其工件加工信息如表 1所示。2台AGV在任意机器之间的运输时间如表 2所示。
| 表 1 FJSP算例的工件加工信息 Table 1 Processing information of FJSP examples |
| 表 2 各机器之间AGV的运输时间 Table 2 Transportation time of AGV between machines min |
根据工件加工信息,给出一组染色体编码见图 3,表示一个可行调度解。算例中有3个工件加工,依次对应的工序数为2、4、2,染色体长度为
|
图 3 基于工序、机器、AGV的3层编码结构 Fig. 3 The three-layer coding structure of operation, machine and AGV |
考虑AGV约束的柔性作业车间调度问题解码时,比传统的车间调度问题更加复杂。除了要确定每个工件的每道工序的开工时间和完工时间,还要确定AGV运送工件的空载、负载开始和完成时间。针对1个工件的某道工序Oij加工过程,如图 1所示,设计解码方法如下。
1) 确定AGV运送工序Oij空载、负载开始和完成时间,具体步骤如下。
步骤1:读取由上述编码方式生成的染色体信息,工序顺序P、对应加工机器Mk和运送小车编号Rv。
步骤2:记录AGV当前位置及其走过的路径。
步骤3:判断本道工序Oij是否为工件i的第1道工序。若是,跳转步骤4;若否,跳转步骤6。
步骤4:判断AGV的当前位置是否在装载台M0。
① 若是,AGV空载运输时间t'=0。
② 若不是,AGV需要从当前位置Mh行驶到装载台M0领取工件,AGV空载运输时间t'=Mh→M0。
步骤5:AGV从装载台M0运送工件行驶到本道工序的加工机器Mk处,AGV负载运输时间t=M0→Mk。
步骤6:判断AGV的当前位置是否在紧前工序加工机器Mk'处。
① 若是,AGV空载运输时间t'=0。
② 若不是,AGV需要从当前位置Mh行驶至该工件的前一道工序的加工机器Mk'领取工件。若该工件正在机器Mk'上加工,需等待加工完成后再搬运。AGV空载运输时间t'=Mh→Mk'。
步骤7:AGV从紧前工序加工机器Mk'运送工件行驶到本道工序的加工机器Mk处,AGV负载运输时间t=Mk'→Mk。
步骤8:输出AGV空载开始和完成时间,负载开始和完成时间。
2) 确定工序Oij的开工时间和完工时间。
| $ p_{i j k}^{\mathrm{s}}=\max \left\{p_{i^{\prime} j^{\prime} k}^{\mathrm{c}},\left(p_{i(j-1) k^{\prime}}^{\mathrm{c}}+t\right),\left(t_{i j v}^{\mathrm{s}^{\prime}}+t^{\prime}+t\right)\right\}, $ | (10) |
| $ p_{i j k}^{\mathrm{c}}=p_{i j k}^{\mathrm{s}}+p_{i j k} 。$ | (11) |
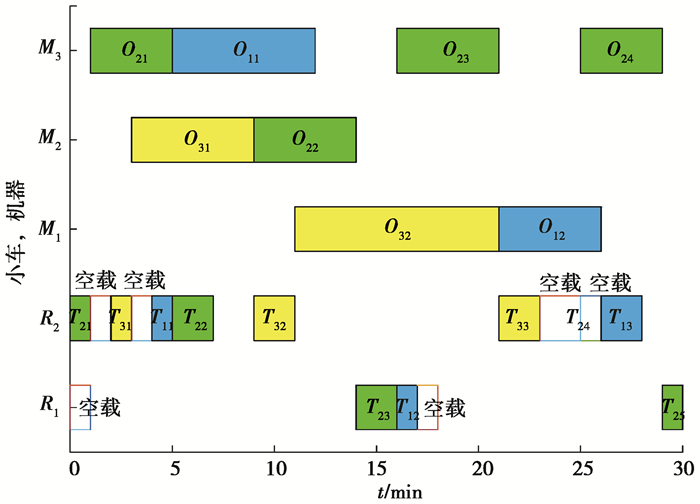
根据设计的编码和解码方法,结合工件的加工信息和2台AGV的运输信息,随机产生一个可行调度方案,其甘特图如图 4所示。分析甘特图可知,工件加工过程和小车的运输过程具体如下,其中“*→”表示AGV空载运行。
|
图 4 调度方案的甘特图 Fig. 4 Gantt chart of scheduling scheme |
R1的运输过程:M0*→M2(取工件2)→M3(加工O23并取工件1)→M1(等待加工O12)*→M3(取工件2)→M4(工件2完成加工后运到卸载台)。
R2的运输过程:M0(取工件2)→M3(加工O21)*→M0(取工件3)→M2(加工O31)*→M0(取工件1)→M3(加工O11并取工件2)→M2(等待加工O22并取工件3)→M1(加工O32)→M4(工件3完成加工后运到卸载台)*→M3(加工O24)*→M1(取工件1)→M4(工件1完成加工后运到卸载台)。
2.2.2 全局搜索根据上述编码方式,为了使个体直接在离散域搜索,以提高算法搜索速度,对DE算法的操作算子进行了改进。
1) 变异操作。从目标种群X中随机选择3个不同的个体Xr1t、Xr2t和Xr3t进行变异操作生成变异个体Vit。
| $ V_{i}^{t}=F \otimes G\left(F \otimes G\left(X_{r 2}^{t}, X_{r 3}^{t}\right), X_{r 1}^{t}\right), $ | (12) |
式中:目标种群Xt={X1t, X2t, …,XPt},变异种群Vt={V1t, V2t, …,VPt},r1, r2, r3, i∈[1, 2, …, P],t为当前运行代数,F为变异概率。
式(12)由2个部分构成。首先,由目标个体Xr2t和Xr3t采用如下操作生成差分矢量Δit。生成一个随机数r∈[0, 1],若r小于变异概率,差分矢量Δit=G(Xr2t, Xr3t);否则,Δit=Xr2t。
| $ \varDelta_{i}^{t}=F \otimes G\left(X_{r 2}^{t}, X_{r 3}^{t}\right)= \begin{cases}G\left(X_{r 2}^{t}, X_{r 3}^{t}\right), & r<F 。\\ X_{r 2}^{t}, & \text { 其他。}\end{cases} $ | (13) |
然后,第二部分由差分矢量Δit和目标个体Xr1t采用如下操作生成变异个体Vit,操作同上。
| $ V_{i}^{t}=F \otimes G\left(\varDelta_{i}^{t}, X_{r 1}^{t}\right)= \begin{cases}G\left(\varDelta_{i}^{t}, X_{r 1}^{t}\right), & r<F 。\\ \varDelta_{i}^{t}, & \text { 其他。}\end{cases} $ | (14) |
其中,G(Xr2t, Xr3t)和G(Δit, Xr1t)表示对染色体进行变换操作,生成可能更优的个体。由于染色体编码分为3个部分,需要对3行基因分别进行操作。
对基于工序编码的基因串,采用IPOX交叉[18]。其具体交叉过程为:将工件集{1, 2, …, n}随机分为非空互补的两个子集S1和S2,复制父代染色体P1中包含S1的工件号到子代染色体C1,复制P1中包含S2的工件号到C2,保留它们的位置;同样复制P2中包含S1的工件号到C1,复制P1中包含S1的工件号到C2,也保留它们的位置,如图 5所示。
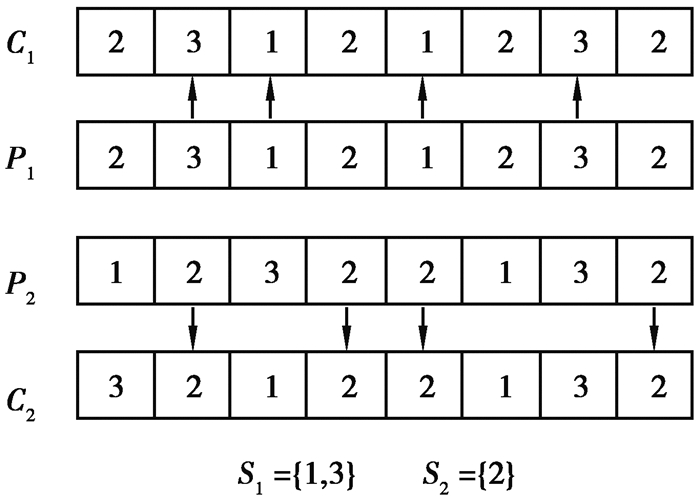
|
图 5 IPOX交叉过程图 Fig. 5 Crossover process of IPOX |
对基于机器编码的基因串,采用MPX交叉[18]。其具体交叉过程为:首先随机产生一行长度与父代染色体相等,由0和1组成的基因串。将父代染色体P1中1对应位置的机器号复制到子代染色体C2,父代染色体P2中1对应位置的机器号复制到C1,P1中剩余的机器号保留到子代C1,P2中剩余的机器号保留到子代C2,如图 6所示。
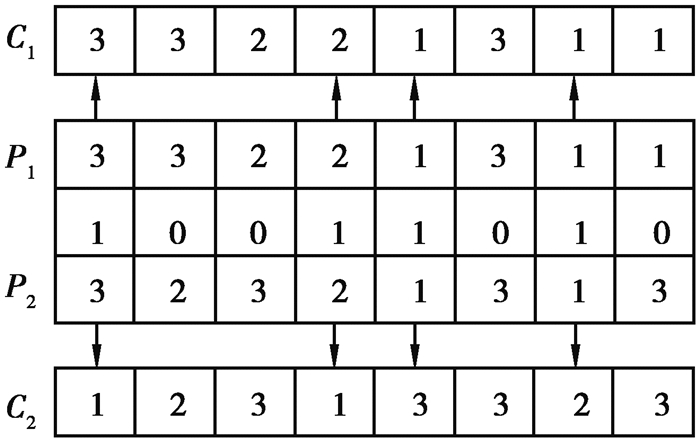
|
图 6 MPX交叉过程 Fig. 6 Crossover process of MPX |
对基于AGV编码的基因串,采用简单的两点交叉。
2) 交叉操作。选择变异个体Vit和目标个体Xit进行交叉操作生成试验个体Uit,操作过程同上。
| $ U_{i}^{t}=C_{\mathrm{r}} \otimes G\left(V_{i}^{t}, X_{i}^{t}\right)= \begin{cases}G\left(V_{i}^{t}, X_{i}^{t}\right), & r<C_{\mathrm{r}}, \\ V_{i}^{t}, & \text { 其他。}\end{cases} $ | (15) |
式中:试验种群Ut={U1t, U2t, …,UPt};i∈[1, 2, …, P];Cr为交叉概率。
3) 选择操作。基本DE算法的选择操作采用“一对一”贪婪思想,比较试验个体Uit和目标个体Xit的适应度值,选择适应度值更高的个体进入下一代。但这种选择方式可能会淘汰与最优解距离很近的较差个体,导致算法的收敛速度和搜索质量下降。研究中引入模拟退火算法中解的接受准则,即按一定概率接受较差个体,且概率受温度变化控制,随着温度的降低,接受较差个体的概率变小。
选择操作如下:当f(Uit) < f(Xit)时,选择目标函数值更小的个体Uit进入下一代;否则按概率
| $ X_{i}^{t+1}=\left\{\begin{array}{l} U_{i}^{t}, f\left(U_{i}^{t}\right)<f\left(X_{i}^{t}\right) 。\\ U_{i}^{t}, f\left(U_{i}^{t}\right) \geqslant f\left(X_{i}^{t}\right) \text { 且 } r<\exp \left(-\frac{f\left(U_{i}^{t}\right)-f\left(X_{i}^{t}\right)}{T}\right) 。\\ X_{i}^{t}, \text { 其他。} \end{array}\right. $ | (16) |
式中,T为退火温度,为了提高算法搜索效率,采用自适应变温方法,不进行循环。T的变化见式(17)。
| $ T=T \times\left(1-\frac{G}{G_{\max }+1}\right) \text { 。} $ | (17) |
变邻域搜索算法比单一的邻域搜索算法性能更强,它通过改变算法的邻域结构来扩大其搜索范围,从而找到更优解。文中对当前种群中的最优个体执行变邻域搜索,以提高DE算法的局部搜索能力。
设计VNS算法首先需要构造邻域结构,算法采用了以下3种邻域结构来产生局部最优解:
1) 邻域结构N1。在基于工序编码的染色体上,随机选择2个基因位置,所选的2个位置对应2道不同工件的工序,互换这2个位置。
2) 邻域结构N2。在基于机器编码的染色体上,随机选择1个基因位置,所选位置对应工序的可加工机器不唯一,重新从该工序的可选机器集合中选择不同的机器替换该位置的机器。
3) 邻域结构N3。在基于AGV编码的染色体上,随机选择1个基因位置,从可选AGV集合中选择不同的AGV编号替换该位置的AGV编号。
基于上述3种邻域结构,变邻域搜索算法的操作步骤如下。
步骤1:算法初始化,将全局搜索得到的最优解设为初始解X,设置q←1,qmax=3,cmax=40。
步骤2:判断循环终止条件q>qmax是否满足,若满足,输出最优个体;否则,转到步骤3。
步骤3:振动环节。初始解X通过邻域结构Nq搜索得到1个扰动解。
步骤4:局部搜索。
① 以振动后的新解作为局部搜索的初始解X',设置c←1。
② 判断循环终止条件c>cmax是否满足,若满足,输出局部最优解X';否则转到步骤③。
③ 使当前解X'在Nq中搜索得到一个新解X",若满足f(X") < f(X'),令X'←X"。
④ 设置c←c+1,返回步骤②循环。
步骤5:判断邻域移动条件f(X') < f(X)是否满足,若满足,令X←X',并继续在邻域Nq内搜索;否则,设置q←q+1,返回步骤2循环。
3 实验分析实验测试以MATLAB2016b为开发环境,运行环境为Intel Core i5-6200 CPU,2.40 GHz主频,4 GB内存。
为了验证IDDE-VNS算法的性能,展开以下测试实验:
1) 算法对比试验。针对遗传算法、差分进化算法和混合变邻域搜索的改进差分进化算法,对比这3种算法产生的解的质量,为客观评价提出的改进方法提供依据。
2) 非柔性算例实验。选取Bilge等[2]提出的82个算例中的一部分进行实验,与其他文献使用各种优化算法得到的计算结果进行对比,为客观评价IDDE-VNS算法的性能提供依据。
3) 柔性算例实验。选取Zhang等[10]提出的柔性算例进行计算,并与Zhang等[10]得到的优化结果对比,为客观评价IDDE-VNS算法作用在柔性作业车间时的性能提供依据。
3.1 算法对比实验为了验证提出的改进方法的有效性和可行性,采用Bilge等[2]提出的测试算例中的EX11算例进行实验。将遗传算法,差分进化算法和混合变邻域的改进差分进化算法分别命名为GA、DE、IDDE-VNS,重复运行20次,对比3种算法的迭代曲线和优化结果。
3种算法的种群规模、迭代次数和小车数量都设为:P=80,Gmax=200,Nagv=2;GA的交叉概率和变异概率设为:Pc=0.8,Pm=0.4;DE的变异概率和交叉概率设为:F=0.7,Cr=0.5;IDDE-VNS的变异概率、交叉概率和初始退火温度设为:F=0.7,Cr=0.5,T0=20。
3种算法的搜索过程曲线如图 7所示,红色实线为GA,蓝色虚线为DE,黄色点划线为IDDE-VNS。由收敛曲线图可知,GA能快速收敛到一个较优解,但易陷入局部最优;DE在进化前期较GA收敛得慢,但在搜索后期发现更优解的可能性更大,使搜索最终得到更好的解;改进后的IDDE-VNS的收敛速度在GA和DE之间,在进化后期,由于引入了变邻域搜索算法增强了DE算法的局部搜索能力,使其最终搜索到的解的质量在3种算法中最好。
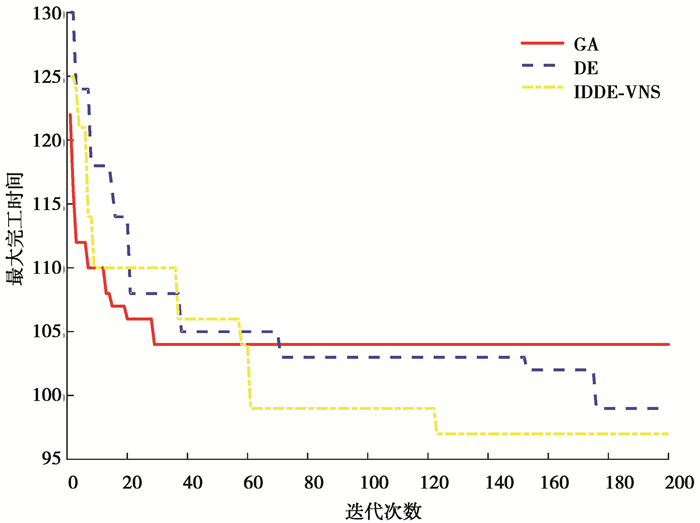
|
图 7 3种算法收敛曲线对比 Fig. 7 Comparison of convergence curves of three algorithms |
3种算法计算EX11算例的优化结果如表 3所示,采用GA进行实验20次,得到的最优解的平均值为100.5,搜索到全局最优解96的概率为5%;采用DE进行实验20次,得到的最优解的平均值为98.5,搜索到全局最优解96的概率为10%;采用IDDE-VNS进行实验20次,得到的最优解的平均值为97.1,搜索到全局最优解96的概率为35%。由此可得,3种算法搜索到的解的质量和稳定性的关系为IDDE-VNS>DE>GA。
| 表 3 3种算法求解EX11算例实验结果 Table 3 Experimental results of three algorithms for EX11 example |
综上所述,IDDE-VNS比GA、DE的稳定性和寻优能力更好,证明了文中提出的改进方法是有效可行的。
3.2 非柔性算例实验Bilge等[2]提出了82个算例用来测试算法的有效性,由装载台、卸载台、4台加工机器和2台AGV构成的4种不同布局和10个不同的工件集组成。EX后面的数字中第一个表示工件集编号,第二个表示布局编号,如“EX32”表示工件集3-布局2。为了验证IDDE-VNS相比其他算法的优越性,选取其中一部分算例进行了测试。IDDE-VNS算法的控制参数设置为:种群规模P=80,最大迭代次数Gmax=500,变异概率F=0.7,交叉概率Cr=0.5,初始退火温度T0=20,小车数量Nagv=2。
每个算例独立计算20次取最优值,与其他文献得到的最优解进行对比,如表 4所示。其中STW表示文献[2]采用滑动时间窗求得的最优解,AGA表示文献[3]采用遗传算法混合启发式方法求得的最优解,FDE表示文献[9]采用差分进化算法求得的最优解,FMAS表示文献[19]采用基于MAS方法求得的最优解。
| 表 4 非柔性算例实验结果 Table 4 Experimental results of non-flexible examples |
由表 4可知,IDDE-VNS算法计算测试算例时,其中100%的解优于或等于STW和AGA的实验结果;85%的解优于或等于FDE的实验结果;90%的解优于或等于FMAS的实验结果。特别地,IDDE-VNS算法计算EX71和EX92的解在对比实验中结果最好。由此可看出,IDDE-VNS在计算机器与AGV同时调度问题时表现优秀,与其他优秀算法相比有较高的搜索质量,证明了IDDE-VNS算法的优越性。
3.3 柔性算例实验上述算例中工件的每道工序可选择的加工机器是唯一的,没有体现生产系统的柔性。在FMS中,不同加工机器的选择会影响AGV路线的选择,从而影响AGV的空载时间和负载时间以及工序的开工时间和完工时间。为了更好体现IDDE-VNS算法在FMS中的作用,借鉴Zhang等[10]给出的柔性作业车间集成调度算例,由6个工件、6台机器和4台AGV构成。
IDDE-VNS算法的控制参数设置与非柔性算例实验一致,其中最大迭代次数与文献[10]一致,小车数量改为Nagv=4,运行10次取最优值,最优实验结果的调度甘特图见图 8,最大完工时间为75.6 min。对比Zhang等[10]采用改进粒子群优化算法得到的最大完工时间85 min,IDDE-VNS算法搜索到的解的质量更好,证明了IDDE-VNS算法求解FMS中机器与AGV同时调度问题的优越性。
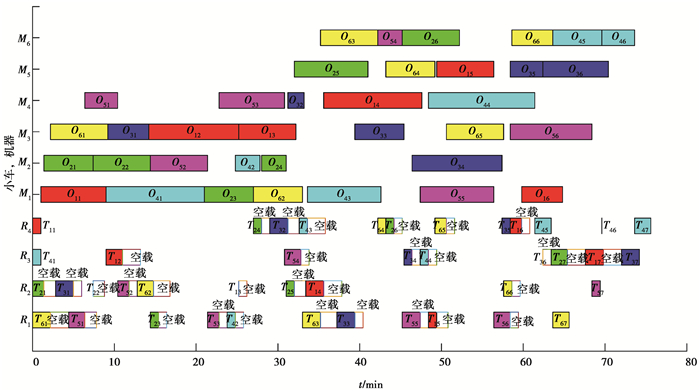
|
图 8 柔性算例调度方案的甘特图 Fig. 8 Gantt chart of flexible example scheduling scheme |
针对FMS中机器与AGV同时调度问题,提出了IDDE-VNS算法。
1) 基于工序、机器、AGV的3层编码方案,提出了改进离散差分进化算法,使个体直接在离散域搜索,提高了算法的全局搜索能力和搜索速度。
2) 将变邻域搜索算法嵌入改进差分进化算法中,并按策略对种群进行扰动操作,增加了种群多样性,提高了算法跳出局部最优的能力,从而获得质量更好的解。
3) 实验结果和比较证明了IDDE-VNS算法求解FMS中机器与AGV同时调度问题的有效性,稳定性和优越性。
4) 在文中研究问题基础上,结合实际生产情况,下一步将考虑更多影响因素和约束条件,如小车冲突问题,或多目标问题。
| [1] |
付建林, 张恒志, 张剑, 等. 自动导引车调度优化研究综述[J]. 系统仿真学报, 2020, 32(9): 1664-1675. Fu J L, Zhang H Z, Zhang J, et al. Review on AGV scheduling optimization[J]. Journal of System Simulation, 2020, 32(9): 1664-1675. (in Chinese) |
| [2] |
Bilge V, Ulusoy G. A time window approach to simultaneous scheduling of machines and material handling system in an FMS[J]. Operations Research, 1995, 43(6): 1058-1070. DOI:10.1287/opre.43.6.1058 |
| [3] |
Abdelmaguid T F, Nassef A O, Kamal B A, et al. A hybrid GA/heuristic approach to the simultaneous scheduling of machines and automated guided vehicles[J]. International Journal of Production Research, 2004, 42(2): 267-281. DOI:10.1080/0020754032000123579 |
| [4] |
龙传泽, 杨煜俊. 基于遗传算法的柔性机器人制造单元调度问题研究[J]. 组合机床与自动化加工技术, 2015(11): 141-144, 148. Long C Z, Yang Y J. Research of flexible robotic manufacturing cell scheduling problem based on hybrid genetic algorithm[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2015(11): 141-144, 148. (in Chinese) |
| [5] |
Umar U A, Ariffin M K A, Ismail N, et al. Hybrid multiobjective genetic algorithms for integrated dynamic scheduling and routing of jobs and automated-guided vehicle (AGV) in flexible manufacturing systems (FMS) environment[J]. The International Journal of Advanced Manufacturing Technology, 2015, 81(9/10/11/12): 2123-2141. |
| [6] |
Nouri H E, BelkahlaDriss O, Ghédira K. Simultaneous scheduling of machines and transport robots in flexible job shop environment using hybrid metaheuristics based on clustered holonicmultiagent model[J]. Computers & Industrial Engineering, 2016, 102: 488-501. |
| [7] |
Lin J T, Chiu C C, Chang Y H. Simulation-based optimization approach for simultaneous scheduling of vehicles and machines with processing time uncertainty in FMS[J]. Flexible Services and Manufacturing Journal, 2019, 31(1): 104-141. DOI:10.1007/s10696-017-9302-x |
| [8] |
Lyu X F, Song Y C, He C Z, et al. Approach to integrated scheduling problems considering optimal number of automated guided vehicles and conflict-free routing in flexible manufacturing systems[J]. IEEE Access, 2019, 7: 74909-74924. DOI:10.1109/ACCESS.2019.2919109 |
| [9] |
Kumar M V S, Janardhana R, Rao C S P. Simultaneous scheduling of machines and vehicles in an FMS environment with alternative routing[J]. The International Journal of Advanced Manufacturing Technology, 2011, 53(1/2/3/4): 339-351. |
| [10] |
Zhang F Q, Li J J. An improved particle swarm optimization algorithm for integrated scheduling model in AGV-served manufacturing systems[J]. Journal of Advanced Manufacturing Systems, 2018, 17(3): 375-390. DOI:10.1142/S0219686718500221 |
| [11] |
徐云琴, 叶春明, 曹磊. 含有AGV的柔性车间调度优化研究[J]. 计算机应用研究, 2018, 35(11): 3271-3275. Xu Y Q, Ye C M, Cao L. Research on flexible Job-Shop scheduling problem with AGV constraints[J]. Application Research of Computers, 2018, 35(11): 3271-3275. (in Chinese) DOI:10.3969/j.issn.1001-3695.2018.11.017 |
| [12] |
Saidi-Mehrabad M, Dehnavi-Arani S, Evazabadian F, et al. An ant colony algorithm (ACA) for solving the new integrated model of job shop scheduling and conflict-free routing of AGVs[J]. Computers & Industrial Engineering, 2015, 86: 2-13. |
| [13] |
刘二辉, 姚锡凡, 陶韬, 等. 基于改进花授粉算法的共融AGV作业车间调度[J]. 计算机集成制造系统, 2019, 25(9): 2219-2236. Liu E H, Yao X F, Tao T, et al. Improved flower pollinaton algorithm for job shop scheduling problems integrated with AGVs[J]. Computer Integrated Manufacturing Systems, 2019, 25(9): 2219-2236. (in Chinese) |
| [14] |
Pan Q K, Wang L, Qian B. A novel differential evolution algorithm for bi-criteria no-wait flow shop scheduling problems[J]. Computers & Operations Research, 2009, 36(8): 2498-2511. |
| [15] |
杨锋英, 刘会超. AGV作业调度模型及改进的DE算法研究[J]. 计算机工程与应用, 2014, 50(9): 225-230. Yang F Y, Liu H C. Research on AGV job scheduling model and improved differential evolution algorithm[J]. Computer Engineering and Applications, 2014, 50(9): 225-230. (in Chinese) DOI:10.3778/j.issn.1002-8331.1309-0055 |
| [16] |
吴秀丽, 刘夏晶. 差分进化算法求解分布式柔性作业车间调度问题[J]. 计算机集成制造系统, 2019, 25(10): 2539-2558. Wu X L, Liu X J. Differential evolution algorithm for solving distributed flexible job shop scheduling problem[J]. Computer Integrated Manufacturing Systems, 2019, 25(10): 2539-2558. (in Chinese) |
| [17] |
崔琪, 吴秀丽, 余建军. 变邻域改进遗传算法求解混合流水车间调度问题[J]. 计算机集成制造系统, 2017, 23(9): 1917-1927. Cui Q, Wu X L, Yu J J. Improved genetic algorithm variable neighborhood search for solving hybrid flow shop scheduling problem[J]. Computer Integrated Manufacturing Systems, 2017, 23(9): 1917-1927. (in Chinese) |
| [18] |
张超勇, 董星, 王晓娟, 等. 基于改进非支配排序遗传算法的多目标柔性作业车间调度[J]. 机械工程学报, 2010, 46(11): 156-164. Zhang C Y, Dong X, Wang X J, et al. Improved NSGA-Ⅱ for the multi-objective flexible job-shop scheduling problem[J]. Journal of Mechanical Engineering, 2010, 46(11): 156-164. (in Chinese) |
| [19] |
Sahin C, Demirtas M, Erol R, et al. A multi-agent based approach to dynamic scheduling with flexible processing capabilities[J]. Journal of Intelligent Manufacturing, 2017, 28(8): 1827-1845. DOI:10.1007/s10845-015-1069-x |
 2021, Vol. 44
2021, Vol. 44


