2. 洛阳拖拉机研究所有限公司, 河南 洛阳 471039;
3. 一汽集团有限公司研发总院, 长春 130000
2. Research Institute of Luoyang Tractor, Luoyang 471039, Henan, P. R. China;
3. China FAW Group Corporation, Changchun 130000, P. R. China
齿轮箱作为拖拉机、汽车重要的传动部件,其可靠性和耐久性至关重要,经常需要进行台架试验。齿轮箱的典型故障包括齿轮的齿面点蚀、剥落、齿面磨损及断齿,轴承的点蚀和剥落,轴的断裂以及壳体断裂。在齿轮箱疲劳寿命试验过程中,齿轮箱若发生严重故障,将可能导致试验设备的损坏以及试验人员的伤害。因此,齿轮箱的疲劳寿命试验都需要同时进行齿轮箱的故障监控,以确保及时发现故障停机,而且故障的早期发现也有利于对故障的原因进行分析。
近年来,数据分析方法的广泛应用,齿轮箱故障诊断有了长足发展。米林等[1]应用基于模糊支持向量机方法进行研究,试验结果表明该方法在变速器产品疲劳失效辨识中具有较高的准确性;金光等[2]研究得出可以运用阶次分析在故障发生初期来定位失效零件位置;王卫群[3]开发了变速器故障诊断专家系统,系统采用阶次分析方法和经典专家系统理论,诊断效果得到了试验验证;丁伟等[4]利用形态小波与排列熵结合的方法来进行变速器齿轮故障识别,最终得出原始信号进行形态小波降噪后所求得的排列熵能有效分类不同故障模式;梅自元等[5]应用基于经验模态分解与核马氏距离的方法进行研究,结论表明该方法可以有效识别出滚动轴承的故障程度并且可持续跟踪故障的发展趋势;He等[6]应用小波包变换评估齿轮箱不同种类的故障,具有较高的准确性;Zhou等[7]将EEMD(集合经验模态分解)算法用于在线监测并诊断齿轮的磨损状态;Smith[8]提出局部均值分解法对齿轮故障振动信号进行分解,然后提取出各个分量的调制信息以此进行故障诊断;Inoue等[9]采用二阶循环谱密度函数将调频信号信息分成了低频调频和高频载波频段2个循环频率域,然后再提取出相应的调制信息。以上的故障诊断方法都具有较强的数据处理能力,而且能够在齿轮箱的故障诊断中给出较为准确的判断,但同时也存在诊断系统对环境要求较高,系统本身价格高昂,而且有时不能满足特定试验条件下的监测需求等不足之处。
齿轮箱在发生故障前,箱体的振动信号会逐渐加剧,通过在齿轮箱箱体安装振动加速度传感器来测试振动信号可以实现故障的判断。由于齿轮、轴承所对应的不同故障类型的振动频率不同,对振动信号的频域分析可以定位典型故障源。
综上所述,针对齿轮箱疲劳试验,笔者开发出一套齿轮箱故障诊断系统,以齿轮箱的故障特征和信号的处理为基础,通过检测箱体的振动信号,在不停机和不拆箱的前提下,进行试验台架的实时监测与故障检测,通过时频域分析算法进行故障判定及其位置诊断,在故障出现的初期进行预警,并给出故障诊断结果。
1 基于振动信号的故障诊断在齿轮箱的疲劳寿命试验中,齿轮箱产生异常振动的主要原因是齿轮发生齿面磨损或轮齿根部产生裂纹甚至断齿等故障[10]。因此利用振动加速度时域信号幅值的变化可以判定故障的发生,但要确定故障类型,则需要进行频域分析。
时域信号x(t),样本长度为T,对其进行均匀采样后,可得到离散时间序列x(n),如果在该样本长度T内采集N个数据,则这个时域信号x(t)的离散傅里叶变换为
| $ \begin{aligned} X(k)=\sum\limits_{n=0}^{N-1} x(n) \mathrm{e}^{-j \frac{2 \pi}{N} k n} &=\sum\limits_{n=0}^{N-1} x(n)\left[\cos \left(\frac{2 \pi}{N} k n\right)-j \sin \left(\frac{2 \pi}{N} k n\right)\right], \\ k &=0, 1, \cdots, N-1 。\end{aligned} $ | (1) |
根据式(1)的实部XR(k)与虚部Xl(k)即可计算得出信号的幅值谱F和功率谱P,即
| $ F=\frac{2|\mathrm{DFT}(k)|}{N}=\frac{2}{N} \sqrt{X_{\mathrm{R}}^{2}(k)+X_{1}^{2}(k)}, $ | (2) |
| $ P=\frac{4|\mathrm{DFT}(k)|^{2}}{N^{2}}=\frac{4}{N^{2}}\left[X_{\mathrm{R}}^{2}(k)+X_{1}^{2}(k)\right] 。$ | (3) |
对原始信号进行处理得到的功率谱图中,某些频率处可能因为信号分布密集,区分度较低而无法清晰地分辨出相邻的谱峰,频谱细化分析能够把整个频率范围内的某段区域局部放大,获得更高的频率分辨率。
基于复解析带通滤波器的复调制细化是在传统复调制细化谱分析基础上,利用复解析带通滤波器进行选带细化谱分析,大大减少了计算工作量,提高了细化精度和细化倍数。具体原理为:首先确定采样频率fs、点数N以及新的谱线数M,原始频率分辨率ΔF=fs/N,要求在频带fa~fb处进行细化分析,则根据以上数据计算可得细化后的频率分辨率ΔF1=(fa-fb)/M,细化倍数D=ΔF1/ΔF,构造一个复解析带通滤波器,对时域信号每隔D点或2D点进行选抽滤波,然后对选抽后的复信号进行移频,将细化的起始频率移到零频点,最后进行FFT变换和谱分析,即可得到细化频谱。
2 故障诊断系统设计 2.1 硬件部分图 1所示为系统硬件结构框图。选用一个压电式加速度传感器采集齿轮箱振动信号,电荷放大器对信号进行放大滤波。温度传感器用于监测被试齿轮箱箱体内润滑油温度;转速传感器选用霍尔传感器,测试齿轮箱输入轴转速,输出脉冲信号。当诊断系统判断有故障发生时,通过IO端口驱动报警装置,利用蜂鸣器发声及指示灯闪烁进行提示。数据采集卡选用NI公司的PCI6014,实现AD转换、脉冲信号输入及IO输出。
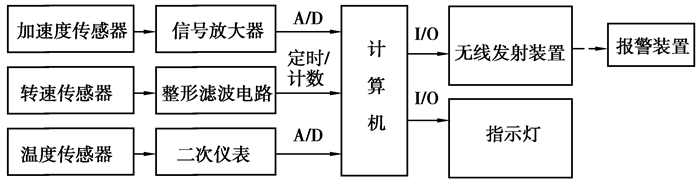
|
图 1 硬件系统框图 Fig. 1 Hardware system block diagram |
加速度传感器需要安装在靠近齿轮箱发生故障的部位,以缩短故障信号的传递路径,减少传递过程中的干扰,获取到更加丰富准确的故障信号,加速度传感器安装时,主轴轴线方向应与被测振动方向一致。
为了拆卸试件的方便,加速度传感器采用磁座吸附在齿轮箱箱体上,并调整位置以保证磁座紧密牢固地和箱体接触,图 2为加速度传感器安装图。

|
图 2 传感器安装位置 Fig. 2 Sensor installation location |
采用低通滤波器对加速度传感器采集的信号进行滤波,可以降低高频噪声对信号的干扰,在频谱分析时能够得到更好的处理效果。试验中采用北戴河实用电子研究所的SD-5A电荷放大器,具有2个通道的多级放大和低通滤波功能,对传感器输出的较小信号先进行适当放大,然后滤波后再进行输出放大,并具有过载保护功能。
2.2 软件功能与设计采用Matlab软件编写测试软件,实现用户交互、数据处理和故障诊断。软件的控制界面和实时监控界面如图 3所示。用户通过控制界面可选择试件类型,输入试件结构参数及试验设定值。试验进行过程中,实时监控界面展示测试信号的时域及频域信息。
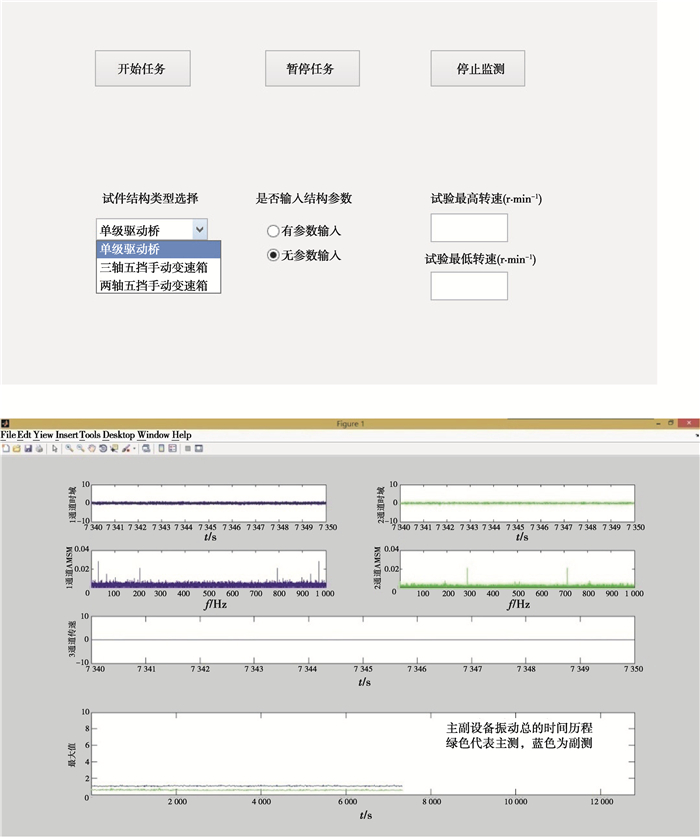
|
图 3 测试软件主界面 Fig. 3 The main interface of the test software |
图 4所示为测试软件程序流程图。系统首先通过录入的被试件结构参数及测试的输入轴转速确定结构特征频率,然后在试验之初通过自学习阶段确定故障停机阈值,最后对实时采样的数据进行时域频域分析处理,给出故障诊断结果。
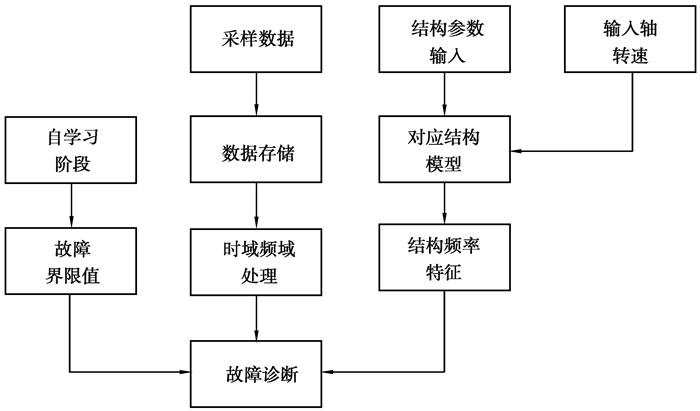
|
图 4 测试软件程序流程图 Fig. 4 Test software program flowchart |
对于运转中的被试件,其振动信号的幅值可以直接反映故障状态,在试验初期,采集获取试件正常工作状态下的平均振动水平,进而确定故障判定阈值,此即自主学习模块的主要功能。此外,为判定故障类型,需要根据试件结构参数及试验工况设置参数(输入转速、变速器挡位)计算特征频率,此为自主学习模块的另一功能。自主学习模块流程如图 5所示。
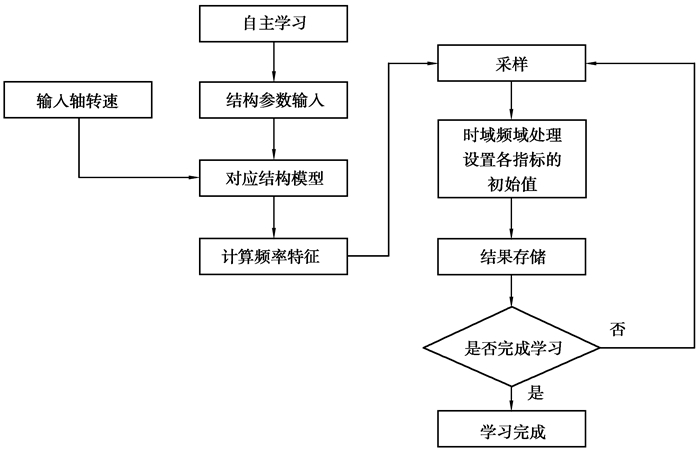
|
图 5 自主学习模块流程图 Fig. 5 Flow chart of autonomous learning module |
试验前输入结构参数,系统根据结构参数找到对应的结构模型同时参考输入转速计算出各特征频率。正式试验开始前对齿轮箱进行磨合,该系统自动检测齿轮箱的运行状态,当处于稳态工况时,系统会连续采样100周期的数据进行时频域分析,将计算结果进行相应处理求出均值,根据振动监测参考标准将均值乘以一定的系数获得报警界限值。最后将计算结果存储,供试验过程中故障诊断及试验后数据分析。
2.2.2 故障诊断算法故障诊断算法首先需要判定故障是否发生,进而确定故障的类型,定位发生故障的零件。利用自主学习模块获得的故障报警阈值可以判定故障的发生,在这之后,为进一步判定故障类型,需建立故障特征向量。
首先分析齿轮箱的结构,确定其主要零件的特征频率计算方法,然后根据不同故障形式建立故障特征向量。以驱动桥主动齿轮为例,设其齿数为n1,输入轴转频为f,则其特征频率f1(齿轮啮合频率)为
| $ f_{1}=f \cdot n_{1} 。$ | (4) |
定义诊断向量为
| $ \boldsymbol{P}=\left(P_{-2}, P_{-1}, P_{0}, P_{1}, P_{2}\right), $ | (5) |
式中P-2,P-1,P0,P1,P2分别为对应频率f1-2f,f1-f,f1,f1+f,f1+2f处的幅值,即啮合频率f1及两侧间隔为1倍、2倍转频的边频所对应幅值。
令学习阶段获得的诊断向量为基准向量P0,故障出现后的诊断向量为P1,定义特征向量F为故障后向量值和基准向量值的差值,点除以基准向量值,即:
| $ \boldsymbol{F}=\left(\boldsymbol{P}_{1}-\boldsymbol{P}_{0}\right) \cdot / \boldsymbol{P}_{0} 。$ | (6) |
根据特征向量各分量的大小就能够判断主动齿轮是否发生故障以及其类型。若只有中心频率对应的中间值较大,则为主动齿轮的均匀磨损;若中间值和边频对应的两侧数值均较大,则是产生不均匀性故障如局部磨损。故障诊断算法流程图如图 6所示。
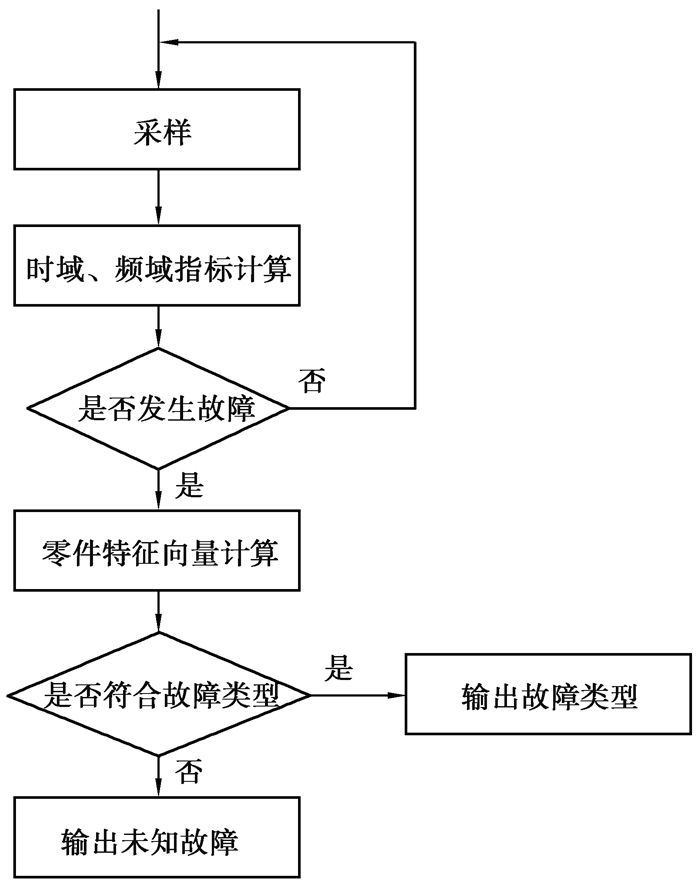
|
图 6 故障诊断算法流程图 Fig. 6 Flow chart of fault diagnosis algorithm |
在试验台进行某轻型载货汽车驱动桥疲劳试验,图 7所示为驱动桥闭式试验台。根据国家标准《汽车驱动桥台架试验方法》,设置各试验参数为输入转速200 r/min,加载满载扭矩1 000 N·m,采样频率1 000 Hz,目标转数为50万转,本次试验的30个试件中有1个试件在试验过程中系统发出故障预警而停机。

|
图 7 试验台 Fig. 7 Test bench |
在试验进行到14 h约17万转后,故障诊断系统报警停机。图 8所示是驱动桥箱体振动信号在停机前的4 100 s内的时域变化曲线,试验初始阶段的振动信号均值为0.44 g,停机阈值设为1.35 g。
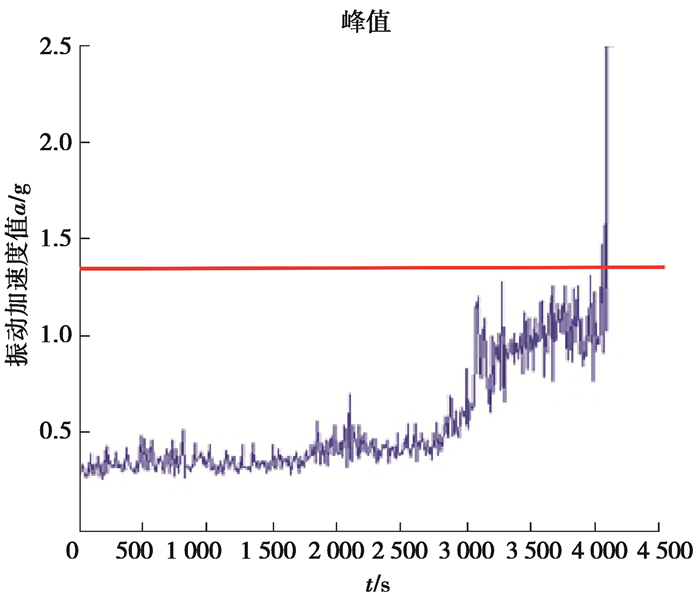
|
图 8 时域峰值图 Fig. 8 Time domain peak graph |
由图 8可以清晰发现时域峰值在故障前的这段时间内开始出现明显上升,尤其是在4 000 s处时域峰值急剧升高,说明此时振动激烈加剧,箱体内部故障开始恶化。
3.2 故障类型判定软件算法依据特征向量进行故障类型判定。已知输入转速为200 r/min,即频率为3.33 Hz,主动锥齿轮齿数为9,从动锥齿轮齿数为38,计算可得齿轮啮合频率为30 Hz,输出轴转动频率为0.79 Hz。分别对学习阶段(10 s)和故障发生时(4 000 s)的啮合频率及其两侧边频的幅值进行提取,其结果如表 1所示,代入公式(5)获得基准向量和故障向量,再利用公式(6)计算可表征主动锥齿轮故障的特征向量。
| 表 1 齿轮各频率处幅值 Table 1 The amplitude of each frequency of the gear |
基准向量:P0=(0.001,0.006,0.008,0.004,0.002);
故障向量:P1=(0.015,0.006,0.033,0.022,0.010);
特征向量:F=(14.000,0.000,3.125,4.500,4.000)。
由特征向量分析可知,中心频率和边频的幅值都有明显增加,表明主动锥齿轮产生了严重的局部磨损。
通过对试验过程中采集的振动信号进行时频域分析,也可得到相同结论。如图 9所示为设备停机前采集到的信号三维频谱图。
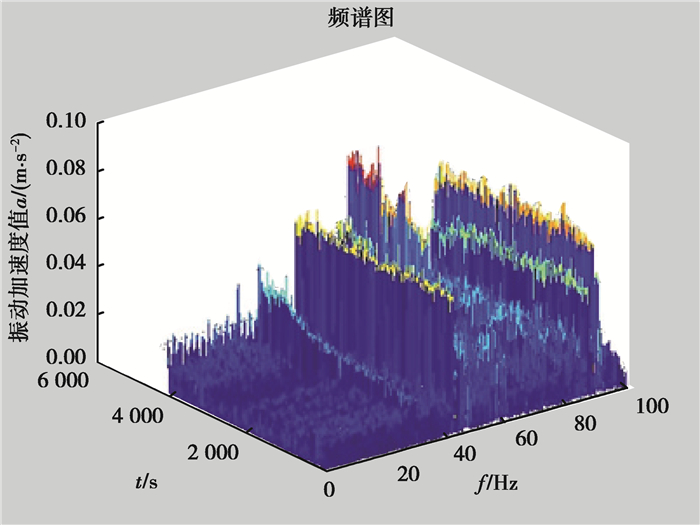
|
图 9 三维频谱图 Fig. 9 Three-dimensional spectrum |
图 9中x轴为0到100 Hz的频率轴,y轴为0到4 100 s的时间轴。可以看出信号频率分布随时间的变化情况,能够大体发现随着故障加剧,某些特定频率处幅值有明显升高。
由于图 9中频率的谱峰杂乱繁多,无法甄别有效信息,需要对图 9进一步处理。截取三维频谱图在10 s、4 000 s处的时间断面,如图 10所示。
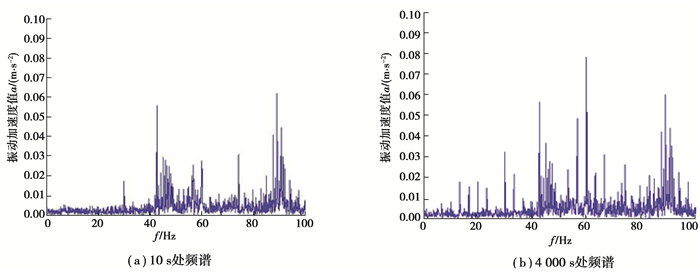
|
图 10 两处幅值谱图 Fig. 10 Two amplitude spectra |
对比图 10中(a)(b)2图可以发现:
1) 在0~20 Hz低频区域处,谱图于3.3 Hz整数倍频率处,即6.7,10.0,13.3,16.7,20.0 Hz等处出现谱峰。
2) 在30和60 Hz附近区域处,谱峰较试验开始时出现明显增加,两侧可见间隔为3.3 Hz的调制现象。
3) 在45和90 Hz附近区域处,边频带较多,幅值有所增加。
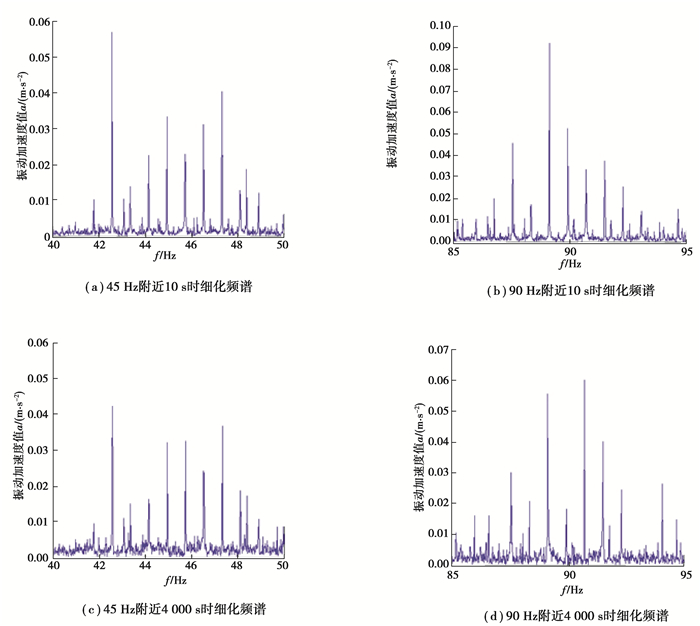
针对45和90 Hz附近的频谱,进行10倍的ZFFT细化频谱处理,得到如图 11所示的细化谱。
|
图 11 45,90 Hz处细化谱 Fig. 11 High resolution spectrum on 45 Hz and 90 Hz |
由图 11可知:
1) 0~20 Hz区域出现的3.3 Hz为输入转频,出现3.3 Hz倍频说明输入轴的振动信号产生波动。
2) 30 Hz是齿轮的啮合频率,60 Hz即是该频率的2倍频,对应频谱幅值的明显增加说明主动齿轮处发生故障。
3) 45 Hz和90 Hz处由细化谱可以看出其附近的调制频率为输出转频,说明该振动信号是由从动部分所产生,并且全程无明显变化,说明从动齿轮尚未发生故障。
由以上分析可知,齿轮在故障发展中首先表现为均匀磨损故障,随着时间进行,主动齿轮首先出现严重的局部磨损故障。
设备停机进行开箱检查时,可以看到主动锥齿轮的轮齿表面磨损非常严重,齿面产生裂缝,见图 12,证明了之前通过分析得到的齿轮故障发展过程的结论。

|
图 12 故障结果 Fig. 12 Failure results |
1) 设计开发了故障诊断系统,系统硬件采用加速度传感器测取被试齿轮箱箱体振动信号,系统软件实现故障预判算法和故障识别算法,在故障预判算法中利用学习模式自主确定故障诊断阈值,在故障识别算法中利用故障特征向量判别故障类型。
2) 将所开发的故障诊断系统应用于驱动桥疲劳试验,试验结果表明该系统可以实现故障监控和典型故障的故障识别。
| [1] |
米林, 王苏磊, 谭伟, 等. 基于模糊支持向量机的变速器新产品疲劳失效辨识方法[J]. 重庆理工大学学报(自然科学), 2017, 31(5): 1-5. Mi L, Wang S L, Tan W, et al. Study of fatigue failure identification method for transmission new product based on fuzzy support vector machine[J]. Journal of Chongqing University of Technology (Natural Science), 2017, 31(5): 1-5. (in Chinese) |
| [2] |
金光, 袁照丹, 姜冠伊, 等. 变速器总成耐久试验早期故障诊断[J]. 汽车技术, 2019(6): 53-58. Jin G, Yuan Z D, Jiang G Y, et al. Transmission premature failure diagnosis of transmission in durability test[J]. Automobile Technology, 2019(6): 53-58. (in Chinese) |
| [3] |
王卫群. 汽车变速器故障诊断专家系统研究[D]. 北京: 机械科学研究总院, 2006. Wang W Q. Study on expert system for diagnosis of automobile transmission faults[D]. Beijing: China Academy of Machinery Science and Technology, 2006. (in Chinese) |
| [4] |
丁伟, 张志刚, 姚练红, 等. 基于形态小波与排列熵的变速器齿轮故障识别方法[J]. 机械传动, 2019, 43(10): 165-168. Ding W, Zhang Z G, Yao L H, et al. Fault recognition method of transmission gear based on morphological wavelet and permutation entropy[J]. Journal of Mechanical Transmission, 2019, 43(10): 165-168. (in Chinese) |
| [5] |
梅自元, 钟维, 齐振峰. 基于EMD与核马氏距离的变速器轴承故障程度评估研究[J]. 江西化工, 2019(5): 56-58. Mei Z Y, Zhong W, Qi Z F. Study of gear box bearing fault degree based on fusion of EMD and nuclear mahalanobis distance[J]. Jiangxi Chemical Industry, 2019(5): 56-58. (in Chinese) |
| [6] |
He Q B, Yan R Q, Gao R X. Wavelet packet base selection for gearbox defect severity classification[C]//2010 Prognostics and System Health Management Conference. January 12-14, 2010, Macao, China. IEEE, 2010: 1-5.
|
| [7] |
Zhou Y Q, Tao T, Mei X S, et al. Feed-axis gearbox condition monitoring using built-in position sensors and EEMD method[J]. Robotics and Computer-Integrated Manufacturing, 2011, 27(4): 785-793. DOI:10.1016/j.rcim.2010.12.001 |
| [8] |
Smith J S. The local mean decomposition and its application to EEG perception data[J]. Journal of the Royal Society, Interface, 2005, 2(5): 443-454. DOI:10.1098/rsif.2005.0058 |
| [9] |
Inoue T, Sueoka A, Kanemoto H, et al. Detection of minute signs of a small fault in a periodic or a quasi-periodic signal by the harmonic wavelet transform[J]. Mechanical Systems and Signal Processing, 2007, 21(5): 2041-2055. DOI:10.1016/j.ymssp.2006.09.002 |
| [10] |
史同杰. 汽车传动箱故障诊断系统研究[D]. 长春: 吉林大学, 2014. Shi T J. Research on the fault diagnosis system of automotive transmission[D]. Changchun: Jilin University, 2014. (in Chinese) |
 2021, Vol. 44
2021, Vol. 44


