机器人的路径规划在一定程度上反映了机器人的研发水平[1]。研究学者在机器人路径规划方面已经研发出了较多的规划方法。由于当下仍处于优化阶段,不同规划路径方法均有自身特点及其优劣性,不同规划方法面向的应用领域也不尽相同[2-3]。对移动机器人路径规划的主要目的是获取机器人从某一位置起始点到需要到达的位置点的可行路径。在众多可行路径中通过对移动路径的行走距离、移动时间及机器人能耗等不同指标进行择优即为对机器人路径规划的优化。通过在机器人上装置传感器从而满足对周围环境进行探测,通过对外界障碍物的位置进行感知可以有效改变运动路径,规避障碍物从而实现避障[4-5]。
在路径规划中可以分为传统的路径规划算法和智能规划算法两大类[6]。在实际规划中,通常有衍生出各算法的改进算法以及混合算法[7]。机器人路径规划中最基础的算法为遗传算法,该算法是一种使用随机迭代进行搜索运动路径的规划方法[8]。该算法引用生物遗传学对自然法则进行延伸并在路径规划中广泛应用[9],通过消除迭代过程中不满足的因素,能够实现最优路径的搜索[10]。该算法在解码种群适应度函数时会存在较大的计算量,从而导致系统处理时间较长,效率低下。改进算法主要是对算法中适应度函数问题进行改进[11]。鲸鱼算法主要是对鲸鱼的群体捕食方法进行模拟。
文献[3]运用传统遗传算法对行走机器人的路径进行规划,使用该算法一般会存在收敛耗时较长、结果不稳定等规划问题。
文献[7]中使用了鲸鱼优化法来对机器人进行路径规划,该算法通过反复迭代来搜索目标,但是对于路径复杂情况,此算法迭代次数过多,不能快速地搜索到最终目标。
为弥补传统遗传算法的不足,笔者将改进遗传算法和鲸鱼优化法融合,增强移动机器人路径规划对动态环境的适应性能,以提高原算法的求解速度和准确率。
1 环境建模根据现实环境构建仿真环境来进行机器人的路径规划[12]。对于环境模型的创建不仅需要对其机器人实际移动路径有客观真实的反映,同时需要赋予算法良好的鲁棒性和稳定性。鲁棒性即针对创建的环境或构建的系统及规划流程本体变化所能保持的能力。稳定性即为构建的系统针对初始条件变化后自身所能保持的能力。为达到环境建模目的需要制定必要措施:
1) 当设定机器人处在二维平面移动时,机器人运动时可将其视为具有尺寸的圆在平面中进行移动,不再考虑三维环境中的高度因素。
2) 若二维平面中两个障碍物间的距离小于圆的直径(机器人长宽尺寸),则视其为整体障碍物,不能满足机器人通过。
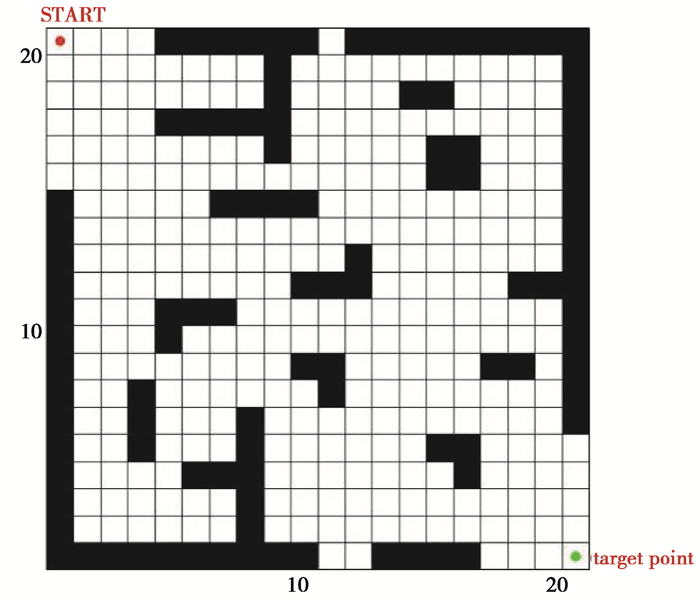
3) 路径规划过程使用网格设定机器人整体运动区间,建立二维结构化空间后,将障碍物网格和自动空间网格进行区分,如图 1所示,图中所有阴影区域为障碍物网格,其余为自由网格,每个网格尺寸相同,并适当选取2个位置点设定为机器人起始点(start)和目标点(target point)进行机器人路径规划前提。
|
图 1 环境模型 Fig. 1 Environment model |
采用鲸鱼算法与改进算法结合,预先使用鲸鱼算法对种群进行整体优化,提高整体种群质量;使用改进算法与鲸鱼算法相融合寻求最优解,可以有效解决遗传算法中存在的收敛耗时长,优化结果不稳定等规划时产生的问题,更快实现搜索目标提炼出最优算子,同时也可提高遗传算法的准确率。
2.1 改进遗传算法传统的遗传算法在对适应度函数进行求解时需要进行大量的计算,改进算法即是使用种群差异度之和的均值对适应度函数进行改进,改进遗传算法能运用于全局,加快机器人到达目标点的时间[13]。
2.1.1 改进遗传算法的设计为使目标函数最小化,将其定义为
| $ F_{\mathrm{it}}=\sum\limits_{l=1}^{N} F(l) / F(t) 。$ | (1) |
运用差异度函数D(t),适应度函数为D(t)与Fit的乘积, 产生的差异度是:
| $ D(i, j)=\frac{1}{K} \sum\limits_{l=1}^{K}\left(x_{i l}-x_{j l}\right), i, j=1,2, \ldots, N, $ | (2) |
| $ x_{i k}-x_{j k}= \begin{cases}0 & x_{i k}=x_{j k}, \\ 1 & x_{i k} \neq x_{j k},\end{cases} $ | (3) |
其中xik和xjk二者代表个体xi和xj第k位的值。
D(t)表示除t以外群体差异度之和的均值:
| $ D(t)=\frac{1}{N-1} \sum\limits_{i \neq t}^{N} D(t, i) \quad i \neq t 。$ | (4) |
适应度函数是:
| $ F_{\mathrm{it}}=D(t) \cdot \sum\limits_{l=1}^{N} F(l) / F(t) 。$ | (5) |
遗传算法中选择算子是从群体中选择个体优良、排除劣质,它通过个体适应性能评估后将劣质个体替换掉,保存优秀个体[14]。具体步骤如下:
Step1:对种群适应度数值F进行统计,对最短和最长路径Fmin,Fmax的适应度值分别进行记录。
Step2:F'即在[Fmin,Fmax]区间内出现。
Step3:依次用F'与各个体的数值进行比较,得出高个体和低个体。
Step4:将Sep3中的个体进行替换,即高个体替换低个体。
Step5:循环上述步骤,直到得出高个体数目。
通过上述步骤选择保存优胜个体数,使种群多样性得到保障且避免算法提前收敛结束。
2.1.3 交叉算子研究中使用交叉算子中的两点交叉,使用该算子进行编码时可以在两点交叉后对部分基因进行交换。具体操作步骤为:
1) 随机设置两两相配的编码交叉点。
2) 将两个交叉点之间的部分个体进行交换。
2.1.4 修正算子在机器人运行空间中,若只通过随机取值不易得到可靠路径,需要多次重复算子,此时需要修正算子。由沿墙导航法可知在对未知路径进行修正时,需要通过检测不同路径择优选取可行路径,再对存在障碍物的路径段进行修正[15]。
2.1.5 优化算子在使用改进遗传算法对机器人路径进行规划时,有时会出现上代种群适应度会优于下代适应度的情况。为更好选出最优适应度算子,一般运用个体保留法,即将上下代中的最优个体进行比较,如果上代个体更优,则记录上代最优个体为当前最优个体。反之,使用下代最优个体对当前最优个体进行替换,从而可以良好保持种群的进化。
2.2 鲸鱼优化算法该算法通过对鲸鱼群体捕猎进行研究提出的一种算法,对捕猎过程进行模拟。根据鲸鱼捕食的搜索策略,此算法不需大规模网络搜索,经过多次送代实现收敛的最优解。使用该优化方法的参数较少且容易布局,拥有科学的局部优化机制且可实现全局智能搜索。
2.2.1 包围猎物通过不断接近或者围捕猎物位置,当最佳座头鲸位置产生后其他搜索将向该位置靠近,其公式为
| $ X(j+1)=X(j)-A \cdot D, $ | (6) |
| $ D=\left|C \cdot X^{*}(j)-X(j)\right|, $ | (7) |
式中:A,C分别代表变量的系数;X*(j)指代最优鲸鱼位;X(j)为当前鲸鱼位;j为进行迭代搜索的次数。A和C的求解公式为
| $ A=2 a \times r-a, $ | (8) |
| $ C=2 r, $ | (9) |
式(8)和(9)中a是一个常数,其区间为[0, 2],以递减形式呈现,更新方式为
| $ a=2-\frac{2 j}{M}, $ | (10) |
其中M代表最终迭代次数,r的取值范围是0~1。
2.2.2 发泡网主要针对鲸鱼吐气泡的捕食方式进行数字模拟。
1) 包围并收缩:将式(8)中的a值进行减少,A的区间原定为[-a,a],a的取值会随着包围范围大小变化而改变,当a为确定数值时即确定了包围位置和收缩范围。
2) 螺旋式位置更新:分析出鲸鱼群体位置,然后计算猎物具体位置,引入螺旋式位置
| $ X(m+1)=D^{\prime} \mathrm{e}^{b l} \cos (2 {\rm{ \mathsf{ π} }} d)+X^{*}(m), $ | (11) |
| $ D^{\prime}=\left|X_{m}^{*}-X_{m}\right|, $ | (12) |
式中:b为常数;D'为鲸群与猎物间距离;m范围为[-1, 1]。
捕猎时,鲸鱼通过螺旋游动逼近猎物并不断压缩范围,位置更新阅值为1/2时公式为
| $ X(m+1)= \begin{cases}X(m)-A \cdot D, & p<0.5, \\ D^{\prime} \mathrm{e}^{b l} \cos (2 {\rm{ \mathsf{ π} }} d)+X(m) & p \geqslant 0.5,\end{cases} $ | (13) |
式中p为[0, 1]上的任意数值。
2.2.3 搜索猎物鲸鱼一般在特定范围内进行随机捕猎食物,只需捕捉位置最近的猎物而并非要捕食每个鲸鱼的目标猎物。因此,当A不在[-1, 1]时,鲸鱼会放弃之前的意向目标转为捕捉与自身位置最近的目标猎物。公式为
| $ D=\left|C \cdot X_{\text {rand }}-X(m)\right|, $ | (14) |
| $ X(m+1)=X_{\text {rand }}-A \cdot D, $ | (15) |
式(14)与(15)中Xrand表示鲸鱼个体随机位置。
2.2.4 移动机器人路径规划步骤Step 1:设定种群的数量规模X,并随机分布鲸鱼的位置点。
Step2:对每只鲸鱼各自的适应度值进行计算并进行对比,获取适应度值最优的个体X'。
step3:当P < 0.5且A < 1,则鲸鱼群体中每个个体均以公式(6)来实现位置点的变化,否则按照公式(15)更新鲸鱼个体位置。如果P≥0.5,则运用公式(13)更新。
Step4:在全局最优状态下对鲸鱼种群进行重新评估,获取鲸鱼及其各自位置信息。
Step5:若达到该算法的终止条件则停止迭代,获取最大迭代次数;若未达到终止条件会继续转入Step2中进行再次迭代。
step6:输出全局最优解X。
3 仿真研究 3.1 静态环境路径规划仿真上述通过理论分析2种算法融合的优点,现对改进鲸鱼融合算法在静态环境上进行路径规划时的优越性进行验证。试验中使用matlab软件根据算法进行路径规划仿真分析。在模拟出相同的环境下使用3种算法进行验证,以证实改进遗传鲸鱼融合算法相对于遗传算法、改进遗传算法的优势所在。
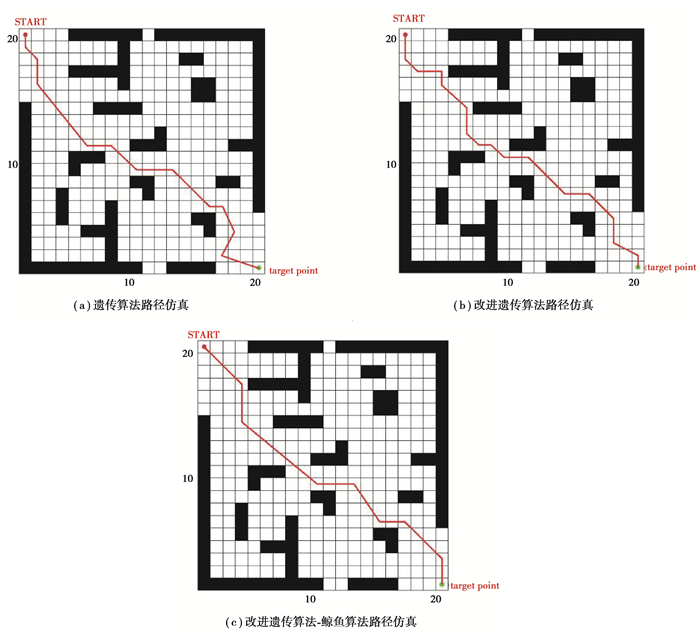
试验中建立20 m×20 m的栅格作为整体环境模型,使用3种不同算法进行仿真分析,并对遗传算法、改进遗传算法和改进遗传鲸鱼融合算法的路径进行对比分析。在matlab软件中进行仿真,设定遗传算法初始种群,通过精英选择法确定算子,该算法参数涵盖了:遗传算法种群规模M=100,交叉概率Pc=0.7,变异概率Pm=0.01,最大迭代次数T=100。为满足对比需要,鲸鱼算法的种群规模及迭代次数与遗传算法的参数相同。经过仿真试验分析,3种算法规划出的最佳运动路径分别如图 2(a)(b)(c)所示,静态仿真适应度函数曲线如图 3所示。
|
图 2 在静态环境下的3种算法的路径仿真对比 Fig. 2 Comparison of the path simulation of three algorithms in static environment |
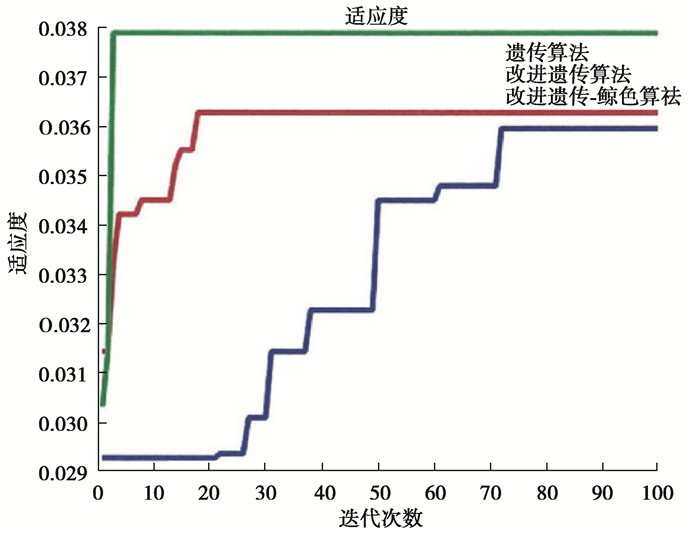
|
图 3 适应度函数曲线 Fig. 3 Adaptability function curve |
实验表明遗传算法运动路径为31.67 m,改进遗传算法运动路径为31.34 m,改进遗传鲸鱼融合算法的机器人运动路径位移为30.34 m。通过分析适应度函数,遗传算法经过75次迭代后终止迭代,系统运算的收敛速率慢。改进算法通过19次迭代后进入稳定。使用改进遗传鲸鱼融合算法进行2次迭代后状态稳定。数据对比如表 1所示。
| 表 1 3种算法位移与时间对比 Table 1 Comparison of displacement and time of three algorithms |
通过分析实验数据可知,将优化后的两种算法结合能够大幅度提升收敛速度并且可避免陷入局部循环,综合运用两种模式搜索移动机器人最优路径时,产生的效果要优于传统的遗传算法和改进遗传算法。
3.2 动态环境路径规划仿真上诉仿真实验中仅使用算法在静态环境下进行路径规划分析。现设定动态环境使用3种算法分别进行实验分析,验证在不同的模拟环境下,改进遗传鲸鱼融合算法相对于遗传算法、改进遗传算法的优势所在,下面对3种算法进行机器人动态环境路径规划仿真试验分析。
仿真实验中同样采用栅格环境,设定机器人传感器探测半径为1 m,机器人与环境中存在的障碍物之间的安全阈值为0.1 m,设定2个动态障碍物为D1,D2。其中D1的运动路径为图中绿色标识,D2运动路径为蓝色标识,2个动态障碍物匀速往返于各自设定轨迹。对于机器人在遇到上述2个障碍物的情形下,采用3种算法规划全局路径。
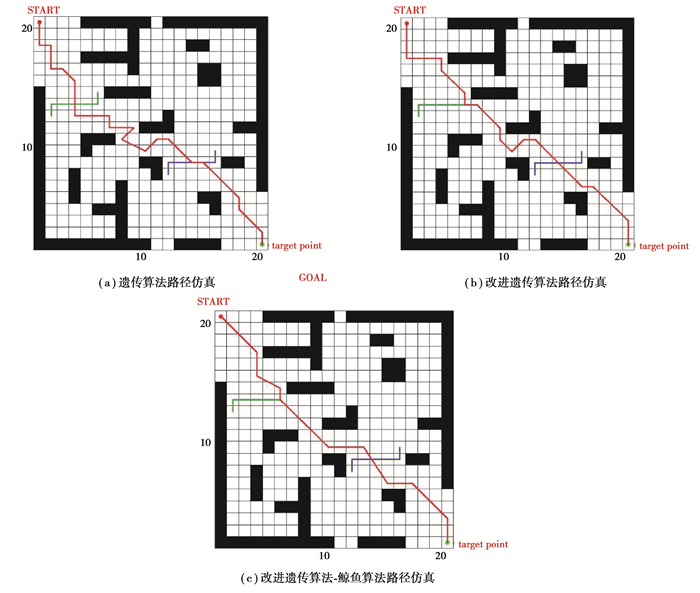
经过matlab软件对机器人运动路径在动态环境下仿真试验分析后,3种算法规划出的最佳运动路径分别如图 4(a)(b)(c)所示,动态仿真适应度函数曲线如图 5所示。
|
图 4 在动态环境下的3种算法的路径仿真对比 Fig. 4 Comparison of the path simulation of three algorithms in dynamic environment |
|
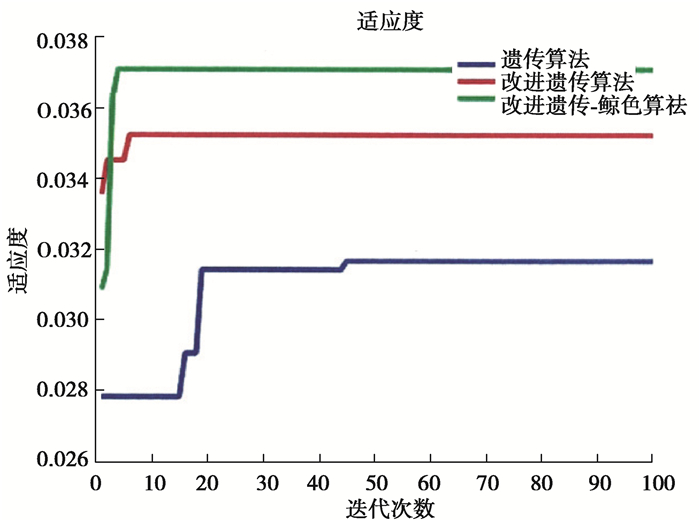
图 5 适应度函数曲线 Fig. 5 Adaptability function curve |
实验表明遗传算法路径位移为33.34 m,改进遗传算法路径位移为29.67 m,改进遗传鲸鱼融合算法的机器人运动路径位移为28.71 m。通过分析适应度函数,遗传算法经过48次迭代后终止迭代,改进算法经过7次迭代后停止,而融合算法仅经过2次迭代。数据对比如表 2所示。
| 表 2 位移与时间对比 Table 2 Comparison of displacement and time |
3种算法在遇到动态障碍物均进行了实时局部路径规划。根据位移和用时明确得到:改进遗传鲸鱼融合算法得到的路径规划结果优于遗传算法和改进遗传算法。
4 结语通过运用改进遗传算法与鲸鱼算法结合并通过设定的静态障碍物环境和动态障碍物环境2种状态下对机器人进行路径规划试验。机器人运动路径规划分别运用遗传算法、改进遗传算法、融合算法3种方法进行仿真实验,并通过试验对比验证了融合算法自身的优越性。减少了迭代次数,缩短了机器人路径规划时长,并实现了机器人运动路径的位移长度缩短,从而达到了最佳路径规划目的。现实路径规划存在于动态环境中,障碍物都有一定程度的复杂因素,深入探索复杂环境,实时反馈传感器信息,提升路径规划,进一步优化算法是未来研究方向。
| [1] |
刘云, 肖雪. 基于邻域维护准则的特征选择算法优化研究[J]. 重庆大学学报, 2019, 42(3): 58-64. Liu Y, Xiao X. Research on optimization of feature selection algorithm based on neighborhood preservation criterion[J]. Journal of Chongqing University, 2019, 42(3): 58-64. (in Chinese) |
| [2] |
褚鼎立, 陈红, 王旭光. 基于自适应权重和模拟退火的鲸鱼优化算法[J]. 电子学报, 2019, 47(5): 992-999. Chu D L, Chen H, Wang X G. Whale optimization algorithm based on adaptive weight and simulated annealing[J]. Acta Electronica Sinica, 2019, 47(5): 992-999. (in Chinese) DOI:10.3969/j.issn.0372-2112.2019.05.003 |
| [3] |
龙建全. 复杂环境下移动机器人的路径规划[D]. 绵阳: 西南科技大学, 2019. Long J Q. Path planning of mobile robots in complex environment[D]. Mianyang, China: Southwest University of Science and Technology, 2019. (in Chinese) |
| [4] |
Fang W, Sun J, Chen H H, et al. A decentralized quantum-inspired particle swarm optimization algorithm with cellular structured population[J]. Information Sciences, 2016, 330: 19-48. DOI:10.1016/j.ins.2015.09.055 |
| [5] |
Li Z J, Deng J, Lu R Q, et al. Trajectory-tracking control of mobile robot systems incorporating neural-dynamic optimized model predictive approach[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2016, 46(6): 740-749. DOI:10.1109/TSMC.2015.2465352 |
| [6] |
裴以建, 杨亮亮, 杨超杰. 基于一种混合遗传算法的移动机器人路径规划[J]. 现代电子技术, 2019, 42(2): 183-186. Pei Y J, Yang L L, Yang C J. Mobile robot path planning based on a hybrid genetic algorithm[J]. Modern Electronics Technique, 2019, 42(2): 183-186. (in Chinese) |
| [7] |
梁凯, 陈志军, 闫学勤. 移动机器人路径规划仿真研究[J]. 现代电子技术, 2018, 41(17): 167-172. Liang K, Chen Z J, Yan X Q. Simulation study on effective path planning for mobile robot[J]. Modern Electronics Technique, 2018, 41(17): 167-172. (in Chinese) |
| [8] |
Ardizzon G, Cavazzini G, Pavesi G. Adaptive acceleration coefficients for a new search diversification strategy in particle swarm optimization algorithms[J]. Information Sciences, 2015, 299: 337-378. DOI:10.1016/j.ins.2014.12.024 |
| [9] |
Chen C L P, Wen G X, Liu Y J, et al. Observer-based adaptive backstepping consensus tracking control for high-order nonlinear semi-strict-feedback multiagent systems[J]. IEEE Transactions on Cybernetics, 2016, 46(7): 1591-1601. DOI:10.1109/TCYB.2015.2452217 |
| [10] |
Zhang Y Y, Li S. Distributed biased Min-consensus with applications to shortest path planning[J]. IEEE Transactions on Automatic Control, 2017, 62(10): 5429-5436. DOI:10.1109/TAC.2017.2694547 |
| [11] |
侯翔. 基于人工势场和量子遗传算法的移动机器人路径规划方法[J]. 计算机应用与软件, 2018, 35(6): 263-266, 333. Hou X. Mobile robot path planning method based on artificial potential field and quantum genetic algorithm[J]. Computer Applications and Software, 2018, 35(6): 263-266, 333. (in Chinese) DOI:10.3969/j.issn.1000-386x.2018.06.048 |
| [12] |
王功亮, 王好臣, 李振雨, 等. 基于优化遗传算法的移动机器人路径规划[J]. 机床与液压, 2019, 47(3): 37-40, 100. Wang G L, Wang H C, Li Z Y, et al. Path planning for mobile robots based on optimized genetic algorithm[J]. Machine Tool & Hydraulics, 2019, 47(3): 37-40, 100. (in Chinese) |
| [13] |
Al Dabooni S, Wunsch D. Heuristic dynamic programming for mobile robot path planning based on Dyna approach[C]//2016 International Joint Conference on Neural Networks (IJCNN). July 24-29, 2016, Vancouver, BC, Canada. IEEE, 2016: 3723-3730.
|
| [14] |
Gavrilov A V, Lenskiy A. Mobile robot navigation using reinforcement learning based on neural network with short term memory[C]//Advanced Intelligent Computing, 2012: 210-217.
|
| [15] |
Zhang Y Y, Li S, Guo H L. A type of biased consensus-based distributed neural network for path planning[J]. Nonlinear Dynamics, 2017, 89(3): 1803-1815. DOI:10.1007/s11071-017-3553-7 |
 2021, Vol. 44
2021, Vol. 44


