2. 新疆工程学院 煤矿机电工程技术研究中心, 乌鲁木齐 830023
2. Coal-mine Electromechanical Engineering Technology Research Center, Xinjiang Institute of Engineering, Urumqi 830023, P. R. China
风能作为一种清洁可再生能源,具有容量大、开发和维护成本低的优势,近年里在全球范围内得到了大规模发展。全球风能理事会统计数据[1]表明风能已经成为全球能源结构的重要组成部分,对缓解环境污染发挥着越来越重要的作用。风电叶片作为风电机组的关键部件是能量吸收的载体,占据机组约20%的成本,同时也是风电机组载荷的主要来源,风电叶片的强度和可靠性对风电机组的寿命和能量输出至关重要。
Haselbach等[2]采用内聚力和三维实体单元建立了包含分层损伤的叶片段模型,探讨了梁帽初始分层对叶片承载能力的影响。结果表明当初始分层缺陷位于梁帽表层时,在操作工况下叶片梁帽发生屈曲,且分层位置应力显著增加;当初始缺陷位于梁帽中间层时,设计载荷下叶片梁帽承载能力未见明显下降,承载能力满足设计要求。Chen等[3]对52.3 m叶片进行极限强度测试,发现叶片过渡段的梁帽和腹板分层是叶片失效的主要原因,而叶片局部屈曲引起的面外变形对叶片失效起重要作用。Overgaard等[4-5]对25 m叶片进行失效测试和数值仿真分析,发现分层和局部屈曲是叶片失效的主要原因。丹麦Risø可再生能源国家实验室的Jensen等[6]对34 m玻璃纤维/环氧预浸料复合材料叶片进行挥舞极限强度测试,实验结果和有限元分析均显示叶片失效从外层壳体胶接脱粘开始,紧接着是叶片屈曲分层。Francisco等[7]通过叶片段加载试验发现摆振加载条件下叶片尾缘屈曲是叶片发生破坏的起始失效模式,对叶片结构的失效发展有重要影响。
薛彩虹等[8]采用FiberSIM、CATIA以及有限元软件对40 m水平轴风电机组叶片进行屈曲分析,根据德国船级社GL规范[9],考察了4个极限工况下叶片的屈曲行为和载荷因子。结果表明4个方向的线性屈曲载荷因子均满足规范要求。针对叶片最大弦长处易发生屈曲的现象,苏成功等[10]对叶片最大弦长10~14 m截面段进行数值建模,分析了夹芯厚度、补强、以及增加剪切腹板对叶片段屈曲载荷的影响,得出尾缘中部增加剪切腹板是提高尾缘屈曲载荷的最有效方法。靳交通等[11]通过实验和有限元方法得出叶片结构屈曲是导致叶片进一步破坏的主因。牛春辉[12]在分析某2.5 MW风电机组叶片后缘开裂失效事故时得出叶片后缘8~12 m区域局部稳定性不足是叶片失效的主要原因。袁巍华等[13]在100 kW叶片基础上建立叶片有限元模型,分析了不同尾缘增强方法对叶片特征值屈曲的影响,结果表明增加尾缘复合材料铺层可以有效提高叶片的抗屈曲载荷,但也明显增加了叶片的重量。黄吉等[14]采用内聚力单元和三维实体单元建立叶片段有限元模型,分析了叶片复合材料和结构胶失效、屈曲以及胶结脱粘,结果表明在摆振载荷下叶片段首先出现非线性屈曲失稳,然后是复合材料失效、胶接脱粘以及结构胶断裂。
可以看出,叶片复合材料失效和屈曲失稳是导致叶片结构强度不足的重要原因。笔者建立了风电叶片复合材料结构非线性有限元模型,依据GL规范对载荷和安全因子的具体要求,探讨了叶片复合材料强度和结构屈曲稳定性,为叶片结构设计和强度校核提供参考。
1 叶片结构强度叶片不仅受到结构刚度和叶尖挠度的约束,还需要满足材料强度和结构稳定性的要求,使得叶片在极限外载荷作用下不发生材料失效和结构失稳。
1.1 复合材料强度现代大型风电叶片由纤维增强聚合物基复合材料制造,不同于传统各向异性材料,复合材料的失效规律更加复杂。因此在判断叶片复合材料失效时,本研究中采用蔡吴失效准则,该失效准则考虑复合材料各向异性,被广泛应用于复合材料失效的判据[15],其表达式为:
| $ {{F_{11}}\sigma _1^2 + 2{F_{12}}2{\sigma _1}{\sigma _2} + {F_{22}}\sigma _2^2 + {F_{66}}\tau _{12}^2 + {F_1}{\sigma _1} + {F_2}{\sigma _2} = 1,} $ | (1) |
| $ {{F_1} = \frac{1}{{{X_{\rm{t}}}}} - \frac{1}{{{X_{\rm{c}}}}},} $ | (2) |
| $ {{F_{11}} = \frac{1}{{{X_{\rm{t}}}{X_{\rm{c}}}}},} $ | (3) |
| $ {{F_2} = \frac{1}{{{Y_{\rm{t}}}}} - \frac{1}{{{Y_{\rm{c}}}}},} $ | (4) |
| $ {{F_{22}} = \frac{1}{{{Y_{\rm{t}}}{Y_{\rm{c}}}}},} $ | (5) |
| $ {{F_{66}} = \frac{1}{{{S^2}}},} $ | (6) |
式中:F11、F12、F22、F66、F1以及F2为张量系数;Xt和Xc分别为复合材料沿纤维主方向的拉伸和压缩强度;Yt和Yc分别为复合材料垂直于纤维主方向的拉伸和压缩强度;S为复合材料平面内的剪切强度;s1为纤维方向的应力;s2为垂直纤维方向的应力;τ12为面内剪切应力。
1.2 结构线性和非线性屈曲屈曲稳定性是叶片复合材料薄壳结构安全性分析的重要方面。根据经典结构稳定性理论[16],线性屈曲为经典的特征值屈曲,根据线弹性前屈曲载荷位移关系,则有
| $ {P_0} = {\mathit{\boldsymbol{K}}_{\rm{e}}}{u_0}, $ | (7) |
式中:Ke为弹性刚度矩阵;u0为施加载荷P0的位移。
假设前屈曲位移很小,在任意状态下,载荷P、位移u以及应力σ的增量平衡方程为
| $ \Delta P = ({\mathit{\boldsymbol{K}}_{\rm{e}}} + {\mathit{\boldsymbol{K}}_\sigma }(\sigma ))\Delta u, $ | (8) |
式中Kσ(σ)为某应力状态下计算的初始应力矩阵。
假设前屈曲行为是一个外加载荷P0的线性函数,P=λP0,u=λu0,σ=λσ0,这里的σ0为与u0对应的应力,则可得,
| $ {\mathit{\boldsymbol{K}}_\sigma }(\sigma ) = \lambda {\mathit{\boldsymbol{K}}_\sigma }({\sigma _0}), $ | (9) |
式中:λ为载荷比例因子;Kσ(σ0)为σ0应力状态下计算的初始应力矩阵。
因此,整个前屈曲范围内的增量平衡方程变为
| $ \Delta P = ({\mathit{\boldsymbol{K}}_{\rm{e}}} + \lambda {\mathit{\boldsymbol{K}}_\sigma }({\sigma _0}))\Delta u。$ | (10) |
在不稳定性开始时(屈曲载荷Pcr),在P0=0的情况下,结构会出现一个变形Δu。
把表达式ΔP0=0代入前屈曲范围内的增量平衡方程(10),则有
| $ ({\mathit{\boldsymbol{K}}_{\rm{e}}} + \lambda {\mathit{\boldsymbol{K}}_\sigma }({\sigma _0}))\Delta u = 0。$ | (11) |
上述关系表达式为经典的屈曲特征值问题。
为了满足表达式(11),则有
| $ {\rm{det}}({\mathit{\boldsymbol{K}}_{\rm{e}}} + \lambda {\mathit{\boldsymbol{K}}_\sigma }({\sigma _0})) = 0。$ | (12) |
对于n个自由度的有限元模型,式(12)产生特征值λ的n阶多项式,这种情况下,特征向量表示屈曲时叠加到系统上的变形,由计算出λ的最小值给定弹性临界载荷Pcr。
在实际结构中,由于存在扰动、结构缺陷以及非线性行为,很难达到临界载荷。因此采用特征值屈曲一般产生非保守解。而非线性屈曲考虑真实扰动和非线性因素的影响,在预测结构稳定性方面更接近真实失稳载荷。
2 叶片模型 2.1 叶片载荷对于极限计算,采用GL windclass 2A,其50年一遇极端风(3S)达到59.5 m/s。对于疲劳计算,湍流风模型采用Kaimal模型。载荷工况基于GL规范[9]进行定义。结构分析采用FOCUS 5软件中的Farob模块。采用的载荷工况不考虑地震、风场特定风况和极端温度影响,但考虑结冰工况,维修和运输工况也作为极限工况进行载荷评估。适用风场类型为GL-2010 2A,参考风速取为42.5 m/s,平均风速取8.5 m/s,空气密度取1.225 kg/m3。除了EWM风模型的指数取0.11外,其他风模型垂直风廓线指数为0.2。为了考虑山地引起的入流风速变化,取风的入流倾角为8°。图 1为叶片极限载荷分布,分别为最小挥舞载荷、最大挥舞载荷、最小摆振载荷以及最大摆振载荷。
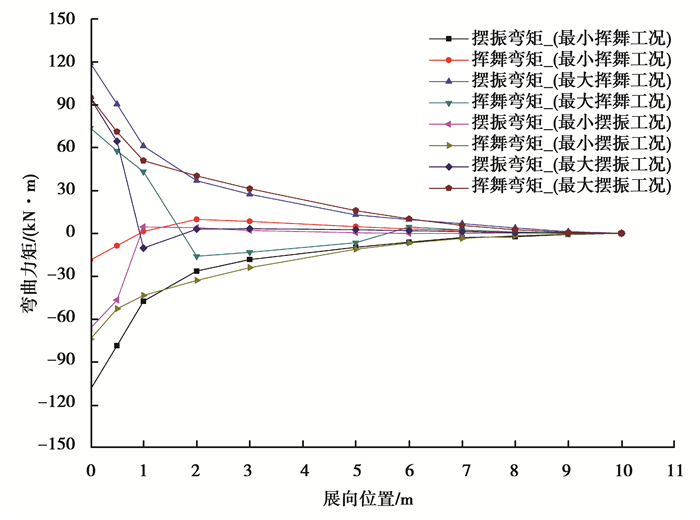
|
图 1 叶片极限载荷 Fig. 1 The extreme loads of the 100 kW blade |
采用ANSYS建立全尺寸叶片有限元模型,叶片复合材料结构采用Shell181层合单元描述,该单元为4结点6自由度单元,分别为3个平动和3个转动自由度。适合模拟薄壳和中等厚度壳体结构,适用于线性、大扭转和应变非线性计算。
根据气动设计得到的翼型沿叶片长度方向的弦长和扭角分布,在ANSYS前处理中建立叶片几何模型,根据叶片结构设计过程中得到的叶片铺层位置和结构,划分叶片铺层分布区域,建立叶片壳体层合板和夹芯结构铺层分区。然后划分叶片模型网格并完成叶片铺层结构设置,约束叶片根部截面所有自由度(图 2(a))。将叶片极限弯矩转换成剪力载荷,确保叶片截面所承受的弯矩载荷不小于设计值。针对每一个载荷施加截面(图 2(b)),选取叶片截面段上梁帽位置的结点施加剪切力载荷。选择叶片段梁帽的加载方式具有两方面优势:既有利于避免载荷施加点的应力集中,又可避免载荷直接施加在夹芯或者薄层复合材料上。
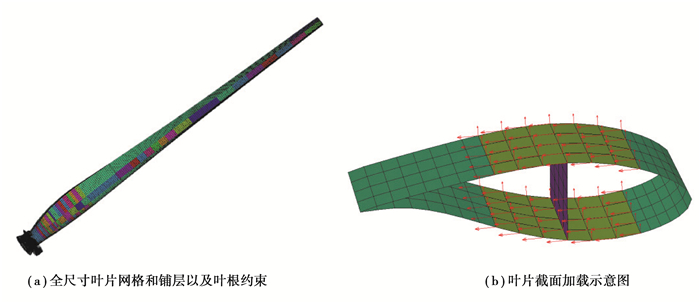
|
图 2 叶片有限元模型 Fig. 2 The finite element model of the wind blade |
叶片实测总质量为245 kg;数值模型叶片质量206 kg,包括叶片根部、腹板、蒙皮、梁帽结构,不包括电缆、结构胶、螺栓套和楔形条,其中结构胶、螺栓套以及楔形条质量约36 kg;数值模型计算出的叶片质量与实测偏差为1.2%。在叶片质量方面,数值模型与实测值具有很好的一致性。
3 结果分析 3.1 极限强度非线性分析在叶片极限强度分析中,考虑叶片大变形非线性效应,采用蔡吴失效准则判断叶片强度。
3.1.1 最小挥舞在最小挥舞载荷下叶片展向应变和失效因子分布如图 3所示(其中,上图为压力面,下图为吸力面)。由图 3(a)可以看出,较大的应变主要分布在叶片根部圆柱段与最大弦长之间的过渡段和叶片中部区域,且最大拉和压应变值分别为0.195 2%和0.162 5%,根据GL规范,当应变值小于0.250 0%时,材料极限强度无需进行额外的校核即可满足强度的要求。由图 3(b)可以看出,叶片压力面和吸力面失效安全因子分布相对应变比较均匀,说明该叶片复合材料铺层设计比较合理,没有明显的复合材料铺层过渡和结构刚度突变。考虑GL规范要求的材料分项安全系数(Sm=2.205),则复合材料的最小安全系数为:Sfm=1/(0.15×Sm)=3.02。
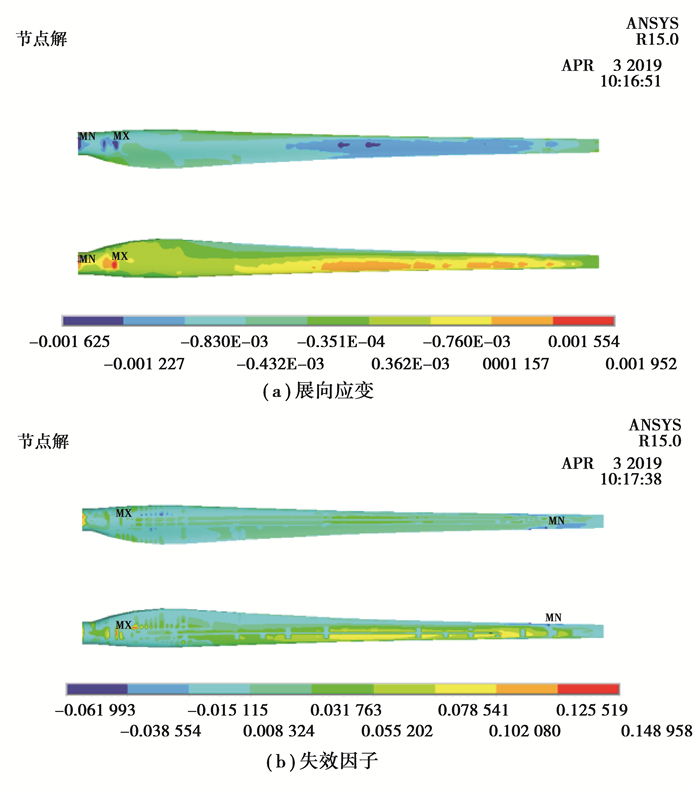
|
图 3 最小挥舞载荷下叶片复合材料强度 Fig. 3 The strength of the composite of the 100 kW blade under the minimum flap-wise load |
在最大挥舞载荷下叶片展向应变和失效因子分布如图 4所示。由图 4(a)可以看出,较大的应变主要分布在叶片根部圆柱段与最大弦长之间的过渡段和叶片中部区域,且最大拉和压应变值分别为0.255 6%和0.234 4%。由图 4(b)可以看出,叶片吸力面失效安全因子分布相对压力面更均匀。考虑规范要求的材料分项安全系数,则复合材料的最小安全系数为:Sfm =1/(0.19×Sm)=2.39。
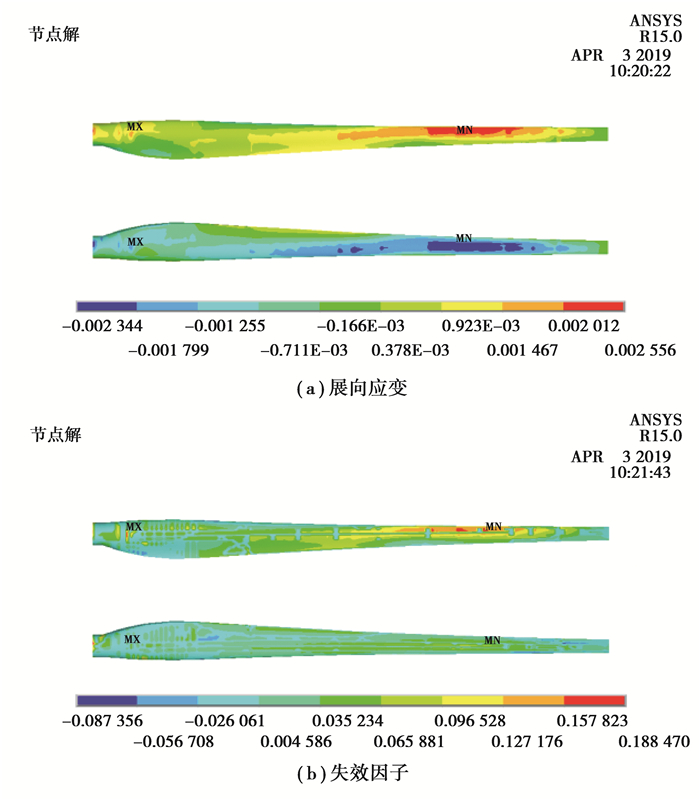
|
图 4 最大挥舞载荷下叶片复合材料强度 Fig. 4 The strength of composite of the 100 kW blade under maximum flap-wise load |
在最小摆振载荷下叶片展向应变和失效因子分布如图 5所示。由图 5(a)可以看出,较大的应变主要分布在叶片中部尾缘区域,且最大拉和压应变值分别为0.432 6%和0.238 2%。由图 5(b)可以看出,叶片吸力面和压力面失效安全因子分布比较均匀。考虑规范要求的材料分项安全系数,则材料的最小安全系数为:Sfm =1/(0.31×Sm)=1.46。

|
图 5 最小摆振载荷下叶片复合材料强度 Fig. 5 The strength of composite of the 100 kW blade under minimum edge-wise load |
在最大摆振载荷下叶片展向应变和失效因子分布如图 6所示。由图 6(a)可以看出,较大的应变主要分布在叶片中部尾缘区域,且最大拉和压应变值分别为0.287 9%和0.540 0%。由图 6(b)可以看出,叶片吸力面和压力面失效安全因子分布比较均匀。考虑规范要求的材料分项安全系数,则材料的最小安全系数为:Sfm =1/(0.45×Sm)=1.01。最危险位置在叶片前缘较小区域,位于沿叶片根部圆柱段至最大弦长之间,绝大部分区域安全因子很小,因此,有必要对叶片前缘较小区域作适当铺层优化,以提高叶片在最大摆振载荷下的安全性。
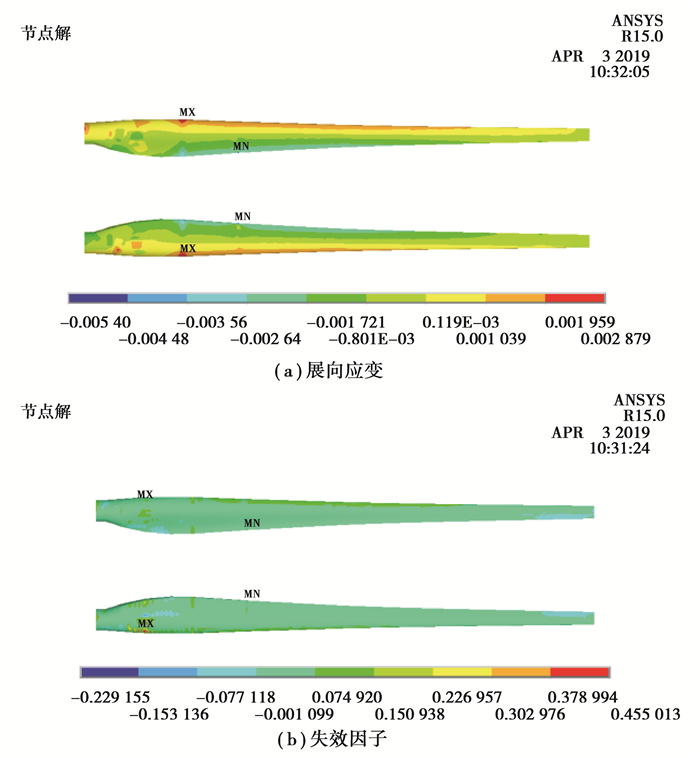
|
图 6 最大摆振载荷下叶片复合材料强度 Fig. 6 The strength of composite of the 100 kW blade under maximum edge-wise load |
有限元模型网格大小对屈曲分析有重要的影响,在计算时太大的网格可能遗漏某些重要的屈曲模态,太小的网格则大幅增加计算量。因此,有必要进行有限元模型网格密度的验证,在满足精度要求的前提下尽可能减少计算量。GL导则规定:当网格密度增加一倍,屈曲载荷因子误差小于5%则认为网格满足计算的要求[9]。当网格大小设置为50 mm时,最小挥舞载荷下第1阶特征值屈曲载荷系数为3.506;当网格大小设置为25 mm时,载荷系数为3.457,与网格大小为50 mm对比,相对误差为1.4%;当网格大小设置为12.5 mm时,载荷系数为3.453,与网格大小为25 mm相比,相对误差为0.1%。因此,在屈曲分析时,选择尺寸大小为50 mm的有限元网格。
3.2.1 最小挥舞在最小挥舞载荷下叶片第1阶屈曲模态和非线性屈曲变形如图 7所示。由图 7(a)可以看出,叶片的第1阶屈曲发生区域为靠近叶片尖部梁帽位置。由图 7(b)可以看出,叶片非线性屈曲发生在靠近叶片尖部梁帽的压力面。
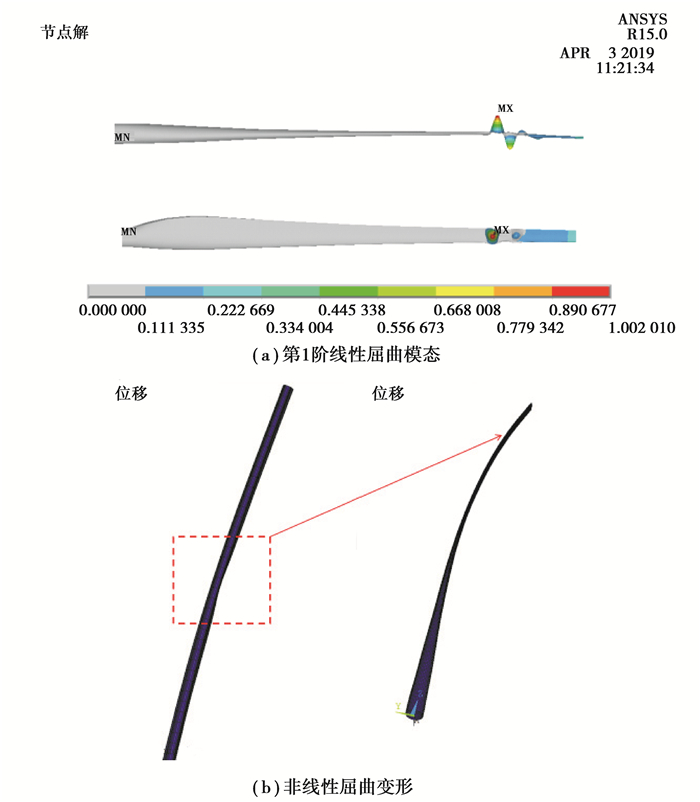
|
图 7 最小挥舞载荷下叶片的屈曲行为 Fig. 7 The buckling behavior of the 100 kW blade under minimum flap-wise load |
在最大挥舞载荷下叶片第1阶屈曲模态和非线性屈曲变形如图 8所示。由图 8(a)可以看出,叶片的第1阶屈曲发生区域为靠近叶片尖部梁帽位置。由图 8(b)可以看出,叶片非线性屈曲发生在靠近叶片尖部梁帽的吸力面。
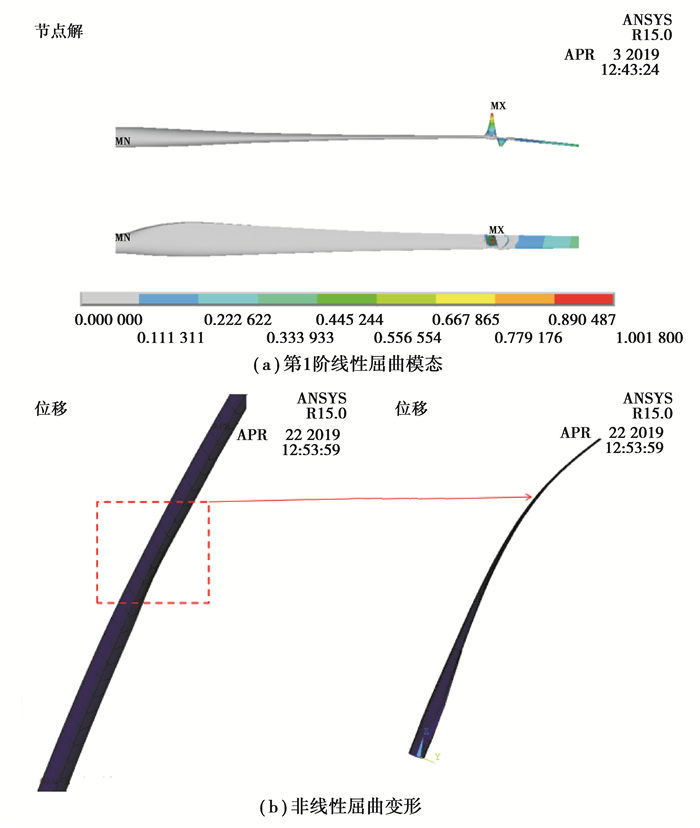
|
图 8 最大挥舞载荷下叶片屈曲行为 Fig. 8 The buckling behavior of the 100 kW blade under maximum flap-wise load |
在最小摆振载荷下叶片第1阶屈曲模态和非线性屈曲变形如图 9所示。叶片的第1阶屈曲和非线性屈曲均发生在叶片最大弦长截面前缘位置。
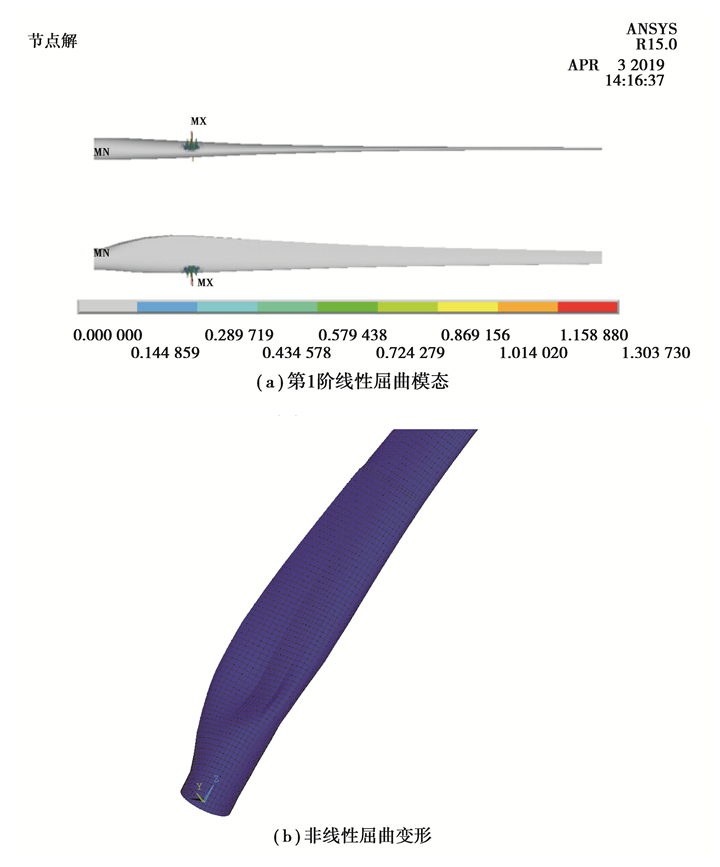
|
图 9 最小摆振载荷下叶片屈曲行为 Fig. 9 The buckling behavior of the 100 kW blade under minimum edge-wise load |
在最大摆振载荷下叶片第1阶屈曲模态和非性屈曲变形如图 10所示。叶片的第1阶屈曲和非线性屈曲均发生在叶片最大弦长截面尾缘位置。

|
图 10 最大摆振载荷下叶片屈曲行为 Fig. 10 The buckling behavior of the 100 kW blade under maximum edge-wise load |
叶片在4个方向最大极限载荷的第1阶线性屈曲载荷因子和非线性屈曲载荷因子如图 11所示。特征值载荷因子均大于非线性屈曲载荷因子,与理论吻合,线性屈曲预测结构的稳定性存在一定的风险。从屈曲载荷因子大小可以看出,最小摆振和最小挥舞工况下,叶片屈曲稳定性更高。挥舞方向非线性屈曲载荷因子与线性载荷因子差别较大,摆振方向差别较小,从而说明位于叶片梁帽附近的缺陷对叶片挥舞载荷下屈曲稳定性比叶片前尾缘的缺陷对于摆振方向稳定性更为敏感。尽管叶片前缘和尾缘因为几何外形和刚度的急剧变化容易发生屈曲,但是位于叶片翼型最大厚度处的缺陷也不能忽视。
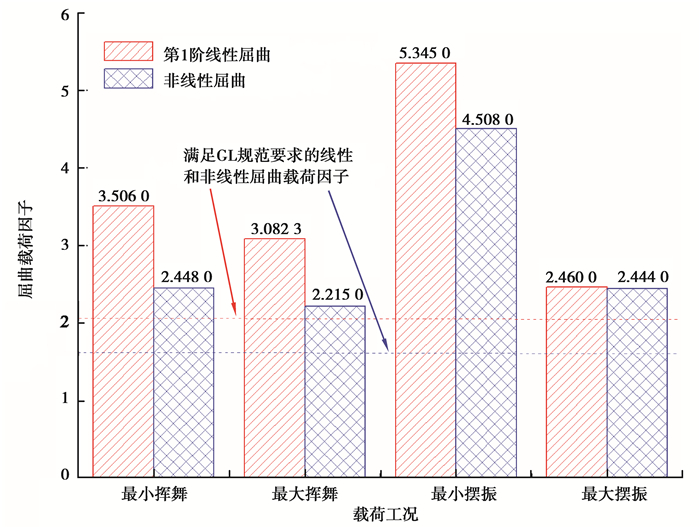
|
图 11 叶片线性和非线性屈曲载荷因子 Fig. 11 The linear and nonlinear load factors of the 100 kW blade |
考虑风电规范对叶片稳定性的分项安全因子的不同要求,其中线性屈曲分项安全系数为2.042,非线性屈曲分项安全系数为1.633 5。屈曲安全系数Sfb通过屈曲载荷系数除以屈曲分项安全系数得到,4个方向极限载荷下线性和非线性屈曲安全系数如表 1所示。可以得出,在挥舞方向载荷条件下,采用非线性分析方法比线性方法更加保守;考虑摆振方向载荷条件下,采用线性分析方法比非线性方法更加保守。
| 表 1 叶片线性和非线性屈曲安全系数 Table 1 The linear and nonlinear buckling safety factors of the 100 kW blade |
以100 kW钝尾缘叶片为对象,建立了叶片复合材料结构三维非线性有限元模型,依据GL规范分析了4个方向极限载荷工况下叶片复合材料的应变和安全系数分布,并对比分析了叶片线性和非线性屈曲稳定性。
1) 在最小和最大挥舞载荷下,较大的展向应变主要分布在叶片根部圆柱段与最大弦长之间的过渡段和叶片中部区域,材料的最小安全系数分别为3.02和2.39。叶片失效安全因子分布相对应变比较均匀,说明该叶片复合材料铺层设计比较合理。在最小和最大摆振载荷下,叶片较大的展向应变主要分布在叶片中部尾缘区域,材料的最小安全系数分别为1.46和1.01。
2) 在最小和最大挥舞载荷下,叶片的第1阶线性和非线性屈曲均发生在靠近叶片尖部梁帽位置;在最小和最大摆振载荷下,叶片的第1阶线性和非线性屈曲分别发生在叶片最大弦长截面的前缘和尾缘位置。
3) 在4个方向的极限载荷条件下,叶片第1阶特征值屈曲载荷因子均大于非线性屈曲载荷因子;最小摆振和最小挥舞工况下,叶片屈曲稳定性更高。
4) 位于叶片梁帽附近的缺陷对叶片挥舞载荷下屈曲稳定性比叶片前尾缘的缺陷对于摆振方向稳定性更为敏感;在挥舞方向载荷条件下,采用非线性分析方法比线性方法更加保守;考虑摆振方向载荷条件下,采用线性分析方法比非线性方法更加保守。
| [1] |
Global Wind Energy Council. Global wind statistics 2017[R]. Brussels: Global Wind Energy Council, 2018.
|
| [2] |
Haselbach P U, Bitsche R D, Branner K. The effect of delaminations on local buckling in wind turbine blades[J]. Renewable Energy, 2016, 85: 295-305. DOI:10.1016/j.renene.2015.06.053 |
| [3] |
Chen X, Zhao W, Zhao X, et al. Failure test and finite element simulation of a large wind turbine composite blade under static loading[J]. Energies, 2014, 7(4): 2274-2297. DOI:10.3390/en7042274 |
| [4] |
Overgaard L C T, Lund E. Structural collapse of a wind turbine blade. Part B: progressive interlaminar failure models[J]. Composites Part A: Applied Science and Manufacturing, 2010, 41(2): 271-286. DOI:10.1016/j.compositesa.2009.10.012 |
| [5] |
Overgaard L C T, Lund E, Thomsen O T. Structural collapse of a wind turbine blade. Part A: static test and equivalent single layered models[J]. Composites Part A: Applied Science and Manufacturing, 2010, 41(2): 257-270. DOI:10.1016/j.compositesa.2009.10.011 |
| [6] |
Jensen F M, Falzon B G, Ankersen J, et al. Structural testing and numerical simulation of a 34m composite wind turbine blade[J]. Composite Structures, 2006, 76(1/2): 52-61. |
| [7] |
Lahuerta F, De Ruiter M J, Espinosa L, et al. Assessment of wind turbine blade trailing edge failure with sub-component tests[C/OL]//Proceedings of 21st International Conference on Composite Materials, August 20-25, 2017, Xi'an.[2019-03-15]. https://www.researchgate.net/publication/319211257_Assessment_of_wind_turbine_blade_trailing_edge_failure_with_sub-component_tests.
|
| [8] |
薛彩虹, 李军向, 王超, 等. 复合材料风电叶片有限元建模和屈曲稳定性分析[J]. 玻璃钢/复合材料, 2014(1): 4-7. Xue C H, Li J X, Wang C, et al. Finite element modeling and buckling stability analysis of composite material wind blades[J]. Fiber Reinforced Plastics/Composites, 2014(1): 4-7. (in Chinese) |
| [9] |
Germanischer Lloyd. Rules and guidelines IV industrial services: Part I: guideline for the certification of wind turbines[M]. Hamburg, Germany: Germanischer Lloyd, 2010: 389.
|
| [10] |
苏成功, 李成良, 鲁晓锋. 大型风电叶片后缘最大弦长区域稳定性研究[J]. 玻璃钢/复合材料, 2015(6): 58-63. Su C G, Li C L, Lu X F. Buckling stability research on the maximum chord region of wind turbine blade trailing edge[J]. Fiber Reinforced Plastics/Composites, 2015(6): 58-63. (in Chinese) |
| [11] |
靳交通, 邓航, 侯彬彬, 等. 大尺寸复合材料风机叶片破坏试验机理[J]. 机械设计与研究, 2015, 31(2): 74-76. Jin J T, Deng H, Hou B B, et al. Structural collapse investigation of the large-scale composite wind turbine blade in static test[J]. Machine Design & Research, 2015, 31(2): 74-76. (in Chinese) |
| [12] |
牛春辉. 哈密烟墩某风电场2.5 MW机组叶片后缘开裂事故分析[J]. 硅谷, 2014, 7(24): 208-209. Niu C H. The accident analysis of 2.5 MW blade trailing edge crack at Hamiyandun[J]. Silicon Valley, 2014, 7(24): 208-209. (in Chinese) |
| [13] |
袁巍华, 吴玉国, 王国付, 等. 风电叶片尾缘结构稳定性研究[J]. 玻璃钢/复合材料, 2018(1): 12-17. Yuan W H, Wu Y G, Wang G F, et al. Study on the stability of wind turbine blade trailing edge strcture[J]. Fiber Reinforced Plastics/Composites, 2018(1): 12-17. (in Chinese) |
| [14] |
黄吉, 王继辉, 秦志文, 等. GFRP风电叶片段结构强度三维有限元分析[J]. 复合材料学报, 2019, 36(8): 1964-1872. Huang J, Wang J H, Qin Z W, et al. Three-dimensional finite element analysis of the structural strength of GFRP wind turbine blade segment[J]. Acta Materiae Compositae Sinica,, 2019, 36(8): 1964-1872. (in Chinese) |
| [15] |
Li S G, Sitnikova E, Liang Y N, et al. The Tsai-Wu failure criterion rationalised in the context of UD composites[J]. Composites Part A: Applied Science and Manufacturing, 2017, 102: 207-217. DOI:10.1016/j.compositesa.2017.08.007 |
| [16] |
Bak M. Nonlinear buckling analysis using Workbench V15[R]. CAE Associates, 2014.
|
 2021, Vol. 44
2021, Vol. 44


