1a. 长安大学 汽车运输安全保障技术交通行业重点实验室, 西安 710064;
2. 西北工业大学 机电学院, 西安 710072
1a. Key Laboratory of Automotive Transportation Safety Techniques of Ministry of Transport, Chang'an University, Xi'an 710064, P. R. China;
2. School of Mechanical Engineering, Northwestern Polytechnical University, Xi'an 710072, P. R. China
准双曲面齿轮广泛应用于车辆主减速器,其齿面复杂且加工难度大。目前在汽车工业中运用最广泛的是刀倾半展成铣齿法(HFT),其齿面设计、加工一直是研究的重点。国内外学者对准双曲面齿轮的齿面设计、加工方法等进行了大量研究:局部综合法[1]、高阶传动误差齿面[2]、主动设计方法[3]、全局综合法[4]、刀倾全展成切齿法[5]及双螺旋切齿法[6]等,主要集中于修正摇台型机床运动参数的抛物线传动误差齿面,尽管这种局部共轭齿面可有效避免齿面边缘应力集中现象,但造成了齿轮副失配量过大,导致强度降低及承载变形过大,因此不能从根本上改善齿轮副动态啮合特性。
为了更为直观控制齿面失配量,一种相对于共轭齿面的修形即齿面ease-off修形技术已成为螺旋锥齿轮齿面设计与加工的研究热点,其较传统的修形方法不仅直观而且避免了复杂的齿面曲率计算。文献[7-8]结合齿面承载接触分析(loaded tooth contact analysis, LTCA)方法进行最优ease-off修形准双曲面齿轮设计,其关键技术不详。文献[9-10]结合齿面接触分析(tooth contact analysis, TCA)方法,给定传动误差和接触区域大小设计弧齿锥齿轮ease-off曲面,再通过齿面离散,反求机床加工参数。文献[11]建立螺旋锥齿轮副共轭差曲面修形量与相对曲率、共轭接触线以及接触迹线之间的联系,设计ease-off曲面。文献[12]构造弧齿锥齿轮ease-off差齿面的密切曲面,通过二阶密切曲面拓扑、接触区可控参数综合确定小轮齿面的接触参数,进而通过数值方法求解小轮的加工参数。目前,基于ease-off的复杂齿面修形方法主要是通过修正加工参数获得ease-off修形曲面,再结合轻载下的TCA方法进行接触区域匹配仿真验证,其不能反映受载工况下齿轮副的啮合性能,且无法实现自由ease-off修形齿面的设计。
拓扑修形在均化齿面载荷和改善齿轮综合性能方面有显著作用,基于ease-off螺旋锥齿轮拓扑修形齿面很复杂,传统的基于摇台型机床的齿面修正技术[13-16]可调加工参数有限,不能实现高精度拓扑修形齿面修正。文献[17-18]研究了螺旋锥齿轮刀具刃形和刀具几何参数对齿面误差及接触质量的影响,基于CNC机床运动和刀具刃形误差敏感性的齿面高阶修正技术[19],可实现自由ease-off修形齿面的修正,但求解方法较为困难,必须给出合理的修正参数边界,特别是旋转轴展成运动系数边界,否则将产生较大修正误差。
为了进一步提高汽车驱动桥品质,笔者预设齿间间隙与齿面法向间隙,对HFT法小轮齿面进行自由ease-off曲面设计,小轮修形齿面表示为ease-off曲面与大轮的全共轭齿面叠加;结合LTCA方法,优化ALTE最小获得最优ease-off曲面,并推导其相对小轮理论齿面的目标修形量。基于刀具和CNC机床各运动轴齿面误差敏感性的修正模型,推导合理的参数边界,进而通过优化方法确定了最优ease-off齿面的加工参数,该方法可直接对齿面进行任意自由修形设计与加工。
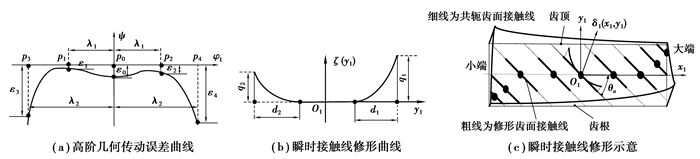
1 Ease-off修形齿面数学模型点接触齿面齿轮副传动性能与重合度有很大关系,其受载荷后的实际重合度受啮合位置多齿对轮齿初始接触间隙的影响很大。轮齿初始间隙可以用齿轮几何传动误差和接触线法向间隙表达,齿轮几何传动误差可转化为齿面法向位移即齿间间隙,齿间间隙与接触线法向间隙之和定义为初始间隙。修形齿面是对共轭齿面几何的微观修正,其表达式无法脱离共轭齿面,可以表达为共轭齿面与ease-off修形曲面的叠加,进而确定其准确的解析表达式。根据摇台型机床的准双曲面齿轮加工参数及切齿模型,可确定其理论齿面,该理论齿面为点接触齿面,按照齿轮啮合理论和齿轮副安装关系,用大轮理论齿面按照名义传动比与小轮啮合,可获得与大轮完全共轭的小轮齿面。齿间间隙与接触线法向间隙各自反映着齿轮传动性能的不同方面,因此,需要结合齿间间隙与齿面法向间隙产生的机理进行ease-off修形曲面设计。齿间间隙可通过图 1(a)所示的高阶传动误差(参数为λ1,λ2及ε0~ε4)曲线表示,通过图 1(b)所示曲线(参数为d1, d2, q1, q2及θa)经旋转变换映射后得到齿面法向间隙如图 1(c)所示。基于ease-off的修形准双曲面齿轮齿面数学模型详见文献[20]。
|
图 1 基于齿轮几何传动误差与接触线修形的ease-off修形曲面设计 Fig. 1 Design of ease-off flank modification surface based on transmission error and contact line |
齿轮承载传动误差幅值(amplitude of loaded transmission error, ALTE)是工作过程中振动的直接激励,是产生振动、噪声的重要因素。结合TCA、LTCA优化齿面的最大载荷与ALTE最小,可确定齿间接触间隙参数和齿面法向接触间隙参数进而确定最优ease-off修形齿面。
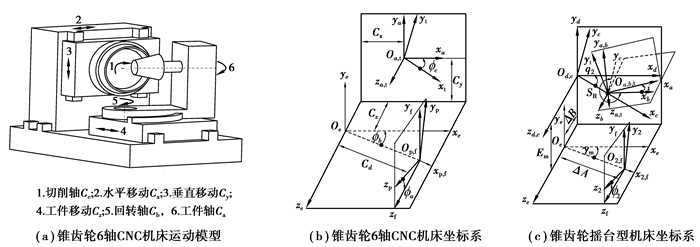
2 准双曲面齿轮数控切齿模型图 2(a)~(b)为6轴CNC锥齿轮机床模型及坐标系,其中坐标系St, Sp分别固联于刀具与工件。Sa,Se为固定坐标系且各坐标轴平行。辅助坐标系Sf与工件箱固连,其绕ye轴旋转后偏离φb角度,并移动Cd距离。St相对Sa绕za轴旋转角为φc;Sp相对Sf绕xf轴旋转角为φa。Cd为工件节锥顶至固定坐标系原点Oe的距离,为机床常参数。刀盘与工件的相对运动被分解为X,Y,Z3个方向的直线运动和绕Ca,Cb,Cc轴的3个回转运动,通过复合空间运动来完成实际展成运动。理论上CNC锥齿轮机床可以模拟任何带刀倾和变性机构的传统机床。采用端面铣齿刀盘和X,Y,Z,Ca及Cb5轴联动可以展成格里森制齿面;采用端面滚齿刀盘和X,Y,Z,Ca,Cb及Cc6轴联动可以展成奥利康制齿面。
|
图 2 准双曲面齿轮机床模型及坐标系 Fig. 2 Coordinate systems and generator model for the six-axis CNC hypiod gear generator |
从摇台型机床向free-form型机床的运动等效转换原则是保证刀具与工件的相对位置和姿态在任意时刻都相同。摇台型机床坐标系如图 2(c)所示,刀盘动坐标系St绕辅助坐标系Sa的za轴的旋转角为β;Sa相对辅助坐标系Sb的yb轴旋转刀倾角度为i;Sb相对摇台坐标系Sc的zc轴旋转刀转角度为j,并沿xc轴平移径向刀位SR;Sc相对机床固定坐标系Sd的zd轴旋转摇台初始转角为q。坐标系Se,Sf为确定被加工齿轮安装位置的辅助坐标系,S1为工件动坐标系,γm为轮坯安装角,Em为垂直轮位,ΔB为床位,ΔA为水平轮位,φ1为工件转角。由于刀倾结构的存在,工件轴和刀具轴之间的最短距离矢量(大小和方向)是不断变化的,而在CNC锥齿轮机床中两者最短距离矢量的方向是不变的,并且始终平行于某一轴,如何保证刀盘和工件的相对位置和姿态相同的具体推导过程见文献[21-22],可以得到:
| $ {M_{1{\rm{t}}}^{\rm{c}} = M_{1{\rm{f}}}^{\rm{c}}\left( {{\varphi _1}} \right)M_{{\rm{ft}}}^{\rm{c}}\left( {{C_x},{C_y},{C_z},\Delta {\varphi _a},{\varphi _b},\Delta {\varphi _c}} \right),} $ | (1) |
| $ {M_{1{\rm{t}}}^{\rm{u}} = M_{1{\rm{f}}}^{\rm{u}}\left( {{\varphi _1}} \right)M_{{\rm{ft}}}^u\left( {i,j,q,{S_{\rm{r}}}{E_{\rm{m}}},\Delta A,\Delta B,{\gamma _{\rm{m}}},{R_a}} \right),} $ | (2) |
| $ M_{{\rm{ft}}}^{\rm{u}}\left( {i,j,q,{S_{\rm{r}}}{E_{\rm{m}}},\Delta A,\Delta B,{\gamma _{\rm{m}}},{R_a}} \right) = \left[ {\begin{array}{*{20}{c}} {{e_{11}}}&{{e_{12}}}&{{e_{13}}}&{{e_{14}}}\\ {{e_{21}}}&{{e_{22}}}&{{e_{23}}}&{{e_{24}}}\\ {{e_{31}}}&{{e_{32}}}&{{e_{33}}}&{{e_{34}}}\\ 0&0&0&1 \end{array}} \right], $ | (3) |
| $ \left\{ {\begin{array}{*{20}{l}} {{C_x} = \left( {{e_{14}} + {C_d}} \right)\cos {\varphi _b} - \left( {{e_{34}}\cos \Delta {\varphi _a} + {e_{24}}\sin \Delta {\varphi _a}} \right)\sin {\varphi _b};}\\ {{C_y} = {e_{24}}\cos \Delta {\varphi _a} - {e_{34}}\sin \Delta {\varphi _a};}\\ {{C_z} = - \left( {{e_{14}} + {C_d}} \right)\sin {\varphi _b} - \left( {{e_{34}}\cos \Delta {\varphi _a} + {e_{24}}\sin \Delta {\varphi _a}} \right)\cos {\varphi _b};}\\ {{\varphi _b} = {{\sin }^{ - 1}}{e_{13}},{C_b} = {\varphi _b};}\\ {\Delta {\varphi _a} = {{\tan }^{ - 1}}\left( {{e_{23}}/{e_{33}}} \right),{C_a} = \Delta {\varphi _a} + {\varphi _1};}\\ {\Delta {\varphi _c} = {{\sin }^{ - 1}}\left( {{e_{12}}/{e_{11}}} \right),{C_c} = \Delta {\varphi _c} = {\varphi _1}/{R_a}}。\end{array}} \right. $ | (4) |
式中:
在已知加工参数确定的理论齿面基础上,修正铣刀盘切削刃曲线、刀盘半径及CNC机床各轴高阶运动参数,可实现复杂修形齿面的校正;然而,ease-off曲面是相对共轭齿面的法向修形量,因此,需要将其转化为相对理论齿面的修形量。工件齿轮目标ease-off修形齿面位矢Rm表示为
| $ {\mathit{\boldsymbol{R}}_{\rm{m}}} = {\mathit{\boldsymbol{R}}_{10}} + {\delta _{\rm{m}}}{\mathit{\boldsymbol{N}}_{10}}, $ | (5) |
式中:δm为最优ease-off修形量,R10, N10为小轮共轭齿面位矢及法矢量。设小轮理论齿面的ease-off修形量为δg,则其位矢Rg表示为
| $ {\mathit{\boldsymbol{R}}_{\rm{g}}} = {\mathit{\boldsymbol{R}}_{10}} + {\delta _{\rm{g}}}{\mathit{\boldsymbol{N}}_{10}}。$ | (6) |
结合式(5)(6)可得最优ease-off拓扑修形齿面相对理论齿面的修形量δmg为
| $ {\delta _{{\rm{mg}}}} = \left( {{\mathit{\boldsymbol{R}}_{\rm{m}}} - {\mathit{\boldsymbol{R}}_{\rm{g}}}} \right) \cdot {\mathit{\boldsymbol{N}}_{\rm{g}}} = \left( {{\delta _{\rm{m}}} - {\delta _{\rm{g}}}} \right)\left( {{\mathit{\boldsymbol{N}}_{10}} \cdot {\mathit{\boldsymbol{N}}_{\rm{g}}}} \right)。$ | (7) |
式中:Ng为小轮理论齿面单位法矢。根据CNC螺旋锥齿轮机床的5个联动轴的瞬时运动位置,可选参数φ1(或φc)为各轴之间的联系参数,实际加工中φ1为时间的函数,进而可拟合出5个联动轴的表达式。各运动轴的位置展成6阶多项式为
| $ {C_k} = {a_{k0}} + {a_{k1}}{\varphi _1} + {a_{k2}}\varphi _1^2 + {a_{k3}}\varphi _1^3 + {a_{k4}}\varphi _1^4 + {a_{k5}}\varphi _1^5 + {a_{k6}}\varphi _1^6\quad (k = a,b,x,y,z)。$ | (8) |
根据微分几何最优ease-off拓扑修形齿面相对理论齿面的法向修形量δmg表示为
| $ {\delta _{{\rm{mg}}}}\left( {{u_i},{l_i}} \right) = \sum\limits_{i = 1}^q {\frac{{\partial {\mathit{\boldsymbol{R}}_{\rm{m}}}\left( {{u_i},{l_i},{\zeta _j}} \right){\mathit{\boldsymbol{N}}_{\rm{g}}}\left( {{u_i},{l_i}} \right)}}{{\partial {\zeta _j}}}} {\zeta _j}\quad (i = 1,2, \cdots ,p,j = 1,2, \cdots ,q)。$ | (9) |
简化可用矩阵表示为
| $ {\delta _{{\rm{mg}}}} = \mathit{\boldsymbol{S\zeta }}, $ | (10) |
式中:ζ为附加运动参数系数ζj(即Cx,Cy,Cz,Ca、Cb多项式系数及刀具刃形和半径修形参数共计46个)组成的列向量; S为齿面敏感矩阵,由网格节点i (i=1, 2, …, p,p为齿面网格点个数取9×15=135)处的齿面误差敏感系数组成的行向量Si构成。式(10)为一个超定线性方程组,由于S通常为病态矩阵,有时甚至奇异,求解得到的加工参数调整量可能会超出实际调整范围;其次通过微分求解的理论齿面上的某网格点i的微分只能在微小的范围变化,否则会导致计算误差;通过分析验证可知,对于旋转轴其运动系数的变化是很有限的,因此求解被视为一个合理约束边界下的优化问题:
| $ F(\zeta ) = \min \sum\limits_{i = 1}^p {\delta _{{\rm{mg}}}^2} \quad \left( {{\lambda _1} \le \zeta \le {\lambda _2}} \right)。$ | (11) |
给定某一个轴的任意一个运动参数扰动,通过比较式(10)引起的齿面误差和该参数对应加工参数变化引起的齿面误差的一致性确定边界
| $ \max \left\{ {\left| {\mathit{\boldsymbol{S\zeta }} - \left( {{\mathit{\boldsymbol{R}}_{\rm{g}}}\left( {C_k^0 + {\lambda _j}} \right) - {\mathit{\boldsymbol{R}}_{\rm{g}}}\left( {C_k^0} \right)} \right) \cdot {\mathit{\boldsymbol{N}}_{\rm{g}}}} \right|} \right\} \le 0.1{\kern 1pt} {\kern 1pt} {\kern 1pt} \mu {\rm{m,}} $ | (12) |
式中:
以一对弧齿准双曲面齿轮的工作面为例,大轮额定扭矩为600 N·m;齿轮副几何参数见表 1,理论齿面加工参数见表 2,CNC机床常参数Cd=0。优化的最优ease-off拓扑修形曲面参数见表 3。
| 表 1 准双曲面齿轮副几何参数 Table 1 Geometric parameters of hypoid gears |
| 表 2 准双曲面齿轮加工参数 Table 2 Cutting parameters of hypoid gears |
| 表 3 最优ease-off拓扑修形曲面参数 Table 3 Parameters of the best ease-off topological modification surface |
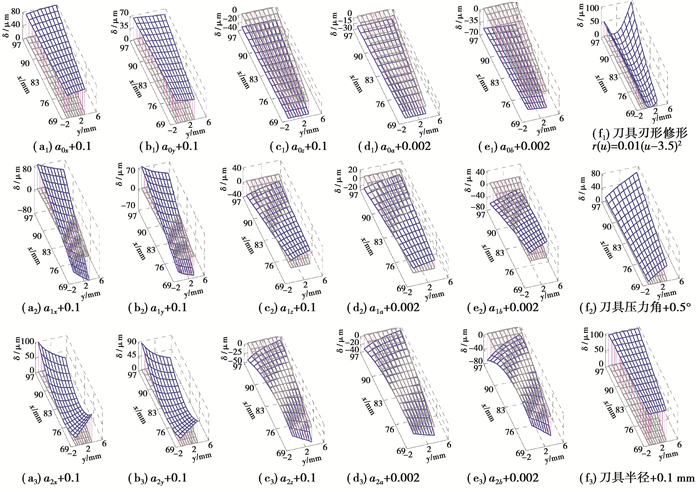
图 3为CNC机床各运动轴齿面误差敏感性仿真,图中注释例如“aij+0.1”表示:j轴的i阶运动系数变化+0.1。1)0阶参数变化引起齿厚修正(见图 3(a1), (b1), (c1), (d1), (e1));2)1阶参数变化引起齿面反向对角修正,即同时引起齿高方向的压力角和齿宽方向的螺旋角修正(见图 3(a2), (b2), (c2), (d2), (e2));3)2阶参数变化引起齿面同向对角修正(见图 3(a3), (b3), (c3), (d3), (e3));4)各轴系数随阶次增加,对齿面整体校正量减小即敏感性降低;5)对凹面的校正主要体现在小端齿顶处和大端齿根处;6)各轴校正敏感性为:工件安装角轴(Cb)>工件旋转轴(Ca)>刀具中心移动轴(Cx)=刀具中心移动(Cy)>工件移动轴(Cz);7)刀具刃形、压力角校正引起齿廓校正(见图 3(f1), (f1)),刀盘半径变化引起齿厚校正(见图 3(f3))。可见螺旋锥齿轮CNC铣齿机各运动轴的附加运动主要引起齿厚误差和对角误差(齿向方向)校正,刀具刃形修形主要产生齿廓修形。
|
图 3 CNC机床各运动轴0阶、1阶及2阶系数齿面误差敏感性仿真 Fig. 3 Simulation of flank error sensitivity to 0, 1 and 2 order coefficients of kinematic axes for the CNC hypoid generator |
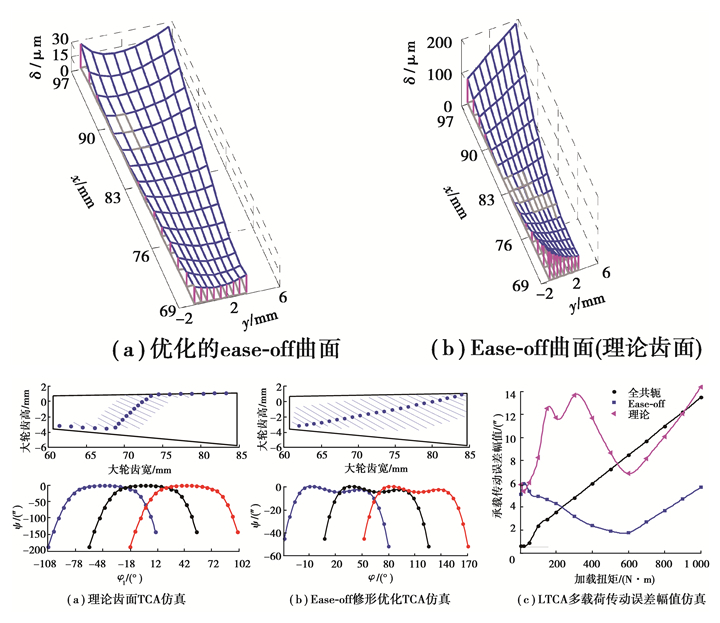
优化的最优ease-off拓补修形曲面见图 4(a),其与理论齿面的ease-off曲面(图 4(b))分别与接触区域(图 4(c)(d))匹配一致。最优ease-off齿面接触椭圆长轴较长,因此接触线法向间隙对重合度的影响较小,随载荷增加重合度呈现“增加不变”趋势,在重合度转换点(600 N·m)处ALTE出现单个最小极值点。
|
图 4 TCA及承载传动误差幅值仿真 Fig. 4 Simulation of both TCA and ALTE on loads |
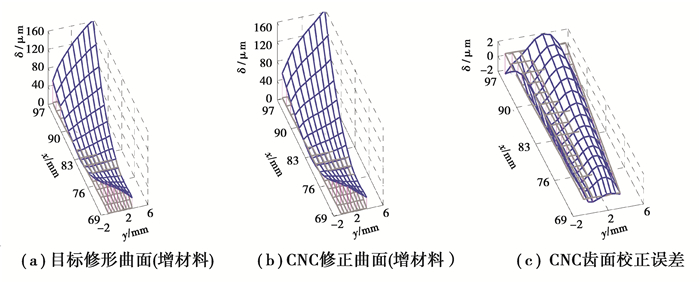
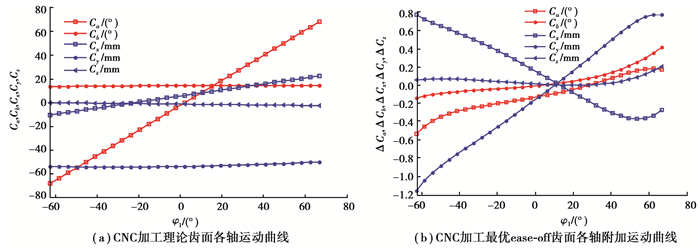
齿面CNC修正仿真:1)最优ease-off齿面主要为齿廓修形和齿向修形,在大端齿顶、小端齿根处最大修形量分别为23,17 μm,其相对理论齿面的修形量(目标修形量)如图 5(a)所示,注意为增材料,在大端齿顶、小端齿根处最大修形量分别为-160,-68 μm。CNC修正后的曲面如图 5(b)所示,校正误差主要为齿廓误差,最大误差为2 μm(≤1%, 见图 5(c));2)CNC各轴运动曲线接近线性,工件旋转轴(Ca)和刀具中心移动轴(Cx)运动变化较大(见图 6(a));3)工件安装角轴Cb,Ca及刀具中心移动轴(Cx和Cy)有较大的附加运动。结合图 3可见Ca,Cb和Cx主要引起小端齿顶减材料修正,而Cy主要引起大端齿根减材料修正,其变化趋势与目标修形量变化趋势基本一致(见图 6(b));表 4为修形前后加工参数表达式,各阶系数有微小变化;通过计算获得的Ca轴运动系数边界λ=±0.01,Cb轴运动系数边界λ=±0.002。
|
图 5 5轴联动CNC修正ease-off拓扑修形准双曲面齿轮仿真 Fig. 5 Simulation of ease-off flank correction based on a five linked axis CNC hypoid generator |
|
图 6 5轴CNC机床加工准双曲面齿轮运动曲线仿真 Fig. 6 Simulation curves of kinematic axis based on the five-axis CNC hypoid gear generator |
| 表 4 5轴CNC加工准双曲面齿轮参数表达式 Table 4 Parameter expression of kinematic positions based on the five-axis CNC hypoid gear generator |
需要说明的是实际应用中,对于一般安装精度的车辆主减速器齿轮,可以仅仅通过修正铣齿机各运动轴参数主要产生的齿向修形来改善安装误差敏感性,进而改善传动性能。尽管齿向修形非常有利于降低安装误差的敏感性,但是也易导致齿面适配量较大,降低重合度;因此,对于高精度安装的齿轮副,为了保证齿轮副有较大的重合度(正如渐开线圆柱齿轮),齿面通常需要较小的齿向修形,主要是对齿顶和齿根进行齿廓修形来改善传动性能,而齿顶或齿根修形主要是通过对刀具横截面刃形的修正实现的,因此需选用这一刀具参数。刀具刃形的修正工艺较为复杂,且刀具成本较高,易产生磨损,而机床附加运动的修正更为柔性,因此,对于一般安装精度齿轮主要考虑减小安装误差敏感性时,可不考虑刀具刃形的修形。对于高精度及高精度安装的拓扑修形齿轮,除了考虑机床运动参数的修正,还需要考虑刀具刃形的修形。
5 结语1) 预设齿间间隙与齿面法向间隙进行自由ease-off曲面设计,小轮ease-off修形齿面表示为ease-off曲面与大轮的全共轭齿面叠加;结合LTCA方法,优化ALTE最小,获得最优ease-off曲面。
2) 椭圆长轴设计较大时,齿间间隙对重合度的影响较小,随载荷增加重合度呈现“增加不变”,因此ALTE呈现“减小增加”趋势,在重合度转换点处出现单一最小极值点。
3) 基于理论齿面加工参数,获得齿面误差敏感性系数矩阵的方法求解修形齿面加工参数时,需要确定合理的旋转轴运动参数边界。
4) 螺旋锥齿轮CNC铣齿机各运动轴主要引起齿厚误差和对角误差校正,自由ease-off拓扑修形齿面的修正需要增加刀具刃形修正;该研究为高精度、高性能螺旋锥齿轮的齿面设计与加工提供理论方法。
| [1] |
Litvin F L, Zhang Y, Handschuh R F. Local synthesis and tooth contact analysis of face-milled spiral bevel gears: 91-C-039[R]. NASA, 1991.
|
| [2] |
Wang P Y, Fong Z H. Fourth-Order kinematic synthesis for face-milling spiral bevel gears with modified radial motion (MRM) correction[J]. Journal of Mechanical Design, 2006, 128(2): 457-467. DOI:10.1115/1.2168466 |
| [3] |
周凯红, 唐进元, 严宏志. 基于预定啮合特性的点啮合齿面设计方法[J]. 航空动力学报, 2009, 24(11): 2612-2617. Zhou K H, Tang J Y, Yan H Z. Research on meshing characteristics-based design of point-contact tooth surface[J]. Journal of Aerospace Power, 2009, 24(11): 2612-2617. (in Chinese) |
| [4] |
Wang P, Zhang Y, Wan M. Global synthesis for face milled spiral bevel gears with zero transmission errors[J]. Journal of Mechanical Design, 2016, 138(3): 033302-1-9. |
| [5] |
王星, 方宗德, 李声晋, 等. HGT准双曲面齿轮精确建模和加载接触分析[J]. 四川大学学报: 工程科学版, 2015, 47(4): 181-185. Wang X, Fang Z D, Li S J, et al. Precise modeling of HGT hypoid gear and loaded tooth contact analysis[J]. Journal of Sichuan University: Engineering Science Edition, 2015, 47(4): 181-185. (in Chinese) |
| [6] |
Zhang Y, Yan H Z. New methodology for determining basic machine settings of spiral bevel and hypoid gears manufactured by duplex helical method[J]. Mechanism and Machine Theory, 2016, 100: 283-295. DOI:10.1016/j.mechmachtheory.2016.02.015 |
| [7] |
Kolivand M, Kahraman A. An ease-off based method for loaded tooth contact analysis of hypoid gears having local and global surface deviations[J]. Journal of Mechanical Design, 2010, 132(7): 071004-1-8. |
| [8] |
Artoni A, Kolivand M, Kahraman A. An ease-off based optimization of the loaded transmission error of hypoid gears[J]. Journal of mechanical design, 2010, 32(1): 011010-1-9. |
| [9] |
Shih Y P. A novel ease-off flank modification methodology for spiral bevel and hypoid gears[J]. Mechanism and Machine Theory, 2010, 45(8): 1108-1124. DOI:10.1016/j.mechmachtheory.2010.03.010 |
| [10] |
苏进展, 贺朝霞. 弧齿锥齿轮齿面的高精度修形方法[J]. 华南理工大学学报(自然科学版), 2014, 42(4): 91-96. Su J Z, He Z X. High-precision modification of tooth surface for spiral bevel gears[J]. Journal of South China University of Technology(Natural Science Edition), 2014, 42(4): 91-96. (in Chinese) |
| [11] |
张卫青, 马朋朋, 郭晓东. 基于共轭差曲面的螺旋锥齿轮接触特性控制方法[J]. 北京工业大学学报, 2018, 44(7): 1024-1031. Zhang W Q, Ma P P, Guo X D. Contact characteristics control method of spiral bevel gears based on ease-off[J]. Journal of BeiJing University of technology, 2018, 44(7): 1024-1031. (in Chinese) |
| [12] |
魏冰阳, 邓效忠, 仝昂鑫. 曲面综合法弧齿锥齿轮加工参数计算[J]. 机械工程学报, 2016, 52(1): 20-25. Wei B Y, Deng X Z, Tong A X. Surface synthesis method on generating parameters computation of spiral bevel-gears[J]. Journal of Mechanical Engineering, 2016, 52(1): 20-25. (in Chinese) |
| [13] |
Lin C Y, Tsay C B, Fong Z H. Computer aided manufacturing of spiral bevel and hypoid gears by applying optimization techniques[J]. Journal of Materials Processing Technology, 2001, 114(1): 22-35. DOI:10.1016/S0924-0136(01)00734-8 |
| [14] |
田程, 丁炜琦, 桂良进. 基于回归分析的准双曲面齿轮齿面误差修正[J]. 清华大学学报(自然科学版), 2017(2): 141-146. Tian C, Ding W Q, Gui L J. Flank error correction of hypoid gears based on regression analyses[J]. Journal of Tsinghua University (Science and Technology), 2017(2): 141-146. (in Chinese) |
| [15] |
唐进元, 聂金安, 王智泉. 螺旋锥齿轮HFT法加工的反调修正方法[J]. 中南大学学报(自然科学版), 2012, 43(6): 2142-2149. Tang J Y, Nie J A, Wang Z Q. Reverse correction of spiral bevel gear HFT method[J]. Journal of Central South University (Science and Technology), 2012, 43(6): 2142-2149. (in Chinese) |
| [16] |
郭晓东, 张卫青, 张明德, 等. 螺旋锥齿轮切齿调整参数的精确反调[J]. 重庆大学学报, 2011, 34(3): 34-39. Guo X D, Zhang W Q, Zhang M D, et al. The machine setting reverse method of spiral bever gear[J]. Journal of Chongqing University, 2011, 34(3): 34-39. (in Chinese) |
| [17] |
梁成成, 宋朝省, 朱才朝, 等. 基于刀具法向基准的奥利康准双曲面齿轮精确建模与验证[J]. 重庆大学学报, 2020, 43(2): 1-11. Liang C C, Song C S, Zhu C C, et al. Accurate modeling and verification of Oerlikon hypoid gears based on tool normal benchmark[J]. Journal of Chongqing University, 2020, 43(2): 1-11. |
| [18] |
Lee Y H, Fong Z H. A mathematical model for grinding a stick blade profile to cut hypoid gears[J]. Journal of Mechanical Design, 2020, 142: 053401-1-11. |
| [19] |
Shih Y P, Fong Z H. Flank correction for spiral bevel and hypoid gears on a six-axis CNC hypoid gear generator[J]. Journal of Mechanical Design, 2008, 130(6): 062604-1-11. |
| [20] |
蒋进科, 方宗德, 刘钊. Ease-off拓扑修形准双曲面齿轮齿面多目标优化设计方法[J]. 西安交通大学学报, 2019, 53(6): 44-53. Jiang J K, Fang Z D, Liu Z. Design of multi-objective tooth optimization for hypoid gear with ease-off topological modification[J]. Journal of Xi'an Jiao Tong University, 2019, 53(6): 44-53. (in Chinese) |
| [21] |
Simon V V. Generation of hypoid gears on CNC hypoid generator[J]. Journal of Mechanical Design, 2011, 133(12): 121003-19. |
| [22] |
陈书涵, 严宏志, 明兴祖, 等. 螺旋锥齿轮六轴五联动数控加工模型[J]. 农业机械学报, 2008, 39(10): 198-201. Chen S H, Yan H Z, Ming X Z, et al. Spiral bevel gear's numerical control machining model with six axes five linkages[J]. Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(10): 198-201. (in Chinese) |
 2021, Vol. 44
2021, Vol. 44


