在轴承故障信息诊断和识别分类方面,人工神经网络和支持向量机(support vector machines, SVM)均取得了显著的成果,然而传统的人工神经网络主要采用后向反馈网络结构,随着网络层数的增加误差不断累积,对分类的结果产生一定的影响[1-2]。SVM在对故障信息诊断方面具有很好的性能,但SVM的参数选择将直接影响其模型的学习能力和性能,如何得到SVM最优的参数组合是学者必须考虑的问题[3-5]。因此,众多学者采用智能优化算法研究SVM最优模型参数,常用有遗传算法、蚁群算法、粒子群算法及其改进算法,例如:文献[6-7]。上述算法在SVM参数优化中取得了一定的效果,但其本身还存在着一些不足,例如:遗传算法存在搜索速度慢、编解码增加了计算的复杂度、对初始种群的选择有一定的依赖性等问题;蚁群算法存在搜索时间较长、易产生停滞情况、本质上是离散性限制了算法的应用范围等问题;粒子群优化算法存在易陷入局部最优、后期收敛性较差等问题。另外,大多改进的优化算法引入更多的控制参数,增加了算法的复杂度。
针对上述问题,提出单形进化算法(surface-simplex swarm evolution, SSSE)优化的SVM滚动轴承故障识别方法。该方法的思想是将单形进化算法[8]引入到SVM中进行学习,优化SVM的参数。其中,单形进化算法是通过全随机的搜索机制建立粒子所在的单形邻域,在减少算法的控制参数的同时保证了算法的收敛性,也减少了算法对初始值的依赖;并通过建立粒子的多角色态进化搜索策略,来保持粒子的多样性,避免算法陷入局部的极值点。为验证单形进化算法优化的SVM优越性,采用集总经验模态分解(ensemble empirical mode decomposition, EEMD)方法分解滚动轴承故障信号,选取前6个固有模态分量(intrinsic mode function, IMF),计算其能量,构造故障特征数据,来训练和测试单形进化优化的SVM,并实现滚动轴承信号的诊断和识别。
1 单形进化优化的SVM算法 1.1 SVM原理传统SVM的作用是一个分类器,对于非线性问题需通过核函数映射到线性可分的空间。多数文献中详细地描述了SVM的基本原理和方法[7],文中不再赘述。实际中针对不同的数据特点,核函数的选择影响着SVM的分类效果。为了使优化后的SVM滚动轴承故障诊断方法获得较好的性能和推广性,采用3类常用核函数进行对比实验,计算公式为
| $ \begin{aligned} &\text { 高斯核函数 }: K\left(x, x_{i}\right)=\exp \left(-\frac{\left\|x_{i}-x\right\|^{2}}{2 \sigma^{2}}\right) \text { , } \end{aligned} $ | (1) |
| $ \begin{aligned} &\text { Sigmoid 核函数 }: K\left(x, x_{i}\right)=\exp \left(-\frac{\left\|x_{i}-x\right\|}{2 \beta^{2}}\right), \end{aligned} $ | (2) |
| $ \begin{aligned} &\text { 线性核函数: } K\left(x, x_{i}\right)=x_{i} \cdot x+\theta, \end{aligned} $ | (3) |
式中:x为核函数的中心(即支持向量),xi为样本数据,σ、β和θ为常参数,为了简化实验,将σ、β定义为1,θ定义为0。由文献[4]可知,将特征数据映射到高维空间的最优分类函数:
| $ f(x) = {\rm{sgn}} \left( {\sum\nolimits_{i = 1}^l {{\omega ^*}{y_i}K({x_i},x) + {b^*}} } \right) $ | (4) |
式中:ω*为SVM机之间的连接权值,b*为SVM的偏置。由上述分析可知,SVM有3个主要的参数有待优化,即:核函数的中心X、权值W、偏置B。
1.2 单形进化算法单形进化算法融合单形凸集逼近、随机二维度更新、多角色态的搜索机制[9-10]。其原理是:随机选取二维子空间,利用定义的粒子单形邻域,实现单形凸集逼近搜索,提高算法勘探局部区域的能力与收敛性能。同时,在搜索策略中引入粒子多角色态,实现粒子的多样化,提高搜索的全局性。另外,算法采用全随机方式,所以仅有一个控制参数:群体个数。单形进化算法的参数和收敛特性详见参考文献[8],具体步骤如下:
1) 初始化SSSE算法参数。m个粒子初始化定位方式如下:
| $ X_{i}^{l}(0)=\underline{{{X}^{l}}}+\operatorname{rand}(0,1)\times \left( \overline{{{X}^{l}}}-\underline{{{X}^{l}}} \right), $ | (5) |
式中:Xil(0)是第i个粒子在Rn搜索子空间第l维度上的位置,
2) 建立群体粒子搜索策略。在搜索空间Rn中随机选取p和q两个维度,构建搜索子空间。在p、q空间,定义群体粒子的单形邻域搜索算子:
| $ {X_{i,c1}^{p,q}(n + 1) = {r_{11}} \times X_{i,c}^{p,q}(n) + {r_{12}} \times X_{j,[l,g]}^{p,q}(n) + \left( {1 - {r_{11}} - {r_{12}}} \right) \times X_{j,c}^{p,q}(n),} $ | (6) |
| $ {X_{i,c2}^{p,q}(n + 1) = {r_{21}} \times X_{i,c}^{p,q}(n) + {r_{22}} \times \bar X_{j,[l,g]}^{p,q}(n) + \left( {1 - {r_{21}} - {r_{22}}} \right) \times X_{j,c}^{p,q}(n),} $ | (7) |
| $ {X_{i,c3}^{p,q}(n + 1) = {r_{31}} \times X_{i,c}^{p,q}(n) + {r_{32}} \times \bar X_{j,[l,g]}^{p,q}(n) + \left( {1 - {r_{31}} - {r_{32}}} \right) \times \bar X_{j,c}^{p,q}(n),} $ | (8) |
| $ {X_{i,c4}^{p,q}(n + 1) = {r_{41}} \times X_{i,c}^{p,q}(n) + {r_{42}} \times X_{j,[l,g]}^{p,q}(n) + \left( {1 - {r_{41}} - {r_{42}}} \right) \times \bar X_{j,c}^{p,q}(n),} $ | (9) |
式中:
3) 更粒子新角色位置。每个粒子i,利用步骤2,搜到的4个新中心位置:Xi, c1p, q(n+1),Xi, c2p, q(n+1),Xi, c3p, q(n+1),Xi, c4p, q(n+1),在保持维度位置不变的情况下,更新4个新中心角色位置:Xi, c1(n+1),Xi, c2(n+1),Xi, c3(n+1),Xi, c4(n+1)。
4) 确定三角色态。根据误差函数J评价粒子的优劣,确定粒子的3个角色态。分别如下,
中心角色态:最优位置Xi, c(n+1)。
开采角色态:最新位置,即
| $ {X_{i,l}}(n + 1) = \{ {X_{i,c1}}(n + 1),{X_{i,c2}}(n + 1),{X_{i,c3}}(n + 1),{X_{i,c4}}(n + 1)\} 。$ | (10) |
勘探角色态:搜索空间以均匀分布搜索的位置Xi, g(n+1)。
5) 判断算法是否收敛。记录最优粒子位置:Xo, c(n+1),判断J是否收敛或到最大迭代次数,否则返回(2),直至结束搜索。
1.3 单形进化优化的SVM算法确定了SVM的优化参数(X、W、B)后,基于单形进化智能优化算法的SVM训练算法的步骤如下:
1) 设置滚动轴承特征矩阵T为输入,期望输出为Y(即n输出的组合输出编码),
| $ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {{E_{11}}}&{{E_{12}}}& \cdots &{{E_{1N}}}\\ {{E_{21}}}&{{E_{22}}}& \cdots &{{E_{2N}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{E_{m1}}}&{{E_{m2}}}& \cdots &{{E_{mN}}} \end{array}} \right],\quad \mathit{\boldsymbol{Y}} = \left[ {\begin{array}{*{20}{c}} {{y_{11}}}&{{y_{12}}}& \cdots &{{y_{1n}}}\\ {{y_{21}}}&{{y_{22}}}& \cdots &{{y_{2n}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{y_{m1}}}&{{y_{m2}}}& \cdots &{{y_{mn}}} \end{array}} \right], $ |
式中:Eij表示第i个训练样本的第j个能量特征,yij表示第i个测试样本在第j个SVM下识别结果,m为训练集样本数,n=log2K为SVM的输出个数,K为识别的类数。
2) 设置核函数中心、权值和偏置的搜索边界。
3) SVM的误差函数J定义为优化算法的评价函数:
| $ J = \sum\nolimits_{i = 1}^m {\sum\nolimits_{j = 1}^n {{{\left( {y_{ij}^\prime - {y_{ij}}} \right)}^2}} } , $ | (11) |
式中:y′ij表示第i个样本的第j个SVM期望输出,yij代表第i个样本的第j个SVM的实际输出。
4) 利用单形进化的智能优化算法对SVM的模型参数进行优化,搜索在允许误差内的最优位置为:Xo, c(n+1)、Wo, c(n+1)、Bo, c(n+1)。
5) 将粒子搜索到的全局最优位置Xo, c(n+1)、Wo, c(n+1)、Bo, c(n+1)作为SVM的3个参数的训练结果;
6) 将测试样本送入已经训练好的SVM,完成故障诊断。
在故障诊断时,优化SVM的粒子数为20,核函数中心X、连接权值W和偏置B的搜索范围分别为:[-1, 1]×10n、[-1, 1]×10n、[-1, 1]×10n(n=1)。期望误差设置为0.01。
2 EEMD方法的特征提取EEMD对非线性信号处理具有显著的优点,相对于经验模态分解、局部均值分解和变分模态分解更加成熟[11-14]。滚动轴承故障信号作为一种非平稳信号,采用EEMD方法可以获取信号隐含的特征信息,假定将要进行分解的信号是x(t),其步骤如下。
1) 对x(t)加上一定幅度且是一次次产生的白噪声wi(t),从而得到信号:
| $ {x_k}(t) = x(t) + {w_i}(t),\quad k = 1,2, \cdots ,L, $ | (12) |
式中L是白噪声所产生的次数,也是实现集总平均的次数。
2) 对xk(t)做EMD,得到它的IMF分量cjk(t),下标j表示的是xk(t)的第j个IMF分量,k=1, 2, …, L。
3) 集总平均得到信号x(t)各个IMF分量,即:
| $ {c_j} = \frac{1}{L}\sum\nolimits_{k = 1}^L {{c_{jk}}} (t)。$ | (13) |
上面3个步骤即完成了集总经验模态分解。由于滚动轴承信号由EEMD分解之后,能量主要集中在前几个模态分量,考虑支持向量机学习算法的特点,避免数据冗长,以及保持故障诊断时数据一致性,故选择前6个模态分量作为研究对象,并计算其能量作为该数据的特征。提取特征的具体步骤:
1) 对数据进行EEMD分解(L取200),得到若干个固有模态分量。
2) 计算前m模态分量的能量Ei,构建能量特征向量Tij,其中
3) 构建各组数据EEMD能量特征矩阵。
4) 对特征数据进行归一化处理,得特征矩阵为T。
3 仿真实验为了验证本文方法的有效性,采用2组不同的轴承数据进行实验。实验数据I来自于美国西储大学轴承数据中心(CWRU)[15],文中选择主轴转速1 797 r/min、采样频率12 kHz的8种状态数据,数据类型如表 1所示。实验数据Ⅱ来自于机械故障预防技术学会(MFPT)[16],文中选择主轴转速1 500 r/min、采样频率97 656 Hz的3种状态数据,数据类型如表 2所示。
| 表 1 故障类型及标签(实验数据Ⅰ) Table 1 Fault types and labels(case I) |
| 表 2 故障类型及标签(实验数据Ⅱ) Table 2 Fault types and labels(caseⅡ) |
实验数据Ⅰ:每种状态选取120 300个数据点,每组802个数据点,共150组。实验数据Ⅱ:每种状态选取140 000个数据点,每组2 000个数据点,共70组。将上述2组实验数据,按照上文的方法提取特征,限于篇幅,仅列出了部分特征数据,如表 3所示。
| 表 3 滚动轴承信号的特征数据(实验数据Ⅰ) Table 3 Characteristic data of rolling bearing signals(case I) |
由表 3可以看出,对于不同的故障类型,振动信号的第一模态分量的能量具有明显的差异,随着分解的进行,差异逐渐减少,因此证明了实验选取前6个模态分量的合理性。
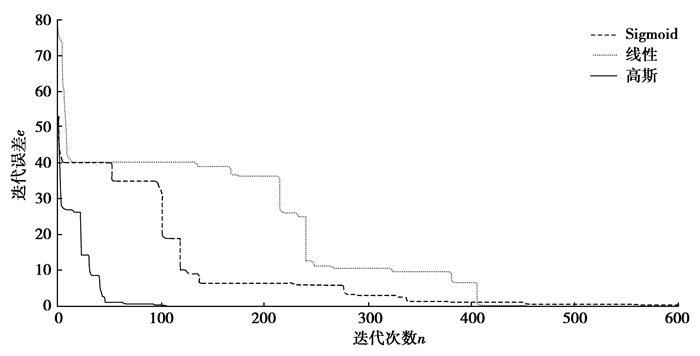
虽然表 3已经可以看出不同故障程度类型的差异,但在大量数据的情况下难以区分,为了进一步精准、快速以及智能化地实现滚动轴承信号的识别,将所提出的单形进化优化的SVM用于滚动轴承故障信号的故障诊断与识别。由于核函数的选取将对SVM的识别分类效果有很大影响,因此,选取式(1)~(3)三个核函数进行对比实验,以判断核函数在本文实验数据下的效果。实验数据Ⅰ每类选择120组训练,30组测试,最大迭代次数1 000;实验数据Ⅱ每类40组训练,30组测试,最大迭代次数600。3种常用核函数的SVM的单形进化寻优过程和测试结果如表 4~5和图 1~2所示。
| 表 4 不同核函数的单形进化SVM统计结果(实验数据Ⅰ) Table 4 SVM of SSSE statistical results of different kernel functions(case Ⅰ) |
| 表 5 不同核函数的单形进化SVM统计结果(实验数据Ⅱ) Table 5 SVM of SSSE statistical results of different kernel functions(case Ⅱ) |

|
图 1 不同核函数的SVM优化过程(实验数据Ⅰ) Fig. 1 SVM optimization process for different kernel functions(case I) |
|
图 2 不同核函数SVM优化过程(实验数据Ⅱ) Fig. 2 SVM optimization process for different kernel functions(case Ⅱ) |
由表 4~5和图 1~2可知,采用不同的核函数,在参数寻优的过程中,单形进化算法均能搜索到期望最优解,其中更快达到最优解并且能够以更高的准确率完成信号诊断的是高斯核函数。由此可见,单形进化算法在SVM参数寻优上具有较好的性能。
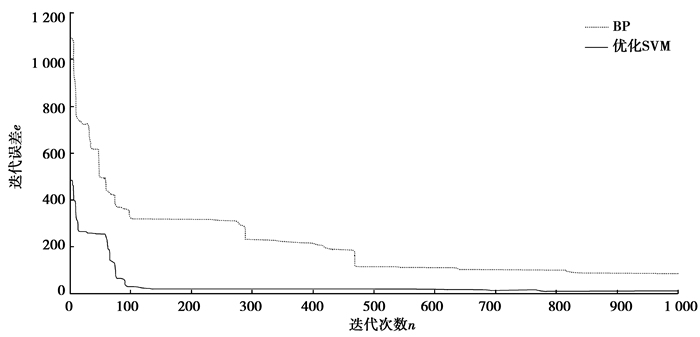
为了进一步验证单形进化算法优化的SVM在滚动轴承故障诊断上的效果,将提取的特征数据用于BP神经网络,并统计结果与优化后的SVM进行分析比较,其中优化的SVM采用高斯函数作为核函数。统计结果如表 6~7和图 3~4所示。
| 表 6 两种方法的诊断精度(实验数据Ⅰ) Table 6 Diagnostic accuracy of the two methods(case Ⅰ) |
| 表 7 两种方法的诊断精度(实验数据Ⅱ) Table 7 Diagnostic accuracy of the two methods(case Ⅱ) |
|
图 3 两种方法的寻优过程(实验数据Ⅰ) Fig. 3 Optimization process of the two methods(case Ⅰ) |

|
图 4 两种方法的寻优过程(实验数据Ⅱ) Fig. 4 Optimization process of the two methods(case Ⅱ) |
从表 6~7和图 3~4可知,单形进化优化的SVM滚动轴承故障识别方法在参数寻优的过程中收敛速度和诊断精度与BP神经网络相比有明显优势。从表 6可知,对于实验数据Ⅰ,采用BP神经网络在滚动轴承诊断时误判样本为18个,总体识别率在92.50%。而优化后的SVM,仅在第八类有2个样本误判,并且总体识别率达到99.17%,与BP神经网络的识别方法相比提高了6.67%。从表 7可知,对于实验数据Ⅱ,优化后的SVM对3种轴承状态的识别率可以达到100%,与BP神经网络的识别方法相比提高了5.56%。
为了验证本文方法与其他算法的优势,与文献[6][17]和[18]中的方法作比较。从表 8可知,本文与文献[6]提出的OFS与量子遗传算法优化的SVM相比总体识别率提高了3.67%,与文献[17]提出的变分模态分解和SVM方法相比总体识别率提高了0.92%,比文献[18]提出的LMD分解的多尺度熵概率神经网络方法提高了0.87%。
| 表 8 不同算法的对比结果 Table 8 Comparison results of different algorithms |
单形进化算法通过单形随机搜索和全随机机制保证算法收敛的同时实现算法单个控制参数,提高算法的可靠性,相较于经典优化算法体现较强的优势,利用多角色态的搜索策略保持群体的多样性,平衡算法的局部勘探能力和全局搜索能力。提出的单形进化算法优化的SVM将优化算法引入到SVM中实现模型参数优化,减少了传统优化算法在优化SVM时的控制参数,并提高了SVM的学习能力。通过滚动轴承信号实验,表明单形进化算法可以很好应用于SVM算法结构参数的寻优,并且EEMD模态能量和单形进化优化的SVM在滚动轴承故障诊断上有更好的效果。
| [1] |
杨蒙蒙, 钱伟. 基于神经网络预测的网络化控制系统故障检测[J]. 信息与控制, 2018, 47(1): 36-40, 47. Yang M M, Qian W. Fault detection of networked control systems based on neural network prediction[J]. Information and Control, 2018, 47(1): 36-40, 47. (in Chinese) |
| [2] |
于德亮, 李妍美, 丁宝, 等. 基于思维进化算法和BP神经网络的电动潜油柱塞泵故障诊断方法[J]. 信息与控制, 2017, 46(6): 698-705. Yu D L, Li Y M, Ding B, et al. Failure diagnosis method for electric submersible plunger pump based on mind evolutionary algorithm and back propagation neural network[J]. Information and Control, 2017, 46(6): 698-705. (in Chinese) |
| [3] |
Aburomman A A, Ibne Reaz M B. A novel SVM-kNN-PSO ensemble method for intrusion detection system[J]. Applied Soft Computing, 2016, 38: 360-372. DOI:10.1016/j.asoc.2015.10.011 |
| [4] |
Wang X P. An innovative SVM for wheat seed quality estimation[J]. Journal of Information and Computational Science, 2015, 12(1): 223-233. DOI:10.12733/jics20105188 |
| [5] |
Tao P Y, Sun Z, Sun Z X. An improved intrusion detection algorithm based on GA and SVM[J]. IEEE Access, 2018, 6: 13624-13631. DOI:10.1109/ACCESS.2018.2810198 |
| [6] |
许迪, 葛江华, 王亚萍, 等. 量子遗传算法优化的SVM滚动轴承故障诊断[J]. 振动.测试与诊断, 2018, 38(4): 843-851, 879. Xu D, Ge J H, Wang Y P, et al. Rolling bearing fault diagnosis of SVM based on improved quantum genetic algorithm[J]. Journal of Vibration, Measurement & Diagnosis, 2018, 38(4): 843-851, 879. (in Chinese) |
| [7] |
杉山将. 图解机器学习[M]. 许永伟, 译. 北京: 人民邮电出版社, 2015: 80-97. Sugiyama M. Diagram machine learning[M]. Xu Y W, trans. Beijing: Posts & Telecom Press, 2015: 80-97. (in Chinese) |
| [8] |
Quan H Y, Shi X L. A surface-simplex swarm evolution algorithm[J]. Wuhan University Journal of Natural Sciences, 2017, 22(1): 38-50. DOI:10.1007/s11859-017-1214-9 |
| [9] |
魏巍, 全海燕. 基于单形进化的径向基网络训练算法[J]. 应用科学学报, 2019, 37(4): 459-468. Wei W, Quan H Y. Radial basis network training algorithm based on surface-simplex swarm evolution[J]. Journal of Applied Sciences, 2019, 37(4): 459-468. (in Chinese) |
| [10] |
高略, 全海燕. 基于一种新智能优化算法与谱相关方法对重力固体潮的分析[J]. 地震工程学报, 2018, 40(3): 535-541. Gao L, Quan H Y. Analysis of gravity earth tide using a new intelligent optimization algorithm and spectral correlation method[J]. China Earthquake Engineering Journal, 2018, 40(3): 535-541. (in Chinese) |
| [11] |
胡广书. 现代信号处理教程[M]. 北京: 清华大学出版社, 2012: 423-428. Hu G S. Modern signal processing course[M]. Beijing: Tsinghua University Press, 2012: 423-428. (in Chinese) |
| [12] |
石瑞敏, 杨兆建. 基于LMD能量特征的滚动轴承故障诊断方法[J]. 振动.测试与诊断, 2015, 35(5): 832-836, 988. Shi R M, Yang Z J. Fault diagnosis of rolling bearing based on energy feature of local mean decomposition[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(5): 832-836, 988. (in Chinese) |
| [13] |
Wang Y X, Markert R, Xiang J W, et al. Research on variational mode decomposition and its application in detecting rub-impact fault of the rotor system[J]. Mechanical Systems and Signal Processing, 2015, 60/61: 243-251. DOI:10.1016/j.ymssp.2015.02.020 |
| [14] |
Colominas M A, Schlotthauer G, Torres M E. Improved complete ensemble EMD: a suitable tool for biomedical signal processing[J]. Biomedical Signal Processing and Control, 2014, 14: 19-29. DOI:10.1016/j.bspc.2014.06.009 |
| [15] |
The Center for Bearing Data. Seeded fault test data[DB/OL].[2020-02-21] https://csegroups.case.edu/bearingdatacenter.
|
| [16] |
Eric B. Fault data sets[DB/OL].[2020-02-21] https://mfpt.org/fault-data-sets/.
|
| [17] |
王新, 闫文源. 基于变分模态分解和SVM的滚动轴承故障诊断[J]. 振动与冲击, 2017, 36(18): 252-256. Wang X, Yan W Y. Fault diagnosis of roller bearings based on the variational mode decomposition and SVM[J]. Journal of Vibration and Shock, 2017, 36(18): 252-256. (in Chinese) |
| [18] |
孟宗, 胡猛, 谷伟明, 等. 基于LMD多尺度熵和概率神经网络的滚动轴承故障诊断方法[J]. 中国机械工程, 2016, 27(4): 433-437. Meng Z, Hu M, Gu W M, et al. Rolling bearing fault diagnosis method based on LMD multi-scale entropy and probabilistic neural network[J]. China Mechanical Engineering, 2016, 27(4): 433-437. (in Chinese) |
 2021, Vol. 44
2021, Vol. 44


