随着空间技术的快速发展,大尺寸、轻量化的空间机械臂已经被广泛地用于空间站的组装、修理和检测,航天员舱外活动,空间飞行器捕获等,其可靠性对于整个空间任务至关重要。空间机械臂动力学分析涉及运动过程中大变形和间隙碰撞问题,且结构参数存在不确定性,因此,要建立精确的空间机械臂动力学模型就需要考虑各种因素。
Flores等[1]对多种间隙模型进行了研究,通过对含间隙机构进行动力学分析发现间隙严重影响机构动力学特性。Zhao等[2]对含间隙空间机器人进行了动力学特性研究,研究发现间隙尺寸会显著影响机器人动力学特性。Erkaya[3]建立了含间隙焊接机械臂的动力学模型。Varedi-Koulaei等[4]采用粒子群算法对含间隙的3-RRR并联机械手进行了优化设计,以减小间隙碰撞对该机械手动力学特性的影响。Megahed等[5]对含多间隙机构进行了研究,结果表明间隙位置,运行速度和间隙大小都会显著影响机构动力学特性。谷勇霞等[6]研究了间隙尺寸和间隙关节数量对漂浮空间机械臂动力学特性的影响。考虑到构件柔性,Khemili等[7]对含间隙平面柔性机构进行了动力学分析,结果显示构件柔性能够有效控制碰撞力峰值。任武等[8]建立了考虑间隙的多柔体臂架的刚柔混合模型。Ben Abdallah等[9]对含多间隙的柔性机构进行了研究。考虑到机械臂在运动过程中存在大变形,Tian等[10]基于绝对节点坐标法[11]对含PD控制器的双连杆柔性机械臂进行了控制精度分析。然而,在建模过程中忽略了间隙对机械臂控制精度的影响。
上述研究都认为机械臂为理想情况,然而由于材料不均匀、加工误差、摩擦、磨损等,真实的机械臂中普遍存在不确定性。Li等[12]研究了存在随机不确定性的含间隙机械臂动力学特性和运动精度问题,建模过程中忽略了机械臂存在的变形。Wang等[13]采用Chebyshev多项式方法对存在区间不确定性参数的刚柔耦合空间机械臂进行了动力学分析,建模过程中忽略了间隙碰撞。笔者将系统考虑大变形、间隙碰撞和不确定性对机械臂动力学特性和控制精度的影响,研究含区间铰间隙的柔性机械臂动力学建模和控制精度分析方法。
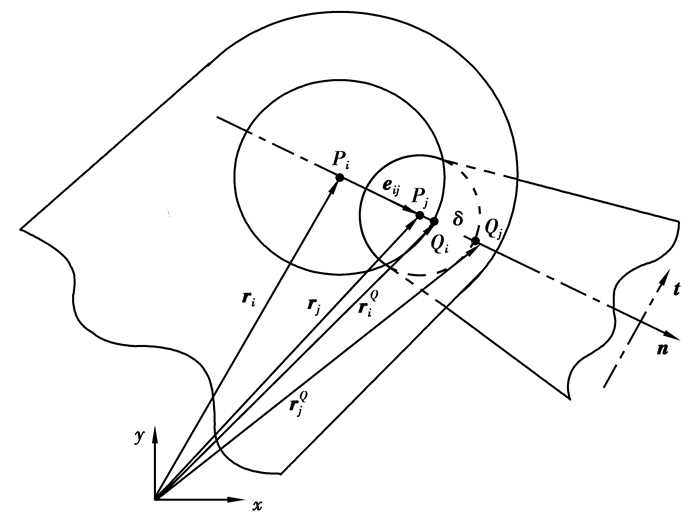
1 旋转铰间隙建模 1.1 旋转铰间隙数学模型如图 1所示,体i, j之间存在平面间隙转动副,轴承是体i的部件,轴是体j的部件。整体坐标系为xy。点Pi和Pj分别为轴承和轴的中心,对应的位置矢量分别为ri和rj。轴与轴承的中心距矢量eij可表示为
| $ {\mathit{\boldsymbol{e}}_{ij}} = {\mathit{\boldsymbol{r}}_j} - {\mathit{\boldsymbol{r}}_i}。$ | (1) |
|
图 1 旋转铰间隙模型 Fig. 1 Revolute joint with clearance |
轴与轴承中心距为
| $ {e_{ij}} = \sqrt {\mathit{\boldsymbol{e}}_{ij}^{\rm{T}}{\mathit{\boldsymbol{e}}_{ij}}} 。$ | (2) |
垂直轴承与轴接触表面的单位法向量为
| $ {\mathit{\boldsymbol{n}} = \frac{{{\mathit{\boldsymbol{e}}_{ij}}}}{{{e_{ij}}}}}。$ | (3) |
当轴承与轴碰撞时,嵌入深度为
| $ {\delta = {e_{ij}} - c,} $ | (4) |
式中c为间隙大小,c=Ri-Rj,Ri和Rj分别为轴承和轴半径。
体i, j的接触点分别为Qi和Qj,基于绝对节点坐标法接触点的全局位置为
| $ \mathit{\boldsymbol{r}}_k^Q = {\mathit{\boldsymbol{r}}_k} + {R_k}\mathit{\boldsymbol{n}}\quad (k = i,j)。$ | (5) |
全局坐标系下接触点Qi和Qj的速度可以通过将式(5)对时间求导得到
| $ \mathit{\boldsymbol{\dot r}}_k^Q = {{\mathit{\boldsymbol{\dot r}}}_k} + {R_k}\mathit{\boldsymbol{n}}\quad (k = i,j)。$ | (6) |
接触点的法向相对速度vN和切向相对速度vT可表示为
| $ {{v_{\rm{N}}} = {{\left( {\mathit{\boldsymbol{\dot r}}_j^Q - \mathit{\boldsymbol{\dot r}}_i^Q} \right)}^{\rm{T}}}\mathit{\boldsymbol{n}},} $ | (7) |
| $ {{v_{\rm{T}}} = {{\left( {\mathit{\boldsymbol{\dot r}}_j^Q - \mathit{\boldsymbol{\dot r}}_i^Q} \right)}^{\rm{T}}}\mathit{\boldsymbol{t}},} $ | (8) |
式中切向量t通过向量n逆时针旋转90°得到。
1.2 接触碰撞力模型Hertz接触力模型是应用最广泛的接触力模型,该模型认为接触表面为完全弹性碰撞,因此不能描述碰撞过程中的能量耗散。为了描述接触碰撞过程中的能量损耗,基于Hertz模型,Lankarani,Herbert和Lee等提出了多种含能量耗散项的接触碰撞力模型[14]。Liu等[15]研究发现Hertz接触力模型仅仅适用于间隙相对较大且载荷较小的情况。对于小间隙情况,计算结果将无法满足精度要求。针对上述问题,Bai等[16]构建了一种基于Lankarani-Nikravesh碰撞力模型和WEF(Winkler elastic foundation)模型的混合碰撞力模型,该碰撞力模型可以表示为
| $ {F_{\rm{n}}} = {K_{\rm{n}}}{\delta ^n} + {D_{{\rm{mod}}}}\dot \delta , $ | (9) |
式中:Fn为法向碰撞力,
| $ {{K_{\rm{n}}} = \frac{1}{8}{\rm{ \mathsf{ π} }}{E^*}\sqrt {\frac{{2\delta {{\left( {3{R_i} - 3{R_j} + 2\delta } \right)}^2}}}{{{{\left( {{R_i} - {R_j} + \delta } \right)}^3}}}} ,} $ | (10) |
| $ {{D_{{\rm{mod}}}} = \frac{{3{K_{\rm{n}}}\left( {1 - c_{\rm{e}}^2} \right){{\rm{e}}^{2\left( {1 - {c_{\rm{e}}}} \right)}}{\delta ^n}}}{{4{{\dot \delta }^{( - )}}}},} $ | (11) |
式中:
| $ \frac{1}{{{E^*}}} = \frac{{1 - v_i^2}}{{{E_i}}} + \frac{{1 - v_j^2}}{{{E_j}}}, $ | (12) |
式中:vk(k=i, j)和Ek(k=i, j)分别是接触材料的泊松比和弹性模量。该间隙碰撞力模型能够普遍适用于大间隙和小间隙情况,通过与有限元仿真结果比较,该碰撞力模型的精度高于Hertz接触力模型。
1.3 摩擦力模型Coulomb摩擦模型是最简单的摩擦力模型。该模型的摩擦力方向与切向速度方向相反,并且摩擦力大小与法向接触力成正比。Coulomb摩擦模型在切向速度趋近于零时会产生不连续的摩擦力,这将有可能导致计算不收敛。为了解决该问题,Ambrósio[17]将速度引入Coulomb摩擦模型,建立了如下形式的摩擦力模型,
| $ {F_{\rm{T}}} = - {c_{\rm{f}}}{c_{\rm{d}}}{F_{\rm{N}}}\frac{{{\mathit{\boldsymbol{v}}_{\rm{T}}}}}{{{v_{\rm{T}}}}}, $ | (13) |
式中:cf为摩擦系数,vT为相对切向速度。cd为动态修正系数,可表示为
| $ {c_{\rm{d}}} = \left\{ {\begin{array}{*{20}{l}} 0&{{\rm{ if }}\quad {v_{\rm{T}}} \le {v_0},}\\ {\frac{{{v_{\rm{T}}} - {v_0}}}{{{v_1} - {v_0}}}}&{{\rm{ if }}\quad {v_0} \le {v_{\rm{T}}} \le {v_1},}\\ 1&{{\rm{ if }}\quad {v_{\rm{T}}} \ge {v_1},} \end{array}} \right. $ | (14) |
式中:v0和v1是为计算动态修正系数给定的速度极限值。Ambrósio摩擦力模型如图 2所示。

|
图 2 Ambrósio摩擦力模型 Fig. 2 Ambrósio friction model |
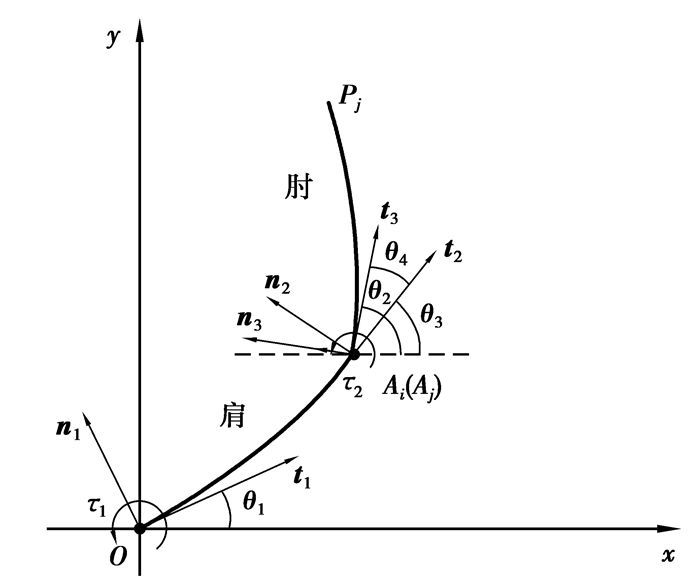
含间隙柔性机械臂模型如图 3所示。连杆OAi在O点处的运动副为理想平面转动副,连杆OAi与连杆AjPj在A处的运动副为平面间隙转动副。τ1和τ2分别为作用于连杆OAi和连杆AjPj的驱动力矩,n1和t1为连杆OAi在O点处的单位法向量和切向量,n2和t2为连杆OAi在Ai点处的单位法向量和切向量,n3和t3为连杆AjPj在Aj点处的单位法向量和切向量,θ1为连杆OAi在O点处的转角,θ3为连杆OAi在Ai点处的转角,θ2为连杆AjPj在Aj点处的转角。考虑到运动过程中连杆OAi和连杆AjPj存在大变形,采用绝对节点坐标法对连杆OAi和连杆AjPj进行动力学建模。
|
图 3 含间隙柔性机械臂 Fig. 3 Flexible manipulator with clearance |
基于绝对节点坐标法[9],平面梁单元上任意一点全局位置可表示
| $ \mathit{\boldsymbol{r}} = \mathit{\boldsymbol{S}}{\mathit{\boldsymbol{e}}^k}, $ | (15) |
式中S为由参数x决定的单元形函数,参数x∈[0 l]表示未变形时特定点的轴向坐标,l为单元初始长度,单元形函数表示为:
| $ \mathit{\boldsymbol{S}} = \left[ {\begin{array}{*{20}{l}} {{S_1}{\mathit{\boldsymbol{I}}_2}}&{{S_2}{\mathit{\boldsymbol{I}}_2}}&{{S_3}{\mathit{\boldsymbol{I}}_2}}&{{S_4}{\mathit{\boldsymbol{I}}_2}} \end{array}} \right], $ | (16) |
式中,I2为2×2的单位矩阵;
| $ {\mathit{\boldsymbol{e}}^k} = {\left[ {\mathit{\boldsymbol{r}}_m^{\rm{T}}\quad {{\left( {\frac{{\partial {\mathit{\boldsymbol{r}}_m}}}{{\partial x}}} \right)}^{\rm{T}}}\quad \mathit{\boldsymbol{r}}_n^{\rm{T}}\quad {{\left( {\frac{{\partial {\mathit{\boldsymbol{r}}_n}}}{{\partial x}}} \right)}^{\rm{T}}}} \right]^{\rm{T}}}。$ | (17) |
ri(i=m, n)表示节点i(i=m, n)位置矢量,∂ri/∂x(i=m, n)为节点i(i=m, n)的位置矢量对x方向的二维偏导数矢量。
基于上述描述,梁单元的动能可表示为
| $ {T_{\rm{e}}} = \frac{1}{2}\int_V \rho {{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}\mathit{\boldsymbol{\dot r}}{\rm{d}}V = \frac{1}{2}{\left( {{{\mathit{\boldsymbol{\dot e}}}^k}} \right)^{\rm{T}}}{{\bf{M}}_{\rm{e}}}{{\mathit{\boldsymbol{\dot e}}}^k}, $ | (18) |
式中Me为梁单元的常数质量矩阵,可通过式(19)计算得到,
| $ {\mathit{\boldsymbol{M}}_{\rm{e}}} = \frac{1}{2}\int_V \rho {\mathit{\boldsymbol{S}}^{\rm{T}}}\mathit{\boldsymbol{S}}{\rm{d}}V, $ | (19) |
式中:ρ和V分别为单元密度和体积。
梁单元的弹性势能可表示为
| $ {U_{\rm{e}}} = \frac{1}{2}\int_V {{\mathit{\boldsymbol{\sigma }}^{\rm{T}}}} \mathit{\boldsymbol{\varepsilon }}{\rm{d}}V, $ | (20) |
式中:σ和ε分别为应力矢量和应变矢量。
驱动力矩τ1和τ2所做的虚功可以表示为
| $ \delta W = {\tau _1}\delta {\theta _1} + {\tau _2}\delta {\theta _4} = {\tau _1}\delta {\theta _1} + {\tau _2}\delta {\theta _2} - {\tau _2}\delta {\theta _3}。$ | (21) |
对于一维两节点柔性梁θ1的变分可以表示为
| $ \delta {\theta _1} = \frac{{\partial r_{Ox}^i/\partial x\delta \left( {\partial r_{Oy}^i/\partial x} \right) - \partial r_{Oy}^i/\partial x\delta \left( {\partial r_{Ox}^i/\partial x} \right)}}{{f_1^2}}{\rm{ , }} $ | (22) |
式中:
| $ {\left. {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{Q}}_1} = \left[ {\begin{array}{*{20}{l}} 0&0&{ - {\tau _1}\left( {\partial r_{Oy}^1/\partial x} \right)/f_1^2} \end{array}} \right.}&{{\tau _1}\left( {\partial r_{Ox}^1/\partial x} \right)/f_1^2}&0&0&0&0 \end{array}} \right]^{\rm{T}}}。$ | (23) |
同理可以得到τ2的等效广义力。基于虚功原理和Baumgarte方法[18],该含间隙柔性机械臂的动力学方程表示为
| $ \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{M}}&{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_\mathit{\boldsymbol{q}}^{\rm{T}}}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_\mathit{\boldsymbol{q}}}}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\ddot q}}}\\ \mathit{\boldsymbol{\lambda }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{B\tau }} - \mathit{\boldsymbol{F}} + {\mathit{\boldsymbol{F}}_{\rm{c}}}}\\ {\gamma - 2\alpha \mathit{\boldsymbol{ \boldsymbol{\dot \varPhi} }} - {\beta ^2}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \end{array}} \right], $ | (24) |
式中:M为机械臂的常数质量矩阵,λ为拉格朗日乘子,F和Fc分别为广义弹性力和广义间隙碰撞力,Φ和Φq分别为约束方程及其对广义坐标q的偏导数矩阵,
由于材料不均匀、加工误差、磨损等原因,机械臂广泛存在不确定性,如间隙尺寸、部件杨氏模量等。这些不确定性因素会显著的影响机械臂动力学特性和控制精度,考虑到间隙尺寸和杨氏模量数据的不完备性,这里将间隙尺寸和杨氏模量处理为区间变量,式(24)变为
| $ \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{M}}&{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_\mathit{\boldsymbol{q}}^{\rm{T}}}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_\mathit{\boldsymbol{q}}}}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\ddot {\tilde q}}}}\\ {\mathit{\boldsymbol{\tilde \lambda }}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{B\tilde \tau }} - \mathit{\boldsymbol{\tilde F}} + {{\mathit{\boldsymbol{\tilde F}}}_{\rm{c}}}}\\ { - 2\alpha \mathit{\boldsymbol{\dot { \boldsymbol{\tilde \varPhi} }}} - {\beta ^2}\mathit{\boldsymbol{ \boldsymbol{\tilde \varPhi} }}} \end{array}} \right], $ | (25) |
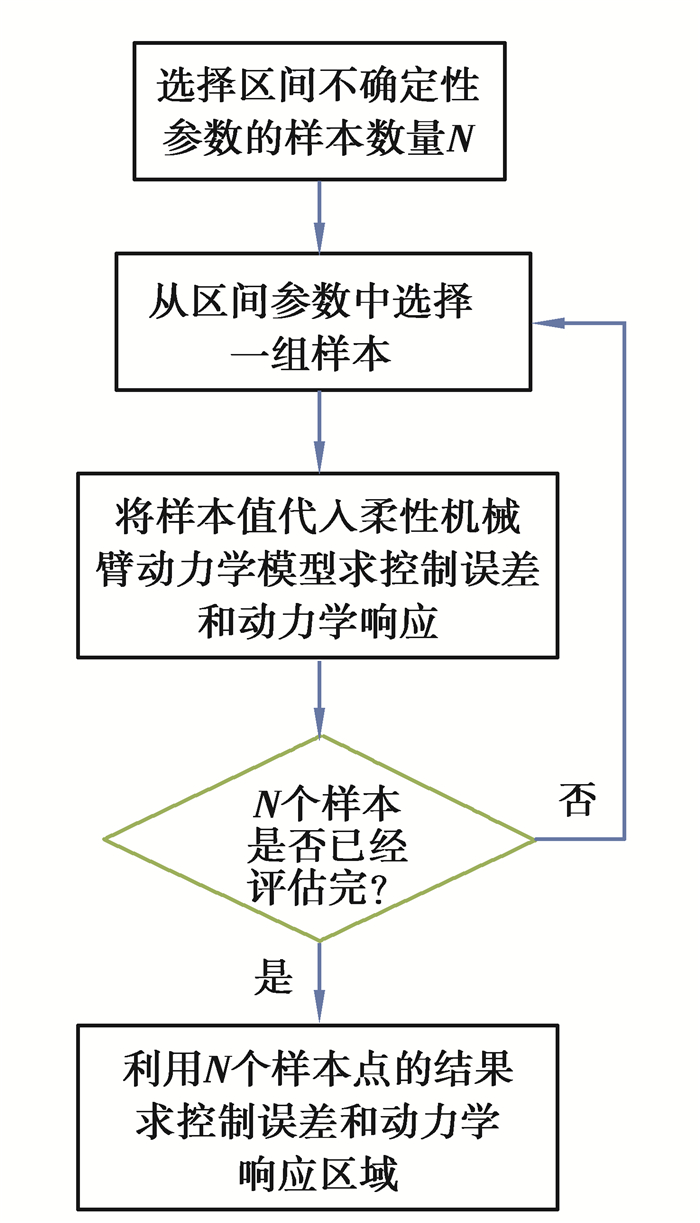
式中上标表示该值与区间变量(c, E)有关。式(25)为含区间不确定性变量和控制器的微分代数方程,对其进行求解将非常困难。这里将提出该动力学模型的求解方法,图 4列出了该方法的主要步骤,具体为:
|
图 4 含区间铰间隙柔性机械臂不确定性分析 Fig. 4 Uncertainty analysis of flexible manipulator with clearance |
1) 选择区间不确定性的抽样数量N。
2) 从每一个区间参数中选择一个样本(ci, Ei)。
3) 在给定区间参数(ci, Ei)的情况下,通过计算动力学方程(24)得到柔性机械臂末端控制误差ei(t)=(xis(t)-xid(t),yis(t)-yid(t))((xis, yis)和(xid, yid)分别为实际和理想情况末端坐标)、末端加速度
4) 判断区间不确定性的N个样本是否已经全部分析。如果否,回到步骤(2);如果是,继续步骤(5)。
5) 找出末端控制误差、末端加速度和驱动力矩上边界和下边界,该上边界和下边界围成的区域即为考虑区间不确定性时末端控制误差、末端加速度和驱动力矩可能的区域。
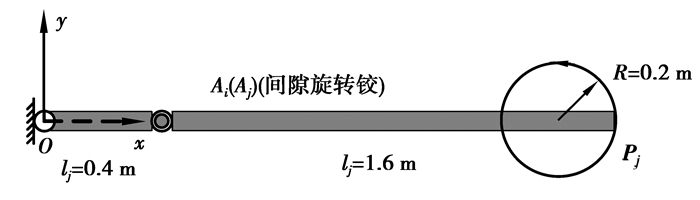
4 仿真分析该含间隙柔性机械臂末端点进行圆轨迹跟踪控制,如图 5所示。连杆OAi和连杆AjPj长度分别为0.4 m和1.6 m。连杆OAi划分为2个单元,连杆AjPj划分为4个单元。连杆OAi和AjPj具有相同的截面形状和材料参数,截面积为2.5×10-3 m2,截面惯性矩为5.208×10-7 m4,杨氏模量为30 GPa,密度为6 000 kg/m3。该机械臂的材料属性及动力学分析相关参数如表 1所示。仿真时间为10 s,跟踪圆轨迹的角速度为
| $ \omega = - \frac{{{\rm{6 \mathsf{ π} }}}}{{500}}\left( {{t^2} - 10t} \right)。$ | (26) |
|
图 5 含间隙柔性机械臂末端圆轨迹跟踪 Fig. 5 End circular tracking of flexible manipulator with clearance |
| 表 1 机械臂仿真参数表 Table 1 Simulation parameter table of manipulator |
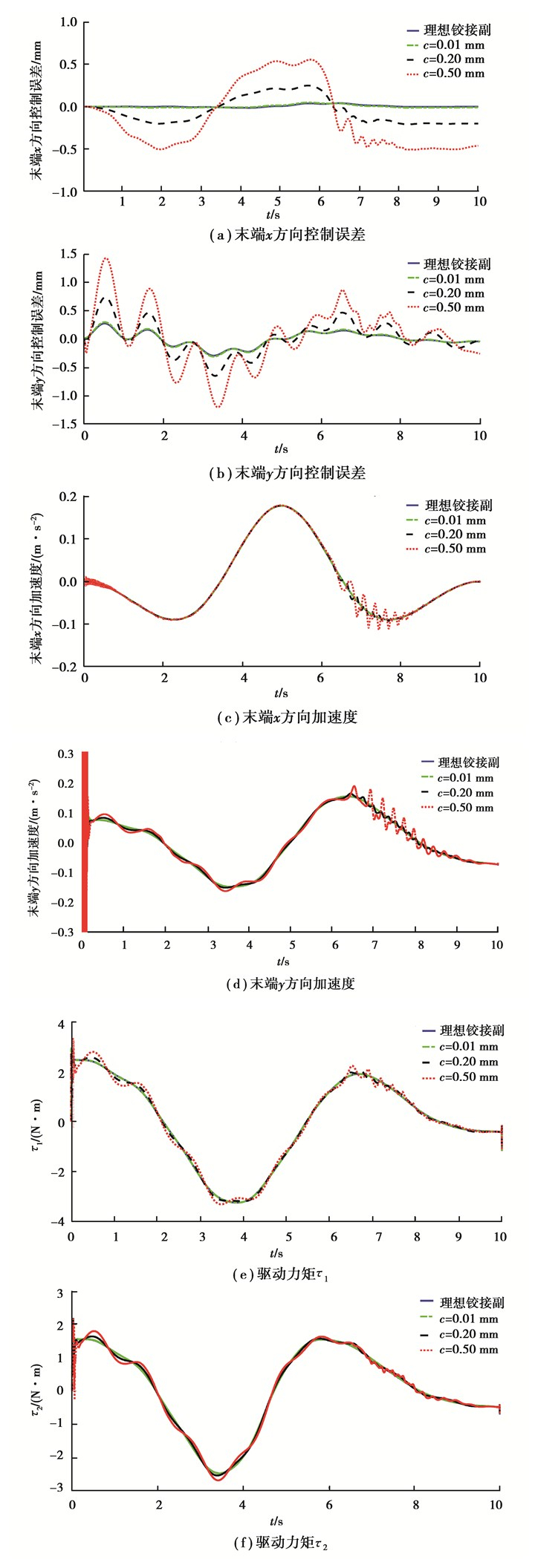
为了研究间隙对机械臂动力学特性和控制精度的影响,分别取间隙c=0.01 mm,c=0.2 mm和c=0.5 mm,摩擦系数cf=0.1,将上述多种间隙情况计算得到的响应结果与理想铰接副的响应结果进行比较。图 6为3种间隙情况下的末端控制误差图、末端加速度图和驱动力矩图。由图 6可知:当间隙大小为0.01 mm时,间隙对末端控制误差、末端加速度和驱动力矩几乎没有影响;当间隙大小为0.2 mm和0.5 mm时,间隙对末端控制误差的影响非常显著,而且间隙越大控制精度越差;当间隙大小为0.2 mm和0.5 mm时,间隙对末端加速度和驱动力矩的影响依然不显著。通过对图 7(d)进一步分析发现初始时刻机械臂末端y方向的加速度扩展较大,其原因在于:初始时刻间隙铰中的轴与轴承存在剧烈碰撞,导致初始时刻机械臂末端y方向的加速度较大。
|
图 6 末端控制误差、末端加速度和驱动力矩图 Fig. 6 Tip error, tip acceleration and driving moment |
|
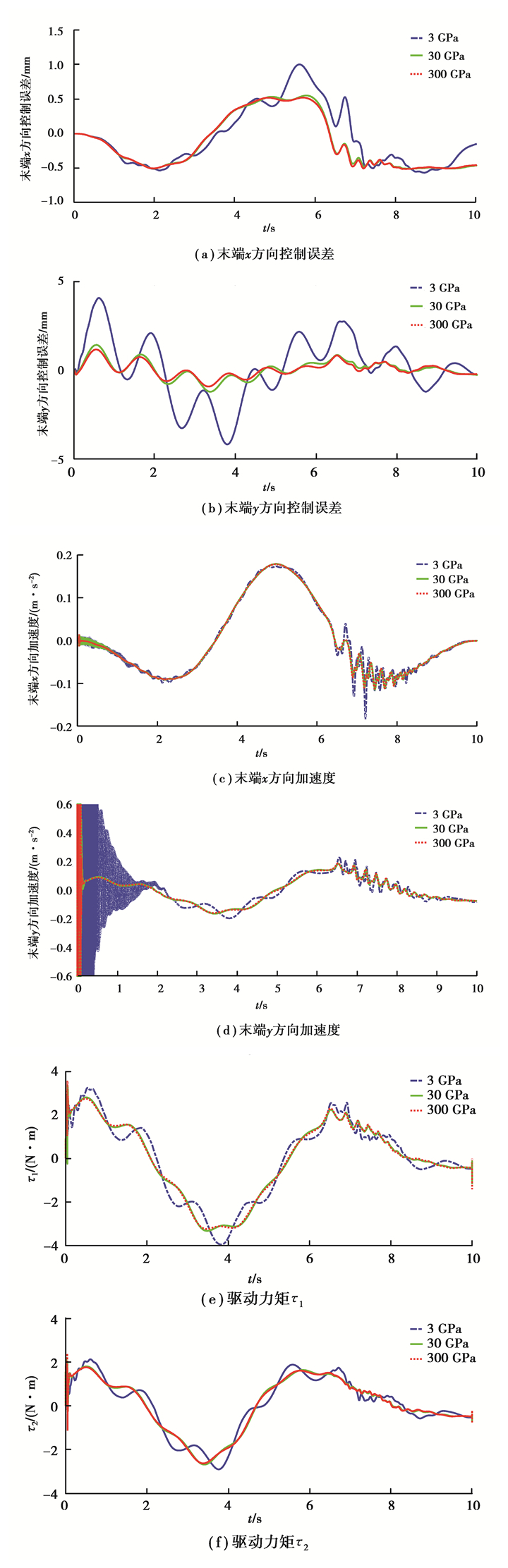
图 7 不同杨氏模量末端控制误差、末端加速度和驱动力矩图 Fig. 7 Tip error, tip acceleration and driving moment under different Young's modulus |
为了分析部件柔性对机械臂动力学特性和控制精度的影响,取连杆杨氏模量为3,30,300 GPa,3种工况下的间隙c=0.5mm。末端控制误差、末端加速度和驱动力矩如图 7所示。可以发现:当杨氏模量为3 GPa时,末端控制误差、末端加速度和驱动力矩与杨氏模量为30 GPa的分析结果存在明显差异,而且弹性模量较低时,末端剧烈抖动持续时间将增加;当杨氏模量为30 GPa和300 GPa时,两种工况的末端控制误差、末端加速度和驱动力矩差异不显著。因此,当连杆弹性模量较小时,连杆柔性会显著的影响控制误差和机械臂的动力学特性,而连杆弹性模量较大时,连杆柔性对该机械臂的控制精度和动力学特性的影响将不显著。
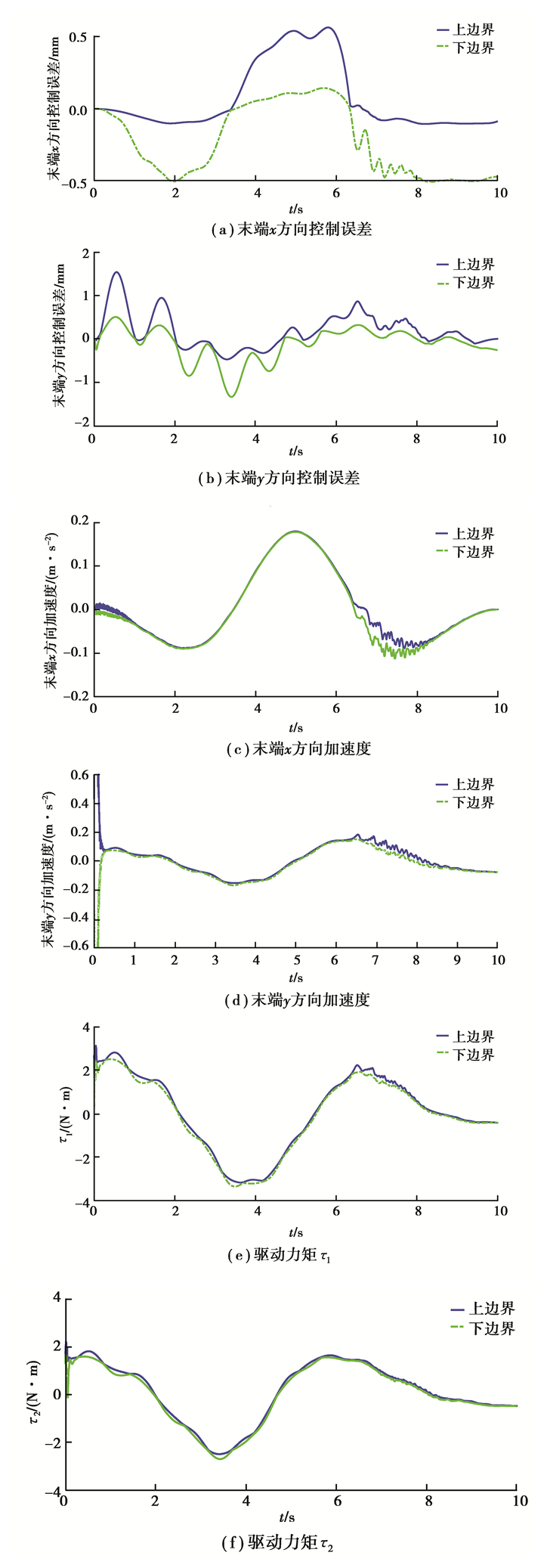
由于间隙尺寸和连杆柔性会显著影响该机械臂控制精度和动力学特性,这里考虑间隙尺寸和杨氏模量为区间变量,其取值范围分别为c=[0.1 0.5mm],E=[20 30]GPa。采用本文中提出的方法对机械臂进行动力学特性和控制精度分析。末端控制误差、末端加速度和驱动力矩如图 8所示。可以发现:考虑不确定性时,末端控制误差将扩张,从而导致控制精度降低;末端加速度和驱动力矩也会扩展,从而影响该机械臂的动力学特性。
|
图 8 末端控制误差、末端加速度和驱动力矩区域图 Fig. 8 Upper and lower bounds of tip error, tip acceleration and driving moment |
1) 当间隙尺寸较小时,间隙对末端控制误差、末端加速度和驱动力矩几乎没有影响。当间隙尺寸较大时,间隙对末端控制误差的影响非常显著,而且间隙越大控制精度越差。然而,较大间隙情况下,间隙对末端加速度和驱动力矩的影响依然不显著。
2) 部件柔性会显著的影响末端控制误差、末端加速度和驱动力矩。当部件弹性模量较低时,末端会剧烈抖动。
3) 参数不确定性会显著的降低该机械臂的控制精度,而且也会影响该机械臂的动力学特性。
| [1] |
Flores P, Ambrósio J. Revolute joints with clearance in multibody systems[J]. Computers & Structures, 2004, 82(17/18/19): 1359-1369. |
| [2] |
Zhao Y, Bai Z F. Dynamics analysis of space robot manipulator with joint clearance[J]. Acta Astronautica, 2011, 68(7/8): 1147-1155. |
| [3] |
Erkaya S. Investigation of joint clearance effects on welding robot manipulators[J]. Robotics and Computer-Integrated Manufacturing, 2012, 28(4): 449-457. DOI:10.1016/j.rcim.2012.02.001 |
| [4] |
Varedi-Koulaei S M, Daniali H M, Farajtabar M, et al. Reducing the undesirable effects of joints clearance on the behavior of the planar 3-RRR parallel manipulators[J]. Nonlinear Dynamics, 2016, 86(2): 1007-1022. DOI:10.1007/s11071-016-2942-7 |
| [5] |
Megahed S M, Haroun A F. Analysis of the dynamic behavioral performance of mechanical systems with multi-clearance joints[J]. Journal of Computational and Nonlinear Dynamics, 2012, 7(1): 011002-1. DOI:10.1115/1.4004263 |
| [6] |
谷勇霞, 张玉玲, 赵杰亮, 等. 考虑含间隙关节的漂浮基空间机械臂动力学输出特性研究[J]. 机械工程学报, 2019, 55(3): 99-108. Gu Y X, Zhang Y L, Zhao J L, et al. Dynamic characteristics of free-floating space manipulator with joint clearance[J]. Journal of Mechanical Engineering, 2019, 55(3): 99-108. (in Chinese) |
| [7] |
Khemili I, Romdhane L. Dynamic analysis of a flexible slider-crank mechanism with clearance[J]. European Journal of Mechanics-A, 2008, 27(5): 882-898. DOI:10.1016/j.euromechsol.2007.12.004 |
| [8] |
任武, 吴运新, 张赵威. 计及铰间隙的多柔体机械臂动力学特性[J]. 振动.测试与诊断, 2015, 35(3): 563-567, 597. Ren W, Wu Y X, Zhang Z W. Dynamic characterization analysis of flexible multibody manipulator with joint clearance[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(3): 563-567, 597. (in Chinese) |
| [9] |
Ben Abdallah M A, Khemili I, Aifaoui N. Numerical investigation of a flexible slider-crank mechanism with multijoints with clearance[J]. Multibody System Dynamics, 2016, 38(2): 173-199. DOI:10.1007/s11044-016-9526-7 |
| [10] |
Tiao Q, Zhang Y Q, Chen L P, et al. Two-link flexible manipulator modelling and tip trajectory tracking based on the absolute nodal coordinate method[J]. International Journal of Robotics and Automation, 2009, 24(2): 103-114. |
| [11] |
Shabana A A. Finite element incremental approach and exact rigid body inertia[J]. Journal of Mechanical Design, 1996, 118(2): 171-178. DOI:10.1115/1.2826866 |
| [12] |
Li J L, Huang H Z, Yan S Z, et al. Kinematic accuracy and dynamic performance of a simple planar space deployable mechanism with joint clearance considering parameter uncertainty[J]. Acta Astronautica, 2017, 136: 34-45. DOI:10.1016/j.actaastro.2017.02.027 |
| [13] |
Wang Z, Tian Q, Hu H Y. Dynamics of spatial rigid-flexible multibody systems with uncertain interval parameters[J]. Nonlinear Dynamics, 2016, 84(2): 527-548. DOI:10.1007/s11071-015-2504-4 |
| [14] |
Machado M, Moreira P, Flores P, et al. Compliant contact force models in multibody dynamics: evolution of the Hertz contact theory[J]. Mechanism and Machine Theory, 2012, 53: 99-121. DOI:10.1016/j.mechmachtheory.2012.02.010 |
| [15] |
Liu C S, Zhang K, Yang R. The FEM analysis and approximate model for cylindrical joints with clearances[J]. Mechanism and Machine Theory, 2007, 42(2): 183-197. DOI:10.1016/j.mechmachtheory.2006.02.006 |
| [16] |
Bai Z F, Zhao Y. Dynamic behaviour analysis of planar mechanical systems with clearance in revolute joints using a new hybrid contact force model[J]. International Journal of Mechanical Sciences, 2012, 54(1): 190-205. DOI:10.1016/j.ijmecsci.2011.10.009 |
| [17] |
Ambrósio J A C. Impact of rigid and flexible multibody systems: deformation description and contact models[M]//Virtual Nonlinear Multibody Systems. Dordrecht: Springer Netherlands, 2003: 57-81.
|
| [18] |
Baumgarte J. Stabilization of constraints and integrals of motion in dynamical systems[J]. Computer Methods in Applied Mechanics and Engineering, 1972, 1(1): 1-16. DOI:10.1016/0045-7825(72)90018-7 |
| [19] |
Dwivedy S K, Eberhard P. Dynamic analysis of flexible manipulators, a literature review[J]. Mechanism and Machine Theory, 2006, 41(7): 749-777. DOI:10.1016/j.mechmachtheory.2006.01.014 |
 2021, Vol. 44
2021, Vol. 44


