汽车在坡长而陡的山区公路行驶时经常需要在低速挡下工作,且制动器需要长时间持续制动,导致刹车摩擦片性能高温退化、材料变形甚至开裂[1],行车安全系数降低, 并伴随噪声和粉尘污染。在中国国家标准《机动车运行安全技术条件》[2]中规定部分汽车应装备缓速器或其他辅助制动装置,使车辆具有持续制动能力,提升行车安全性、舒适性和环保性。缓速器一般采用磁作用非接触摩擦制动方式,可分为电涡流缓速和永磁缓速。
电涡流制动技术比较成熟,已经广泛应用在中大型车辆上。永磁制动尚处研究阶段,由于其具有节约电能、体积相对较小等优点,中外学术界对永磁非摩擦制动的研究越来越重视,但国内高校在这方面的研究还不多,且还没有能够实现可靠无级制动的报道。美国德克萨斯州农工大学的Gay等[3]根据客车制动要求,提出了一种制动器和永磁缓速器联合制动的结构方案,该缓速器只有制动和非制动2种工作状态且结构复杂。2014年广西大学黄亦其教授带领团队展开了对装有永磁缓速器客车联合制动性能的研究[4],结果表明如果缓速器能实现多级制动将极大提高客车的制动安全性和行驶舒适性。2015年江苏大学何仁教授课题组开展了永磁缓速器的设计理论和仿真分析研究[5],同时提出了一种最大制动力矩600 N·m的分级式永磁缓速器设计方案,但其只能实现三级制动,制动力矩小且漏磁严重。2018年北京工业大学叶乐志团队分析了永磁缓速器制动力矩受温度和不同材料的影响[6], 经实验表明仿真分析方法准确可靠,因此在本研究中笔者参照了该团队的建模及分析方法。
无级永磁缓速比分级式具有更强的制动适应性,提高了制动器寿命和行车安全性[7]。所以, 笔者提出一种能够实现无级制动的缓速器方案,进行了结构优化,并建立三维电磁场模型,利用Ansoft软件进行静态、瞬态分析,验证该结构的合理性。
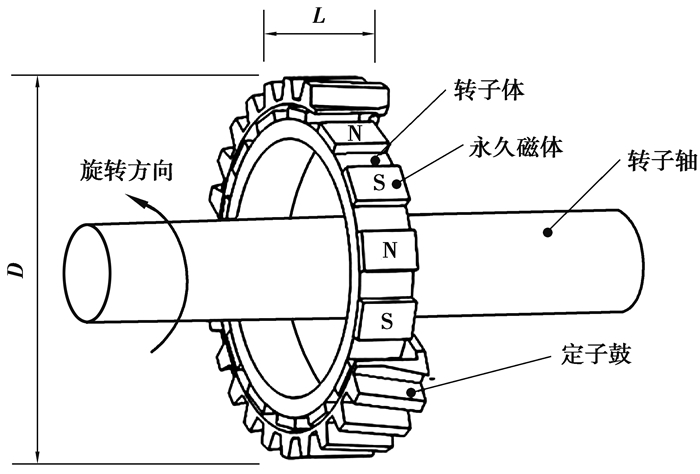
1 工作原理及制动力矩分析 1.1 永磁无级缓速器工作原理缓速器的原理如图 1所示,转子总成通过轴承与转子轴连接。汽车正常行驶时,气缸将转子总成沿轴向完全拉离定子鼓,定子鼓不切割磁感线,无制动力矩产生。
|
图 1 缓速器结构原理示意图 Fig. 1 Structural principle diagram of he retarder |
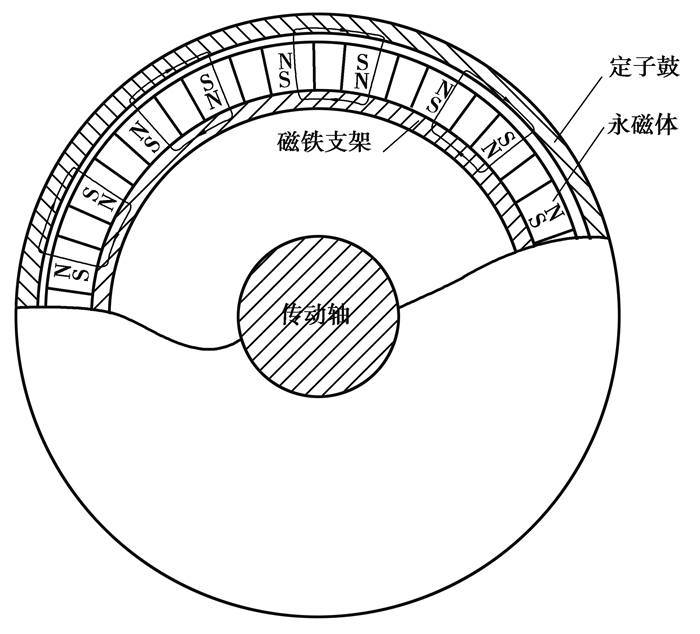
当需要制动时,转子总成沿轴向运动至预定位置并产生磁回路如图 2所示。磁感线从磁体N极出发通过定子鼓与永磁体之间的气隙和定子鼓,然后回到相邻磁体的S极和磁铁支架构成回路。定子鼓表面产生感应电流,感应电流产生的感应磁场阻碍永磁体磁场的运动,从而产生制动力矩实现刹车。连续改变永磁体与定子鼓轴向重合的尺寸产生不同的制动力矩,从而实现缓速器的无级制动。
|
图 2 缓速器磁感应示意图 Fig. 2 Magnetic induction diagram of the retarder |
永磁缓速器磁场分布具有很强的规律性,图 2中产生的电磁场可用Maxwell方程组来描述[8],忽略位移电流效应,其微分方程如式(1)所示。
| $ \left. \begin{array}{l} \nabla \times \boldsymbol{H} = \boldsymbol{J}\\ \nabla \times \boldsymbol{E} = - \frac{{\partial \boldsymbol{B}}}{{\partial t}}\\ \nabla \;\boldsymbol{B} = 0 \end{array} \right\}, $ | (1) |
式中:
磁感应强度B与磁场强度H的关系为
| $ \boldsymbol{B} = \mu \boldsymbol{H}, $ | (2) |
式中μ为磁导率,H/m。引入矢量磁位A,磁感应强度B可表示为
| $ \boldsymbol{B} = \nabla \times \boldsymbol{A}。$ | (3) |
由式(1)~式(3)得
| $ \nabla \times \frac{1}{\mu }\left( {\nabla \times \boldsymbol{A}} \right) = \boldsymbol{J}。$ | (4) |
汽车永磁缓速器求解区域分为导体区Ω1、永磁体区Ω2、空气和定子鼓区Ω3,每个区域控制方程为[6]
| $ \left. \begin{array}{l} {\mathit{\Omega} _1}:\nabla \times \frac{1}{\mu }\left( {\nabla \times \boldsymbol{A}} \right) = \sigma \left( {\frac{{ - \partial \boldsymbol{A}}}{{\partial t}} + \boldsymbol{\upsilon} \times \nabla \times \boldsymbol{A}} \right)\\ {\mathit{\Omega} _2}:\nabla \times \frac{1}{\mu }\left( {\nabla \times \boldsymbol{A} - {\boldsymbol{B}_{\rm{r}}}} \right) = - \sigma \frac{{ - \partial \boldsymbol{A}}}{{\partial t}}\\ {\mathit{\Omega} _3}:\nabla \times \frac{1}{\mu }\left( {\nabla \times \boldsymbol{A}} \right) = - \sigma \frac{{ - \partial \boldsymbol{A}}}{{\partial t}} \end{array} \right\}。$ | (5) |
式中:σ为电导率,S/m;υ为定子鼓与转子的相对运动速度,m/s;Br为永磁体剩磁,A/m。
求解矢量磁位A后即可得到磁感应强度B和电流密度J。在得到磁感应强度和电流密度后即可得到制动力矩表达式
| $ \boldsymbol{T} = \frac{1}{2}\left[ {\int_{r2}^{r1} {\left( {{\boldsymbol{J}_{\rm{e}}} \times \boldsymbol{B}} \right){\rm{d}}r} } \right]{\rm{d}}V{\rm{.}} $ | (6) |
式中:Je为定子鼓电流密度,A/m2;r2、r1分别为定子鼓的内、外半径,m;V为定子鼓涡流区域体积,m3。
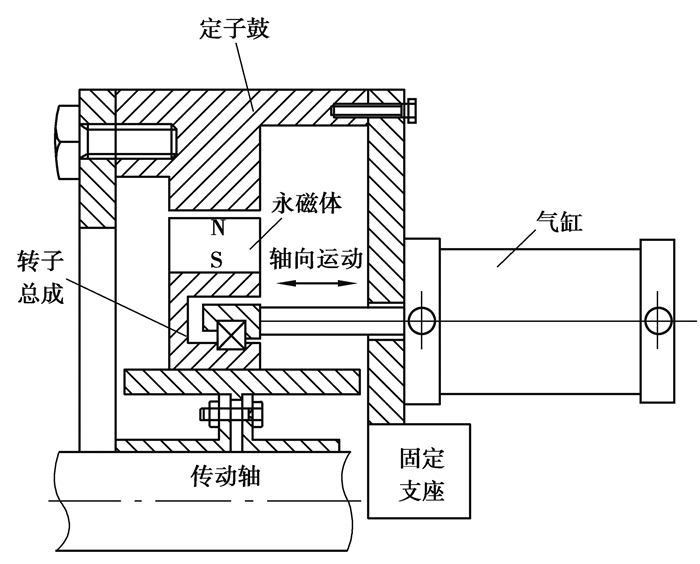
2 永磁无级缓速器结构设计本研究中设计的汽车永磁无级缓速器整体机械结构如图 3所示,主要由永磁体、定子鼓、转子总成、操作机构等组成。永磁体固定在转子体上,定子鼓固定在汽车后桥上,转子总成固定在传动轴上做旋转运动,通过气缸带动其轴向运动实现缓速器无级制动。
|
图 3 缓速器结构简图 Fig. 3 Structure of the retarder |
定子鼓是缓速器中质量最大的关键构件,直接影响制动力矩的大小,有必要进行优化。以定子鼓质量最轻建立目标函数,以车辆空间尺寸和定子鼓热容量要求建立约束条件,建立优化模型如下:
| $ \left. \begin{array}{l} {m_{{\rm{s, min}}}} = \rho {\rm{ \mathsf{ π} }}\left( {r_1^2 - r_2^2} \right){l_{\rm{w}}}\\ 0 < {r_1} \le {d_1}\\ 0 < {r_2} < {d_2}\\ 0 < {l_{\rm{w}}} \le {l_1}\\ m{C_{\rm{d}}}{\delta _{\rm{t}}} \ge \frac{{mg{v^2}}}{{25.98g}} \end{array} \right\}。$ | (7) |
式中:ρ为定子鼓密度,kg/m3;ms, min为定子鼓最小质量,kg;lw为定子鼓宽度,m;m为定子鼓实心部分质量,kg;Cd定子鼓比热容,J/(kg·K);δt为定子鼓许用温升,K;d1, d2,l1分别为车辆缓速器的安装空间尺寸,m; g为重力加速度。
利用Matlab的fmicon模块中二阶非线性函数的中型算法进行了编程解算,设定迭代终止量ε=10-6。优化后的定子鼓在满足性能的前提下重量最轻,实现轻量化设计。
永磁体作为励磁源,其尺寸大小对制动力矩的大小起决定性作用,但其成本较贵,从节省成本的角度出发,在满足性能的前提下磁铁总体积越小越好,按照相同的优化方法进行了尺寸优化。经过2次优化,最终设计出一款制动力矩为900 N·m的永磁无级缓速器,主要参数如下表 1所示。
| 表 1 缓速器主要结构的尺寸大小 Table 1 The size of the main structure of the retarder |
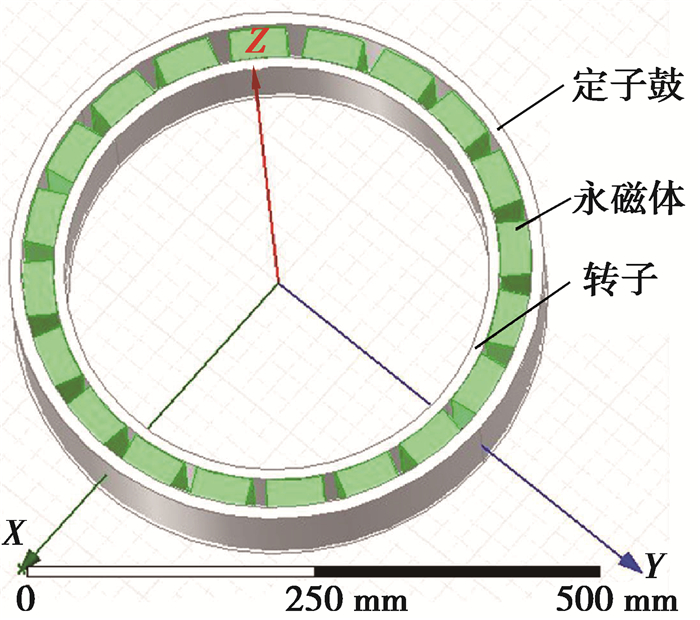
为了验证理论设计和计算的准确性,利用Ansoft Maxwell软件进行制动力仿真。由于目前不具备试验条件,仿真模型的建立和仿真条件的设置参照文献[5]进行。首先进行合理简化:①去除复杂结构,转子和定子用圆环代替;②各零件以及永磁体各向同性,忽略温升对永磁体磁导率和退磁的影响;③忽略缓速器端部的漏磁和功率损耗。
简化后的模型如图 4所示,定子鼓上的永磁体径向充磁,呈N-S极相间布置。
|
图 4 简化模型 Fig. 4 Simplified model |
各部分材料参数如表 2所示。
| 表 2 材料参数 Table 2 Material parameters |
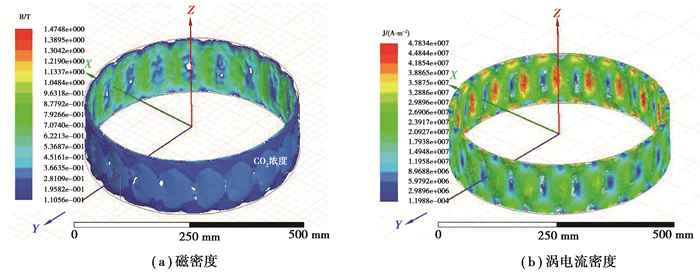
磁场由20块永磁体产生,图 5为静态时定子鼓上磁密度和涡电流密度云图。
|
图 5 定子鼓的仿真云图 Fig. 5 Simulation cloud picture of stator drum |
从图 5中可以看出,在永磁体边缘对应的定子鼓表层部位磁密度最大,符合集肤效应的规律,也说明了分析模型的合理性。热量与制动力的产生均在定子鼓的表层,所以从轻量化角度考虑,定子鼓厚度在满足制动性能和强度前提下应尽可能小。
对比图 5(a)和(b),每个磁体对应的定子鼓上的涡流云图近似环形,且涡流区个数与磁体个数相等,涡电流密度主要集中在磁极正上方。
4.2 瞬态磁场分析开展瞬态分析,观察转子总成轴向移动瞬时的制动力矩波动情况,以及转子总成在不同轴向位置时产生的制动力矩大小。
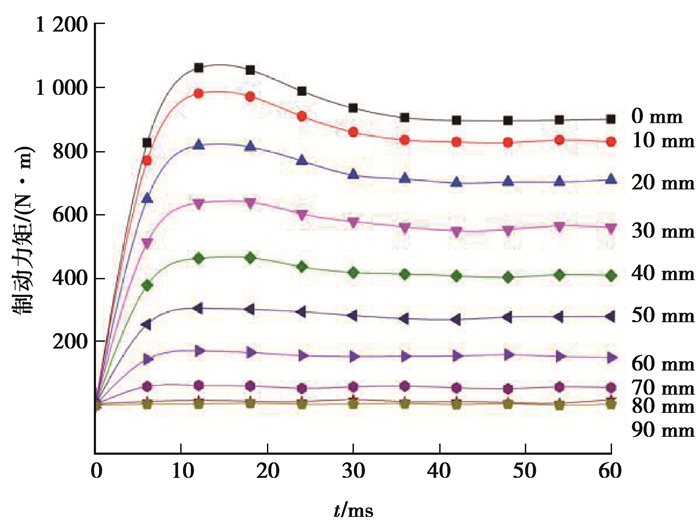
根据仿真计算,模拟缓速器的工作过程,连续轴向移动转子总成,即连续改变永磁体与定子鼓的相对面积,模拟计算制动力矩。将仿真分析得到的结果导出到Origin中(图 6)。
|
图 6 不同转子位置的制动力矩曲线图 Fig. 6 Brake torque curves at different rotor positions |
以10 mm为步长改变转子总成与定子鼓的轴向相对位置,其中0 mm代表转子完全接入磁回路中,80 mm时转子总成已经与定子鼓完全分离,剩下的90 mm与100 mm作为两组对照组。可以看出在转子总成向定子鼓靠拢的过程中制动力矩不断增加,而且当转子总成接入磁回路的面积改变后,制动力矩能够在25~30 ms内达到稳定值,制动响应迅速,制动力矩可连续变化,改善了传统缓速器制动迟缓、顿挫的弊端。
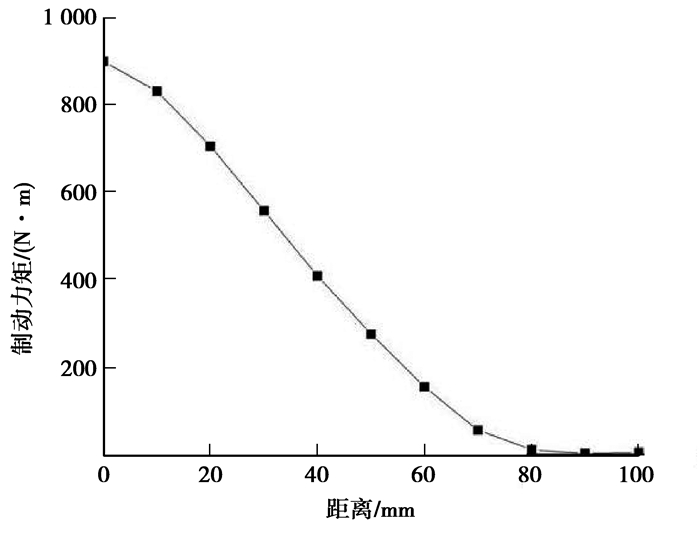
为了更好地说明缓速器无级制动的效果,取各组数据中的稳定制动力矩的平均值,绘制出稳定制动力矩随转子总成轴向位移变化的趋势如图 7所示。
|
图 7 制动力矩变化趋势图 Fig. 7 Brake torque variation trend chart |
可以看出,当转子总成完全接入时,制动力矩最大达到900 N·m,满足工作要求。当转子拉开,位移达到80 mm处制动力矩很小,约为10 N·m,继续拉开至100 mm处,制动力矩下降得很少,约为7 N·m,缓速器基本不起作用。另外,制动力矩与转子轴向位移近成似线性关系,表明通过连续改变转子的轴向位移可实现良好的无级制动,而且可控性好,对缓速器的设计和优化有一定的指导意义。
本论文的仿真结果以笔者所在实验室与西北工业大学合作的国家自然基金——永磁涡流耦合传动特性研究的有限元方法和试验研究为基础[9],同时以北京工业大学叶乐志课题组进行的永磁缓速器试验结果为参照[6],共同验证了优化结果和仿真方法的可靠性,能够满足设计要求。
5 结论文中提出的永磁缓速器设计方案能够实现稳定的无级制动功能,通过理论计算和Matlab优化分析确定了缓速器各个部件的结构参数。从三维瞬态仿真数据可以看出缓速器具有良好的线性控制能力,有利于实现不同路况下的最佳缓速效果。调整转子总成轴向位移后改变的制动力矩能在25~30 ms内收敛到稳定力矩值,峰值力矩与稳定力矩相差不大,可控性好。永磁缓速器能够在进一步完善的基础上进入应用阶段,实现良好的缓速效果。
| [1] |
张应旗. 山区高速公路纵坡路段半挂汽车列车行驶特性研究[D]. 重庆: 重庆交通大学, 2017. Zhang Y Q. Research on the driving characteristics of tractor-semitrailer vehicle in longitudinal slope of mountainous expressway[D]. Chongqing: Chongqing Jiaotong University, 2017.(in Chinese) |
| [2] |
公安部道路交通管理标准化技术委员会, 公安部交通管理科学研究所. 国家标准GB 7258-2017《机动车运行安全技术条件》条文释义[M]. 北京: 中国标准出版社, 2018. Technical Committee for Road Traffic Management Standardization of the Ministry of Public Security, Traffic Management Research Institute of the Ministry of Public Security. Interpretation of the national standard GB 7258-2017 The Provisions on Safety and Technical Conditions for the Operation of Motor Vehicles[M]. Beijing: Standards Press of China, 2018. (in Chinese) |
| [3] |
Gay S E, Ehsani M. Parametric analysis of eddy-current brake performance by 3-D finite-element analysis[J]. IEEE Transactions on Magnetics, 2006, 42(2): 319-328. DOI:10.1109/TMAG.2005.860782 |
| [4] |
张培栋. 装用永磁式缓速器的客车制动性能研究[D]. 南宁: 广西大学, 2014. Zhang P D. Study on braking performance of passenger cars equipped with permanent magnet retarder[D]. Nanning: Guangxi University, 2014.(in Chinese) |
| [5] |
何仁, 王晶, 王亮, 等. 分级式永磁缓速器的设计[J]. 重庆交通大学学报(自然科学版), 2015, 34(5): 155-159, 174. He R, Wang J, Wang L, et al. Design of graded permanent magnet retarder[J]. Journal of Chongqing Jiaotong University(Natural Sciences), 2015, 34(5): 155-159, 174. (in Chinese) |
| [6] |
Ye L Z, Cao M G, Liu Y P, et al. Multi-field coupling analysis and demagnetization experiment of permanent magnet retarder for heavy vehicles (MAY 2018)[J]. IEEE Access, 2019, 7: 50734-50745. DOI:10.1109/ACCESS.2018.2884236 |
| [7] |
Kuwahara T. Composite magnet of electromagnet and permanent magnet, and eddycurrent retarder: US6756870[P].2004-06-29..
|
| [8] |
Wang W J, Li D S, Zhang L X, et al. Research on the influence of different stator materials on the braking torque of liquid-cooled eddy current retarder with dual salient poles[J]. Australian Journal of Mechanical Engineering, 2017, 15(2): 84-92. DOI:10.1080/14484846.2015.1093259 |
| [9] |
何富君, 仲于海, 张瑞杰, 等. 永磁涡流耦合传动特性研究[J]. 机械工程学报, 2016, 52(8): 23-28. He F J, Zhong Y H, Zhang R J, et al. Research on characteristics of permanent magnet eddy-current coupling drive[J]. Journal of Mechanical Engineering, 2016, 52(8): 23-28. (in Chinese) |
 2021, Vol. 44
2021, Vol. 44


