b. 重庆大学 航空航天学院, 重庆 400044
b. College of Aerospace Engineering, Chongqing University, Chongqing 400044, P. R. China
汽车碰撞属于严重的交通事故,一旦发生对人们的生命以及财产安全都将构成极大的威胁,所以研究汽车碰撞安全性问题一直是汽车发展的热点问题之一。提升汽车的碰撞安全性,设计更加合理的结构,对减少碰撞事故带来的危害具有重要意义[1]。
自1889年美国纽约街头发生第一次汽车碰撞事故以来,已有不少采用实车碰撞实验研究汽车碰撞安全性的报道[2, 3]。随着计算机硬件和计算力学方法和软件的发展,数值模拟已成为研究汽车碰撞的重要手段[4, 5]。1986年LS-DYNA首次成功模拟了整车碰撞变形全过程[6]。黄金陵等[7]以闭口等截面薄壁直梁件为研究对象进行了汽车正面碰撞仿真和数值模拟,并将研究成果应用于红旗轿车车身结构正面碰撞仿真模拟中。Hu等[8]以长安SC6350汽车为研究对象,采用数值模拟和实验相结合的方法,改进了该汽车的正面碰撞性能。由于汽车结构极为复杂,碰撞过程数值模拟代价依然高昂。
近年,随着人工智能技术的发展,机器学习方法在工程领域的应用研究受到越来越多的重视。张晓云[9]首次将有限元和神经网络技术与汽车碰撞事故再现相结合,分析了事故发生瞬间的事故车辆关键点的测量值,对汽车结构安全设计提供指导。聂隐愚等[10]针对高速列车,将Kriging模型和Legendre多项式回归应用于车辆动力学建模与仿真分析,提出了一种基于数据驱动的列车建模和仿真方法,优化了车辆多体动力学表达高度非线性力学行为的计算精度。Tang等[11]利用有限元仿真获得列车碰撞响应数据,建立了一种以数据驱动的列车碰撞动力学模型。
汽车碰撞过程中的碰撞力-位移曲线反应了汽车碰撞过程中的吸能特性,是汽车安全性设计中关注的重要数据。采用机器学习算法建立代理模型,可以大幅度提高计算效率。目前尚未见到采用代理模型预测汽车碰撞过程的碰撞力-位移关系的报道。笔者以某型皮卡车为对象,建立整车三维有限元模型,模拟汽车对刚性墙碰撞和两车相向对撞的动态过程,得到碰撞力-位移曲线,并基于BP神经网络和数值模拟结果建立代理模型。采用碰撞代理模型,可以快速得到不同初始速度下汽车碰撞的力-位移曲线,对汽车的安全设计提供依据,具有重要的理论意义和应用前景。
1 汽车碰撞动态过程数值模拟以某型皮卡车为对象,建立三维实体有限元模型,采用ABAQUS有限元软件,模拟该汽车与刚性墙壁碰撞和两车相向碰撞的动态响应过程。考虑5种不同初始速度的情况,模拟结果为代理模型的建立提供数据。
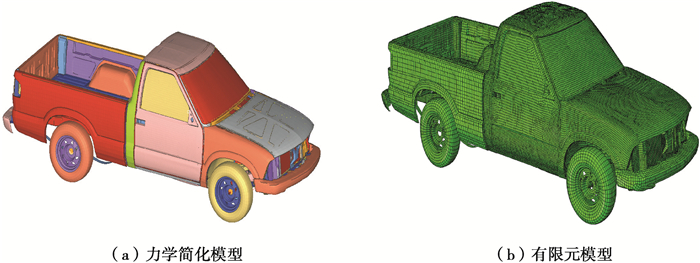
1.1 汽车有限元模型汽车结构复杂,且碰撞过程涉及大变形非线性动态问题,计算模拟代价高。先在本节中建立某型皮卡车的有限元模型。为了提高计算效率,在保证精度的前提下对结构进行简化。整车模型主要包括白车身、动力总成、车门总成、车轮等,由226个部件组成,如图 1(a)所示。其中白车身主要由薄壁板件组成,为保证模拟结果的正确性和精度,模型中对关键部位和部件仅对小的细节进行简化[12]。动力总成主要包括发动机和变速器两大部件,其结构极其复杂,微小部件多,忽略它们的变形在碰撞过程中对整体结构的影响,将其简化成刚体。
|
图 1 某皮卡车整车分析模型 Fig. 1 Analytical model of a pickup truck |
建立的有限元模型见图 1(b)。车身采用四节点壳单元、六面体单元、梁单元、杆单元等进行离散,单元总数为194 924个。各部之间的连接方式为点焊连接、螺栓连接、铰链连接、粘合等。其中点焊连接采用Beam单元进行模拟,螺栓连接采用耦合连接进行处理,铰链连接采用joints连接关系进行简化,采用Adhesive单元模拟部件之间的粘合。
该车车身大部分构件采用钢和铝。轮胎由橡胶和多种材料组成,但不是模拟所关注的重点,将其简化为各向同性均匀材料。当材料发生塑性变形时,均采用双线性各项同性材料模型,其本构关系如下
| $ \begin{array}{l} {\rm{if}}\;\left| \varepsilon \right| \le {\varepsilon _{\rm{s}}}, \sigma = E\varepsilon , \\ {\rm{if}}\;\left| \varepsilon \right| \le {\varepsilon _{\rm{s}}}, \sigma = \left[ {{\sigma _{\rm{s}}} + E'\left( {\left| \varepsilon \right| - {\varepsilon _{\rm{s}}}} \right)} \right]{\rm{sign}}{\sigma _{\rm{s}}}, \end{array} $ | (1) |
式中:σ为应力,ε为应变,σs为屈服应力,εs为屈服应变,E为杨氏模量,E′为强化杨氏模量。材料的参数如表 1所示。
| 表 1 某皮卡车的材料参数 Table 1 Material parameters of a pickup truck |
汽车对刚性墙的碰撞模型如图 2所示,汽车以不同速度正面与刚性墙碰撞。采用ABAQUS/Explicit模拟汽车分别以36,54,72,90,108 km/h等5种初始速度碰撞刚性墙面的情况。图 3所示为汽车与刚性墙面碰撞典型时刻的变形。

|
图 2 皮卡车与刚性墙的碰撞模型 Fig. 2 Collision model of a truck colliding against a rigid wall |

|
图 3 两种不同速度下汽车与刚性墙碰撞典型时刻的变形 Fig. 3 Deformation of the pickup truck colliding against a rigid wall with different initial velocities at typical time |
在汽车安全性设计中,需要确定汽车发生碰撞过程中刚度的变化,或汽车发生碰撞的过程中接触力随质心点位移的变化,这一变化可用碰撞力-位移曲线来反映汽车碰撞吸能的特性。汽车碰撞过程中的碰撞力可由刚性面承受的碰撞力进行计算,图 4所示为不同碰撞速度下碰撞力-位移曲线,以汽车与刚性面开始接触时的位置为参考点。从图 4中可见,不同初速度下碰撞力-位移曲线的变化规律基本相同,均出现了2个峰值,说明车身内部发生了二次碰撞。

|
图 4 汽车以不同速度与刚性墙碰撞时的碰撞力-位移曲线 Fig. 4 Collision force-displacement curves of the pickup truck colliding against a rigid wall |
两车相向相撞是指两辆相同的汽车以大小相同、方向相反的初始速度发生正面碰撞,模型如图 5所示。初始速度仍然选择36, 54, 72, 90, 108 km/h等5种速度。汽车的材料参数不变。典型初始速度下碰撞过程中典型时刻的变形如图 6所示。

|
图 5 两车相向碰撞 Fig. 5 Collision between two trucks |

|
图 6 典型速度下两车相向碰撞过程中典型时刻的变形 Fig. 6 Deformation of trucks during collision with two different initial velocities at typical time |
在这种碰撞情况下,利用其中一辆车的前保险杠碰撞接触力随质心点位移的变化来反映汽车碰撞过程中的刚度变化。图 7所示为各种速度下两车相向碰撞过程中碰撞力-位移曲线,其以两车开始碰撞接触时的质心位置作为参考点。从图 7中可见,碰撞开始时接触力较大,随后车身碰撞吸能,接触力减小,且存在波动,直至两车分离碰撞接触力消失。

|
图 7 不同速度下两车相向碰撞过程中碰撞力-位移曲线 Fig. 7 Collision force-displacement curves during collision between two trucks with different initial velocities |
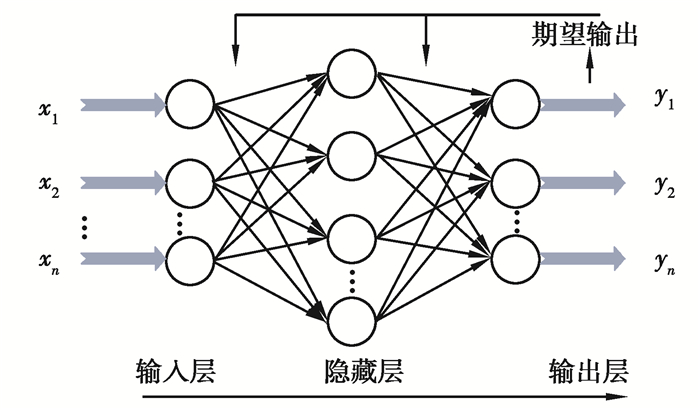
神经网络是一种机器学习方法,其在对输入数据进行学习和误差修正的基础上,建立一个基于数据的回归模型[13]。人工神经网络拥有多种不同结构,包括BP神经网络、卷积神经网络、循环神经网络等。这里采用BP神经网络,其具有分层结构,如图 8所示。BP神经网络包括正向传播和误差的反向传播两个过程,其中正向传播过程每一层的神经元从上一层接收数据,经过计算产生输出数据,输出到下一层神经元继续处理,最后一层神经元输出的是神经网络最终的输出值,而误差的反向传播主要是神经网络的训练算法,其目的在于对权值和阀值的调整,从而调整正向传播中的计算误差,使神经网络达到最优[14]。
|
图 8 BP神经网络结构 Fig. 8 BP neural network structure |
利用前述汽车碰撞过程的有限元模拟结果,得到不同初速度下汽车的力-位移曲线,以反映碰撞发生时汽车的刚度变化。进而从有限元仿真结果中收集不同初速度下的碰撞数据作为神经网络的训练数据,建立一个全速度域的汽车碰撞动力学代理模型。
神经网络的构建包括网络设计、参数配置以及优化算法选择。网络设计包括输入层、隐含层和输出层,输入层节点数应与输入变量个数相同,输出层节点数应与输出变量个数保持一致。这里建立的汽车碰撞BP神经网络结构中的隐含层包括3层神经元,每层128个节点。采用Dropout方法防止过拟合现象,Dropout原理是在前向传播的时候,让某个神经元的激活值以一定的概率停止工作,有利于增强模型的泛化能力,不会过于依赖某些局部特征。神经网络的激活函数描述上层节点输出和下层节点输入之间关系的函数,对于识别率以及收敛速度都有显著影响,这里采用了relu激活函数,relu函数不存在梯度消失问题,会使得模型的收敛速度维持在一个稳定的状态。
将数值模拟得到的数据划分为训练数据和测试数据。将碰撞速度分别为36, 54, 90, 108 km/h的力-位移曲线作为训练数据,将速度72 km/h对应的力-位移曲线作为测试数据。参数配置中将初始学习率设为0.001,学习率影响网络的收敛性和收敛速度,学习率过小虽然可以保证网络收敛,但是收敛较慢,学习率过大则可能导致网络不收敛,不能达到学习效果。选择均方差作为损失函数,均方差损失函数是真实值与预测值差值的平方的均值,能够较好评估回归模型的效果。选择Adam算法作为优化算法,该算法是一种随机梯度下降算法,具有计算高效、方便实现、能够较好处理噪音样本和较好处理稀疏梯度等优势[15]。
神经网络训练的目的在于对权值和阀值的不断调整,在保证模型精度的前提下,使模型进行尽可能多的训练,直到模型的损失函数值达到收敛,误差达到最小[16]。对训练数据采用重采样方法和K-Flod交叉验证使数据充分学习并且得到验证。
针对汽车与刚性墙壁碰撞和两车相向碰撞问题,利用前述方法分别建立相应的代理模型,模型训练的收敛性如图 9所示,可见,建立的两个神经网络模型均具有良好的收敛性。

|
图 9 BP神经网络模型训练收敛性 Fig. 9 Training convergence of BP neural network models |
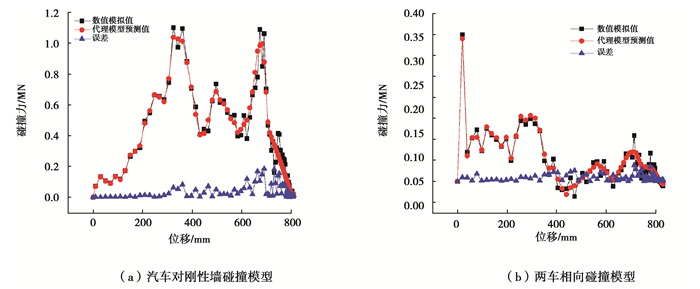
利用前述两个训练完备的BP神经网络代理模型,分别预测汽车以初始速度72 km/h与刚性墙碰撞和两车相向撞时的力-位移响应曲线,并与数值结果进行比较,其结果如图 10所示。从图 10中可见,预测结果与数值模拟结果吻合较好,特别是所关心的碰撞后的初始阶段,预测曲线和模拟曲线变化趋势基本一致。
|
图 10 汽车碰撞代理模型预测及误差 Fig. 10 Prediction by the surrogate model and its errors for collisions of a truck against a rigid wall and between two trucks at an initial velocity of 72km/h |
从图 10中误差曲线可以看到,碰撞开始时和碰撞过程中误差较小,在碰撞接近结束的后阶段误差较大。从汽车安全性设计的角度,主要考虑碰撞后响应最大的初始阶段,对于后面响应较小阶段并不关注。汽车对墙碰撞的预测与数值模拟力-位移响应曲线中,两个最大峰值的相对误差分别为7.49%和9.6%;两车相向碰撞的力-位移响应曲线中,最大峰值的相对误差仅为2.74%。可见,建立的两个汽车代理模型能准确预测力-位移响应曲线,具有很高的效率和足够的精度。
值得一提的是,在建立该代理模型时,模拟的训练样本的参数选择基于汽车设计规范的取值范围,即对于该型汽车,设计中考虑的汽车发生碰撞的初始速度是在36~108 km/h范围内,所以没有讨论该速度范围以外模型的预测精度。
3 结论利用ABAQUS有限元软件建立某皮卡车有限元模型,模拟在不同初始速度下汽车对刚性墙碰撞以及两车相向碰撞的动态过程,基于数值模拟结果和BP神经网络算法,建立了代理模型。得到如下结论:
1) 建立的汽车碰撞有限元模型,以及基于碰撞动态过程模拟得到的力-位移响应结果合理。
2) 针对汽车与刚性墙碰撞和两车相向碰撞问题,基于数值模拟结果和BP神经网络算法建立的代理模型合理。
3) 得到的代理模型在给定的初始碰撞速度范围36~108 km/h内具有足够的预测精度。然而,由于没有讨论碰撞初始速度在该范围之外的泛化能力,因此不能保证碰撞初始速度在该速度范围之外的预测精度。
4) 汽车实车碰撞试验代价高昂,采用代理模型能够高效快速地预测汽车碰撞后的力-位移响应曲线,为汽车碰撞安全性设计提供依据。
| [1] |
李俊峰. 中国汽车被动安全标准探讨: 浅谈汽车柱状碰撞试验[C]//市场践行标准化: 第十一届中国标准化论坛论文集. 成都: 第十一届中国标准化论坛, 2014. Li J F. Discussion on Chinese passive safety standard for automobiles-brief talk on cylindrical collision test of automobiles[C]//Market Fulfilling Standardizaiton: Proceedings of the 11th China Standardization Forum. Chengdu: The 11th China Standardization Forum, 2014. (in Chinese) |
| [2] |
王婷. 我国合资汽车企业效率比较及相关因素研究[D]. 上海: 东华大学, 2012. Wang T. Study on efficiency of joint ventures in automotive industry and related factors[D]. Shanghai: Donghua University, 2012. (in Chinese) |
| [3] |
邓子兵. 乘用车车身结构件安全性试验系统的研制[D]. 上海: 上海交通大学, 2008. Deng Z B. Research and development of a safety test system for vehicle body structure[D]. Shanghai: Shanghai Jiao Tong University, 2008. (in Chinese) |
| [4] |
张静, 栾寅征. 那些年, "碰撞"垫底的车型[J]. 汽车观察, 2012(7): 94-99. Zhang J, Luan Y Z. In those years, colliding car remains in bottom place[J]. Automotive Observer, 2012(7): 94-99. (in Chinese) |
| [5] |
王强. 汽车追尾碰撞安全性及乘员损伤仿真分析[D]. 沈阳: 东北大学, 2010. Wang Q. Simulation analysis of automobile crash at the rear end and safety of passengers[D]. Shenyang: Northeastern University, 2010. (in Chinese) |
| [6] |
昝竹青. 冲压成型工艺对轿车车门碰撞性能的影响研究[D]. 哈尔滨: 哈尔滨工程大学, 2013. Zan Z Q. Influence of forming result on crash behavior of car door[D]. Harbin: Harbin Engineering University, 2013. (in Chinese) |
| [7] |
黄金陵, 贾洪波. 车身碰撞仿真技术在红旗轿车车身开发中的应用[J]. 汽车工程, 1998, 20(5): 257-261, 301. Huang J L, Jia H B. Application of numerical simulation techniques in car body design process of "HONGQI"[J]. Automotive Engineering, 1998, 20(5): 257-261, 301. (in Chinese) |
| [8] |
Hu Y M, Chen W, Deng Z X. Frontal crash-worthiness simulation of the Changan S6350 using the explicit finite element method[C]//The 11th International Pacific Conference on Automotive Engineering(IPC-11), November 6-9, 2001, Shanghai, China. 2001: 9.
|
| [9] |
张晓云. 基于有限元法和神经网络技术的汽车碰撞事故再现[J]. 机械工程学报, 2007, 43(3): 143-147, 153. Zhang X Y. Vehicle crash accident reconstruction based on FEM and neural networks[J]. Chinese Journal of Mechanical Engineering, 2007, 43(3): 143-147, 153. (in Chinese) |
| [10] |
聂隐愚. 数据驱动的车辆动力学建模与仿真研究[D]. 成都: 西南交通大学, 2016. Nie Y Y. Data-driven dynamics modelling and simulation research for railway vehicles[D]. Chengdu: Southwest Jiaotong University, 2016. (in Chinese) |
| [11] |
Tang Z, Zhu Y, Nie Y, et al. Data-driven train set crash dynamics simulation[J]. Vehicle System Dynamics, 2017, 55(2): 149-167. DOI:10.1080/00423114.2016.1249377 |
| [12] |
Chen Y J, Tyan T, Farugue O. Dynamic testing and CAE modeling of engine mounts for application in vehicle crash analysis[C/OL]//SAE 2003 Warld Congress & Exhibition. USA: SAE International, 2003(2003-03-03)[2019-11-25]. https://doilorg/10.4271/2003-01-0257.
|
| [13] |
Mohri M, Rostamizadeh A, Talwalkar A. Foundations of Machine Learning[M]. The MIT Press, 2012.
|
| [14] |
Lanzi L, Bisagni C, Ricci S. Neural networks systems to reproduce crash behavior of structural components[J]. Computers & Structures, 2004, 82(1): 93-108. |
| [15] |
张良军. Python数据分析与挖掘实战[M]. 北京: 机械工业出版社, 2017. Zhang L J. Python practice of data analysis and mining[M]. Beijing: China Machine Press, 2017. (in Chinese) |
| [16] |
Rodolfo B. Building machine learning projects with tensorflow[M]. UK: Packet Pulishing, 2016.
|
 2021, Vol. 44
2021, Vol. 44


