2. 四川大学 空天科学与工程学院, 成都 610065
2. School of Aeronautics and Astronautics, Sichuan University, Chengdu 610065, P. R. China
随着机器人应用领域不断扩大,机器人关节小型化、轻量化、集成化及模块化已成必然发展趋势。现有机器人关节是由驱动电机作为动力源,经由波发生器旋转带动柔轮变形与刚轮啮合传动,从而实现机械臂单自由度摆动或旋转,空间利用率不高且在低速运行快速响应等应用领域发展受限[1]。近年来不同形式波发生器构成的谐波传动构想不断涌现,包括液压驱动[2]、压电驱动[3]、电磁驱动[4]及磁致伸缩驱动[5]等多种形式。其中,基于超磁致伸缩材料具有伸缩系数大、机电耦合系数高、响应速度快、输出功率大、易于驱动等特点[6],朱林剑等[5]提出利用超磁致伸缩材料制作稀土超磁致伸缩驱动器(giant magnetostrictive actuator, 简称GMA)来直接驱动柔轮变形,经谐波传动输出的集驱动、传动于一体的构想备受关注。
因其独特的材料性能,GMM(giant magnetostrictive material)被广泛应用于驱动器与传感器等现代尖端科技元器件研究与开发。基于磁致伸缩正效应基础模型理论的建立,国内外学者开展了广泛的超磁致伸缩驱动器应用研究。Eda等[7]研制出大功率超精密金刚石加工车床微驱动系统,该车床用于加工陶瓷等硬脆材料, 尺寸精度和表面粗糙度均可达纳米级。基于动态Preisach非线性控制模型,Tong等[8]研制出用于校正高频切削力扰动误差的微位移GMA,该驱动器可用于补偿机床加工的系统跟踪误差。Karunanidhi等[9]研制出具有挠曲放大机构的高频喷嘴伺服阀GMA,该驱动器执行具有良好的动态响应与静态抗压性能。同样地,基于磁致伸缩材料的磁致伸缩逆效应,国内外学者对磁机电模型与传感器设计制作进行了深度研究。Baudendistel等[10]采用降噪自感方法研制出环形磁致伸缩传感器,该传感器解决了传统电阻应变传感器的电磁干扰敏感性问题。基于线性耦合磁机耦合模型,Calkins等[11]研究了预压力与感应电压之间关系并以此对输出力进行量化分析,实现输入力测量。郭沛飞等[12]研究了铁磁材料压磁模型,基于此模型研制出静态压磁式力传感器并完成测试系统搭建。目前利用单一磁致伸缩正逆效应研究和应用较为广泛,但正逆效应耦合特性研究及其相关元器件开发偏少。基于GMM正逆耦合效应以及双向能量转换特性,Wang等[13]对兼具执行和传感功能的自感知GMA研究进行了初步探索,研制出了一种GMA驱动的海水液压自感知控制阀。受此文启发,笔者以自感知谐波驱动器为研究对象,采用参数化建模有限元分析法,分析波发生器和柔轮受力情况,根据波发生器尺寸结构和GMM棒刚度、强度以及压杆稳定性条件求解GMM棒几何参数。研究线圈内驱动磁场和偏置磁场叠加强度计算模型并初定驱动磁场和偏置磁场强度大小。通过研究驱动器电磁机三场耦合模型,得出内置永磁体结构参数对磁场均匀性、位移输出特性以及GMM棒应力的影响规律。
1 GMM棒几何参数设计谐波减速器由柔轮、刚轮以及波发生器三大基本构件组成。波发生器为椭圆形零件,尺寸与柔轮存在一定过盈量,其长轴长度比柔轮内经略长,短轴长度比柔轮内径略短,装配过后波发生器旋转迫使柔轮发生弹性形变并与刚轮发生啮合,从而柔轮旋转输出形成谐波传动。谐波驱动器可用于替代波发生器直接驱动柔轮形变并经谐波传动输出,扩展传统电机驱动谐波传动模式,提高系统空间利用率。
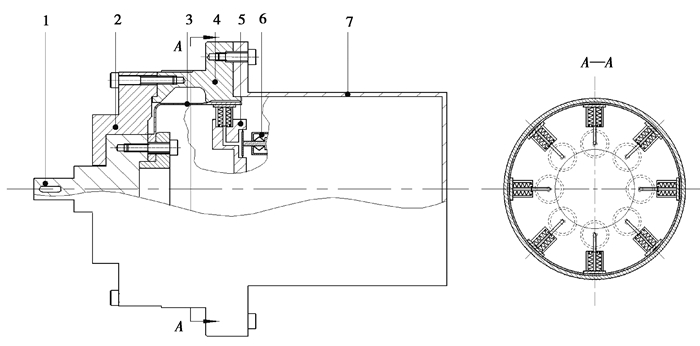
由于谐波减速柔轮内部空间狭小且GMM棒线性伸长率有限,无法在柔轮内部直接均匀周向布置谐波驱动器。故考虑将谐波驱动器外置轴向分布,利用液压传动易实现方向控制的优点,设计小体积液压微位移放大机构嵌入柔轮杯内以实现轴向位移与径向位移之间的转换。建立如图 1所示的超磁致伸缩材料驱动的谐波传动整体结构模型,该结构由输出轴、前端盖、柔轮、刚轮、液压微位移放大机构、谐波驱动器、后端盖、装配螺钉以及轴承组成。通过控制驱动电源信号使得8个圆周方向均布的驱动器以固定相位差产生规律性轴向伸缩,驱动器输出轴向位移推动液压放大机构运动,液压微位移放大机构输出离散均布径向位移迫使柔轮产生周期性谐波变形并与刚轮差齿啮合,以此驱动与柔轮连接的输出轴输出谐波运动。
|
1.输出轴; 2.前端盖; 3.柔轮; 4.刚轮; 5.液压微位移放大机构; 6.谐波驱动器; 7.后端盖 图 1 超磁致伸缩材料驱动的谐波传动整体结构图 Fig. 1 Overall structure of a harmonic drive driven by giant magnetostrictive material |
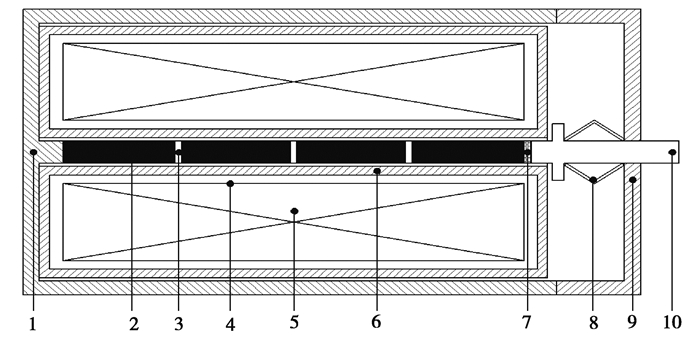
对图 1中谐波驱动器结构进行简化,建立如图 2所示的谐波驱动器总体结构模型,驱动器主要由外壳、GMM棒、驱动线圈、线圈骨架、回路导磁体、上顶盖、预压碟簧、位移输出杆以及霍尔传感器组成。其中外壳、碟簧与位移输出杆均采用非导磁材料,实验仿真中设计闭合磁路结构可以降低漏磁并有效提高磁场均匀度[14]。设置永磁体提供偏置磁场可消除倍频效应,设置预压碟簧给GMM棒施加适当的预压力可提高GMM的伸缩应变以及机电耦合率,设置霍尔传感器可采集磁致伸缩逆效应带来的磁通量变化,希望通过一系列信号提取、信号处理、参数识别控制等操作实现对GMA受力大小进行反映。
|
1.外壳; 2.GMM棒; 3.永磁片; 4.线圈骨架; 5.驱动线圈; 6.回路导磁体; 7.霍尔传感器; 8.预压碟簧; 9.上顶盖; 10.位移输出杆 图 2 超磁致伸缩驱动器(GMA)结构图 Fig. 2 Structure of the giant magnetostrictive actuator(GMA) |
GMM棒设计涉及材料选择、几何形状以及尺寸设计。在本次研究中,GMM棒材料选择Terfenol-D(Tb0.3Dy0.7Fe1.92),棒材形状选择圆柱形。根据甘肃天星稀土功能材料有限公司提供的相关实验数据,其详细物理性能参数如表 1所示。
| 表 1 Tb0.3Dy0.7Fe1.92相关参数 Table 1 Related parameters of Tb0.3Dy0.7Fe1.92 |
对于直动性GMA,其输出位移与GMM棒伸缩量相等,GMA的设定最大伸缩量Xmax与GMM棒长度Lg关系可表示为
| $ {L_{\rm{g}}} = \frac{{\mathit{\Delta }{l_{\max }}}}{{{\lambda _{\rm{g}}}}} = \frac{{{X_{\max }}}}{{\delta {\lambda _{\rm{g}}}}}, $ | (1) |
式中: Lg为GMM棒的长度;Δlmax为GMM棒的最大伸长量;λg为饱和磁致伸缩系数;δ为数学比例因子,为设计工作给予一定的工作余量,一般取线性工作位移为饱和伸长量的一半,但由于谐波驱动器小体积与轻量化要求,取δ=0.8。
由于GMM棒受预压力和负载时须保证刚度、强度以及压杆稳定性满足要求,即GMM棒直径需满足如下条件[5]:
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _p} \ge {n_{\rm{s}}}\left( {{\sigma _0} + {\sigma _1}} \right),}\\ {{F_{{\rm{cr}}}} = \frac{{{{\rm{ \mathsf{ π} }}^2}EI}}{{L_{\rm{g}}^2}} \ge {n_{\rm{s}}}\left( {{F_0} + {F_1}} \right),}\\ {E{A_{\rm{g}}}{\lambda _{\rm{g}}} \ge {F_0} + {F_{10}}}。\end{array}} \right. $ | (2) |
式中: σp为GMM抗压强度;ns为压杆安全系数,一般取3~5;σ0和σ1分别为预压应力和外界负载机械应力;Fcr为临界失稳力;E和I分别为材料弹性模量和转动惯量;F0和F1分别为预压力和外负载机械力;Ag为GMM棒横截面积,其中I和Ag与GMM棒直径dg有如下关系:
| $ \left\{ {\begin{array}{*{20}{l}} {I = \frac{{{\rm{ \mathsf{ π} }}d_{\rm{g}}^4}}{{64}},}\\ {{A_{\rm{g}}} = \frac{{{{\rm{ \mathsf{ π} }}^2}d_{\rm{g}}^2}}{{64}}}。\end{array}} \right. $ | (3) |
谐波减速器CSF-25-80-2UH相关参数如表 2所示。
| 表 2 谐波减速器CSF-25-80-UD结构参数 Table 2 Structural parameters of the CSF-25-80-UD harmonic reducer |
其中,波发生器凸轮长轴Lwgl为45.928 mm,凸轮短轴Lwgs为44.272 mm,若使GMA输出位移满足柔轮径向变形量要求,则GMA的设定最大伸缩量Xmax需满足:
| $ {X_{{\rm{max}}}} = \frac{1}{{{Q_{\rm{A}}}}}\left( {{L_{{\rm{wgl}}}} - \frac{{{L_{{\rm{wgl}}}} + {L_{{\rm{wgs}}}}}}{2}} \right), $ | (4) |
式中QA为微位移放大机构放大倍数,根据文献[15]基于帕斯卡原理的液压微位移放大机构,取放大倍数QA为10。对谐波减速器CSF-25-80-2UH进行力学分析,讨论波发生器在旋转过程中受到的应力载荷情况。通过SolidWorks对谐波减速器进行建模,运用ANSA对减速器模型进行网格划分,其中对波发生器外壁和柔轮内壁划分六面体网格以保持网格精度并且使模型运算收敛性更好。然后将模型导入有限元软件,通过ANSYS Workbench对减速器进行应力仿真分析,根据图 3仿真结果可得减速器波发生器外壁最大应力为59.426 MPa,近似取σ1为60 MPa,即取液压微位移放大机构承受最大应力为60 MPa。根据帕斯卡原理,液压传动机构两端应力相等,因此GMM棒顶杆承受最大应力也为60 MPa。由于GMM抗压强度为300~800 MPa, 故满足要求。

|
图 3 CSF-25-80-2UH波发生器应力分布 Fig. 3 Stress distribution of the CSF-25-80-2UH wave generator |
根据文献[16],超磁致伸缩材料在预压应力σ0为8~12 MPa时伸缩性能最好,结合甘肃天星稀土功能材料有限公司提供的相关实验数据,预压应力σ0取10 MPa,磁场强度取60~100 kA/m,线性伸缩性能较好,此时超磁致伸缩材料的饱和磁致伸缩系数λg为10-3。根据式(1) ~ (4)计算可得,GMM棒长度Lg和直径dg应满足
| $ \left\{ {\begin{array}{*{20}{l}} {{L_{\rm{g}}} \ge 103.5,}\\ {{d_{\rm{g}}} \ge 7.2}。\end{array}} \right. $ | (5) |
根据上述计算结果,为计算简便且有一定的工作余量,结合甘肃天星稀土功能材料有限公司GMM棒产品系列规格列表,取GMM棒长度Lg为120 mm,GMM棒直径dg为10 mm。
2 驱动器磁场强度分析设驱动器体积域为V,封闭边界为∂V,自由空间为V*,电_磁_机耦合三场模型由磁静态方程(安培定律和高斯磁性定律)与磁力学方程描述,Navier方程弱解形式为
| $ \int\limits_V {\left[ {\mathit{\boldsymbol{T}} \cdot \delta \mathit{\boldsymbol{S}} + \rho \frac{{{\partial ^2}\mathit{\boldsymbol{u}}}}{{\partial {t^2}}} \cdot \delta \mathit{\boldsymbol{u}} + c\frac{{\delta \mathit{\boldsymbol{u}}}}{{\delta t}} \cdot \delta \mathit{\boldsymbol{u}}} \right]} {\rm{d}}\mathit{\boldsymbol{V}} = \int\limits_{\partial V} \mathit{\boldsymbol{t}} \cdot \delta \mathit{\boldsymbol{u}}{\rm{d}}\mathit{\boldsymbol{V}} + \int\limits_V {{f_{\rm{B}}}} \cdot \delta \mathit{\boldsymbol{u}}{\rm{d}}\mathit{\boldsymbol{V}}, $ | (6) |
式中:T和fB分别为GMM应力张量与外界负载; t为作用于边界∂V的牵引矢量; S和u是域V中每个点的应变张量和位移,其中应变张量S与位移u满足如下关系[17]:
| $ \mathit{\boldsymbol{S}} = \frac{1}{2}(\nabla \mathit{\boldsymbol{u}} + \nabla {\mathit{\boldsymbol{u}}^{\rm{T}}})。$ | (7) |
同样地,自由空间中磁性材料介质磁静态控制方程弱解为
| $ \int_\varepsilon {{\mathop{\rm grad}\nolimits} {\kern 1pt} } \delta \mathit{\boldsymbol{\phi}} \cdot \mathit{\boldsymbol{B}}{\rm{d}}\mathit{\boldsymbol{V}} = 0, $ | (8) |
式中:ϕ是磁势,与磁场强度H有关,且-grad ϕ=H。此外ε≡V∪V*为包含驱动器体积域V和自由空间V*的欧氏空间。驱动器应力以及空间磁感应强度非线性本构方程为
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{T}} = \mathit{\boldsymbol{C}}[\mathit{\boldsymbol{S}} - \mathit{\boldsymbol{\lambda }}(\mathit{\boldsymbol{T}},\mathit{\boldsymbol{H}})],}\\ {\mathit{\boldsymbol{B}} = {\mu _0}[\mathit{\boldsymbol{H}} + \mathit{\boldsymbol{M}}(\mathit{\boldsymbol{T}},\mathit{\boldsymbol{H}})]}。\end{array}} \right. $ | (9) |
式中:C为柔度矩阵;λ(T, H)和M(T, H)分别为磁致伸缩张量与磁化矢量。由于驱动器采用轴对称螺旋线圈为GMM棒提供驱动磁场,故采用柱坐标系对磁场进行分析求解。根据麦克斯韦方程组可得
| $ \left\{ {\begin{array}{*{20}{l}} {\nabla \times \mathit{\boldsymbol{E}} = - \frac{{\partial \mathit{\boldsymbol{B}}}}{{\partial t}},}\\ {\nabla \times \mathit{\boldsymbol{H}} = J + \frac{{\partial \mathit{\boldsymbol{D}}}}{{\partial t}},}\\ {\nabla \cdot \mathit{\boldsymbol{B}} = 0,}\\ {\nabla \cdot \mathit{\boldsymbol{D}} = \frac{\rho }{{{\varepsilon _0}}}}。\end{array}} \right. $ | (10) |
式中:J为电流密度;D为电位移;ρ为电荷密度;ε0为真空电容率。以单匝线圈为研究对象,由于螺线管直径远大于线圈导线直径,可将模型简化为导线直径无限小的理想情况考虑[18]。设驱动线圈轴线为Z轴,取垂直于轴线的线圈切面为研究对象,线圈半径为R,线圈电流为I,圆环平面圆心Z坐标为M。根据毕奥萨伐尔定律,磁场中任意一点P(x, y, z)矢量磁位A(P)为
| $ \mathit{\boldsymbol{A}}(P) = \frac{{{\mu _o}}}{{4{\rm{ \mathsf{ π} }}}}\oint_l {\frac{{{\rm{d}}l(Q)}}{\mathit{\boldsymbol{a}}}} , $ | (11) |
式中:l为线圈回路;μo为真空磁导率;Q(x′, y′, z′)为线圈导线上任意一点;dl(Q)是其切线方向矢量微分,方向与电流方向一致;a为点Q到点P的矢量。
| $ {{\rm{d}}l = {\rm{d}}{x^\prime }i + {\rm{d}}{y^\prime }j + {\rm{d}}{z^\prime }k,} $ | (12) |
| $ {R = {{\left[ {{{\left( {x - {x^\prime }} \right)}^2} + {{\left( {y - {y^\prime }} \right)}^2} + {{\left( {z - {z^\prime }} \right)}^2}} \right]}^{1/2}}}。$ | (13) |
将式(8)(9)代入式(7),P点矢量磁位A(x, y, z)为
| $ \mathit{\boldsymbol{A}}(x,y,z) = \frac{{{\mu _o}I}}{{4{\rm{ \mathsf{ π} }}}}\oint_l {\frac{{{\rm{d}}{x^\prime }i + {\rm{d}}{y^\prime }j + {\rm{d}}{z^\prime }k}}{{{{\left[ {{{\left( {x - {x^\prime }} \right)}^2} + {{\left( {y - {y^\prime }} \right)}^2} + {{\left( {z - {z^\prime }} \right)}^2}} \right]}^{1/2}}}}} , $ | (14) |
直角坐标系与柱坐标系转换关系为
| $ \left\{ {\begin{array}{*{20}{l}} {\rho = {x^2} + {y^2},}\\ {\phi = \arctan \left( {\frac{y}{x}} \right),}\\ {z = z}。\end{array}} \right. $ | (15) |
从而P点矢量磁位在柱坐标下可表示为
| $ \mathit{\boldsymbol{A}}(\rho ,\phi ,z) = \frac{{{\mu _{\rm{o}}}IR}}{{4\pi }}\int_0^{{\rm{2 \mathsf{ π} }}} {\frac{{\left[ {\sin \left( {\phi - {\phi ^\prime }} \right){\mathit{\boldsymbol{e}}_p} + \cos \left( {\phi - {\phi ^\prime }} \right){\mathit{\boldsymbol{e}}_\phi }} \right]{\rm{d}}{\phi ^\prime }}}{{{{\left[ {{\rho ^2} + {R^2} - 2\rho R\cos \left( {\phi - {\phi ^\prime }} \right) + {{(z - r)}^2}} \right]}^{1/2}}}}} , $ | (16) |
式中ep和eϕ分别为P点的径向与切向单位矢量,令θ=ϕ-ϕ',P点矢量磁位A(ρ, ϕ, z)可表示为
| $ \mathit{\boldsymbol{A}}(\rho ,\phi ,z) = \frac{{{\mu _{\rm{o}}}IR}}{{4\pi }}\left\{ {\int_0^{{\rm{2 \mathsf{ π} }}} {\frac{{{\mathit{\boldsymbol{e}}_\phi }\cos \theta {\rm{d}}\theta }}{{{{\left[ {{\rho ^2} + {R^2} - 2\rho R\cos \theta + {{(z - r)}^2}} \right]}^{1/2}}}}} + \int_{ - {\rm{ \mathsf{ π} }}}^{\rm{ \mathsf{ π} }} {\frac{{{\mathit{\boldsymbol{e}}_p}\sin \theta {\rm{d}}\theta }}{{{{\left[ {{\rho ^2} + {R^2} - 2\rho R\cos \theta + {{(z - r)}^2}} \right]}^{1/2}}}}} } \right\}, $ | (17) |
式中,第2个被积函数是关于θ的奇函数,其值为零。因此,式(13)可以简化为
| $ \mathit{\boldsymbol{A}}(\rho ,\phi ,z) = \frac{{{\mu _{\rm{o}}}IR}}{{{\rm{4 \mathsf{ π} }}}}\int_0^{{\rm{2 \mathsf{ π} }}} {\frac{{{\mathit{\boldsymbol{e}}_\phi }\cos \theta {\rm{d}}\theta }}{{{{\left[ {{\rho ^2} + {R^2} - 2\rho R\cos \theta + {{(z - r)}^2}} \right]}^{1/2}}}}} 。$ | (18) |
由式(18)可知,矢量磁位仅有切向分量,其他方向分量均为零。因此,到轴线距离为r的点的磁场强度Hr为
| $ {H_r} = \frac{{IR}}{{2{{({R^2} + {r^2})}^{3/2}}}}。$ | (19) |
忽略GMM棒放入后相对磁导率的变化以及涡流对磁场的反作用,设螺线管内径为R1,螺线管外径为R2,螺线管长度为l,线圈匝数为n,可得线圈内距离轴线r处的M磁场强度为
| $ {H_{r1}} = \frac{{nI}}{2}\left\{ {\left( {r + \frac{l}{2}} \right)\ln \frac{{{R_2} + {{\left[ {{R_2} + {{(r + l/2)}^2}} \right]}^{1/2}}}}{{{R_1} + {{\left[ {{R_1} + {{(r + l/2)}^2}} \right]}^{1/2}}}} - \left( {r - \frac{l}{2}} \right)\ln \frac{{{R_2} + {{\left[ {{R_2} + {{(r - l/2)}^2}} \right]}^{1/2}}}}{{{R_1} + {{\left[ {{R_1} + {{(r - l/2)}^2}} \right]}^{1/2}}}}} \right\}。$ | (20) |
为消除倍频效应,GMA需在驱动磁场和偏置磁场共同作用下控制GMM棒的伸长与缩短。目前偏置磁场主要分为电流线圈偏置式和内置永磁偏置式两种方式,其中电流线圈偏置式对偏执磁场控制精度更高,但是偏置线圈容易与驱动线圈产生互感,影响磁场控制精度[19]。相比之下内置永磁偏置式使得GMA整体结构更加紧凑,同时可以降低系统能耗以及避免线圈互感提高磁场控制精度[20]。
采用内置永磁圆片产生偏置磁场,根据文献[5]说明,在永磁圆片作用下,距离轴线为r的点的M磁场强度Hr2为:
| $ {H_{r2}} = \int_z^{{t_p} + z} {\frac{m}{{{\rm{2 \mathsf{ π} }}}}} \cdot \frac{1}{{\sqrt {{r_p} + {r^2}} }}{\rm{d}}r, $ | (21) |
式中:m为永磁圆片剩余磁化强度;tp为永磁圆片厚度;rp为永磁圆片半径。所以线圈内磁场总强度为
| $ \begin{array}{*{20}{c}} {{H_{\rm{t}}} = \frac{{nI}}{2}\left\{ {\left( {r + \frac{l}{2}} \right)\ln \frac{{{R_2} + {{\left[ {{R_2} + {{(r + l/2)}^2}} \right]}^{1/2}}}}{{{R_1} + {{\left[ {{R_1} + {{(r + l/2)}^2}} \right]}^{1/2}}}} - \left( {r - \frac{l}{2}} \right)\ln \frac{{{R_2} + {{\left[ {{R_2} + {{(r - l/2)}^2}} \right]}^{1/2}}}}{{{R_1} + {{\left[ {{R_1} + {{(r - l/2)}^2}} \right]}^{1/2}}}}} \right\} + }\\ {\int_z^{{t_p} + z} {\frac{m}{{{\rm{2 \mathsf{ π} }}}}} \cdot \frac{1}{{\sqrt {{r_p} + {r^2}} }}{\rm{d}}r}。\end{array} $ | (22) |
结合甘肃天星稀土功能材料有限公司提供的材料参数,当线圈内总磁场强度满足60 kA/m≤Ht≤100 kA/m时,GMA有较好线性伸缩性能且饱和伸缩系数较大,因此取驱动磁场Hr1和偏置磁场Hr2分别为80和10 kA/m时满足使用条件,此时螺线管线圈和永磁圆片结构参数可通过式(20)(21)初步研究计算。
结合GMM棒相关尺寸参数,初定驱动线圈长度、GMM棒长度与永磁片组厚度之和保持一致。由于驱动GMM棒产生磁致伸缩效应需要较大的磁场强度,许多GMA采用小电流、多匝数的方案,但是线圈匝数增多会使线圈电感增大,从而影响GMA的响应速度[21]。所以本研究中采用大电流、少匝数的方案,在满足磁场强度要求的同时提升GMA的响应速度。
3 驱动器磁场均匀性和位移输出特性分析根据前述关于驱动磁场、内置偏置磁场的结构参数以及相关设计方法研究,使用小电流、多匝数的驱动线圈并内置永磁片提供驱动和偏置磁场容易造成磁场分布不均匀问题,需要对线圈磁场均匀性予以分析。理论上,根据上节可求解驱动磁场以及偏置磁场强度,但由于引入非线性GMM棒后模型复杂性增加,只可通过有限元法求解式(20)和式(21)微分方程可得出磁场强度。使用COMSOL Multiphysics有限元软件中采用数值分析方法对谐波GMA简易模型进行求解与分析,建立GMA电磁机三场耦合模型,分析在不同条件下GMA内部尤其是GMM棒附近区域磁场分布情况,为确定合理的GMA结构参数设计、驱动磁场与偏置磁场布置提供理论依据。
为降低模型计算成本和分析难度,将三维轴对称的GMA模型简化为二维轴对称模型求解,假设驱动电流为稳定直流电且呈准静态变化,计算过程中忽略电感效应[22]。使用COMSOL中的参数化扫描特征,使驱动线圈中的电流密度逐渐升高,从而得到不同条件下GMM棒附近区域磁场分布情况以及非线性磁致伸缩与磁场强度的关系[23]。根据驱动器的结构特点,对GMM棒以及内置永磁片四边形映射进行网格划分,设置最大网格尺寸为0.8 mm,对其他部分采用自适应网格划分,网格尺寸为超细化。设计有限元仿真模型及其网格划分情况如图 4所示。

|
图 4 谐波GMA简易模型网格划分 Fig. 4 Meshing of the harmonic GMA model |
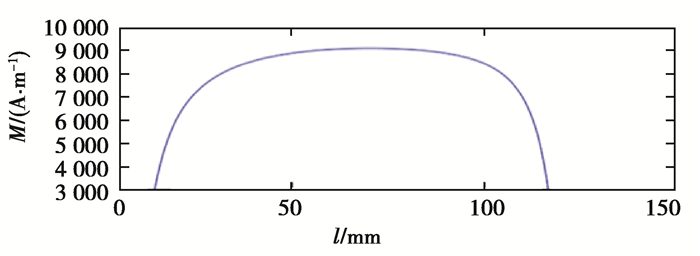
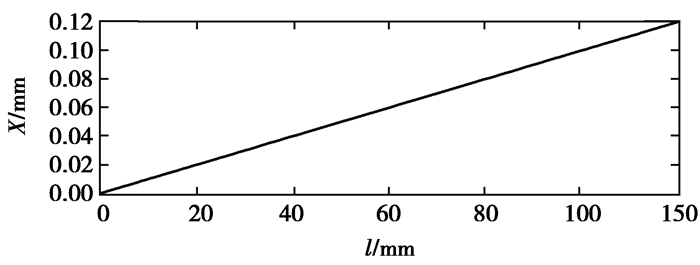
轴心线磁场强度M和位移X分布情况如图 5和图 6所示,取GMA轴线为研究对象,在没有设置永磁片即GMM棒未被分段时,对GMA系统进行磁机耦合分析。结果显示,在驱动线圈内部,磁场分布均匀,磁场能达到预设的场强80 kA/m左右,此时GMA的位移输出线性度很好,最大输出位移能达到0.12 mm,大于GMA的设定最大伸缩量Xmax= 0.082 8 mm,满足设计要求。
|
图 5 无偏置磁场时驱动线圈内部磁场分布 Fig. 5 Internal magnetic field distribution without a bias magnetic field |
|
图 6 无偏置磁场时GMA输出位移曲线 Fig. 6 GMA output displacement curve without a bias magnetic field |
为消除倍频效应,必须设置偏置磁场。但由于GMA结构紧凑,内置永磁片的布局会影响驱动磁场分布。在GMM棒总长度Lg以及直径dg保持不变的基础上,分析永磁片的个数以及GMM棒段数对驱动线圈内部磁场均匀性分布的影响。由第2节可得,GMM棒长度Lg为120 mm,直径dg为10 mm。同时,为保持GMA伸缩部分整体结构均匀性,取永磁圆片直径dp也为10 mm,永磁圆片总长度Lp为15 mm。设定永磁片Br= 1.2 T, Hc= 960 kA/m。将永磁圆片平均分为n片,GMM棒平均分为n+1段,则每片永磁圆片长度Lgn和永磁圆片厚度Lpn分别为
| $ \left\{ {\begin{array}{*{20}{l}} {{L_{{\rm{g}}n}} = \frac{{{L_{\rm{g}}}}}{n},}\\ {{L_{{\rm{p}}n}} = \frac{{{L_{\rm{p}}}}}{n}。} \end{array}\quad (n = 1,2,3, \cdots )} \right. $ | (23) |
取驱动线圈内部区域为研究对象,采用控制变量法,依次改变n值,得到GMM棒和永磁圆片不同分段情况下驱动线圈内部磁场分布情况(见图 7)。

|
图 7 不同n取值条件下驱动线圈内部磁场分布图 Fig. 7 Internal magnetic field distribution with different number of permanent magnets n |
类比数据标准差计算公式,定义磁场均匀性度量标准η计算公式为
| $ \eta = \frac{{\sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{({H_i} - {H_{{\rm{avg}}}})}^2}} } }}{{{H_{{\rm{avg}}}}}} \times 100\% , $ | (24) |
式中:N为GMM棒轴向等距获取的采样点数;Hi为第i个采样点处磁场强度;Havg为N个采样点的平均磁场强度。度量标准η值越小,说明磁场均匀度越好。经过对图 7(a)到(e)每间隔10 mm设置一个采样点,用最小二乘法对η值变化曲线进行数据拟合,得到η值随永磁体片数n变化情况如图 8所示。

|
图 8 磁场均匀性η随均布永磁体片数n变化情况 Fig. 8 Magnetic field uniformity η with different number of permanent magnets n |
由图 8可得,当永磁体片数n取1和2时,磁场均匀性较差,靠近永磁片附近区域磁场变化较大,远离永磁片的GMM棒中段磁场均匀性较好,GMM棒的伸缩应变可能受到影响。随着永磁体片数逐渐增加,驱动线圈内部磁场强度小幅度下降,这是由于永磁体平均布置,磁场互相抵消降低了总体磁场强度。同时,随着永磁体片数增多,单片永磁体厚度减小,磁场均匀性η从44%降低到26%且下降程度逐渐放缓,线圈内部磁场均匀性逐渐改善。
同时,为了验证均布永磁体偏置磁场方案的可行性,对GMA的输出位移进行研究。根据图 9可得,5种条件下GMA输出位移都大于初设最大伸缩量Xmax,满足位移大小要求。但随着永磁体片数逐渐增加且单片厚度不断减小,GMA输出位移的线性度逐渐提高,可见永磁体的均匀分布可以改善GMA输出位移均匀度,进而自感知谐波驱动器具有更好的动态性能以及工作稳定性。

|
图 9 不同n取值条件下GMA输出位移分布图 Fig. 9 GMA output displacement distribution with different number of permanent magnets n |
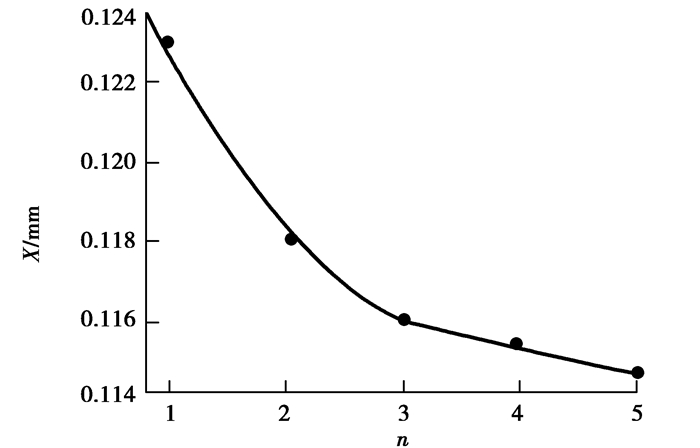
以GMA输出末端截面圆心为研究对象,提取不同n取值条件下GMA输出最大位移,如图 10所示,随着永磁体片数逐渐增加,GMA输出最大位移从0.123 mm下降到0.114 mm,最大输出位移下降7.32%,且下降趋势逐渐放缓,根据趋势预测如继续增加永磁片数量n,最大输出位移会逼近0.110 mm左右。
|
图 10 不同n取值条件下GMA输出最大位移变化 Fig. 10 Maximum displacement of GMA output with different number of permanent magnets n |
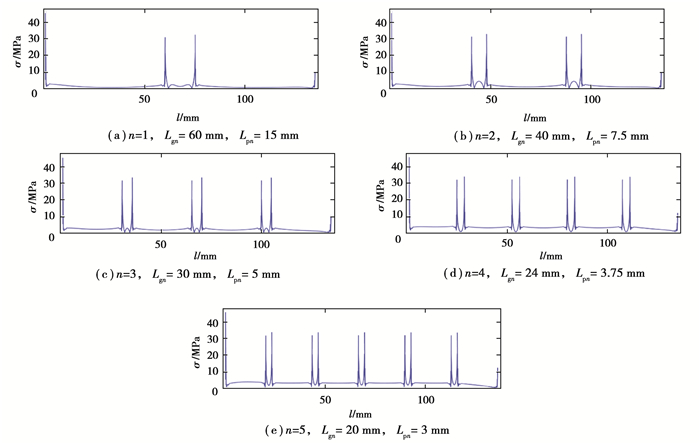
分析GMA工作时不同位置应力分布情况(见图 11),在永磁片和GMM棒交界处应力集中明显,最大应力可达32.5 MPa,GMM棒整体应力稳定在3.5 MPa左右。随着永磁体片数逐渐增加,最大应力基本稳定在32.5 MPa左右,但应力集中区域增多,应力分布关于位置中心对称性很好。可以推断,如果永磁体片数继续增加,系统应力集中区域也会随之增加。
|
图 11 不同n取值条件下GMA应力分布图 Fig. 11 Stress distribution of GMA with different number of permanent magnets n |
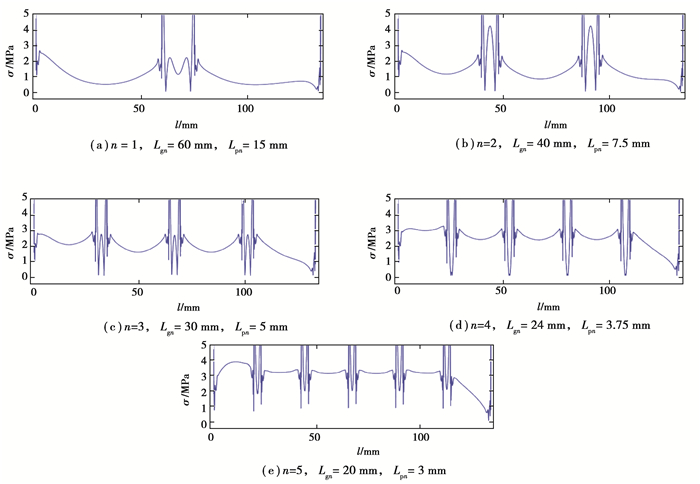
主要考察GMM棒应力分布情况,截取应力分析区间为0~5 MPa。如图 12所示,随着永磁体片数逐渐增加,GMM棒应力分布均匀性逐渐改善,符合前述磁场均匀性相关规律。尤其是当n取5的时候,中间4根GMM棒应力基本稳定在3.1 MPa左右,整根棒应力值波动小于10%,说明在偏置磁场尤其是均布偏置磁场对GMM棒受力均匀性有较大改善。
|
图 12 不同n取值条件下GMM棒应力分布图 Fig. 12 Stress distribution of GMM rods with different number of permanent magnets n |
综合考虑永磁体段数n对磁场分布、位移特性以及应力分布影响,永磁体段数n越大,磁场分布均匀度变化与位移输出均匀度越好,最大位移输出越小,GMM应力均匀度越好。由于最大位移输出影响较小,且即使n取5时最大位移输出也能满足设计要求,但内置永磁片过多会增加系统结构的冗杂性。故在驱动器最大位移输出满足一定要求的前提下,如系统结构允许,可布置较大数量的内置永磁片以提高GMA系统磁场均匀度和应力均匀度,从而改善GMA系统的综合性能。
4 结论1) 基于GMM正逆效应耦合特性,提出了集驱动、传动、传感于一体的新型自感知谐波驱动器构想。建立了基于GMM的谐波传动整体结构模型,求解了波发生器应力分布并根据帕斯卡原理确定GMM棒承受最大应力,根据谐波减速器工作条件确定驱动器输出参数,计算得出超磁致伸缩棒的长度和直径分别为120 mm和10 mm。
2) 基于毕奥萨伐尔定律推导了驱动线圈内部磁场求解方程,综合对比两种偏置磁场布置方式的利弊,选取了内置永磁体提供偏置磁场的布置方式,初定驱动磁场和偏置磁场强度分别为80 kA/m和10 kA/m。
3) 改变GMM棒以及内置永磁体段数,对线圈内部磁场分布、位移输出以及应力分布进行有限元仿真分析,在永磁体总长度不变情况,对永磁体实行内置均匀布置,随着永磁体片数逐渐增加,磁场均匀度从44%降低到26%,输出最大位移从0.123 mm下降到0.114 mm,GMM棒应力分布均匀度显著提高。
| [1] |
刘二乐, 陈纯, 王方成. 谐波减速器的传动精度分析[J]. 机械工程师, 2014(2): 3-5. Liu E L, Chen C, Wang F C. Transmission accuracy analysis of harmonic reducer[J]. Mechanical Engineer, 2014(2): 3-5. (in Chinese) |
| [2] |
李国康, 吕小乔. 液力谐波减速器波发生器流体特性研究[J]. 沈阳理工大学学报, 2017, 36(1): 42-45. Li G K, Lv X Q. Study on fluid characteristics of wave generator on hydraulic harmonic reducer[J]. Transactions of Shenyang Ligong University, 2017, 36(1): 42-45. (in Chinese) |
| [3] |
李霞, 郭正阳, 张三川, 等. 一种新型压电谐波电动机的研究[J]. 微特电机, 2014, 42(6): 4-7. Li X, Guo Z Y, Zhang S C, et al. Research on a novel piezoelectric harmonic motor[J]. Small & Special Electrical Machines, 2014, 42(6): 4-7. (in Chinese) |
| [4] |
Rens J, Clark R, Calverley S, et al. Design analysis and realization of a novel magnetic harmonic gear[C/OL]//2008 18th International Conference on Electrical Machines. Piscataway, NJ: IEEE, 2008(2018-05-16)[2020-07-29]. https://doi.org/10.1109/ICELMACH.2008.4800163.
|
| [5] |
朱林剑, 曹向峥, 陆玉前. 超磁致伸缩谐波电机致动器设计方法与特性研究[J]. 机械工程学报, 2018, 54(22): 204-211. Zhu L J, Cao X Z, Lu Y Q. Design method and characteristics study on actuator of giant magnetostrictive harmonic motor[J]. Journal of Mechanical Engineering, 2018, 54(22): 204-211. (in Chinese) |
| [6] |
刘慧芳, 贾振元. 超磁致伸缩材料力传感执行器关键技术研究[J]. 机械工程学报, 2014, 50(4): 69-69. Liu H F, Jia Z Y. Research on the key technologies of force sensing actuator with giant magnetostrictive materials[J]. Chinese Journal of Mechanical Engineering, 2014, 50(4): 69-69. (in Chinese) |
| [7] |
Eda H, Ohmura E, Sahashi M, et al. Ultraprecise machine tool equipped with a giant magnetostriction actuator: development of new materials, tbx Dy1-x, (fey Mn1-y)n, and their application[J]. CIRP Annals, 1992, 41(1): 421-424. DOI:10.1016/S0007-8506(07)61235-9 |
| [8] |
Tong D, Veldhuis S C, Elbestawi M A. Control of a dual stage magnetostrictive actuator and linear motor feed drive system[J]. The International Journal of Advanced Manufacturing Technology, 2007, 33(3/4): 379-388. DOI:10.1007/s00170-006-0769-y |
| [9] |
Karunanidhi S, Singaperumal M. Design, analysis and simulation of magnetostrictive actuator and its application to high dynamic servo valve[J]. Sensors and Actuators A: Physical, 2010, 157(2): 185-197. DOI:10.1016/j.sna.2009.11.014 |
| [10] |
Baudendistel T A, Turner M L. A novel inverse-magnetostrictive force sensor[J]. IEEE Sensors Journal, 2007, 7(2): 245-250. DOI:10.1109/JSEN.2006.886876 |
| [11] |
Calkins F T, Flatau A B. Terfenol-D sensor design and optimization[J]. Institute of Noise Control Engineering, 1997, 373-382. |
| [12] |
郭沛飞, 贾振元, 杨兴, 等. 压磁效应及其在传感器中的应用[J]. 压电与声光, 2001, 23(1): 26-29. Guo P F, Jia Z Y, Yang X, et al. Magnetoelastic effect and its application in sensors[J]. Piezoelecrics & Acoustooptics, 2001, 23(1): 26-29. (in Chinese) |
| [13] |
Wang X H, Wang S M, Liu J Y, et al. Research on a new type of sea water hydraulic servovalve driven by diphase oppositing giant magnetostrictive self-sensing actuator[C/OL]//2009 International Conference on Measuring Technology and Mechatronics Automation. Piscataway, NJ: IEEE, 2009(2009-08-18)[2020-07-29]. https://doi.org/10.1109/ICMTMA.2009.643.
|
| [14] |
Rong C, He Z B, Li D W, et al. Dynamic modeling and analysis of stack giant magnetostrictive actuator[J]. Sensors and Actuators A: Physical, 2018, 276: 205-218. DOI:10.1016/j.sna.2018.04.020 |
| [15] |
朱优兵, 朱林剑, 苑顺鹏, 等. 超磁致伸缩谐波电机的微位移放大器研究[J]. 微特电机, 2016, 44(10): 13-17. Zhu Y B, Zhu L J, Yuan S P, et al. A research of micro displacement amplifier on the giant magnetostrictive harmonic motor[J]. Small & Special Electrical Machines, 2016, 44(10): 13-17. (in Chinese) |
| [16] |
Bak C, Son H. Magnetostrictive actuator for chatter vibration suppression of boring bar[C/OL]//2018 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM). Piscataway, NJ: IEEE, 2018(2018-09-03)[2020-07-29]. https://doi.org/10.1109/AIM.2018.8452250.
|
| [17] |
Atulasima J, Flatau A B, Cullen J R. Erratum: "Energy-based quasi-static modeling of the actuation and sensing behavior of single-crystal iron-gallium alloys"[J]. Journal of Applied Physics, 2008, 103(6): 069901. DOI:10.1063/1.2903964 |
| [18] |
薛光明, 张培林, 何忠波, 等. 超磁致伸缩致动器的等效电路研究及驱动波形设计[J]. 电机与控制学报, 2016, 20(3): 20-28. Xue G M, Zhang P L, He Z B, et al. Equivalent circuit and driving voltage suitable for giant magnetostrictive actuator in electric injector[J]. Electric Machines and Control, 2016, 20(3): 20-28. (in Chinese) |
| [19] |
Zhao T, Yuan H, Pan H, et al. Study on the rare-earth giant magnetostrictive actuator based on experimental and theoretical analysis[J]. Journal of Magnetism and Magnetic Materials, 2018, 460: 509-524. DOI:10.1016/j.jmmm.2018.01.047 |
| [20] |
Xue G, He Z, Li D, et al. Analysis of the giant magnetostrictive actuator with strong bias magnetic field[J]. Journal of Magnetism and Magnetic Materials, 2015, 394: 416-421. DOI:10.1016/j.jmmm.2015.06.083 |
| [21] |
闫荣格, 王博文, 曹淑瑛, 等. 超磁致伸缩致动器的磁-机械强耦合模型[J]. 中国电机工程学报, 2003, 23(7): 107-111. Yan R G, Wang B W, Cao S Y, et al. Magneto-mechanical strong coupled model for a giant magnetostrictive actuator[J]. Proceedings of the CSEE, 2003, 23(7): 107-111. (in Chinese) |
| [22] |
Hu H, Qi X, Wang C S. Finite element analysis on magnetic field in the actuator of giant magnetostrictive linear motor with Ansoft[C/OL]//2008 IEEE International Conference on Industrial Technology. Piscataway, NJ: IEEE, 2008(2008-08-26)[2020-07-29]. https://doi.org/10.1109/ICIT.2008.4608342.
|
| [23] |
郑佳伟, 何忠波, 周景涛, 等. 阀用超磁致伸缩致动器偏置磁场分布结构设计[J]. 液压与气动, 2018(9): 33-37. Zheng J W, He Z B, Zhou J T, et al. Distribution structure design on bias magnetic field of giant magnetostrictive actuator for hydraulic valve[J]. Chinese Hydraulics & Pneumatics, 2018(9): 33-37. (in Chinese) |
 2021, Vol. 44
2021, Vol. 44

