电阻炉是利用电流使电热元件升温,通过热传递加热炉内物体的装置。在制造业中,电加热装置是耗能大户,其耗电占据企业总耗电的25%~60%,全国热处理电热装置总装机量约15万台,年总耗能电量约100亿度[1]。对工业电阻炉制定科学合理的能耗分析方法与生产计划能提高能源效率,实现可持续的清洁生产和节能降耗[2]。因此,工业电阻炉的能耗预测研究具有深远的意义。
传统的工业电阻炉能耗预测研究主要是通过数值分析法来建立的理论数学模型,模拟加热时炉内的热传递辐射。Fu等[3]基于计算流体动力学(computational fluid dynamics,CFD)软件FLUENT数值模拟了高温合金坯在电阻炉内的加热过程,对炉膛内自然对流和表面热辐射进行了数值分析,预测了高温合金的温度分布和平衡时间。Jang等[4]采用共轭梯度法和打靶法相结合的优化方法,研究表明随着预热区温度降低,能耗也显著降低。以上传统的数学建模方法需要提供详细的数据信息,模型建立困难,预测误差大,不够精确。
近年来,基于数据驱动的能耗预测得到广泛运用[5]。数据驱动技术如人工神经网络(artificial neural network,ANN)、支持向量机(support vector machine,SVM)等在能耗研究方面取得了一定的研究成果。Chen等[6]采用ANN方法根据硅、焦炭、煤和电极的效率和电耗进行了建模,用于指导较低电力消耗和较高效率下的埋弧炉硅生产。王俊凯等[7]将支持向量机引入烧结生产系统,提高了能耗及性能指标预测的精度。Gajic等[8]基于人工神经网络对电弧炉的不锈钢生产过程进行了建模,分析不锈钢化学成分的波动来预测电能消耗。以上研究采集历史生产数据作为模型的输入,仅能预测整个生产周期内的总能耗,因此对具有非线性和时变特性的工业电阻炉,上述方式不能实现短期时间内的准确能耗预测。对于具有时序特征的数据,赫聚显等[9]提出一种基于时间序列的BP神经网络模型,实现0.5 h后的热风炉煤气消耗量的预测。De等[10]提出通过Bagging-ARIMA(bootstrap aggregating-autoregressive integrated moving average model)和平滑指数法预测中长期的电力消耗。Li等[11]提出一种与ANN结合的新型进化算法用于建筑物的短期能耗预测,模型的收敛速度和预测精度都高于遗传算法、粒子群优化算法结合下的ANN模型,适合于在线能耗预测。Subodh等[12]用支持向量机对低能耗建筑进行能耗建模与预测,采用具有代表性的数据集建模,提高了预测精度。以上数据驱动的研究都只是基于时间序列,或基于少参数进行的能耗预测,但在实际中,电能消耗往往受到多种因素影响,因此单参数或少参数的能耗预测无法满足较高的精度需求。
综上所述,虽然能耗预测在各方面研究早已开展,但具有非线性、大惯性、时变性特点[13]的大功耗的工业电阻炉,目前还没有给出泛化性高的多参数预测方法。因此笔者对电阻炉工作状态下的多个过程参数进行研究,分析各个加热阶段的能耗特性,基于数据驱动下建立小样本、非线性的多参数能耗预测模型,并以粒子群优化算法(particle swarm optimization,PSO)对支持向量回归的超参数进行寻优,提高模型精度。
1 工业电阻炉能耗分析 1.1 工业电阻炉能耗特性分析工业电阻炉工作阶段按不同工艺可分为预热阶段、加热阶段、保温阶段和冷却阶段。预热阶段是将电阻炉升温到预热温度后放入工件为止;加热阶段是在工件放入后加热达到电阻炉的工作温度为止;保温阶段是电阻炉持续保持工作温度到设定时长为止;冷却阶段是保温结束后关闭温度控制系统,使工件随炉冷却到一定温度,直到将其从电阻炉中取出为止。
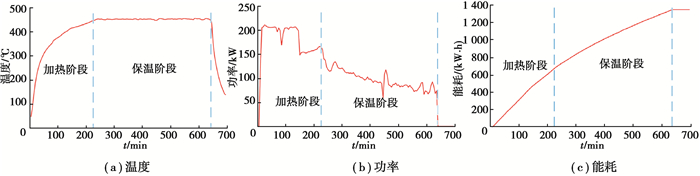
经现场采集三相电输出数据,绘制电阻炉能耗趋势图,如图 1所示。
|
图 1 电阻炉温度、功率、耗电趋势图 Fig. 1 Trend of temperature, power and power consumption of resistance furnace |
由图 1可知,工件放入,打开电阻炉开关后开始记录能耗数据,可以看到加热阶段持续到炉内温度达到设定值。此阶段的功率为电阻炉额定输出功率Pheat,即加热电阻导电后的发热功率。该炉电阻丝为星形接法,根据三相电路功率公式,总功率等于各相功率之和:
| $ {{P_{{\rm{heat }}}} = {P_{\rm{A}}} + {P_{\rm{B}}} + {P_{\rm{C}}},} $ | (1) |
其中
| $ {{P_{\rm{A}}} = \frac{{U_{\rm{A}}^2}}{{{R_{\rm{A}}}}} \cdot \cos \varphi }。$ | (2) |
式中:UA为A相电压;cos φ为功率因数;RA为A相负载电阻的阻值;PA为三相电路A相有功功率,三相电阻炉因为是纯阻性负载,电流与电压没有相位差,所以功率因数取1,PB,PC以此类推。因此电阻炉的加热阶段能耗可表示为
| $ {E_{{\rm{heat }}}} = \sum\limits_{i = 1}^n {{P_{{\rm{heat }}}}} \cdot {t_i}(i = 1,2, \cdots ,n), $ | (3) |
式中ti是加热阶段的采样时间。
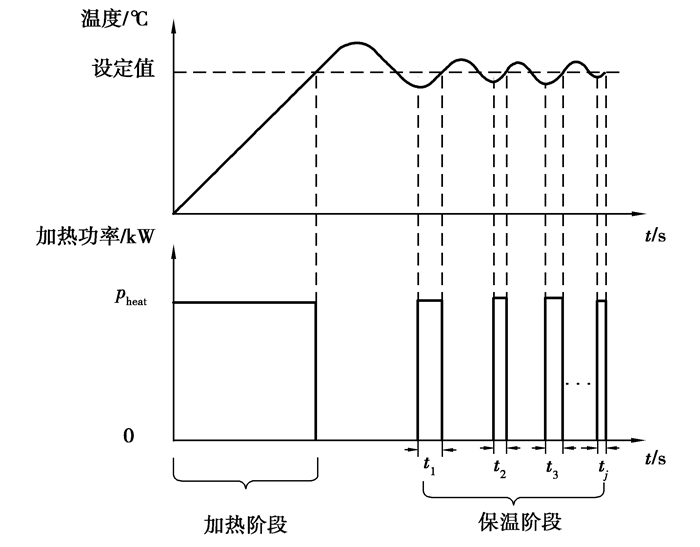
1.1.2 工业电阻炉保温阶段能耗分析当炉温达到设定温度后,此时PID温度控制系统开始工作,控制继电器通断电路改变电阻炉有功功率,如图 2所示。
|
图 2 加热与保温阶段温度、功率对照图 Fig. 2 Comparison of temperature and power in heating and holding stage |
图 2中t1,t2,…,tj表示加热电阻保温阶段的运行时长,此时电阻炉的保温阶段能耗可表示为
| $ E_{\text {keep }}=\sum\limits_{j=1}^{n} P_{\text {keep }} \cdot t_{j}(j=1,2, \cdots, n)。$ | (4) |
由于保温过程使用PID温度控制器根据传感器采集的温度自动调节,在工程应用中,无法精确测量加热电阻保温状态下的运行时长。因此,为便于保温过程的能耗分析,提出平均功率计算方法,即在单位时间t内采集电表上的读数,记为单位能耗Ekeep(j),可获得单位时间内的平均功率
| $ {\hat P_{{\rm{keep }}}}(j) = \frac{{{E_{{\rm{keep }}}}(j)}}{t}。$ | (5) |
由图 2加热与保温阶段温度、功率对照图可知,保温过程是PID温度控制器控制设定温度的幅值趋近于0的过程,是
电阻炉的精确稳定运行受温控系统的控制,控制系统包括上位机监控终端和PID温控仪,其功率消耗相对稳定,受负载影响较小,因此实际输入功率可用额定功率Pe代替。在放入和取出工件的过程中,电阻炉机械动力系统也会消耗一定电量,动力系统的额定功率为Pm。加热与保温阶段需开启安装在炉顶的循环风扇,保证炉内热流循环以及各炉区温度均匀,风扇额定功率为Pf。工业电阻炉辅助系统的能耗Eaux为
| $ {E_{{\rm{aux }}}} = {P_{\rm{e}}}\left( {{t_{{\rm{heat }}}} + {t_{{\rm{keep }}}} + {t_{{\rm{cool }}}}} \right) + 4{P_{\rm{m}}}{t_{\rm{m}}} + {P_{\rm{f}}}\left( {{t_{{\rm{heat }}}} + {t_{{\rm{keep }}}}} \right), $ | (6) |
式中:theat,tkeep,tcool分别为加热、保温、冷却的时长;tm为炉门打开或关闭过程电机运行时长。
1.2 工业电阻炉工作阶段能耗模型由式(3)(4)及(6),电阻炉工作能耗可近似为
| $ {E_{{\rm{work}}}} = {E_{{\rm{heat }}}} + {E_{{\rm{keep }}}} + {E_{{\rm{cool }}}} + {E_{{\rm{aux }}}}。$ | (7) |
Fu等[14]指出电阻炉在加热阶段,加热元件的热量通过辐射到电阻炉内壁表面,内壁表面吸收辐射后转化为热流遍布整个区域,此时炉内空气介质、内壁、耐火炉衬、隔热层以及外壳等吸收加热电阻散发的热量,通过对流传热和辐射传导至周围环境中;Cheng等[15]提出此过程会产生加热能耗损失Ehl和保温能耗损失Ekl。
| $ {{E_{{\rm{hl}}}} = \sum\limits_{i = 1}^n {\int\limits_S {{K_{{\rm{out}}}}} } \left( {{T_{\rm{s}}} - {T_{\rm{e}}}} \right){t_{\rm{h}}}{\rm{d}}S,} $ | (8) |
| $ {{E_{{\rm{kl}}}} = \sum\limits_{i = 1}^n {\int\limits_S {{K_{{\rm{out}}}}} } \left( {{T_{\rm{s}}} - {T_{\rm{e}}}} \right){t_{\rm{k}}}{\rm{d}}S}。$ | (9) |
| $ {{\rm{其中}}\ \ \ \ \ \ \ \ {K_{{\rm{out}}}} = \frac{q}{{{T_{\rm{s}}} - {T_{\rm{e}}}}},q = \lambda \frac{{{T_{{\rm{inner}}}} - {T_{\rm{s}}}}}{S}}。$ | (10) |
式中:S为炉壁厚度;th,tk为加热阶段、保温阶段持续时间;Ts为炉外表面温度;Te为环境温度;Tinner为炉内温度;Kout为外壁传热系数;q为热通量;λ为导热系数。根据以上公式,电阻炉理论能耗模型为
| $ {E_{{\rm{real}}}} = {E_{{\rm{heat }}}} + {E_{{\rm{keep }}}} + {E_{{\rm{cool }}}} + {E_{{\rm{aux }}}} + {E_{{\rm{hl}}}} + {E_{{\rm{kl}}}}。$ | (11) |
在工程实际中,电阻炉的实际损失能耗与多种因素有关,如炉的内外壁的传热系数随着温度提高不断改变;炉内各个加热区由于辐射换热、对流换热,温度场分布有一定差异;炉内气体并不是理想气体等,从而难以进行精确计算。为简化模型,假设电阻炉的电源输入能耗等于发热电阻的能耗与损失能耗之和,则理论模型如式(12)。
| $ {{E_{{\rm{total }}}} = {E_{\rm{A}}} + {E_{\rm{B}}} + {E_{\rm{C}}} + {E_{{\rm{aux }}}}}。$ | (12) |
| $ {{\rm{其中}}\ \ \ \ \ \ \ \ {E_{\rm{A}}} = \sum\limits_{i = 1}^n {{U_{\rm{A}}}} {I_{\rm{A}}}\cos \varphi \cdot {t_i}}。$ | (13) |
式中:UA,IA、是三相电A相的相电压、电流;EA是A相有功功率与采样时间之积的累加;EB,EC同理可得。
2 基于数据驱动的电阻炉多参数能耗预测方法利用数据采集平台动态获取电阻炉工作参数,通过功率特征判断电阻炉的运行状态,将该状态下的电流、炉内外温度、功率、能耗等各个特征信息输入模型训练,运用多个评价指标评价模型,获得最佳预测方法。
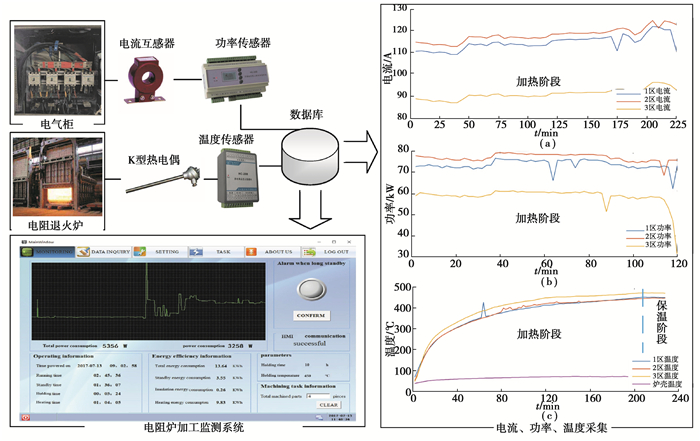
2.1 多参数数据采集及特征提取采集系统中的功率传感器、温度传感器与主机通讯,实时获取电阻炉3个加热区(1区、2区及3区)的功率、电流以及炉内、外壳温度信息。采集信息流程如图 3所示,图(a)(b)中3条曲线分别代表 1区、2区及3区的电流、功率,图(c)中采集3个区的温度以及电阻炉外壳温度。
|
图 3 采集信息流程图 Fig. 3 Information collection process |
为了实时反映炉内外温度、电流及功率的变化,剔除波动较大或明显异常的采样点。图 3中的温度曲线在加热阶段具有明显的非平稳性,而保温阶段序列是平稳的,电流与功率在加热阶段也是平稳的。如果对以上电流、功率以及温度3组采集数据均提取时域特征,导致数据维度过大,直接使用机器学习建模将增大模型的复杂度。由于电阻炉的功率、发热与三相电流的大小息息相关,因此只提取电流信号的时域特征参数,包括3个加热区的测量电流I,3个区的电流方差Ivar、均方根Irms、峰峰值Iptp与偏度Iske共12个时域特征参数作为电流信号的特征量,以及3个加热区的炉内温度、炉壳温度、室温及电阻炉总功率共21个参数作为模型的输入向量。
2.2 基于数据驱动的电阻退火炉多参数能耗预测模型 2.2.1 回归型支持向量机预测模型支持向量机(SVM)是Corinna Cortes和Vapnik[16]在1995年提出的机器学习方法,在分类和回归任务中已得到许多运用。支持向量回归(support vector regression,SVR)是SVM中的一项重要应用分支[17],近年来在回归估计和非线性问题的解决中受到越来越多的重视。SVR是将原始数据向高维特征空间的非线性映射,将其转化为线性回归关系。假设一个回归函数F,训练样本为{(xi, yi)}, 其中xi是输入,yi是输出。SVR使用线性方程预测目标值,即
| $ F(x) = {\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{\varphi }}(x) + b, $ | (14) |
式中: F(x)为输出;w为权向量;b为偏差;φ(x)为高维的实际输入向量;权向量w和偏差b是通过最小化风险函数计算所得。最小化风险函数的推理过程如式(15)~(21)。
| $ R(F) = C\sum\limits_{i = 1}^n {{L_\varepsilon }} \left( {{y_i},{F_i}} \right) + \frac{1}{2}{\left\| \boldsymbol{w} \right\|^2}, $ | (15) |
| $ \text { 其中 } L_{\varepsilon}\left(y_{i}, F_{i}\right)=\left\{\begin{array}{lc} 0 & \left|y_{i}-F_{i}\right| \leqslant \varepsilon; \\ \left|y_{i}-F_{i}\right|-\varepsilon & \text { 其他。} \end{array}\right. $ | (16) |
式(15)中,第1项采用不敏感损失函数ε来表示实际值与回归值之间的偏差,第2项用于估计函数的模糊性。C为惩罚参数,用于表达函数复杂度和损失之间的权衡,C值越高代表对误差的惩罚就越高,使回归训练的模型误差也越小,泛化程度越小,且容易过拟合。实际问题中,难以准确确定ε,为确保大部分数据点在ε内,引入松弛变量ξi,ξi*。式(15)可转换为如下形式:
| $ {R(w) = \min \left[ {\frac{1}{2}{{\left\| \mathit{\boldsymbol{w}} \right\|}^2} + C\sum\limits_{i = 1}^n {\left( {{\xi _i} + \xi _i^*} \right)} } \right],} $ | (17) |
| $ {{\rm{ Subject}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{to }}\left\{ {\begin{array}{*{20}{l}} {{y_i} - {\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{\varphi }}(x) - b \le \varepsilon + \xi _i^*,}\\ {{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{\varphi }}(x) + b - {y_i} \le \varepsilon + {\xi _i},}\\ {{\xi _i},\xi _i^* \ge 0,i = 1,2, \cdots ,n}。\end{array}} \right.} $ | (18) |
式(14)可考虑非线性回归的情况、特征空间的映射以及添加拉格朗日乘子转换为以下形式:
| $ F = \sum\limits_{i = 1}^n {\left( {{\alpha _i} - \alpha _i^*} \right)} \left( {\mathit{\boldsymbol{\varphi }}\left( {{x_i}} \right)\mathit{\boldsymbol{\varphi }}\left( {{x_j}} \right)} \right) + b, $ | (19) |
其中αi,αi*是拉格朗日乘子,向量内积φ(xi)φ(xj)可用核函数k(xi, xj)代替,式(19)变为
| $ F = \sum\limits_{i = 1}^n {\left( {{\alpha _i} - \alpha _i^*} \right)} k\left( {{x_i},{x_j}} \right) + b。$ | (20) |
最常用的核函数是RBF函数,其定义如下:
| $ K\left( {{x_i},{x_j}} \right) = \exp \left( {\frac{{ - {{\left\| {{x_i} - {x_j}} \right\|}^2}}}{{2\gamma }}} \right){\rm{ , }} $ | (21) |
其中γ表示RBF函数的宽度,γ值越大映射的维度越高,训练的结果越好,但是容易引起过拟合,即泛化能力低。
2.2.2 模型参数寻优方法1) 粒子群优化算法。
粒子群优化算法(PSO)由Kennedy和Eberhart[18]在1995年受到鸟类捕食的启发而设计一种无质量的粒子来模拟鸟群的群聚行为。粒子群优化算法是一种基于总体的并行全局搜索策略,它具有更快的收敛速度,在解决大量维数问题的方面具有优势。在优化过程中,每个粒子都有自己的速度、位置和适应度。每次迭代,粒子会根据经过的单个最佳位置Pbest和全局最佳位置gbest来更新其速度和位置。对于维度为D的第i个粒子其更新速度和位置的公式如下:
| $ {V_{i,D}^{t + 1} = \omega v_{i,D}^t + {c_1}{r_1}\left( {P_{{\rm{best}}i{\rm{ }},D}^t - x_{i,D}^t} \right) + {c_2}{r_2}\left( {g_{{\rm{best}}i,D}^t - x_{i,D}^t} \right),} $ | (22) |
| $ {X_{i,D}^{t + 1} = X_{i,D}^t + V_{i,D}^t,} $ | (23) |
其中t是迭代数;c1,c2是学习因子;r1,r2是0到1之间的随机数,ω是用于平衡全局和局部搜索的权重系数。
2) 基于PSO优化SVR。
SVR的泛化能力在很大程度上取决于超参数,即惩罚因子C和核函数γ,但是通过先验知识很难确定这些参数的适当值,且手动调整参数的过程非常耗时。为使模型评估更加准确可信,采用粒子群优化算法(PSO)对式(15)与式(21)中的C和γ参数进行寻优。
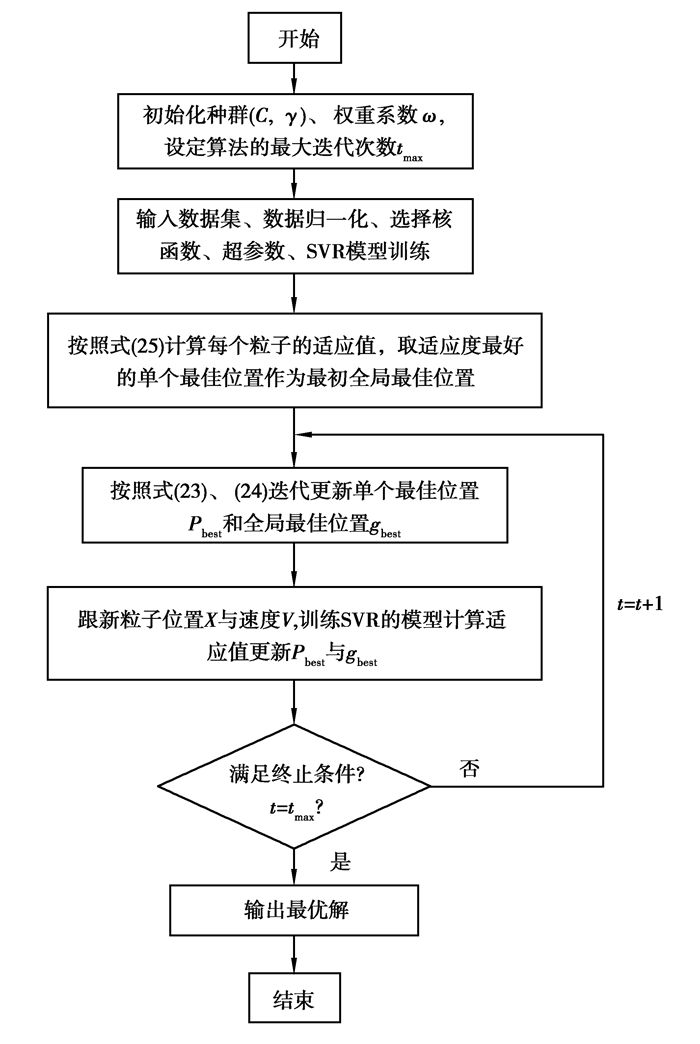
PSO-SVR参数优化算法流程图如图 4所示。
|
图 4 PSO-SVR参数优化算法流程图 Fig. 4 Process of PSO-SVR parameter optimization algorithm |
为了评估文中模型性能,需应用不同评估标准,标准包括平均绝对误差Wmae、均方差Wmse、平均绝对百分比误差Wmape以及决定系数R2。
| $ {{W_{{\rm{mae }}}} = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {{y_i} - {{\hat y}_i}} \right|} ,} $ | (24) |
| $ {{W_{{\rm{mse }}}} = \frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} ,} $ | (25) |
| $ {{W_{{\rm{mape }}}} = \frac{{100\% }}{n}\sum\limits_{i = 1}^n {\left| {\frac{{{{\hat y}_i} - {y_i}}}{{{y_i}}}} \right|} ,} $ | (26) |
| $ {{R^2} = 1 - \frac{{\sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} }}{{\sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} }}}。$ | (27) |
式中:n为样本数;yi为当前能耗观测值;
本案例以重庆某公司退火炉车间为平台,以重庆大学自主研发的退火炉实时状态监控系统获取加工任务和加工状态信息。功率的实时监测通过HC-33D6L功率传感器实现,温度监测通过HC-208温度采集模块与K型热电偶实现,分别采集退火炉的输入功率、电流、炉内外温度等信息,通过Modbus-RTU通信协议传输至智能终端。数据采集系统软硬件平台如图 5所示。

|
图 5 数据采集系统软硬件平台 Fig. 5 Software and hardware platform of the data acquisition system |
实验对象为间歇式炉,加热工件为铝绞线(BLVV),截面积120 mm2,长度9 000 m,工作时长10 h,采样时长设置为2 min,采集获得外界温度Te、炉壳温度Ts、3个加热区的炉内温度Tin、功率P、能耗E、3个加热区的电流I,提取电流特征参数:方差Ivar、均方根Irms、峰峰值Iptp及偏度Iske,获得数据整理表 1、表 2所示。
| 表 1 电阻炉温度、电流、能耗参数(2 min采样时长) Table 1 Temperature, current and energy consumption parameters of the resistance furnace (2 min sampling time) |
| 表 2 电流特征参数 Table 2 Characteristic parameters of the current |
本次案例中共收集326组数据,使用交叉验证法对训练数据和测试数据进行划分,其中训练数据与测试数据的比例为3∶1。
1) 多参数PSO-SVR、SVR、GPR、ANFIS模型对比。
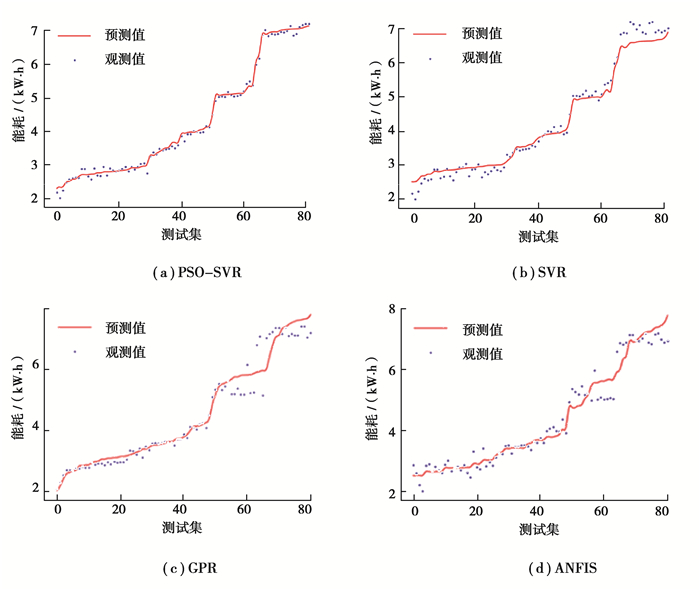
高斯过程回归(Gaussian process regression,GPR)和自适应模糊神经推理系统(adaptive network-based fuzzy inference system,ANFIS)是两种常用的能耗预测算法。为验证SVR算法效果,使用以上两种建模方法与SVR进行对比分析。将表 1中Te,Ts,3个加热区的Tin、3个加热区的电流I,P,E以及表 2中电流特征参数:Ivar,Irms,Iptp,Iske,带入集合{(xi, yi)}中,E作为输出y,其余作为输入x,导入PSO-SVR、SVR、GPR、ANFIS模型中得到测试集图像对比图,如图 6所示。
|
图 6 PSO-SVR、SVR、GPR、ANFIS预测结果对比 Fig. 6 Comparison of prediction results of PSO-SVR, SVR, GPR and ANFIS |
3种预测模型训练集与测试集评价指标如表 3所示。
| 表 3 3种预测模型训练集与测试集评价指标对比 Table 3 Comparison of evaluation indexes of three prediction models |
由图 6、表 3可知,PSO-SVR模型的评价指标均优于SVR、GPR、ANFIS模型,在测试集中PSO-SVR与SVR相比Wmae减少了48.46%,Wmse减少了83.65%,Wmape减少了35.06%,R2提高了2.09%。PSO-SVR、SVR、GPR、ANFIS模型中,GPR采用高斯核函数,模型对超参数的调优有一定要求;ANFIS采用自学习生成模糊规则的特点,难以准确表达函数关系,需要凭借专家经验来手动调整模糊规则。实验表明PSO-SVR模型的评价指标明显优于SVR、GPR和ANFIS模型,因此,PSO优化下的SVR模型具有更高的精度、更好的泛化性和拟合能力。
2) 单参数与多参数PSO-SVR模型对比。
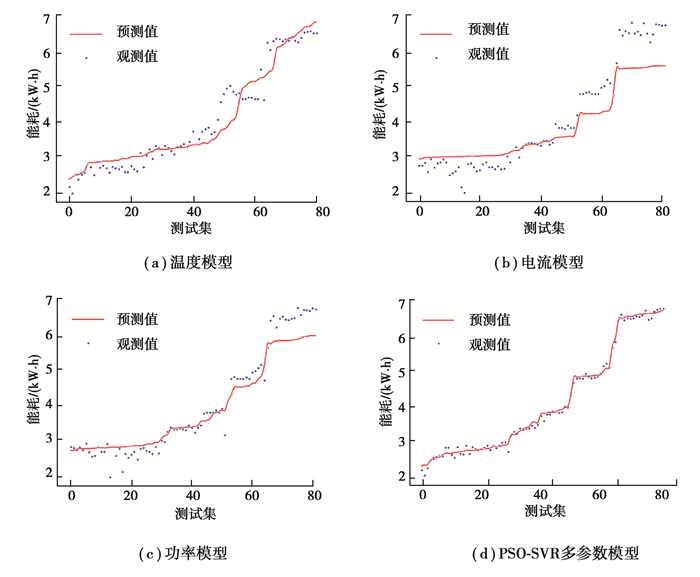
将表 1中的温度、电流、功率分别带入模型中得到预测结果与多参数模型对比,如图 7所示。
|
图 7 单参数与多参数模型预测结果对比 Fig. 7 Comparison of prediction results between single parameter model and multi-parameter model |
3种预测模型训练集与测试集评价指标如表 4所示。
| 表 4 单参数与多参数预测模型训练集与测试集评价指标对比 Table 4 Comparison of evaluation indexes of single parameter and multi-parameter model |
由图 7、表 4可知,电阻炉能耗受温度、电流、功率等多种参数影响,模型精度与模型输入数据维度成正相关,Wmae、Wmse、Wmape的多参数模型指标相比温度、电流、功率建立的单参数模型指标明显减小,R2也显著增大。这是因为多参数预测模型的输入是基于理论模型中的参数,再提取主要特征,能较好地表示输入输出向量的相关性,而单参数预测模型在非线性、大惯性的时变系统中拟合性能较差。因此,多参数模型各项评价指标均优于单参数模型指标,基于数据驱动的电阻炉多参数能耗预测模型比单参数预测模型有更高的精度和更好的泛化性。
3) 数据驱动模型与理论模型对比。
根据公式(12)基于功率和时间信息建立退火炉工作的理论能耗模型,各个评价指标如表 5所示。
| 表 5 PSO-SVR多参数数据驱动模型与理论模型评价指标对比 Table 5 Comparison of evaluation indexes between PSO-SVR multi-parameters data driven model and theoretical model |
从表 5中可知,理论模型的各项评价指标均低于数据驱动建立的PSO-SVR模型。理论模型是基于功率、时间建模,建模因素单一,并且理论模型中的功率为瞬时功率,其大小受到瞬时电流、加热电阻阻值、对流换热等多种因素影响,导致建立的模型精度较低,只能在一段时间内粗略预估电阻炉的能耗,而基于数据驱动下的多参数模型输入根据实际系统的实验分析获得,克服了理论建模精度不高的缺点,能实时追踪电阻炉工作状态,实现电阻炉能耗的动态预测。
4 结论1) 分析了工业电阻炉各个加工阶段的工作状态,结合电阻炉的特征,基于功率、时间建立了理论能耗模型。
2) 根据所测得环境温度、炉外表温度、炉内温度、功率、电流、以及提取的电流特征向量,建立了PSO-SVR、SVR、GPR及ANFIS能耗预测模型,通过Wmae、Wmse、Wmape以及R2指标分析,证明基于数据驱动下的PSO-SVR多参数能耗预测模型具有更高的精度和更好的泛化性。
3) 对比理论能耗模型与数据驱动多参数模型的各项评价指标,实验表明数据驱动的多参数模型具有实时系统的分析能力,能反映电阻炉的实时工作状态,提供可靠的动态能耗预测数据,为优化退火工艺、电炉的检修或更改生产计划提供详细的数据支持。
| [1] |
吴光治, 吴越, 袁蓉, 等. 热处理电阻炉的节能减排[J]. 热处理, 2015, 30(1): 1-10. Wu G Z, Wu Y, Yuan R, et al. Energy saving and reduction in pollutant discharge of electric resistance furnace for heat treatment[J]. Heat Treatment, 2015, 30(1): 1-10. (in Chinese) |
| [2] |
Liu Z F, Yan J, Cheng Q, et al. The mixed production mode considering continuous and intermittent processing for an energy-efficient hybrid flow shop scheduling[J]. Journal of Cleaner Production, 2020, 246: 119071. DOI:10.1016/j.jclepro.2019.119071 |
| [3] |
Fu Z L, Yu X H, Shang H L, et al. A new modelling method for superalloy heating in resistance furnace using FLUENT[J]. International Journal of Heat and Mass Transfer, 2019, 128: 679-687. DOI:10.1016/j.ijheatmasstransfer.2018.08.105 |
| [4] |
Jang J Y, Huang J B. Optimization of a slab heating pattern for minimum energy consumption in a walking-beam type reheating furnace[J]. Applied Thermal Engineering, 2015, 85: 313-321. DOI:10.1016/j.applthermaleng.2015.04.029 |
| [5] |
李聪波, 尹誉先, 肖溱鸽, 等. 数据驱动下基于元动作的数控车削能耗预测方法[J]. 中国机械工程, 2020, 31(21): 2601-2611. Li C B, Yin Y X, Xiao Q G, et al. Data-driven Energy Consumption Prediction Method of CNC Turning Based on Meta-action[J]. China Mechanical Engineering, 2020, 31(21): 2601-2611. (in Chinese) |
| [6] |
Chen Z J, Ma W H, Wu J J, et al. Predicting the electricity consumption and the exergetic efficiency of a submerged arc furnace with raw materials using an artificial neural network[J]. Silicon, 2018, 10(2): 603-608. DOI:10.1007/s12633-016-9499-4 |
| [7] |
王俊凯, 乔非, 祝军, 等. 基于支持向量机的烧结能耗及性能指标预测模型[J]. 同济大学学报(自然科学版), 2014, 42(8): 1256-1260. Wang J K, Qiao F, Zhu J, et al. SVR-based predictive models of energy consumption and performance criteria for sintering[J]. Journal of Tongji University (Natural Science), 2014, 42(8): 1256-1260. (in Chinese) |
| [8] |
Gajic D, Savic-Gajic I, Savic I, et al. Modelling of electrical energy consumption in an electric arc furnace using artificial neural networks[J]. Energy, 2016, 108: 132-139. DOI:10.1016/j.energy.2015.07.068 |
| [9] |
郝聚显, 赵贤聪, 韩玉召, 等. 热风炉煤气消耗量中期预测模型[J]. 中国冶金, 2018, 28(2): 17-22. Hao J X, Zhao X C, Han Y Z, et al. Medium-term prediction model for byproduct gas consumption in hot blast stove[J]. China Metallurgy, 2018, 28(2): 17-22. (in Chinese) |
| [10] |
de Oliveira E M, Cyrino Oliveira F L. Forecasting mid-long term electric energy consumption through bagging ARIMA and exponential smoothing methods[J]. Energy, 2018, 144: 776-788. DOI:10.1016/j.energy.2017.12.049 |
| [11] |
Li K J, Xie X M, Xue W P, et al. A hybrid teaching-learning artificial neural network for building electrical energy consumption prediction[J]. Energy and Buildings, 2018, 174: 323-334. DOI:10.1016/j.enbuild.2018.06.017 |
| [12] |
Paudel S, Elmitri M, Couturier S, et al. A relevant data selection method for energy consumption prediction of low energy building based on support vector machine[J]. Energy and Buildings, 2017, 138: 240-256. DOI:10.1016/j.enbuild.2016.11.009 |
| [13] |
Strommer S, Niederer M, Steinboeck A, et al. Hierarchical nonlinear optimization-based controller of a continuous strip annealing furnace[J]. Control Engineering Practice, 2018, 73: 40-55. DOI:10.1016/j.conengprac.2017.12.005 |
| [14] |
Fu Z L, Yu X H, Shang H L, et al. A new modelling method for superalloy heating in resistance furnace using FLUENT[J]. International Journal of Heat and Mass Transfer, 2019, 128: 679-687. DOI:10.1016/j.ijheatmasstransfer.2018.08.105 |
| [15] |
Cheng Q, Gong J L, Xiao G, et al. Research on energy-saving production planning of periodic forging resistance furnace[J]. Journal of Cleaner Production, 2020, 275: 122897. DOI:10.1016/j.jclepro.2020.122897 |
| [16] |
Cortes C, Vapnik V. Support-vector networks[J]. Machine Learning, 1995, 20(3): 273-297. DOI:10.1023/A%3A1022627411411 |
| [17] |
赵静, 王选仓, 丁龙亭, 等. 基于灰色关联度分析和支持向量机回归的沥青路面使用性能预测[J]. 重庆大学学报, 2019, 42(4): 72-81. Zhao J, Wang X C, Ding L T, et al. Performance prediction of asphalt pavement based on grey relational analysis and support vector machine regression[J]. Journal of Chongqing University (Natural Science Edition), 2019, 42(4): 72-81. (in Chinese) |
| [18] |
Ebeehart R, Kennedy J. A new optimizer using particle swarm theory[C]//Proceedings of the Sixth International Symposium on Micro Machine and Human Science. Nagoya, Japan: IEEE, 1995: 39-43.
|
 2021, Vol. 44
2021, Vol. 44

