2. 青岛大学 环境科学与工程学院, 山东 青岛 266071
2. College of Environmental Science and Engineering, Qingdao University, Qingdao, shandong 266071, P. R. China
抗浮锚杆以地层适应能力强、锚固力高、造价低、工期短、受力合理等诸多优势备受青睐,在建筑物地下室、地下停车场、污水处理池、地铁与隧道、地下综合管廊、储油罐及港工、水工构筑物等土木工程多个领域得到了广泛的应用[1-4]。尤其在坚硬的岩石地基中,施工大直径抗浮桩非常困难,工效低,抗浮锚杆的优势更加凸显,具有显著的经济效益[5]。
抗浮锚杆作为抵抗地下水浮力的结构构件,受地下水位变化的影响较大,锚筋常选用螺纹钢筋。调查发现,抗浮锚杆在实际工程的应用往往超前理论研究。近年来,国内外学者对抗浮锚杆的研究取得了较多成果。在试验和测试方面,贾金青[6]、柳建国[7]、张明义[8]、白晓宇[9-10]等通过现场试验得到抗浮锚杆的极限抗拔承载力和荷载传递特性。在理论研究方面,陈棠茵[11]、龙照[12]、董天文[13]、白晓宇[14]等讨论了抗浮锚杆的应力应变分布规律及其长期抗拔承载力。在数值模拟方面,马占峰[15]、Kim[16]、贾科科[17]、赵天杨[18]等基于FLAC、ANSYS、ABAQUS等软件分析了抗浮锚杆的锚固性能及其锚固体和岩土体的应力分布特征。在实际工程中,由于抗浮措施选用不当,导致地下车库、地下室、地铁道床上浮的事故屡见不鲜,主要是对抗浮锚杆的承载机制认识不足。此外,由于抗浮锚杆的基本试验开展较少,人们对其承载力和变形很难确切把握;另一方面,中国目前尚无抗浮锚杆的国家及行业标准,加上岩石成因类型及分布较为广泛,规范提供的设计参数分布范围较大,参数选取非常困难;由于设计标准不确定,很多工程中抗浮锚杆设计很长,造成资源浪费。鉴于此,有必要系统开展岩石地层中全长黏结抗浮锚杆试验,确定其合理锚固长度及其极限抗拔承载力,为岩石地基中抗浮锚杆的设计、施工与检测提供参考,为编制抗浮锚杆的技术标准提供理论支持。
1 现场试验方案及过程 1.1 试验场地概况试验场地位于已开挖岩石基坑内,场区内为中风化花岗岩,岩体呈块状构造,节理裂隙发育,厚度约为3.5~16.7 m,地下水位埋深约为1.7~7.2 m。中风化花岗岩的力学指标, 如表 1所示。
| 表 1 岩层力学指标 Table 1 Mechanical index of rock layer |
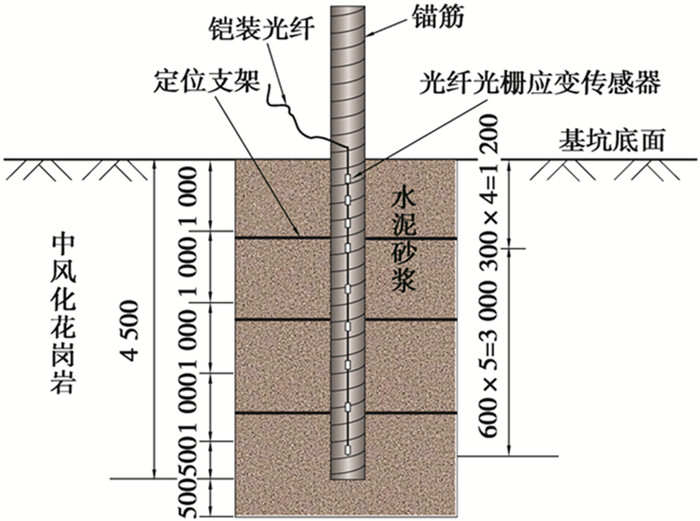
试验共设置13根试验锚杆,间距均为3.0 m,锚杆孔直径为120 mm,孔深超过锚筋的黏结长度50 cm。杆体材料选用HRB400螺纹钢筋,屈服强度标准值为400 MPa,弹性模量为200 GPa。锚固体材料选用M30商品水泥砂浆,锚杆的试验参数如表 2所示。为确定锚筋沿锚固深度的荷载传递深度以及锚筋与锚固体之间的剪应力分布规律,在锚筋SA4.5-01表面安装了9个光纤光栅应变传感器,传感器通过两端的支座焊接在锚筋上,地表附近传感器间距较密,离地表较远处传感器布置的相对稀疏,光纤光栅应变传感器的设置情况如图 1所示,1 000 mm为锚杆定位支架的间距,300 mm和600 mm分别为光纤光栅应变传感器的中心距离,500 mm为锚筋距锚杆孔底部的距离。
| 表 2 抗浮锚杆试验参数 Table 2 Experimental parameters of anti-floating anchor |
|
图 1 锚杆SA4.5-01传感器布置示意图(单位:mm) Fig. 1 Arrangement of the sensors in anchor SA4.5-01 (unit : mm) |
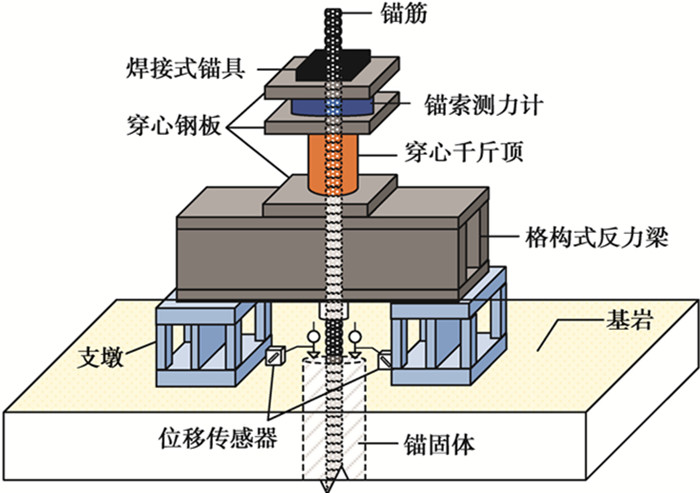
整平场地后,利用潜孔钻机成孔,锚杆孔垂直向下,将装有定位支架的锚筋送入锚杆孔内,当锚筋到达预定的标高后,开始灌注水泥砂浆,同时浇筑2组立方体试件用于测试锚固体的抗压强度。锚固体的强度达到15 MPa或达到设计强度的75%后进行现场抗拔试验,抗浮锚杆试验装置如图 2所示,与文献[19]类似,只是将锚具直接焊接在锚筋外表面,锚具为厚度3 cm、边长10 cm的方形铁板,中央开直径为3 cm的圆孔,抗浮锚杆的具体试验流程, 如图 3所示。
|
图 2 锚杆拉拔装置示意图 Fig. 2 Schematic diagram of the pullout device |

|
图 3 锚杆试验流程 Fig. 3 Anchor experimental process |
试验为极限荷载下的拉拔试验,采用逐级单调加载,荷载的施加顺序为0→40→80→120→160 kN……,每级荷载稳压时间不少于15 min,直至锚杆发生破坏。荷载值由锚索测力计直接量测,锚固体顶面位移的测读、终止加载条件、锚杆的破坏标准以及极限抗拔承载力的确定均按《建筑基坑支护技术规程》(JGJ120—2012)[20]执行。
2 试验结果分析与讨论 2.1 破坏现象与特征分析试验中,抗浮锚杆主要发生以下3种破坏形态,即锚筋-锚固体界面剪切滑移破坏、锚固体-周围岩体界面剪切滑移破坏以及锚筋拔断。13根抗浮锚杆的试验结果如表 3所示,破坏形态如图 4所示。
| 表 3 锚杆试验结果汇总 Table 3 Summary of the anchor experimental results |

|
图 4 抗浮锚杆破坏形态 Fig. 4 Failure modes of the anti-floating anchors |
试验中,抗浮锚杆SA2、SA3的破坏形态主要为锚筋-锚固体界面剪切滑移破坏和锚固体-周围岩体界面剪切滑移破坏。随着拉拔荷载的增加,锚固体顶面位移逐渐增大,当荷载水平超过240 kN后,各锚杆表现出压力加不上,锚固体顶面位移不断上升的现象,由于锚筋的黏结长度不足,此时第一界面或第二界面出现不同程度的滑移痕迹,甚至脱黏现象。而抗浮锚杆SA4.5、SA6.5主要出现锚筋拔断现象。锚固体顶面位移随拉拔荷载增加而增大,加载后期锚筋进入屈服阶段,当荷载水平超过320 kN时,在距锚固体顶面5~10 cm的范围内,锚筋出现明显缩颈现象,此时千斤顶加载困难,加载端的锚筋飞出,锚筋被拔断,断裂部位均出现在距锚固体顶面7~8 cm处,锚固体产生宽度为5~7 mm的裂缝。
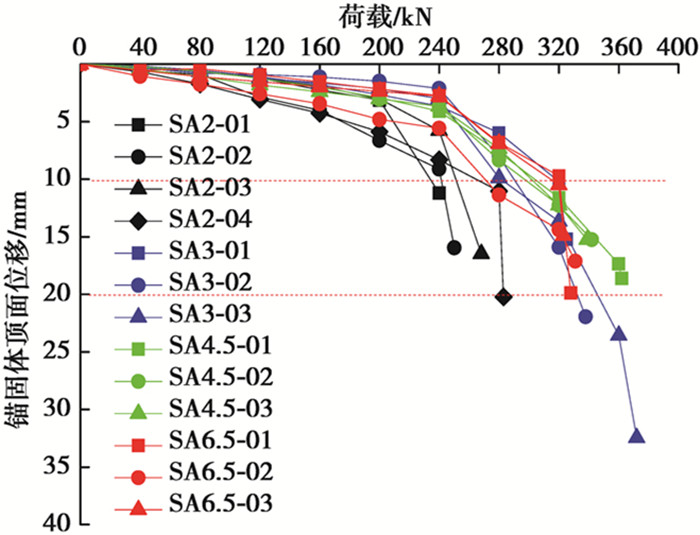
2.2 极限抗拔承载力分析荷载锚固体顶面位移曲线能够从宏观上反映抗浮锚杆在不同荷载水平下的荷载传递特性和破坏规律,13根抗浮锚杆的荷载-锚固体顶面位移曲线, 如图 5所示。
|
图 5 荷载-锚固体顶面位移关系曲线 Fig. 5 Load-anchorage body head displacement curve |
图 5和表 3显示,13根抗浮锚杆的荷载-锚固体顶面位移曲线表现出相同的变化规律,基本呈缓变型。锚杆受荷初期,荷载与锚固体顶面位移呈线性关系,随拉拔荷载的增加,锚固体顶面位移持续增大,逐渐向非线性过渡,进入塑性变形阶段,锚固体顶面位移的变化速率逐渐增大,抗浮锚杆SA2、SA3、SA4.5、SA6.5的破坏荷载分别为240~284 kN,325~372 kN,339~362 kN,323~331 kN,由于每组试验锚杆极限抗拔承载力的极差均小于30%,根据《建筑基坑支护技术规程》(JGJ120—2012)[20]的判定标准,得到黏结长度为2 m的抗浮锚杆SA2-01、SA2-02、SA2-03、SA2-04的极限抗拔承载力分别为200、240、240、280 kN。在试验条件下,直径为28 mm、黏结长度为2 m、锚固体强度为M30时,抗浮锚杆的极限抗拔承载力为240 kN。同样可以得到抗浮锚杆SA3、SA4.5、SA6.5的极限抗拔承载力分别为333、333、320 kN,黏结长度为3 m的抗浮锚杆与黏结长度为2 m的相比,极限抗拔承载力提高38.8%。总体来看,锚筋材料、锚筋直径、锚固体强度均相同的条件下,抗浮锚杆的极限抗拔承载力随黏结长度的增加而提高;然而,并不是黏结长度越长,极限抗拔承载力就越高,存在一个临界黏结长度,高丹盈[21]和曾宪明[22]等研究结果说明了这一现象。
以上是根据破坏荷载确定抗浮锚杆的极限抗拔承载力,也有学者通过锚固体顶面位移给出了取值标准。陈根全[23]和张明义[24]根据锚固体顶面位移和相应的荷载水平取10~20 mm范围内的较小值作为抗浮锚杆的极限抗拔承载力。贾金青等[6]则把荷载-位移曲线中位移变化较大的拐点所对应的荷载看作是锚杆的极限抗拔承载力。王贤能等[25]针对岩石锚杆给出了相应的确定标准,即取锚固体顶面位移20 mm对应荷载作为岩石抗浮锚杆的极限抗拔承载力。英国则以25 mm的位移对应的荷载作为极限抗拔承载力。从试验得到的锚固体顶面位移结果,按文献[6]确定抗浮锚杆的极限抗拔承载力则较小,根据文献[25]确定锚杆的极限抗拔承载力则较大。以锚固体顶面位移10~20 mm范围内荷载的较小值作为抗浮锚杆的极限抗拔承载力较为合理。依此确定4组抗浮锚杆SA2、SA3、SA4.5、SA6.5的极限抗拔承载力分别为259、335、348、327 kN,这一取值结果与史佩栋[26]提出抗拔桩桩顶上拔量的控制标准相吻合,这样将有利于结构物的安全。
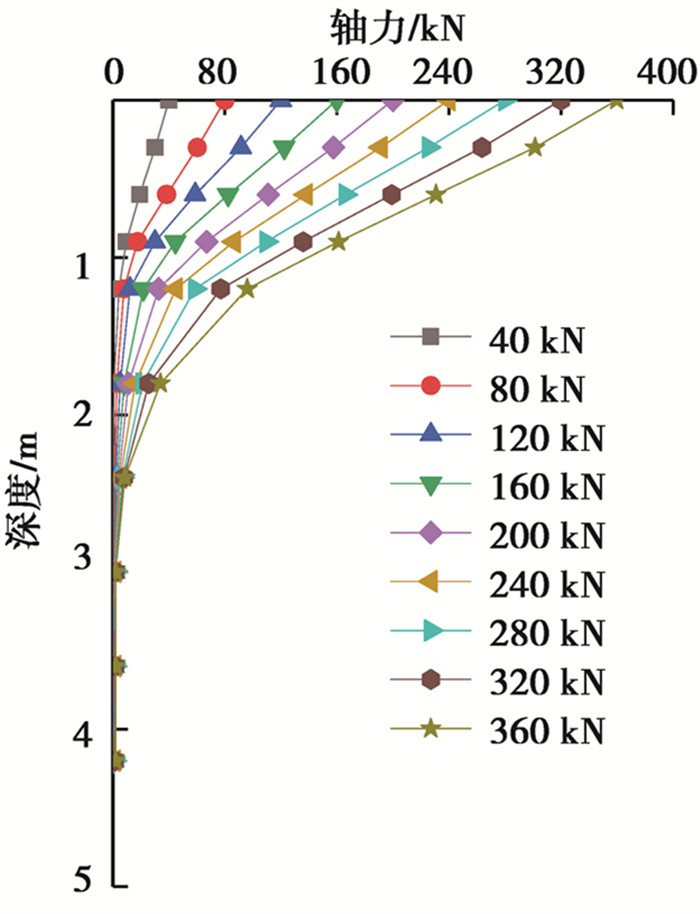
2.3 锚筋轴力沿深度传递特征分析笔者前期的研究表明[27],在试验时间较短的情况下,可忽略温度变化对锚筋应力变化的影响。通过光纤光栅应变传感器计算锚筋轴力与剪应力的原理与文献[28]相同。锚筋SA4.5-01轴力沿深度的变化规律如图 6所示。随着荷载水平的增加,锚筋轴力传递深度逐渐加大,总体来看,轴力的传递深度在2.4 m以内。在地表附近,锚筋轴力及其随荷载的增幅均达到峰值,在1.2 m以内,锚筋轴力衰减较快。荷载水平越高,锚筋轴力自上而下衰减速率越快。随着锚固深度的增加,锚筋轴力的衰减速率逐渐减小。在2.5 m以下,锚筋轴力已衰减到较低的水平,从距锚固体顶面3.0 m开始,锚筋轴力几乎衰减为零。说明锚筋与锚固体之间的黏结力并不是在锚固深度范围内均匀分布,而是自上而下逐步发挥,但并非沿锚固深度完全发挥出来。因此,当锚筋的黏结长度达到某一定值后,仅靠增加黏结长度并不能提高抗浮锚杆的极限抗拔承载力,这与Kilic[29]和曾宪明[30]等研究结果一致。试验中,2组抗浮锚杆SA4.5和SA6.5均发生锚筋拔断现象,进一步说明黏结长度为4.5 m和6.5 m的抗浮锚杆,锚固长度足够,结合表 3和图 5可以确定,直径28 mm、锚固体为M30水泥砂浆、中风化花岗岩中抗浮锚杆的应力传递深度不超过3.0 m。考虑到岩土层的局部差异、抗浮锚杆施工工艺的不同和经济性,以及永久性锚杆足够的应力储备,试验条件下,建议在中风化花岗岩中,锚筋直径为28 mm、锚固体为M30水泥砂浆的全长黏结抗浮锚杆的合理锚固长度为3.5~4.0 m。
|
图 6 锚筋轴力沿深度的分布规律 Fig. 6 Distribution rule of the rod axial force alone depth |
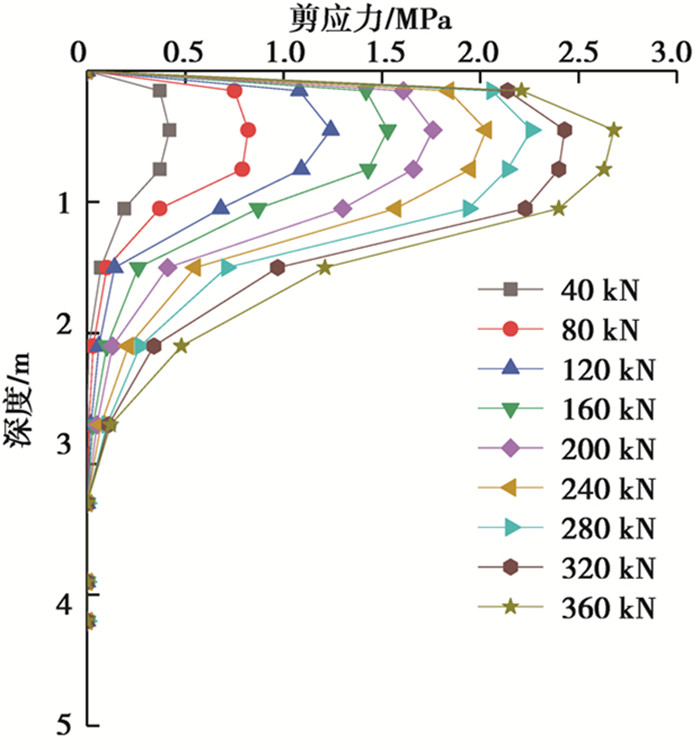
锚筋SA4.5-01表面剪应力沿深度的分布规律如图 7所示。锚筋剪应力沿深度呈先增大后减小的趋势,在锚固体顶面附近,剪应力具有数值大和分布集中的特点。在锚固体顶面处剪应力为零,在距锚固体顶面迅速增加到最大值,随后逐渐衰减,在距锚固体顶面3.3 m的位置减小到零。随着荷载水平的增加,剪应力的分布范围逐渐增大,剪应力峰值也随之增大,剪应力在0.45 m的位置达到最大值,在荷载水平为360 kN时,峰值剪应力约为2.7 MPa。
|
图 7 锚筋剪应力沿深度的分布规律 Fig. 7 Distribution rule of the rod shear stress alone depth |
锚筋承受剪应力的大小与荷载水平成正比,荷载水平越高,剪应力越大,而且不同荷载水平下剪应力的分布规律基本一致。另外,Coates等[31]研究发现,除荷载水平外,Er/Ea(Er为岩土体弹性模量,Ea为锚筋弹性模量)是影响剪应力大小和分布规律的另一个主要因素,Er/Ea越小,锚固体顶面附近的剪应力分布越均匀,试验也说明了这一点。
2.5 锚筋-锚固体界面黏结强度黏结强度是评价抗浮锚杆锚固效果的基本参数。这里所述的黏结强度是锚筋与锚固体之间的黏着力、摩擦力和咬合力共同作用结果,或称为摩阻力更为贴切。将极限抗拔承载力与锚筋和锚固体有效黏结面积的比值定义为锚筋-锚固体界面平均黏结强度,有效黏结面积指有效黏结长度范围内的接触面积。计算公式为[32]
| $ {\tau _{\rm{a}}} = {T_{\rm{u}}}/{\rm{ \mathsf{ π} }}d{l_{\rm{a}}}, $ | (1) |
式中:Tu为抗浮锚杆的极限抗拔承载力, kN;d为锚筋直径, mm;la为锚筋的有效黏结长度, m;τa为锚筋-锚固体界面的平均黏结强度, MPa。
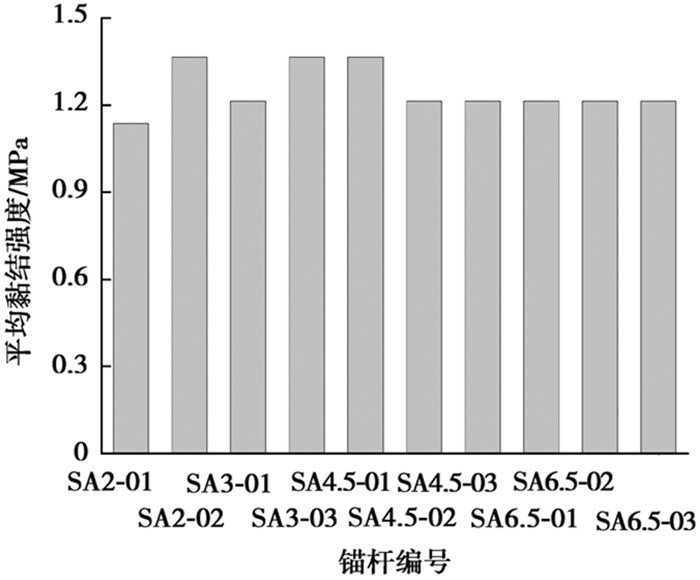
因抗浮锚杆SA2-01、SA2-02、SA3-01、SA3-03在锚筋-锚固体界面处发生剪切滑移破坏,抗浮锚杆SA4.5-01、SA4.5-02、SA4.5-03、SA6.5-01、SA6.5-02、SA6.5-03发生锚筋拔断现象,计算时取有效黏结长度,即la=3.0 m。因此,锚筋-锚固体界面平均黏结强度柱状图,如图 8所示。
|
图 8 锚筋-锚固体界面平均黏结强度柱状图 Fig. 8 Histogram for the average bonding strength of the rod-anchorage body interface |
10根抗浮锚杆的锚筋-锚固体界面平均黏结强度介于1.14~1.36 MPa之间,均值为1.25 MPa。当水泥砂浆或水泥净浆的强度等级介于M25~M40时,《岩土锚杆(索)技术规程》(CECS:22—2005)[33]建议锚固体与螺纹钢筋的黏结强度标准值为2.0~3.0 MPa;水泥砂浆强度等级介于M25~M35时,《建筑边坡工程技术规范》(GB 50330—2013)[34]建议锚固体与螺纹钢筋的黏结强度标准值为2.1~2.7 MPa;对于永久性锚杆,锚固体抗压强度分别为25、30、40 MPa时,《岩土锚杆与喷射混凝土支护工程技术规范》(GB50086—2015)[35]建议锚固体与螺纹钢筋的黏结强度设计值分别为0.8、0.9、1.0 MPa,随着锚固体抗压强度的提高,锚筋-锚固体界面的黏结强度增大。试验得到的锚筋与锚固体界面的平均黏结强度均低于《岩土锚杆(索)技术规程》、《建筑边坡工程技术规范》和《岩土锚杆与喷射混凝土支护工程技术规范》推荐的下限值。因《岩土锚杆与喷射混凝土支护工程技术规范》给出的是锚固体与螺纹钢筋的黏结强度设计值,对于永久性锚杆,其界面黏结强度标准值分别不低于1.6、1.8、2.0 MPa。分析原因,是由于试验锚杆的黏结长度超过其临界锚固长度,临界锚固长度为一定值,与荷载水平无关,锚筋黏结长度超过临界锚固长度后,抗浮锚杆的极限抗拔承载力不会因黏结长度的增加而提高。需要说明的是,试验开始之前,测试得到同条件养护下锚固体抗压强度的均值为34.1 MPa,因此,锚筋与锚固体界面平均黏结强度偏低并非锚固体强度不足所致。
通过公式(1)求得的锚筋-锚固体界面平均黏结强度实际上是黏结长度范围内剪应力的平均值。而抗浮锚杆受荷载作用时,其极限抗拔承载力为
| $ {T_{\rm{u}}} = \smallint _{{u_0}}^l\frac{{{\rm{ \mathsf{ π} }}{d^2}\tau \left( x \right)}}{4}{\rm{d}}x, $ | (2) |
式中,τ(x)为极限承载状态下锚筋上的应力分布函数。
2.6 锚固体-岩土体界面黏结强度锚固体与岩土体界面的平均黏结强度计算公式为
| $ {f_{\rm{a}}} = {T_{\rm{u}}}/{\rm{ \mathsf{ π} }}D{L_a}, $ | (3) |
式中:Tu为抗浮锚杆的极限抗拔承载力, kN;D为锚固体的直径, mm;La为锚固体与岩土体的锚固长度, m;f为锚固体与岩土体的平均黏结强度, MPa。
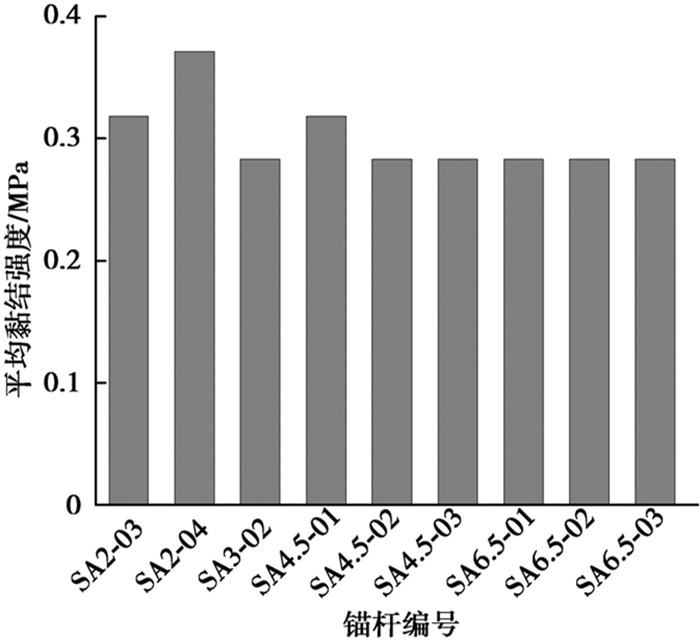
因抗浮锚杆SA2-03、SA2-04、SA3-02在锚固体-岩土体界面处发生剪切滑移破坏,抗浮锚杆SA4.5-01、SA4.5-02、SA4.5-03、SA6.5-01、SA6.5-02、SA6.5-03发生锚筋拔断现象,计算时取有效黏结长度,La=3.0 m。图 9为锚固体-岩土体界面平均黏结强度柱状图。
|
图 9 锚固体-岩土体界面平均黏结强度柱状图 Fig. 9 Histogram for the average bonding strength of the anchorage body-surrounding rock interface |
钻孔直径为120 mm的条件下,9根抗浮锚杆的锚固体-岩土体界面平均黏结强度介于0.28~0.37 MPa之间,均值为0.30 MPa。当锚固体强度等级为M30时,关于较硬岩石与锚固体的黏结强度标准值,《岩土锚杆(索)技术规程》(CECS:22—2005)[33]推荐取1.2~1.6 MPa,《建筑边坡工程技术规范》(GB 50330—2013)[34]推荐取0.55~0.90 MPa,《岩土锚杆与喷射混凝土支护工程技术规范》(GB 50086—2001)[35]推荐取1.0~1.5 MPa。不难发现,试验得到的锚固体-岩土体界面平均黏结强度均低于上述3项技术标准的推荐值。锚固体-岩土体界面力的传递是锚筋受荷后经锚固体传递的,同锚筋的应力传递规律类似,也是自上而下逐步发挥,但传递深度与锚筋相比更浅,白晓宇等[28]试验结果验证了这一点。因此,在计算时选用的黏结长度较长,试验得到的锚固体-岩土体界面平均黏结强度偏低。另一方面,试验场区的花岗岩为中生代晚期形成的侵入岩,物理力学指标和其它地区的花岗岩相比会出现不同程度的降低,这是导致锚固体-岩土体界面平均黏结强度偏低的另一个因素。可见,抗浮锚杆的承载力会受到岩石区域性差异的影响,在抗浮锚杆设计和施工过程中这种影响因素应当加以重视。此外,钻孔直径也会对锚固体-岩土体界面黏结强度造成一定的影响,黄志怀等[36]试验发现,在围岩条件、注浆工艺、锚固体强度等级、锚固长度均相同的条件下,锚固体-岩土体界面黏结强度随钻孔直径的增大而提高。
3 结论1) 试验条件下,抗浮锚杆主要出现锚筋-锚固体界面剪切滑移破坏、锚固体-周围岩体界面剪切滑移破坏及锚筋拔断3种破坏形态。
2) 中风化花岗岩中,钻孔直径为120 mm、锚筋直径为28 mm、水泥砂浆强度等级为M30时,黏结长度为2.0 m的抗浮锚杆其极限抗拔承载力为240 kN,黏结长度为不小于3.0 m的抗浮锚杆其极限抗拔承载力不低于320 kN,单筋抗浮锚杆的承载力高、变形小,能够满足抗浮要求。建议以锚固体顶面位移10~20 mm范围内荷载的较小值来确定抗浮锚杆的极限抗拔承载力。
3) 抗浮锚杆的荷载-锚固体顶面位移曲线总体呈缓变型,随荷载水平的增加,锚杆由弹性变形逐渐向弹塑性阶段过渡,且塑性区有逐渐向下移动的趋势。
4) 锚筋轴力沿深度并非均匀分布。随荷载水平的增加,锚筋轴力的传递深度逐渐增大;荷载水平越高,锚筋轴力自上而下衰减速率越快,锚筋在距锚固体顶面3.0 m以下范围内基本不受力。考虑到岩土层的局部差异、锚杆施工工艺的不同和经济性,以及永久性锚杆要有足够的应力储备,试验条件下,建议全长黏结抗浮锚杆的黏结长度设计值取3.5~4.0 m。
5) 锚筋剪应力沿深度呈先增大后减小的趋势。随着荷载水平的增加,剪应力的分布范围逐渐增大,剪应力峰值也随之增大,剪应力在0.45 m的位置达到峰值,在荷载水平为360 kN时,峰值剪应力约为2.7 MPa。
6) 锚筋锚固体界面平均黏结强度介于1.14~1.36 MPa之间,而锚固体-岩土体界面平均黏结强度介于0.28~0.37 MPa之间,锚固体-土体界面的黏结强度具有显著的区域差异性。
| [1] |
白晓宇, 张明义, 王永洪, 等. 岩石GFRP抗浮锚杆承载性能室内试验与机理分析[J]. 土木建筑与环境工程, 2018, 40(5): 78-85. Bai X Y, Zhang M Y, Wang Y H, et al. Full-scale test and mechanism analysis on bearing capacity of GFRP anti-floating anchor socket into rock[J]. Journal of Civil, Architectural & Environmental Engineering, 2018, 40(5): 78-85. (in Chinese) |
| [2] |
付文光, 柳建国, 杨志银. 抗浮锚杆及锚杆抗浮体系稳定性验算公式研究[J]. 岩土工程学报, 2014, 36(11): 1971-1982. Fu W G, Liu J G, Yang Z Y. Formulae for calculating stability of anti-floating anchor and anchor anti-floating system[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(11): 1971-1982. (in Chinese) |
| [3] |
Ni P, Mei G, Zhao Y. Numerical investigation of the uplift performance of prestressed fiber-reinforced polymer floating piles[J]. Marine Georesources & Geotechnology, 2017, 35(6): 829-839. |
| [4] |
曹洪, 朱东风, 骆冠勇, 等. 临江地下结构抗浮计算方法研究[J]. 岩土力学, 2017, 38(10): 2973-2979. Cao H, Zhu D F, Luo G Y, et al. Study of anti-buoyancy calculation method for underground structures near riverside[J]. Rock and Soil Mechanics, 2017, 38(10): 2973-2979. (in Chinese) |
| [5] |
白晓宇, 张明义, 匡政, 等. 全长黏结岩石GFRP抗浮锚杆变形特性分析[J]. 广西大学学报(自然科学版), 2018, 43(4): 1466-1473. Bai X Y, Zhang M Y, Kuang Z, et al. Deformation of full-length bonded GFRP anti-floating anchor in rock foundation[J]. Journal of Guangxi University(Nat Sci Ed), 2018, 43(4): 1466-1473. (in Chinese) |
| [6] |
贾金青, 宋二祥. 滨海大型地下工程抗浮锚杆的设计与试验研究[J]. 岩土工程学报, 2002, 24(6): 769-771. Jia J Q, Song E X. The design and test on anti-floating anchorage of large substructure in coastal region[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(6): 769-771. (in Chinese) |
| [7] |
柳建国, 吴平, 尹华刚, 等. 压力分散型抗浮锚杆技术及其工程应用[J]. 岩石力学与工程学报, 2005, 24(21): 3948-3953. Liu J G, Wu P, Yin H G, et al. Pressure-dispersive anti-float anchor technique and its application to engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(21): 3948-3953. (in Chinese) |
| [8] |
张明义, 张健, 刘俊伟, 等. 中风化花岗岩中抗浮锚杆的试验研究[J]. 岩石力学与工程学报, 2008, 27(增刊1): 2741-2746. Zhang M Y, Zhang J, Liu J W, et al. Experimental investigation on anti-floating anchor in moderately weathered granite[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(s1): 2741-2746. (in Chinese) |
| [9] |
白晓宇, 张明义, 刘鹤, 等. 风化岩地基全螺纹玻璃纤维增强聚合物抗浮锚杆承载特征现场试验[J]. 岩土力学, 2014, 35(9): 2464-2472. Bai X Y, Zhang M Y, Liu H, et al. Field test on load-bearing characteristics of full-thread GFRP anti-floating anchor in weathered rock site[J]. Rock and Soil Mechanics, 2014, 35(9): 2464-2472. (in Chinese) |
| [10] |
白晓宇, 张明义, 闫楠. 两种不同材质抗浮锚杆锚固性能的现场对比试验研究与机理分析[J]. 土木工程学报, 2015, 48(8): 38-46, 59. Bai X Y, Zhang M Y, Yan N. Field contrast test and mechanism analysis on anchorage performance of anti-floating anchors with two different materials[J]. China Civil Engineering Journal, 2015, 48(8): 38-46, 59. (in Chinese) |
| [11] |
陈棠茵, 王贤能. 抗浮锚杆应力-应变状态的线弹性理论分析[J]. 岩土力学, 2006, 27(11): 2034-2036. Chen T Y, Wang X N. Linear elastic analysis of stress-strain state of anti-float anchor[J]. Rock and Soil Mechanics, 2006, 27(11): 2034-2036. (in Chinese) |
| [12] |
龙照, 赵明华, 张恩祥, 等. 锚杆临界锚固长度简化计算方法[J]. 岩土力学, 2010, 31(9): 2991-2994. Long Z, Zhao M H, Zhang E X, et al. A simplified method for calculating critical anchorage length of bolt[J]. Rock and Soil Mechanics, 2010, 31(9): 2991-2994. (in Chinese) |
| [13] |
董天文, 许彬, 王家伟, 等. 无降水深基坑抗浮锚杆-旋喷体封底阻水体设计[J]. 岩土工程学报, 2018, 40(5): 848-856. Dong T W, Xu B, Wang J W, et al. Design of sealing bottom water-stop body of anti-floatage anchor-jetting body in non-dewatering deep foundation pits[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(5): 848-856. (in Chinese) |
| [14] |
白晓宇, 张明义, 张舜泉. 全长黏结螺纹玻璃纤维增强聚合物抗浮锚杆蠕变试验研究[J]. 岩石力学与工程学报, 2015, 34(4): 804-813. Bai X Y, Zhang M Y, Zhang S Q. Creep testing on anti-floating anchors of full-length bonding thread glass fiber reinforced polymer (GFRP)[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(4): 804-813. (in Chinese) |
| [15] |
马占峰. 拉力型抗浮锚杆的现场测试与数值分析[D]. 北京: 中国地质大学, 2008: 48-59. Ma Z F. Field testing and numerical analysis on tensile type anti-float anchor[D]. Beijing: China University of Geosciences, 2008: 48-59. (in Chinese) |
| [16] |
Kim S J, Smith S T. Pullout strength models for FRP anchors in uncracked concrete[J]. Journal of Composites for Construction, 2010, 14(4): 406-414. |
| [17] |
贾科科, 张明义, 李伟伟, 等. GFRP抗浮锚杆在混凝土底板中荷载传递机制的数值模拟[J]. 青岛理工大学学报, 2016, 37(1): 22-26. Jia K K, Zhang M Y, Li W W, et al. Numerical simulation on load transport mechanisms of GFRP anti-floating anchor in the concrete floor[J]. Journal of Qingdao University of Technology, 2016, 37(1): 22-26. (in Chinese) |
| [18] |
赵天杨, 白晓宇, 张明义, 等. 钢筋抗浮锚杆承载特性现场试验与数值仿真[J]. 科学技术与工程, 2018, 18(7): 38-43. Zhao T Y, Bai X Y, Zhang M Y, et al. Field test and numerical simulation of bearing capacity of steel reinforcement anti-floating anchor[J]. Science Technology and Engineering, 2018, 18(7): 38-43. (in Chinese) |
| [19] |
白晓宇, 张明义, 寇海磊. 基于裸光纤光栅传感技术GFRP抗浮锚杆荷载传递机制的原位试验研究[J]. 工程力学, 2015, 32(8): 172-181. Bai X Y, Zhang M Y, Kou H L. Field experimental study of load transfer mechanism of GFRP anti-floating anchors based on embedded bare fiber bragg grating sensing technology[J]. Engineering Mechanics, 2015, 32(8): 172-181. (in Chinese) |
| [20] |
中华人民共和国国家标准编写组. JGJ 120-2012建筑基坑支护技术规程[S]. 北京: 中国建筑工业出版社, 2012. The Professional Standards Compilation Group of People's Republic of China. JGJ 120-2012 Technical specification for retaining and protection of building foundation excavations[S]. Beijing: China Architecture and Building Press, 2012. (in Chinese) |
| [21] |
高丹盈, Brahim B. 纤维聚合物筋混凝土的粘结机制及锚固长度的计算方法[J]. 水利学报, 2000(11): 70-78. Gao D Y, Brahim B. Bonding mechanism and calculating method for embedded length of fiber reinforced polymer rebars in concrete[J]. Journal of Hydraulic Engineering, 2000(11): 70-78. (in Chinese) |
| [22] |
曾宪明, 林大路, 李世民, 等. 锚固类结构杆体临界锚固长度问题综合研究[J]. 岩石力学与工程学报, 2009, 28(增刊2): 3609-3625. Zeng X M, Lin D L, Li S M, et al. Comprehensive research of critical anchorage length problem of rod of anchorage structure[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(s2): 3609-3625. (in Chinese) |
| [23] |
陈根全. 锚杆桩的抗拔试验[J]. 工程勘察, 1997, 25(2): 15-16, 19. Chen G Q. The pullout test of uplift pile[J]. Geotechnical Investigation & Surveying, 1997, 25(2): 15-16, 19. (in Chinese) |
| [24] |
张明义, 寇海磊, 白晓宇, 等. 玻璃纤维增强聚合物抗浮锚杆抗拔性能试验研究与机制分析[J]. 岩土力学, 2014, 35(4): 1069-1076. Zhang M Q, Kou H L, Bai X Y, et al. Experimental study and mechanism on the anti-pulling behavior of GFRP anti-float anchor[J]. Rock and Soil Mechanics, 2014, 35(4): 1069-1076. (in Chinese) |
| [25] |
王贤能, 曾卫东, 徐金台. 岩石抗浮锚杆的应用及分析[C]//中国岩石力学与工程学会第七次学术大会论文集. 西安: [s. n. ], 2002: 831-835. Wang X N, Zeng W D, Xu J T. Engineering application of anti-float anchor rod in rock mass and it's analysis[C]//Proceedings of the Seventh Conference of Chinese Society for Rock Mechanics and Engineering. Xi'an: [s. n. ], 2002: 831-835. (in Chinese) |
| [26] |
史佩栋. 实用桩基工程手册[M]. 北京: 中国建筑工业出版社, 1999: 180-190. Shi P D. Practical handbook of pile foundation[M]. Beijing: China Architecture and Building Press, 1999: 180-190. (in Chinese) |
| [27] |
白晓宇, 张明义, 匡政, 等. 光纤光栅传感技术在GFRP抗浮锚杆现场拉拔试验中的应用[J]. 岩土力学, 2018, 39(10): 3891-3899. Bai X Y, Zhang M Y, Kuang Z, et al. Application of fiber grating sensing technology in pull-out test on glass fiber reinforced polymer anti-floating anchor[J]. Rock and Soil Mechanics, 2018, 39(10): 3891-3899. (in Chinese) |
| [28] |
白晓宇, 张明义, 朱磊, 等. 全长黏结GFRP抗浮锚杆界面剪切特性试验研究[J]. 岩石力学与工程学报, 2018, 37(6): 1407-1418. Bai X Y, Zhang M Y, Zhu L, et al. Experimental study on shear characteristics of interface of full-bonding glass fiber reinforced polymer anti-floating anchors[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(6): 1407-1418. (in Chinese) |
| [29] |
Kilic A, Yasar E, Celik A G. Effect of grout properties on the pull-out load capacity of fully grouted rock bolt[J]. Tunnelling and Underground Space Technology, 2002, 17(4): 355-362. |
| [30] |
曾宪明, 赵林, 李世民, 等. 锚固类结构杆体临界锚固长度与判别方法试验研究[J]. 岩土工程学报, 2008, 30. Zeng X M, Zhao L, Li S M, et al. Critical rod anchorage length and discrimination method of anchorage type structure[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(s1): 404-409. (in Chinese) |
| [31] |
Coates D F, Yu Y S. Three-dimensional stress distributions around a cylindrical hole and anchor[C]//Proceedings of the 2nd International Conference on Rock Mechanics. Belgrade, 1970, 3: 175-182.
|
| [32] |
Won J P, Park C G, Kim H H, et al. Effect of fibers on the bonds between FRP reinforcing bars and high-strength concrete[J]. Composites Part B: Engineering, 2008, 39(5): 747-755. |
| [33] |
中华人民共和国国家标准编写组. CECS 22: 2005岩土锚杆(索)技术规程[S]. 北京: 中国计划出版社, 2005. The Professional Standards Compilation Group of People's Republic of China. CECS 22: 2005 Technical specification for ground anchors[S]. Beijing: China Planning Press, 2005. (in Chinese) |
| [34] |
中华人民共和国国家标准编写组. GB50330-2013建筑边坡工程技术规范[S]. 北京: 中国建筑工业出版社, 2013. The Professional Standards Compilation Group of People's Republic of China. GB50330-2013 Technical code for building slope engineering[S]. Beijing: China Architecture and Building Press, 2013. (in Chinese) |
| [35] |
中华人民共和国国家标准编写组. GB50086-2015岩土锚杆与喷射混凝土支护技术规范[S]. 北京: 中国计划出版社, 2015. The Professional Standards Compilation Group of People's Republic of China. GB50086-2015 Technical code for engineering of ground anchorages and shotcrete support[S]. Beijing: China Planning Press, 2015. (in Chinese) |
| [36] |
黄志怀, 李国维, 王思敬, 等. 不同围岩条件玻璃纤维增强塑料锚杆结构破坏机制现场试验研究[J]. 岩石力学与工程学报, 2008, 27(5): 1008-1018. Huang Z H, Li G W, Wang S J, et al. Field test on pullout behaviors of anchorage structures with glass fiber reinforced plastic rods for different surrounding rock masses[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(5): 1008-1018. (in Chinese) |
 2021, Vol. 44
2021, Vol. 44

