2. 四川大学 水利学与山区河流开发保护国家重点实验室, 成都 610065
2. State Key Laboratory of Hydraulics and Mountain River Engineering, Sichuan University, Chengdu 610065, P. R. China
在外力或内力作用下,材料内局部源迅速释放能量而产生瞬态弹性波的现象称为声发射,其本质上是一种频率和模式丰富的弹性波[1]。声发射作为一种重要的无损检测手段,有着灵敏度高、反应及时和全周期实时监测等诸多优点,在工程安全监测领域拥有广阔的应用前景。工程材料特性对弹性波传播模式有重要影响,因此必须首先理解所研究材料中弹性波的传播规律及衰减特性等。Worlton[2]通过实验验证了板波在铝板中的频散效应。Habeger等[3]通过实验分析了纸板中板波的传播规律。王佳明[4]通过试验进行混凝土材料声发射特性的研究,分析了声波波速在混凝土材料中的衰减,并为玄武岩纤维混凝土的推广和声发射技术在混凝土结构健康监测领域的应用提供了基础研究。赵永川等[5]利用超声波传感器研究了弹性波在中粒砂岩圆柱体内传播不同距离后的衰减特性和波形变化特征。Goodfellow等[6]以枫丹白露砂岩为研究对象,采用主动和被动超声波方法研究了真三轴变形过程中弹性波的衰减特性,结果表明初始衰减各向异性主要是由粒间摩擦引起的,之后由于宏观垂直裂缝形成波的散射,导致高频谱的衰减。Li等[7]对嵌入混凝土中的钢绞线进行了4组AE衰减试验,试验结果表明:随着覆盖层深度和水灰比的增加,AE强度的衰减率分别呈近似指数函数和线性关系变化,并随着孔隙水饱和度的增加而减小。王子振等[8]研究了岩石介质中孔隙结构对弹性波衰减的影响,发现孔隙密度及形状与信号衰减密切相关。
尽管国内外学者对岩石等材料中弹性波的传播和衰减规律进行了研究,并取得了大量成果,但材料内部颗粒特征对弹性波传播的影响规律相关研究还不多见,尤其是工程混凝土材料由不同粒径骨料构成,这将影响到弹性波传播与衰减规律并与检测准确度直接相关。因此,本文利用不同粒径的砂作为骨料制作成混凝土试样,以声发射设备作为研究手段,分析骨料粒径对弹性波衰减的影响规律与机制。
1 试验 1.1 试件制备实验步骤主要包括了砂粒制备、试件制作、传感器校准、断铅试验与信号监测、结果分析等。以普通天然河沙为原料,利用高频振动筛分别筛选粒径为0.1~0.25 mm,0.5~1 mm,1~2 mm和2~5 mm的4种砂(图 1(a)~(d))作为试件的骨料,PO42.5普通硅酸盐水泥为胶凝材料。为获得混凝土骨料粒径对弹性波参数衰减的影响规律,试件需要有较高的骨料比例,综合相关文献[9]和多次预制结果,最后确定了试样的质量配合比,即水泥∶砂∶水=1∶2∶0.5。按照上述质量比分别将原料进行混合搅拌均匀后(图 1(e))倒入100 mm×40 mm×400 mm的混凝土试件专用模具中成型并保湿养护7 d;试样脱模后如图 1(f)所示,从左到右依次为骨料粒径0.1~0.25 mm,0.5~1 mm,1~2 mm,2~5 mm的混凝土试样。

|
图 1 混凝土试件制作 Fig. 1 Concrete specimen production |
试验采用的声发射监测系统为北京软岛公司开发的DS5-16型声发射测试定位仪,主机采样频率为3 MHz,采用RS-2A型陶瓷压电传感器,频率范围为100~400 kHz。沿试件上表面中心长轴方向上标注断铅点和声发射传感器位置,在第20 mm处设置断铅位置,在第80,140,200,260,320,380 mm处分别设置1#~6#传感器,如图 2所示。

|
图 2 试验原理图 Fig. 2 Test schematic |
试验开始前在每个标注点上用细砂纸打磨光滑,并在传感器和试件表面用硅胶耦合剂贴合以提高换能效率,减少信号损失与失真。在图 2中断铅点位置采用ф0.5 mm、型号为HB的铅芯与试件平面按30°夹角进行断铅测试,每种试件按相同方法断铅4次,分别命名为Test 1、Test 2、Test 3、Test 4。通过1#~6#传感器收集断铅测试过程的全部波形信号,将信号导入MATLAB中,按照传感器参数设计滤波器,再利用自编代码进行信号滤波、频谱转换、参数统计及曲线拟合等方式处理,分析骨料粒径对弹性波在混凝土试件中衰减过程的影响机制,以及波形特征参数的演化规律。
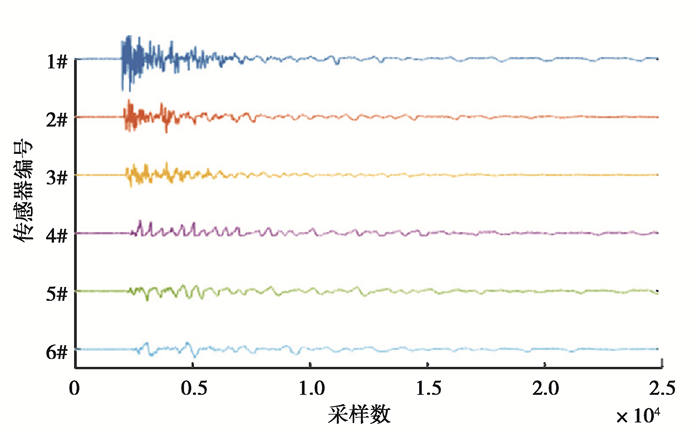
2 试验数据分析 2.1 弹性波幅值衰减规律断铅试验产生的弹性波在混凝土试件中传播,其能量不断地衰减,信号特征参数的衰减程度是源信号强度和介质物理性质(骨料粒径等)的函数。以0.1~0.25 mm骨料试件第一次断铅实验(Test 1)为例,在相同坐标尺度下绘出6个传感器监测到的时域信号,如图 3所示。该次事件产生的突发型信号特征较为清晰,弹性波按传播距离依次到达1#~6#传感器,波形幅值逐渐降低。
|
图 3 时域信号对比 Fig. 3 Time domain signal comparison |
由于混凝土材料属非完全弹性体,应力波在其传播过程中都要发生波动能量损失。根据应力波传播衰减理论、品质因子Q理论[10-11],声发射波在传播过程中振幅的变化可表示为
| $ A\left( x \right) = {A_0}{\rm{exp}}\left( { - \frac{{{\rm{ \mathsf{ π} }}f}}{{VQ}}x} \right) = {A_0}{\rm{exp}}\left( { - \alpha x} \right), $ | (1) |
式中:A(x)为声发射传播距离x处的振幅,dB;A0为声发射信号初始振幅,dB;f为声发射信号频率,Hz;x为声发射信号传播距离,m;V为声发射信号传播速度,m/s;Q为砂岩体介质的品质因子;α为声发射信号衰减系数。
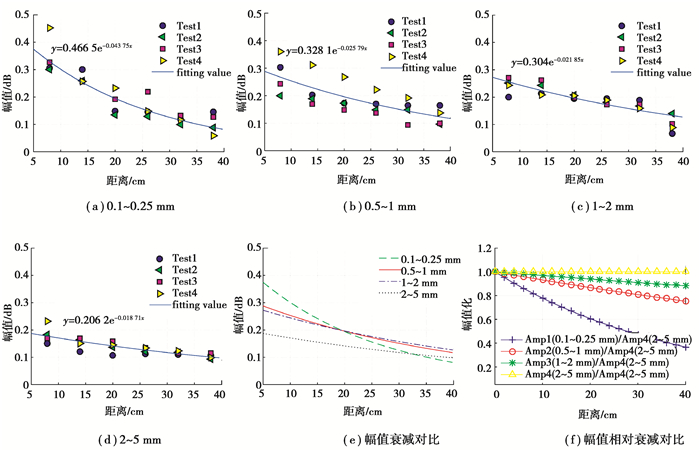
因此,弹性波信号振幅随着传播距离的增大呈负指数函数衰减,衰减的快慢取决于式(1)中的衰减系数α。提取不同传感器监测到的混凝土试件断铅测试的幅度峰值并分别进行拟合,得到了沿传播距离方向上声发射信号幅值衰减函数关系,图 4(a)~(d)。从拟合结果来看,随着传播距离的增大,所有试件中的声发射信号幅值均近似符合负指数函数衰减,为判断和评价回归模型拟合优度,对回归方程进行决定系数检验(R2),4种试件拟合决定系数分别为0.768 3,0.535 8,0.734 5,0.671 2,可以看出在置信区间95%以下,幅值随距离的衰减变化均呈现出良好的负指数相关。
|
图 4 不同粒径试样幅值衰减规律 Fig. 4 Attenuation law of amplitude of samples with different particle sizes |
经拟合得到,0.1~0.25 mm,0.5~1 mm,1~2 mm和2~5 mm试件的弹性波幅值衰减系数分别为0.043 75,0.025 79,0.021 85,0.018 71,如图 4(e)所示,即骨料粒径越小,弹性波幅值的衰减速度越快。为进一步说明骨料粒径对幅值衰减的影响,利用不同粒径的拟合曲线分别除以2~5 mm试件拟合曲线,并进行归一化处理,结果如图 4(f)所示,可见骨料粒径越小的混凝土试件,其弹性波幅值衰减的相对速度就越快。
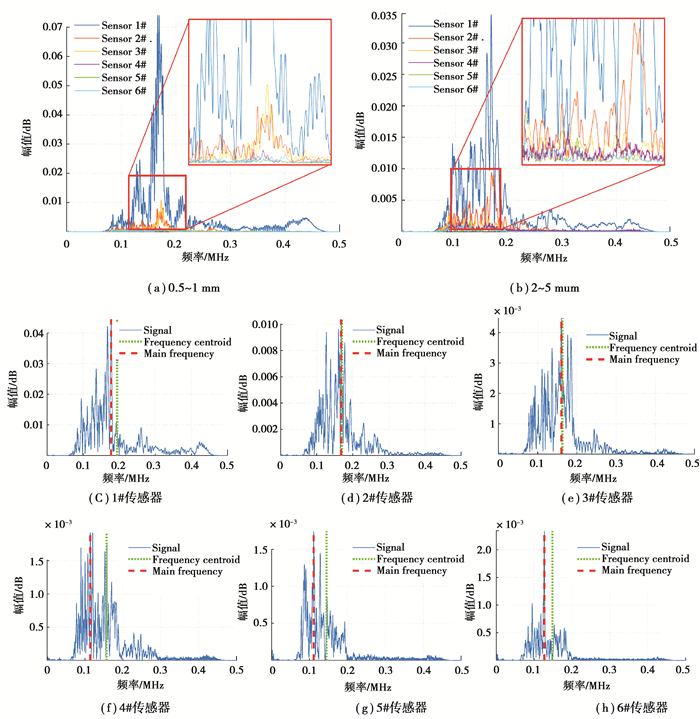
2.2 弹性波频谱演化规律从理论上讲,声发射源发出的信号都含有反应其本质特征的信息,频谱分析是对时域信号的补充,以期在时域信号中不能发现的信息在频域中得以反映[5]。为分析不同频率信号在传播过程中的衰减特性,利用快速傅里叶变换(FFT, fast fourier transform)得到信号的频域信息,结果表明:1)1#传感器在几乎所有频谱上幅值都是最大,2#~6#接近依次减小,说明随着传播距离的增加,各频率段的信号强度都会逐渐衰减;2)在衰减速度方面,小骨料粒径试件在个频率段衰减速度较快,而较大骨料粒径试件中各频率段信号衰减速度较慢。图 5(a)~(b)为0.5~1 mm和2~5 mm试件的频谱图。
|
图 5 试样频谱衰减分析 Fig. 5 Spectral attenuation analysis |
事实上,随着弹性波传播距离的增大,信号的衰减不仅体现在幅值上,构成信号的频率分布也出现了显著变化。以2~5 mm粒径试样(Test 1)为例,将1#~6#传感器中监测到的弹性波信号依次经快速傅里叶变换得到频谱图,如图 5(c)~(h)所示。可以发现,在距离声发射源距离最的1#传感器频谱图(图 5(c))上,0.2~0.3 MHz及0.3 MHz以上高频信号有相对较高的比例,2#传感器频谱中(图 5(d))0.3 MHz以上高频迅速衰减至极低水平,而0.2~0.3 MHz频率段信号相对衰减不多,其后3#和4#传感器频谱(图 5(e)~(f))中0.2~0.3 MHz频率段强度继续减少,而5#和6#传感器频谱图(图 5(g)~(h))中0.2~0.3 MHz频率段也衰减至极低水平,几乎仅剩下了0.2 MHz以下的低频部分。由此可见,弹性波信号沿传播方向的衰减速度与频率直接相关,高频部分信号衰减速度更快。断铅试验产生的弹性波在传播过程中衰减的主要原因是弹性波在传播过程中以波动即微颗粒振动的形式进行扩散,同等振动幅度下频率越高,振动越快,颗粒间的摩擦阻尼越显著,使得高频信号衰减更加显著。
以上分析了不同频率段信号衰减速度差异,为将声发射频率演化趋势进行量化,选取信号主频(峰值频率,即最大幅值对应的频率)和频谱重心作为指标进行分析。经计算得到1#~6#传感器信号主频分别为0.194,0.169 7,0.162 8,0.158 5,0.144 9,0.148 3 MHz,如图 5(e)~图 5(h)中红色虚线所示,近似呈线性下降;为克服主频描述多频率信号的片面性,将信号的频率按照幅值作为加权的依据得到频谱信号的频谱重心,频谱重心位置如图 5(e)~(h)中绿色虚线所示,分别为0.177 4,0.167 4,0.160 3,0.115 3,0.110 9,0.126 8 MHz。由此可见,无论是主频还是频谱重心参数都反应出声发射信号随传播距离的增加,高频部分衰减速度快,低频部分衰减速度慢,因此随传播距离增加,低频信号所占比例越来越大。
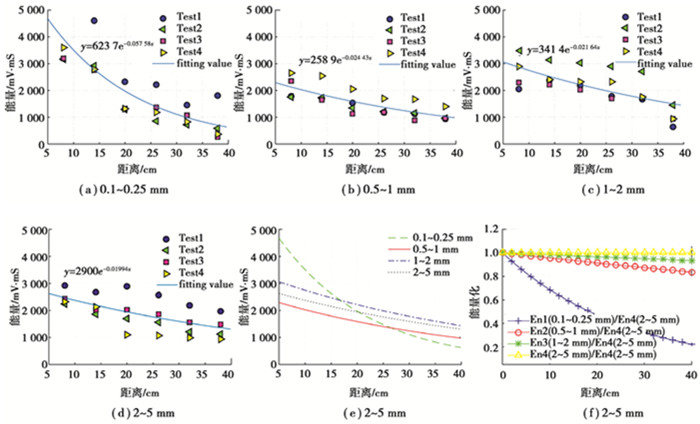
2.3 弹性波能量衰减规律幅值的衰减表示着波形振动最大幅值的变化规律,而能量是时间信号检波包络线下的面积,是所有频率信号的能量总和,考虑了幅值、振铃计数、频率和持续时间等因素,是一个综合反映信号强度的物理量[12]。不同位置传感器接收到的能量变化规律如图 6(a)~图 6(d)的散点图所示,传播过程中的能量呈现近似指数变化规律,将试验结果按指数函数(y=a exp(bx))进行拟合,图中蓝色虚线为能量拟合曲线,在距离声发射源较近处能量较大,随后迅速降低。经拟合得到,0.1~0.25 mm,0.5~1 mm,1~2 mm和2~5 mm试件的弹性波能量衰减系数分别为0.057 58,0.024 43,0.021 64,0.019 94,如图 6(e)所示。由此可见,骨料粒径越小的混凝土试件,弹性波能量的衰减速度越快。
|
图 6 不同粒径试样能量衰减规律 Fig. 6 Attenuation law of energy of samples with different particle sizes |
为对比相对衰减速度,将各拟合曲线分别除以2~5 mm试件拟合曲线,并进行归一化处理,结果如图 6(f)所示,可见骨料粒径越小的混凝土试件,其弹性波能量衰减的相对速度就越快。
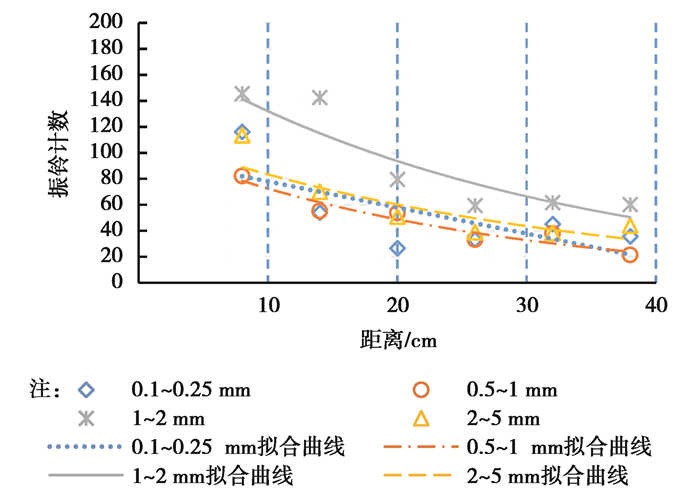
2.4 振铃计数变化规律当声发射信号幅值超过设定的阀值电压时将产生一个矩形脉冲,超过阈值电信号的每一个震荡波称为一个振铃计数[13]。振铃计数能粗略地反映信号强度和频率,在试验中,随着传播距离的增加,信号幅值不断下降,超过门槛值并触发振铃计数次数也在逐渐减少。试验真实的平均振铃计数和拟合结果如图 7所示。由此可见,在不同粒径混凝土试件中,振铃计数的变化规律类似,均随传播距离的增加而呈对数函数减少。
|
图 7 振铃计数衰减规律 Fig. 7 Attenuation law of count |
以4种不同粒径骨料制作的混凝土试件为研究对象,分析了弹性波特征参数随传播距离增加而出现的衰减演化规律,以及骨料粒径对弹性波衰减变化的影响,主要结论如下:
1) 弹性波在混凝土试件中传播时其幅值不断地降低,可采用负指数函数对其进行拟合,得到0.1~0.25 mm,0.5~1 mm,1~2 mm和2~5 mm试件的弹性波幅值衰减系数分别为0.043 75,0.025 79,0.021 85,0.018 71,即骨料粒径越小,则弹性波幅值的衰减相对速度越快。
2) 分析频域变化特征后发现,弹性波信号沿传播方向的衰减速度与频率直接相关。随着传播距离的增加,各频率段的信号都会逐渐衰减,且粒径较小试件下降更快;随传播距离增加,信号主频和频谱重心都会逐渐偏向低频区,即高频信号衰减更快,低频信号所占比例则越来越大。
3) 弹性波的能量随着传播距离的增大呈负指数函数衰减,拟合分别得到4种试件的能量衰减系数为0.057 58, 0.024 43,0.021 64,0.019 94,即骨料粒径越小的混凝土试件,其弹性波能量衰减的相对速度就越快,这与幅值衰减规律相一致。
4) 振铃计数能近似反映信号强度和频率,试验结果表明,随着传播距离的增加,声发射信号振铃计数大致呈对数函数减少,且4种不同粒径试件的振铃计数衰减规律较为近似。
| [1] |
马波, 陈健飞, 李标, 等. 玻璃纤维复合材料板声发射信号传播特性[J]. 无损检测, 2017, 39(1): 16-18, 23. Ma B, Chen J F, Li B, et al. Acoustic emission signal propagation characteristics of glass fiber composite material plate[J]. Nondestructive Testing, 2017, 39(1): 16-18, 23. (in Chinese) |
| [2] |
Worlton D C. Experimental confirmation of lamb waves at megacycle frequencies[J]. Journal of Applied Physics, 1961, 32(6): 967-971. DOI:10.1063/1.1736196 |
| [3] |
Habeger C C, Mann R W, Baum G A. Ultrasonic plate waves in paper[J]. Ultrasonics, 1979, 17(2): 57-62. DOI:10.1016/0041-624X(79)90096-9 |
| [4] |
王明佳. 基于声发射参数的玄武岩纤维混凝土抗弯断裂及声波衰减特性研究[D]. 长春: 吉林大学, 2017. Wang M J. Research on flexural fracture and acoustic attenuation characteristics of basalt fiber reinforced concrete based on acoustic emission parameters[D]. Changchun: Jilin University, 2017. (in Chinese) |
| [5] |
赵永川, 杨天鸿, 肖福坤, 等. 弹性波在中粒砂岩内传播衰减特性分析[J]. 振动.测试与诊断, 2018, 38(2): 285-291, 418. Zhao Y C, Yang T H, Xiao F K, et al. Study on the attenuation of elastic wave propagating in medium-grained sandstone[J]. Journal of Vibration, Measurement & Diagnosis, 2018, 38(2): 285-291, 418. (in Chinese) |
| [6] |
Goodfellow S D, Tisato N, Ghofranitabari M, et al. Attenuation properties of fontainebleau sandstone during true-triaxial deformation using active and passive ultrasonics[J]. Rock Mechanics and Rock Engineering, 2015, 48(6): 2551-2566. DOI:10.1007/s00603-015-0833-8 |
| [7] |
Li F M, Huang L, Zhang H X, et al. Attenuation of acoustic emission propagation along a steel strand embedded in concrete[J]. KSCE Journal of Civil Engineering, 2018, 22(1): 222-230. DOI:10.1007/s12205-017-0844-y |
| [8] |
王子振, 王瑞和, 李天阳, 等. 孔隙结构对干岩石弹性波衰减影响的数值模拟研究[J]. 地球物理学进展, 2014, 29(6): 2766-2773. Wang Z Z, Wang R H, Li T Y, et al. Numerical-modeling of pore structure effects on acoustic attenuation in dry rocks[J]. Progress in Geophysics, 2014, 29(6): 2766-2773. (in Chinese) |
| [9] |
申艳军, 荣腾龙, 杨更社, 等. 类砂岩相似材料配合比方案试验研究[J]. 水利水电科技进展, 2016, 36(4): 75-79. Shen Y J, Rong T L, Yang G S, et al. Experimental study on ratio of quasi-sandstone similar material[J]. Advances in Science and Technology of Water Resources, 2016, 36(4): 75-79. (in Chinese) |
| [10] |
李建功. 应力波在弹塑性煤岩体中传播衰减规律研究[D]. 青岛: 山东科技大学, 2008. Li J G. Study on the stress wave propagation attenuation laws in the elastoplastic coal and rock[D]. Qingdao: Shandong University of Science and Technology, 2008. (in Chinese) |
| [11] |
文光才, 李建功, 邹银辉, 等. 矿井煤岩动力灾害声发射监测适用条件初探[J]. 煤炭学报, 2011, 36(2): 278-282. Wen G C, Li J G, Zou Y H, et al. Preliminary study on the application conditions of acoustic emission monitoring dynamic disasters in coal and rock[J]. Journal of China Coal Society, 2011, 36(2): 278-282. (in Chinese) |
| [12] |
Wanniarachchi W A M, Ranjith P G, Perera M S A, et al. Assessment of dynamic material properties of intact rocks using seismic wave attenuation: an experimental study[J]. Royal Society Open Science, 2017, 4(10): 170896. DOI:10.1098/rsos.170896 |
| [13] |
郭军杰, 程晓阳. 循环载荷下煤样变形及声发射特征试验研究[J]. 中国安全科学学报, 2017, 27(11): 109-115. Guo J J, Cheng X Y. Experimental study on deformation and acoustic emission characteristics of coal samples under cyclic loading[J]. China Safety Science Journal, 2017, 27(11): 109-115. (in Chinese) |
 2021, Vol. 44
2021, Vol. 44

