2. 国网智能科技股份有限公司, 济南 250101;
3. 华通科技有限公司, 重庆 400112;
4. 重庆大学 机械传动国家重点实验室, 重庆 400044
2. State Grid Intelligent Technology Co., Ltd., Jinan 250101, P. R. China;
3. Huatong Technology Co., Ltd., Chongqing 400112, P. R. China;
4. The State Key Laboratory of Mechanical Transmissions, Chongqing University, Chongqing 400044, P. R. China
随着工业、农业的迅速发展和社会用电需求的不断增加,人们对输电线路供电可靠性、供电质量的要求越来越高, 但变电站的鸟害故障、电缆损伤、电网波形畸变等严重影响了电网系统的安全运行及使用寿命。随着科技不断发展,变电站智能化的步伐也不断加快,巡检机器人、驱鸟机器人等智能辅助设备的使用为降低变电站维运部门的人力物力、保证人身安全提供了新的途径。智能机器人的全线路自主运行,需要频繁进行电能补给,而电流谐波会使得机器人充电设备内的元件出现过热现象,导致系统出现紊乱,降低机器人的正常寿命,加速设备的老化。此外,谐波电流还会对整流装置产生不良影响,降低电力系统中设备的利用率和经济效益,造成电网波形畸变、电力品质下降[1]。因此,准确测量电流谐波参数,掌握电网谐波实际情况,对保证充电系统与接入设备安全使用、提高电网负载能力、维护电力系统的经济稳定运行具有重要意义[2]。
目前,电网谐波检测方法主要包括快速傅里叶变换(FFT,fast Fourier transform)检测方法、小波检测方法、神经网络检测方法、参数化检测方法等。但各种方法均存在局限性,如基于小波变换的谐波检测方法[3],由于不同尺度的小波函数在频域中存在互相干扰,难以分离频率较近的谐波和间谐波成分;基于神经网络的谐波检测方法[4],需要大量的训练样本,且在电网频率波动情况下的训练存在较大误差;参数化谐波检测方法,如拓展Prony方法[5],具有较高的频率分别率,但模型参数计算复杂,计算量大,且抗噪能力较差;基于FFT的谐波检测方法,由于算法简单、处理速度快等特点,是目前使用最广泛的谐波检测方法。但由于电网基波频率变化,导致非同步采样或非整周期截断而产生较严重的频谱泄漏,使测量精度降低;而基于FFT频谱校正的谐波检测方法,如加窗插值算法[6-8],当FFT谱泄漏严重或分辨率较低时,相邻谐波成分相互干扰,造成谐波检测精度降低。文献[9]使用全相位时移相位差法检测谐波,但需要计算两次全相位FFT(apFFT, all-phase FFT), 增加了计算量。
综上,传统的谐波检测方法往往在资源有限的实际设备上运行时检测速度较慢,无法实现谐波的快速定位,实时性较差。结合谱线插值算法和apFFT方法特点,论文提出基于全相位谱线插值的电力谐波检测新方法。该方法利用apFFT得到高精度的谐波相位,并利用谐波实际频点附近的三根离散谱线对全相位谱进行插值校正。由于全相位谱中旁谱线相对于主谱线按平方项衰减,再结合旁瓣衰减速度快的Nutall四项五阶余弦窗,可有效抑制基于FFT的谱线插值法相邻谐波成分的相互干扰,提高测量精度。该方法能准确提取谐波信息,又降低了运算量,提高了检测的实时性。
1 全相位FFT相较于传统FFT截断,apFFT考虑了某样点的全部截断情况,并通过循环移位对齐该采样点,获得N个“全相位子分段”,最后对所有“全相位子分段”的FFT谱求和获得全相位FFT谱。FFT与apFFT的关系如图 1所示。
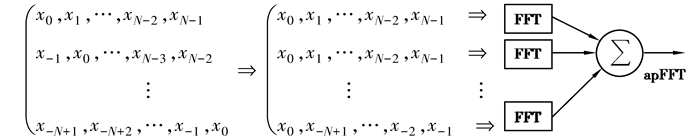
|
图 1 FFT与apFFT关系 Fig. 1 Relationship between FFT and apFFT |
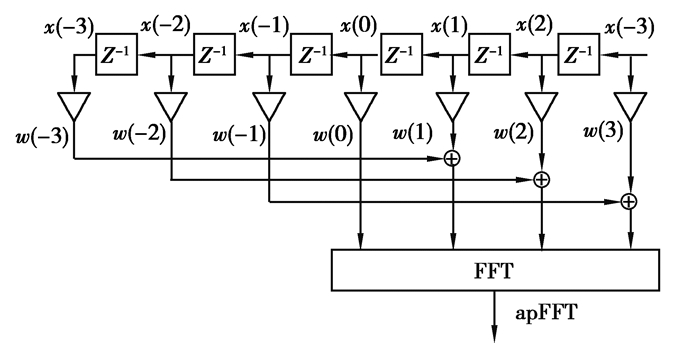
根据线性时不变系统的齐次性和叠加性,全相位谱分析过程可转换为图 2所示的过程。
|
图 2 全相位谱分析结构 Fig. 2 Structure of apFFT |
图 2中,利用卷积窗w对中心样点x(0)前后2N-1个数据加权,并令间隔为N的加权数据相加获得N点全相位预处理数据,将这N点数据进行傅里叶变换即得到全相位谱。卷积窗w由前窗f和反转的后窗b卷积得到:
| $ w(n)=f(n) * b(-n),-N+1 \leqslant n \leqslant N-1 。$ | (1) |
当前窗和后窗相同,且为对称窗时,窗谱为:
| $ W(j \omega)=F(j \omega) F^{*}(j \omega)=\left|F_{g}(\omega)\right|^{2}, $ | (2) |
式中,Fg(ω)为窗f的幅值谱。文中仅研究上述情况下的apFFT。对于单频复指数序列x(n),设其幅值为A,频率为ω0,相位为θ0。
| $ x(n)=A\ \mathrm{e}^{j\left(\omega_{0} n+\theta_{0}\right)}, n \in Z。$ | (3) |
其加f窗的傅里叶变换为:
| $ \begin{array}{c} X(k)=A F_{g}\left(k \Delta \omega-\omega_{0}\right) \mathrm{e}^{j\left(\theta_{0}-\tau\left(k \Delta \omega-\omega_{0}\right)\right)}, \\ \tau=(N-1) / 2。\end{array} $ | (4) |
根据图 1,使用f双窗的apFFT谱为
| $ X_{a}(k)=A F_{g}^{2}\left(k \Delta \omega-\omega_{0}\right) \mathrm{e}^{j \theta_{0}}。$ | (5) |
比较式(4)和式(5),传统傅里叶变换离散谱线上的相位值与其对应的频率偏离值有关,而全相位谱的相位值即为中心样点x(0)的理论相位值,故全相位谱主谱线上的相位值无需校正,即可得到较高的精确度;另外,在全相位谱中,窗旁瓣谱线相对于主谱线按按平方项衰减,使主谱线更为突出,即可有效抑制频谱泄漏。
2 全相位谱线插值通过apFFT可以得到较高的相位精度,但通过离散谱线获得的幅值和频率精度较差。文中结合谱线插值算法,对全相位谱进行幅值和频率校正。
2.1 窗函数性质窗函数的特性对谱线插值算法的影响较大,一般选择旁瓣衰减大且迅速的窗函数用于谱线插值校正。文中选择四项五阶Nuttall窗作为全相位分析窗,其旁瓣衰减-60.95 dB,旁瓣衰减速率42 dB/otc。窗函数时域表达式为
| $ w(n)=\sum\limits_{m=0}^{3}(-1) m a_{m} \cos (2 {\rm{ \mathsf{ π}}} n m / N), 0 \leqslant n \leqslant N-1, $ | (6) |
式中:a0=0.312 5, a1=0.468 75, a2=0.187 5, a3=0.031 25。窗函数的频谱函数为
| $ W(\omega)=\sum\limits_{m=0}^{3}(-1) m \frac{a_{m}}{2}\left[W_{R}\left(\omega-\frac{2 {\rm{ \mathsf{ π}}}}{N} m\right)+W_{R}\left(\omega+\frac{2 {\rm{ \mathsf{ π}}}}{N} m\right)\right], $ | (7) |
式中,
| $ W(k)=\sin (k {\rm{ \mathsf{ π}}}) e^{-j k {\rm{ \mathsf{ π}}}} e^{j k {\rm{ \mathsf{ π}}} / N} \sum\limits_{m=0}^{3}(-1) m \frac{a_{m}}{2} \cdot\left[\frac{\mathrm{e}^{-j {\rm{ \mathsf{ π}}} m / N}}{\sin \frac{\rm{ \mathsf{ π}}}{N}(k-m)}+\frac{e^{j {\rm{ \mathsf{ π}}} m / N}}{\sin \frac{\rm{ \mathsf{ π}}}{N}(k+m)}\right]。$ | (8) |
在实际电力谐波检测中,N一般较大,故根据式(8)将窗函数的幅值谱简化为
| $ W(k)=\frac{45 N \sin (k {\rm{ \mathsf{ π}}})}{4 k {\rm{ \mathsf{ π}}}\left(1-k^{2}\right)\left(4-k^{2}\right)\left(9-k^{2}\right)}。$ | (9) |
当对信号非同步采样或非整周期截断时,由于栅栏效应,实际的谐波频率f0=k0Δf很难恰好落在离散谱线的频点上,即k0不为整数。设全相位谱频点附近的最大离散谱线为第k条谱线,则定义δ= k0-k,-0.5≤δ≤0.5。根据式(5)和式(8)有
| $ \alpha = \frac{{\sqrt {\left| {{X_a}(k)} \right|} + \sqrt {\left| {{X_a}(k + 1)} \right|} }}{{\sqrt {\left| {{X_a}(k)} \right|} + \sqrt {\left| {{X_a}(k - 1)} \right|} }} = \frac{{|W( - \delta )| + |W(1 - \delta )|}}{{|W( - \delta )| + |W( - 1 - \delta )|}}。$ | (10) |
由式(9)得:α=(4+δ)/(4-δ),整理得:
| $ \delta = 4(\alpha - 1)/(\alpha + 1)。$ | (11) |
获得δ后即可对频率和幅值进行校正:
| $ {{f_0} = (k + \delta )\Delta f,} $ | (12) |
| $ {A = \frac{{\left| {{X_a}(k)} \right|}}{{|W( - \delta ){|^2}}}}。$ | (13) |
当谐波频率实际谱线的偏离量很小,即δ接近于0时,直接使用式(9)校正幅值,W(k)分子、分母都接近0,难以保证计算精度。故对W(k)分子项进行泰勒展开后得
| $ W(k) = \frac{{45N\left( {1 - \frac{{{{\rm{ \mathsf{ π} }}^2}{k^2}}}{{3!}} + \frac{{{{\rm{ \mathsf{ π} }}^4}{k^4}}}{{5!}} - \frac{{{{\rm{ \mathsf{ π} }}^6}{k^6}}}{{7!}} + \frac{{{{\rm{ \mathsf{ π} }}^8}{k^8}}}{{9!}}} \right)}}{{4\left( {1 - {k^2}} \right)\left( {4 - {k^2}} \right)\left( {9 - {k^2}} \right)}}。$ | (14) |
为保证计算精度,当δ接近0时使用式(14)进行幅值校正。
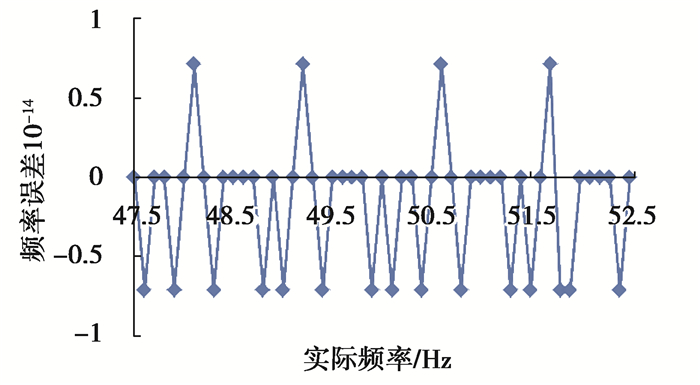
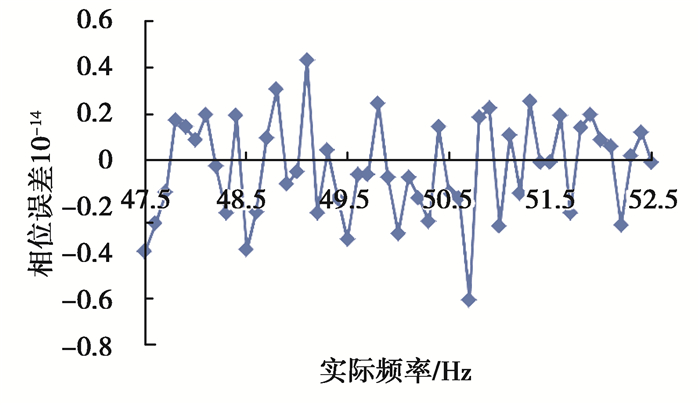
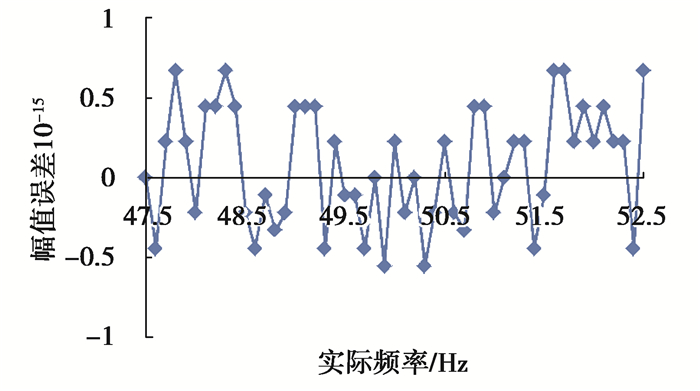
3 仿真验证 3.1 单频信号仿真设单频信号为x(n)=cos(2πf0n/fs),0≤n≤N-1,采样率fs为10 240 Hz,根据IEC谐波检测标准,使频率分辨率为5 Hz,故取N为2 048。为保证全相位谱分辨率,在实际电力谐波检测中,需要保存x(0)前的N-1个数据用于加权。仿真信号频率f0在47.5 Hz和52.5 Hz以0.1 Hz为步长均匀变化,即δ在-0.5到0.5之间以0.02为步长均匀变化。全相位加权卷积窗由式(6)生成的窗序列及其反转序列卷积得到。仿真得到的频率误差、相位误差、幅值误差分别如图 3~图 5所示。
|
图 3 频率测量误差 Fig. 3 Error of frequency |
|
图 4 相位测量误差 Fig. 4 Error of phase |
|
图 5 幅值测量误差 Fig. 5 Error of amplitude |
从图 3~图 5可看出,文中提出全相位谱线插值方法对单频谐波的频率检测误差小于10-14,相位检测误差小于0.6×10-14,幅值的检测误差维持在10-15以下,并且各个检测精度并不随着谐波频率而产生较大波动,可见文中提出的谐波检测方法具有较好的鲁棒性与稳定性。
3.2 复杂信号仿真复杂信号模型为
| $ x(n) = \sum\limits_{i = 1}^{19} {{A_i}} \cos \left( {2{\rm{ \mathsf{ π} }}i{f_1}n/{f_s} + {\theta _i}} \right), $ | (15) |
其中,基波频率f1为50.5 Hz,采样信息与单频信号仿真相同。谐波的幅值、相位参照文献[10]设计,具体参数见表 1。
| 表 1 仿真信号基波及谐波成分 Table 1 Components of the simulated harmonic signal |
通过表 2与表 3的对比可以看出,采用全相位谱线插值算法各谐波幅值的检测误差的数量级基本保持e×10-11~e×10-15之间,而相位的检测误差在e×10-9~e×10-13之间。三谱插值法的幅值与相位检测误差的数量级分别在e×10-6~e×10-9,e×10-3~e×10-8之间,全相位的幅值检测误差的数量级基本维持在e×10-4或e×10-5, 而其相位检测精度在e×10-4~e×10-7之间。可见,文中采用的方法因结合了三谱插值与全相位2种算法的优点,对谐波幅值与相位的检测精度都要远高于其他2种传统方法。文中提出的全相位谱线插值法通过选择旁瓣衰减大且衰减速度快的Nuttall窗和全相位2种方法抑制频谱泄漏,减小相邻谐波成分的相互干扰,因此得到的精度优于仅选择了一种频谱泄漏抑制方式的谱线插值法和全相位分析方法。
| 表 2 幅值相对误差对比 Table 2 Comparisons of relative errors of amplitudes |
| 表 3 相位与基频绝对误差对比 Table 3 Comparisons of absolute errors of phases |
文章提出了的基于全相位谱线插值的谐波检测方法,集合了全相位分析和谱线插值算法的优点。利用全相位分析旁瓣谱线相对于主谱线按平方项衰减的特点,并选择旁瓣衰减大且衰减速度快的Nuttall窗生成全相位卷积窗,极大程度地抑制了频谱泄漏,减小了相邻谐波成分频谱泄漏的相互干扰,提高了检测精度。仿真对比结果表明,全相位谱线插值法提高了谐波检测的精度。研究将为电力谐波的治理提供可靠的检测信息,在提高电能质量,保证充电系统、用电设备的安全稳定运行方面有较好的应用价值,且有利于提高智能巡检机器人和驱鸟机器人的工作寿命和巡检性能。
| [1] |
Maurya I, Gupta S K, Maurya P. An efficient harmonic detection approach for shunt active filter based on wavelet transform[J]. Ain Shams Engineering Journal, 2018, 9(4): 2833-2839. DOI:10.1016/j.asej.2018.01.003 |
| [2] |
Liu G, Chen B D, Wang K, et al. Selective current harmonic suppression for high-speed PMSM based on high-precision harmonic detection method[J]. IEEE Transactions on Industrial Informatics, 2019, 15(6): 3457-3468. DOI:10.1109/TII.2018.2873652 |
| [3] |
Gadanayak D A, Mallick R K. Interharmonics based high impedance fault detection in distribution systems using maximum overlap wavelet packet transform and a modified empirical mode decomposition[J]. International Journal of Electrical Power & Energy Systems, 2019, 112: 282-293. |
| [4] |
Lin H C. Intelligent neural network-based fast power system harmonic detection[J]. IEEE Transactions on Industrial Electronics, 2007, 54(1): 43-52. DOI:10.1109/TIE.2006.888685 |
| [5] |
Khodaparast J, Fossol O B, Molinas M, et al. EMD-prony for phasor estimation in harmonic and noisy condition[C]//2018 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), 20-22 June 2018, Amalfi, Italy, 2018: 1209-1214.
|
| [6] |
Wen H, Zhang J H, Meng Z, et al. Harmonic estimation using symmetrical interpolation FFT based on triangular self-convolution window[J]. IEEE Transactions on Industrial Informatics, 2015, 11(1): 16-26. DOI:10.1109/TII.2014.2362491 |
| [7] |
刘冬梅, 杨重良, 张艳, 等. 基于Nuttall自卷积窗四谱线插值FFT的电力谐波分析方法[J]. 合肥工业大学学报(自然科学版), 2018, 41(1): 12-17. Liu D M, Yang Z L, Zhang Y, et al. Harmonic analysis of power system based on Nuttall self-convolution window four-spectrum-line interpolation FFT[J]. Journal of Hefei University of technology, 2018, 41(1): 12-17. (in Chinese) |
| [8] |
牛胜锁, 梁志瑞, 张建华, 等. 基于三谱线插值FFT的电力谐波分析算法[J]. 中国电机工程学报, 2012, 32(16): 130-136. Niu S S, Liang Z R, Zhang J H, et al. An algorithm for electrical harmonic analysis based on triple-spectrum-line interpolation FFT[J]. Proceedings of the CSEE, 2012, 32(16): 130-136. (in Chinese) |
| [9] |
汪小平, 黄香梅. 基于全相位FFT时移相位差的电网间谐波检测[J]. 重庆大学学报(自然科学版), 2012, 35(3): 81-84. Wang X P, Huang X M. Measurement of interharmonics in power network based on all phase FFT time shifting and phase difference[J]. Journal of Chongqing University(Natural Science Edition), 2012, 35(3): 81-84. (in Chinese) |
| [10] |
卿柏元, 滕召胜, 高云鹏, 等. 基于Nuttall窗双谱线插值FFT的电力谐波分析方法[J]. 中国电机工程学报, 2008, 28(25): 153-158. Qing B Y, Teng Z S, Gao Y P, et al. An approach for electrical harmonic analysis based on Nuttall window double-spectrum-line interpolation FFT[J]. Proceedings of the CSEE, 2008, 28(25): 153-158. (in Chinese) |
 2021, Vol. 44
2021, Vol. 44


