图像复原问题中，给定观测图像Y由原始清晰图像X经过线性算子A和标准差为σ加性高斯白噪声N退化所生成，即

$ \mathit{\boldsymbol{Y}} = \mathit{\boldsymbol{AX}} + \mathit{\boldsymbol{N}}, $

(1)

为了恢复原始图像X，需要有关原始图像的先验知识。由于维度的原因，对整个图像的全局建模比较困难，因此近年来许多图像复原算法选择通过采用块(或局部)先验来解决建模问题。块尺寸较小更易于建模，流行的模型包括：稀疏模型^[1]，高斯混合模型(GMM, gaussian mixture model)^[2]，ICA^[3]等。尽管块先验对每个去噪块进行了很好的处理，但块的平均化操作破坏了这种行为，因为从聚合图像中提取的结果块可能不再符合局部先验。Zoran和Weiss等人提出的块对数似然期望(EPLL, expected patch log likelihood)算法^[4]改善了上述状况，他们的方案使用全局先验，在图像中去寻找每个选定的块都可能符合的局部先验，为了求解这一先验的最大后验估计(MAP, maximum a posteriori estimation)问题，迭代地对块进行去噪，随着迭代的进行，重叠的块越来越接近局部模型。EPLL最初利用GMM先验，后来扩展到基于稀疏性的块模型^[5]、专家场^[6]、分析稀疏模型^[7]等。这些模型实现通过局部相互作用来形成全局先验。利用块的自相似性块建模是另一种生成全局模型的方法^[8-9]，这一方法对即使相隔较远的相似块，仍能进行协同处理，从而实现非局部处理。但是上述这些方法也无法完全实现“全局化”处理，导致经常出现局部伪影的情况，以及复原图像质量过度平滑的问题。基于块的建模的另一缺点是整体模型的强制局部性，由于使用小的尺寸块，会无视图像中存在的更大范围的相互作用，图像块无论采用简单的平均，还是块之间信息的复杂融合，这个缺陷都是存在的。通过考虑多尺度处理有望缓解上述问题，该方法可以生成由局部所组成的全局图像先验，通过在各种尺度上使用局部模型，即可以保持低维模型的简单性，同时在图像中较大区域实施非局部性。

另一方面，在图像处理和计算机视觉领域中，图像像素或梯度域的直方图提供了图像全局统计信息的简单有效的方法，这种约束可以在数据点之间引入负相关。因此直方图对输出图像的全局统计提供约束，不仅仅在像素值域，也可以对图像的其他变换域(水平梯度、垂直梯度、Laplacian等)的直方图应用这一约束，例如，强度和颜色直方图可以得到图像对比度和色调变化，这些变化可作为图像增强^[10]和检索^[11]中的特征。诸如SIFT^[12]和HOG^[13]之类的图像特征描述子利用的是方向梯度直方图，带通滤波器响应直方图的匹配是纹理分析和合成方法的关键步骤^[14]，图像梯度和小波系数的直方图在零区域出现尖峰其他区域出现重尾特点，这激发了许多参数图像模型的研究，如高斯尺度混合模型^[15]和超拉普拉斯模型^[16]，这些模型已经为应用于各种图像复原任务。通过上述研究表明，图像复原任务可以从这种整体约束中受益，但是以数值稳定的方式将这些约束与现有的复原方法相结合仍然是一个具有挑战性的问题^[17]。

为了对局部块模型施加非局部性及全局统计约束，消除局部伪影，进一步改善图像复原质量，提出一种集成梯度直方图约束的多尺度块先验建模方法，主要如下：

1) 引入多尺度方法，对目标图像滤波及下采样以得到不同尺度的图像，再从中提取的相同大小的尺度块并施加局部低维先验，为了保持尺度不变性，通过在对原尺度图像下采样之前，应用高斯滤波；通过最小化滤波及下采样后图像的块经验分布与局部块模型分布间的KL散度，对滤波器进行参数调整，从而使各尺度块的局部模型可以保持不变，即单个局部模型可用于所有尺度；

2) 将梯度直方图全局统计先验引入到多尺度块先验建模中，以提升图像复原视觉质量。使用二次Wasserstein距离(W₂)来度量复原图像的梯度直方图和参考梯度直方图之间的统计距离，W₂距离可以直接从数据计算而不依赖于密度估计，提供平滑且可微分的形式来测量直方图之间的差异性，将差异约束项集成到多尺度块先验的图像复原框架中，利用半二次分裂和最优传输理论，通过坐标下降优化目标函数，算法具有有效的解析解和良好的收敛性；

3) 在参考直方图的估计方面，针对去噪和去模糊应用，基于广义高斯分布设计不同的参考梯度直方图的估计方法，以更好地适配不同的求解问题；

4) 在去噪及去模糊任务中应用所提出的模型，针对多种噪声标准差及多种模糊核进行实验，并与传统方法进行了对比分析，取得了更好视觉复原量，验证了所提出模型的有效性。

1 相关研究工作 1.1 期望块对数似然模型

图像复原问题中，给定退化图像Y，根据公式(1)，通过求解最大后验估计问题来恢复X。

$ \begin{array}{*{20}{c}} {\mathop {\max }\limits_\mathit{\boldsymbol{X}} p(\mathit{\boldsymbol{X}}\mid \mathit{\boldsymbol{Y}}) = \mathop {\max }\limits_\mathit{\boldsymbol{X}} p(\mathit{\boldsymbol{Y}}\mid \mathit{\boldsymbol{X}})p(\mathit{\boldsymbol{X}}) = }\\ {\mathop {\min }\limits_\mathit{\boldsymbol{X}} ( - \log p(\mathit{\boldsymbol{Y}}\mid \mathit{\boldsymbol{X}}) - p(\mathit{\boldsymbol{X}}))}。\end{array} $

(2)

为此，需要利用图像的全局先验p(X)，块对数似然期望(EPLL)就属于这类先验^[4]，它通过累加本地块对数似然来形成先验。

$ {\mathop{\rm EPLL}\nolimits} (\mathit{\boldsymbol{X}}) = \log p(\mathit{\boldsymbol{X}}) = \sum\limits_i {\log } p\left( {{P_i}\mathit{\boldsymbol{X}}} \right), $

(3)

其中：图像X表示为n×m的向量；P_i为抽取图像X第i个块(表示为s维的向量)的算子。通过将退化模型以及EPLL代于公式(2)中，得到

$ \mathop {\min }\limits_\mathit{\boldsymbol{X}} \frac{\lambda }{2}\left\| {\mathit{\boldsymbol{AX}} - \mathit{\boldsymbol{Y}}} \right\|_2^2 - \sum\limits_i {\log } p\left( {{P_i}\mathit{\boldsymbol{X}}} \right), $

(4)

其中，λ为参数，以平衡保真项和先验项。通过引入辅助变量z _i，借助半二次分裂^[18]来求解这一问题，这简化了优化过程。问题转换为

$ \mathop {\min }\limits_{X,{{\left\{ {{\mathit{\boldsymbol{z}}_i}} \right\}}_i}} \frac{\lambda }{2}\left\| {\mathit{\boldsymbol{AX}} - \mathit{\boldsymbol{Y}}} \right\|_2^2 + \sum\limits_i {\left( {\frac{\beta }{2}\left\| {{P_i}\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{z}}_i}} \right\|_2^2 - \log p\left( {{\mathit{\boldsymbol{z}}_i}} \right)} \right)} , $

(5)

当β→∞，可以得到P_i X = z _i，这样式(5)的解可以收敛到式(4)的解。在实践中，通过对不断增大的β集合进行来迭代求解式(5)。对于每个固定β，使用块坐标下降来降低目标值。

首先，通过固定X，求解关于z _i最小化式(5)，通过局部MAP问题来更新z _i：

$ \mathop {\min }\limits_{{\mathit{\boldsymbol{z}}_i}} \frac{\beta }{2}\left\| {{P_i}\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{z}}_i}} \right\|_2^2 - \log p\left( {{\mathit{\boldsymbol{z}}_i}} \right)。$

(6)

然后，固定z _i，求解关于X最小化式(5)。X通过最小二次问题来求解，可以得到闭式解

$ \boldsymbol{X}=\left(\lambda \boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}+\beta \sum\limits_{i} \boldsymbol{P}_{i}^{\mathrm{T}} \boldsymbol{P}_{i}\right)^{-1}\left(\lambda \boldsymbol{A}^{\mathrm{T}} \boldsymbol{Y}+\beta \sum\limits_{i} \boldsymbol{P}_{i}^{\mathrm{T}} \boldsymbol{z}_{i}\right)=\frac{\boldsymbol{Y}+\beta\left(\sum\limits_{i} \boldsymbol{P}_{i}^{\mathrm{T}} \boldsymbol{P}_{i}\right)^{-1} \sum\limits_{i} \boldsymbol{P}_{i}^{\mathrm{T}} \boldsymbol{z}_{i}}{1+\beta}, $

(7)

其中：P_i^T z_i表示P_i的伴随变换：它创建一个图像，其中块z _i放在其适当的位置，而图像的其余部分设置为零。矩阵$\sum\limits_i {\mathit{\boldsymbol{P}}_i^{\rm{T}}{P_i}} $是大小为nm×nm的对角矩阵，对角线中的每个元素都与一个像素相关联，并且等于包含它的块的数量。

公式(5)一次迭代只执行一次更新。初始时，将X初始化为Y，固定X寻找所有z _i；然后再更新一次X，这一过程是对Y中的退化块进行去噪；最后结合退化算子A的逆对所有块进行平均操作。在基于稀疏的模型中，K-SVD去噪算法^[19]也是采用这种方法来执行迭代，以得到更好的去噪性能。EPLL的关键问题是β的选择问题，以及迭代过程中如何增长，来保证得到不断改进的性能。文献[4]选择简单的固定值的β的设置方法，而文献[5]是通过临时图像X估计得到。

在文献[4]中与EPLL一起使用的局部先验是高斯混合模型，定义为

$ p\left( {{\mathit{\boldsymbol{z}}_i}} \right) = \sum\limits_{k = 1}^K {{{\rm{ \mathsf{ π} }}_k}} N\left( {\left. {{\mathit{\boldsymbol{z}}_i}} \right|0,\sum\nolimits_k {} } \right), $

(8)

其中，第k个高斯分量的协方差和权值分别表示为∑_k和π_k。所有分量的均值设置为0。因为在这一先验下，式(6)中MAP问题并没有闭式解，需要一种在给定X下近似的更新z _i的方法。

首先，选择最有可能被选中的高斯分量。

$ \begin{array}{l} \mathop {\max }\limits_k p\left( {k\mid {\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{X}}} \right) = \mathop {\max }\limits_k p\left( {{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{X}}\mid k} \right)p(k) = \mathop {\min }\limits_k \left( { - \log p\left( {{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{X}}\mid k} \right) - \log p(k)} \right)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \mathop {\min }\limits_k \frac{1}{2}\log \left( {\left| {\sum\nolimits_k {} + \frac{1}{\beta }I} \right|} \right) + \frac{1}{2}{\left( {{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{X}}} \right)^{\rm{T}}}{\left( {\sum\nolimits_k {} + \frac{1}{\beta }I} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{X}}} \right) - \log \left( {{{\rm{ \mathsf{ π} }}_k}} \right), \end{array} $

(9)

然后，利用计算的最优分量$\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over k} $，块复原通过经典的维纳滤波进行即可。

$ {\mathit{\boldsymbol{z}}_i} = \sum\nolimits_{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over k} } {{{\left( {\sum\nolimits_{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over k} } {} + \frac{1}{\beta }I} \right)}^{ - 1}}} {\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{X}}。$

(10)

1.2 多尺度块模型

基于块的图像复原建模是在整体模型上强制局部性，由于使用小尺寸的块，无法考虑图像中存在于较大范围内的相互作用，通过多尺度处理可以缓解这一问题。多尺度块处理与使用多尺度字典学习来去噪的方法相似，Sulam等人通过将图像分解成不同的小波频带来对图像进行去噪，通过基于块的K-SVD独立地对每个波段进行去噪，并应用逆小波变换来获得最终的重建图像^[20]。该方法的困难是图像的高频带将被去噪，而这种频率是具有低信噪比的。因此，通过考虑低频带可以避免了这种问题，因为低频带具有高信噪比，而且随着分辨率的降低，信噪比实际上会上升。Papyan等人应用多个尺度，对原始信号施加低通滤波器，再进行下采样，得到所有的尺度图像，通过一个所有尺度的所有块都必须遵守的惩罚函数，可以融合所有波段^[21]。在不同尺度图像上提取块上施加局部低维先验，通过假设尺度不变性，使尺度块的模型保持不变，即单个模型可用于所有尺度。尽管所有处理过的尺度块都具有相同的尺寸，但是由于下采样，它们在原始目标图像中的占用面积会有所不同。例如尺度为2的情况下，从粗糙图像中抽取的尺度块事实上是2倍于原始图像网格的，通过将这些块约束为遵循局部模型，约束原始图像中2倍于原始图像块的低频信息。

不失一般性，只考虑2个尺度，但这一思路可以推广到尺度金字塔。多尺度的期望块对数似然先验定义为

$ \operatorname{MSEPLL}(\boldsymbol{X})=w_{1} \sum\limits_{i} \log p\left(\boldsymbol{P}_{i} \boldsymbol{X}\right)+w_{2} \sum\limits_{i} \log p\left(\widetilde{\boldsymbol{P}}_{i} \boldsymbol{S} \boldsymbol{X}\right), $

(11)

其中：算子S = DH，H是低通滤波器，D是下采样算子，$\mathit{\boldsymbol{\tilde P}}$算子从退化的信息SX抽取第i个块。权值w_i表示不同尺度的重要性。假定具有尺度不变性，这样通常在滤波和下采样之后获得的块具有相同的局部模型，其先验分布表示为p，当然这需要通过对滤波器的参数进行调整，以使得尺度不变性成立，在后面将给出参数调整方法。

不同尺度的信号是通过对原始信号滤波及采样得到，在所有尺度下提取的块具有相同的大小，无论其原始尺度如何，在所有这些块上强加本地块模型。处理仍然是局部的，但随着尺度的提升，单个块在原始信号上的足迹会越来越宽。这一思路可以很容易地推广到多个滤波器和下采样因子的应用中。

1.3 梯度直方图先验及Wasserstein距离 1.3.1 梯度直方图先验

梯度直方图先验最早应用于纹理合成领域，例如通过小波子带直方图与期望纹理间进行匹配来合理纹理，通过匹配纹理元素的直方图进行非均匀纹理合成等。在图像复原领域，Li等人提出一种两阶段图像复原算法^[22]，该算法首先使用基于样例技术重建图像，然后将重建图像的梯度分布适配为参考梯度分布。Woodford等人^[23]使用称为边缘概率场的MAP估计框架，利用低级特征(例如梯度)的直方图来求解去噪等视觉问题，其使用全局惩罚项来拟合全局分布，边缘概率场要求每个箱体特征形成离散直方图，利用从图像数据库估计出的图像先验，并在重建具有不同纹理的图像使用相同的全局先验。Schmidt等人^[24]通过采样比较梯度分布，这在计算上是非常耗时的，其在使用不同纹理重建图像还使用单个全局先验，这会在平滑区域中产生伪影。Hacohen等人将纹理合成与图像复原相结合^[25]，特别是用于图像上采样问题。为了恢复纹理，它们对退化图像进行分割，并用图像数据库中的纹理替换每个纹理段。Cho等人^[26]提出在反卷积过程中保留重尾边缘梯度分布，增强了复原图像中的视觉细节。然而，他们的方法最小化输出图像梯度和参考分布之间的KL散度，这需要参数密度拟合和复杂的调整权重优化方案。Zuo等人^[27]提出了一种纹理增强去噪方法，该方法将非局部基于块的图像模型与启发式梯度惩罚项相结合。Song等人^[28]提出一种利用超拉普拉斯分布估计梯度直方图，通过梯度直方图保持进行图像去模糊。

综上，将梯度直方图先验这个全局统计信息约束集成到图像复原框架中，有助于提升视觉观感，是很有应用前景的技术。

1.3.2 Wasserstein距离

Wasserstein距离在图像处理领域也被称为“推土机距离”，相比KL散度，Wasserstein距离在比较图像直方图分布方面更有优势：即使2个分布的支撑集没有重叠或者重叠比较少，仍然能够反映2个分布的远近，而此时KL散度可能无意义。

给出2个概率测度p和q，其二次Wasserstein(W₂)距离被定义为以下Monge问题的变分解^[29]：

$ W_2^2(p,q) = \mathop {in{\kern 1pt} f}\limits_\phi \int_{ - \infty }^\infty {{{(x - \phi (x))}^2}} p(x){\rm{d}}x, $

(12)

其中：下确界是针对所有确定函数ϕ: R↦R，ϕ是将分布p的任意随机变量x转移到分布q的新的随机变量ϕ(x)；W₂距离可以看作是由2个给定分布之间的任何映射函数引起的最小l₂干扰。与KL散度不同，W₂距离是概率分布的真正度量，当且仅当p和q相等时，距离为0。

对于给定概率分布p，定义其累积分布函数为${\mathit{\boldsymbol{F}}_p}\left( x \right) = \int_{ - \infty }^x {p\left( \tau \right)} {\rm{d}}\tau $，其百分位函数(也称为F_p(x)的伪逆)为F_p^-1(x)=inf(x: F_p(x)>t}。根据最优传递理论，最小化公式(12)得到最优ϕ的过程具有闭式解^[29]

$ {\phi _{p \to q}}(x) = \mathit{\boldsymbol{F}}_q^{ - 1}\left( {{\mathit{\boldsymbol{F}}_p}(x)} \right), $

(13)

在框架中，需要测量图像X (nm个像素)的直方图h_x与和给定直方图h_q之间的统计距离。大多数直方图距离(卡方、KL散度等)直接比较2个直方图向量。然而从X中提取h_x的过程是对x的不可微分的操作，这妨碍了在图像复原中的应用。相反使用W₂距离的等价定义，将X =(x₁, …, x_nm)^T视为从分布p中抽取的nm个独立样本，并将h_q视为另一个分布q的离散近似。基于公式(12)，引入经验度量${\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over W} _2}$。

$ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over W} _2^2(p,q) = \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over W} _2^2\left( {{h_x},{h_q}} \right) = \mathop {\min }\limits_\phi \frac{1}{{nm}}\sum\limits_{i = 1}^{nm} {{{\left( {{x_i} - {\xi _i}} \right)}^2}} , $

(14)

其中函数ϕ将x_i映射为ξ_i=ϕ(x_i)，这使得变换后的样本ξ=(ξ₁, …, ξ_n)满足直方图分布h_q。类似于连续情形，式(14)的最优$\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \phi } $为^[29]

$ {\xi _i} = {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \phi } }_{{h_x} \to {h_q}}}\left( {{x_i}} \right) = \mathit{\boldsymbol{F}}_{{h_q}}^{ - 1}\left( {{\mathit{\boldsymbol{F}}_{{h_x}}}\left( {{x_i}} \right)} \right), $

(15)

其中：F^-1_hq和F_hx是h_q的百分位函数和h_x的累积分布函数。从公式(15)可以看出对于图像X，$\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \phi } $实际上对应着“直方图匹配”操作，可以用于改进图像对比度。经验${\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over W} _2}$度量重要的特点在于可以通过二次形式计算。另一方面，对于如KL散度这类度量，2个直方图直接比较是X上的非平滑操作，这样与现有的复原算法集成就比较困难。

2 梯度直方图先验约束的多尺度块模型

为了对局部块模型施加非局部性及全局统计约束，进一步提升图像复原性能，提出将多尺度建模与梯度直方图先验结合，在高斯混合模型的局部块先验模型基础上，加入梯度直方图全局统计约束，并结合多尺度块建模，在图像较大区域实施非局部性。所提出模型的目标函数如下

$ \mathop {\min }\limits_\mathit{\boldsymbol{X}} \frac{\lambda }{2}\left\| {\mathit{\boldsymbol{AX}} - \mathit{\boldsymbol{Y}}} \right\|_2^2 - {w_1}\sum\limits_i {\log } p\left( {{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{X}}} \right) - {w_2}\sum\limits_i {\log } p\left( {{{\mathit{\boldsymbol{\tilde P}}}_i}\mathit{\boldsymbol{SX}}} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {h_{TX}} = {h_R}, $

(16)

其中：第一项为数据保真项，表示观测Y与AX的l₂范数，正则项是前述的多尺度的期望块对数似然模型，参数λ用于权衡2个项。约束条件为梯度直方图先验，h_R是参考梯度直方图，矩阵T表示相应的线性变换，h_TX为在线性变换域(例如水平梯度、垂直梯度等)中X的直方图。这里假定不同尺度的图像具有尺度不变性，即所有尺度下局部模型是相等的，在对原始尺度下采样操作之前应用滤波器，并且可以通过调整滤波器参数实现尺度不变性。通过求解公式(16)的约束最小化问题，可以用于大部分复原任务，包括：去噪、去模糊、超分辨等。

使用${\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over W} _2}$度量和惩罚函数方法，将公式(16)转换成下列无约束的最小化问题

$ \mathop {\min }\limits_\mathit{\boldsymbol{X}} \frac{\lambda }{2}\left\| {\mathit{\boldsymbol{Y}} - \mathit{\boldsymbol{AX}}} \right\|_2^2 - {w_1}\sum\limits_i {\log } p\left( {{\mathit{\boldsymbol{P}}_i}\mathit{\boldsymbol{X}}} \right) - {w_2}\sum\limits_i {\log } p\left( {{{\mathit{\boldsymbol{\tilde P}}}_i}\mathit{\boldsymbol{SX}}} \right) + \frac{{{\beta _h}}}{2}\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over W} _2^2\left( {{h_{TX}},{h_R}} \right)。$

(17)

随着惩罚权值β_h→∞，公式(17)的局部最优解会成为公式(22)的局部最优解。

根据公式(15)的定义，引入辅助向量ξ，其维度与TX一致，优化下面的目标函数：

$ \min \limits_{X, \xi} \frac{\lambda}{2}\|\boldsymbol{A} \boldsymbol{X}-\boldsymbol{Y}\|_{2}^{2}-w_{1} \sum\limits_{i} \log p\left(\boldsymbol{P}_{i} \boldsymbol{X}\right)-w_{2} \sum\limits_{i} \log p\left(\boldsymbol{P}_{i} \boldsymbol{X}\right)+\frac{\beta_{h}}{2}\|\boldsymbol{\xi}-\boldsymbol{T} \boldsymbol{X}\|_{2}^{2} \ s . t .\ h_{\xi}=h_{R}。$

(18)

式(18)是所提出模型最终目标函数形式，可以利用坐标下降方法，关于ξ和X来交替最小化式(18)。这个算法能够收敛到局部最小解。首先，固定X，最小化ξ则简化为

$ \min \limits_{\xi} \frac{\beta_{h}}{2}\|\xi-\boldsymbol{T} \boldsymbol{X}\|_{2}^{2} \quad \text { s.t. }\ h_{\xi}=h_{R}。$

(19)

利用公式(15)的结论，最优ξ可以通过类似直方图匹配操作给出

$ {\mathit{\boldsymbol{\xi }}_i} = {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \phi } _{{h_{TX}} \to {h_r}}}\left( {{{(\mathit{\boldsymbol{TX}})}_i}} \right)。$

(20)

然后，固定ξ，关于X的问题是关于2个二次项和2个正则项的优化问题。

$ \min \limits_{\boldsymbol{X}} \frac{\lambda}{2}\|\boldsymbol{Y}-\boldsymbol{A} \boldsymbol{X}\|_{2}^{2}-w_{1} \sum\limits_{i} \log p\left(\boldsymbol{P}_{i} \boldsymbol{X}\right)-w_{2} \sum\limits_{i} \log p\left(\boldsymbol{P}_{i} \boldsymbol{X}\right)+\frac{\beta_{h}}{2}\|\boldsymbol{\xi}-\boldsymbol{T} \boldsymbol{X}\|_{2}^{2}, $

(21)

为了优化式(21)，采用与公式(5)类似的方法，通过引入辅助变量z _i和${\tilde z_i}$，借助半二次分裂^[18]来求解这一问题。z _i和${\tilde z_i}$分别对应原始尺度图像抽取的块和额外尺度抽取的块，得到以下目标函数

$ \begin{array}{c} \min \limits_{X,\left\langle \boldsymbol{z}_{i}\right\},\left\{\tilde{\boldsymbol{z}}_{i}\right\}} \frac{\lambda}{2}\|\boldsymbol{Y}-\boldsymbol{A} \boldsymbol{X}\|_{2}^{2}+w_{1} \sum\limits_{i}\left\{\frac{\beta}{2}\left\|\boldsymbol{P}_{i} \boldsymbol{X}-\boldsymbol{z}_{i}\right\|_{2}^{2}-\log p\left(\boldsymbol{z}_{i}\right)\right\}+ \\ w_{2} \sum\limits_{i}\left\{\frac{2}{}\left\|\widetilde{\boldsymbol{P}}_{i} \boldsymbol{S} \boldsymbol{X}-\tilde{\boldsymbol{z}}_{i}\right\|_{2}^{2}-\log p\left(\tilde{\boldsymbol{z}}_{i}\right)\right\}+\frac{\beta_{h}}{2}\|\boldsymbol{\xi}-\boldsymbol{T} \boldsymbol{X}\|_{2}^{2}。\end{array} $

(22)

随着β→∞和$\tilde \beta \to \infty $，公式(22)将收敛到公式(21)解。这样就得到一个重构的图像，图中每个抽取的块都来自局部模型，额外尺度下采样版本的图像中每个抽取的块也来自于同一局部模型。

下面探讨β与$\tilde \beta $的关系。假定X是原始图像，$\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} }}$表示经过若干次迭代之后重建的图像表示，参考文献[4]的做法，假设$\left( {\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} }} - \mathit{\boldsymbol{X}}} \right){\left( {\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} }} - \mathit{\boldsymbol{X}}} \right)^{\rm{T}}}$的期望等于$\frac{1}{\beta }I$，其中I为单位矩阵，这种已经在原始EPLL工作证明该假设是合理的，可以把参数$\frac{1}{\beta }$看作是对求解图像当前噪声水平的估计。类似地，¹是额外尺度图像的噪声水平的近似值，这样有

$ \frac{1}{{\tilde \beta }} = \frac{1}{s}\left\| {{{\mathit{\boldsymbol{\tilde P}}}_i}\mathit{\boldsymbol{S\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} }} - {{\mathit{\boldsymbol{\tilde P}}}_i}\mathit{\boldsymbol{SX}}} \right\|。$

(23)

表达式除以s(块中像素的数目)是为了归一化，这样得到了一个逐个像素的度量。这个表达式可以进一步简化为

$ \begin{array}{*{20}{c}} {\frac{1}{{\tilde \beta }} = \frac{1}{s}{{\left( {{{\mathit{\boldsymbol{\tilde P}}}_i}\mathit{\boldsymbol{S\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} }} - {{\mathit{\boldsymbol{\tilde P}}}_i}\mathit{\boldsymbol{SX}}} \right)}^{\rm{T}}}\left( {{{\mathit{\boldsymbol{\tilde P}}}_i}\mathit{\boldsymbol{S\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} }} - {{\mathit{\boldsymbol{\tilde P}}}_i}\mathit{\boldsymbol{SX}}} \right) = \frac{1}{s}tr\left( {{{\left( {{{\mathit{\boldsymbol{\tilde P}}}_i}\mathit{\boldsymbol{S\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} }} - {{\mathit{\boldsymbol{\tilde P}}}_i}\mathit{\boldsymbol{SX}}} \right)}^{\rm{T}}}\left( {{{\mathit{\boldsymbol{\tilde P}}}_i}\mathit{\boldsymbol{S\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} }} - {{\mathit{\boldsymbol{\tilde P}}}_i}\mathit{\boldsymbol{SX}}} \right)} \right)}\\ { = \frac{1}{s}tr\left( {(\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} }} - \mathit{\boldsymbol{X}}){{(\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} }} - \mathit{\boldsymbol{X}})}^{\rm{T}}}{{\left( {{{\mathit{\boldsymbol{\tilde P}}}_i}\mathit{\boldsymbol{S}}} \right)}^{\rm{T}}}{\rm{ }}{{\mathit{\boldsymbol{\tilde P}}}_i}\mathit{\boldsymbol{S}}} \right) = \frac{1}{\beta }tr\left( {{{\mathit{\boldsymbol{\tilde P}}}_i}\mathit{\boldsymbol{S}}{\mathit{\boldsymbol{S}}^{\rm{T}}}{\rm{ }}\mathit{\boldsymbol{\tilde P}}_i^{\rm{T}}} \right) = \frac{1}{\beta }tr\left( {{{\mathit{\boldsymbol{\tilde P}}}_i}\mathit{\boldsymbol{DH}}{\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{D}}^{\rm{T}}}{\rm{ }}\mathit{\boldsymbol{\tilde P}}_i^{\rm{T}}} \right)}。\end{array} $

(24)

矩阵${\mathit{\boldsymbol{\tilde P}}_i}\mathit{\boldsymbol{DH}}{\mathit{\boldsymbol{H}}^{\rm{T}}}{\mathit{\boldsymbol{D}}^{\rm{T}}}{\mathit{\boldsymbol{\tilde P}}_i}^{\rm{T}}$是s×s矩阵，对角线元素等于滤波器H的Frobenius范数。因此有

$ \widetilde{\beta}=\beta /\|\boldsymbol{H}\|_{F}^{2}, $

(25)

尽管引入额外的参数$\tilde \beta $，上述分析表明这项参数可以合并调整为一项即可。

对于式(22)，同样可以使用块坐标下降来优化目标。首先，假设重建的图像X是固定的，更新辅助变量z _i和${\tilde z_i}$；之后假定辅助块是固定的，并使用它们来更新重建图像。

#38;为了计算z _i，这是在原始尺度上求解图像块的MAP问题

$ \min \limits_{\left\{\boldsymbol{z}_{i}\right\rangle} \frac{\beta}{2}\left\|\boldsymbol{P}_{i} \boldsymbol{X}-\boldsymbol{z}_{i}\right\|_{2}^{2}-\log p\left(\boldsymbol{z}_{i}\right), $

(26)

更新${\tilde z_i}$是求解另一个MAP问题，此时块是从滤波下采样图像上抽取

$ \min \limits_{\left\{\widetilde{\boldsymbol{z}}_{i}\right\}} \stackrel{2}{\|} \widetilde{\boldsymbol{P}}_{i} \boldsymbol{S} \boldsymbol{X}-\widetilde{\boldsymbol{z}}_{i} \|_{2}^{2}-\log p\left(\widetilde{\boldsymbol{z}}_{i}\right)。$

(27)

2个尺度下的局部先验都是公式(8)定义高斯混合模型。在这一先验下，求解局部MAP问题利用式(9)、(10)求解即可。

在给定z _i和${\tilde z_i}$，X的更新是通过求解二次问题得到。

$ \begin{aligned} X=&\left(\lambda \boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}+w_{1} \beta \sum\limits_{i} {\boldsymbol{P}_{i}}^{\mathrm{T}} \boldsymbol{P}_{i}+w_{2} \widetilde{\beta} \sum\limits_{i} \boldsymbol{S}^{\mathrm{T}} {\widetilde{\boldsymbol{P}}_{i}}^{\mathrm{T}} \boldsymbol{P}_{i} \boldsymbol{S}+\beta_{h} \boldsymbol{T}^{\mathrm{T}} \boldsymbol{T}\right)^{-1} \\ &\left(\lambda \boldsymbol{A}^{\mathrm{T}} \boldsymbol{Y}+w_{1} \beta \sum\limits_{i} {\boldsymbol{P}_{i}}^{\mathrm{T}} \boldsymbol{z}_{i}+w_{2} \widetilde{\beta} \sum\limits_{i} \boldsymbol{S}^{\mathrm{T}} {\widetilde{\boldsymbol{P}}_{i}}^{\mathrm{T}} \widetilde{\boldsymbol{z}}_{i}+\beta_{h} \boldsymbol{T}^{\mathrm{T}} \boldsymbol{\xi}\right)。\end{aligned} $

(28)

综上，提出的框架通过迭代地执行2个主要步骤，直到收敛：通过公式(20)更新ξ；然后通过公式(28)更新X；惩罚权值β和β_h随着迭代计算过程变化而增加。具体的图像复原算法见算法1。

        Algorithm 1：图像复原算法

        Input: 退化图像Y，尺度滤波器H，下采样算子 D，退化算子A

        Output: X

        X ← Y；

        repeat

            根据公式(20)求解ξ；

            repeat

            $\tilde \beta = \beta /\parallel H\parallel _F^2$，

            根据公式(26)(27)求解z _i和${\tilde z_i}$；

            根据公式(28)求解X;

            β←2β;

            until β>β_max

            β_h←2β_h;

        until β_h>β_{h_max}

        return X;

3 尺度不变性和参考直方图估计 3.1 尺度不变性

当处理不同尺度的图像时，期望其保持尺度不变性，即：所有尺度的所有局部模型都是相等的，不需要分别为每个尺度单独训练模型。通过滤波器的调整，可以将相同的先验模型应用于所有尺度建模。给定滤波器H和下采样模式D，从图像X中提取额外尺度图像的块${\mathit{\boldsymbol{\tilde P}}_i}\mathit{\boldsymbol{DHX}}$，下面估计这些块定义的经验分布与局部块先验分布p(z)之间的相似性。首先计算每个块在K个高斯中的概率，给出第i个块的隶属于第k个高斯分量的概率V_{i, k}

$ \boldsymbol{V}_{i, k}=\frac{{\rm{ \mathsf{ π}}}_{k} N\left(\widetilde{\boldsymbol{P}}_{i} \boldsymbol{D} \boldsymbol{H} \boldsymbol{X} \mid 0, \sum_{k}\right)}{\sum\limits_{j=1}^{K} {\rm{ \mathsf{ π}}}_{j} N\left(\widetilde{\boldsymbol{P}}_{i} \boldsymbol{D} \boldsymbol{H} \boldsymbol{X} \mid 0, \sum_{j}\right)}。$

(29)

然后，计算经验高斯混合模型

$ \tilde{p}(z)=\sum\limits_{k=1}^{K} \tilde{\pi}_{k} N\left(z \mid 0, \widetilde{\sum}_{k}\right), $

(30)

其中，不同高斯的经验协方差和权值分别定义为

$ {\widetilde{\sum}_{k}}=\frac{\sum_{i} v_{i, k}\left(\widetilde{\boldsymbol{P}}_{i} \boldsymbol{D} \boldsymbol{H} \boldsymbol{X}\right)\left(\widetilde{\boldsymbol{P}}_{i} \boldsymbol{D} \boldsymbol{H} \boldsymbol{X}\right)^{\mathrm{T}}}{\sum_{i} v_{i, k}}, $

(31)

$ \widetilde{\rm{ \mathsf{ π}}}_{k}=\frac{\sum_{i} v_{i, k}}{\sum_{k} \sum_{j} v_{j, k}}, $

(32)

在给定上述经验分布${\tilde p_z}$后，目标是通过使用KL散度来计算其与局部块先验分布p(z)的相似性。由于GMM之间的KL差异不易进行分析，因此并不是计算精确的KL，而是计算下列形式的上限

$ D_{K L}(\tilde{p} \| p) \leqslant D_{K L}(\tilde{\rm{ \mathsf{ π}}} \| {\rm{ \mathsf{ π}}})+\sum\limits_{k=1}^{K} \widetilde{{\rm{ \mathsf{ π}}}}_{k} D_{K L}\left(N\left(0, \sum_{k}\right) \| N\left(0, \sum_{k}\right)\right), $

(33)

高斯间的KL散度具有闭式解，因此式(33)可以简化为

$ D_{K L}(\tilde{p} \| p) \leqslant \sum\limits_{k=1}^{K} \tilde{\rm{ \mathsf{ π}}}_{k}\left(\log \left(\frac{\tilde{\rm{ \mathsf{ π}}}_{k}}{{\rm{ \mathsf{ π}}}_{k}}\right)+\frac{1}{2}\left(\operatorname{tr}\left(\sum_{k}^{-1} \widetilde{\sum}_{k}\right)-\log \frac{\left|\widetilde{\sum}_{k}\right|}{\left|\sum_{k}^{-1}\right|}\right)\right)。$

(34)

可以利用式(34)的上界来对滤波器H进行调优，以得到尺度不变性。在实验中，设置H是一个居中和各向同性的高斯，并搜索其最佳宽度，以寻找最小近似KL的参数。

3.2 参考直方图估计

为了对模型进行求解，需要知道参考直方图h_R，它是对原始图像X的梯度直方图的估计。参考直方图的生成方法可能会因不同的应用而异，常用的直方图生成的方法如下：

1) 使用外部源指定直方图。Woodfood等人提出用自然图像构建直方图数据库，并使用最接近的匹配直方图用于图像去噪^[26]。

2) 通过用户交互和参数模型指定直方图。众所周知，自然图像的边缘梯度直方图遵循超拉普拉斯模型。通过调整模型的参数，可以很好地估计原始直方图。

3) 对于某些特定的问题，可以直接从退化图像中估计边缘直方图。对于由小的高斯噪声污染的图像，梯度直方图可以通过一维去卷积过程粗略的估计。

针对去噪和去模糊2个不同实验应用场景，设计了不同的参考梯度直方图生成方法。在去噪应用中，假定梯度图像▽X中所有像素是独立同分布的，可以将其视作标量变量的样本，表示为x。这样▽ X的归一化直方图可以看作是x的概率密度函数的离散近似。对于加性高斯白噪声N，可以将其元素建模为一个独立同分布变量n的样本。因为有n~N(0, σ²)，令v=▽n，可以知道v也是独立同分布的高斯分布，其概率密度函数为

$ p_{v}=\frac{1}{2 \sqrt{\pi} \sigma} \exp \left(-\frac{v^{2}}{4 \sigma^{2}}\right)。$

(35)

因为有Y = X + N，因此有：▽ Y =▽ X +▽ N，对▽Y建模为独立同分布的变量y，有y=x+v。令p_x是x的概率密度分布，p_y是y的概率密度分布。因为x和v是独立的，联合概率密度分布p(x, v)为

$ p(x, v)=p_{x} \times p_{v}, $

(36)

因此，p_y的概率密度分布为

$ p_{y}(y=m)=\int_{t} p_{x}(x=t) \times p_{v}(v=(m-t)) \mathrm{d} t。$

(37)

如果使用归一化直方图h_x和h_y来近似p_x和p_y时，可以在离散域中重写公式(37)为

$ h_{y}=h_{x} \otimes h_{v}, $

(38)

其中，⊗表示卷积算子。注意h_v可以通过对p_v离散化而得到。h_y可以直接对噪声观测y计算出来。因此，h_x的估计可以通过建模为一个去卷积的问题

$ h_{R}=\operatorname{argmin}_{h_{x}}\left\{\left\|h_{y}-h_{x} \otimes h_{v}\right\|^{2}+\psi R\left(h_{x}\right)\right\}, $

(39)

其中ψ是一个常量，R(h_x)是自然图像梯度直方图的先验信息。考虑到h_x是p_x的离散版本，而p_x可以建模为一个广义高斯分布。使用广义高斯分布模型对p_x建模，并将其离散化为h_x。

$ p_{x}=\frac{\kappa \ \tau^{1 / \kappa}}{2 \varGamma(1 / \kappa)} \exp \left(-\tau|x|^{\kappa}\right)。$

(40)

对于p_x的估计可以转换为参数τ和κ的估计。考虑自然图像的事实，τ和κ具有相对窄的范围，可以给出这两个参数的范围，来寻找一个参数对使得$\parallel {h_y} - {h_x} \otimes {h_v}{\parallel ^2}$最小。

在去模糊应用中，由于原始图像受到模糊核和噪声污染，梯度直方图的估计更为困难。考虑到图像纹理的分形特性和表面的分段平滑特性，许多纹理是尺度不变的，梯度曲线在尺度上大致相等。因此考虑先进行基本的去卷积操作，然后进行下采样。下采样的图像被用来估计梯度直方图，利用下采样图像梯度分布尺度相对不变的特性，同时在下采样期间也降低了由反卷积引入噪声的影响。这种方法在大部分应用场景下是有效的。

当对退化图像进行去模糊时，使用如下的MAP估计器。

$ \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} }} = \mathop {{\mathop{\rm argmin}\nolimits} }\limits_\mathit{\boldsymbol{X}} \frac{1}{2}\lambda \left\| {\mathit{\boldsymbol{K}} \otimes \mathit{\boldsymbol{X}} - \mathit{\boldsymbol{Y}}} \right\|_2^2 - \tilde \omega \ln {p_x}(\nabla \mathit{\boldsymbol{X}}), $

(41)

其中：K为已知模糊核，p_x的定义如式(40)，设置初始的图像先验参数为[$\bar \omega = 0.1, \kappa = 0.8, \tau = 4$]。求解出粗糙的去卷积结果$\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} }}$'后，再对其下采样得到$\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} }}$。利用$\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} }}$'去拟合其梯度为一个广义高斯分布。

$ \mathop {{\mathop{\rm argmin}\nolimits} }\limits_{\mathit{\boldsymbol{\tau }},\kappa } \left\{ { - \sum\nolimits_i {\ln p} \left( {\nabla {\mathit{\boldsymbol{X}}^\prime }_i;\mathit{\boldsymbol{\tau }},\kappa } \right)} \right\}。$

(42)

利用拟合后的广义高斯分布，离散化后得到参考直方图h_R。虽然通过下采样可能会丢失细节，但根据实验结果来看，估计的参考直方图对于复原任务来说已经足够准确。

4 实验 4.1 实验环境及参数设置

所提出模型应用于图像去噪和去模糊实验中。选择经典合成图像及BSDS部分图像作为评估图像。实验的硬件配置为：Intel(R) Core(TM) i7-8700K@3.70GHz，RAM为32G，在Matlab环境下进行测试。采用峰值信噪比PSNR和结构相似性SSIM作为算法的客观度量。估计图像的质量越高，通常会有更高的PSNR和SSIM值，相比来说SSIM评估更贴近于主观质量评价。

实验中图像块的大小设置为8×8，式(18)中λ设置为s/σ²(s为块维度，σ²为噪声方差)。β和β_h的序列值，在去噪实验中设置为1/σ²{1, 4, 8, 16, 32, 64, 128}；在去模糊实验中设置为15*{1, 4, 8, 16, 32, 64, 128}，收敛性分析将在后面讨论。式(40)中τ和κ的范围分别设置为τ∈[0.001, 5]，κ∈[0.02, 1.5]。滤波器H采用高斯滤波器，下采样因子为2时，设置其标准差为0.8；在下采样因子为4情况下，设置其标准差为1.5。

确定图像复原质量的过程称为图像质量评估(IQA, image quality assessment)。通常，IQA方法包括基于人类观察者的感知评估的主观方法和基于自动预测图像质量的计算模型的客观方法。PSNR和SSIM是两种主流的客观评估方法。

1) 峰值信噪比

峰值信噪比(PSNR, peak signal-to-noise ratio)通常用于测量有损变换的重建质量。给定真实图像I和重构图像$\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over I} }}$，两者都具有N个像素，I和$\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over I} }}$之间的MSE和PSNR(以dB为单位)定义如下

$ {{\rm{MSE}} = \frac{1}{N}\sum\limits_{i = 1}^N {{{(\mathit{\boldsymbol{I}}(i) - \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over I} }}(i))}^2}} ,} $

(43)

$ {{\rm{PSNR}} = 10.{{\log }_{10}}\left( {{L^2}/{\rm{MSE}}} \right)}。$

(44)

在使用8位图像表示情况下，L等于255，并且PSNR的典型值在20—40之间变化，值越高越好。当L固定时，PSNR仅与图像之间的像素级MSE相关，仅关注相同位置处的像素值之间的差异而不是人类视觉感知。这导致PSNR在表现真实场景中的图像的质量方面表现不佳，在这种情况下通常更关注人类感知。PSNR是目前最广泛使用的复原模型评估标准。

2) 结构相似性指数(SSIM, structural similarity index measure)

考虑到人类视觉系统(HVS, human visual system)高度适应从视野中提取结构信息，结构相似性指数被提出用于测量图像之间的结构相似性，基于亮度、对比度和结构3个相对独立分量进行比较。对于具有N个像素的图像I，亮度和对比度分别被估计为图像强度的平均值和标准偏差。由于SSIM从HVS的角度评估重建质量，因此它更好地满足感知评估的要求，并且也被图像复原模型广泛使用。

主要采用PSNR和SSIM作为客观度量标准，而主观方法也用于辅助对于复原方法的评估。

4.2 去噪

为了验证所提出方法在去噪问题的求解性能，在具有不同纹理结构的自然图像上进行实验。同时与一些优秀的去噪算法进行了对比，包括BM3D^[8]、EPLL^[4]、多尺度EPLL^[21]、HOSVDT^[30]、MSDCT^[31]等，对比方法的代码来自于作者公开代码，参数设定来自论文及代码设置。表 1给出方法与其他对比方法的在不同噪声方差下去噪结果对比，单元格值左侧为PSNR值，右侧为SSIM值。从表中可以看出在所有噪声级别上，SSIM指标上研究方法均占有优势。

图 1给出噪声标准差为30情况下的去噪视觉质量对比，总体方法的主观感观更好，并且在SSIM指标上也体现了这一点。从图 2—图 4的裁剪局部放大图也可以得到佐证。图 2为水面区域的局部放大图对比，BM3D方法和EPLL方法的伪影情况较为严重；MEPLL方法尽管一定程度消除了伪影，但是水面区域被过度平滑，尽管取得最好的PSNR值，但是视觉观感较差；MSDCT方法水面区域相比MEPLL方法更为平滑，已经没有任何纹理层次，HOSVDT方法虽然保留一定的纹理，但是噪点较为明显。而方法较好的还原了水面波光粼粼的效果。图 3给出建筑物还原的局部放大图，方法在可视观感上更为优秀，尤其在2个细节处：建筑物中的柱子和建筑物前的桥梁栅栏，这两处方法相比对比方法更为清晰，还原细节较好。从这个实例也可以说明单纯的PSNR指标难以完全反映复原算法的优劣，而SSIM指标则较好的反映了主观视觉质量。

图 4给出上例复原图像各主要方法的水平梯度直方图和垂直直方图的对比，为了提高对比效果，纵坐标做了对数处理。从图中可见，方法复原图像的直方图，相比MEPLL和EPLL能更为接近于估计直方图及原始直方图分布。这也说明了方法将直方图先验与多尺度块先验结合，一方面较好的抑制了图像伪影，尤其是平滑区域的改善，这得益于多尺度的效果；另一方面也提升了纹理区域的细节，改善了视觉质量，这方面更多源自于梯度直方图的全局统计约束的作用力。以上2点正是研究方法相比传统方法最为重要的改进，下节的去模糊实验对这2点有进一步的例证。

4.3 去模糊

在图像去模糊的实验中，对测试用图先施加模糊核，实验测试了3种模糊核：均匀模糊核(9×9)，高斯模糊核(21×21，标准差为1.6)和运动模糊核(len=20，theat=45)。模糊核退化图像后，再加入噪声方差为2的噪声。在实验中，除了原始尺度，额外增加2个尺度，下采样因子分别为2和4。对不同的分量分别指定权值(w₁=1，w₂=0.25，w₃=0.02)，在下采样之前，并没有应用滤波器，因为这样能取得更好的结果。在每次迭代中，通过块平均来重建抽取的图像，一定程度上具有低通滤波器的效果，因此即使没有明确地进行滤波，仍然可以获得平滑效果。对比方法包括：EPLL^[4]、多尺度EPLL^[21]、INSR^[32]、DeblurGAN^[33]等，这些对比方法的代码来自于作者所公开代码，参数设定来自代码及论文设置。表 2给出测试图像在3种不同模糊核下平均去模糊结果对比。从对比结果看，本研究方法在PSNR和SSIM均占有都有优势。

图 5给出butterfly图像在3种模糊核下复原效果对比。方法在所有3种模糊核情况下，都具有更好视觉还原质量及更好客观度量值。

图 6给出图 5运动模糊核下复原结果局部放大区域的视觉质量对比。DeblurGAN由于测试数据集与训练数据集的有一定差异，还原效果比较糟糕，由于生成对抗网络(GAN, generative adversarial networks)建模固有的模型塌陷问题，导致生成图像的多样性不足，通常容易出现复原图像的保真度较差；MEPLL和INSR方法的噪点较多，尤其是INSR方法更为明显，平滑度不足；EPLL方法有点过度平滑，相比研究方法锐度不够，观感度较差；而研究方法较好地兼顾了局部纹理的还原度、锐度及平滑度，这一结果也进一步印证了上节的分析。

为获得最佳性能，实验中发现权值w₂设置为负值，视觉质量更为理想，这一点与文献[21]的实验结果类似。从原始图像中减去其模糊版本，从而获得锐化效果，这有助于进行去模糊的任务。相关的解释源于图像处理中的偏微分方程的领域。EPLL方法是迭代恢复算法，因此，它可以被视为扩散过程。在处理去模糊问题时，普通扩散是不够的，因为它不会在初始图像中向已存在的细节添加新的细节。为了缓解这个问题，可以使用反应扩散过程，也称为前向和后向扩散。前向过程去噪平滑区域，而后向过程增强边缘和特征。后向扩散是试图向后移动并反转扩散过程，以重建丢失的特征。在多尺度先验中的负权重可以被视为向原始EPLL完成的已经存在的前向扩散添加后向扩散过程的尝试。通过改变增加尺度的权重符号，实现反转扩散，从而有助于增强细节。

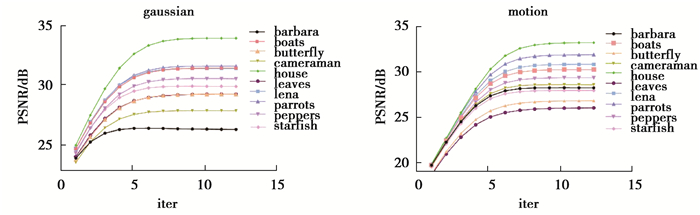
4.4 收敛性分析

研究方法的收敛性实验结果，以去高斯模糊和去运动模糊实验为例，图 7给出部分测试图像随迭代推进PSNR值的变化情况。可以观测到随着迭代的增加，PSNR值显著增长，大部分测试图像在经过6~7轮基本会达到峰值。在实验中统一设置最大迭代次数为7次，总体来说，这一设置能够取得比较好的收敛效果，在视觉质量及效率间取得较好的折衷。通过实验说明了方法的算法收敛性方面表现理想，能在较低的时间复杂度情况下，完成复原工作。

5 结语

提出一种将梯度直方图先验与多尺度块先验集成建模的图像复原方法，以施加非局部性及全局统计约束。首先，利用多尺度块先验，对退化图像执行滤波和下采样过程，通过滤波器的调整实现尺度不变性，在所有尺度图像的块上施加同样的块局部模型；其次，利用Wasserstein距离作为衡量复原图像直方图与参考直方图的相似性度量，来施加直方图全局统计约束；针对不同的复原任务，通过广义高斯分布参数优化调整来估计参考直方图。最后，将所提出模型在图像去噪和去模糊任务中进行了实验，相比传统方法取得了更好的视觉质量。下一步，将把模型扩展应用于图像填充及超分辨等图像复原任务中。