2. 吉林大学 符号计算与知识工程教育部重点实验室, 长春 130012;
3. 吉林大学 计算机科学与技术学院, 长春 130012
2. Key Laboratory of Symbolic Computation and Knowledge Engineering of the Ministry of Education, Jilin University, Changchun 130012, P. R. China;
3. School of Computer Science and Technology, Jilin University, Changchun 130012, P. R. China
图像视觉特征提取与表达是图像检索与分类的关键步骤,同时也是计算机视觉领域的重要研究方向[1]。归纳总结视觉特征研究发展历程,可分为3个阶段:底层视觉特征提取、中间层特征表达,以及最近流行的深度学习方法。1)底层视觉特征提取主要针对图像形状、纹理、颜色等信息进行刻画,提取表征图像外观的视觉特征,如常用的尺度不变特征变换[2]、局部二值模式[3]等。底层视觉特征提取一般计算较简单,但单独使用时难以胜任复杂的计算机视觉任务。2)中间层特征表达是指对底层视觉特征进一步编码和统计,以挖掘更具判别能力的深层特征表示,如经典的视觉词袋模型(BoVW, bag-of-visual-words)[4]。中间层特征表达在一定程度上可以弥补底层视觉特征的缺陷。3)深度学习方法作为一种倍受关注的数据驱动方法,其不需要手工参与设计,直接以图像像素作为初始数据输入,经过多层网络结构,学习图像的潜在深层特征。以卷积神经网络(CNN, convolution neural network)[5]为代表的深度学习方法,发展出一系列高效的网络结构,如AlexNet[5]、VGGNet[6]、ResNet[7]等,被用在高光谱图像分类[8]、人体行为识别[9]与表情识别[10]等多个领域。CNN虽然在自然场景图像分类中取得巨大成功,但仍然存在一些缺陷,如依赖海量样本数据、可解释性较差、难以推理、较难描述和理解图像内容模式的含义等,这使得CNN在处理小样本和对语义特性要求较高的多目标图像时面临许多挑战。
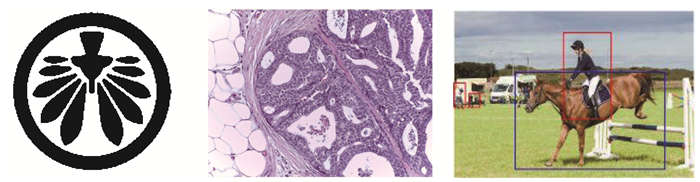
空间关系建模作为一种实现图像语义表达的重要手段,可有效增强视觉特征表达性能。相较于纹理、形状、颜色等底层视觉特征,通过刻画图像基元之间的空间关系来识别图像,更符合人类的视觉认知习惯。空间关系刻画可有效跨越和缩小底层视觉特征到高层语义之间的“语义鸿沟”,在计算机视觉与模式识别领域具有重要的地位,尤其是对于医学影像等多目标图像识别具有至关重要的判别能力[11-12]。然而,现有工作研究的空间关系模型存在诸多缺陷,如描述目标简单、基本关系数量有限、缺少有效的推理与相似性度量方法,难以满足视觉特征表达的现实需求。表 1总结了目前代表性的空间关系模型,其中RCC-8[13]等经典空间关系模型仅有少数种空间关系;CRString[14]虽然具有完备的空间关系表示,但其目标仅针对凸区域;前期研究成果DTString[15]研究了简单区域的完备拓扑空间关系表示,但其不适用于具有复杂区域的多目标图像场景。如图 1所示,商标、医学和目标分割后的场景图像均为具有复杂区域空间关系的多目标图像。
| 表 1 代表性空间关系模型总结 Table 1 Summary of representative topological relation models |
|
图 1 多目标图像示例 Fig. 1 The examples of multi-object images |
针对上述空间关系描述简单、图像视觉特征表达不充分、语义信息缺失的问题,主要研究复杂图像的空间关系建模与深度特征融合,提出一种能满足视觉特征表达需求的空间关系模型来刻画复杂区域的空间拓扑结构,并与深度特征融合,应用于多目标图像检索,提高检索性能,同时为增强深度学习可解释性创造有利条件。主要贡献包括:1)针对复杂区域表示,提出了一种新的精细拓扑结构表示模型,不仅具有完备的拓扑关系描述性能,还提供了有效的拓扑不变量推理算法和拓扑结构相似性度量方法;2)基于精细拓扑表示模型,提出了融合复杂空间关系特征和深度特征的多目标图像检索算法,取得优于现有方法的性能。
1 精细拓扑结构表示模型提出一种新的精细拓扑结构表示模型(DTSRM, detailed topological structure representation model)来刻画多目标的复杂区域,主要包括精细拓扑结构的表示、定性推理和相似性计算3个部分。这3个部分从理论到应用层层递进。为便于介绍,首先给出一些通用符号说明,如表 2所示。
| 表 2 通用符号说明 Table 2 Description of universal symbols |
首先逐步给出复杂区域的形式化定义。平面上同胚于圆盘的区域称之为简单区域,而带洞的简单区域则定义如下。
定义1(带洞的简单区域) 给定c0, c1, …, cn为简单区域,若满足1)1≤i≤n,有ci⊂c0,且|∂ci∩∂c0| ≤1;(2)对于1≤i, j≤n(i≠j),|ci∩cj ≤1,则称A=c0\∪i=1ncio为带洞的简单区域,ci(i≥1)称为A的洞。
定义2(复杂区域) 设A为平面上的区域,若A由若干个简单区域或带洞的简单区域组成,则称A为复杂区域。
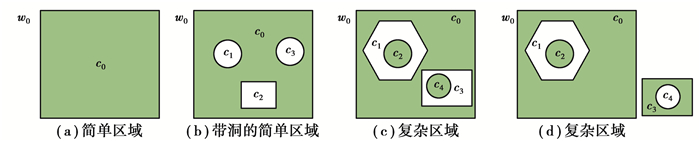
图 2展示了简单区域、带洞的简单区域以及复杂区域的区别。给定一个有界的平面区域A,称A°为正成分,如图 2(b)中c0;Ae为负成分,且负成分可进一步划分为两种类型,一种是有界的,如图 2(b)中c1、c2、c3;一种是无界的,如w0。容易发现,一个区域至少包含一个正成分和一个负成分,且Ae有唯一一个无界的开放区域(即w0)。
|
图 2 简单区域与复杂区域示意图 Fig. 2 The examples of simple regions and complex regions |
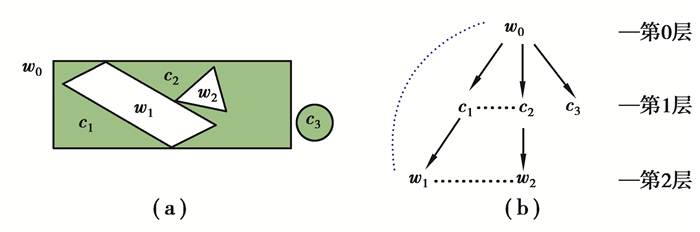
基于上述定义,针对多目标复杂区域描述提出精细拓扑结构表示模型DTSRM。如图 3(a)所示,在多目标复杂区域中,对于任意2个成分ai和aj之间有2种连接关系:1)强连接关系,若ai和aj闭包的交集包含至少一条曲线;2)弱连接关系,若ai和aj闭包的交集仅包含一个或多个离散点。
|
图 3 精细拓扑结构表示模型(DTSRM) Fig. 3 The detailed topological structure representation model (DTSRM) |
定义3(精细拓扑结构表示模型) 复杂区域A的精细拓扑结构表示定义为一个四元组G={V, E1, E2, L},其中V是A中所有成分的集合;E1表示成分之间强连接关系的集合,E2表示成分之间弱连接关系的集合,即rij∈E1和rij∈E2分别表示成分ai和aj之间存在强连接关系(即图 3中的有向边)或者弱连接关系(即图 3中的无向边);L则表示每个成分的标签,可根据需要由视觉特征描述后聚类得到。此外,在集合V中,唯一的根节点表示开放背景区域(即w0),记根节点w0在第0层,w0的子节点c1、c2、c3在第1层,c1、c2、c3的子节点在第2层,以此类推,由此得到精细拓扑结构表示模型为图 3所示。
下面通过一个直观的例子阐述提出的DTSRM模型相比现有方法的优势。图 4展示了3种具有相似拓扑结构的复杂区域,但是在局部细节上存在较大的差异。使用CRString[14]和DTString[15]模型无法对3种拓扑结构进行区分,因其无法描述复杂区域。使用树表示模型[16]无法将点连通区域分开,即将(a)和(b)视为同一种拓扑结构;分层图模型[17]则无法区分弱连接关系,即无法区分(a)和(c)2种情况。而提出的精细拓扑结构表示模型综合考虑了强连接和弱连接关系,能够有效区分图 4中3种情况,实现了更精确和完备的拓扑结构表达。值得说明的是,将DTSRM模型应用于多目标图像刻画时,考虑到像素采样的误差与粘连,弱连接关系中目标边界交集的离散点可以根据需要抽象为若干个邻域像素集合。

|
图 4 三种不同的拓扑结构 Fig. 4 Example of three different topological structures |
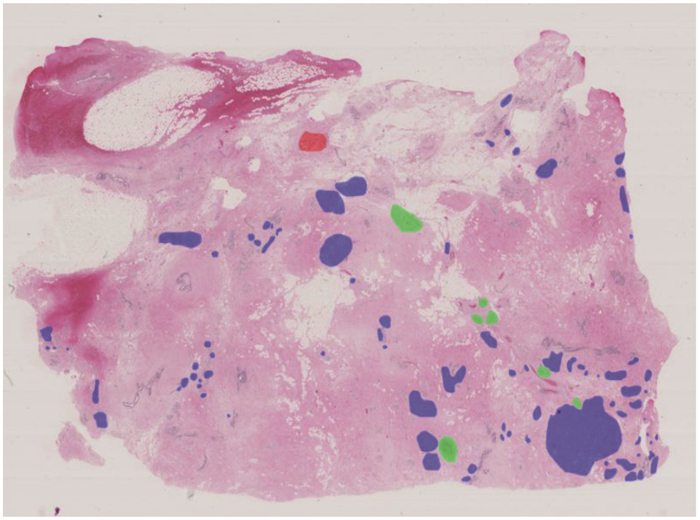
实际上,DTSRM模型通过有效区分强连接与弱连接关系不仅有助于增强语义特性,对于描述医学影像等尤其注重细节内容差别的图像具有重要的意义。如图 5所示的乳腺癌全扫描切片(来自2018年international conference on image analysis and recognition组织的乳腺癌图像分析大赛[18]),其中病理组织(背景区域)、良性(红色区域)、原位癌病变区域(绿色部分)、浸润性癌病变区域(蓝色区域)彼此之间构成复杂区域,并且区域之间体现出强连接关系和弱连接关系,对他们之间的空间组织形式与拓扑结构进行表达,可有效协助医生对癌细胞转移进行分析与判断。
|
图 5 乳腺癌图像中的复杂区域 Fig. 5 The complex region in breast cancer images |
设复杂区域A以及它的精细拓扑结构表示G={V, E1, E2, L}。实际上,如图 6所示,G可划分为一个有向子图G1={V, E1, L}和一个无向子图G2={V, E2, L}构成。

|
图 6 DTSRM模型可划分为有向子图和无向子图表示 Fig. 6 DTSRM model divided into a directed sub-graph and a undirected sub-graph |
定理1 设c为A的非根节点,G′1⊂G1为从G1中移除c所形成的子图,则c没有洞当且仅当G′1依然是连通的。
证明:首先证明必要性。设c没有洞,如果c存在子孙节点b,假设从根节点到b之间的路径均经过c,根据模型定义3,这意味着b的闭包只与c的闭包存在交集,即b是c的子节点,假设与前提条件矛盾。因此,从根节点到b之间必然存在一条路径没有经过c,即在G1中移除c得到的G′1依然是连通的。
接着证明充分性。设G′1是连通的,假设c存在洞b,则从根节点w0到b的每条路径必然经过c,在G1中移除c后将造成G′1是不连通。假设与前提条件矛盾,因此c没有洞。综上所述,即得证。
定理2 设c为A的非根节点,如果从G1中移除c将产生一个或多个连通子图,这些子图可以进一步划分为两种类型:1)唯一一个包含根节点的子图w0; 2)其他不包含根节点w0的子图gi(c), 1≤i≤k,则gi(c)即是c的洞。
证明:从定理1可知,如果c存在洞bi,若从G1中移除c将使得bi与根节点是不连通的,则bi可看成等价的子图gi(c),即得证。
下面给出一个直观的例子。在如图 6所示的复杂区域和它的精细拓扑结构表示,只有c2节点存在洞b2,因为在G1中移除c2之后,b2单独形成一个不包括根节点w0的子图。
由上述定理1和定理2,可在O(n)时间复杂度内(n为节点的数量),直接从DTSRM表示模型中推导出每个子区域包含洞的数量,不需要额外的图形或者几何计算,从而大大地降低了计算复杂度,同时也提供了具有语义特性的拓扑不变量。
1.2.2 环绕子区域推理设复杂区域A以及它的拓扑结构表示G={V, E1, E2, L}, 假定c为A的任意成分(子区域),一个切实的问题是能否仅根据G就推导出c由哪些其他子区域环绕,以及如何确定环绕子区域的顺序。这些信息不仅是拓扑不变的,而且对于基于知识表示的图像重构也具有重要意义。下面提出子区域推理来回答上述问题。
定理3 设c为G的节点,S(c)定义为如下集合:S(c)={vi⊂V|(c, vi)∈E1或(vi, c) ∈E1, 1≤i≤k},则S(c)为c的围绕子区域集合。并且,如果每个vi∈S(c)恰恰形成E2中的回路R=(r1r2…rkr1),则(r1r2…rkr1)即为c环绕的子区域序列。
证明:首先,设任意节点vi满足:∂vi∩∂c包含一条简单曲线,即vi和c是强连接的,则vi是c的子节点或者父节点,即(c, vi)∈E1或(vi, c)∈E1。由定义3易知,∂c的每个线段分量只与其父节点或子节点存在交集,因此S(c)恰为c的围绕子区域集合。再者,c的任意2个相邻围绕子区域必然存在弱连接关系(以一个点或多个点相连),而模型在E2中恰恰描述了这种弱连接关系。因此,只需要在E2中找到关于S(c)中所有节点的回路(r1r2…rkr1),即为c的环绕子区域的序列。特别的,如果S(c)中仅包括一个节点,意味着c是一个某个子区域的洞,被其父节点所环绕。
举例如图 6所示,其中图 6(b)和图 6(c)分别为有向子图G1={V, E1}和无向子图G2={V, E2}。以计算b4的环绕子区域序列为例,由图G1易知:S(b4)={c2, c3, c4, c5},而S(b4)中的所有节点在G2中恰恰存在回路(c2c3c4c5c2),因此(c2c3c4c5c2)即为b4的环绕子区域序列,在图 6(a)中可得到验证。同理,可计算w0和c1分别被G2中回路(c2c5c4c3c1c2), (b1b3w0b1)所环绕,同时上述环路中的节点在G1中也分别是w0和c1的子节点或者父节点。
由上述几个定理可以发现,所提出的精细拓扑结构表示模型不仅能实现对拓扑结构的精细刻画,同时提供简易有效的推理,使得拓扑不变量可以由表示模型直接推导得到,并可进一步应用于空间查询与图像视觉特征表达。
1.3 基于精细拓扑结构表示模型的相似性度量相似性度量是空间关系模型应用于视觉特征表达的重要基础。由于精细图表示模型G可划分为一个有向图G1={V, E1, L}和一个无向图G2={V, E2, L}组成,分别对2个子图进行相似性度量。
1.3.1 有向图相似性度量由于G1是有唯一根节点和层次信息的有向图,因此G1亦可被看成类似树的结构。采用最大相似子树来计算2个有向图的相似度。首先,假设T1和T2是2个有向图,其节点集合分别为V1和V2,如果存在U1⊆V1和U2⊆V2,对于任意双射f: U1→U2,使得子图U1和U2具有相同的邻接关系,则称该双射为一个子图同构。接着,一旦获得2个有向图的子图同构f之后,即计算子图同构的相似度W
| $ W\left( f \right) = \sum\limits_{u \in {U_1}} {\phi \left( {u, f\left( u \right)} \right)} , $ | (1) |
其中: ϕ(u, v)表示使用模糊形状描述算子[19]计算2个节点(子区域)的形状相似度。表 3给出了2个同构子图相似度的计算方法,则2个T1和T2的所有子图同构中具有最大的相似度称之为最大子图同构,其相似度定义为
| $ {S_g} = \mathop {\max }\limits_f W\left( f \right)。$ | (2) |
| 表 3 计算子图相似度的算法 Table 3 The algorithm of computing sub-graph similarity |
考虑到在复杂图像表示的实际应用中,目标区域间的弱连接关系图G2是稀疏的,提取无向图的图谱特征作为相似度量方法。具体的,给定G2={V, E2},首先计算其邻接矩阵的n个特征值,并将其按绝对值大小排序,即得t=[λ1, λ2, …, λn],λ1≥λ2≥…≥λn,为表征G2的图谱特征。图谱特征能较好的反应无向图的特性,具有拓扑不变性,且计算较简单。对于任意精细图表示模型G和G′,获取最大子图同构之后,相应的节点组成的2个无向图即可计算其图谱特征的欧氏距离来刻画相似度,记为Su。
2 基于精细拓扑结构表示与深度特征融合的图像检索深度学习方法因其在场景图像分类等任务中的优异性能受到广泛的关注。深度学习方法虽然能有效获取深度特征,但其依赖于大量学习样本,并且缺乏语义信息。而空间关系模型蕴含着大量的语义信息,与深度特征融合能够充分利用两者的优势,有望提升视觉特征的表达性能与可解释性。
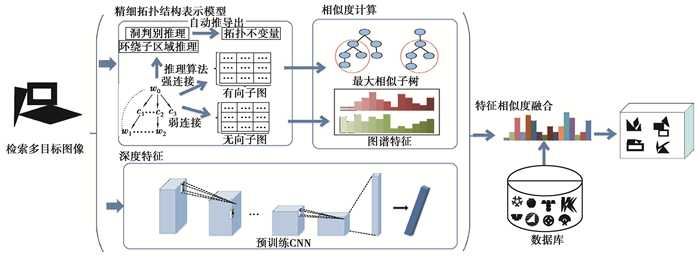
提出基于复杂空间关系特征与深度特征融合的多目标图像检索框架,如图 7所示。首先,给定查询图像I,使用提出的精细拓扑结构表示模型刻画I与检索数据集中的样本,获取最大子图同构,分别计算有向子图相似度Sg和无向子图的相似度Su。接着,使用训练好的卷积神经网络提取多目标图像的第一个全连接层特征作为I的深度特征Fd,使用欧式距离计算任意2个图像深度特征相似度,记为Sd。最终,任意2个多目标图像的相似度定义为
| $ S({I_i}, {I_j}) = {w_1}{s_g} + {w_2}{s_u} + {w_3}{s_d}, $ | (3) |
|
图 7 基于精细拓扑结构表示和深度特征融合的多目标图像检索框架 Fig. 7 Multi-objet image retrieval framework based on DTSRM and deep feature fusion |
其中:w1, w2, w3为权重系数。
3 实验与结果分析实验采用多目标图像数据集,该数据集一部分来自MPEG-7形状数据集[21],一部分来自商标数据集[22],包括20个类别的多目标二值图像,每个类别包含30~100不等的数据样本。使用图像检索领域常用指标查准率(precision)和查全率(recall)作为评价标准。实验机器配置为:Intel Core i9-7900X CPU, NVIDIA TITAN XP GPU, 16 GB内存,使用MATLAB 2019a及深度学习工具箱作为实验平台。分别构建基于拓扑不变量的空间查询、基于内容的图像检索两组实验。
3.1 基于拓扑不变量的空间查询实验在该实验中,输入“子区域数量”、“洞的数量”2组拓扑不变量,基于精细拓扑结构表示模型及拓扑不变量推理算法,在数据集中查询满足条件的图像。图 8给出了3组不同查询条件下的检索示意图。

|
图 8 多目标图像查询示意图 Fig. 8 Examples of multi-objet image retrieval |
从图 8的查询结果可以发现,当查询拓扑不变量较简单时,检索返回的图像视觉差异较大;但随着拓扑不变量越复杂,检索返回的图像不仅在在拓扑结构上体现出拓扑同构或者相似的结构特性,在视觉上也具有更大的相似性。
值得说明的是,这种空间查询方式主要为了验证拓扑不变量及相关推理算法的性能,并未使用形状、深度学习等其他特征。实验结果表明,对于多目标图像而言,当限定了多个拓扑不变量同时满足条件查询时,检索出来的图像之间已然具有一定的相似性,并携带着一定的语义特性。随着查询的拓扑不变量越复杂,检索的结果在语义和视觉上越相似,这表明拓扑不变量蕴含着一定的判别能力。研究提出的精细拓扑结构表示模型和推理算法,可以直接在表示模型的基础上推导出拓扑不变量,而不需要繁复的图像计算,这对于空间和语义查询十分便利。
3.2 基于内容的图像检索实验在该实验中,输入一个查询图像,在数据集中检索相似图像。
首先,对2种方法进行评估,一是单独使用所提出的精细拓扑结构表示模型和相似性度量方法,记为DTSRM,二是融合了深度特征的方法(如公式3),其中CNN网络结构选用AlexNet[5]和VGGNet[6],分别记为DTSRM +AlexNet和DTSRM+VGGNet。为了评估复杂空间关系特征与深度特征的融合权重系数对检索结果的影响,计算不同权重系数下的平均查准率。即分别从每类数据集中随机抽取10副图像作为查询图像进行检索,共执行200次查询,抽取前12张最相似的图像计算平均查准率,表 4展示了研究方法在不同权重系数下的平均查准率。
| 表 4 研究方法在不同权重系数下的平均查准率(%) Table 4 The average precision of proposed method with different weight |
由表 3实验结果表明,1)结合表征弱连接关系相似性权重(即w2≠0时)的检索精度要高于仅考虑强连接关系的检索精度(即w2=0时),这说明刻画目标之间的弱连接关系是对精细拓扑结构表达性能的完善。2)无论是在AlexNet还是VGGNet网络结构下,融合深度特征后的检索精度有了进一步提高,这主要因为复杂空间关系特征与深度特征在表达多目标图像中形成一种良好的互补。3)总体来说,复杂空间关系特征与深度特征的融合体现了一定的鲁棒性,即不同的权重组合方式均较原有基础有了较大提升,其中(w1=0.4,w2=0.2,w3=0.4)的权重组合取得最好的性能,被应用于后续实验。
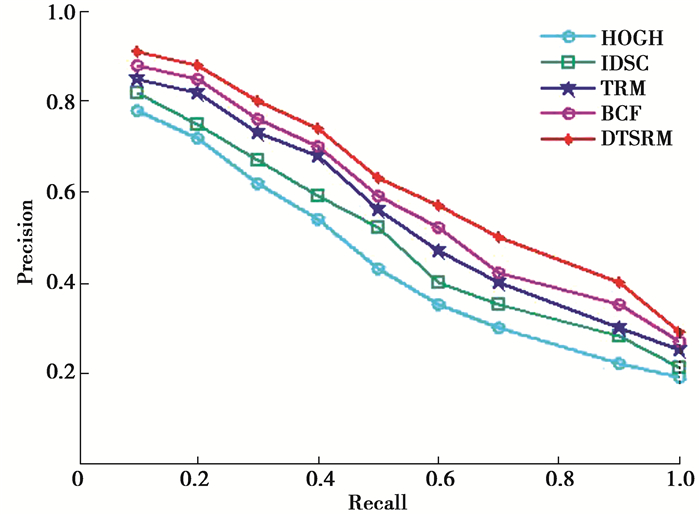
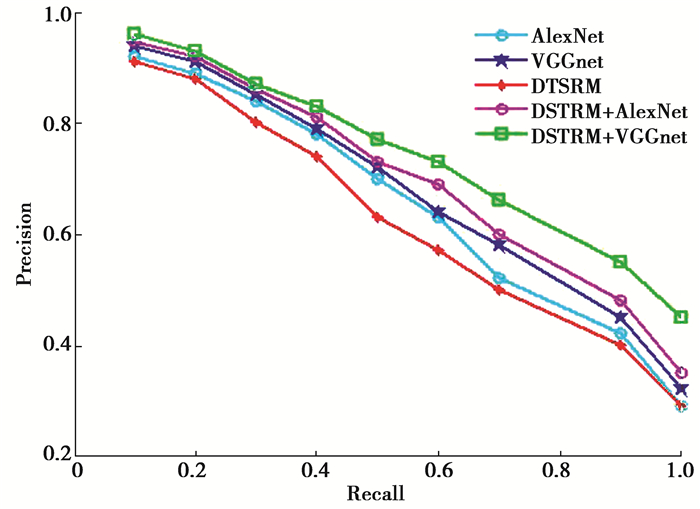
接着,分别对比了代表性手工设计特征方法HOGH[23],IDSC[24], TRM[16], BCF[25],以及深度特征学习方法AlexNet,VGGNet,它们的查全率和查准率曲线图分别如图 9和图 10所示。图 11展示了5种对比方法的检索结果示意图,其中加框的检索结果为返回的不同类别图像。
|
图 9 与手工特征方法的查准率与查全率曲线对比图 Fig. 9 Recall-Precision curves comparison of the proposed method and handcrafted features |
|
图 10 与深度学习方法的查准率与查全率曲线对比图 Fig. 10 Recall-Precision curves comparison of the proposed method and deep learning features |

|
图 11 5种对比方法进行检索的结果 Fig. 11 The retrieval results of five compared methods |
分析上述实验结果,可以得到以下结论:1)由图 9可知,提出的精细空间表示模型DTSRM单独使用时要优于其他手工特征表达方法,如HOGH、TRM、IDSC等,这是因为所提出的模型具有完备的拓扑结构描述性能,能有效的刻画多目标的复杂空间关系特征,提供更具判别能力的视觉特征。2) 由图 10可知,无论是在AlexNet还是VGGNet网络结构下,DTSRM与深度特征融合后,均相比深度特征单独使用时有了较大提升;此外由图 11可知,研究方法所检索的结果具有更相似性的拓扑结构,这是主要因为DTSRM模型携带了一定的语义信息,与深度特征形成良好的互补,非常适用于多目标图像检索。3)DTSRM+VGGNet获得了最高的检索精度,这可能得益于VGGNet更复杂的网络结构,并与复杂空间关系特征进行了较好地融合。
3.3 时间复杂度分析图像检索主要包括特征提取、相似度计算两个环节,其中特征提取分为有监督特征提取和无监督特征提取,如BCF方法需要训练视觉词袋模型、CNN方法需要利用训练集进行fine-tuning,属于有监督特征提取;而其他的手工特征方法直接从单张图像中提取特征,属于无监督特征提取。表 5展示了不同对比方法在特征提取、相似度计算及模型训练过程花费的平均时间。从中可以看出,DTSRM方法在特征提取阶段花费时间最少,在相似度计算中涉及最大相似子图计算问题,需要花费O(n2)时间复杂度,其中n为图表示模型中的节点数,通常节点数小于30。因此,在无监督多目标图像检索任务中,DTSRM单独使用可取得较好的检索效果;如果综合考虑精度与时间复杂度,DTSRM与深度特征融合则是一种更好的选择。
| 表 5 对比方法的时间复杂度 Table 5 The temporal complexity of the proposed method |
主要研究了复杂多目标图像的空间关系特征表示与深度特征融合问题,为增强图像的视觉特征表达与语义特性提供了新的思路。首先提出了一种新的精细拓扑结构模型,该模型最大创新之处在于它不仅具有完备的拓扑描述性能,还支持两种重要拓扑不变量的推理,使得拓扑不变量可由知识表示直接推理而来。其次,设计了基于精细拓扑表示的相似性度量方法,并提出面向多目标图像检索的空间关系特征与深度特征的融合方法。实验结果表明,所提出的方法在多目标图像检索中取得优于传统手工特征和目前流行的深度学习方法,并且对于不同参数选择具有一定的鲁棒性。在未来研究工作中,进一步考虑将研究方法扩展应用在医学图像分析与场景图像分类中,挖掘具有语义特性的视觉特征。
| [1] |
Cheng Q M, Zhang Q, Fu P, et al. a survey and analysis on automatic image annotation[J]. Pattern Recognition, 2018, 79: 242-259. DOI:10.1016/j.patcog.2018.02.017 |
| [2] |
Zheng L, Yang Y, Tian Q. SIFT meets CNN: a decade survey of instance retrieval[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(5): 1224-1244. DOI:10.1109/TPAMI.2017.2709749 |
| [3] |
Pietikäinen M, Zhao G. Two decades of local binary patterns: A survey[M]. Advances in Independent Component Analysis and Learning Machines. Academic Press, 2015: 175-210.
|
| [4] |
Jabeen S, Mehmood Z, Mahmood T, et al. An effective content-based image retrieval technique for image visuals representation based on the bag-of-visual-words model[J]. PloS One, 2018, 13(4): e0194526. DOI:10.1371/journal.pone.0194526 |
| [5] |
LeCun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015, 521(7553): 436-444. DOI:10.1038/nature14539 |
| [6] |
Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition[EB/OL]. 2014: arXiv: 1409.1556[cs. CV]. https://arxiv.org/abs/1409.1556
|
| [7] |
He K, Zhang X, Ren S, et al. Deep residual learning for image recognition[C]//The IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, USA: IEEE, 2016: 770-778.
|
| [8] |
Zhang M M, Li W, Du Q. Diverse region-based CNN for hyperspectral image classification[J]. IEEE Transactions on Image Processing, 2018, 27(6): 2623-2634. DOI:10.1109/TIP.2018.2809606 |
| [9] |
刘智, 冯欣, 张杰. 基于深度卷积神经网络和深度视频的人体行为识别[J]. 重庆大学学报, 2017, 4(11): 99-106. Liu Z, Feng X, Zhang J. Action recognition based on deep convolution neural network and depth sequences[J]. Journal of Chongqing University, 2017, 4(11): 99-106. (in Chinese) DOI:10.11835/j.issn.1000-582X.2017.11.012 |
| [10] |
Liu Y Y, Yuan X H, Gong X, et al. Conditional convolution neural network enhanced random forest for facial expression recognition[J]. Pattern Recognition, 2018, 84: 251-261. DOI:10.1016/j.patcog.2018.07.016 |
| [11] |
Gong C, Anders R A, Zhu Q, et al. Quantitative characterization of CD8+ T cell clustering and spatial heterogeneity in solid tumors[J]. Frontiers in Oncology, 2018, 8: 649-690. |
| [12] |
于瑞云, 苏展, 谢青, 等. 基于空间分割的人体模型骨骼提取算法[J]. 计算机学报, 2019, 42(9): 2049-2061. Yu R Y, Su Z, Xie Q, et al. Skeleton extraction of character model based on space segmentation[J]. Chinese Journal of Computers, 2019, 42(9): 2049:2061. (in Chinese) |
| [13] |
Chen J, Cohn A G, Liu D, et al. A survey of qualitative spatial representations[J]. The Knowledge Engineering Review, 2015, 30(1): 106-136. DOI:10.1017/S0269888913000350 |
| [14] |
Li S J, Liu W M. Topological relations between convex regions[C]//The Twenty-Fourth AAAI Conference on Artificial Intelligence, Atlanta, USA: AAAI, 2010: 321-326.
|
| [15] |
Wang S S, Liu D, Zhang C, et al. Representation, reasoning and similar matching for detailed topological relations with DTString[J]. Information Sciences, 2014, 276: 255-277. DOI:10.1016/j.ins.2014.02.059 |
| [16] |
Alajlan N, Kamel M S, Freeman G H. Geometry-based image retrieval in binary image databases[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 30(6): 1003-1013. DOI:10.1109/TPAMI.2008.37 |
| [17] |
Li S J. A layered graph representation for complex regions[C]//The 12th International Conference on Principles of Knowledge Representation and Reasoning, Toronto, Canada, Morgan Kuafmann, 2010: 581-583.
|
| [18] |
Aresta G, Araújo T, Kwok S, et al. Bach: Grand challenge on breast cancer histology images[J]. Medical Image Analysis, 2019, 1-19. |
| [19] |
Escalera S, Alicia Fornés, Pujol O, et al. Blurred shape model for binary and grey-level symbol recognition[J]. Pattern Recognition Letters, 2009, 30(15): 1424-1433. DOI:10.1016/j.patrec.2009.08.001 |
| [20] |
Lyzinski V, Fishkind D E, Fiori M, et al. Graph matching: relax at your own risk[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 38(1): 60-73. |
| [21] |
Abbas S, Farhan S, Fahiem M A, et al. Efficient shape classification using zernike moments and geometrical features on MPEG-7 dataset[J]. Advances in Electrical and Computer Engineering, 2019, 19(1): 45-51. DOI:10.4316/AECE.2019.01006 |
| [22] |
Wei C H, Li Y, Chau W Y, et al. Trademark image retrieval using synthetic features for describing global shape and interior structure[J]. Pattern Recognition, 2010, 42(3): 386-394. |
| [23] |
Ni H, Guo Z H, Huang B Q. Binary patent image retrieval using the hierarchical oriented gradient histogram[C]//2015 International Conference on Service Science (ICSS), Weihai, China: IEEE, 2015: 23-27.
|
| [24] |
Zhang Z, Tang P, Duan R. Dynamic time warping under pointwise shape context[J]. Information Sciences, 2015, 315: 88-101. DOI:10.1016/j.ins.2015.04.007 |
| [25] |
Wang X G, Feng B, Bai X, et al. Bag of contour fragments for robust shape classification[J]. Pattern Recognition, 2014, 47(6): 2116-2125. DOI:10.1016/j.patcog.2013.12.008 |
 2021, Vol. 44
2021, Vol. 44


