目前,燃料电池汽车因无污染、零排放、能量转换效率高等优点受到人们的广泛关注[1]。但由于燃料电池动力响应慢且不能储存能量,大多数燃料电池汽车采用混合动力系统[2-3]。为此,各种能量管理策略被提出,以降低能源消耗,提高动态响应[4]。在许多控制策略中,道路坡度信息非常重要。例如,获得道路坡度等相关参数后,燃料电池的输入(空气压力、氢气压力等)可根据相应的控制算法及时进行调节,缓解动态响应的滞后现象[5]。
道路坡度的估计方法主要有两类。第一类是基于传感器的估计方法,主要在车辆上安装额外的传感器来直接或间接地测量道路坡度值。文献[6]将角位移传感器安装在车辆上,直接测量汽车倾角,但动态误差较大;文献[7]结合全球定位系统(GPS)和其他传感器来间接测量道路坡度;文献[8]通过地理信息系统(GIS)读取道路坡度信息。但当GPS/GIS信号较差时,此类方法并不适用。第二类是基于汽车动力学模型的估计方法,主要通过各类算法对汽车纵向或横向动力学模型进行解耦,同时估计汽车质量和道路坡度。例如,文献[9]使用了卡尔曼滤波算法进行解耦;文献[10-11]使用了最小二乘法进行解耦;文献[12-13]使用了状态观测法进行解耦。由于需要对复杂的动力学模型进行解耦,此类方法计算复杂度较高。同时,建模的准确度严重影响了估计算法的性能。
综上所述,目前的道路坡度估计方法有着各种制约,需要使用额外的传感器或需要对动力学模型进行复杂的解耦。因此,笔者根据道路坡度的时变特性,提出了一种基于智能算法(长短期神经网络)的道路坡度估计方法,该方法不需要安装额外的传感器,只从CAN总线读取汽车行驶的相关数据,并通过实车实验验证了该方法的有效性。
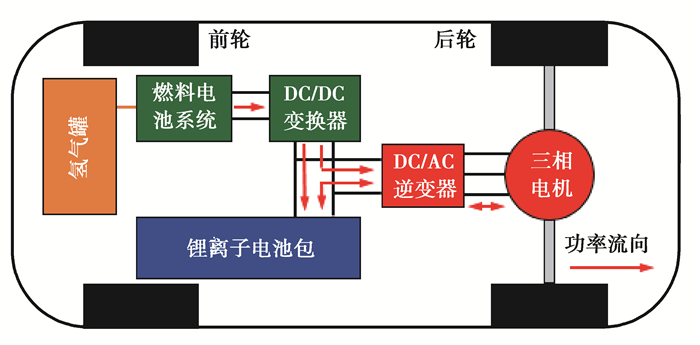
1 燃料电池汽车配置研究基于一辆由双座电动车改装的燃料电池混合动力汽车(FCHV),如图 1所示。表 1列出了该车的基本参数。动力系统由燃料电池系统、单向DC/DC变换器、电池包、DC/AC逆变器和交流电机组成,如图 2所示。高压锂电池包与直流母线相连,燃料电池系统通过单向DC/DC变换器与直流母线相连,两个动力源提供的能量可经过DC/AC逆变器到达交流电机,驱动车辆行驶。

|
图 1 实验车辆 Fig. 1 Experimental vehicle |
| 表 1 实验车辆基本参数 Table 1 Basic parameters of the FCHV |
|
图 2 动力系统结构简图 Fig. 2 Structural sketch of the FCHV |
在智能算法中,输入变量的选择非常重要,它决定了网络的具体结构和复杂度[14]。因此,分析了燃料电池汽车行驶动力模型,以选择合适的汽车行驶参数作为网络输入。
根据车辆动力学理论,总牵引功率Ptrac(t)可表示为
| $ \left.\begin{array}{c} P_{\text {trac }}(t)=v(t)\left(m a(t)+F_{\text {roll }}(t)+F_{\text {aero }}(t)+F_{\text {gra }}(t)\right), \\ F_{\text {acro }}(t)=\frac{1}{2} \rho C_{\mathrm{x}} A v(t)^{2}, \\ F_{\text {roll }}(t)=m C_{\mathrm{r}} g \cos \theta(t), \\ F_{\text {gra }}(t)=m g \sin \theta(t)。\end{array}\right\} $ | (1) |
式中:v(t)为汽车速度;a(t)为汽车加速度;θ(t)为道路坡度;m为汽车质量;Froll(t)为滚动阻力;Faero(t)为空气阻力;Fgra(t)为重力阻力;ρ为空气密度;Cx为空气阻力系数;A为汽车迎风面积;Cr为滚动阻力系数;g为重力加速度。
公式(1)中的总牵引力Ptrac(t)、汽车速度v(t)、道路坡度θ(t)为时变参数,而其他参数一般视为常量。因此,道路坡度可表示为:
| $ \theta(t)=f_{1}\left(v(t), a(t), P_{\text {trac }}(t)\right), $ | (2) |
其中总牵引功率Ptrac(t)可由以下3种行驶阶段决定。
行驶阶段1 驱动行驶阶段,Ptrac(t)为总驱动功率,定义为大于0,即
| $ P_{\text {trac }}(t)=P_{\mathrm{DC}_{\text {_bus }}}(t) \times \eta_{\text {drive }}>0, $ | (3) |
式中:PDC_bus(t)为流经直流总线的功率(大于0);ηdrive为驱动系统总功率。
行驶阶段2 制动过程, Ptrac(t)为再生制动系统回收的功率,定义为小于0, 即
| $ P_{\text {trac }}(t)=P_{\text {DC_bus }}(t) \times \eta_{\text {regen }}<0,$ | (4) |
式中:PDC_bus为制动回收时流经直流总线的功率(小于0);ηregen为再生制动系统效率。
行驶阶段3再生制动系统未工作时的滑行阶段:
| $ P_{\text {trac }}(t)=P_{\text {DC_bus }}(t)=0。$ | (5) |
考虑以上3个阶段:在行驶阶段1中,只有油门踏板开度大于0;在行驶阶段2中,只有制动踏板开度大于0;在行驶阶段3中,油门踏板开度和制动踏板开度都等于0。由此可见,行驶阶段与制动踏板开度αbra(t)、加速踏板开度αacc(t)和汽车速度v(t)密切相关。因此,总牵引功率Ptrac(t)可表示为
| $ P_{\text {trac }}(t)=f_{3}\left(P_{\mathrm{DC}_{\text {_bus }}}(t), \alpha_{\text {acc }}(t), \alpha_{\text {bra }}(t), v(t)\right) \text { 。} $ | (6) |
根据公式(2)和公式(6),道路坡度α(t)可表示为
| $ \theta(t)=f\left(\alpha_{\text {acc }}(t), \alpha_{\text {bra }}(t), v(t), a(t), P_{\text {DCbus }}(t)\right)。$ | (7) |
公式(7)中相关参数都随时间变化,实际上,道路坡度是一个与车辆行驶参数高度相关的时变序列。由于长短期神经网络(LSTM)在时间序列预测方面有良好的性能[15],基于该算法来预测道路坡度这一时序数据。作为对比,还应用了一个更简单的多层感知器算法(MLP)。
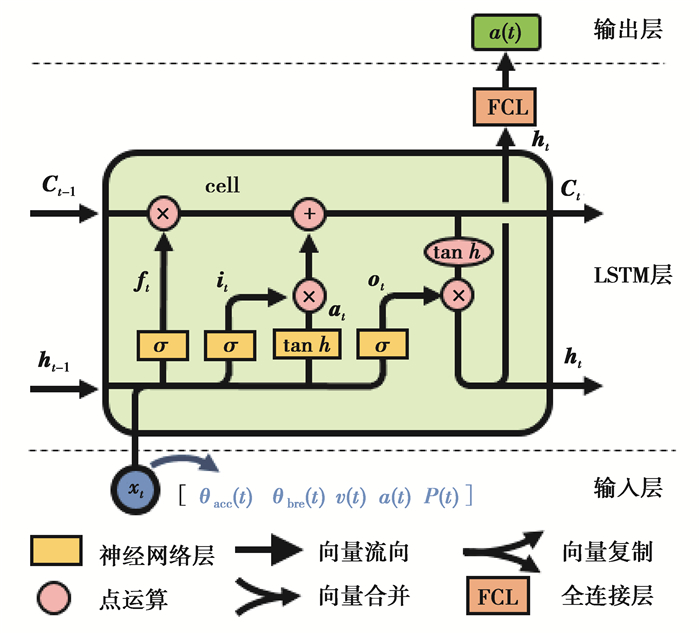
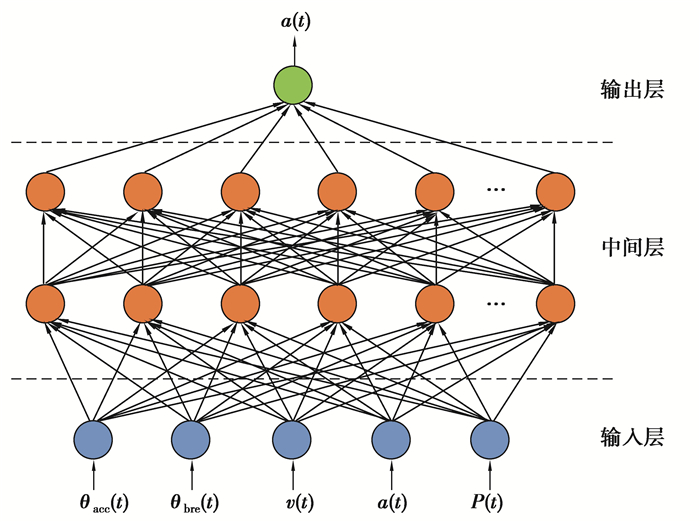
图 3和图 4分别展示了LSTM和MLP 2个算法的网络结构。2个网络有相同的5个输入(油门踏板开度、制动踏板开度、汽车速度、汽车加速度和直流母线功率)和相同的1个输出(当前的道路坡度值)。其中,MLP算法中间层为2层,每一层有32个节点,采用了sigmoid激活函数。LSTM网络的具体公式如式(8)所示。
|
图 3 LSTM网络结构 Fig. 3 LSTM network structure |
|
图 4 MLP网络结构 Fig. 4 MLP network structure |
| $ \left.\begin{array}{c} \boldsymbol{f}_{t}=\sigma\left(\boldsymbol{W}_{\mathrm{f}} \boldsymbol{h}_{t-1}+\boldsymbol{U}_{\mathrm{f}} \boldsymbol{x}_{t}+\boldsymbol{b}_{\mathrm{f}}\right) \\ \boldsymbol{i}_{t}=\sigma\left(\boldsymbol{W}_{i} \boldsymbol{h}_{t-1}+\boldsymbol{U}_{\mathrm{i}} x_{t}+\boldsymbol{b}_{\mathrm{i}}\right), \\ \boldsymbol{a}_{t}=\tan h\left(\boldsymbol{W}_{\mathrm{a}} \boldsymbol{h}_{t-1}+\boldsymbol{U}_{\mathrm{a}} \boldsymbol{x}_{t}+\boldsymbol{b}_{\mathrm{a}}\right) \\ \boldsymbol{o}_{t}=\sigma\left(\boldsymbol{W}_{\mathrm{o}} \boldsymbol{h}_{t-1}+\boldsymbol{U}_{\mathrm{o}} \boldsymbol{x}_{t}+\boldsymbol{b}_{\mathrm{o}}\right), \\ \boldsymbol{C}_{t}=\boldsymbol{C}_{t-1} \odot \boldsymbol{f}_{t}+\boldsymbol{i}_{t} \cdot \boldsymbol{a}_{t}, \\ \boldsymbol{h}_{t}=\boldsymbol{o}_{t} \odot \tan h\left(\boldsymbol{C}_{t}\right), \\ \alpha_{t}=\boldsymbol{W}_{\mathrm{FO}} \tan h\left(\boldsymbol{W}_{\mathrm{FI}} \boldsymbol{h}_{t}+\boldsymbol{b}_{\mathrm{FI}}\right)+b_{\mathrm{FO}}。\end{array}\right\} $ | (8) |
式中:Wf, Wi, Wa, Wo, WFO, WFI, Uf, Ui, Ua, Uo为网络权重;bf, bi, ba, bobFI, bFO为网络偏置;Ct为LSTM网络状态变量;ht为网络中间输出;符号⊙表示哈达玛积;符号σ表示sigmoid函数,即(σ(x)=1/(1+ e-x));xt= θacc(t) θbre(t) v(t) a(t) P(t) 为网络输入向量。
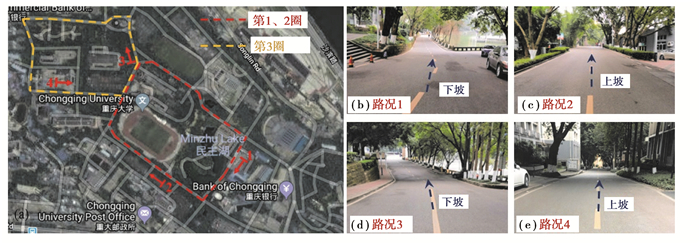
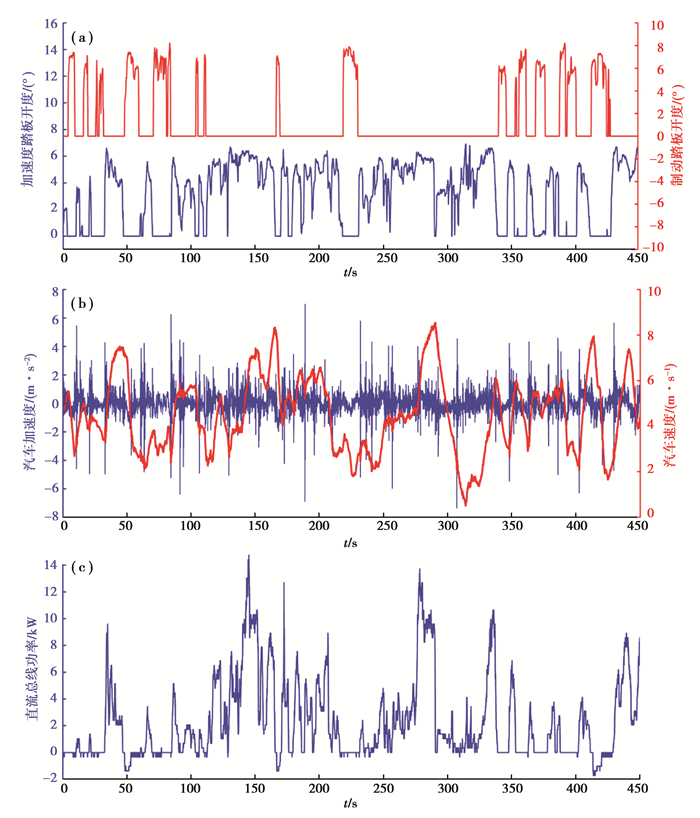
3 实验结果与讨论一辆小型燃料电池汽车被用于实车实验,为了清晰地展示估计算法的性能,一段坡度快速变化的道路被选作实验路线。图 5左侧虚线标出了实验路线,右侧列出了该路线上的4种路况。总里程为3.198 km,平均速度为16.63 km/h,最大速度为34.63 km/h。其中,第1圈的数据用作训练集,第2圈和第3圈的数据用作测试集。图 6展示了测试集部分的输入变量,由CAN总线通过10 Hz的采样频率采集。同时,为了验证该算法的有效性,真实道路坡度由坡度测量模块采集,该模块由陀螺仪和带卡尔曼滤波的倾角仪组成。
|
图 5 实车实验路线 Fig. 5 Real-world driving schedule |
|
图 6 测试集输入 Fig. 6 Input variables of the test set |
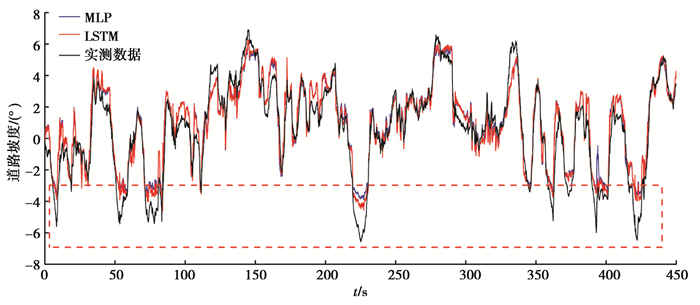
图 7展示了LSTM和MLP两种算法的估计道路坡度和真实道路坡度。同时,为了评价两种算法的性能,表 2列出了估计结果的均方根误差值(fRMSE)和皮尔逊相关系数(r),计算公式为[16]
|
图 7 LSTM和MLP算法估计结果 Fig. 7 Estimation results of LSTM and MLP |
| 表 2 智能算法的评价指标 Table 2 Statistic performance of the intelligent algorithms |
| $ f_{\text {RMSE }}=\frac{\sqrt{\sum\left(P_{i}-T_{i}\right)^{2}}}{n}, $ | (9) |
| $ r=\frac{n\left(\sum P_{i} \cdot T_{i}\right)-\left(\left(\sum P_{i}\right) \cdot\left(\sum T_{i}\right)\right)}{\sqrt{\left(n \sum P_{i}^{2}-\left(\sum P_{i}\right)^{2}\right) \cdot\left(n\left(T_{i}^{2}-\sum T_{i}\right)^{2}\right)}},$ | (10) |
式中:Pi和Ti分别为道路坡度的第i个估计值和第i个真实值;n为数据总量。
由表 2可知,两种算法的估计结果和真实数据的皮尔逊相关系数(r)皆大于0.9,因此两种智能算法都具备道路坡度的估计能力。但相比于MLP算法,LSTM算法的均方根误差值(fRMSE)更小且皮尔逊相关系数(r)更大,这意味着LSTM算法的准确性更高。由图 8可见,LSTM算法估计的坡度曲线比MLP算法估计的坡度曲线更接近真实值。这是因为LSTM算法通过网络状态量将该时刻的信息传递给下一时刻,即预测当前值时充分利用之前的信息。但在红色虚线包围的矩形部分中,即道路坡度小于-3°时,两种算法的估计值与真实值有较大的误差,表明该智能算法在汽车下陡坡时性能较差。但考虑道路坡度被应用于FCHV的能量管理策略中,当道路坡度小于-3°时,汽车往往处于刹车状态,所需功率为0。因此,当汽车下陡坡时,估计结果误差较大是可以接受的。同时,由于网络的训练和预测是分离的,整个测试集的计算在0.1 s内完成,所以该方法在实际应用时计算复杂度较低。
此外,该算法还与其他文献中的几种不同算法进行了比较,见表 3。由于各文献的实验是在不同环境下完成,汽车、传感器类型有所差别,直接比较估计结果的均方根误差值(fRMSE)是不公平的。为了减少不同实验条件对算法的影响,采用估计结果的归一化均方根误差值(fNRMSE)作为更公平的参数来比较性能,其计算方法为[17]
| $ f_{\text {NRMSE }}=\frac{f_{\text {RMSE }}}{\left|\theta_{\max }-\theta_{\min }\right|}, $ | (11) |
| 表 3 几种不同方法的归一化均方根误差值 Table 3 The normalized root mean square error of some different methods |
式中θmax和θmin分别为真实坡度的最大值和最小值。
由表 3可见,该智能算法的均方根误差值较小,仅大于文献[18]中的估计方法,但文献[18]中的估计方法利用了精确的GPS及多个传感器的信息。因此,在不使用额外传感器的情况下,该算法具有较好的估计性能。
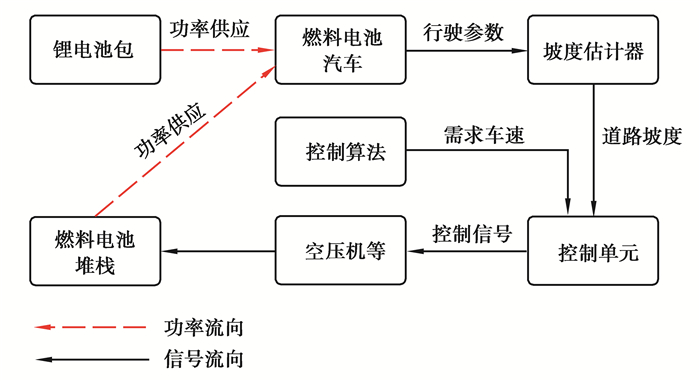
许多研究者提出,道路坡度可用于各种控制策略,以减少混合动力汽车的能耗[21]。因此,估计的实时道路坡度可用于改善FCV车辆的动态性能和燃油经济性,如图 8所示。例如,为了保持期望车速,当汽车上坡时需求功率通常大于0,当汽车下坡时需求功率通常等于0。因此,可以根据实时道路坡度及时调整燃料电池堆的输入(空气压力,氢气压力等),减轻动态响应的滞后,减少燃料消耗。
|
图 8 道路坡度在控制策略中的应用 Fig. 8 Application |
实际上,基于车辆基本参数(如电机输出转矩、电机输出转速和踏板开度等),该方法同样可用于部分其他类型的车辆,如纯电动汽车。
4 结语考虑道路坡度的时变特性,提出了一种基于长短期神经网络的道路坡度估计方法,并通过汽车行驶动力模型选择合适的行驶参数作为网络输入。该方法仅利用了CAN总线数据,不需要安装额外的传感器,适用性较强,成本较低。同时,与其他方法的比较表明,该方法可以有效地估计道路坡度值,且具有较高的精度,可以用于各种能量管理策略中。
尽管此方法能较准确地估计出当前时刻的道路坡度值,但目前有很多燃料电池汽车控制策略也利用到未来短时间内的预测数据实现前瞻性控制,所以,在此基础上,进一步设计出能够预测未来短时间内道路坡度的算法是一个可行的研究方向。
| [1] |
Tanç B, Arat H T, Baltacıoǧ lu E, et al. Overview of the next quarter century vision of hydrogen fuel cell electric vehicles[J]. International Journal of Hydrogen Energy, 2019, 44(20): 10120-10128. DOI:10.1016/j.ijhydene.2018.10.112 |
| [2] |
Zhang C Z, Liu Z T, Zhou W J, et al. Dynamic performance of a high-temperature PEM fuel cell-An experimental study[J]. Energy, 2015, 90: 1949-1955. DOI:10.1016/j.energy.2015.07.026 |
| [3] |
孙冬野, 陈元, 范曾雁. 搭载回流式动力传动系统的PHEV参数优化[J]. 重庆大学学报, 2019, 42(6): 42:1-12. Sun D Y, Chen Y, Fan Z Y. Optimization of PHEV parameters with reflux power coupling transmission system[J]. Journal of Chongqing University, 2019, 42(6): 42:1-12. (in Chinese) |
| [4] |
Ettihir K, Boulon L, Agbossou K. Energy management strategy for a fuel cell hybrid vehicle based on maximum efficiency and maximum power identification[J]. IET Electrical Systems in Transportation, 2016, 6(4): 261-268. DOI:10.1049/iet-est.2015.0023 |
| [5] |
Liu T, Hu X S, Li S E, et al. Reinforcement learning optimized look-ahead energy management of a parallel hybrid electric vehicle[J]. IEEE/ASME Transactions on Mechatronics, 2017, 22(4): 1497-1507. DOI:10.1109/TMECH.2017.2707338 |
| [6] |
Mangan S, Wang J, Wu Q H. Measurement of the road gradient using an inclinometer mounted on a moving vehicle[C]//Proceedings of IEEE International Symposium on Computer Aided Control System Design. September 20-20, 2002, Glasgow, UK. IEEE, 2002: 80-85.
|
| [7] |
汪旭明. 道路坡度测试方法试验研究[J]. 农业装备与车辆工程, 2015, 53(2): 53:6-11. Wang X M. Experimental research on test methods of road slope[J]. Agricultural Equipment & Vehicle Engineering, 2015, 53(2): 53:6-11. (in Chinese) |
| [8] |
Kock P, Weller R, Ordys A W, et al. Validation methods for digital road maps in predictive control[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(1): 339-351. DOI:10.1109/TITS.2014.2332520 |
| [9] |
Sun Y, Li L, Yan B J, et al. A hybrid algorithm combining EKF and RLS in synchronous estimation of road grade and vehicle mass for a hybrid electric bus[J]. Mechanical Systems and Signal Processing, 2016, 68/69: 416-430. DOI:10.1016/j.ymssp.2015.08.015 |
| [10] |
Kim S, Shin K, Yoo C, et al. Development of algorithms for commercial vehicle mass and road grade estimation[J]. International Journal of Automotive Technology, 2017, 18(6): 1077-1083. DOI:10.1007/s12239-017-0105-6 |
| [11] |
李光宇. 整车质量与道路坡度识别及其对纯电动汽车换挡规律的影响[D]. 长春: 吉林大学, 2016. Li G Y. Estimation of vehicle mass and road slope and their influence on shift schedule[D]. Changchun: Jilin University, 2016. (in Chinese) |
| [12] |
Yang J, Na J, Guo Y, et al. Adaptive estimation of road gradient and vehicle parameters for vehicular systems[J]. IET Control Theory & Applications, 2015, 9(6): 935-943. |
| [13] |
Li B Y, Zhang J W, Du H P, et al. Two-layer structure based adaptive estimation for vehicle mass and road slope under longitudinal motion[J]. Measurement, 2017, 95: 439-455. DOI:10.1016/j.measurement.2016.10.045 |
| [14] |
Zeng T, Zhang C Z, Hu M H, et al. Modelling and predicting energy consumption of a range extender fuel cell hybrid vehicle[J]. Energy, 2018, 165: 187-197. DOI:10.1016/j.energy.2018.09.086 |
| [15] |
Vidal C, Kollmeyer P, Chemali E, et al. Li-ion battery state of charge estimation using long short-term memory recurrent neural network with transfer learning[C]//2019 IEEE Transportation Electrification Conference and Expo (ITEC). June 19-21, 2019, Detroit, MI, USA. IEEE, 2019: 1-6.
|
| [16] |
李哲, 郑玲, 胡一明, 等. 轮毂驱动电动汽车振动负效应及抑制方法[J]. 重庆大学学报, 2019, 42(2): 20-29. Li Z, Zheng L, Hu Y M, et al. Negative vibration effects of in-wheel motor electric vehicles and the method for suppressing them[J]. Journal of Chongqing University, 2019, 42(2): 20-29. (in Chinese) |
| [17] |
Hari Krishna E, Sivani K, Ashoka Reddy K. On the use of EMD based adaptive filtering for OFDM channel estimation[J]. AEU-International Journal of Electronics and Communications, 2018, 83: 492-500. DOI:10.1016/j.aeue.2017.11.002 |
| [18] |
Sahlholm P, Henrik Johansson K. Road grade estimation for look-ahead vehicle control using multiple measurement runs[J]. Control Engineering Practice, 2010, 18(11): 1328-1341. DOI:10.1016/j.conengprac.2009.09.007 |
| [19] |
McIntyre M L, Ghotikar T J, Vahidi A, et al. A two-stage Lyapunov-based estimator for estimation of vehicle mass and road grade[J]. IEEE Transactions on Vehicular Technology, 2009, 58(7): 3177-3185. DOI:10.1109/TVT.2009.2014385 |
| [20] |
Liao X Y, Huang Q G, Sun D H, et al. Real-time road slope estimation based on adaptive extended Kalman filter algorithm with in-vehicle data[C]//201729th Chinese Control And Decision Conference (CCDC). May 28-30, 2017, Chongqing. IEEE, 2017: 6889-6894.
|
| [21] |
Xu S B, Li S E, Cheng B, et al. Instantaneous feedback control for a fuel-prioritized vehicle cruising system on highways with a varying slope[J]. IEEE Transactions on Intelligent Transportation Systems, 2017, 18(5): 1210-1220. DOI:10.1109/TITS.2016.2600641 |
 2021, Vol. 44
2021, Vol. 44


