近年来,基于全氟磺酸质子交换膜(proton exchange membrane, PEM)的低温燃料电池取得了巨大的进展[1-2],燃料电池汽车等基于质子交换膜燃料电池(PEMFC)的产品已经实现了小规模的商业化。质子交换膜燃料电池具有启动速度快、效率高、功率密度大等优点[3],然而,它的大规模商业化受限于材料成本、系统集成和燃料需求等几个因素[4]。与PEMFC相比,碱性阴离子交换膜燃料电池(anion exchange membrane fuel cell, AEMFC)因其碱性工作环境可以使用非贵金属催化剂以及具有较高的电化学动力学特性[5],在近年来受到了国内外的广泛关注[6-7]。目前,AEMFC面临着功率密度、水热管理、耐久性、催化剂选择和膜电极(membrane electrode assembly, MEA)制造等方面的挑战[8-14]。与PEMFC类似,AEMFC的性能取决于MEA中水的分布,因为大多数传输特性(如离子电导率、气体扩散率等)对水的存在非常敏感[15]。对于AEMFC,水在阳极生成,阴极消耗,并在膜中传输,如果阳极生成的水没有及时排出,会稀释KOH电解液以及造成水淹现象,导致性能下降;如果阴极水含量较多,也会稀释KOH电解液,过少会减缓阴极的反应。与PEMFC水管理丰富的研究成果不同,AEMFC水管理的相关研究文献较少,其中Li等[16]通过离线测量的方法测试总结出Tokuyama A201型碱性阴离子交换膜的传输特性;Deng等[17]通过实验表明高催化剂、适当入口气体湿度可以提升电池性能;在Duan等[18]的实验研究中,对A201膜在不同温度下的导电率进行了测量,并给出了膜中水含量与气态水活性、膜的电导率与膜中水含量的函数关系,实验为研究提供了参考数据,但不能直观地观察电池内部水传输状态。Huo等[18]的研究基于Li等的实验数据进行建模,研究主要集中在液态水的输运,而对水在电极中的作用缺乏严谨的建模和验证。
笔者通过制备MEA,组装实验室规模的AEMFC单电池,完成特定条件下性能测试,利用CFD软件COMSOL旨在建立一个计算高效的二维稳态等温模型,模型综合考虑了水在膜中的扩散和电渗拖拽两种传输机制,研究了电流密度、进气湿度对电池性能以及电池内部水传输和水分布的影响。
1 实验设计实验中使用的MEA采用CCM(catalyst coated membrane)型膜电极和两极气体扩散层(gas diffusion layer, GDL)、微孔层(Microporous Layer, MPL)组成。实验过程中使用的设备和材料规格分别如表 1和表 2所示。
| 表 1 膜电极制备和单个燃料电池测试设备参数 Table 1 Equipment used for catalyst layer fabrication and single fuel cell tests |
| 表 2 制备MEA所需材料参数 Table 2 Materials for MEA fabrication |
MEA的制造过程包括以下步骤:
步骤1 制备催化剂墨水。对于5 cm×5 cm的CCM活性区域,所需催化剂的标称质量为150 mg,其相应的电解质溶液/溶剂(去离子水)体积分别为1.2 mL和3.0 mL。将上述规格的催化剂、去离子水和电解质加入烧杯中,超声处理10 min。水浴(室温)条件下,在搅拌器中搅拌12~24 h使催化剂和电解质溶液均匀混合。
步骤2 切割膜并称质量,在真空烘箱中进行干燥处理。
步骤3 将催化剂墨水装入喷枪之前,超声处理10 min。将干燥的膜安装到MEA框架中,该框架由3片不锈钢板和8个夹子组成。使用喷枪手动进行喷涂,采用垂直和水平交替喷涂的方法以实现尽可能均匀的喷涂。喷涂膜的一面后,将其放入真空干燥箱干燥。
步骤4 重复步骤3以涂覆膜的另一面。
步骤5 最后,将干燥的CCM与两极MPL和GDL热压成MEA,将MEA存储在2个装有Ar气的塑料袋中。
步骤6 每个MEA在首次使用前都要进行激活,该实验将电池的电压设置在一定范围内运行70 min后性能达到稳定。
2 数学模型 2.1 模型假设笔者针对典型的碱性阴离子交换膜燃料电池(AEMFC),建立了一个二维稳态等温模型。为了简化分析做了以下假设:
1) 电池内部温度处处相等;
2) 反应气体被视为理想气体,适用理想气体方程;
3) 燃料电池在稳态条件下运行,流动为层流;
4) MEA和双极板材料均具有各向同性和均匀性。
2.2 控制方程在模型中求解了O2,H2,H2O(包括膜态水和气态水)和带电粒子OH-,e-的守恒方程。由于在实验装置中产生的电流小且能够有效地进行传热,所以假设工作温度在计算域内均匀分布(等温状态),求解过程中不考虑能量守恒方程。由于产生电流小,MEA中液态水的形成和影响也被忽略。
连续性方程即质量守恒方程:
| $ \nabla \cdot(\rho u)=S_{g}, $ | (1) |
式中:ρ为燃料/氧化剂的混合气密度;u为反应气体的流速;Sg为源项,在催化层为反应物和生成物质量变化之和,在其他区域为0。
气体组分守恒:
| $ \nabla \cdot\left\{-\rho_{g} D_{i}^{\mathrm{m}}\left(\nabla \omega_{i}+\omega_{i} \frac{\nabla M_{\mathrm{n}}}{M_{\mathrm{n}}}\right)\right\}=S_{\mathrm{o}}, $ | (2) |
| $ D_{i}^{\mathrm{m}}=\frac{1-\omega_{i}}{\sum\nolimits_{k \neq i} \frac{x_{k}}{D_{i k}}} , $ | (3) |
| $ M_{\mathrm{n}}=\left(\sum\limits_{i} \frac{\omega_{i}}{M_{i}}\right)^{-1} , $ | (4) |
| $ \rho_{g}=\frac{P\;M_{\mathrm{n}}}{R T}。$ | (5) |
式中:ωi为质量分数;Dim为扩散系数;Mn为平均分子质量;Mi为相对分子质量;ρg为密度;x为摩尔分数。
催化层中各组分源项So可由方程(6)(7)(8)计算。
| $ S_{\mathrm{H}_{2}}=\left\{\begin{array}{c} -\frac{i_{\mathrm{a}}}{2 F} M_{\mathrm{H}_{2}}, \text { in }\quad \mathrm{aCL} ; \\ 0, \text { other }。\end{array}\right. $ | (6) |
| $ S_{\mathrm{O}_{2}}=\left\{\begin{array}{c} -\frac{i_{\mathrm{c}}}{4 F} M_{\mathrm{O}_{2}}, \text { in } \quad \mathrm{cCL} ; \\ 0, \text { other }。\end{array}\right. $ | (7) |
| $ S_{\mathrm{H}_{2} \mathrm{O}}=\left\{\begin{array}{c} \frac{i_{\mathrm{a}}}{F} M_{\mathrm{H}_{2} \mathrm{O}}-\rho_{\mathrm{m}} \kappa_{\mathrm{pc}}\left(\lambda_{\mathrm{e}}-\lambda\right) M_{\mathrm{H}_{2} \mathrm{O}}, \text { in } \quad \mathrm{aCL} ; \\ -\frac{i_{\mathrm{c}}}{2 F} M_{\mathrm{H}_{2} \mathrm{O}}-\rho_{\mathrm{m}} \kappa_{\mathrm{pc}}\left(\lambda_{\mathrm{e}}-\lambda\right) M_{\mathrm{H}_{2} \mathrm{O}}, \text { in } \quad \mathrm{cCL}_{0}。\end{array}\right. $ | (8) |
式中:ia和ic分别为阳极和阴极电流密度;κpc为相变速率;λe为饱和膜态水含量;λ为膜态水含量;F为法拉第常数,取值96 485 C/mol; aCL和cCL分别表示阳极和阴极催化层。
膜态水守恒:
| $ \nabla \cdot\left(-\rho_{\mathrm{m}} D_{\lambda} \nabla \lambda+n_{d} \frac{J}{F}\right)=S_{d}, $ | (9) |
式中:ρm为膜的密度;J为电流密度。膜态水含量λ定义为[19]:当303.15 < T < 313.15时,
λ=1.401-0.004T-(0.23T-90.824)a-(0.57T-130.796)a2+(0.48T-111.312)a3。
当313.15 < T < 323.15时,
| $ \lambda=4.908-0.0153 T-(0.205 T-87.596 .824) a-(0.85 T-313.878) a^{2}-(0.48 T-189.312) a^{3} 。$ | (10) |
Dλ为水扩散系数,定义为[20]
| $ D_{\lambda}=0.0051 \lambda \cdot T-1.44 \lambda \cdot 10^{-10}。$ | (11) |
nd为电渗系数,与膜态水含量λ有关,通过对实验数据[16]进行拟合得到:
| $ n_{d}=0.183 \lambda+1.3 \text { , } $ | (12) |
源项Sd的计算式为
| $ S_{d}=\rho_{\mathrm{m}} \kappa_{\mathrm{pc}}\left(\lambda_{\mathrm{e}}-\lambda\right)。$ | (13) |
电荷守恒:
考虑的带电粒子为离子和电子,电荷守恒分别以离子势和电势表示,即
| $ \nabla \cdot\left(-\sigma_{\mathrm{m}} \nabla \phi_{\mathrm{m}}\right)=S_{\mathrm{m}}, $ | (14) |
| $ \nabla \cdot\left(-\sigma_{\mathrm{s}} \nabla \varphi_{\mathrm{s}}\right)=S_{\mathrm{s}} , $ | (15) |
| $ S_{\mathrm{m}}+S_{\mathrm{s}}=0。$ | (16) |
式中:ϕm为离子势;φs为电势;σm为离子传导率;σs为电子传导率;S为在催化剂层中产生的局部电流。
在催化层中进行两种电化学反应,即阳极氢氧化反应(HOR):
| $ \mathrm{H}_{2}+2 \mathrm{OH}^{-} \rightarrow \mathrm{H}_{2} \mathrm{O}+2 \mathrm{e}^{-}, E^{0}=0.83 \mathrm{~V}, $ | (17) |
阴极氧化还原反应(ORR):
| $ \frac{1}{2} \mathrm{O}_{2}+\mathrm{H}_{2} \mathrm{O}+2 \mathrm{e}^{-} \rightarrow 2 \mathrm{O} \mathrm{H}^{-}, E^{0}=0.40 \mathrm{~V}。$ | (18) |
阳极和阴极动力学表达式类型由浓度相关动力学决定:
| $ i_{\mathrm{a}}=a_{\mathrm{va}} \cdot i_{\mathrm{e}, \mathrm{a}}\left[C_{\mathrm{R}} \cdot \exp \left(\frac{\alpha_{\mathrm{a}} F}{R T} \eta\right)-C_{0} \cdot \exp \left(-\frac{\alpha_{\mathrm{c}} F}{R T} \eta\right)\right] 。$ | (19) |
| $ i_{\mathrm{c}}=a_{\mathrm{vc}} \cdot i_{\mathrm{e}, \mathrm{c}}\left[C_{\mathrm{R}} \cdot \exp \left(\frac{\alpha_{\mathrm{a}} F}{R T} \eta\right)-C_{0} \cdot \exp \left(-\frac{\alpha_{\mathrm{c}} F}{R T} \eta\right)\right], $ | (20) |
| $ \eta=\varphi_{\mathrm{s}}-\varphi_{1}-E^{0}。$ | (21) |
式中:ava, avc分别为阳极和阴极反应面积;ie, a, ie, c分别为阳极和阴极交换电流密度;αa, αc分别为阳极电荷转移系数和阴极电荷转移系数;CR, C0分别为还原物和氧化物的浓度;η为过电压;R为理想气体常数,取值8.314 J/(mol·K)。
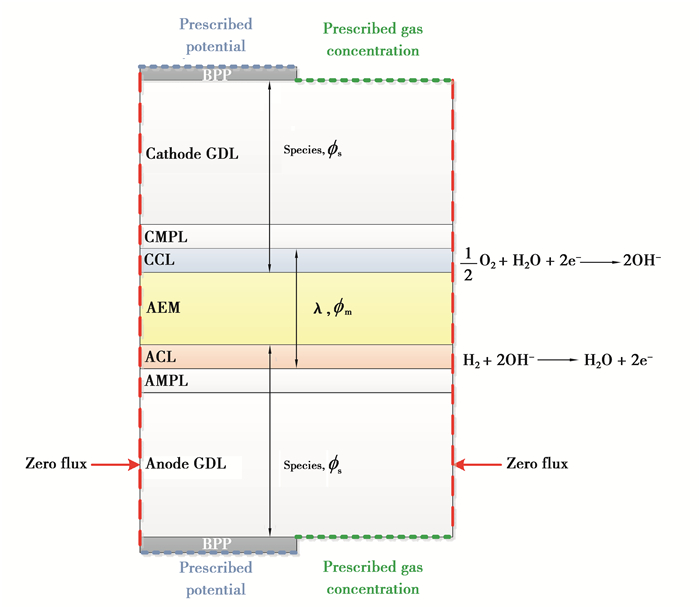
2.3 计算域和边界条件图 1为碱性阴离子交换膜燃料单电池模型示意图,该模型的计算域包括双极板(BPP)、气体扩散层(GDL)、微孔层(MPL)、催化剂层(CL)和碱性交换膜(AEM),由于电池结构的对称特性,计算域设置为半电池,模型具体参数见表 3。
|
图 1 计算域和边界条件 Fig. 1 Computational domain and boundary conditions |
| 表 3 燃料电池的结构参数和材料参数 Table 3 Cell properties |
利用COMSOL软件求解控制方程组,将两个垂直边界上所有主要变量设置为零通量,对两极双极板设置电位如下:
| $ \varphi_{\mathrm{S}}^{\mathrm{a}}=0 , $ | (22) |
| $ \varphi_{\mathrm{S}}^{\mathrm{c}}=V_{\text {cell }}。$ | (23) |
式中:φSa是阳极双极板边界电位;φSc是阴极双极板边界电位。
进气口组分的摩尔分数设置如下:
| $ x_{\mathrm{H}_{2} \mathrm{O}, \mathrm{in}}^{\mathrm{a}}=\varphi_{\mathrm{a}} \frac{P_{\mathrm{in}}}{P_{\mathrm{in}}^{\mathrm{a}}}, $ | (24) |
| $ x_{\mathrm{H}_{2}, \mathrm{in}}^{\mathrm{a}}=1-x_{\mathrm{H}_{2} \mathrm{O}, \mathrm{in}}^{\mathrm{a}}, $ | (25) |
| $ x_{\mathrm{H}_{2} \mathrm{O}, \mathrm{in}}^{\mathrm{c}}=\varphi_{\mathrm{c}} \frac{P_{\mathrm{in}}}{P_{\mathrm{in}}^{\mathrm{c}}}, $ | (26) |
| $ x_{\mathrm{O}_{2}, \mathrm{in}}^{\mathrm{c}}=0.209\left(1-x_{\mathrm{H}_{2} \mathrm{O}, \mathrm{in}}^{\mathrm{c}}\right), $ | (27) |
| $ x_{\mathrm{N}_{2}, \mathrm{in}}^{\mathrm{c}}=1-x_{\mathrm{H}_{2} \mathrm{O}, \mathrm{in}}^{\mathrm{c}}-x_{\mathrm{O}_{2}, \mathrm{in} }^{\mathrm{c}}。$ | (28) |
式中:φa和φc分别为阳极进气相对湿度和阴极进气相对湿度。
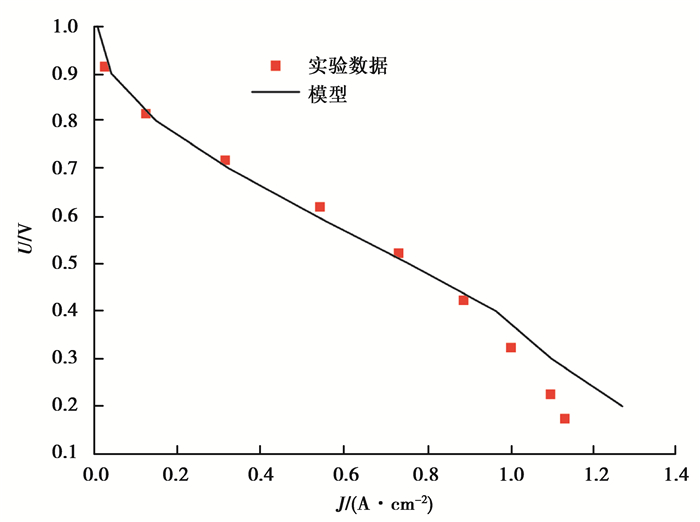
3 结果与讨论 3.1 模型验证为了验证模型的正确性和真实性,对其进行了实验对照。如图 2所示,在特定条件(阳极进气相对湿度φa=阴极进气相对湿度φc=95%,T=323.15 K,Pa=Pc=2×105Pa)下模型预测的极化曲线与实验数据吻合良好,并且可以看出燃料电池3个工作区域的特点:活化极化、欧姆极化、浓差极化。证明了模型的合理性。
|
图 2 实验与模拟对比 Fig. 2 Model validation |
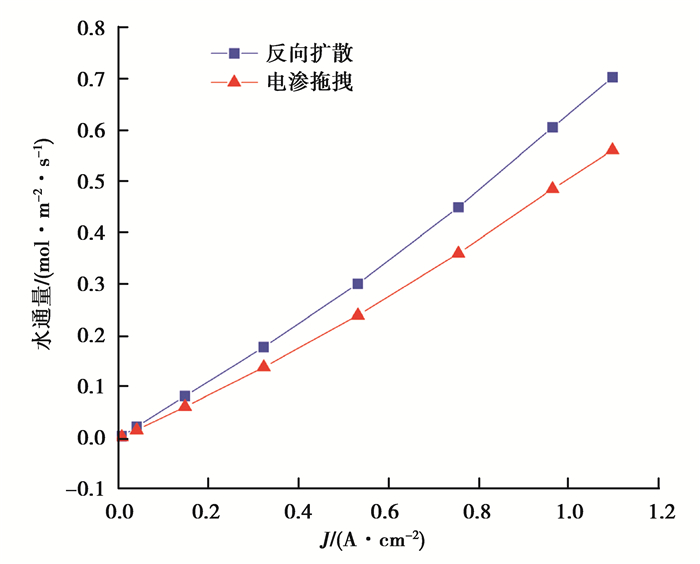
图 3为电池在特定条件(φa=φc=95%,T=323.15 K,Pa=Pc=2×105Pa)下水的迁移通量的变化。由于阳极产生水和阴极消耗水的特性,水的扩散方向是由阳极向阴极。随着电流密度的增加,扩散通量和电渗通量都增大,说明电流密度的增加对膜两侧的扩散作用和电渗作用都加强。由此看来,电流密度较小时,阳极侧水量有限,两极浓度差较小,扩散作用较弱,随着电流密度增加,阳极反应产生并积累了较多的水,浓度差增大,扩散作用逐渐增强,电渗通量与电流成正比,电流密度增加加强了电渗作用,由于扩散作用比电渗作用增强快,使得水从阳侧到阴极的净迁移增强。
|
图 3 水的迁移通量随电流密度的变化 Fig. 3 The flux of water with various current densities |
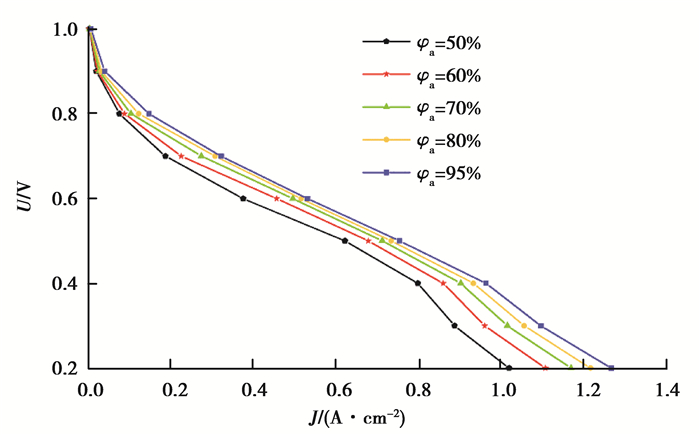
图 4为在温度为323.15 K,阴极和阳极进气压力均为2×105 Pa,阴极充分加湿(φc=95%)的情况下,电池性能随着阳极进口相对湿度(φa)变化的情况。由图 4可以看出,随着阳极进气湿度从50%增加到95%,阳极进气相对湿度越大,电流密度越大,但随着阳极进气湿度逐渐增大,对性能提升的作用越来越小。由极化曲线可以看出,当阳极进气相对湿度增加,AEMFC的欧姆极化损失和浓差极化损失减小,说明动力学在碱性介质中的水依赖性,进气湿度越大,动力学损失越小,因此对阳极适当加湿是必要的。
|
图 4 不同阳极进口湿度的极化曲线 Fig. 4 Polarization curves at different anode inlet relative humidity |
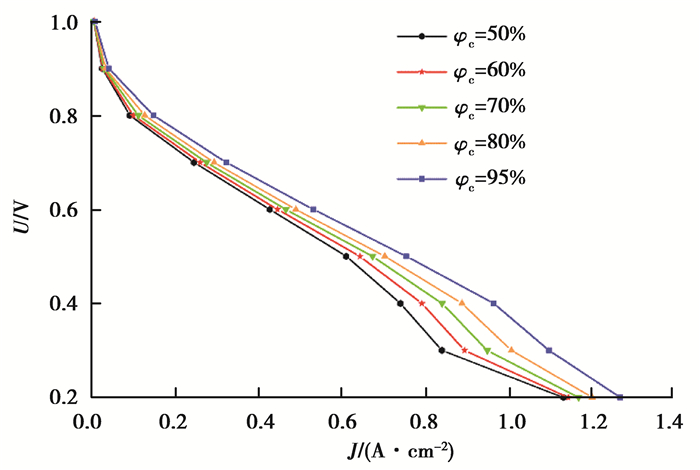
由于阴极反应消耗水,为了防止阴极脱水需要进行适当的加湿,从而提高电池性能。在保持其他条件不变,阳极进气充分加湿(φa=95%)的情况下,如图 5分析了不同阴极进气加湿水平下电池电压随电流密度的变化。由图 5可以看出,在低电流密度时,不同进气湿度的极化曲线相似,随着电流密度的增加,电池电压的差异越来越明显,此阶段是由欧姆极化引起的,由于此模拟设定阳极进气相对湿度和进气组分浓度相同,可以推断欧姆损失的变化是由阴极相对湿度引起的,即阴极反应不断消耗水,造成阴极湿度减小,电解质膜局部干燥,欧姆阻抗增大,从而导致电池性能降低。在高电流密度时,阴极进气相对湿度过小会产生较大的浓度极化损失。由图 5看出,阴极加湿对电池性能的提升主要体现在高电流密度,说明阴极加湿减小了阴极侧的质量传输损失。
|
图 5 不同阴极进口湿度的极化曲线 Fig. 5 Polarization curves at different cathode inlet relative humidity |
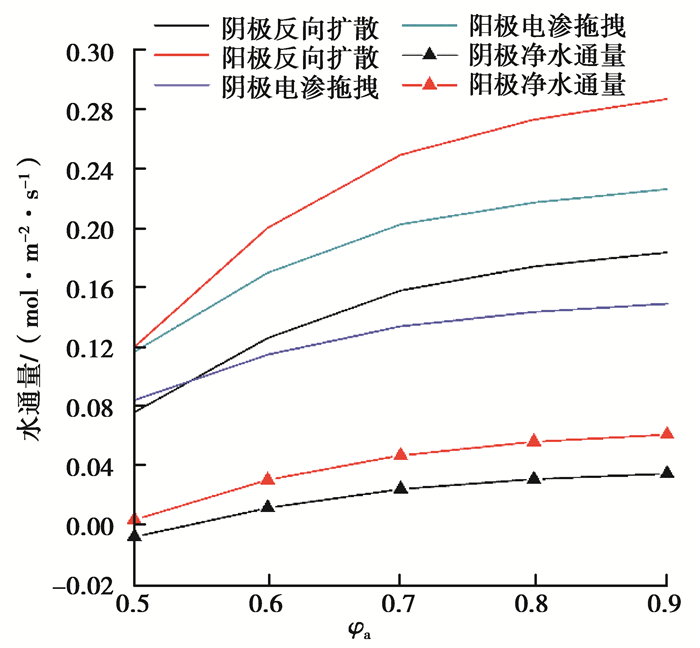
图 6为在温度为323.15 K,电压为0.6 V,阴极和阳极进气压力均为2×105 Pa,阴极充分加湿(φc=90%)的情况下,水的迁移通量随阳极进气加湿的变化情况。由图 6可以看到,随着阳极进气相对湿度增大,膜两侧电渗通量和扩散通量均增大,扩散通量在低湿度(50%~70%)下随着湿度增加得相对迅速;随着阳极进气湿度的增大,净迁移通量逐渐增大。这说明在0.6 V的电压条件下,阳极湿度越高,电流密度越高,电渗通量越大,随着阳极进气湿度增大,膜两侧的浓度差增大,扩散作用增强,且扩散通量比电渗作用增强得快,增加阳极湿度可以加快阳极侧的水向阴极侧传输,从而为阴极侧提供反应所需要的水。
|
图 6 不同阳极进口湿度的水通量 Fig. 6 Water transport with anode inlet relative humidity from 50% to 90% |
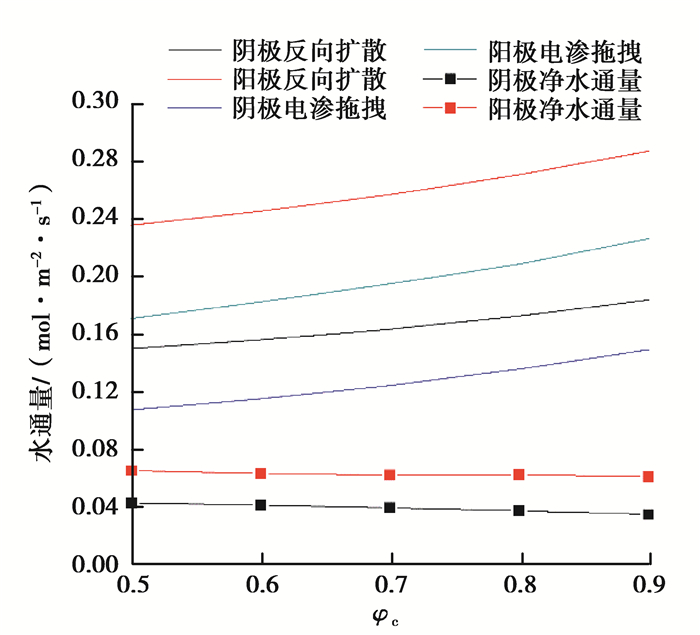
图 7为其他工况不变,阳极充分加湿(φa=90%)的情况下,水的迁移通量随阴极进气加湿的变化情况。由图 7可以看到,随着阴极进气相对湿度增大,膜两侧电渗通量和扩散通量均增大;随着阴极进气湿度的增大,净迁移量变化不明显,说明随着阴极进气湿度的增大,水从阳极侧向阴极侧的传输速率稳定。
|
图 7 不同阴极进口湿度的水通量 Fig. 7 Water transport with cathode inlet relative humidity from 50% to 90% |
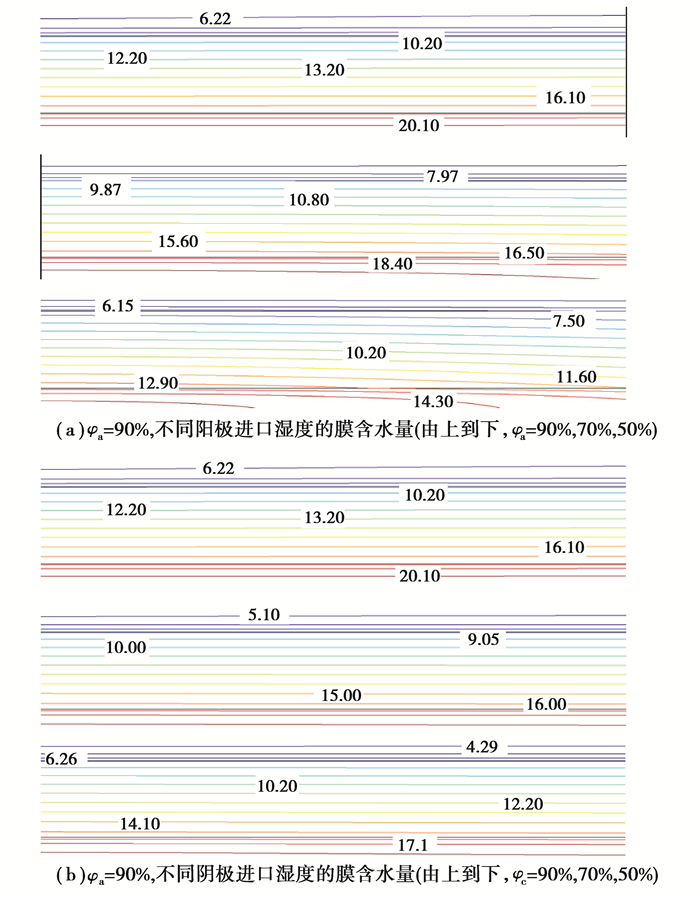
图 8表示不同进口湿度的膜含水量。图 8(a)表示阴极进气充分湿润(φc=90%),不同阳极进气相对湿度的情况下膜中含水量的分布图。从图 8(a)可以看出,当阳极进气相对湿度从90%下降到50%时,阳极侧催化层含水量较为明显地从20左右下降到14左右,膜中的含水量大范围下降说明降低阳极进气湿度不仅使膜的阳极侧含水量降低,对扩散作用存在一定的影响,也使得膜中含水量下降,影响离子传导能力,电池性能降低。图 8(b)表示阳极进气充分湿润(φa=90%),不同阴极进气相对湿度的情况下膜中含水量的分布图。从图 8(b)可以看出,当阴极进气相对湿度从90%下降到50%时,同图 8(a)趋势相同,含水量均有下降,不同的是此下降幅度不明显,说明在0.6 V电压对应的电流密度下,欧姆极化损失差异不明显,印证了3.3图 5的结果。
|
图 8 不同进口湿度的膜含水量 Fig. 8 Membrane water content with different inlet humidity |
通过制备MEA并组装测试了AEMFC单电池性能,建立了AEMFC二维稳态等温模型,通过实验和模拟得出以下结论:
1) 实验数据和模型预测结果吻合良好,为AEMFC水管理等研究工作提供了一个高效的工具,未来可利用进出水平衡实验对模型进一步优化。
2) 随着电流密度的增加,扩散作用和电渗拖拽作用均增强。
3) 提高阳极进气湿度可以加快水从阳极到阴极的净迁移。
4) 两极进气相对湿度过小都会影响电池性能,较低电流密度下阴极进气湿度对电池性能影响较小,在较高电流密度下阴极进气湿度过小会造成较大的欧姆极化损失和浓差极化损失。
5) 该模型假设电池内部温度均匀分布,此假设与实际情况不符,拟在后续设计中引入传热过程,优化模型设计。
| [1] |
Kiani M, Zhang J, Luo Y, et al. Recent developments in electrocatalysts and future prospects for oxygen reduction reaction in polymer electrolyte membrane fuel cells[J]. Journal of Energy Chemistry, 2018, 27(4): 1124-1139. DOI:10.1016/j.jechem.2018.01.019 |
| [2] |
郑道友, 钟振忠. 微型燃料电池设计与三维数值模拟分析[J]. 重庆大学学报, 2014, 37(Z2): 264-270. Zheng D Y, Zhong Z Z. Design and 3d numerical simulation of micro fuel cell[J]. Journal of chongqing university, 2014, 37(Z2): 264-270. (in Chinese) |
| [3] |
Han I S, Park S K, Chung C B. Modeling and operation optimization of a proton exchange membrane fuel cell system for maximum efficiency[J]. Energy Conversion and Management, 2016, 113: 52-65. DOI:10.1016/j.enconman.2016.01.045 |
| [4] |
Jiao K, Ni M. Challenges and opportunities in modelling of proton exchange membrane fuel cells (PEMFC)[J]. International Journal of Energy Research, 2017, 41(13): 1793-1797. DOI:10.1002/er.3798 |
| [5] |
Brouzgou A, Podias A, Tsiakaras P. PEMFCs and AEMFCs directly fed with ethanol: a current status comparative review[J]. Journal of Applied Electrochemistry, 2013, 43(2): 119-136. DOI:10.1007/s10800-012-0513-2 |
| [6] |
Varcoe J R, Atanassov P, Dekel D R, et al. Anion-exchange membranes in electrochemical energy systems[J]. Energy Environ Sci, 2014, 7(10): 3135-3191. DOI:10.1039/C4EE01303D |
| [7] |
赵卓, 吴爱华, 栾胜基, 等. 燃料电池用阴离子交换膜的研究进展[J]. 高分子通报, 2015(8): 52-62. Zhao Z, Wu A H, Luan S J, et al. Research and development of anion exchange membrane for fuel cell[J]. Polymer Bulletin, 2015(8): 52-62. (in Chinese) |
| [8] |
Gottesfeld S, Dekel D R, Page M, et al. Anion exchange membrane fuel cells: Current status and remaining challenges[J]. Journal of Power Sources, 2018, 375: 170-184. DOI:10.1016/j.jpowsour.2017.08.010 |
| [9] |
Pan Z F, An L, Zhao T S, et al. Advances and challenges in alkaline anion exchange membrane fuel cells[J]. Progress in Energy and Combustion Science, 2018, 66: 141-175. DOI:10.1016/j.pecs.2018.01.001 |
| [10] |
Cheng J, He G H, Zhang F X. A mini-review on anion exchange membranes for fuel cell applications: Stability issue and addressing strategies[J]. International Journal of Hydrogen Energy, 2015, 40(23): 7348-7360. DOI:10.1016/j.ijhydene.2015.04.040 |
| [11] |
Krewer U, Weinzierl C, Ziv N, et al. Impact of carbonation processes in anion exchange membrane fuel cells[J]. Electrochimica Acta, 2018, 263: 433-446. DOI:10.1016/j.electacta.2017.12.093 |
| [12] |
Ponce-González J, Whelligan D K, Wang L Q, et al. High performance aliphatic-heterocyclic benzyl-quaternary ammonium radiation-grafted anion-exchange membranes[J]. Energy & Environmental Science, 2016, 9(12): 3724-3735. |
| [13] |
Zhu L, Pan J, Wang Y, et al. Multication side chain anion exchange membranes[J]. Macromolecules, 2016, 49(3): 815-824. DOI:10.1021/acs.macromol.5b02671 |
| [14] |
Amel A, Gavish N, Zhu L, et al. Bicarbonate and chloride anion transport in anion exchange membranes[J]. Journal of Membrane Science, 2016, 514: 125-134. DOI:10.1016/j.memsci.2016.04.027 |
| [15] |
Hibbs M R, Hickner M A, Alam T M, et al. Transport properties of hydroxide and proton conducting membranes[J]. Chemistry of Materials, 2008, 20(7): 2566-2573. DOI:10.1021/cm703263n |
| [16] |
Li Y S, Zhao T S, Yang W W. Measurements of water uptake and transport properties in anion-exchange membranes[J]. International Journal of Hydrogen Energy, 2010, 35(11): 5656-5665. DOI:10.1016/j.ijhydene.2010.03.026 |
| [17] |
Deng H, Wang D W, Wang R F, et al. Effect of electrode design and operating condition on performance of hydrogen alkaline membrane fuel cell[J]. Applied Energy, 2016, 183: 1272-1278. DOI:10.1016/j.apenergy.2016.09.091 |
| [18] |
Duan Q J, Ge S H, Wang C Y. Water uptake, ionic conductivity and swelling properties of anion-exchange membrane[J]. Journal of Power Sources, 2013, 243: 773-778. DOI:10.1016/j.jpowsour.2013.06.095 |
| [19] |
Huo S, Deng H, Chang Y F, et al. Water management in alkaline anion exchange membrane fuel cell anode[J]. International Journal of Hydrogen Energy, 2012, 37(23): 18389-18402. DOI:10.1016/j.ijhydene.2012.09.074 |
| [20] |
Ong A L, Saad S, Lan R, et al. Anionic membrane and ionomer based on poly(2, 6-dimethyl-1, 4-phenylene oxide) for alkaline membrane fuel cells[J]. Journal of Power Sources, 2011, 196(20): 8272-8279. DOI:10.1016/j.jpowsour.2011.06.015 |
 2021, Vol. 44
2021, Vol. 44


