2. 重庆科技学院 机械与动力工程学院, 重庆 401331
2. School of Mechanical and Power Engineering, Chongqing University of Science and Technology, Chongqing 401331, P. R. China
智轨电车是一种融合了现代有轨电车和公共汽车各自优势的交通工具,投资成本低、建设周期短、运营灵活[1]。然而,由于智轨电车具有3节及以上编组,整体车身超过20 m,在车辆行驶过程中极易出现跑偏、甩尾及双向驾驶性能不一致等现象,需对车轴及铰接盘角度进行精密测量[2]。
目前采用角度和尺寸测量仪进行智轨电车角度测量,整车完成测量耗时1 d,效率低、劳动强度大且测量误差大[3]。为实现智轨电车车轮及铰接盘角度快速、精密测量,提出了一种基于四目立体视觉的测量框架,解决车身过长引起的测量视野范围问题;通过方向性标靶的识别及二次优化,解决车轮目标空间姿态的高精度求解问题;通过空间向量计算各轮转向角及铰接盘夹角,构建相关角度视觉测量模型;通过V3D模型建立车身平面测量基准,解决车厢前后左右不平产生的误差,实现了智轨电车车轮及铰接盘角度大视野、高效率、高精度测量。
1 智轨电车的几何参数智轨电车角度测量需构造测量基准,定义电车在车轮零转向角时为零位置状态,以车身平面为基准建立各角度间数学关系式,如图 1所示,连接同一车厢左右两侧车轮位置得到两个轮毂线AC、BD,将轮毂线的中点E、F连接以得到虚轨对准线EF,取虚轨对准线的垂线GH,由车轮法向的法向量与垂线得到夹角∠A、∠B、∠C、∠D,视为车轮转向角。将虚轨对准线EF延长,与相邻车厢的虚轨对准线形成夹角∠β1、∠β2,视为铰接盘转向角。

|
图 1 几何参数示意图 Fig. 1 Schematic diagram of geometric parameters |
基于空间向量,以车身平面为基准建立车轮转动角度、铰接盘夹角及其零度,获取智轨电车几何参数,不受零点偏移影响,可自动消除由于车厢前后左右不水平产生的测量误差,提高测量精度。
2 四目立体视觉利用4台相机分别识别各车轮上的目标靶,实现大视野景象拍摄。相机间安装位置关系如图 1,相机1,2和相机3,4分别位于车厢同一侧,相机1,4采用对角线的安装方式。采用的4台相机,需对相机内外参数进行标定。
相机内参数表示线性透视变换参数和非线性畸变参数, 线性透视变换参数表示计算机图像和相机坐标系间的关系[4-7],如式(1)。
| $ \boldsymbol{A}=\left[\begin{array}{ccc} a_{x} & r & u_{0} \\ 0 & a_{y} & v_{0} \\ 0 & 0 & 1 \end{array}\right], $ | (1) |
式中:(u0, v0)为计算机图像原点; r为图像物理坐标u轴和v轴不垂直因子; ax,ay分别为u轴、v轴的尺度因子。
相机外参数表示相机坐标系和世界坐标系间的位姿关系,包含旋转矩阵和平移矩阵:
| $ \boldsymbol{R}=\left[\begin{array}{lll} r_{1} & r_{2} & r_{3} \\ r_{4} & r_{5} & r_{6} \\ r_{7} & r_{8} & r_{9} \end{array}\right], \boldsymbol{T}=\left[\begin{array}{c} t_{x} \\ t_{y} \\ t_{z} \end{array}\right], $ | (2) |
式中:R表示综合旋转矩阵;T表示综合平移向量,r1-r9、tx-tz分别表示R,T展开数值。
考虑相机径向畸变,首先通过1维平台,分别实现单相机内参数TSAI标定[8-11]。然后将4台相机分别安装在工字形相机架四端进行多相机标定,标定步骤如下:
1) 完成相机2相对于相机1关系的R12T12标定。
2) 完成相机4相对于相机2关系的R24T24标定,计算得到相机4相对于相机1关系的R14T14。
3) 完成相机3相对于相机4关系的R43T43标定,计算得到相机3相对于相机1关系的R13T13。
系统外参数包含3对相机间的相对位置关系,求解原理相同。以相机1和相机2求解为例。现场标定时,保证4台相机同时拍摄到对应标靶上的合作标识特征,相机1坐标系与相机2坐标系间的变换矩阵就是相机外参R12T12。因此,只需求解两相机坐标系下相同点数的三维点集间的刚性变换关系即可求得相机外参R12T12 [12]。
于是问题简化为
| $ \boldsymbol{N}_{i}^{\prime}=\boldsymbol{R}_{12} N_{i}+\boldsymbol{T}_{12}+\boldsymbol{Z}_{i}, $ | (3) |
式中:N′i为相机2坐标系下的三维点集;R12为3×3旋转矩阵;Ni为相机1坐标系下的三维点集;T12为平移向量;Zi为图像噪声,可通过递归算法排除图像噪点,提高测量精度。
则目标函数为
| $ \boldsymbol{Q}\left(\boldsymbol{R}_{12}, \boldsymbol{T}_{12}\right)=\sum\limits_{i=1}^{N}\left|X_{i}^{\prime}-\left(\boldsymbol{R}_{12} \boldsymbol{N}_{i}+\boldsymbol{T}_{12}\right)\right|^{2}。$ | (4) |
通过奇异值分解求得目标解,提高测量结果准确性。其余待解参数同理。
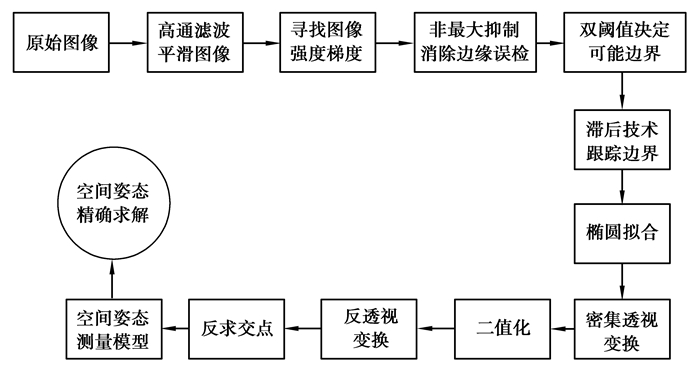
3 标靶图高精度识别及优化以圆形和圆环为合作标识,设计平面标靶如图 2所示,减小由机械加工造成的精度影响。标靶图高精度识别及优化流程如图 3所示。分为合作标识识别及优化处理两部分。

|
图 2 平面标靶示意图 Fig. 2 Schematic diagram of plane target |
|
图 3 识别及优化过程流程图 Fig. 3 Flow chart of identification and optimization process |
首先通过高斯高通滤波对图像进行平滑处理,去除图像噪声,完成边缘提取与增强,其函数为
| $ H(u, v)=1-\mathrm{e}^{-D^{2}(u, v) / 2 D_{0}^{2}}, $ | (5) |
式中:u,v属计算机图像坐标系;D(u, v)为傅立叶变换中心原点的距离;D0为截止频率。
将滤波后的图像利用边缘检测算法寻找图像强度梯度,利用公式(6)求得每一个像素点的梯度幅值,通过非极大抑制清晰模糊边界,利用双阈值确定边界阈值,利用滞后技术跟踪边界。
| $ G=\sqrt{G_{x}^{2}+G_{y}^{2}}, $ | (6) |
式中Gx和Gy分别表示沿水平x方向和垂直y方向的梯度。
鉴于合作标识在成像过程中的旋转、扭曲等现象,设定圆点面积范围、长短轴比例关系剔除非标识点并补充缺失点,然后对合作标识进行椭圆拟合,得到圆心坐标(x0, y0),对其进行最小二乘法曲线拟合求交补齐,得到更精确的圆心坐标[13-14],即
| $ \left\{\begin{array}{l} x_{0}=\frac{\sum\limits_{x} \sum\limits_{y} x I(x, y)}{\sum\limits_{x} \sum\limits_{y} I(x, y)} ,\\ y_{0}=\frac{\sum\limits_{x} \sum\limits_{y} y I(x, y)}{\sum\limits_{x} \sum\limits_{y} I(x, y)}。\end{array}\right. $ | (7) |
完成合作标识初步识别后,对其进行二次优化处理得到更高精度的标靶空间姿态。首先通过透视变换将合作标识成像投影到一个新的平面,读取坐标数组,如式(8):
| $ \left[x^{\prime}, y^{\prime}, w^{\prime}\right]=[u, v, w]\left[\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right], $ | (8) |
式中:
将式(8)展开后得到
| $ \left\{\begin{array}{l} x=\frac{x^{\prime}}{w^{\prime}}=\frac{a_{11} u+a_{21} v+a_{31}}{a_{13} u+a_{23} v+a_{33}}, \\ y=\frac{y^{\prime}}{w^{\prime}}=\frac{a_{12} u+a_{22} v+a_{32}}{a_{13} u+a_{23} v+a_{33}}。\end{array}\right. $ | (9) |
带入合作标识点获得此次透视变换的变换矩阵,通过自适应阈值将图像二值化,找到圆心坐标,后通过逆透视变换求解各圆心精确坐标。
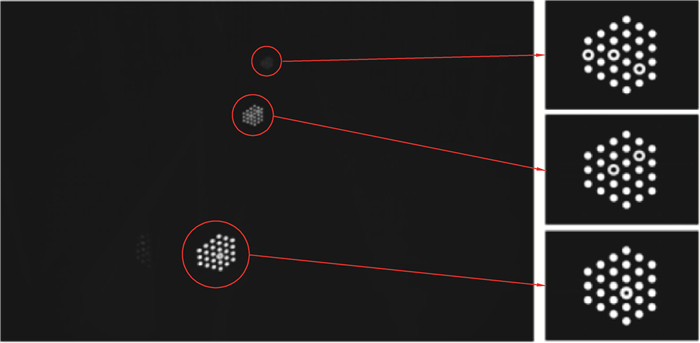
利用上述方法对合作标识进行高精度识别及优化处理,得到透视变换图像如图 4所示,实测受光照和环境影响更小,测量结果精度更高和更稳定。
|
图 4 标靶高精度识别及优化结果测试图 Fig. 4 High-precision target identification and optimization results test chart |
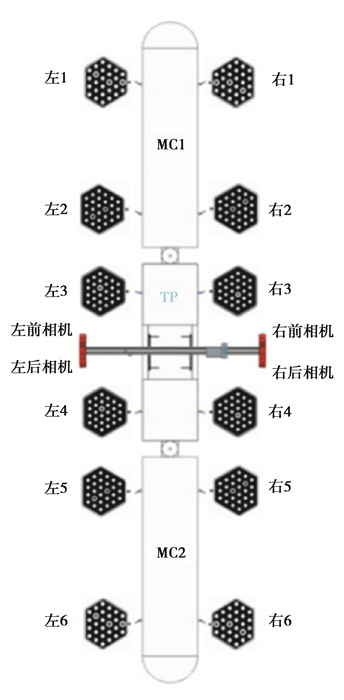
将本系统应用于3节编组的智轨电车标定中,测量系统硬件安装示意图如图 5所示,采用工字形架构,3种型号的标靶通过夹具按图中顺序将其分别固定在电车各轮,将4台2 000万红外相机及LED光源分别置于横梁四端配合对应标靶成像。
|
图 5 测量系统示意图 Fig. 5 Schematic diagram of measurement system |
智轨电车参数测量软件基于C/S架构提高程序处理速度,通过递归算法排除采样噪点提高图像质量,借助OpenCV丰富的函数库对标靶图像进行识别优化,得到更高精度的标靶空间姿态。软件测量界面如图 6所示,实验测量数据及计算结果见表 1及表 2。

|
图 6 测试采集图 Fig. 6 Test capture diagram |
| 表 1 车轮转向角测量数据及计算结果 Table 1 Measurement data and calculation results of wheel steering Angle |
| 表 2 铰接盘转向角测量数据及计算结果 Table 2 Measurement data and calculation results of hinged disc steering angle |
实验误差主要来源于环境干扰、相机分辨率及标靶图像处理等误差的累积。分组多次测量待测参数,根据车轮转向角测量数据及计算结果可知,测量相对误差均不超过±0.1°;在铰接盘转向角测量实验中,改变铰接盘夹角,从实验数据中可知相对误差均不超过±0.05°。
结果表明依靠研发的测量方法可实现智轨电车参数高效率、高精度测量,测量耗时1 h/车,精度均优于±0.1°。四目立体视觉保证大视野测量,有效解决了由智轨电车车身过长引起的相关问题。
5 结论针对智轨电车参数测量存在车身过长、测量精度及测量效率等问题,通过研究四目立体视觉及标靶图像识别与优化技术,研发了一套基于四目立体视觉的智轨电车参数测量系统,并应用于中车相应车辆标定中,结论如下:
1) 通过四台相机解决由车身过长引起的测量视野范围问题,并分布进行相机标定。首先通过1维平台实现单相机内参数TSAI标定,再分布完成多相机标定,避免由联合标定造成的系统误差,准确有效,成功率高。
2) 对拍摄标靶图像进行高精度识别及优化处理,基于边缘检测完成合作标识初步识别,基于透视变换原理得到更精确的圆心坐标,达到车轮转向角测量精度优于±0.1°,铰接盘夹角测量精度优于±0.05°。
3) 研发了基于C/S架构的智轨电车参数测量系统并应用于中车相应车辆标定中,测量时间由之前的1 d/车缩短为1 h/车,有效提高了测量效率。
| [1] |
冯江华, 肖磊, 胡云卿. 智能轨道快运系统[J]. 控制与信息技术, 2020(1): 1-12, 31. Feng J H, Xiao L, Hu Y Q. Autonomous-rail rapid transit[J]. Control and Information Technology, 2020(1): 1-12, 31. (in Chinese) |
| [2] |
彭京, 冯江华, 肖磊, 等. 智轨电车自主导向与轨迹跟随技术研究[J]. 控制与信息技术, 2020(1): 27-31. Peng J, Feng J H, Xiao L, et al. Research on autonomous guidance and track following technology of autonomous-rail rapid tram[J]. Control and Information Technology, 2020(1): 27-31. (in Chinese) |
| [3] |
陈超录, 罗煌, 董其爱, 等. 智轨电车低压配电与数据采集系统研究[J]. 控制与信息技术, 2020(1): 58-61, 65. Chen C L, Luo H, Dong Q A, et al. Research on the low-voltage distribution and data acquisition system of autonomous-rail rapid tram[J]. Control and Information Technology, 2020(1): 58-61, 65. (in Chinese) |
| [4] |
黄荣娟, 仲思东, 屠礼芬. 基于四目立体视觉的三维全自动建模[J]. 计算机工程与设计, 2015, 36(2): 36:431-435. Huang R J, Zhong S D, Tu L F. Automatic three-dimensional modeling based on four-view stereo vision[J]. Computer Engineering and Design, 2015, 36(2): 36:431-435. (in Chinese) |
| [5] |
Ma W P, Li W X, Cao P X. Binocular vision object positioning method for robots based on coarse-fine stereo matching[J]. International Journal of Automation and Computing, 2020, 17(4): 562-571. DOI:10.1007/s11633-020-1226-3 |
| [6] |
Liu S L, Jin P, Liu J H, et al. Accurate measurement method for tube's endpoints based on machine vision[J]. Chinese Journal of Mechanical Engineering, 2017, 30(1): 152-163. DOI:10.3901/CJME.2016.0516.066 |
| [7] |
任海蕾. 基于多相机标定的全景合成方法研究[D]. 西安: 西安电子科技大学, 2019. Ren H L. Research on panorama synthesis method based on multi-camera calibration[D]. Xi'an: Xidian University, 2019. (in Chinese) |
| [8] |
舒娜. 摄像机标定方法的研究[D]. 南京: 南京理工大学, 2014. Shu N. Research on camera calibration method[D]. Nanjing: Nanjing University of Science and Technology, 2014. (in Chinese) |
| [9] |
Peng E, Li L. Camera calibration using one-dimensional information and its applications in both controlled and uncontrolled environments[J]. Pattern Recognition, 2010, 43(3): 1188-1198. DOI:10.1016/j.patcog.2009.08.003 |
| [10] |
Zhu Z M, Wang X Y, Liu Q X, et al. Camera calibration method based on optimal polarization angle[J]. Optics and Lasers in Engineering, 2019, 112: 128-135. DOI:10.1016/j.optlaseng.2018.09.009 |
| [11] |
刘金凤. 数码相机标定及相关技术的研究[D]. 重庆: 重庆大学, 2010. Liu J F. Research on digital camera calibration and related technology[D]. Chongqing: Chongqing University, 2010. (in Chinese) |
| [12] |
权力奥. 基于整体最小二乘的标靶特征提取算法研究[D]. 重庆: 重庆大学, 2017. Quan L A. Research on target feature extraction algorithm based on total least squares[D]. Chongqing: Chongqing University, 2017. (in Chinese) |
| [13] |
周传德, 王见, 尹爱军. 基于平面标靶的物体空间姿态精确测量[J]. 重庆大学学报, 2011, 34(8): 34:66-70. Zhou C D, Wang J, Yin A J. Accurate measurement for objects space attitude based on planar target[J]. Journal of Chongqing University, 2011, 34(8): 34:66-70. (in Chinese) |
| [14] |
王海菊, 谭常玉, 王坤林, 等. 自适应高斯滤波图像去噪算法[J]. 福建电脑, 2017, 33(11): 33:5-6. Wang H J, Tan C Y, Wang K L, et al. Image denoising algorithm based on adaptive Gaussian filtering[J]. Fujian Computer, 2017, 33(11): 33:5-6. (in Chinese) |
| [15] |
Gajek A, Strzępek P. The analysis of the accuracy of the wheel alignment inspection method on the side-slip plate stand[J]. IOP Conference Series: Materials Science and Engineering, 2016, 148: 012037. DOI:10.1088/1757-899X/148/1/012037 |
| [16] |
Baek D, Cho S, Bang H. Wheel alignment inspection by 3D point cloud monitoring[J]. Journal of Mechanical Science and Technology, 2014, 28(4): 1465-1471. DOI:10.1007/s12206-014-0133-3 |
 2021, Vol. 44
2021, Vol. 44


