2. 香港理工大学 工业与系统工程系, 香港 999077
2. Department of Industrial and Systems Engineering, the Polytechnic University of Hong Kong, Hong Kong 999077, P. R. China
随着微纳米技术和材料科学的兴起和迅猛发展,微机电系统、微制造、微操作、微装配等技术领域的研究不断取得进步[1-4]。微胶接作为微装配技术领域中应用最广泛的连接方式,在生命科学[5]、电子封装[6]、快速制造[7]等尖端领域有着重要的地位。
目前,胶液的微量喷射多采用精度高、响应快的压电陶瓷驱动器和一体化柔顺机构来实现。面向常规的封装要求,点胶频率不得小于100 Hz,推杆行程范围为0~300 μm[8-9]。近年来,国内外专家学者对微点胶机构的设计与分析做了许多有益探索。史亚莉等[10]设计了一种3D半自动装配点胶系统,基本满足末端直径10 μm的微管和孔径12 μm的微球装配和胶接要求。韩萌萌[11]设计了一种基于压电原理的微点胶机构,仿真结果表明机构可实现皮升(pL)级点胶量。陈从平等[12]研究了点胶微通道结构参数对胶体挤出过程影响的规律,表明微通道结构微参数的变化对胶体通过微通道时的压力和流速有影响。胡俊峰等[13]设计了一种压电式微点胶系统,采用桥式机构和杠杆机构将压电陶瓷输出位移放大,得到了系统的最大驱动力、输出位移和频率特性,获得了形成正常胶滴所需的条件。Nguon等[14]设计了一种精密液体分配阀,可实现高重复性和高精密地分配胶体。Deng等[15]设计了一种压电式微喷射分配器,其针头速度较传统点胶机构增大了1.8倍。Lu等[16]设计了一种压电陶瓷驱动的喷射分配器,仿真和实验表明系统可较好地分配胶滴流量。Yao等[17]对非接触式微量液体的分配进行了模拟与实验研究,为非接触式控制的优化提供一定的依据。
以上研究为微点胶机构的设计与应用提供了广泛的思路,但多数微点胶机构采用刚性构件和传统铰链作为传递机构,极大地影响了点胶精度,且不利于机构的小型化。柔性机构利用材料的弹性变形来实现力和运动的传递,具有零件少、无需装配和润滑、无运动副间隙、高精度和高可靠性等优点[18-20]。针对目前微点胶机构行程小、精度低和速度慢等问题,笔者面向芯片封装领域元器件连接和焊膏,基于柔顺机构设计了具有大行程、结构紧凑、适合高频微量液体分配的点胶机构。
1 微点胶机构设计 1.1 材料选择微点胶机构的运动范围受限于柔性铰链的转动范围,而铰链的转动范围由材料的属性和铰链缺口类型决定,因此,机构材料的属性直接影响系统的性能。机构在运转过程中,柔性铰链不仅需要有较大的弹性形变,还要有较高的屈服强度来防止应力过大而受到损坏。因此,要求材料的弹性模量E较小,屈服强度与弹性模量的比值σ/E较大;同时,需综合考虑材料的价格和性能等因素。表 1对比了4种典型材料,铝合金7075-T6(SN)的各项性能参数较好,且具有密度小、性能高、价格低等优势,因此,选其作为机构的本体材料。
| 表 1 材料参数对比 Table 1 Material parameter comparison |
点胶方式按点胶过程中喷射口是否与基板接触分为接触式和非接触式。接触式点胶是通过喷嘴与基板接触来实现胶体分配;非接触式点胶则是在驱动力作用下,使喷嘴处的胶体获得足够的速度,利用惯性力克服表面张力和粘性力将胶体喷出。接触式点胶又分为撞针式点胶、活塞式点胶和时间压力式点胶,3种点胶方式的示意图和优缺点对比分别如图 1和表 2所示。活塞式点胶是通过活塞直接推动胶体流向喷射口实现点胶,由表 2可知,活塞式点胶一致性较好,出胶量受黏度影响小,相较于撞针式点胶,更易于控制点胶量。综上所述,根据机构的驱动和传动方式,选择基于活塞的接触式点胶。
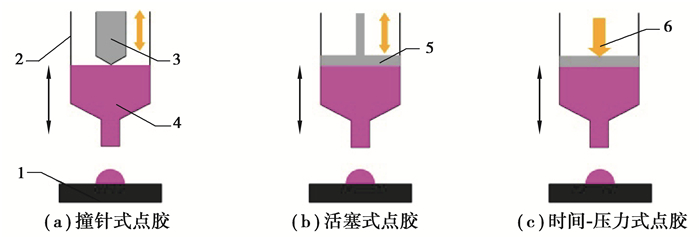
|
1—基板;2—喷嘴;3—撞针;4—胶体;5—活塞;6—脉动空气 图 1 三种接触式点胶方式 Fig. 1 Three contact dispensing methods |
| 表 2 三种接触式点胶方式的优缺点对比 Table 2 Comparison of three typical contact dispensing methods |
为补偿压电陶瓷驱动器的行程,考虑各种放大机构的特性,综合杠杆机构、桥式机构和Scott-Russel(SR)机构,设计了结构紧凑的混合位移放大机构。3种放大机构的示意图及运动链如图 2所示。
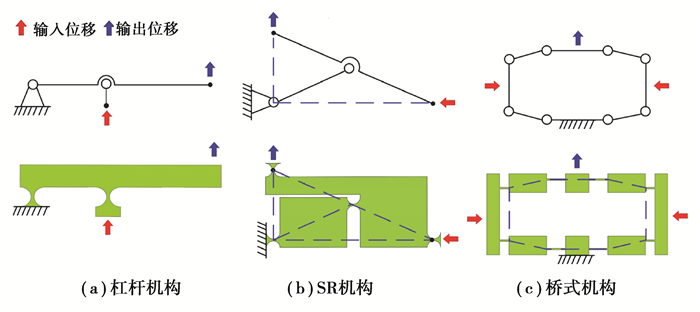
|
图 2 三种放大机构 Fig. 2 Three amplification mechanisms |
微量液体分配系统如图 3所示,由驱动装置、推塞、推塞阀、供胶装置和喷射嘴组成。点胶系统在实际工作中,处于竖直状态,喷嘴朝下,其中柔性机构和底座通过端部4个螺栓实现装配。供胶装置与推塞阀的胶液入口相连,胶液进入阀体后,在推塞的往复推动下经喷射嘴形成胶滴,完成点胶操作,其工作原理如图 4所示。为更好地控制点胶量,提高点胶一致性,该设计在活塞式点胶的基础上,把推塞的顶部变成了流线型。
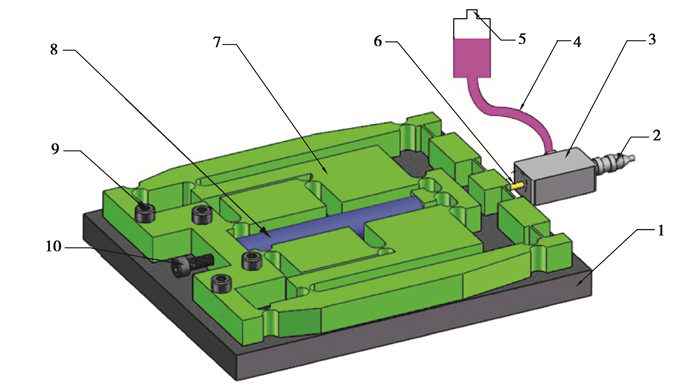
|
1—底座;2—喷射嘴;3—推塞阀;4—胶液;5—供胶装置;6—推塞;7—三级位移放大机构;8—压电陶瓷驱动器;9—紧固平台用螺钉;10—紧固压电陶瓷用螺钉 图 3 微量胶体分配示意图 Fig. 3 Assembly of micro-dispensing mechanism |
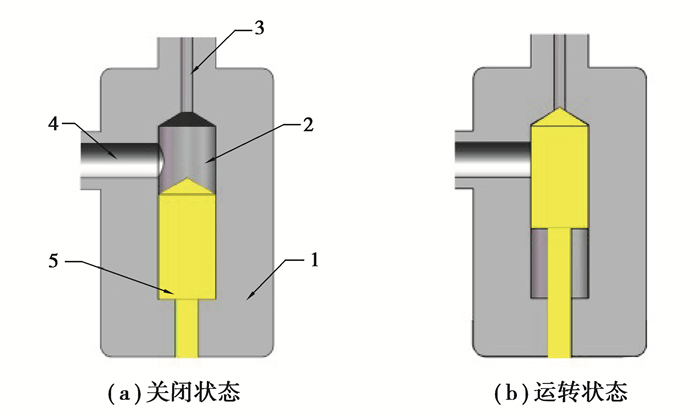
|
1—阀体;2—阀室;3—喷射口;4—入胶口;5—推塞 图 4 工作原理图 Fig. 4 Operation principle |
点胶机构如图 5所示,其中传递机构由SR机构、杠杆机构和桥式机构组成,放大机构将力和位移传递给推塞,并放大行程。当压电陶瓷在y方向产生位移时,经由SR机构进行1级放大,杠杆机构进行2级放大,桥式机构最终将位移进行第3级放大,传递至推塞处。
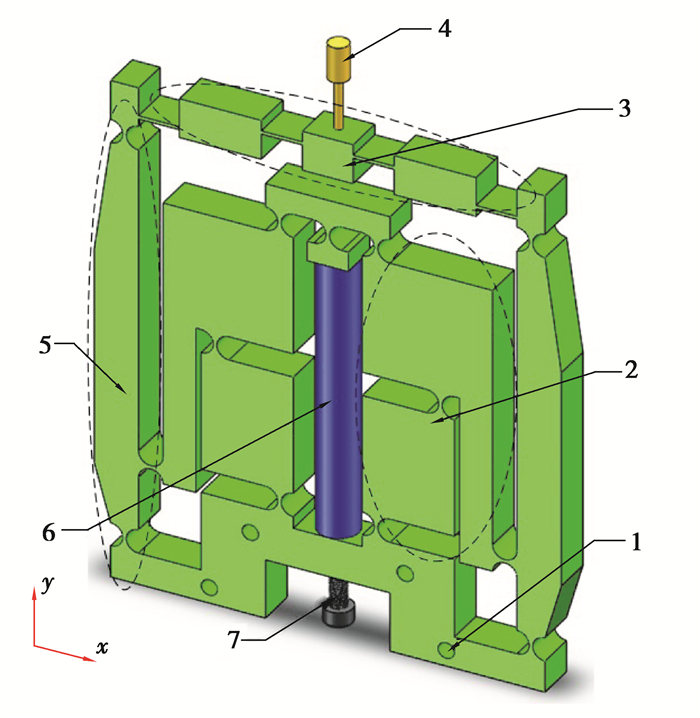
|
1—固定孔;2—SR机构;3—桥式机构;4—推塞;5—杠杆机构;6—压电陶瓷驱动器;7—预紧螺栓 图 5 微点胶机构 Fig. 5 Structure of the micro-dispensing mechanism |
由图 5可知,放大机构是由SR机构、杠杆机构、桥式机构组成的混合放大机构,为得到机构的放大倍数,依次对这3种机构的放大率进行分析。
2.1 SR机构放大倍数分析SR机构被视为具有固定放大倍数的直线放大机构,其运动链如图 6所示,图中B为固定铰链,A为位移输入端,D为位移输出端。其中,AC=CD=BC=l0,∠BAD=θ。
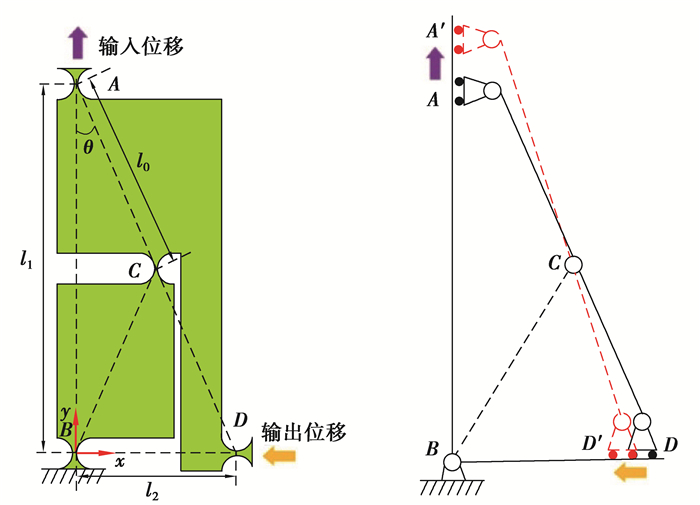
|
图 6 SR机构及其运动链示意图 Fig. 6 Diagram of SR mechanism and kinematic chain |
依据三角形的原理可知
| $ l_{1}^{2}+l_{2}^{2}=4 l_{0}^{2}。$ | (1) |
当A端在y方向输入位移为ΔyA,相应的D端将会输出x方向的位移ΔxD,由于变化很微小,有
| $ \left(\Delta y_{A}+l_{1}\right)^{2}+\left(\Delta x_{D}+l_{2}\right)^{2} \approx 4 l_{0}^{2}。$ | (2) |
对式(2)进行计算求解,可得
| $ \lambda_{1} \approx \frac{-\sqrt{4 l_{0}^{2}-l_{1}^{2}}}{l_{1}}=-\tan \theta。$ | (3) |
由式(3)可知,如果0 < θ < π/40 < θ < π/4,当A端沿y轴输出小位移为ΔyA时,D端沿x轴将会输出放大位移ΔxD=(-tan θ)ΔyA。负号表示ΔyA减小,将导致ΔxD增大。
2.2 杠杆机构放大倍数分析杠杆机构及其运动链如图 7所示,N端为固定端,Di为可动铰链。为防止机构运转过程中杠杆机构因N、V两端受到过大的压力发生压弯变形而影响机构的位移放大输出,同时为提高机构的响应速度对传统杠杆机构的形状做了一定的改变[21]。依据杠杆原理,在Di端输入位移时,在V端会输出位移。
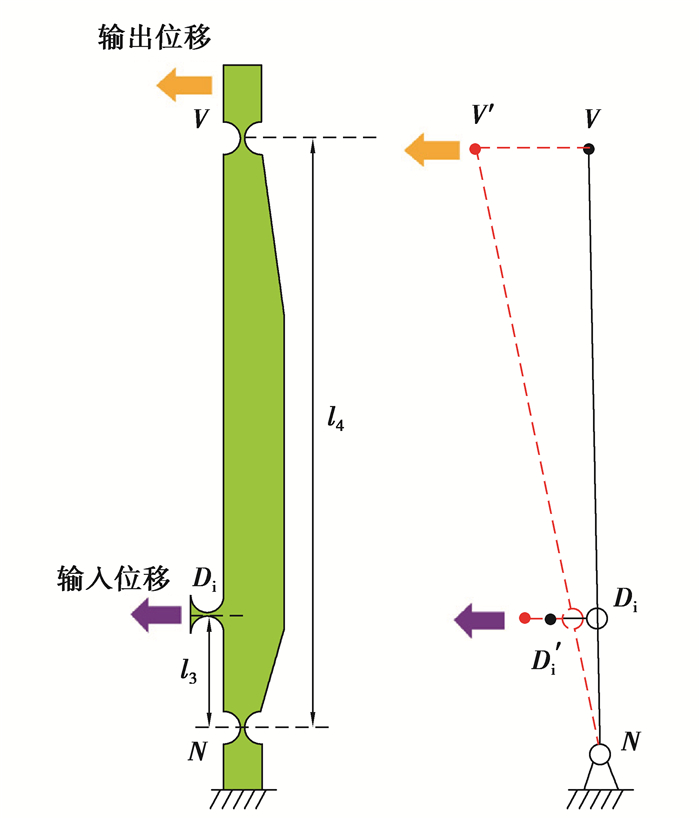
|
图 7 杠杆机构及其运动链示意图 Fig. 7 Diagram of lever mechanism and kinematic chain |
由相似三角形原理,可知
| $ {\lambda _2} = \frac{{{l_4}}}{{{l_3}}}。$ | (4) |
由上式可知,Di、V铰链与铰链N的距离决定着杠杆机构的放大倍数。同时,还需考虑杠杆机构中柔性铰链V的作用效果,杠杆机构将位移传递至桥式机构时,柔性铰链V的主要作用在于使桥式机构拥有充足的向上输出变形的空间,防止其向下输出变形。由于柔性铰链V的弹性变形及轴漂特性,最终输出的位移会受到影响,产生位移损失。
2.3 桥式机构放大倍数分析该柔性机构采用桥式机构的二分之一作为输出端,其机构和运动链如图 8所示。在杠杆机构传动作用下,桥式机构两端的输入位移为Δx,输出的位移为Δy。
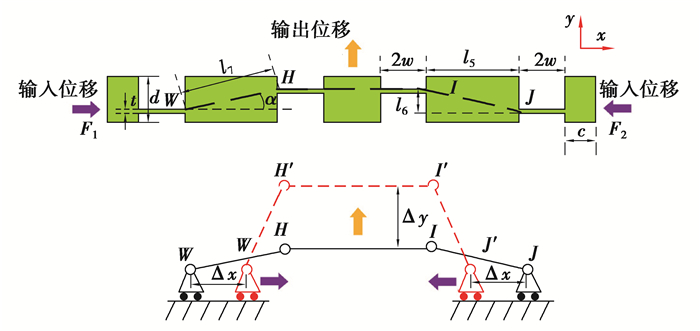
|
图 8 桥式机构及其运动链示意图 Fig. 8 Diagram of bridge mechanism and kinematic chain |
由图可知,机构的放大倍数为λ3=Δy/2Δx。图中,F1、F2分别为输入位移时,对应桥式机构两端所受到的力,两力在铰链H、I处分别产生的力矩为M1、M2。桥式机构采用对称结构,由受力平衡,可得F1=F2=Fx,M1=M2=M=Fxl6/2。Fx表示桥式机构两直梁型铰链输出时所受到的x方向上的力;M表示两直梁型铰链输出时所受到的力矩作用;l6为两铰链之间的垂直距离,α表示两个铰链之间的偏转角,l7为两铰链之间的距离,l5为两铰链之间的水平距离。
在桥式机构的放大率分析中,仅考虑柔性铰链的平面变形,基于柔度矩阵法可将直梁型铰链输出简化为[22]:
| $ \left[\begin{array}{c} \Delta x_{i} \\ \Delta y_{i} \\ \Delta \theta \end{array}\right]=\left[\begin{array}{ccc} \frac{2 w}{E b t} & 0 & 0 \\ 0 & \frac{32 w^{3}}{3 E b t^{3}}+\frac{2 w}{G b t} & \frac{24 w^{2}}{E b t^{3}} \\ 0 & \frac{24 w^{2}}{E b t^{3}} & \frac{24 w}{E b t^{3}} \end{array}\right]\left[\begin{array}{c} F_{x} \\ 0 \\ M \end{array}\right]。$ | (5) |
式中:Δxi和Δyi分别为柔性铰链沿x、y方向在平面的变形,Δθ为柔性铰链的旋转角度,E、G分别为材料的杨氏模量和剪切模量,2w、t、b分别为铰链的缺口宽度、最小厚度、宽度。
为进一步研究桥式机构的变形,需要考虑放大过程中桥臂的变形,由此可得:
| $ \Delta l=\frac{F_{x} l_{7} \cos \alpha}{E S}。$ | (6) |
式中S=bd为桥臂的横截面积。考虑到铰链变形、桥臂的旋转和压缩,得出:
| $ \left\{\begin{array}{l} \Delta x=2 \Delta x_{\mathrm{i}}+l_{7} \sin \alpha \Delta \theta+\Delta l \cos \alpha ,\\ \Delta y=2 \Delta y_{\mathrm{i}}+l_{7} \cos \alpha \Delta \theta+\Delta l \sin \alpha 。\end{array}\right. $ | (7) |
联立式(5)~(7),得输入位移和输出位移分别为:
| $ \left\{\begin{array}{c} \Delta x=\left(\frac{4 w}{E b t}+\frac{12 w l_{6}^{2}}{E b t^{3}}+\frac{l_{5}^{2}}{E S l_{7}}\right) F_{x} ,\\ \Delta y=\left(\frac{24 w^{2} l_{6}+12 w l_{5} l_{6}}{E b t^{3}}+\frac{l_{5} l_{6}}{E S l_{7}}\right) F_{x} 。\end{array}\right. $ | (8) |
由式(8)可得,桥式机构的放大倍数为
| $ \lambda_{3}=\frac{\Delta y}{2 \Delta x}=\frac{\frac{24 w^{2} l_{6}+12 w l_{5} l_{6}}{b t^{3}}+\frac{l_{5} l_{6}}{S l_{7}}}{\frac{8 w}{b t}+\frac{24 w l_{6}^{2}}{b t^{3}}+\frac{2 l_{5}^{2}}{S l_{7}}}。$ | (9) |
由式(9)可知,铰链参数w、t、b,以及铰链相对位置和桥臂横截面积对机构的放大倍数均有影响,因此桥式机构的设计需综合考虑各项参数影响,才得到较为精确的放大倍数模型。依据式(3)(4)(9),得出柔性机构的总放大倍数为
| $ \lambda=-\frac{\tan \theta l_{4}}{l_{3}}\left(\frac{\frac{24 w^{2} l_{6}+12 w l_{5} l_{6}}{b t^{3}}+\frac{l_{5} l_{6}}{S l_{7}}}{\frac{8 w}{b t}+\frac{24 w l_{6}^{2}}{b t^{3}}+\frac{2 l_{5}^{2}}{S l_{7}}}\right)。$ | (10) |
由式(10)可知,SR机构与杠杆机构中l2、l4和l1、l3两组参量分别以正比和反比的关系影响λ的大小。以w、t、l5、l6、l7和S为自变参量,其对机构总放大倍数的影响如图 9所示。
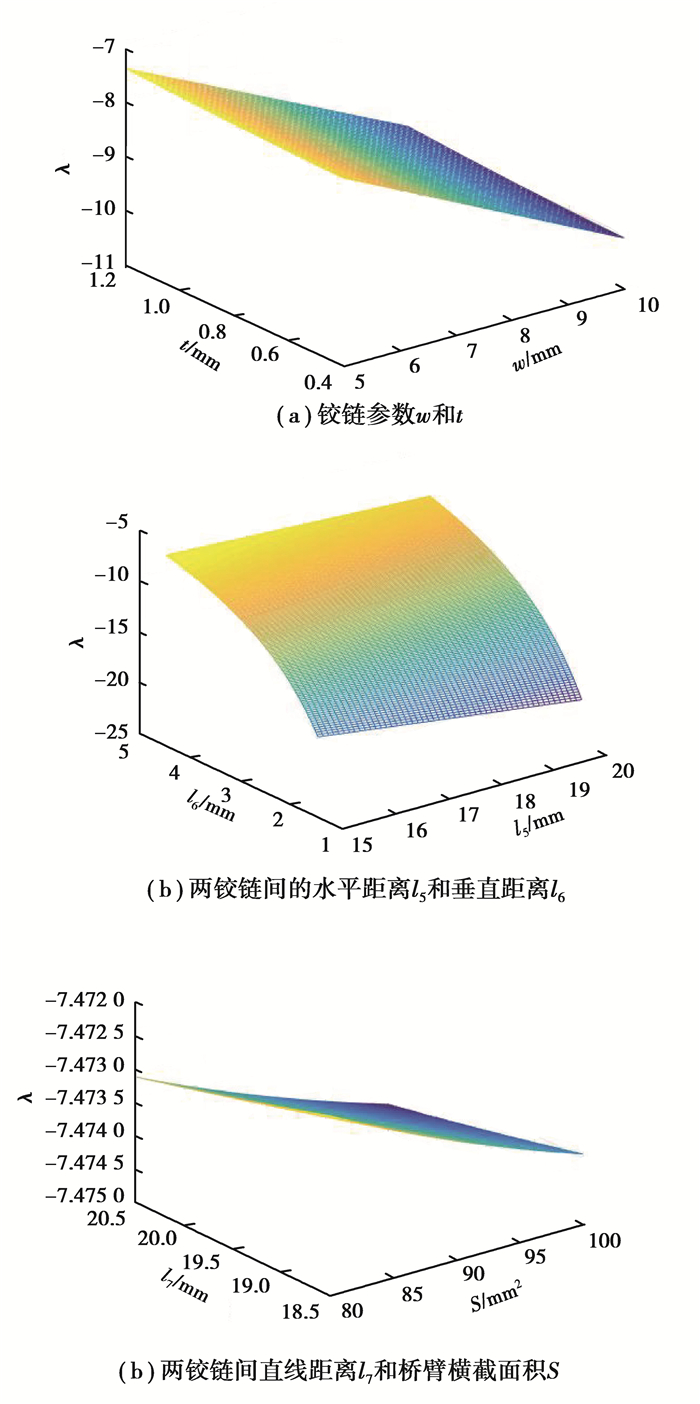
|
图 9 变量对放大率影响仿真 Fig. 9 Simulation of the effects of variables on the amplification |
由图 9可知,上述3组参量中w、l6、S对λ的相对影响权重较大,前2者均以正比的拟合关系影响λ的大小,S以反比的拟合关系影响λ的大小。
3 机构力学性能分析为了解机构在压电陶瓷驱动力作用下各构件的受力情况以及对机构输出位移的影响,对机构的受力情况、刚度和固有频率进行了分析,机构各项参数如图 10所示。图中的J1、J2分别为SR机构中ADi、BC构件分别绕柔性铰链C、B转动的转动惯量,J3为杠杆机构绕柔性铰链N转动的转动惯量,J4为桥式机构中桥臂在铰链W、H作用下产生转动的转动惯量;m1为推塞的质量。
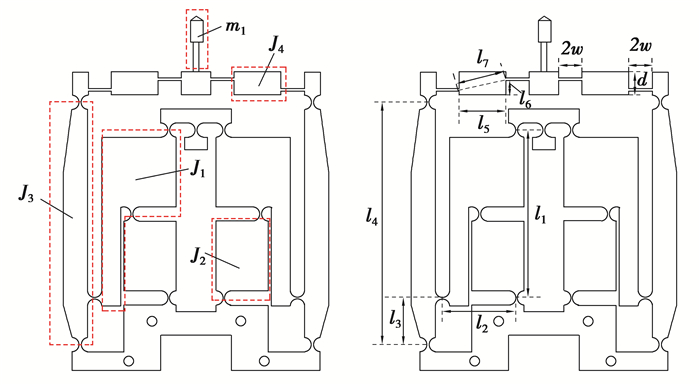
|
图 10 机构参数示意图 Fig. 10 Architecture parameters of the designed mechanism |
在驱动力作用下,机构各构件的受力情况如图 11所示。其中,(a)(b)所示两构件共同组成SR机构的受力情况,(c)所示为杠杆机构的受力情况,(d)所示为桥式机构的四分之一受力情况。
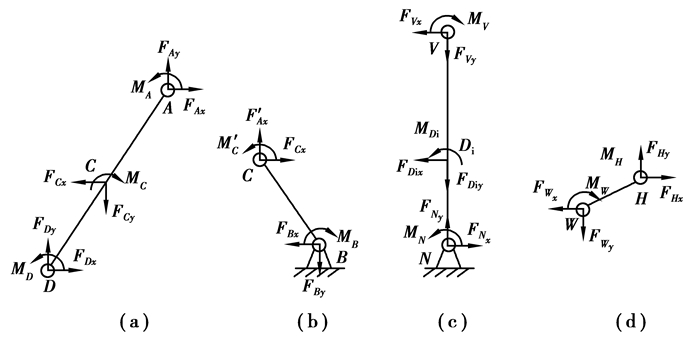
|
图 11 构件受力示意图 Fig. 11 Schematic of components loading condition |
依据平衡的原理,可知SR机构、杠杆机构、桥式机构的受力等式组分别为
| $ {\left\{ {\begin{array}{*{20}{c}} {{F_{Ay}} + {F_{Dy}} = {F_{By}},}\\ {{M_A} + {M_D} + {F_{Ay}}{l_2} = {M_B} + {F_{By}}{l_2}}。\end{array}} \right.} $ | (11) |
| $ \left\{ {\begin{array}{*{20}{l}} {{F_{Ny}} = {F_{Diy}} + {F_{Vy}},}\\ {{M_N} + {M_{Di}} = {M_V}}。\end{array}} \right. $ | (12) |
| $ \left\{ {\begin{array}{*{20}{c}} {{F_{Wy}} = {F_{Hy}},}\\ {{M_H} + {F_{Hy}}{l_5} = {M_W}}。\end{array}} \right. $ | (13) |
可知压电陶瓷驱动力的大小Fin,便可得到
| $ F_{A y}=\frac{1}{2} F_{\text {in }}。$ | (14) |
同时,在已知柔性铰链的转角刚度k、转角θ′的条件下,依据
| $ M_{z}=k \theta^{\prime} \text { , } $ | (15) |
可得到各柔性铰链处的转动力矩Mz。因此,确定压电陶瓷驱动力的大小及方向,再结合各机构运转的几何关系,便可求解出各处的受力。
3.2 刚度分析为求解输入力和输出位移的关系,应用拉格朗日定理对机构y输出方向的刚度进行了分析。由于机构的对称性,同时也为方便计算和观察,取机构的一侧进行分析。在驱动力条件下,机构的运动链如图 12所示。

|
图 12 机构运动链示意图 Fig. 12 Schematic diagram of kinematic chain |
机构主要采用正圆型铰链和直梁型铰链,两柔性铰链如图 13所示。图中各铰链坐标系的建立是以铰链连接杆截面中心为坐标圆心,中心轴的方向作为y轴的指定方向,x轴的指向与铰链两端连接方向相一致,z轴与铰链的转动平面相互垂直。h为两种柔性铰链的高度,r为正圆型铰链圆弧的圆半径,Mz为两铰链所受到的力矩。正圆型和直梁型铰链的转角刚度k1、k2分别为[23]:
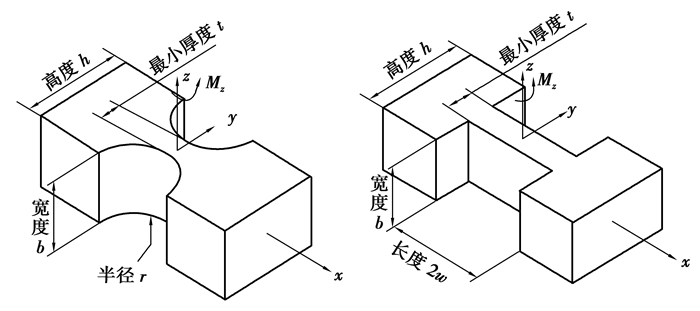
|
图 13 柔性铰链示意图 Fig. 13 Architecture parameters of flexible joints |
| $ {k_1} = \frac{{2Eb{t^{5/2}}}}{{9{\rm{ \mathsf{ π} }}{r^{1/2}}}}, $ | (16) |
| $ {k_2} = \frac{{Eb{t^3}}}{{24w}}。$ | (17) |
机构在力的作用下运动时,产生相应的动能与势能。由图 10、图 12可知,机构的动能与势能可分别表示为
| $ \left\{\begin{array}{l} E_{\mathrm{m}}=\frac{1}{2} J_{1} \dot{\theta}_{1}^{2}+\frac{1}{2} J_{2} \dot{\theta}_{1}^{2}+\frac{1}{2} J_{3} \dot{\theta}_{3}^{2}+\frac{1}{2} J_{4} \dot{\theta}_{4}^{2}+\frac{1}{2} m_{1} \dot{y}_{\mathrm{out}}^{2} ,\\ E_{\mathrm{p}}=\frac{1}{2} k_{1} \theta_{1}^{2} \times 3+\frac{1}{2} k_{1} \theta_{2}^{2}+\frac{1}{2} k_{1} \theta_{3}^{2} \times 2+\frac{1}{2} k_{2} \theta_{4}^{2} \times 2 。\end{array}\right. $ | (18) |
式中:θ2为柔性铰链C因受构件ADi、BC同时作用而产生的转角;Em、Ep分别为机构整体的动能与势能。
| $ \left\{\begin{array}{c} \theta_{1}=\frac{x_{\text {in }}}{l_{1}}=-\frac{l_{2}}{l_{1}^{2}} y_{\text {in }} ,\\ \theta_{2}=2 \theta_{1}=-\frac{2 l_{2}}{l_{1}^{2}} y_{\text {in }}, \\ \theta_{3}=\frac{x_{\text {in }}}{l_{3}}=-\frac{l_{2}}{l_{1} l_{3}} y_{\text {in }}, \\ \theta_{4}=\frac{x_{\text {out }}}{l_{6}}=-\frac{l_{2} l_{4}}{l_{1} l_{3} l_{6}} y_{\text {in }}。\end{array}\right. $ | (19) |
式(18)可进一步写为
| $ \left\{\begin{array}{c} E_{\mathrm{m}}=\frac{1}{2}\left(\frac{J_{1} l_{2}^{2} l_{3}^{2} l_{6}^{2}+2 J_{2} l_{2}^{2} l_{3}^{2} l_{6}^{2}+J_{3} l_{1}^{2} l_{2}^{2} l_{6}^{2}+J_{4} l_{1}^{2} l_{2}^{2} l_{4}^{2}+m_{1} \lambda_{3}^{2} l_{1}^{2} l_{2}^{2} l_{4}^{2} l_{6}^{2}}{l_{1}^{4} l_{3}^{2} l_{6}^{2}}\right) \dot{y}_{\mathrm{in}}^{2}, \\ E_{\mathrm{p}}=\frac{1}{2}\left(\frac{3 k_{1} l_{2}^{2} l_{3}^{2} l_{6}^{2}+4 k_{1} l_{2}^{2} l_{3}^{2} l_{6}^{2}+2 k_{1} l_{1}^{2} l_{2}^{2} l_{6}^{2}+2 k_{2} l_{1}^{2} l_{2}^{2} l_{4}^{2}}{l_{1}^{4} l_{3}^{2} l_{6}^{2}}\right) y_{\mathrm{in}}^{2}。\end{array}\right. $ | (20) |
机构的刚度K可表示为
| $ K=\frac{3 k_{1} l_{2}^{2} l_{3}^{2} l_{6}^{2}+4 k_{1} l_{2}^{2} l_{3}^{2} l_{6}^{2}+2 k_{1} l_{1}^{2} l_{2}^{2} l_{6}^{2}+2 k_{2} l_{1}^{2} l_{2}^{2} l_{4}^{2}}{l_{1}^{4} l_{3}^{2} l_{6}^{2}}。$ | (21) |
由刚度分析可知,机构的等效质量meq可表示为
| $ m_{\mathrm{eq}}=\frac{J_{1} l_{2}^{2} l_{3}^{2} l_{6}^{2}+2 J_{2} l_{2}^{2} l_{3}^{2} l_{6}^{2}+J_{3} l_{1}^{2} l_{2}^{2} l_{6}^{2}+J_{4} l_{1}^{2} l_{2}^{2} l_{4}^{2}+m_{1} \lambda_{3}^{2} l_{1}^{2} l_{2}^{2} l_{4}^{2} l_{6}^{2}}{l_{1}^{4} l_{3}^{2} l_{6}^{2}}。$ | (22) |
依据拉格朗日定理,系统动力学方程如下:
| $ \frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial T}{\partial \dot{q}_{i}}-\frac{\partial T}{\partial q_{i}}+\frac{\partial U}{\partial q_{i}}=F_{i}, i=1,2, \cdots, n。$ | (23) |
式中:T为系统势能,U为系统动能,qi为广义坐标,Fi为非有势力,n为系统自由度数。由此得出,在机构y输出方向上
| $ {m_{{\rm{eq}}}}{{\ddot y}_{in}} + K{y_{{\rm{in }}}} = 0。$ | (24) |
式(24)中,yin取得非零解的条件为:
| $ \left| {K - {{\left( {2{\rm{ \mathsf{ π} }}{f_i}} \right)}^2}{m_{{\rm{eq}}}}} \right| = 0。$ | (25) |
依据式(21)和(22),进一步得到机构的固有频率表达式为
| $ f = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\sqrt {\frac{{3{k_1}l_2^2l_3^2l_6^2 + 4{k_1}l_2^2l_3^2l_6^2 + 2{k_1}l_1^2l_2^2l_6^2 + 2{k_2}l_1^2l_2^2l_4^2}}{{{J_1}l_2^2l_3^2l_6^2 + 2{J_2}l_2^2l_3^2l_6^2 + {J_3}l_1^2l_2^2l_6^2 + {J_4}l_1^2l_2^2l_4^2 + {m_1}\lambda _3^2l_1^2l_2^2l_4^2l_6^2}}} 。$ | (26) |
为验证理论分析的正确性,利用Workbench对该机构的位移行程、刚度进行仿真验证。机构采用的材料为铝合金7075-T6(SN),泊松比μ为0.33,各项材料参数和机构主要参数如表 1和3所示。
| 表 3 机构主要参数表 Table 3 Architecture parameters |
将机构的三维模型导入有限元软件,建立有限元模型,推塞网络划分的最小单元为1.3 mm,在所有定位孔的内圆柱面施加固定约束,在提前建立的加载节点进行位移加载,模型的位移云图及应力变形如图 14所示。

|
图 14 机构位移仿真 Fig. 14 Displacement simulation |
经仿真分析求解,得到一组对应的输入位移与输出位移的数据,其放大倍数为5.46倍,依据表 4和公式(10)计算得出机构的理论放大倍数为5.97倍,其理论值与仿真值比较如图 15所示。
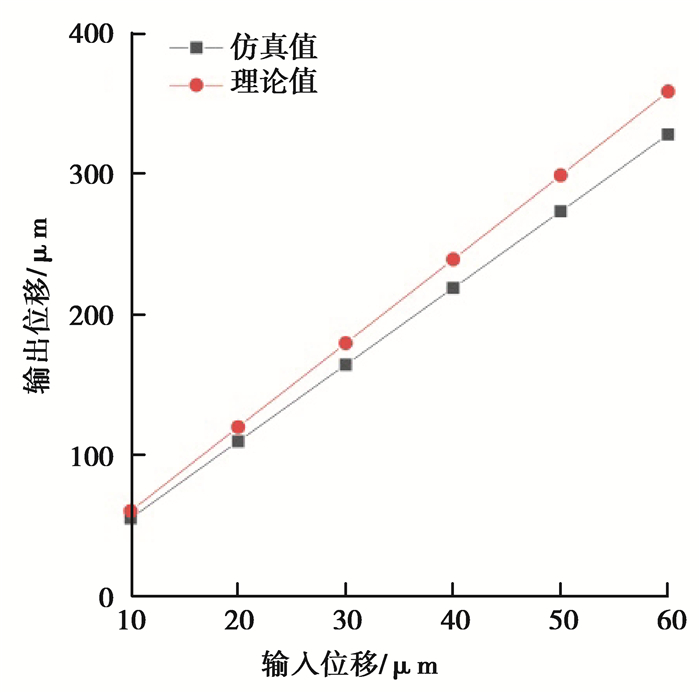
|
图 15 位移理论值与仿真值对比图 Fig. 15 Comparison of theoretical and simulation values of displacement |
由图 15可知,机构放大倍数的仿真值与理论值较为接近,考虑到推塞的弹性变形,会产生一定的误差,两数据的相对误差为8.5%。由仿真结果可知,在一定放大倍数下,可以通过压电陶瓷驱动器输出不同的位移,使推塞获得相应大小的行程,在供胶系统不断提供胶液的条件下,推动胶液,实现点胶。依据工作要求,可选择PZT 150/7/60 VS12封装压电陶瓷,最大出力为900 N,最大抗拉力为300 N,其标称位移为60 μm,可实现机构较大行程范围内的点胶操作。
4.2 刚度仿真分析为了验证机构理论刚度模型的正确性,对机构进行刚度仿真分析,机构的变形图和应力图如图 16所示。
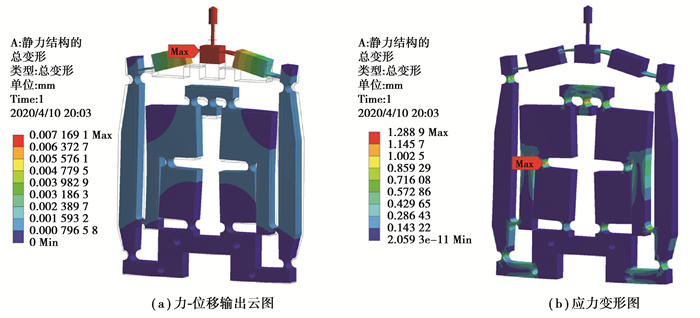
|
图 16 机构刚度仿真 Fig. 16 Stiffness simulation |
通过仿真得出了输入力与输出位移的数据,经计算可得其刚度值为1.40 N/μm。依据表 4和公式(21)可得机构的理论刚度值为1.51 N/μm。机构刚度的理论值与仿真值对比如图 17所示。
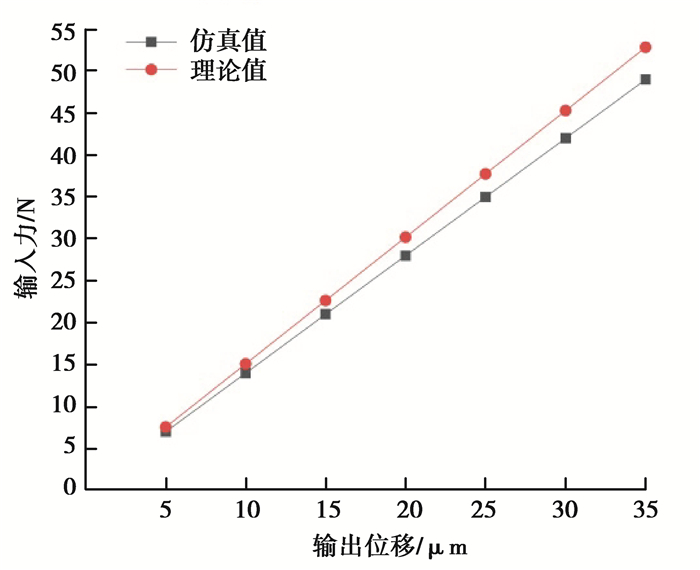
|
图 17 刚度理论值与仿真值对比图 Fig. 17 Comparison of theoretical and simulated stiffness values |
由图 17可知,机构刚度的仿真值与理论值较为接近,两者的相对误差为7.2%,验证了公式(21)具有较高的可靠性。
4.3 模态分析通过机构的模态参数可以了解其动态特性,为机构的振动分析、诊断和预报及机构动力特性的优化设计提供依据。前6阶共振模态形变图和各阶共振频率值如图 18所示,机构的1阶固有频率为122.35 Hz,可以满足100 Hz点胶工作频率要求,机构的性能在下阶段会通过实验进一步验证。
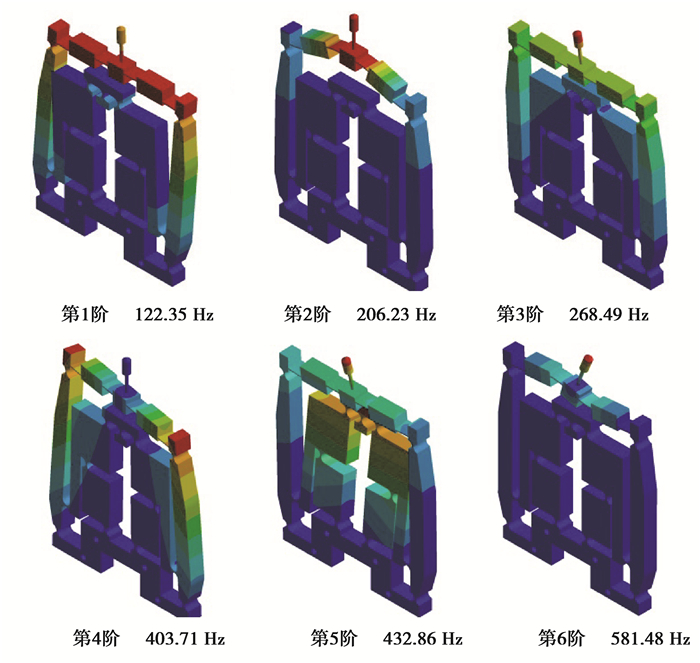
|
图 18 六阶共振模式仿真图 Fig. 18 Mode simulation |
在第1、第2阶频率下,推塞分别在杠杆机构和桥式机构的带动下,沿x、y轴方向发生了平移运动;在第3、第4、第5阶频率下,杠杆机构和桥式机构沿z轴方向产生了一定的偏转;在第6阶频率下,推塞及桥式机构在x、y轴平面内发生了转动。
5 结论笔者基于三级混合放大机构设计了一种适用于微量液体自动分配的点胶机构。以铝合金7075-T6(SN)为机构本体材料,得到了机构位移放大倍数、整体刚度和固有频率的解析表达式,对机构的位移行程和刚度值进行了仿真分析验证,相对误差分别为8.5%、7.2%;仿真与分析存在误差的主要原因在于机构在实际工作运转中,推塞产生一定的弹性变形,使其与理论分析存在一定的偏差;在力的作用下,柔性铰链产生一定的平动拉伸,从而影响机构的理论分析;同时,在进行有限元网络划分的时候,受计算机性能影响,单元尺寸比较粗糙,会与理论计算产生一定的误差。本研究中提出的结构设计与分析具有一定的应用价值,下一阶段将主要围绕样机加工和点胶一致性做实验分析和验证。
| [1] |
Seon J A, Dahmouche R, Gauthier M. On the contribution of adhesion and friction in planning dexterous in-hand micromanipulation[J]. Journal of Micro-Bio Robotics, 2017, 12: 33-44. DOI:10.1007/s12213-017-0096-4 |
| [2] |
李文亚, 曹聪聪, 杨夏炜, 等. 冷喷涂复合加工制造技术及其应用[J]. 材料工程, 2019, 47(11): 53-63. Li W Y, Cao C C, Yang X W, et al. Cold spraying hybrid processing technology and its application[J]. Journal of Materials Engineering, 2019, 47(11): 53-63. (in Chinese) |
| [3] |
丁冰晓, 肖霄, 李杨民. 大行程并联三自由度柔性微操作平台的设计[J]. 天津理工大学学报, 2015, 31(4): 28-32. Ding B X, Xiao X, Li Y M. Design a 3-DOF compliant parallel mechanism with large stroke[J]. Journal of Tianjin University of Technology, 2015, 31(4): 28-32. (in Chinese) |
| [4] |
黄晨灿. 微装配系统的力学特性及精度分析研究[D]. 北京: 北京理工大学, 2017. Huang C C. The mechanical characteristics and precision analysis of flexible automatic assembly system for micro devices[D]. Beijing: Beijing Institute of Technology, 2017. (in Chinese) |
| [5] |
姚玉峰, 路士州, 刘亚欣, 等. 微量液体自动分配技术研究综述[J]. 机械工程学报, 2013, 49(14): 140-153. Yao Y F, Lu S Z, Liu Y X, et al. Research on automated micro-liquid dispensing technology[J]. Journal of Mechanical Engineering, 2013, 49(14): 140-153. (in Chinese) |
| [6] |
Kunchala P, Kappagantula K. 3D printing high density ceramics using binder jetting with nanoparticle densifiers[J]. Materials & Design, 2018, 155: 443-450. |
| [7] |
Chen C L, Wang J P, Huang G M, et al. High-precision rapid prototyping technology for manufacturing linear guides[J]. The International Journal of Advanced Manufacturing Technology, 2017, 92(9/10/11/12): 3137-3142. DOI:10.1007/s00170-017-0378-y |
| [8] |
陈九生, 蒋稼欢. 微流控液滴技术: 微液滴生成与操控[J]. 分析化学, 2012, 40(8): 1293-1300. Chen J S, Jiang J H. Droplet microfluidic technique: mirodroplets formation and manipulation[J]. Chinese Journal of Analytical Chemistry, 2012, 40(8): 1293-1300. (in Chinese) |
| [9] |
孙道恒, 高俊川, 杜江, 等. 微电子封装点胶技术的研究进展[J]. 中国机械工程, 2011, 22(20): 2513-2519. Sun D H, Gao J C, Du J, et al. Advances in fluid dispensing technology for micro-electronics packaging[J]. Chinese Journal of Construction Machinery, 2011, 22(20): 2513-2519. (in Chinese) |
| [10] |
史亚莉, 张正涛, 徐德. 跨尺度微管微球三维半自动装配点胶系统[J]. 光学精密工程, 2015, 23(11): 3121-3128. Shi Y L, Zhang Z T, Xu D. 3D semi-automatic assembly and dispensing system for trans-scale parts of micro-tube and micro-sphere[J]. Optics and Precision Engineering, 2015, 23(11): 3121-3128. (in Chinese) |
| [11] |
韩萌萌. 基于压电原理的微量点胶仿真与实验研究[D]. 哈尔滨: 哈尔滨工业大学, 2014. Han M M. Simulation and experiment research on microdispensing based on piezoelectric drive[D]. Harbin: Harbin Institute of Technology, 2014. (in Chinese) |
| [12] |
陈从平, 张涛, 董小刚. 点胶微通道结构参数对胶体挤出过程影响规律研究[J]. 三峡大学学报(自然科学版), 2013, 35(1): 73-75. Chen C P, Zhang T, Dong X G. Research on influence of micro-channel structure parameters for glue soluting dispensing process[J]. Journal of China Three Gorges University (Natural Sciences), 2013, 35(1): 73-75. (in Chinese) |
| [13] |
胡俊峰, 梁龙, 赵永祥. 基于柔顺机构的压电式微喷点胶系统设计与性能分析[J]. 光学精密工程, 2019, 27(9): 1990-2001. Hu J F, Liang L, Zhao Y X. Design and performance analysis of piezoelectric micro-spray dispensing system based on compliant mechanism[J]. Optics and Precision Engineering, 2019, 27(9): 1990-2001. (in Chinese) |
| [14] |
Nguon B, Jouaneh M. Design and characterization of a precision fluid dispensing valve[J]. The International Journal of Advanced Manufacturing Technology, 2004, 24(3/4): 251-260. DOI:10.1007/s00170-003-1738-3 |
| [15] |
Deng G L, Cui W J, Zhou C, et al. A piezoelectric jetting dispenser with a pin joint[J]. Optik, 2018, 175: 163-171. DOI:10.1016/j.ijleo.2018.08.132 |
| [16] |
Lu S Z, Liu Y X, Yao Y F, et al. Bond-graph model of a piezostack driven jetting dispenser[J]. Simulation Modelling Practice and Theory, 2014, 49: 193-202. DOI:10.1016/j.simpat.2014.09.007 |
| [17] |
Yao Y F, Lu S Z, Liu Y X. Simulation and experiment research of non-contact micro-liquid reagent dispensing[J]. Advance Journal of Food Science and Technology, 2013, 5(5): 514-521. DOI:10.19026/ajfst.5.3119 |
| [18] |
Qin Y D, Zhao X, Shirinzadeh B, et al. Closed-form modeling and analysis of an XY flexure-based nano-manipulator[J/OL]. Chinese Journal of Mechanical Engineering, 2018, 31: 7[2020-02-25]. https: //doi.org/10.1186/s10033-018-0211-z.
|
| [19] |
Zhu B L, Zhang X M, Zhang H C, et al. Design of compliant mechanisms using continuum topology optimization: a review[J]. Mechanism and Machine Theory, 2020, 143: 103622. DOI:10.1016/j.mechmachtheory.2019.103622 |
| [20] |
刘凯, 曹毅, 周睿, 等. 抗压内LET柔性铰链的建模及分析[J]. 工程设计学报, 2016, 23(6): 585-591. Liu K, Cao Y, Zhou R, et al. Modeling and analysis of compressive inside LET flexure hinge[J]. Chinese Journal of Engineering Design, 2016, 23(6): 585-591. (in Chinese) |
| [21] |
Ding B X, Li Y M, Xiao X, et al. Design and analysis of a 3-DOF planar micromanipulation stage with large rotational displacement for micromanipulation system[J]. Mechanical Sciences, 2017, 8(1): 117-126. DOI:10.5194/ms-8-117-2017 |
| [22] |
Li J Y, Yan P, Li J M. Displacement amplification ratio modeling of bridge-type nano-positioners with input displacement loss[J]. Mechanical Sciences, 2019, 10(1): 299-307. DOI:10.5194/ms-10-299-2019 |
| [23] |
Wu Z G, Li Y M, Hu M. Design and optimization of full decoupled micro/nano-positioning stage based on mathematical calculation[J]. Mechanical Sciences, 2018, 9(1): 417-429. |
 2021, Vol. 44
2021, Vol. 44


