超磁致伸缩材料(giant magnetostrictive material,简称GMM)是一种磁控功能的智能材料,可以实现电磁机能量双向转换,与压电材料、形状记忆合金和电致伸缩材料相比,它具有能量转换效率高、形变率较大、驱动电压低、响应更快、工作频带宽等优点[1]。利用超磁致伸缩材料研制的作动器具有结构简单、出力大和反应迅速等特点,在精密定位、振动主动控制、流体控制等领域有非常好的应用前景[2-6]。
在对超磁致伸缩作动器性能研究方面,由于超磁致伸缩作动器输入电流与输出位移及输出力之间存在明显的电磁机非线性耦合场,GMM棒中磁感应强度的大小分布不均匀,将严重破坏作动器的工作性能[7-9]。如果GMM棒处于一个非均匀的磁场环境中,一方面在对其测控时会出现高次谐波而导致谐频输出[10-11];另一方面,根据磁畴唯象理论,由于各磁畴之间的伸缩位移不同导致相邻磁畴之间的拉压性不一致,使GMM棒中的应力分布不均匀,从而大大降低超磁致伸缩棒的力学性能[10]。针对这些问题,国内外学者做了大量的研究,北京航空航天大学的李琳等[12]对超磁致伸缩作动器进行了磁路优化设计的研究,通过增加导磁体形成闭合磁路,从磁能的利用率角度开展研究,研究结果表明经磁路优化后,磁场的均匀度得到了一定的提高。薛光明等[13]对超磁致伸缩作动器中的激励线圈设计进行了大量的研究,以磁场强度的大小和热损失作为评价磁路好坏的一个准则,通过对激励线圈优化后磁场环境得到了很大的改善。Grunwald等[14]提出了超磁致伸缩作动器磁路优化设计的方法,并开展了作动器磁路优化设计的研究。然而,曹海龙等[5]和王修勇等[15]对于超磁致伸缩作动器的性能分析只考虑了磁路中导磁材料的导磁率对磁场均匀性的影响,并没有分析磁路结构及结构参数等对GMM棒中磁感应强度的大小及均匀性的影响。超磁致伸缩作动器在工作过程中,GMM棒中的磁感应强度的均匀性至关重要,但这些学者[16-17]只关注了GMM棒中的磁感应强度大小和作动器的输出特性,并未涉及GMM棒中磁感应强度的均匀性。基于以上研究,国内外的众多学者对磁路进行优化后磁感应强度的大小和均匀性均得到了一定的提高,但是对于磁场的影响因素并没有系统性地考虑,同时对于GMM棒中磁感应强度的均匀性并没有过多的涉及。所以笔者结合相关的电磁学理论,提出以GMM棒中减小磁漏、增大磁感应强度和提高磁感应强度的均匀性为设计原则[18],利用有限元ANSYS软件系统性地分析磁路结构、激励线圈、导磁体和导磁内壁所用的材料参数对超磁致伸缩作动器中磁路磁场的影响,在此基础上对各参数进行优化设计。研究结果表明,经磁路优化设计后,GMM棒的磁感应强度的大小和均匀性都得到了很大程度的提高,这对于高性能GMA的研发设计具有一定的指导意义。
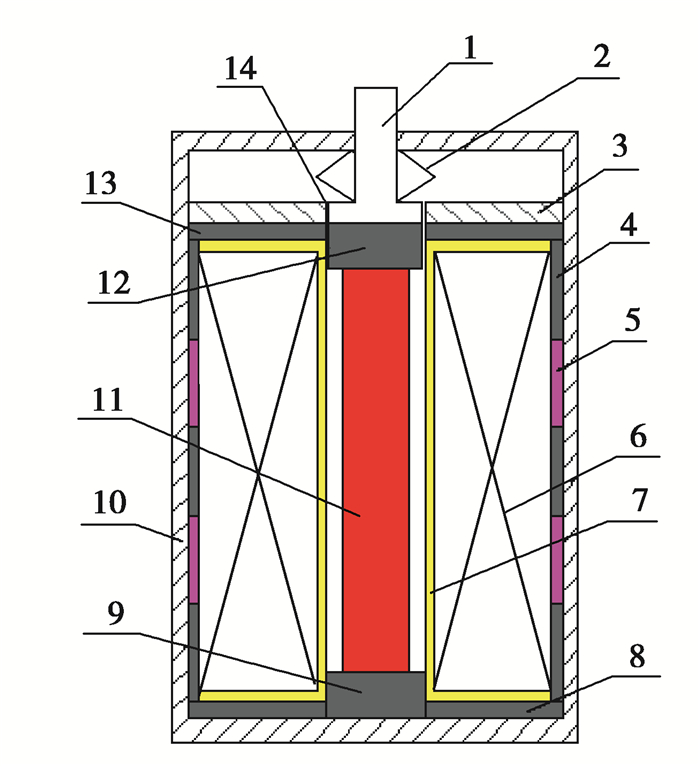
1 GMA的结构和工作原理超磁致伸缩作动器结构如图 1所示。主要包括输出杆、碟形弹簧、端盖、导磁侧壁、导磁环、导磁体、不导磁外壳和GMM棒等,其驱动部分由激励线圈和永磁体组成。超磁致伸缩作动器的工作原理为:以激励线圈产生的磁场作为驱动磁场,在结构上由上下导磁体、空气间隙、上下导磁环、导磁侧壁、永磁体与GMM棒形成闭合磁路[19]。当改变输入电流时,激励线圈会产生变化的磁场;由于GMM棒轴向的磁致伸缩效应,GMM棒会随着磁场的变化而发生伸缩变形,所以作动器会向外界输出位移和力,从而实现电磁能向机械能的转换。通过控制输入电流,可以控制作动器位移和力的输出。永磁体是为了提供偏置磁场而达到消除倍频现象的目的,同时使GMA具有较好的线性输出。蝶形弹簧提供一定的预压力,使GMM棒能够充分发挥材料的性能。
|
1—输出杆;2—碟形弹簧;3—上端盖;4—导磁侧壁;5—永磁体;6—激励线圈;7—线圈骨架;8—下导磁环;9—下导磁体;10—外壳;11—GMM棒;12—上导磁体;13—上导磁环;14—空气间隙 图 1 超磁致伸缩作动器结构简图 Fig. 1 Structure diagram of giant magnetostrictive actuator |
通过静态条件下GMM棒的线性压磁方程式(1)与式(2)[20],可得出应变s和磁感应强度B之间的关系,如式(3)所示。
| $ s=\frac{\sigma}{E_{y}^{H}}+q H, $ | (1) |
| $ B=q \sigma+u^{\sigma} H , $ | (2) |
| $ s=\left(\frac{1}{E_{y}^{H}}-\frac{q^{2}}{u^{\sigma}}\right) \sigma+\frac{q}{u^{\sigma}} B, $ | (3) |
式中:s为磁场作用下的材料应变;σ为GMM棒的预压力;q为GMM棒轴向压磁系数;EyH为材料弹性模量;H为GMM棒的平均磁场强度;B为磁感应强度;uσ为GMM棒的相对磁导率。
由式(3)可知,假定q、EyH、uσ为恒量,当预压力σ一定,应变s与磁感应强度B呈线性关系,此时磁感应强度决定GMA的输出性能。
2 磁路设计对于螺线管产生的磁场H与磁路总磁通ϕ之间的关系如式(4)表达所示[21]。
| $ NI = \phi R{\rm{ , }} $ | (4) |
式中:N为螺线管线圈的匝数;I为线圈中的电流值;ϕ为磁通量;R为磁路中的总磁阻。
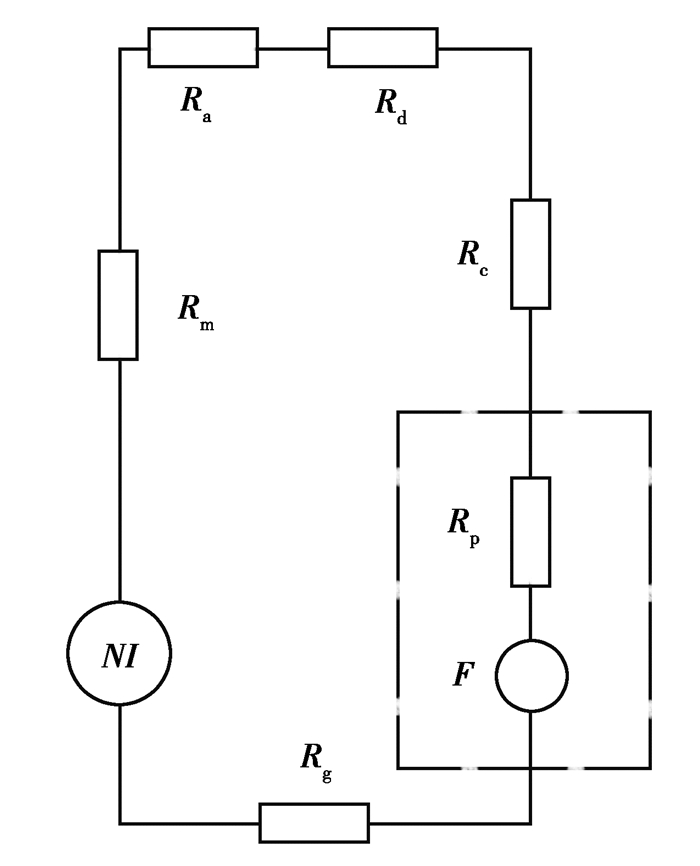
由图 1可知,可以将作动器简化,得到磁路模型如图 2所示。其中NI和F分别表示控制线圈和永磁体的磁动势;Rm、Rd、Rc、Rp、Rg和Ra分别表示GMM棒、上下导磁体、导磁侧壁、永磁体、上下导磁环和空气间隙的等效磁阻[22-23]。
|
图 2 超磁致伸缩作动器磁路模型简图 Fig. 2 Magnetic circuit model of giant magnetostrictive actuator |
其中:
| $ {{R_{\rm{m}}} = \frac{{{L_{\rm{m}}}}}{{{u_0}{u_{\rm{m}}}{A_{\rm{m}}}}},\quad {R_{\rm{d}}} = \frac{{{L_{\rm{d}}}}}{{{u_0}{u_{\rm{d}}}{A_{\rm{d}}}}},\quad {R_{\rm{c}}} = \frac{{{L_{\rm{c}}}}}{{{u_0}{u_{\rm{c}}}{A_{\rm{c}}}}},} $ | (5) |
| $ {{R_{\rm{p}}} = \frac{{{L_{\rm{p}}}}}{{{u_0}{u_{\rm{p}}}{A_{\rm{p}}}}},\quad {R_{\rm{g}}} = \frac{{{L_{\rm{g}}}}}{{{u_0}{u_{\rm{g}}}{A_{\rm{g}}}}},\quad {R_{\rm{a}}} = \frac{{{L_{\rm{a}}}}}{{{u_0}{A_{\rm{a}}}}} = \frac{{\ln \left( {\frac{{{r_2}}}{{{r_1}}}} \right)}}{{2{\rm{ \mathsf{ π} }}{u_0}h}},} $ | (6) |
式中:u0为真空磁导率;um、Am和Lm分别为GMM棒的相对磁导率、等效截面积和有效长度;ud、Ad和Ld分别为上下导磁体的相对磁导率、等效截面积和有效长度;uc、Ac和Lc分别为导磁侧壁的相对磁导率、等效截面积和有效长度;up、Ap和Lp分别为永磁体的相对磁导率、等效截面积和有效长度;ug、Ag和Lg分别为上下导磁环的相对磁导率、等效截面积和有效长度;r1、r2和h分别为上导磁体的外径、上导磁环的内径和空气间隙高度。由式(5)和式(6)可知,在GMA结构设计完成的情况下,要减小外磁路中的磁阻,需要增大导磁材料的磁导率;空气间隙Ra越小,外磁路中的磁阻越小,对GMM棒性能的发挥越有利。
由于超磁致伸缩材料和永磁体的磁导率都很低,因此,在实际的磁路中应考虑到漏磁。本文中所设计的磁路中同时包含激励线圈和永磁体2个磁动势,它们的漏磁强弱是不同的,分别用kf1、kf2定义激励线圈和永磁体的漏磁系数。由磁路欧姆定律可得:
| $ \begin{array}{*{20}{l}} {\phi = B{A_{\rm{m}}} = \frac{{\frac{1}{{{k_{{\rm{f1}}}}}}NI \pm \frac{1}{{{k_{{\rm{f}}2}}}}F}}{{{R_{\rm{m}}} + {R_{\rm{d}}} + {R_{\rm{c}}} + {R_{\rm{p}}} + {R_{\rm{g}}} + {R_{\rm{a}}}}} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\frac{1}{{{k_{{\rm{f}}1}}}}NI \pm \frac{1}{{{k_{{\rm{f}}2}}}}F}}{{\frac{{{L_{\rm{m}}}}}{{{u_0}{u_{\rm{m}}}{A_{\rm{m}}}}} + \frac{{{L_{\rm{d}}}}}{{{u_0}{u_{\rm{d}}}{A_{\rm{d}}}}} + \frac{{{L_{\rm{c}}}}}{{{u_0}{u_{\rm{c}}}{A_{\rm{c}}}}} + \frac{{{L_{\rm{p}}}}}{{{u_0}{u_{\rm{p}}}{A_{\rm{p}}}}} + \frac{{{L_{\rm{g}}}}}{{{u_0}{u_{\rm{g}}}{A_{\rm{g}}}}} + \frac{{\ln \left( {\frac{{{r_2}}}{{{r_1}}}} \right)}}{{2{\rm{ \mathsf{ π} }}{u_0}h}}}}}。\end{array} $ | (7) |
由式(3)和式(7),可得式(8),
| $ s = \left( {\frac{1}{{E_y^H}} - \frac{{{q^2}}}{{{u^\sigma }}}} \right)\sigma + \frac{q}{{{A_{\rm{m}}}{u^\sigma }}}\frac{{\frac{1}{{{k_{{\rm{f}}1}}}}NI \pm \frac{1}{{{k_{{\rm{f}}2}}}}F}}{{\frac{{{L_{\rm{m}}}}}{{{u_0}{u_{\rm{m}}}{A_{\rm{m}}}}} + \frac{{{L_{\rm{d}}}}}{{{u_0}{u_{\rm{d}}}{A_{\rm{d}}}}} + \frac{{{L_{\rm{c}}}}}{{{u_0}{u_{\rm{c}}}{A_{\rm{c}}}}} + \frac{{{L_{\rm{p}}}}}{{{u_0}{u_{\rm{p}}}{A_{\rm{p}}}}} + \frac{{{L_{\rm{g}}}}}{{{u_0}{u_{\rm{g}}}{A_{\rm{g}}}}} + \frac{{\ln \left( {\frac{{{r_2}}}{{{r_1}}}} \right)}}{{2{\rm{ \mathsf{ π} }}{u_0}h}}}}。$ | (8) |
由式(8)可知,磁回路的结构形式、线圈的驱动方式和磁路中的导磁材料等均会对作动器的输出位移产生很大的影响。在作动器结构确定的前提下,对于高性能的GMA,需要对导磁材料的导磁率、上下导磁体的半径和激励线圈的轴向长度等进行优化。
3 磁致伸缩作动器磁场有限元分析 3.1 超磁致伸缩作动器有限元建模电磁场理论主要是通过一套麦克斯韦方程组来描述的,它是用来分析和研究电磁场的[24-25]。如图 1所示,由于GMA是三维轴对称结构,对其结构进行简化,采用平面轴对称单元(轴对称模型)建立有限元模型。利用ANSYS有限元软件对GMA磁回路进行有限元分析,具体的分析过程如下。
1)创建物理环境,选定Magnetic-Nodal,定义相关材料的材料特性,如表 1所示;
| 表 1 模型材料的相关参数 Table 1 Related parameters of model materials |
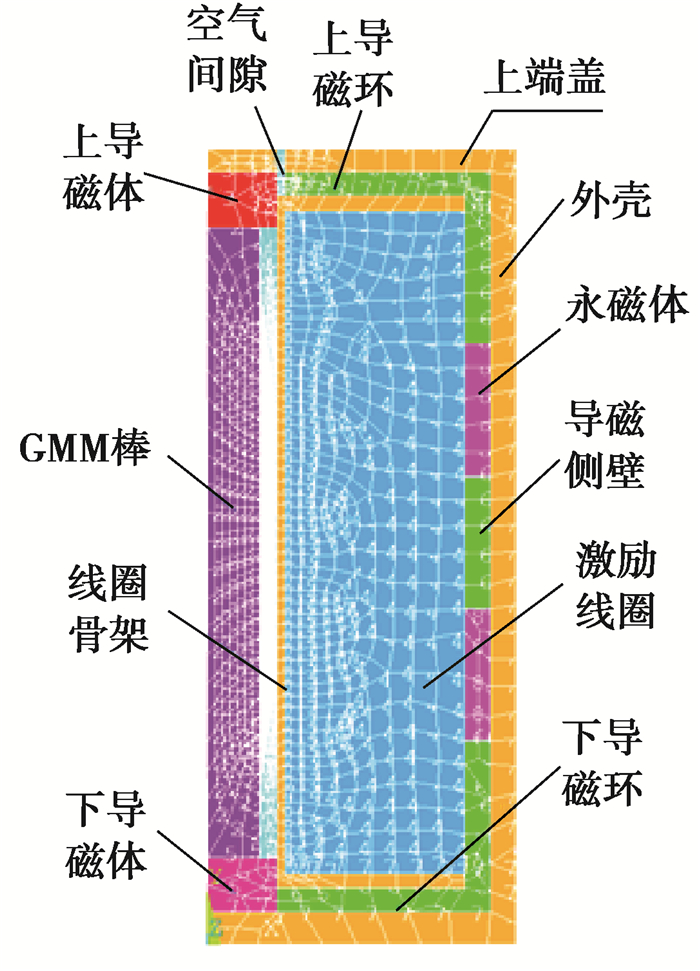
2) 采用面单元plane53建立模型、赋予材料属性、划分网格(图 3),这里采用的网格等级为4。对不同模型网格等级的研究表明,网格影响很小,考虑网格精度影响的结果见表 2;
|
图 3 超磁致伸缩作动器网格划分 Fig. 3 Meshing of giant magnetostrictive actuator |
| 表 2 不同网格等级的磁感应强度与均匀度的对比 Table 2 Comparison of magnetic induction intensity and uniformity at different grid levels |
3) 对所建模型施加磁力线平行边界条件,在线圈上施加电流密度面荷载;
4) 通过MAGSOLV求解得到GMA内部磁感应强度分布以及GMM棒中的磁感应强度;
5) 输出GMM棒磁感应强度计算结果。
以GMM棒中心线处的磁场均匀性作为磁回路优劣评价的标准,其值越接近1表示磁感应强度分布越均匀,表达式为
| $ \omega = \left( {1 - \frac{{{B_{{\rm{max}}}} - {B_{{\rm{min}}}}}}{{{B_{{\rm{max}}}}}}} \right) \times 100\% , $ | (9) |
式中:Bmax为GMM棒中心线处的最大磁感应强度,Bmin为GMM棒中心线处的最小磁感应强度。
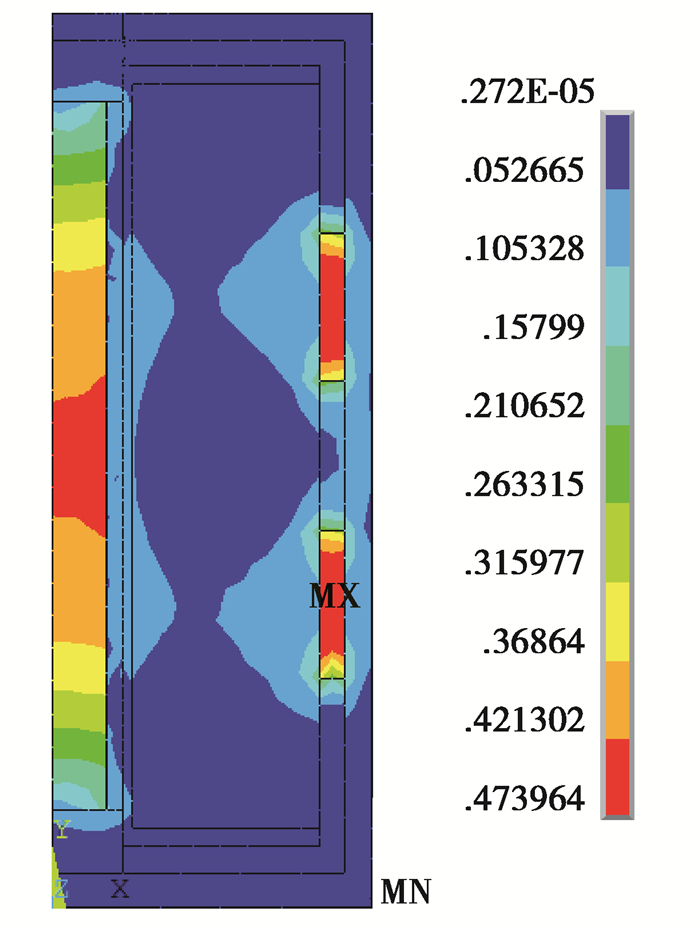
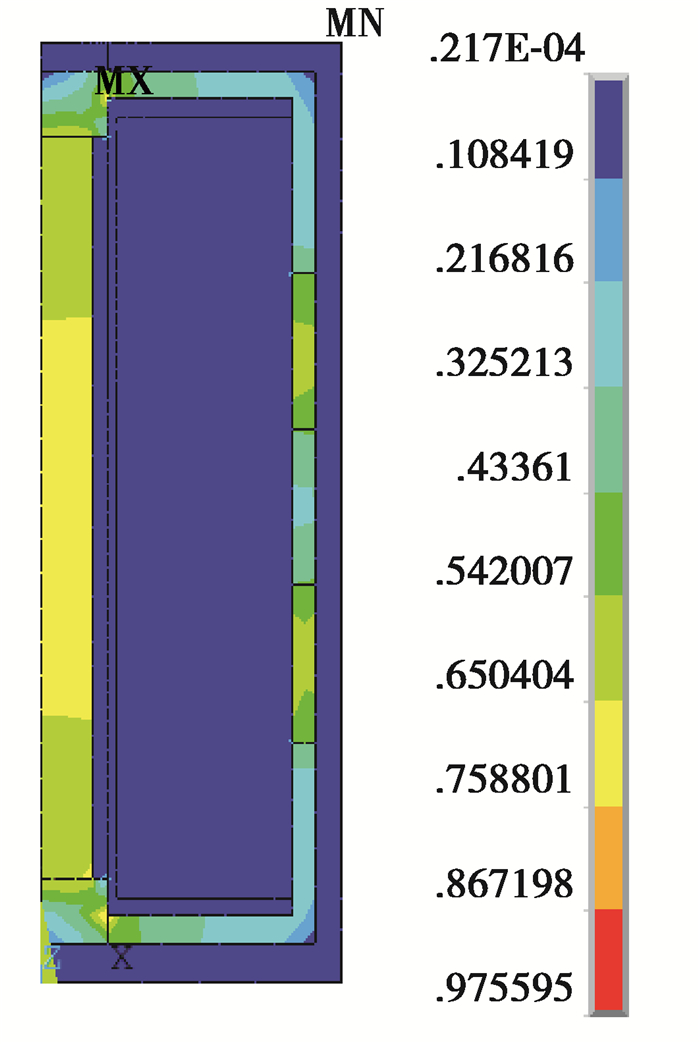
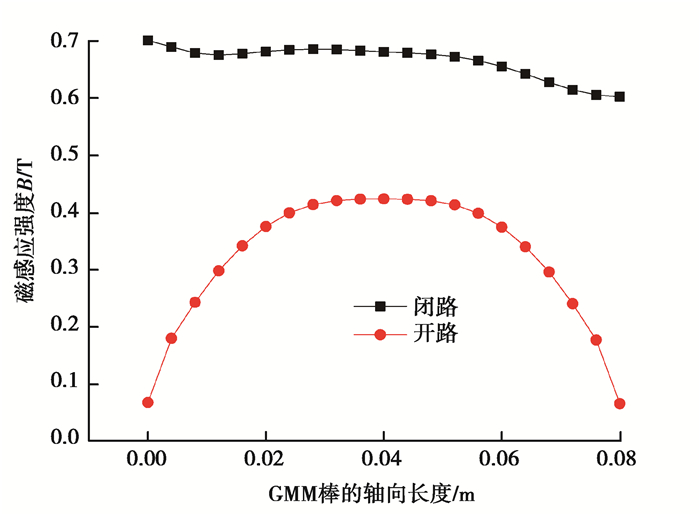
3.2 结构参数对GMM棒的磁场影响 3.2.1 开闭磁路对GMM棒的磁场影响超磁致伸缩作动器内部磁路分别在开路和闭路的情况下,进行磁路分析。其中开路:上下导磁体、上下导磁环、导磁侧壁的相对导磁率均为1;闭路:上下导磁体、上下导磁环和导磁侧壁的相对导磁率均为100;无论开路还是闭路,GMM棒和永磁体的相对导磁率分别为8和5。通过有限元分析,得到开路和闭路时的磁感应强度分布分别如图 4和图 5所示。当磁路为开路时,GMM棒中的磁感应强度分布表现出中间大,两端小,磁感应强度分布极不均匀。当磁路闭合时,GMM棒中的磁感应强度的大小和均匀性均得到了很大的提高。将开路状态和闭路状态进行对比,其结果如图 6所示。从图 6中可以看出,GMA为闭路磁路时,磁感应强度远高于开路磁路的磁感应强度,且GMM棒中心线处的磁感应强度较为均匀。根据式(9)计算得到,开路时的均匀度为15.4%,闭路时均匀度高达85.9%,闭路时的均匀度相对开路时的均匀度提高了70.5%。因此,GMA内部的磁路应设计成闭合的。
|
图 4 开路时磁感应强度分布图 Fig. 4 Distribution of magnetic induction intensity in open circuit |
|
图 5 闭路时磁感应强度分布图 Fig. 5 Distribution of magnetic induction intensity in closed circuit |
|
图 6 GMM棒磁感应强度与开闭磁路的关系 Fig. 6 Relationship between GMM rod magnetic induction intensity and opening and closing magnetic circuit |
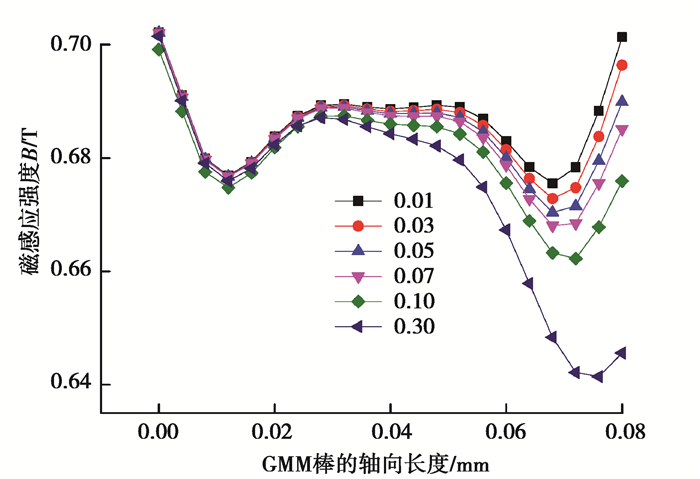
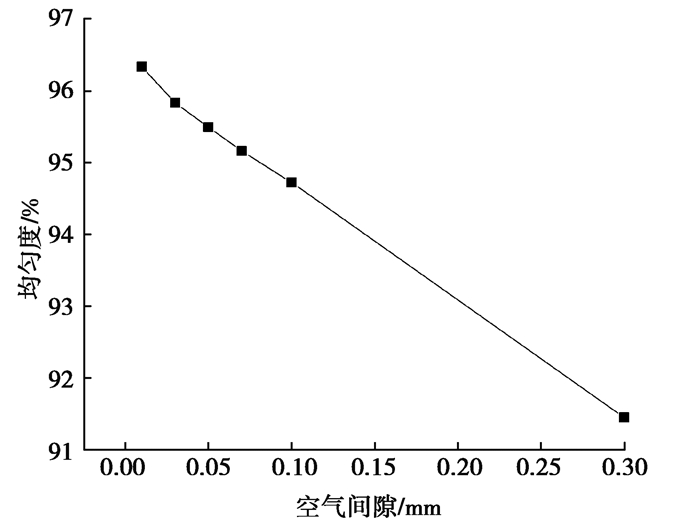
超磁致伸缩作动器在工作时,由于GMM棒的磁致伸缩效应,应该在输出杆与上端盖之间留有一定的空气间隙,便于GMA机械能的输出。而空气间隙的大小对于GMM棒中心线磁场分布影响非常大。空气间隙的大小直接决定漏磁的大小,所以当空气间隙大小分别为0.01,0.03,0.05,0.07,0.10,0.30 mm时,通过有限元分析,得到GMM棒中心线磁感应强度分布如图 7所示,GMM棒磁感应强度的均匀度与空气间隙的关系如图 8所示。
|
图 7 GMM棒磁感应强度与空气间隙的关系 Fig. 7 Relationship between magnetic induction intensity and air gap of GMM rod |
|
图 8 GMM棒均匀度与空气间隙的关系 Fig. 8 Relationship between uniformity of GMM rod and air gap |
从图 7可以看出,GMM棒左端的磁感应强度较右端的大,且随着空气间隙的增大,GMM棒的磁感应强度逐渐减小。GMM棒左端的磁感应强度随着空气间隙的增大基本无变化,GMM棒右端的磁感应强度随着空气间隙的增大呈现大幅度的下降;这是由于空气间隙的增大,使GMM棒右端出现大量的漏磁现象,导致GMM棒右端的磁感应强度大幅减小。从图 8可以看出,随着空气间隙的增大,GMM棒磁感应强度的均匀度逐渐下降,空气间隙为0.01 mm相对空气间隙为0.05 mm,GMM棒中磁感应强度的均匀度只提高了0.84%,空气间隙越小,意味着作动器结构设计成本越高。因此,在制作GMA时,应控制空气间隙小于0.05 mm,即能保证GMM棒中磁感应强度的均匀度高达95.49%。
超磁致伸缩作动器在工作时,应在输出杆与上端盖之间留有一定的空气间隙,便于超磁致伸缩作动器机械能的输出。设计时空气间隙最好小于0.05 mm,为了验证这个普适性,选用不同规格的GMM棒,通过改变模型的参数。分别取GMM棒的模型尺寸(mm×mm)为ϕ8×80、ϕ10×80、ϕ20×80、ϕ12×100和ϕ12×120来分别进行验证,其分析的结果分别如表 3所示。
| 表 3 模型参数空气间隙与最优均匀度 Table 3 Air gap and optimal uniformity in model parameters |
通过以上各种模型的仿真计算,其最终的结果表明,超磁致伸缩作动器设计空气间隙时最好小于0.05 mm,此时GMM棒中的均匀度最高。
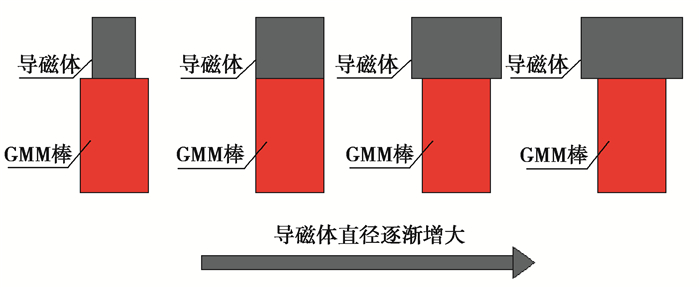
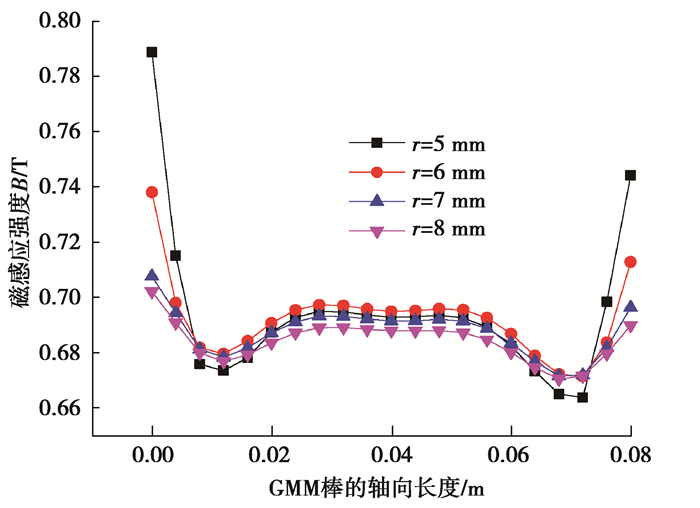
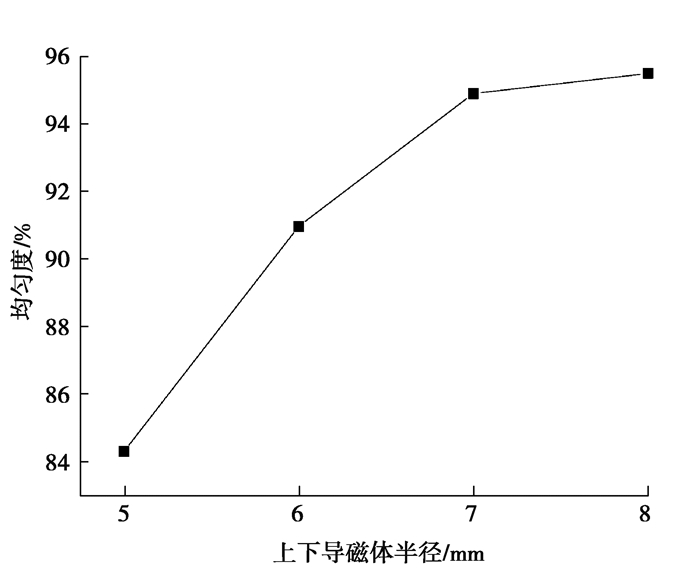
3.2.3 上下导磁体的半径对GMM棒的磁场影响根据磁路第一方程,穿出任意封闭面的磁通量恒等于穿入该封闭面的磁通量。为了改善GMM棒两端的漏磁,需要增加上下导磁体来减少端部的漏磁。由于GMM棒的导磁率仅为空气导磁率的3~10倍左右,因此GMM棒两端应设计高导磁的导磁体,导磁率高的导磁体可以使GMM棒中的磁感应强度更加均匀,导磁体的半径变化如图 9所示。通过有限元分析,得到仿真结果如图 10所示,GMM棒磁感应强度的均匀度与上下导磁体的半径的关系如图 11所示。
|
图 9 导磁体半径的变化情况 Fig. 9 Variation of radius of conducting magnet |
|
图 10 GMM棒磁感应强度与导磁体半径的关系 Fig. 10 Relationship between the magnetic induction intensity of GMM rod and the radius of conducting magnet |
|
图 11 GMM棒均匀度与上下导磁体半径的关系 Fig. 11 Relationship between uniformity of GMM rod and radius of upper and lower magnets |
根据图 10可知,由于右端空气间隙的存在,增大了漏磁,使得每一种对应的导磁体半径左端的磁感应强度总比右端大。GMM棒磁感应强度的均匀度如图 11所示,当导磁体的半径比GMM棒的半径小时,GMM棒中的磁场均匀度最差;当导磁体的半径与GMM棒的半径一致时,GMM棒中的磁感应强度较大,但均匀度相对较低;当导磁体的半径大于GMM棒的直径时,GMM棒中的磁感应强度相对较均匀,且导磁体半径为7 mm与导磁体半径为8 mm相比,GMM棒中的磁感应强度更大,均匀度相差很小。同时考虑到GMM棒易受到激励线圈工作时产生温度的影响,因此,在设计GMA时,导磁体的半径应略大于GMM棒的半径。
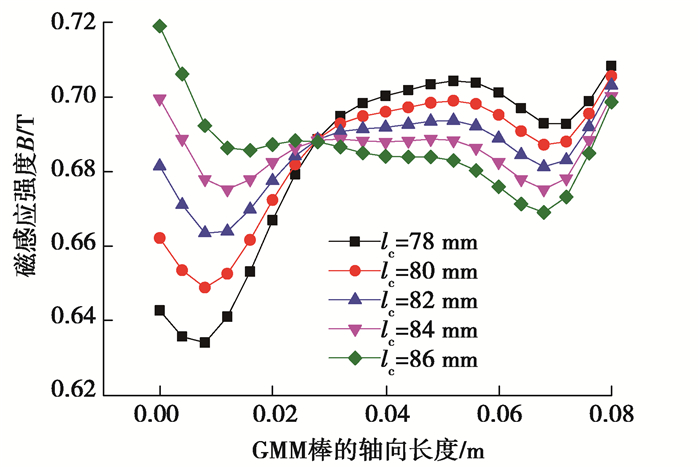
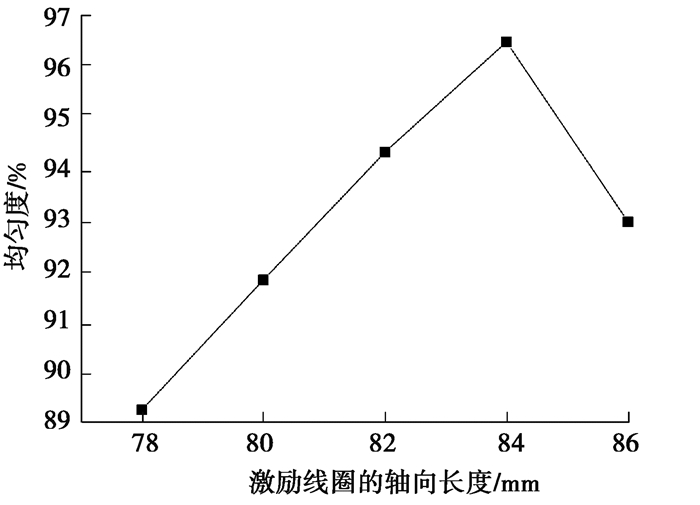
3.2.4 激励线圈轴向长度对GMM棒的磁场影响考虑到空心螺线管端部磁场漏磁较大,因此应尽可能的将GMM棒位于激励线圈的中心位置,以改善GMM棒中心线磁场的均匀性。在保证其他结构参数不变的情况下,改变激励线圈轴向长度;通过有限元分析,得到仿真结果如图 12所示,GMM棒磁感应强度的均匀度与激励线圈的轴向长度的关系如图 13所示。
|
图 12 GMM棒磁感应强度与激励线圈轴向长度的关系 Fig. 12 Relationship between magnetic induction intensity of GMM rod and axial length of excitation coil |
|
图 13 GMM棒均匀度与激励线圈的轴向长度的关系 Fig. 13 Relationship between uniformity of GMM rod and axial length of excitation coil |
从图 12可以看出,不同长度的激励线圈,所对应的磁感应强度是不一样的。通过式(9)计算,计算结果如图 13所示。当激励线圈的轴向长度为84 mm时,GMM棒中心线的磁场均匀性最好,均匀度为96.43%;而当激励线圈的轴向长度为86 mm时,GMM棒中心线的磁场均匀性较低,均匀度为93.05%。并不是激励线圈的轴向长度越长,GMM棒中心线的磁场均匀性越好。因此在设计GMA中激励线圈的轴向长度最好为GMM棒长的1.05倍左右。
激励线圈轴向长度应设计为GMM棒轴向长度的1.05倍左右;为了验证这个普适性,选用不同规格的GMM棒,通过改变主要的模型参数。分别取GMM棒的模型尺寸(mm×mm)为ϕ8×80、ϕ10×80、ϕ20×80、ϕ12×100和ϕ12×120来分别进行验证,其分析的结果如表 4所示。
| 表 4 模型参数中比值与最优均匀度 Table 4 Ratios and optimal uniformity in model parameters |
通过以上各种模型的仿真计算,其最终的结果表明,激励线圈轴向长度应设计为GMM棒轴向长度的1.05倍左右,此时GMM棒中的均匀度最高。
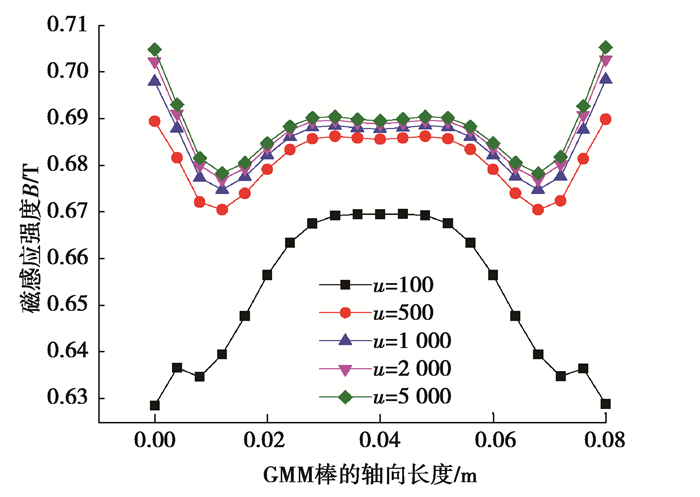
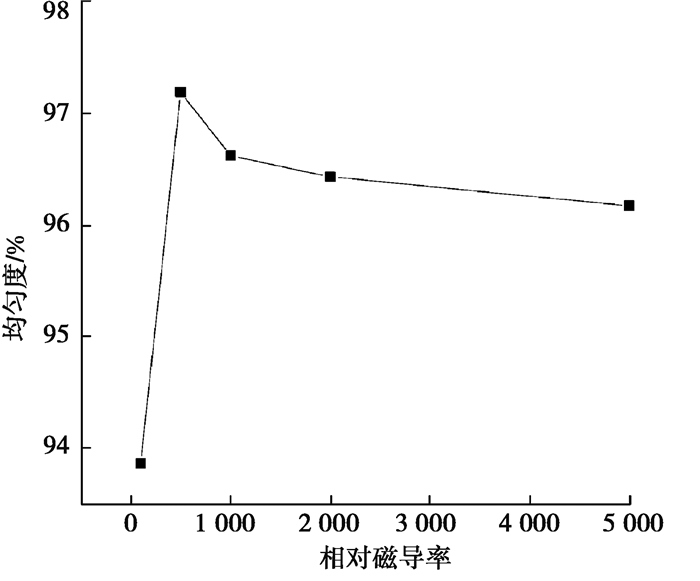
3.2.5 磁路中导磁材料的导磁率对GMM棒的磁场影响闭合磁路中,各导磁材料的相对导磁率的大小对GMM棒中磁场均匀性密切相关。当上下导磁体、上下导磁环和导磁侧壁相对导磁率分别为100,500,1 000,2 000,5 000时,通过有限元分析,得到材料的相对导磁率与GMM棒中磁场强度的关系如图 14所示,GMM棒中磁感应强度的均匀度与导磁材料的导磁率的关系如图 15所示。
|
图 14 GMM棒磁感应强度与导磁材料相对导磁率关系 Fig. 14 Relationship between magnetic induction intensity of GMM rod and relative permeability of magnetic conducting material |
|
图 15 GMM棒均匀度与相对导磁率的关系 Fig. 15 Relationship between uniformity of GMM rod and relative permeability |
从图 14可以看出,当导磁材料的相对导磁率为100时,GMM棒两端的磁感应强度较小,中间磁感应强度大。造成的原因是,由于GMM棒两端的导磁体的相对导磁率低,导致GMM棒两端漏磁较为严重,从而影响GMM棒两端的磁感应强度。而当导磁材料的相对导磁率大于500时,随着导磁材料相对导磁率的增大,GMM棒的磁感应强度也随着增大,但是增大的幅度慢慢减小;GMM棒两端与中间的磁感应强度相差较小,GMM棒中心线磁场分布较为均匀,原因是GMM棒两端导磁体的相对导磁率较高,限制了漏磁。从图 15可以看出,当导磁材料的导磁率大于500时,GMM棒磁感应强度的均匀度变化不大。因此,在设计GMA时,应选择较高的导磁材料,较高的导磁材料对于GMM棒中磁场分布的大小和均匀性都有利。
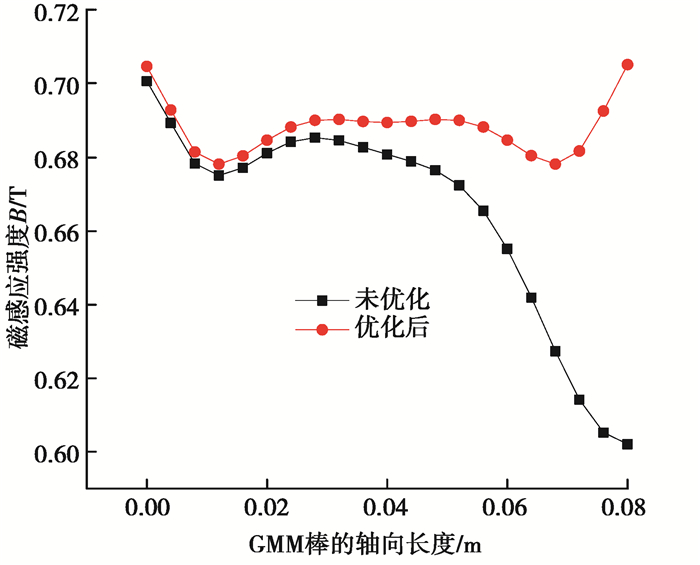
3.3 作动器结构参数优化前后的对比磁路中,采用闭合的形式,空气间隙为0.05 mm,上下导磁体的半径为7 mm,激励线圈的轴向长度为84 mm,同时导磁材料的导磁率为5 000。通过有限元分析,得到最终优化后的仿真结果如图 16所示。从仿真结果来看,GMM棒中的磁感应强度分布非常均匀。将闭合磁路的仿真结果和最终优化结构参数的仿真结果进行对比,结果对比如图 17所示。从整体的仿真结果来看,作动器结构参数优化后,GMM棒中的磁感应强度的大小和均匀性均得到了提高。由于右端空气间隙的存在,增大了GMM棒右端的漏磁,导致GMM棒右端的磁感应强度减小,且均匀性下降,但是经过结构的参数优化,可以避免这种现象的出现。未优化时GMM棒中的磁感应强度的均匀度为85.9%,当进行结构参数的优化后,GMM棒中的磁感应强度的均匀度为96.17%。结构参数优化后相对未优化时,磁感应强度的大小提高了0.1 T,均匀度提高了10.27%。所以通过参数的合理优化,不仅可以提高作动器的磁机转换效率,还可以提高作动器的精准输出。

|
图 16 优化后磁感应强度分布图 Fig. 16 Distribution of magnetic induction intensity after optimization |
|
图 17 GMM棒磁感应强度优化前后的对比 Fig. 17 Comparison before and after optimization of GMM rod magnetic induction intensity |
超磁致伸缩作动器内部磁路比较复杂,基于静态条件下线性磁致伸缩理论,并根据电磁学原理得出应变和磁路结构参数、材料相对导磁率的关系。在此基础上建立GMA的有限元模型,对其进行磁场仿真分析。通过GMA的磁场仿真结果研究,可以得出以下结论:
1) 超磁致伸缩作动器内部的磁路应采用闭合的形式,无论是GMM棒中磁感应强度的大小还是均匀度都得到了大幅度的提高;同时磁回路应采用高导磁率的导磁材料,高磁导率的导磁体对GMM棒中磁感应强度的大小和均匀度都有利。
2) 过长或过短的激励线圈轴向长度都会使GMM棒中磁感应强度的大小和均匀性受到影响,所以激励线圈轴向长度应设计为GMM棒轴向长度的1.05倍左右;为了增大GMM棒中磁感应强度的大小和均匀度,同时减小温度对GMM棒性能的影响,上下导磁体的半径应略大于GMM棒的半径。
3) 输出杆与上端盖之间的空气间隙会使磁回路出现漏磁现象,过大的空气间隙将影响GMM棒磁感应强度的大小和均匀性。因此,设计时空气间隙最好小于0.05 mm。
4) 通过作动器参数优化前后GMM棒中磁感应强度的对比,优化后,GMM棒中磁感应强度的大小提高了0.1 T,且均匀度提高了10.27%。
| [1] |
周寿增, 高学绪. 磁致伸缩材料[M]. 北京: 冶金工业出版社, 2017. Zhou S Z, GAO X X. Magnetostrictive material[M]. Beijing: Metallurgical Industry Press, 2017. (in Chinese) |
| [2] |
王安明, 孟建军, 胥如迅, 等. 大功率超磁致伸缩作动器的仿真与试验[J]. 仪表技术与传感器, 2019(4): 79-85. Wang A M, Meng J J, XU R X, et al. Simulation and experiment of high-power giant magnetostrictive actuator[J]. Instrument Technique and Sensor, 2019(4): 79-85. (in Chinese) |
| [3] |
Luo M Z, Li W J, Wang J M, et al. Development of a novel guided wave generation system using a giant magnetostrictive actuator for nondestructive evaluation[J]. Sensors, 2018, 18(3): 779. DOI:10.3390/s18030779 |
| [4] |
Sun H, Li J, Wang X, et al. Time delay compensation for the active cable vibration control using giant magnetostrictive actuators[J]. Zhendong Yu Chongji/Journal of Vibration and Shock, 2017, 36(14): 208-215. |
| [5] |
曹海龙, 朱石坚, 楼京俊, 等. 超磁致伸缩作动器的磁路设计与仿真分析[J]. 舰船科学技术, 2015, 37(6): 109-113. Cao H L, Zhu S J, Lou J J, et al. Magnetic circuit design and simulation analysis of giant magnetostrictive actuator[J]. Ship Science and Technology, 2015, 37(6): 109-113. (in Chinese) |
| [6] |
Xue G M, Zhang P L, Li X Y, et al. A review of giant magnetostrictive injector (GMI)[J]. Sensors and Actuators A: Physical, 2018, 273: 159-181. |
| [7] |
喻曹丰, 王传礼, 魏本柱. 超磁致伸缩驱动器磁致伸缩模型的有限元分析[J]. 机床与液压, 2016, 44(13): 120-124. Yu C F, Wang C L, WEI B Z. Finite element analysis of magnetostrictive model of giant magnetostrictive actuator[J]. Machine Tool & Hydraulics, 2016, 44(13): 120-124. (in Chinese) |
| [8] |
Zhu Y C, Ji L. Theoretical and experimental investigations of the temperature and thermal deformation of a giant magnetostrictive actuator[J]. Sensors and Actuators A: Physical, 2014, 218: 167-178. DOI:10.1016/j.sna.2014.07.017 |
| [9] |
范文涛, 林明星, 鞠晓君, 等. 圆筒状超磁致伸缩致动器磁场研究与仿真[J]. 功能材料, 2017, 48(5): 05054-05060. Fan W T, Lin M X, Ju X J, et al. Magneticfield calculation and simulation of a cylindrical giant magnetostrictive actuator[J]. Journal of Functional Materials, 2017, 48(5): 05054-05060. (in Chinese) |
| [10] |
闫洪波, 高鸿, 郝宏波, 等. 稀土超磁致伸缩驱动器激励线圈设计与仿真[J]. 机械科学与技术, 2019, 38(10): 1569-1575. Yan H B, Gao H, Hao H B, et al. Design and simulation of exciting coil in rare earth giant magnetostrictive actuator[J]. Mechanical Science and Technology for Aerospace Engineering, 2019, 38(10): 1569-1575. (in Chinese) |
| [11] |
高晓辉, 刘永光, 裴忠才. 超磁致伸缩作动器磁路优化设计[J]. 哈尔滨工业大学学报, 2016, 48(9): 145-150. Gao X H, Liu Y G, Pei Z C. Optimization and design for magnetic circuit in giant magnetostrictive actuator[J]. Journal of Harbin Institute of Technology, 2016, 48(9): 145-150. (in Chinese) |
| [12] |
李琳, 陈亮良, 杨勇. 超磁致伸缩作动器的结构分析[J]. 北京航空航天大学学报, 2013, 39(9): 1269-1274. Li L, Chen L L, Yang Y. Structural analysis of giant magnetostrictive actuator[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(9): 1269-1274. (in Chinese) |
| [13] |
薛光明, 何忠波, 李冬伟, 等. 超磁致伸缩棒磁场强度建模及线圈优化分析[J]. 纳米技术与精密工程, 2014, 12(2): 85-90. Xue G M, He Z B, Li D W, et al. Magnetic field intensity model for giant magnetostrictive rod and coil optimization analysis[J]. Nanotechnology and Precision Engineering, 2014, 12(2): 85-90. (in Chinese) |
| [14] |
Grunwald A, Olabi A G. Design of a magnetostrictive (MS) actuator[J]. Sensors and Actuators A: Physical, 2008, 144(1): 161-175. |
| [15] |
王修勇, 姚响宇, 孙洪鑫, 等. 超磁致伸缩作动器有限元建模与磁场分析[J]. 土木工程学报, 2012, 45(S2): 172-176. Wang X Y, Yao X Y, Sun H X, et al. Finite element model of giant magnetostrictive actuator and its magnetic field analysis[J]. China Civil Engineering Journal, 2012, 45(S2): 172-176. (in Chinese) |
| [16] |
Liu X H, Zhang H, Gao X L, et al. Design and simulation analysis of giant magnetostrictive actuator[J]. Materials Technology, 2015, 30(3): 155-158. |
| [17] |
孟建军, 张扬, 祁文哲, 等. 超磁致伸缩激振器的优化设计及应用分析[J]. 兵器材料科学与工程, 2017, 40(2): 8-12. Meng J J, Zhang Y, Qi W Z, et al. Optimal design and application analysis of giant magnetostrictive vibrator[J]. Ordnance Material Science and Engineering, 2017, 40(2): 8-12. (in Chinese) |
| [18] |
杨旭磊, 朱玉川, 费尚书, 等. 超磁致伸缩电静液作动器磁场分析与优化[J]. 航空动力学报, 2016, 31(9): 2210-2217. Yang X L, Zhu Y C, Fei S S, et al. Magnetic field analysis and optimization of giant magnetostrictive electro-hydrostatic actuator[J]. Journal of Aerospace Power, 2016, 31(9): 2210-2217. (in Chinese) |
| [19] |
Gabdullin N A, Khan S H. Application of change in permeability of magnetic shape memory (MSM) alloys for optimization of magnetic circuit in actuators[C]//9th IET International Conference on Computation in Electromagnetics (CEM 2014), London, UK. Institution of Engineering and Technology, 2014: 4.15-4.15.
|
| [20] |
向红军, 胡仁喜, 康士廷, 等. ANSYS 18.0电磁学有限元分析从入门到精通[M]. 北京: 机械工业出版社, 2018. Xiang H J, Hu R X, Kang S T. Mastering ANSYS 18.0 electromagnetic finite element analysis[M]. Beijing: China Machine Press, 2018. |
| [21] |
赵章荣, 邬义杰, 顾新建, 等. 超磁致伸缩执行器的三维非线性动态有限元模型[J]. 浙江大学学报(工学版), 2008, 42(2): 203-208. Zhao Z R, Wu Y J, Gu X J, et al. Three-dimensional nonlinear dynamic finite element model for giant magnetostrictive actuators[J]. Journal of Zhejiang University(Engineering Science), 2008, 42(2): 203-208. (in Chinese) |
| [22] |
He Z B, Rong C, Li D W, et al. Modeling and analysis of magnetic field distribution for stack giant magnetostrictive actuator[J]. Optics and Precision Engineering, 2017, 25(9): 2347. |
| [23] |
Rong C, He Z B, Li D W, et al. Dynamic modeling and analysis of stack giant magnetostrictive actuator[J]. Sensors and Actuators A: Physical, 2018, 276: 205-218. |
| [24] |
Hsieh C T, Tachikawa Y, Yonekura K. Anomaly of the electromagnetic duality of maxwell theory[J]. Physical Review Letters, 2019, 123(16): 161601. |
| [25] |
Yu Z, Wang T, Zhou M. Study on the magnetic-machine coupling characteristics of giant magnetostrictive actuator based on the free energy hysteresis characteristics[J]. Sensors, 2018, 18(9): 3070. |
 2021, Vol. 44
2021, Vol. 44

