2. 机械工业勘察设计 研究院有限公司, 西安 710043
2. China JIKAN Research Institute of Engineering Investigations and Design, Co. Ltd, Xi'an 710043, P. R. China
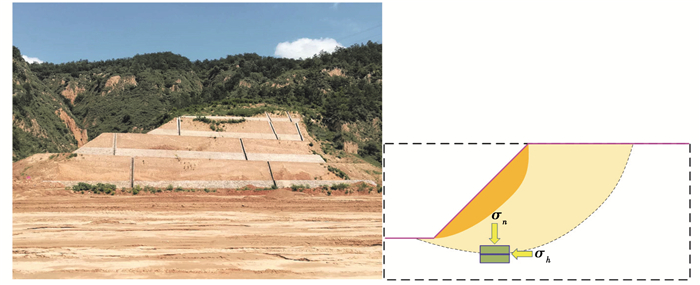
黄土地区是中国工程灾变的主要发生地之一[1-4],目前通过一系列大规模挖填方工程来改善这一工程灾变地区的环境以实现长久发展。大规模挖填方工程现场调查表明填方区边坡较为稳定而挖方区边坡失稳频发[5-6]。图 1为挖方区某边坡,挖方使得边坡内部一点从原始稳定应力状态变成卸荷应力状态,包括竖向和侧向卸荷[7-8]。竖向卸荷又可根据卸荷作业进程分非线性连续卸荷及分阶段卸荷,即在一次连续挖方作业过程中,竖向应力(σn)连续减小且非线性变化,将这种卸荷方式定义为非线性连续卸荷;在多次作业过程中,竖向应力分阶段连续减小(σ'n1>σ'n2>…>σ'nn)忽略σ'n1、σ'n2和σ'nn的连续减小过程,将这种卸荷方式记为竖向分阶段卸荷。而挖方边坡失稳则常发生在连续卸荷过程中,因此,研究非线性连续卸荷过程中黄土的强度特性具有应用价值。
|
图 1 某挖方边坡及垂直剖面内部一点应力状态 Fig. 1 An excavation slope and its internal stress state |
实际挖方工程的应力路径非常复杂,关于卸荷路径对试样力学特性的影响,相关学者采用简化的方法进行研究。如庄心善等[9]采用真三轴仪进行了不排水侧向卸荷试验,发现侧向卸荷情况下土体在较小的应变下发生破坏;张孟喜[10]对不同卸荷应力路径下的土体变形及强度特性进行了研究,发现侧向卸载的试样,其体积变形表现为剪缩性,侧向加载试样,其体积变形表现为剪胀性;张玉[11-12]进行平面应变条件原状黄土侧向卸载试验,试验表明侧向卸载条件下土的破坏应变要比平面应变竖向加载和常规三轴试验小得多;李加贵等[13]建立了侧向卸载过程细观结构演化方程;程相华[14]利用直剪仪对卸荷土体强度特性进行了研究,其发现瞬时卸载快剪强度受卸荷比、先期固结压力等因素的影响;赵春风[15]采用大型直剪试验,分析不同加、卸荷状态下接触面的力学特性,以及卸荷程度、粗糙度等对接触面软化特性和剪胀(缩)性的影响;张伏光[7]针对基坑开挖影响范围内土体的应力路径进行平面应变试验离散元模拟,发现不同卸荷应力路径卸荷土体性质差别较大且与结构性有关。此外Ng[16]和Li[17]等也研究了卸荷过程中的应力路径变化。但以上研究主要以基坑开挖涉及到的侧向卸荷为主,研究手段以常规三轴试验居多,而挖方工程更多涉及的是竖向卸荷,其不同于研究基坑开挖侧向土体的强度与变形。因此,以大规模挖填方工程挖方边坡为背景研究竖向卸荷状态下黄土的强度特性对挖方区边坡失稳机理研究具有重要的理论意义。
综合文献[7-18]可知加荷、卸荷应力路径下土体的强度与变形特性有着显著差异。从工程应用角度出发,根据挖方作业进程将竖向卸荷分为分阶段卸荷和非线性连续卸荷,基于伯努利方程对现有直剪仪进行改造,即利用带水龙头的水箱代替砝码进行加、卸载,模拟一次连续非线性挖方作业过程,以达到研究非线性连续卸荷路径下黄土强度特性的目的。
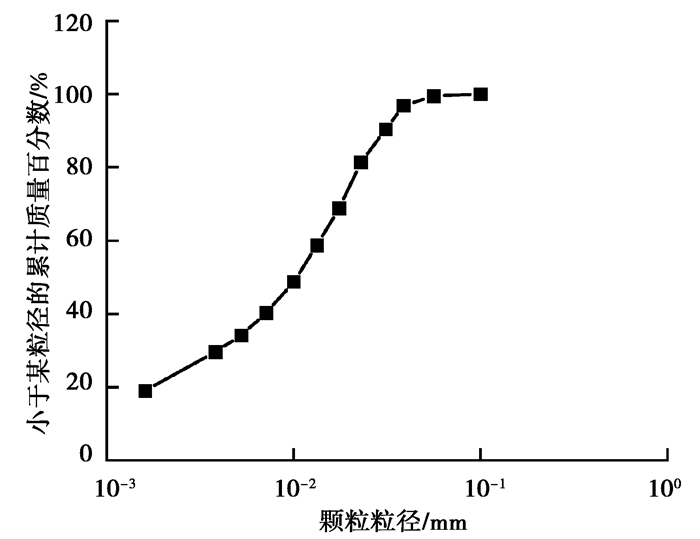
1 试样制备、试验设备及试验方法 1.1 试样制备本试验所用黄土取自陕西省西安市曲江某基坑,土样粒径级配曲线如图 2所示。
|
图 2 土样粒径级配曲线 Fig. 2 Soil particle size grading curve |
根据《土工试验方法标准》测定土样的物理参数,结果如表 1所示。
| 表 1 土样物理性质指标 Table 1 Index of physical property of soil sample |
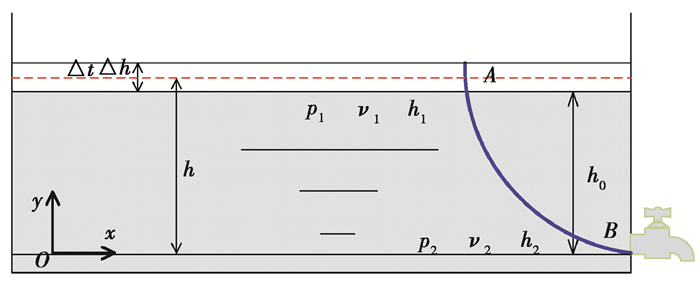
本次试验在应变控制式直剪仪的基础上进行改进,选择卸荷方式为水流连续卸荷,以达到非线性卸荷目的。但为了试验结果的可分析性,须考虑卸荷时间步长一致,且每一卸荷步长卸荷速率应尽量保证匀速,因此基于流体力学理论中的守恒原理设计水箱尺寸。设水箱底面积为S1,开口面积为S2。记水面下降速度为v1,水流流出速度为v2,水面高度为h1,水箱开口高度为h2,取孔口局部阻力系数ζ=0.5。水面及开口处压强相等,均为大气压p0。建立如图 3所示的连续卸荷水流示意图。
|
图 3 水流示意图 Fig. 3 Sketch map of water flow |
如图 3所示,A和B分别为水面和水龙头处的2点,则AB为一条流线。根据伯努利方程,在AB2点有
| $ p_{1}+\frac{1}{2} \rho v_{1}^{2}+\rho g h_{1}=p_{2}+\frac{1}{2} \rho v_{2}^{2}+\rho g h_{2}+\zeta \frac{1}{2} \rho v_{2}^{2}。$ | (1) |
由于水面上A点和水龙头处B点都和大气接触,所以其压强都等于大气压p0,且由式(1)可知水面和孔口的相对高度差y为
| $ y=h_{1}-h_{2}=\frac{3 v_{2}^{2}-2 v_{1}^{2}}{4 g} 。$ | (2) |
又根据连续方程有
| $ v_{1} S_{1}=v_{2} S_{2} 。$ | (3) |
联立式(2)、(3)有
| $ v_{1}=\sqrt{\frac{4 g S_{2}^{2}}{3 S_{1}^{2}-2 S_{2}^{2}} y}。$ | (4) |
令
| $ v_{1}=A \sqrt{y} \text { 。} $ | (5) |
由前所述,非线性连续卸荷试验要求卸荷过程中,一个时步内尽量满足水流速度均匀和水流量均匀变化,即一个时步内尽量控制速度v1不变。由公式(5)可知,卸荷时y不断变化,要使v1的变化最小,应该控制A的值尽可能小。因此,设计的水箱应具备底面积大,开口面积小的特征。根据原有直剪装置的尺寸,设定水箱尺寸为400 mm×200 mm×200 mm,水龙头直径为20 mm,带入式(4)可得最大流速为6.36 mm/s。
室内直剪仪的砝码质量对应于作用在土样的法向压力,如要对试样施加400 kPa的法向压力,需要在杠杆端部安装10.20 kg的砝码。当改用水箱加载时,水箱总质量达到10.20 kg,同样能够对土样施加400 kPa的法向压力。因此只需称量对应于200 kPa,300 kPa,400 kPa法向压力的砝码质量,再在水箱内装好水,使水箱总质量与测得的砝码质量相同,并依次在水箱上对水位线进行标注。
由式(5)可知,卸荷过程流速不恒定,导致法向荷载非线性变化,因而可实现竖向非线性连续卸荷路径,打开不同开关(开口数)也可模拟实际工程中不同的卸荷速率。为了试验数据的可分析性,需要计算在卸荷过程中,法向荷载及卸荷比随时间的变化关系。
| $ \mathrm{d} R=\mathrm{d}\left(\frac{\sigma_{n}-\sigma_{n}^{\prime}}{\sigma_{n}}\right)=\frac{\Delta \sigma_{n}}{\sigma_{n}}=\frac{\alpha \rho}{\sigma_{n}} \mathrm{~d} Q, $ | (6) |
式中: σn为初始固结压力(定值);σ' n为法向荷载(变量)。基于连续方程,可得法向荷载及卸荷比的变化分别为
| $ \Delta \sigma_{n}=\frac{\sqrt{2 h_{0}}}{2} \alpha \rho S_{2} B \Delta t \sum\limits_{i=1}^{n} \sqrt{2+\frac{\Delta t}{t_{0}}-2 \frac{\Delta t}{t_{0}} i} , $ | (7) |
| $ \mathrm{~d} R=\frac{\Delta \sigma_{n}}{\sigma_{n}}=\frac{\sqrt{2 h_{0}}}{2 \sigma_{n}} \alpha \rho S_{2} B \Delta t \sum\limits_{i=1}^{n} \sqrt{2+\frac{\Delta t}{t_{0}}-2 \frac{\Delta t}{t_{0}} i}, $ | (8) |
式中:α为砝码所代表的载荷量与用水质量之间的换算系数;h0为初始水面高度;Δt为卸荷时间步长;B为与水箱尺寸及出口断面有关的一个参数(B=AS1/S2);t0为卸荷总时长。
1.3 试验方案及方法不论是连续卸荷还是分阶段卸荷,由于土体侧向土压力系数基本稳定,侧向土压力/围压也会同时降低,由于采用直剪仪进行试验,暂不考虑侧向土压力(围压)的影响。为了对比分析设计未卸荷、非线性连续卸荷两种工况,具体试验方案见表 2,不同法向荷载对应的水箱加水量见表 3,其中水箱自身重量为1.35 kg。限于篇幅,主要讨论竖向非线性连续卸荷。
| 表 2 竖向连续卸荷试验条件 Table 2 The test condition of vertical continuous unloading |
| 表 3 不同法向荷载对应的水箱加水量 Table 3 The amount of water added to the water tank corresponding to different normal loads |
试验采用固结快剪试验,即先使土样在某一法向压力作用下充分固结,再在不排水条件下打开水龙头边卸荷边剪切,剪切速率为0.8 mm/min。
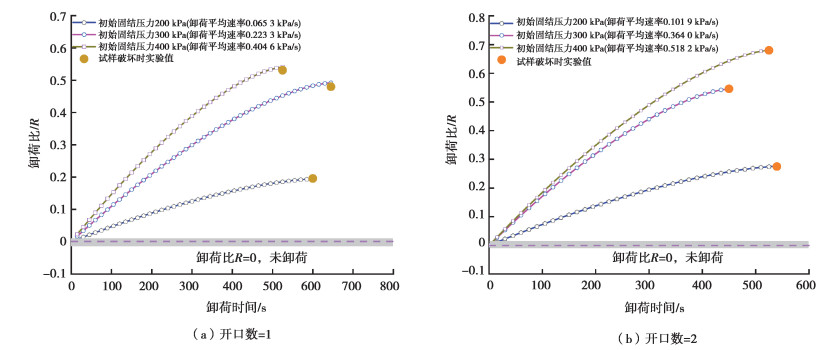
2 剪应力-剪切位移特性 2.1 卸荷时间与卸荷比的关系通过水箱尺寸计算得到S2,B,通过表 3可得到初始水面高度h0,水的密度ρ,换算系数α,将其带入式(7)、(8)并考虑等效开口面积,可计算得到连续卸荷过程中卸荷时间与卸荷比的关系曲线,如图 4所示。
|
图 4 不同固结法向荷载R-t关系 Fig. 4 R-t relationship under different initial consolidation pressure |
由图 4可知,卸荷比R与时间t表现出非线性关系,即连续卸荷过程中,法向荷载随卸荷时间的增加趋于稳定;固结法向荷载σn越大,单位时间内剪切法向荷载的变化量越大;当试样达到破坏时,试验得到的卸荷比与理论计算比较接近,当开口数=1且初始固结压力为200 kPa, 300 kPa, 400 kPa时理论计算与试验结果误差分别为0.8%,2.46%及1.8%,开口数=2时,误差分别为0.28%,0.049%以及0.094%,说明卸荷比的理论推导结果是可信的。进一步据剪切速率可计算得到卸荷过程中剪切位移与卸荷比之间的关系,其对分析非线性连续卸荷强度至关重要。
2.2 剪应力与剪切位移关系分析 2.2.1 卸荷速率对剪应力与剪切位移影响值得注意的是,直剪试验中,试样的剪应力与剪切位移的分布是不均匀的[20],因而通过直剪试验只能获得剪切面上剪应力与剪切位移的关系。由前面的分析可知,连续卸荷过程中,剪应力与剪切位移以及卸荷比均有关,而为了更直观的分析卸荷速率(平均速率)对剪应力的影响,考虑剪应力(τ)-剪切位移(δ)-卸荷比(R)的一个子空间(τ-δ),通过整理试验数据,得初始固结压力为200 kPa,300 kPa,400 kPa,试样在不同卸荷速率下的剪应力τ-剪切位移δ曲线(图 5)。
|
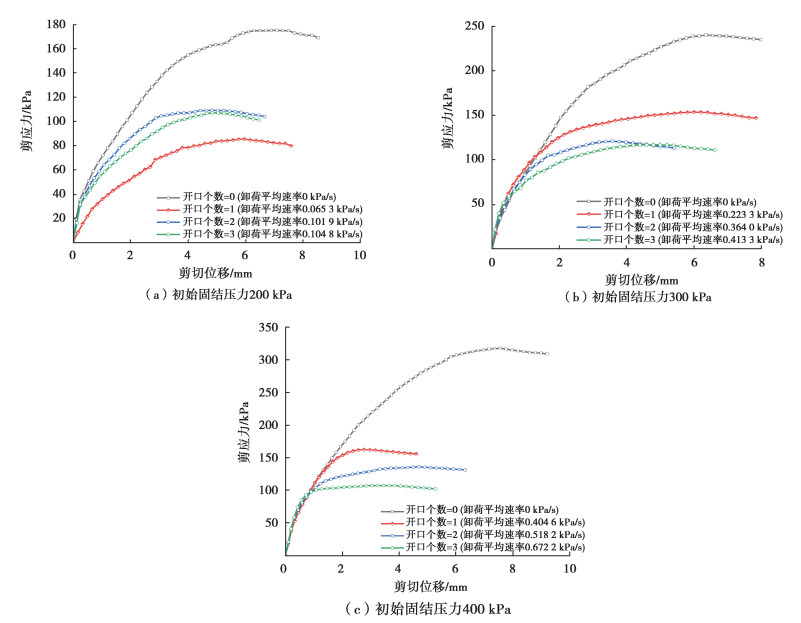
图 5 不同卸荷速率下试样剪应力-剪切位移关系 Fig. 5 Relationship between shear stress and shear displacement under different unloading rates |
由图 5可知,不同初始固结压力未卸荷工况下,随剪切位移增大,剪应力也随之增加,王家全[21],王军[22]等采用双曲线模型描述了直剪试验中剪应力与剪切位移关系,取得了良好效果,因此在τ-δ空间剪应力-剪切位移可考虑用双曲线关系进行描述。连续卸荷工况下,当初始固结压力等于200 kPa时,开口个数为1的曲线剪应力-位移曲线位于最下方,其主要原因是:水箱中水量较小,水位低,当开口个数为2或3时,水流速度较快,试验很快达到未卸荷状态,此过程流速相对稳定;而当开口个数为1时,流速较慢且变化不稳定。因此,开口个数为1的曲线剪应力-位移曲线位于最下方,主要是由仪器改进误差引起,随着初始固结压力增大,水箱水量增加,水位升高,由仪器改进所引起的误差减小。
当初始固结压力等于300 kPa和400 kPa时,非线性连续卸荷工况下,试样在前期卸荷比较小情况下的剪应力-剪切位移曲线基本重合,当卸荷比增大到一定值后,卸荷对剪应力-剪切位移曲线的影响开始凸显,卸荷速率越大,影响越明显,在剪应力达到峰值强度之后,随着剪切位移的增大,剪应力有所减小,曲线出现软化,其主要原因是:1)在非线性连续卸荷后期,法向荷载与未卸荷工况相比减小,赵春风等[15]认为卸荷过程固结法向应力(法向荷载)主要通过影响接触面土体密实度和含水率间接对剪应力产生影响;2)在连续卸荷过程中,土样强度参数发生变化,详见强度特性分析。另外,对于不同初始固结压力,开口个数相同时其卸荷速率也不同,这主要是因为不同初始固结压力,对应的水面高度不同。随着卸荷速率的增加,一方面卸荷速率对剪应力-剪切位移的影响逐渐下降,另一方面由式(6)可知卸荷速率对剪切位移-剪应力的影响蕴含在卸荷比(R)上。因此,后续研究选择开口数为2的试验数据进行分析。
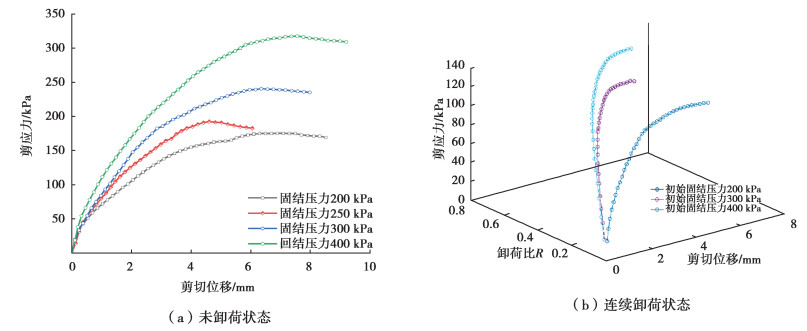
2.2.2 初始固结压力对剪应力-剪位移影响分析非线性连续卸荷过程中剪应力不仅与剪切位移有关,也与卸荷比有关,可用剪应力(τ)-剪切位移(δ)-卸荷比(R)空间中的一条曲线来反映三者之间的关系。由于采用剪切速率为0.8 mm/min,结合图 4(b)开口个数为2卸荷时间与卸荷比的关系,可得剪切位移与卸荷比的关系,同时考虑图 5(a)(b)(c)中开口个数为0和2的试验数据,绘制未卸荷工况剪应力-剪切位移的关系如图 6(a)所示、连续卸荷工况剪切位移与卸荷比R以及剪切应力的关系如图 6(b)所示。
|
图 6 不同初始固结压力下试样剪应力-剪切位移关系 Fig. 6 The relationship between shear stress and shear displacement under different initial consolidation pressure |
庄心善[9]通过研究发现基坑开挖的侧向卸荷使土体抗剪强度降低,抵抗变形的能力减小;张玉[11-12]等人同样得出侧向卸荷侧向应变的发展要快于竖向应变。而由图 6可知,与未卸荷工况相比,竖向非线性卸荷条件下土体剪应力达到峰值强度时的剪切位移明显减小,且竖向固结压力越大,峰值剪切位移的降低程度越大,这表明在竖向卸荷条件下土样同样容易在小变形时发生剪切破坏。
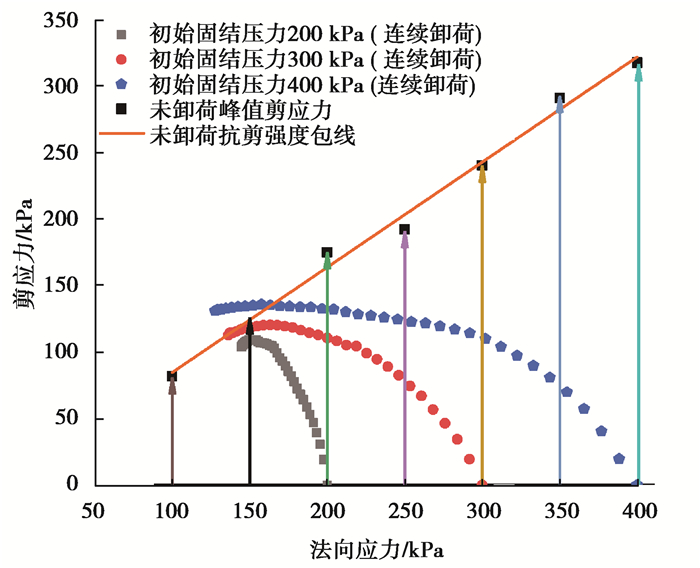
3 强度特性分析根据试验数据,在法向荷载(σ'n)-剪应力(τ)空间绘制未卸荷、竖向非线性连续卸荷两种工况其总应力路径的变化情况,并选择未卸荷情况下峰值剪应力,绘制未卸荷抗剪强度包线,如图 7所示。
|
图 7 不同试验方案总应力路径 Fig. 7 Total stress path for different test protocols |
由图 7可知,对于非线性连续卸荷,当初始固结压力为200 kPa和300 kPa时,其峰值剪应力在未卸荷强度包线之下,但随着初始固结压力增加至400 kPa,初始固结压力对强度的影响开始显现,说明非线性连续卸荷条件下,抗剪强度与初始固结压力有关,随着初始固结压力的增加,超固结效应增强,张俏楚[23]通过研究同样发现了基坑开挖侧向卸荷过程中诱发的土体超固结效应随深度的增加而降低。
本试样为黄土状粉质黏土,其抗剪强度参数由黏聚力与内摩擦角2部分构成,考虑到岩土材料黏聚力和内摩擦的构成及岩土材料发挥出的抵抗变形的能力随外荷载变化而变化,可推断岩土材料表现出的黏聚力和内摩擦是变化的,峰值强度参数是变形过程某一时刻岩土材料的强度特性。目前已有许多学者[24-28]应用黏聚力和内摩擦角随变形发展模型来研究岩土材料的强度和变形。由于卸荷对试样强度产生了明显的影响,为了更好地分析卸荷对强度参数的影响,定量地探讨卸荷比对黏聚力和内摩擦角的影响。
采用Mohr-Coulumb准则描述土体的强度演化特性,卸荷前满足
| $ \tau=\sigma_{n} \tan \varphi+c , $ | (9) |
卸荷后
| $ \tau^{\prime}=\sigma_{n}^{\prime} \tan \varphi^{\prime}+c^{\prime}, $ | (10) |
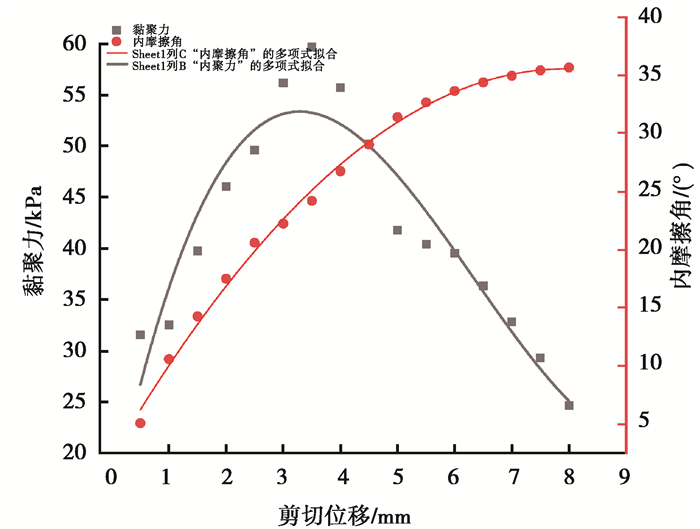
未卸荷工况下,随着剪切位移的增加,试样的黏聚力和内摩擦角在发生变化,参考文献[24-28],计算得到未卸荷时黏聚力与内摩擦角随位移的变化曲线,如图 8所示。
|
图 8 未卸荷工况下强度参数与剪切位移关系 Fig. 8 Relationship between strength parameters and shear displacement under unloaded condition |
由图 8可知,在变形初始阶段,抗剪强度中黏聚力所占的比重较大,随着变形的增加,黏聚力的影响逐渐降低,摩擦提供的强度开始占主导地位,这一结论与[24-28]等的研究结论均一致。
由于非线性连续卸荷试验变量的复杂性,分析过程中如果同时考虑黏聚力与内摩擦角受卸荷比的影响,就会使分析变得困难,基于未卸荷内摩擦角与黏聚力的变化规律,首先假设卸荷前后黏聚力不受卸荷比影响,结合式(9)(10),化简后可得
| $ \tan \varphi^{\prime}=\frac{\left(-\tau+\tau^{\prime}\right)+\sigma_{n} \tan \varphi(\delta)}{\sigma_{n}-R(\delta) \sigma_{n}}。$ | (11) |
将式(11)分别画在内摩擦角(φ)-剪切位移(δ)-卸荷比(R)三维空间及内摩擦角(φ)-剪切位移(δ)二维空间中,如图 9(a)(b)所示。
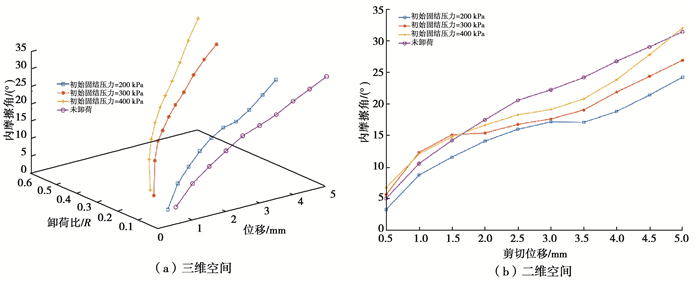
|
图 9 非线性连续卸荷工况下内摩擦角与剪切位移及卸荷比关系 Fig. 9 The relationship among internal friction angle shear displacement and unloading ratio under nonlinear continuous unloading condition |
由图 9可知,当假设卸荷前后黏聚力不变时,得到的内摩擦角在剪切位移小于2 mm时,大于未卸荷,这主要是由于忽略了黏聚力的影响造成的,其不符合实际。结合图 8未卸荷内摩擦角、黏聚力的变化规律,并考虑图 9中假设黏聚力不变得到的内摩擦角随剪切位移变化的关系,可以采用指数衰减的数学模型(式(12))描述卸荷后内摩擦角随卸荷比、位移的变化
| $ \varphi^{\prime \prime}=\varphi^{\prime \prime}(\delta, R)=\varphi(\delta) \times e^{-\chi R(\delta)}, $ | (12) |
其中:χ为与初始固结压力相关的参数;φ(δ)为卸荷前内摩擦角与剪切位移的关系,将式(12)绘制于剪切位移(δ)与内摩擦角(φ)空间,如图 10所示。
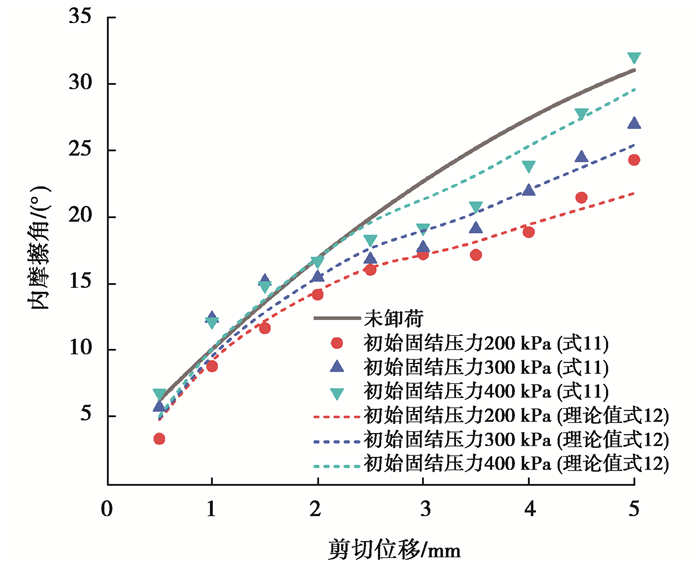
|
图 10 非线性连续卸荷后黏聚力与剪切位移关系 Fig. 10 The relationship between cohesive force and shear displacement after nonlinear continuous unloading |
由图 10可知,当剪切位移大于2 mm时,式(12)可以很好地描述非线性连续卸荷过程中内摩擦角随剪切位移的变化规律,这主要原因是非线性连续卸荷过程中,当剪切位移>2 mm时,黏聚力较小,其对内摩擦角的变化影响较小;而当剪切位移<2 mm时,采用式(12)计算得到的结果位于未卸荷曲线下方,符合实际情况,因此采用式(12)描述非线性连续卸荷过程中内摩擦角随剪切位移的变化规律是合理的。由式(12)进一步根据Mohr-Coulumb准则,可计算得到卸荷后黏聚力随剪切位移的变化关系。
| $ C^{\prime}=\tau^{\prime}-\left(\sigma_{n}-R(\delta) \sigma_{n}\right) \tan \varphi^{\prime \prime}(\delta), $ | (13) |
基于式(13)计算得到的数据,为了在形式上与卸荷后内摩擦角随卸荷比、剪切位移保持一致,同样采用如式(14)所示指数衰减的数学模型来描述卸荷后粘聚力随卸荷比、剪切位移的变化
| $ C^{\prime \prime}=C^{\prime \prime}(\delta, R)=C(\delta) \times \lambda e^{-\kappa R}, $ | (14) |
式中,λ和κ为与竖向固结压力有关的参数。式(13)和式(14)结果如图 11所示,如图 11可知,采用式(14)的形式可以较好地描述非线性连续卸荷过程中,黏聚力随剪切位移的变化关系。利用卸荷比将图 10和图 11横坐标变换为法向荷载,可以更直观地看到非线性连续卸荷过程中黏聚力与内摩擦角随法向荷载的变化,如图 12(a)和图 12(b)所示。由图 12(b)可知,当初始固结压力等于400 kPa时,实验值与理论值相差较大,其主要原因是:当初始固结压力等于400 kPa,主要由内摩擦抵抗剪切变形,而黏聚力基本不随固结压力变化,在抗剪强度成分中所占比重较小,因而忽略内摩擦的影响时,误差较大;同时由12(a)可知,当忽略黏聚力时,内摩擦角与理论较为接近,也说明了当初始固结压力为400 kPa时,主要由内摩擦抵抗变形。
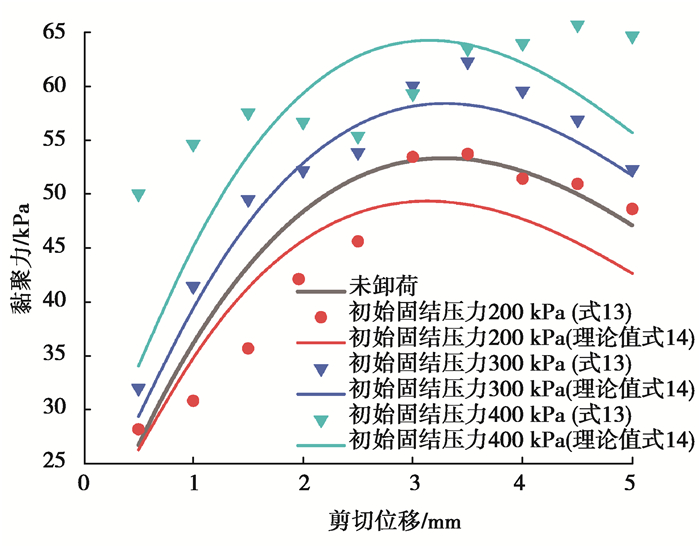
|
图 11 非线性连续卸荷后黏聚力与剪切位移关系 Fig. 11 The relationship between cohesive force and shear displacement after nonlinear continuous unloading |
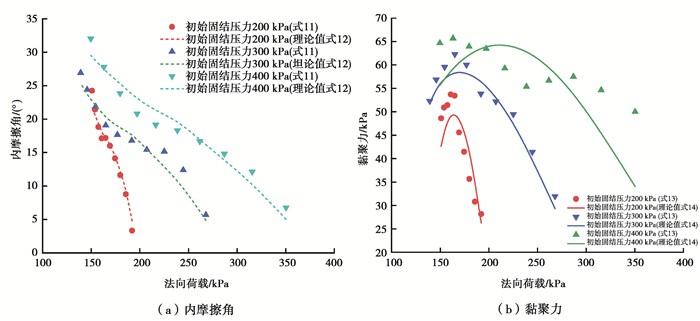
|
图 12 非线性连续卸荷过程中竖向剪切荷载与强度参数之间的关系 Fig. 12 Relationship between vertical shear load and strength parameters in nonlinear continuous unloading process |
采用水箱代替砝码实现连续卸载研究了竖向非线性连续卸荷工况下黄土的强度与变形特性,得到以下结论:
1) 基于伯努利方程推导得到的卸荷比能够很好地描述试样在连续卸荷过程中法向荷载的变化。
2) 在剪应力(τ)-剪切位移(δ)空间中,同一初始固结压力,非线性连续卸荷路径下,试样在变形前期卸荷比较小时剪应力-剪切位移曲线与未卸荷工况基本重合,当卸荷比达到某一值后,卸荷对剪应力-剪切位移曲线的影响开始凸显,卸荷速率越大,影响越明显,在剪应力达到峰值后,随着剪切位移的增大,剪应力有所减小,曲线出现软化特性。
3) 非线性连续卸荷路径下,抗剪强度与初始固结压力有关,随着初始固结压力的增加,超固结效应越明显。
4) 所给出的强度参数(内摩擦角和黏聚力)随剪切位移的变化模型,较好地描述了非线性连续卸荷路径下强度参数演化规律,但由于非线性连续卸荷,涉及到的变量多且难以控制,其关系式仍需进行更深一步的研究。
| [1] |
Tu X B, Kwong A K L, Dai F C, et al. Field monitoring of rainfall infiltration in a loess slope and analysis of failure mechanism of rainfall-induced landslides[J]. Engineering Geology, 2009, 105(1/2): 134-150. |
| [2] |
Zhuang J Q, Peng J B, Wang G H, et al. Distribution and characteristics of landslide in Loess Plateau: a case study in Shaanxi Province[J]. Engineering Geology, 2018, 236: 89-96. DOI:10.1016/j.enggeo.2017.03.001 |
| [3] |
Xu L, Dai F C, Tu X B, et al. Landslides in a loess platform, North-West China[J]. Landslides, 2014, 11(6): 993-1005. DOI:10.1007/s10346-013-0445-x |
| [4] |
Wang J D, Xu Y J, Ma Y, et al. Study on the deformation and failure modes of filling slope in loess filling engineering: a case study at a loess mountain airport[J]. Landslides, 2018, 15(12): 2423-2435. DOI:10.1007/s10346-018-1046-5 |
| [5] |
何思明, 王全才. 人工高切坡的长期强度指标研究[J]. 四川大学学报(工程科学版), 2005, 37(6): 26-30. He S M, Wang Q C. Study on long-term strength index of high cut slope[J]. Journal of Sichuan University (Engineering Science Edition), 2005, 37(6): 26-30. (in Chinese) DOI:10.3969/j.issn.1009-3087.2005.06.006 |
| [6] |
蒲小武, 王兰民, 吴志坚, 等. 兰州丘陵沟壑区挖方黄土高边坡面临的工程地质问题及稳定性分析[J]. 地震工程学报, 2016, 38(5): 787-794. Pu X W, Wang L M, Wu Z J, et al. Engineering geological problems of loess high excavation slope in loess hilly and gully region of Lanzhou and its stability analysis[J]. China Earthquake Engineering Journal, 2016, 38(5): 787-794. (in Chinese) DOI:10.3969/j.issn.1000-0844.2016.05.0787 |
| [7] |
张伏光, 蒋明镜. 基坑土体卸荷平面应变试验离散元数值分析[J]. 岩土力学, 2018, 39(1): 339-348. Zhang F G, Jiang M J. Distinct element analysis of plane strain test on soil unloading around a foundation pit[J]. Rock and Soil Mechanics, 2018, 39(1): 339-348. (in Chinese) |
| [8] |
刘熙媛, 闫澍旺, 窦远明, 等. 模拟基坑开挖过程的试验研究[J]. 岩土力学, 2005, 26(1): 97-100, 104. Liu X Y, Yan S W, Dou Y M, et al. Experimental studies of simulated excavation process[J]. Rock and Soil Mechanics, 2005, 26(1): 97-100, 104. (in Chinese) |
| [9] |
庄心善, 胡恺. 土体侧向卸荷对基坑支护位移的影响[J]. 土工基础, 2009, 23(6): 43-45. Zhuang X S, Hu K. Effect of lateral unloading on foundation pit displacement[J]. Soil Engineering and Foundation, 2009, 23(6): 43-45. (in Chinese) DOI:10.3969/j.issn.1004-3152.2009.06.014 |
| [10] |
张孟喜, 孙钧. 受施工卸载扰动黄土的变形与强度特性研究[J]. 岩石力学与工程学报, 2005, 24(13): 2248-2254. Zhang M X, Sun J. Unloading-induced deformation and strength properties of loess during construction[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(13): 2248-2254. (in Chinese) DOI:10.3321/j.issn:1000-6915.2005.13.008 |
| [11] |
张玉, 何晖, 赵敏, 等. 平面应变条件下原状黄土侧向卸载变形与强度特性分析[J]. 岩土力学, 2017, 38(5): 1233-1242, 1250. Zhang Y, He H, Zhao M, et al. Analysis of lateral unloading deformation and strength characteristics of intact loess under plain strain condition[J]. Rock and Soil Mechanics, 2017, 38(5): 1233-1242, 1250. (in Chinese) |
| [12] |
张玉, 邵生俊. 平面应变加、卸荷条件下黄土的非线性变形特性的研究[J]. 岩土工程学报, 2015, 37(S1): 185-190. Zhang Y, Shao S J. Non-linear deformation behaviors of loess under plane strain state of vertical loading and lateral unloading[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(S1): 185-190. (in Chinese) |
| [13] |
李加贵, 陈正汉, 黄雪峰, 等. Q3黄土侧向卸荷时的细观结构演化及强度特性[J]. 岩土力学, 2010, 31(4): 1084-1091. Li J G, Chen Z H, Huang X F, et al. CT-triaxial shear tests on the meso-structure evolution and strength of unsaturated loess Q3 during unloading confining pressure[J]. Rock and Soil Mechanics, 2010, 31(4): 1084-1091. (in Chinese) DOI:10.3969/j.issn.1000-7598.2010.04.013 |
| [14] |
程相华. 卸荷土体的强度特征[J]. 佳木斯大学学报(自然科学版), 2000, 18(3): 234-238. Cheng X H. The characteristics of shear strength in unloading soil[J]. Journal of Jiamusi University (Natural Science Edition), 2000, 18(3): 234-238. (in Chinese) DOI:10.3969/j.issn.1008-1402.2000.03.008 |
| [15] |
赵春风, 吴悦, 赵程, 等. 考虑卸荷效应的砂土-混凝土接触面剪切特性影响研究[J]. 岩石力学与工程学报, 2018, 37(4): 1020-1029. Zhao C F, Wu Y, Zhao C, et al. Effect of unloading on shear behavior of interface between sand and concrete[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(4): 1020-1029. (in Chinese) |
| [16] |
Ng C W W. Stress paths in relation to deep excavations[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(5): 357-363. DOI:10.1061/(ASCE)1090-0241(1999)125:5(357) |
| [17] |
Li X B, Cao W Z, Zhou Z L, et al. Influence of stress path on excavation unloading response[J]. Tunnelling and Underground Space Technology, 2014, 42: 237-246. |
| [18] |
梅国雄, 陈浩, 卢廷浩, 等. 坑侧土体卸荷的侧向应力-应变关系研究[J]. 岩石力学与工程学报, 2010, 29(S1): 3108-3112. Mei G X, Chen H, Lu T H, et al. Research on lateral stress-strain relation on side of foundation pit with lateral unloading[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S1): 3108-3112. (in Chinese) |
| [19] |
潘林有, 程玉梅, 胡中雄. 卸荷状态下粘性土强度特性试验研究[J]. 岩土力学, 2001, 22(4): 490-493. Pan L Y, Cheng Y M, Hu Z X. Experimental study on the shear strength of clay under the unloading state[J]. Rock and Soil Mechanics, 2001, 22(4): 490-493. (in Chinese) |
| [20] |
潘晨晨, 李卫超. 关于直剪试验若干问题的讨论[J]. 施工技术, 2017, 46(S2): 1-5. Pan C C, Li W C. Discussion on some disadvantages of direct shear test[J]. Construction Technology, 2017, 46(S2): 1-5. (in Chinese) |
| [21] |
王家全, 陈亚菁, 周岳富. 加筋粗粒土大型直剪试验及本构模型适用性研究[J]. 广西科技大学学报, 2016, 27(2): 1-8. Wang J Q, Chen Y J, Zhou Y F. Large direct shear test of reinforced coarse grained soil and study of constitutive model applicability[J]. Journal of Guangxi University of Science and Technology, 2016, 27(2): 1-8. (in Chinese) |
| [22] |
王军, 林旭, 符洪涛. 砂土-格栅筋土界面特性的本构模型研究[J]. 岩土力学, 2014, 35(S2): 75-84. Wang J, Lin X, Fu H T. Study of constitutive model of sand-geogrid interface behavior in geogrid/geotextile reinforced soil[J]. Rock and Soil Mechanics, 2014, 35(S2): 75-84. (in Chinese) |
| [23] |
张俏楚, 刘景锦, 郑刚. 基坑降水开挖对坑底不同深度土体影响的试验研究[J]. 科学技术与工程, 2016, 16(4): 75-82. Zhang Q C, Liu J J, Zheng G. Experimental studies on influence of pit dewatering and excavation on soils at different depths below excavation base[J]. Science Technology and Engineering, 2016, 16(4): 75-82. (in Chinese) |
| [24] |
Li H Z, Xiong G D, Zhao G P. An elasto-plastic constitutive model for soft rock considering mobilization of strength[J]. Transactions of Nonferrous Metals Society of China, 2016, 26(3): 822-834. |
| [25] |
Vermeer P A. Non-associated plasticity for soils, concrete and rock[M]. Dordrecht: Springer Netherlands, 1998: 163-196.
|
| [26] |
Ma L J, Xu H F, Tong Q, et al. Post-yield plastic frictional parameters of a rock salt using the concept of mobilized strength[J]. Engineering Geology, 2014, 177: 25-31. |
| [27] |
Jafarpour M, Rahmati H, Azadbakht S, et al. Determination of mobilized strength properties of degrading sandstone[J]. Soils and Foundations, 2012, 52(4): 658-667. |
| [28] |
Zhang K, Zhou H, Shao J F. An experimental investigation and an elastoplastic constitutive model for a porous rock[J]. Rock Mechanics and Rock Engineering, 2013, 46(6): 1499-1511. DOI:10.1007/s00603-012-0364-5 |
 2021, Vol. 44
2021, Vol. 44


