2. 中国地震局 a. 工程力学研究所; b. 地震工程与工程 振动重点实验室, 哈尔滨 150080;
3. 西南交通大学 土木工程学院, 成都 610031;
4. 抗震工程技术四川省重点实验室, 成都 610031
2. 2a. Institute of Engineering Mechanics; 2b. Key Laboratory of Earthquake Engineering and Engineering Vibration, China Earthquake Administration, Harbin 150080, P. R. China;
3. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, P. R. China;
4. Key Laboratory of Seismic Engineering of Sichuan Province, Chengdu 610031, P. R. China
土木工程结构及其耗能减震控制元件在大震及超大震作用下表现出强非线性特征[1-2]。受到试验设备加载能力及试验费用的制约,传统结构抗震试验方法很难准确检验大型、复杂结构动力灾变过程。结构混合试验将物理试验与数值模拟相结合,从而得到整体结构动力响应。目前,结构混合试验受到了研究者们的广泛关注[3-4]。受到试验室作动器数量的限制,数值子结构将不可避免会进入非线性阶段,数值模型误差将会降低混合试验精度。Bouc-Wen模型采用微分形式的数学表达,非线性模拟精度高和应用普适性强,可以用于模拟结构混合试验中的数值子结构[5]。然而,Bouc-Wen模型参数本身物理意义并不明确,模型参数值对模型输出精度具有较大影响,在混合试验中如何准确给出Bouc-Wen模型参数值是亟需解决的问题。研究者们提出了在线模型更新方法,即利用试验观测数据在线识别试验子结构模型参数,并实时更新数值子结构中Bouc-Wen模型参数[6-7]。
以卡尔曼滤波器为框架的一系列时域在线识别算法,如无迹卡尔曼滤波(unscented Kalman filter, UKF)[8-9]、约束无迹卡尔曼滤波(constrained unscented Kalman filter, CUKF)[10-11]被应用于结构模型更新混合试验,以实现在线数值模型更新。然而,受到试验和监测过程中可能存在的非高斯噪声和Bouc-Wen模型自身强非线性的影响,上述参数识别算法的精度和稳定性会明显降低,从而影响整体混合试验结果精度。因此,找到一种精度更高的非线性参数在线识别算法仍是亟需解决的问题。
粒子滤波(particle filter, PF)算法[12]是一种基于贝叶斯估计和蒙特卡洛方法的在线非线性识别算法,其本质是通过寻找一组在状态空间内传播的随机样本来近似状态概率密度函数,采用离散样本模拟连续函数,以样本均值代替积分运算,从而获得状态最小方差分布的过程。PF算法从理论上具有比扩展卡尔曼滤波器(extended Kalman filter, EKF)和UKF算法更高的识别精度。Merwe等[13]对传统的PF算法进行改进,在重要性采样过程中利用了最新的观测信息,更精确地逼近了后验概率密度函数。Gordon等[14-16]提出了重采样算法,解决粒子退化问题。李烨等[17]和唐和生等[18]采用PF算法解决结构系统的损伤识别问题,与EKF算法相比, 粒子滤波在非高斯噪声条件下具有更高的结构模型参数识别精度。樊学平等[19]采用混合高斯粒子滤波器(mixed gaussian particle filter, MGPF),对监测信息状态变量的后验分布参数和监测值一步向前预测分布参数进行了预测分析。目前,粒子滤波器在土木工程中的研究及应用仍非常有限,如何进一步提高PF算法的重要性采样精度并同时削弱粒子匮乏仍是提高算法精度的关键问题。
文中首先在标准的PF算法基础上拟建立一种改进的辅助无迹粒子滤波算法(auxiliary unscented particle filter, AUPF),给出算法实现步骤。然后,针对单自由度Bouc-Wen模型进行参数在线识别,并与传统的PF算法、EPF算法、UPF算法识别结果进行对比分析,验证改进算法的精度和计算效率。最后,通过隔震支座拟静力试验验证了采用AUPF算法在线识别Bouc-Wen模型参数方法的有效性。
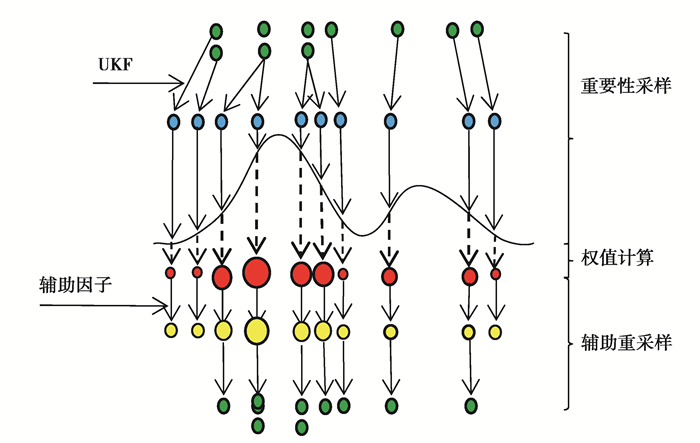
1 辅助无迹粒子滤波算法的建立思路文中提出的AUPF算法在标准粒子滤波算法的基础上主要进行了两方面改进:1)采用UKF算法进行重要性采样,提高非线性系统粒子估计更新精度;2)在重采样过程中引入辅助因子,修改粒子权值,通过增加粒子多样性来削弱粒子退化现象。AUPF算法继承了PF算法原理,理论上可以应用于任意非线性模型参数识别。AUPF算法具体流程如图 1所示,算法主要包括重要性采样、权值计算和辅助重采样3个主要环节。
|
图 1 AUPF算法示意图 Fig. 1 Diagram of the AUPF algorithm |
首先,在重要性采样中,根据第k-1步粒子估计
对于任意一个非线性、非高斯动态系统,系统状态方程、观测方程分别定义为式(1)和式(2):
| $ x_{k}=f\left(x_{k-1}, u_{k-1}\right)+w_{k-1}, $ | (1) |
| $ y_{k}=h\left(x_{k}\right)+v_{k}, $ | (2) |
式中:k为递推步数;xk为系统的状态值,假设xk具有一阶马尔可夫性质。函数f(·)为系统的状态方程,uk为系统的输入;wk-1为系统的过程噪声;yk为系统的观测值;h(·)为系统的观测方程;vk为系统的观测噪声;wk-1和vk为2组相互独立、互不相关的噪声序列,假定已知其概率密度函数;Qk、Rk分别为过程噪声协方差矩阵和观测噪声协方差矩阵。
2.1 重要性函数的选取为了提高粒子非线性变换精度,文中采用UKF算法作为重要性函数。根据k-1步对应于第i个粒子估计均值
| $ \hat{x}^{{i}\ \left[{m}\right] k-1}=\hat{x}_{k-1}^{i}+\tilde{x}^{(i[m])} m=1, \ldots, 2 L , $ | (3) |
| $ \tilde{x}^{(i\ [m])}=\left(\sqrt{L P_{k-1}^{i}}\right)_{m}^{\mathrm{T}} m=1, \ldots, L, $ | (4) |
| $ \tilde{x}^{(i\ [L+m])}=-\left(\sqrt{L P_{k-1}^{i}}\right)_{m}^{\mathrm{T}}, m=1, \ldots, L, $ | (5) |
式中:
将Sigma点
| $ \hat{x}_{k}^{{i}\ \left[{m}\right]}=f\left(\hat{x}^{{i}\ [m] k-1}, u_{k}\right), i=1, \ldots, N ; m=1, \ldots, 2 L, $ | (6) |
通过加权统计,第i个粒子先验估计均值
| $ \hat{x}_{k \mid k-1}^{i}=\sum\limits_{m=1}^{2 L} \omega_{\mathrm{g}}^{m} \hat{x}_{k}^{{i}\ \left[{{m}}\right]}, i=1, \ldots, N ; m=1, \ldots, 2 L, $ | (7) |
先验估计误差协方差Pk|k-1i为
| $ P_{k \mid k-1}^{i}=\sum\limits_{m=1}^{2 L} \omega_{\mathrm{c}}^{m}\left(\hat{x}_{k}^{{i}\ \left[{m}\right]}-\hat{x}_{k \mid k-1}^{i}\right)\left(\hat{x}_{k}^{{i}\ \left[{m}\right]}-\hat{x}_{k \mid k-1}^{i}\right)^{\mathrm{T}}+Q_{k-1}, i=1, \ldots, N ; m=1, \ldots, 2 L, $ | (8) |
式中:ωgm和ωcm分别为第m个Sigma点的均值及协方差权值,即
| $ \omega_{\mathrm{g}}^{m}=\omega_{\mathrm{c}}^{m}=\frac{1}{2 L}, m=1,2, \ldots, 2 L, $ |
然后,将Sigma点
| $ \hat{y}_{k}^{{i}\ \left[{m}\right]}=h\left(\hat{x}_{k}^{{i}\ \left[{m}\right]}\right), $ | (9) |
通过加权统计,第i个观测粒子估计均值
| $ \hat{y}_{k}^{i}=\sum\limits_{m=1}^{2 L} \omega_{\mathrm{g}}^{m} \hat{y}_{k}^{{i}\ \left[{m}\right]}, $ | (10) |
新息协方差Py ik|k-1为
| $ P^{y\ ik \mid k-1}=\sum\limits_{m=1}^{2 L} \omega_{c}^{m}\left(\hat{y}_{k}^{{i}\ \left[{m}\right]}-\hat{y}_{k}^{i}\right)\left(\hat{y}_{k}^{{i}\ \left[{m}\right]}-\hat{y}_{k}^{i}\right)^{\mathrm{T}}+R_{k}, $ | (11) |
交叉协方差Pxy ik|k-1为
| $ P^{x\ y i k \mid k-1}=\sum\limits_{m=1}^{2 L} \omega_{\mathrm{c}}^{m}\left(\hat{x}_{k}^{{i}\ \left[{m}\right]}-x_{k \mid k-1}^{i}\right)\left(\hat{y}_{k}^{{i}\ \left[{m}\right]}-\hat{y}_{k}^{{i}\ \left[{m}\right]}\right)^{\mathrm{T}}, $ | (12) |
卡尔曼增益Kki为
| $ K_{k}^{i}=P^{{xy\ i}\ \left[{m}\right] k \mid k-1}\ \left(P^{y\ i k \mid k-1}\right)-1, $ | (13) |
利用最新的观测yk,计算第k步第i个粒子估计的均值和协方差为
| $ \hat{x}_{k}^{i} =\hat{x}_{k-1}^{i}+K_{k}^{i}\left(y_{k}-\hat{y}_{k}^{i}\right), $ | (14) |
| $ P_{k}^{i} =P_{k-1}^{i}-K_{k}^{i} P_{k}^{i}\left(K_{k}^{i}\right)^{\mathrm{T}}。$ | (15) |
可得到由第k步第i个粒子估计均值
| $ x_{k}^{i} \sim N\left(\hat{x}_{k}^{i}, P_{k}^{i}\right)。$ | (16) |
在整个过程中,AUPF算法通过UKF算法对非线性模型进行直接处理,得到算法的重要性函数,避免了繁琐的雅克比矩阵的求解,降低了计算复杂度,同时使得AUPF算法的重要性函数中包含最新的系统观测信息。
2.2 重要性权值的计算当由公式(14)计算得到第k步粒子的估计值后,需要通过调整每一个粒子重要性权值,并将每个粒子权值进行归一化,以更好地逼近状态后验概率密度函数[21]。归一化后的重要性权值为
| $ \widetilde{\omega}_{k}^{i}=\frac{\omega_{k}^{i}}{\sum\limits_{j=1}^{N} \omega_{k}^{j}}, $ | (17) |
式中,ωki为调整前粒子重要性权值,通过迭代计算。
| $ \omega_{k}^{i}=\omega_{k-1}^{i} \frac{p\left(y_{k} \mid \hat{x}_{k}^{i}\right) p\left(\hat{x}_{k}^{i} \mid \hat{x}_{k-1}^{i}\right)}{q\left(\hat{x}_{k}^{i} \mid \hat{x}_{k-1}^{i}, y_{1: k}\right)}, $ | (18) |
式中
对于多元正态分布,可由似然概率密度qki近似代替粒子的重要性权值[22]:
| $ q_k^i \sim \frac{1}{{(2{\rm{ \mathsf{ π} }})\left| {{R_k}} \right|1/2}}\exp \left( {\frac{{ - {{\left[ {{y_k} - h\left( {\hat x_k^i} \right)} \right]}^{\rm{T}}}R_k^{ - 1}\left[ {{y_k} - h\left( {\hat x_k^i} \right)} \right]}}{2}} \right)。$ | (19) |
当得到新的粒子
| $ \hat{x}_{k}=\frac{1}{N} \sum\limits_{i=1}^{N} \hat{x}_{k}^{i}。$ | (20) |
在重采样过程中,为增加粒子多样性、减小其中权值较小粒子有效信息的丧失,文中在标准PF算法基础上引入的辅助因子λ,重新计算粒子的观测似然函数为
| $ \tilde{q}_{k}^{i}=\frac{(\lambda-1) q_{k}^{i}+\bar{q}_{k}}{\lambda},$ | (21) |
式中:λ为辅助因子,代表调整度;qk为所有qki的样本均值。
当λ→+∞时,正则化的概率
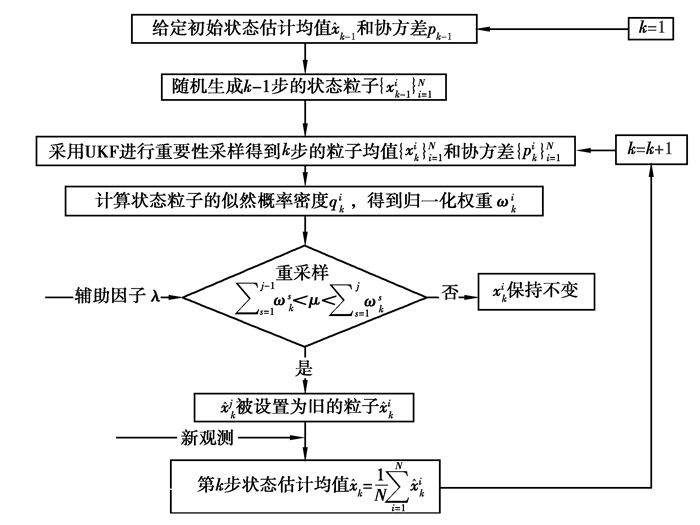
|
图 2 AUPF算法流程 Fig. 2 Flow chart of the AUPF algorithm |
AUPF算法继承了PF算法原理,是一种完全的非线性估计器,可以识别任意非线性模型参数。Bouc-Wen模型是一种具有代表性的强非线性模型,被广泛用来模拟结构和构件恢复力特性。文中以一单自由度Bouc-Wen模型为对象,给出应用AUPF算法进行非线性模型参数在线识别的具体实现方法,检验算法识别精度。结合结构运动方程,Bouc-Wen模型如式(22)~式(24)所示:
| $ \ddot{d}+2 \xi \omega_{\mathrm{n}} \dot{d}+\alpha \omega_{\mathrm{n}}^{2} z=0 ,$ | (22) |
| $ \dot{z}=\dot{d}-\gamma|\dot{d}||z| n-1 z-\beta \dot{d}|z|^{n}, $ | (23) |
| $ F=k_{0} z,$ | (24) |
式中:d、
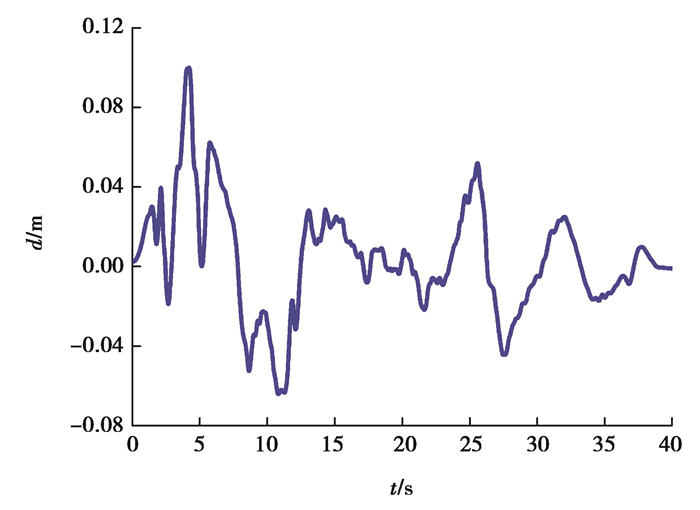
设Bouc-Wen模型参数真实取值为k0=40 kN/m,β=20,γ=20,n=1.1;对模型进行位移控制加载,输入位移激励选用1940年5月19日Imperial Valley地震El Centro(1940,NS)台站测得的地面运动位移记录,位移峰值调整为10 cm,如图 3所示,图中纵坐标d为位移。采用4阶Runge-Kutta数值积分方法计算Bouc-Wen系统恢复力,积分步长Δt=0.01 s,积分步数为4 000步。
|
图 3 位移加载时程曲线 Fig. 3 Displacement loading time curve |
在结构加载过程中,基于当前及之前步结构真实反应和系统输入,采用AUPF算法在线识别Bouc-Wen模型参数,并与PF算法、EPF算法和UPF算法的识别结果进行对比,用以验证AUPF算法参数识别精度。为了能够体现出改进算法在重要性采样及重采样的影响,以上4种算法均采用相同的状态及参数设置。设系统状态为x=[x1, x2, x3, x4, x5]T=[z, k0, β, γ, n]T;系统的观测为yk=Rk,其中,下标k表示步数,Rk为第k步的结构恢复力;假定系统过程噪声vk和观测噪声wk都服从高斯分布,即均值均为0,协方差分别为Q、W。AUPF算法中辅助因子λ取1.1。
假定状态估计初始值为x0=[0, 50, 15, 15, 2]T,过程噪声协方差为Q=diag(10-8,0.0452,0.000 092,0.000 012,0.0072),观测噪声协方差为W =0.015 kN2;状态估计误差初始协方差为P0=diag(10-6,113.9,15.6,12.7,0.65)。
系统状态方程为
| $ \dot{x}=f\left(x, \dot{x}^{\prime}\right)=\left[\begin{array}{c} \dot{x}_{1} \\ \dot{x}_{2} \\ \dot{x}_{3} \\ \dot{x}_{4} \\ \dot{x}_{5} \end{array}\right]=\left[\begin{array}{c} \dot{z} \\ \dot{k} \\ \dot{\beta} \\ \dot{\gamma} \\ \dot{n} \end{array}\right]=\left[\begin{array}{c} \dot{d}-x_{3}|\dot{d}|\left|x_{1}\right|^{x 5-1} x_{1}-x_{4} \dot{d}\left|x_{1}\right|^{x 5} \\ 0 \\ 0 \\ 0 \\ 0 \end{array}\right]+\nu_{k}, $ | (25) |
式中:vk为过程噪声;
| $ \left\{\begin{array}{l} \dot{d}_{k}=\frac{d_{k+1}-d_{k-1}}{2 \Delta t}, k=1,2, \ldots, N-1 ; \\ \dot{d}_{k}=\frac{d_{1}-d_{0}}{\Delta t}, k=0 ; \end{array}\right. $ | (26) |
设系统观测方程为
| $ y_{k}=F_{k}=x_{1, k} x_{2, k}+w_{k}。$ | (27) |
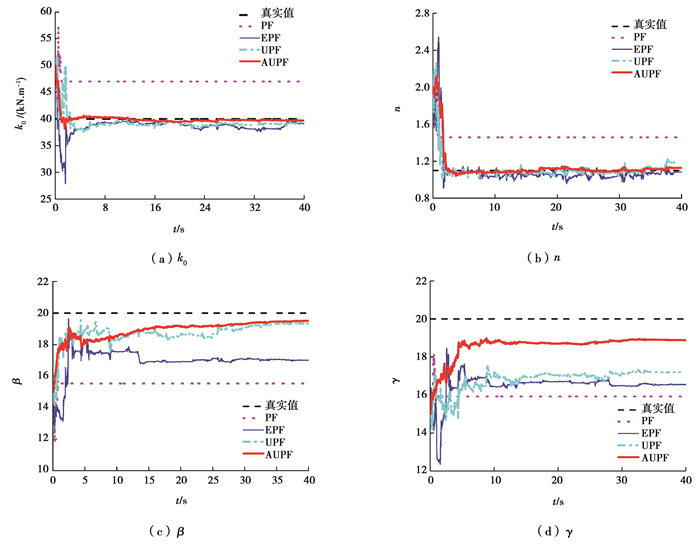
将基于AUPF算法、UPF算法、EPF算法和PF算法得到的Bouc-Wen模型在线参数识别结果进行对比,如图 4所示。可以看出,对于k0和n 2个参数的识别效果4种算法大致相同,基本都收敛到了真实值附近,且收敛速度大致相似,其中AUPF算法得到的识别值同真实值吻合度最好。PF算法、EPF算法、UPF算法、AUPF算法得到的参数β识别终值相对误差分别为22.34%、14.95%、3.33%、2.46%,参数γ识别终值相对误差分别为20.41%、17.25%、14.03%、5.58%。与其他3种算法结果相比,AUPF算法提高了模型参数的识别精度,同时显著减小了参数识别值收敛过程波动幅度。由于Bouc-Wen模型参数β和γ为控制滞回环形状参数,本身无物理意义。在相同的模型输入下,不同参数β和γ的组合可以得到相同的模型输出,因此,导致反问题的参数识别值可能并不唯一,识别误差增大。AUPF算法在重要性采样具有更高的非线性变换精度,在重采样过程中丰富了粒子多样性,有效削弱粒子退化。算法性能决定了算例识别结果的优劣,具有普遍意义。因此,当算例中的Bouc-Wen模型参数的真实值取值发生变化,在相同的条件下,4种算法识别结果仍会有类似的规律,由于篇幅有限,没有给出采取其他参数真实值时的识别结果。
|
图 4 Bouc-Wen模型参数识别值 Fig. 4 Identification values of Bouc-Wen model parameters |
为了能定量评价算法识别精度,定义一次独立仿真的均方根误差(root-mean-square error,RMSE)为
| $ \mathrm{RMSE}=\sqrt{\frac{\sum\limits_{k=1}^{M}\left(\theta_{k}-\hat{\theta}_{k}\right)^{2}}{M}}, $ | (28) |
式中:θk为模型参数真实值;
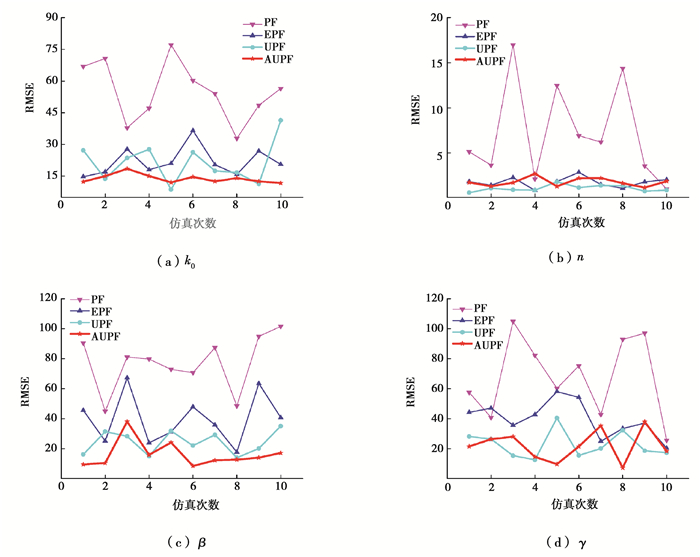
PF算法及其改进的EPF算法、UPF算法和AUPF算法本质上均为随机性参数识别算法,4种算法均基于蒙特卡洛随机采样方法,因此,即使在相同的参数初值条件下,每一种算法在每一次仿真得到的参数识别值都是不同的,即参数识别结果具有随机性。为了检验算法识别结果的随机性,采用4种滤波算法分别进行了10次独立仿真,统计识别结果来对比分析不同算法的识别精度和收敛性,更具有说服性。在本算例中的10次独立仿真中,系统输入、Bouc-Wen模型初始参数和算法初始参数均相同,随机性主要来自算法生产粒子的随机性。4种算法参数识别值的均方根误差与仿真次数的关系曲线如图 5所示,图中的横坐标为仿真次数。
|
图 5 模型参数识别值均方根误差 Fig. 5 RMSEs of parameters identification values of Bouc-Wen model |
可以看出,AUPF算法的参数识别整体误差明显低于PF算法、EPF算法和UPF算法,而且误差波动幅度显著降低。可见,由于AUPF算法利用最新观测信息修正粒子,同时通过引入辅助因子增加了粒子多样性。因此,AUPF算法明显高于PF算法、EPF算法和UPF算法的识别精度。
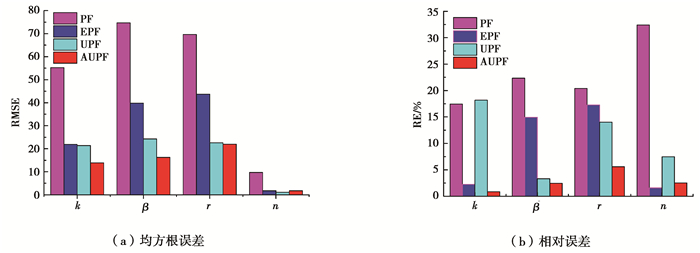
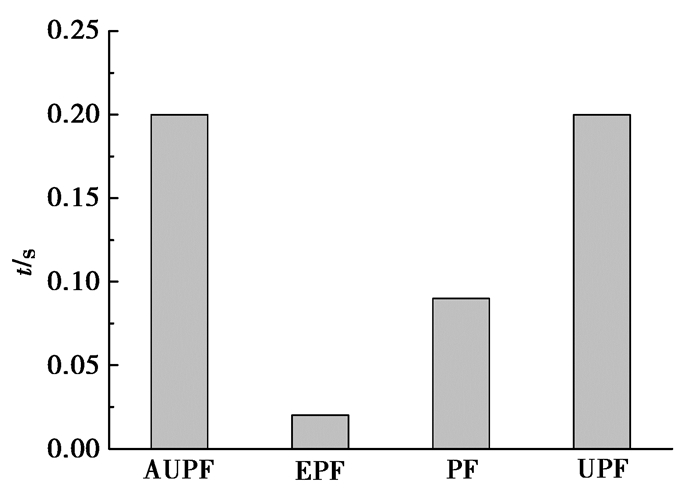
统计10次独立仿真在线参数识别值的均方根误差RMSE均值、相对误差RE(relative error)均值如图 6所示。可以明显看出,文中提出的AUPF算法的参数识别值均方根误差均值和相对误差均值整体上都要小于PF算法、EPF算法和UPF算法参数识别误差。AUPF算法得到的4组参数识别值的均方根误差整体上比PF算法、EPF算法和UPF算法结果误差减小了81.5%、37.7%和8.0%,AUPF算法得到的4组参数识别值的相对误差整体上比PF算法、EPF算法和UPF算法结果误差减小了87.3%、39.0%和61.8%。由此可见,10次仿真4组参数识别值的平均均方根误差和平均相对误差2种评价指标均表明AUPF算法精度均高于其它3种算法。需要注意的是,算法在取得较高参数识别精度同时,也需要付出更多的计算耗时。10次仿真4种算法的单步平均计算耗时如图 7所示。其中,AUPF算法与UPF算法的单步平均计算耗时几乎相同,均为0.20 s,相当于标准粒子滤波算法耗时的2倍和EPF算法的6倍左右。其原因主要是由于AUPF算法和UPF算法在重要性采样时,对于每一个粒子均值均需要采用UKF方法计算,这将显著增加算法的计算耗时。
|
图 6 参数识别值均方根误差及相对误差均值 Fig. 6 Means of RMSEs and relative errors of parameters identification values |
|
图 7 单步平均计算耗时 Fig. 7 Means of computing time-consuming in a single step |
为了验证AUPF算法对于真实物理试验中进行参数识别的有效性,采用直径为300 mm的铅芯橡胶隔震支座拟静力试验所测得的水平剪力和位移数据,进行了在线模型参数识别。参数识别时,假定隔震支座恢复力模型为Bouc-Wen模型。拟静力试验模型为LRB300铅芯橡胶隔震支座,其质量分别为81 kg和82 kg。铅芯橡胶隔震支座的设计承载力为566 kN,橡胶直径为300 mm,橡胶总厚度为48 mm,支座高度为100 mm,一次形状系数为9.375,二次形状系数为6.250,水平等效刚度为1.017 kN/mm,竖向刚度为608 kN/mm。隔震支座实物如图 8所示。试验在哈尔滨工业大学结构与力学实验中心完成,试验加载设备是华龙20 MN动态压剪试验机,竖向最大加载压力为2 000 t,行程为±100 mm;水平最大加载压力为200 t,行程为±500 mm。试验机采样频率为0.01 Hz。隔震支座在工作台上由2块挡板固定下连接板,当工作台移动到试验位置附近时,调节工作台使之居中,并固定上连接板。

|
图 8 LRB300隔震支座实物图 Fig. 8 Physical drawing of LRB300 isolation bearing |
采用AUPF算法进行Bouc-Wen模型在线参数识别时,将真实物理试验中在当前步位移加载路径下的隔震支座位移测量值dk和水平剪力Fk作为AUPF算法当前步的位移输入d和观测量yk。AUPF算法在每一步的参数识别时,仅需要用到当前步及之前步的输入和观测数据,并不需要利用试验结束后全部的试验数据。全部试验数据进行参数识别为离线识别,AUPF算法为参数在线识别,因而具有更大的挑战性。设系统状态为x=[x1, x2, x3, x4, x5]T=[z, k0, β, γ, n]T;状态方程和观测方程分别为式(25)和式(27)。状态初值为x0=[0 1 0.01 0.01 2]T,过程噪声协方差为Q =diag(10-8,10-8,10-8,10-8,10-8),观测噪声协方差为W =0.015 kN2;状态估计误差初始协方差为P =diag(10-6,100,1,1,0.01)。
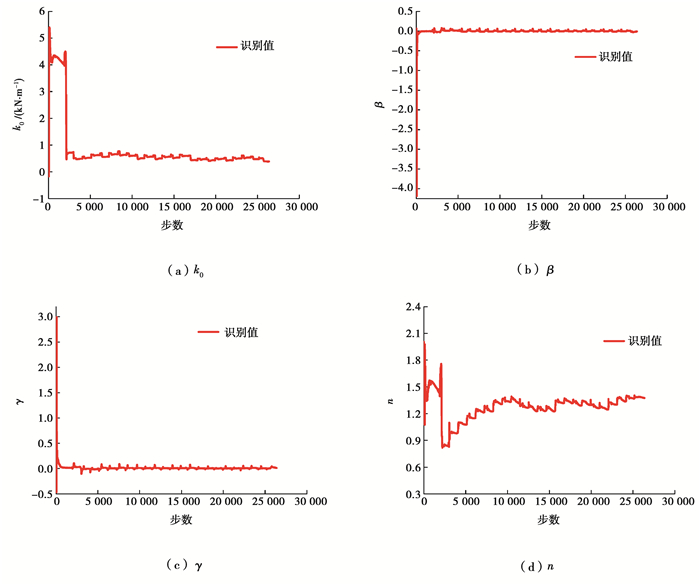
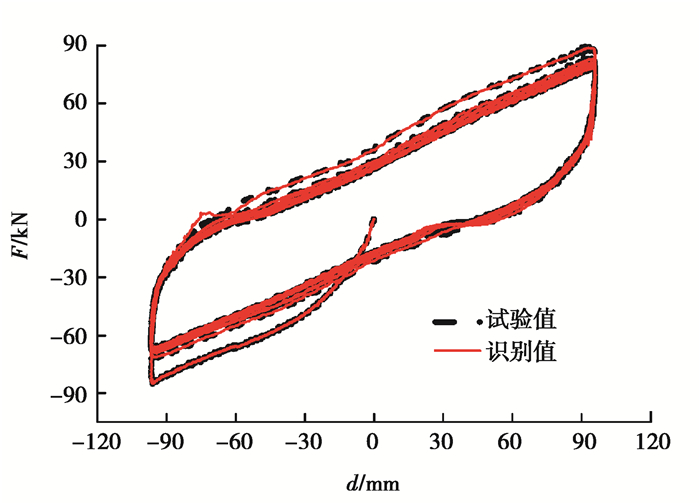
橡胶隔震支座Bouc-Wen模型参数识别时程曲线如图 9所示。参数的识别终值分别为:k0=0.382 8 kN/mm、β=-0.007 73、γ=0.009 6和n=1.374 37。将AUPF算法识别得到的支座滞回曲线与试验真实滞回曲线进行对比,如图 10所示。
|
图 9 Bouc-Wen模型参数识别值 Fig. 9 Parameter identification value of Bouc-Wen model |
|
图 10 隔震支座滞回曲线 Fig. 10 Hysteresis curve of isolation bearing |
可以看出,当基于隔震支座真实试验数据采用AUPF算法进行在线参数识别时,除了Bouc-Wen模型参数n收敛较慢,模型参数k0、β和γ均可以很快地收敛于稳定值。参数n识别值收敛较慢主要有两方面的原因:一是存在模型误差;二是模型具有强非线性。AUPF算法是一种基于模型的参数识别算法,当假定模型与真实系统之间存在模型误差,就会降低算法识别精度。由图 4(b)可见,当识别算法中假定的系统模型和真实系统模型均为相同的Bouc-Wen模型时,即算法不存在模型误差时,模型参数n的识别值收敛较快,基本可以收敛到参数的真实值,可见算法对参数n具有较好的识别效果。由图 9(d)可见,模型参数n的识别值具有一定的波动性,并没有很快地收敛于稳定值,其主要原因是由于识别算法采用Bouc-Wen模型来近似真实的隔震器的滞变关系仍存在一定模型误差,模型误差会降低识别算法的识别精度。另外,模型中的时变滞变位移z为参数n的指数函数,具有较高程度的非线性。以上原因导致参数n识别值具有时变性,以补偿模型误差的不利影响。
由于Bouc-Wen模型参数没有明确的物理意义,很难确定隔震支座所对应的模型参数真实值,因此并不能直接评价参数识别值的精度。为了验证识别参数准确性,将识别参数在线计算得到的水平恢复力和试验测量得到的恢复力进行对比,可以看出,滞回曲线识别值和实验值吻合较好,表明采用AUPF算法在线识别Bouc-Wen模型参数具有较高的识别精度,同时也表明Bouc-Wen模型可以很好地模拟铅芯橡胶隔震支座力学行为。
5 结论采用AUPF算法对一种强非线性Bouc-Wen模型进行了在线参数识别,分析了AUPF算法的精度和计算效率,得到以下结论。
1) 基于标准PF算法提出了一种改进的AUPF算法,采用UKF算法进行粒子重要性采样提高粒子非线性变化精度,同时引入辅助因子提高重采样粒子多样性,削弱粒子退化。
2) 与标准PF算法、EPF算法以及UPF算法相比,提出的AUPF算法得到的Bouc-Wen模型参数识别值的均方根误差整体上减小了81.5%、37.7%和8.0%,并能有效降低模型参数识别过程中的波动幅度,提高了强非线性模型在线参数识别精度。
3) AUPF算法平均单步计算耗时为0.20 s,与PF算法、EPF算法相比,计算耗时有所增加。需考虑减少UKF算法重要性采样计算负荷,提高算法计算效率。
4) 采用铅芯橡胶支座拟静力试验数据,验证了AUPF算法在线识别Bouc-Wen模型参数方法的有效性。
| [1] |
潘毅, 陈侠辉, 赵俊贤, 等. 基于剪力比的黏弹性阻尼腋撑-RC框架结构设计方法[J]. 建筑结构学报, 2018, 39(S1): 79-86. Pan Y, Chen X H, Zhao J X, et al. Seismic design method of RC frame structure with knee brace of viscoelastic damper based on shear ratio[J]. Journal of Building Structures, 2018, 39(S1): 79-86. (in Chinese) |
| [2] |
郭阳照, 潘毅, 吴体, 等. LRB-DSB三维隔震系统的隔震效果分析[J]. 西南交通大学学报, 2018, 53(6): 1195-1204. Guo Y Z, Pan Y, Wu T, et al. Analysis of LRB-DSB three dimensional isolation system's isolating effect[J]. Journal of Southwest Jiaotong University, 2018, 53(6): 1195-1204. (in Chinese) DOI:10.3969/j.issn.0258-2724.2018.06.015 |
| [3] |
Wu B, Ning X Z, Xu G S, et al. Online numerical simulation: a hybrid simulation method for incomplete boundary conditions[J]. Earthquake Engineering & Structural Dynamics, 2018, 47(4): 889-905. |
| [4] |
Ou G, Dyke S J, Prakash A. Real time hybrid simulation with online model updating: an analysis of accuracy[J]. Mechanical Systems and Signal Processing, 2017, 84: 223-240. DOI:10.1016/j.ymssp.2016.06.015 |
| [5] |
关新春, 欧进萍. 磁流变耗能器的阻尼力模型及其参数确定[J]. 振动与冲击, 2001, 20(1): 5-8. Guan X C, Ou J P. Magnetorheological damper's damping force model and the definition of its parameter[J]. Journal of Vibration and Shock, 2001, 20(1): 5-8. (in Chinese) |
| [6] |
Yang G, Wu B, Ou G, et al. HyTest: platform for structural hybrid simulations with finite element model updating[J]. Advances in Engineering Software, 2017, 112: 200-210. DOI:10.1016/j.advengsoft.2017.05.007 |
| [7] |
王涛, 吴斌. 基于约束UKF模型更新的混合试验方法[J]. 地震工程与工程振动, 2013, 33(5): 100-109. Wang T, Wu B. Hybrid testing method based on model updating with constrained unscented Kalman filter[J]. Journal of Earthquake Engineering and Engineering Vibration, 2013, 33(5): 100-109. (in Chinese) |
| [8] |
王涛. 基于模型更新的土木结构混合试验方法[D]. 哈尔滨: 哈尔滨工业大学, 2014. Wang T. Hybrid testing method for civil structures based on model updating[D]. Harbin: Harbin Institute of Technology, 2014. (in Chinese) |
| [9] |
李春来, 张海宁, 杨立滨, 等. 基于无迹卡尔曼滤波神经网络的光伏发电预测[J]. 重庆大学学报, 2017, 40(4): 54-61. Li C L, Zhang H N, Yang L B, et al. Photovoltaic power forecasting based on unscented Kalman filtering neural network[J]. Journal of Chongqing University, 2017, 40(4): 54-61. (in Chinese) |
| [10] |
Shao X Y, Mueller A, Mohammed B A. Real-time hybrid simulation with online model updating: methodology and implementation[J]. Journal of Engineering Mechanics, 2016, 142(2): 04015074. DOI:10.1061/(ASCE)EM.1943-7889.0000987 |
| [11] |
Wu B, Wang T. Model updating with constrained unscented Kalman filter for hybrid testing[J]. Smart Structures and Systems, 2014, 14(6): 1105-1129. DOI:10.12989/sss.2014.14.6.1105 |
| [12] |
Zaritskii V, Svetnik V, Shimelevich L. Monte carlo techniques in problems of optimal information processing[J]. Automation and Remote Control, 1975, 36(3): 2015-2022. |
| [13] |
Merwe R, Wan E. ReBEL-recursive bayesian estimation libaru[EB/OL]. (2006)[2009-07-25]. http://choosh.cse.ogi.edu/rebel/.
|
| [14] |
Gordon N J, Salmond D J, Smith A F M. Novel approach to nonlinear/non-Gaussian Bayesian state estimation[J]. IEE Proceedings F Radar and Signal Processing, 1993, 140(2): 107. DOI:10.1049/ip-f-2.1993.0015 |
| [15] |
Zhang G Y, Cheng Y M, Yang F, et al. Particle filter based on PSO[C]//2008 International Conference on Intelligent Computation Technology and Automation (ICICTA). October 20-22, 2008, Changsha, China. IEEE, 2008: 121-124.
|
| [16] |
朱磊, 樊继壮, 赵杰, 等. 改进粒子滤波器的移动机器人同步定位与地图构建方法[J]. 重庆大学学报, 2014, 37(4): 39-45. Zhu L, Fan J Z, Zhao J, et al. A method for mobile robot SLAM based on modified particle filter[J]. Journal of Chongqing University, 2014, 37(4): 39-45. (in Chinese) |
| [17] |
李烨, 王建, 李青, 等. 基于粒子滤波器的结构损伤识别研究[J]. 建筑结构, 2007, 37(S1): 281-284. Li Y, Wang J, Li Q, et al. Particle filter based on structural system identification[J]. Building Structure, 2007, 37(S1): 281-284. (in Chinese) |
| [18] |
唐和生, 张伟, 陈镕, 等. 基于自适应粒子滤波的结构损伤识别[J]. 振动、测试与诊断, 2008, 28(3): 211-215, 299. Tang H S, Zhang W, Chen R, et al. Structural damage identification method based on adaptive particle filtering[J]. Journal of Vibration, Measurement & Diagnosis, 2008, 28(3): 211-215, 299. (in Chinese) |
| [19] |
樊学平, 刘月飞, 吕大刚. 应用高斯粒子滤波器的桥梁可靠性在线预测[J]. 哈尔滨工业大学学报, 2016, 48(6): 164-169. Fan X P, Liu Y F, Lyu D G. On-line reliability prediction of bridges based on Gaussian particle filter[J]. Journal of Harbin Institute of Technology, 2016, 48(6): 164-169. (in Chinese) |
| [20] |
Dan Simon. 最优状态估计: 卡尔曼, H∞及非线性滤波[M]. 张勇刚, 李宁, 奔粤阳, 译. 北京: 国防工业出版社, 2013. Dan S. Optimal state estimation[M]. Zhang Y G, Li N, Ben Y Y, trans. Beijing: National Defense Industry Press, 2013. (in Chinese) |
| [21] |
胡士强, 敬忠良. 粒子滤波原理及其应用[M]. 北京: 科学出版社, 2010. Hu S Q, Jing Z L. Particle filter principle and its application[M]. Beijing: Science Press, 2010. (in Chinese) |
| [22] |
朱志宇. 粒子滤波算法及其应用[M]. 北京: 科学出版社, 2010. Zhu Z Y. Particle filter algorithm and its application[M]. Beijing: Science Press, 2010. (in Chinese) |
 2021, Vol. 44
2021, Vol. 44



