静液压无极变速器(HST,hydrostatic transmission)是由液压泵、液压马达和其他液压元件组成的传动系统,具有无极调速、变矩,对外部载荷自适应的特点,被广泛应用于农业机械和部分工程机械中[1]。HST的操控性是影响主体机械经济性和适用性的关键,因此,HST的研究对农业机械现代化发展具有极其重要的作用。
HST的传统控制方法有电液伺服控制[2-3]和PID(比例、积分、微分)控制,电液伺服控制虽然动态响应快、控制精度高、使用寿命长,但其抗污染能力差,制造成本高,并且电液伺服控制的主要设备大多由国外公司提供,且以硬件方式集成在泵中,设备后期的维护及升级困难。而传统PID控制通过PID参数的线性组合,直接输出被控量,降低控制难度,被广泛应用于机械系统的控制。但在传统的PID控制中,系统的动态品质对PID增益的变化敏感,PID参数整定成一个难点。相关报道在PID控制中引入模糊控制算法可以实现控制参数的自适应调整,能一定程度上降低传统PID在线参数整定难度,及非线性系统控制效果差等缺陷。朱从民[4]运用模糊自适应PID控制器对静液压系统进行复合控制研究,解决了静液压传动系统的时变非线性控制效果差的问题。李和言和陈宝瑞[5]设计了模糊自适应PID同步控制器,仿真结果表明,基于该控制器的静液压传动系统在负载干扰变化时转速能快速达到设定值,具有良好鲁棒性。但模糊控制方法主要根据经验对控制规则进行调整,导致控制规则的确定具有一定难度,且经模糊处理后系统的动态品质下降,控制精度降低[6]。
BP神经网络(BP neural network)是20世纪80年代在人工智能领域兴起的一种控制方法。该方法不但具有传统控制方法的优点,而且能对复杂系统进行模型逼近,是一种适用于复杂非线性系统的有效控制方法。在汽车、机械、传动等领域,相关文献[7-9]报道了利用BP神经网络的自学习、自适应及非线性逼近功能,拟合复杂的系统模型,实现快速且高精度预测。将BP神经网络嵌入传统PID控制方法中,一方面能有效克服传统PID控制方法对非线性时变系统控制效果差的缺点;另一方面,BP神经网络通过自身训练,在线整定参数,使被控系统输出不断逼近期望值,可实现精确控制。汪伟[10]引入BP神经网络对无轴承异步电机的PID控制器参数进行在线调整,实现转子的稳定悬浮,且启动超调量小,静、动态特性较好。针对液压系统的时变性、大惯性、高度非线性和无法获得数学模型的特点,刘浩[11]提出一种多级自适应电压激励与BP神经网络联合控制的策略,用以减小控制误差,实现对液压缸位移的精确控制。Ikbal Eski[12]在汽车电子节气门控制系统中采用3种神经网络控制器来控制车辆速度,仿真结果表明,基于自适应神经网络的模糊推理控制系统具有更好的控制性能。
HST中变量泵变量马达系统因其能量传递效率高,调速范围广而被广泛应用于工程机械中。但由于变量泵变量马达系统是高耦合、非线性系统,泵和马达的解耦控制难度大。而分段控制可以减小系统的控制难度,也可以降低系统功率消耗,提高系统性能,是目前较为普遍采用的控制方式。王岩[13]使用Bang-Bang变结构控制算法对泵和马达分段控制,实现系统快速响应。郑琦[14]针对变量泵采用滑模变结构控制,对变量马达采用引入扰动观测器的PID控制,可以抑制系统的非线性扰动和负载扰动,提高波动压力下的稳态精度。Leon Liebenberg[15]使用PID控制器分别控制泵和马达,使静液压传动系统处于高效区,实现传动系统较为节能的动力匹配。李飞龙[16]同样使用PID控制器分别控制泵和马达,使采用静液压传动技术的风力机实现变速恒频功能。陈宝瑞等[17]则采用模糊控制算法对变量泵变量马达进行分段调节,相对于传统的PID控制,能保证系统在较好的响应速度下有效减小超调量。王岩[18]采用单神经元PID控制变量泵,模糊控制算法对变量马达排量预测控制,相对于传统的控制方法,可以提高系统的响应速度,减少溢流损失。然而,目前现有文献大多采用传统控制方法对泵和马达进行分段控制研究,而BP神经网络与传统PID控制方法相结合的控制研究鲜有。
基于此,提出基于BP神经网络的PID控制方法,对HST中马达输出转速的动态响应特性进行研究。首先,建立静液压传动系统的数学模型,分别采用传统PID控制、模糊控制以及BP神经网络PID控制3种方法对变量泵定量马达的静液压系统的转速进行了仿真试验,以验证BP神经网络PID控制在静液压传动系统中的可行性和控制优势。其次,基于BP神经网络PID控制方法对具有更大马达转速变化范围的变量泵变量马达传动系统进行研究,采用分段控制分别对泵和马达进行调控,以提高控制精度和响应速度,减小系统溢流,并在不同的控制算法下,分析不同负载等效转动惯量对HST系统的影响。
1 静液压传动系统建模为了提高变量泵变量马达系统的控制性能,采用基于BP神经网络的PID方法对泵和马达进行分段控制研究。
1.1 HST模型简化考虑采用的变量泵—变量马达静液压传动系统模型如图 1所示,该模型的主要假设条件如下[19]:
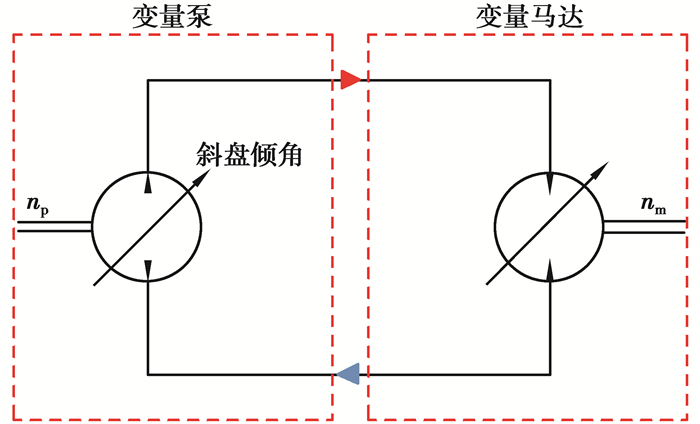
|
图 1 变量泵—变量马达系统简图 Fig. 1 Variable pump-Variable motor system diagram |
1) 油液的粘性不变;
2) 不考虑泵和马达的脉动性;
3) 液压泵和液压马达的泄露油流为层流;
4) 液压泵的吸油口和液压马达的回油口压力为零;
5) 不考虑油液的液阻和液感及管路中的动态过程,仅考虑液容。
1.2 HST数学模型变量泵的排量:静液压传动系统工作中,泵的斜盘倾角越大,内部柱塞的行程越长,产生的高压油的流量也就越大,变量泵的排量方程为
| $ {q_p} = {k_p} \times {x_p}, $ | (1) |
式中:xp为变量泵的调节参数;Kp为泵的每转排量梯度;qp为泵的排量。
泵的流量连续性方程
| $ {Q_P} = {n_p}{q_p} - ({C_{ip}} + {C_{ep}})P, $ | (2) |
式中:Qp为泵的流量;np为泵的转速;P为压力油腔压力;Cip、Cep分别为泵的内泄露系数和外泄露系数。
马达输出转速不仅受自身排量的影响,还受变量泵输出高压油的流量大小影响,其流量连续方程为
| $ {Q_P} = ({C_{im}} + {C_{em}})P + {n_m}{q_m} + \frac{{{V_0}}}{{{\beta _e}}}\frac{{{\rm{d}}p}}{{{\rm{d}}t}}, $ | (3) |
式中:nm为马达输出转速;qm为马达排量;V0为压力油腔总容积;βe为油液的体积弹性系数;Cim、Cem分别为马达的内泄露系数和外泄露系数。
马达的转矩平衡方程
| $ {q_m}P = J\frac{{{\rm{d}}{n_m}}}{{{\rm{d}}t}} + B{n_m} + {\mathit{\boldsymbol{T}}_l}, $ | (4) |
式中:J为马达及负载折算到马达轴上的等效转动惯量;B粘性阻尼系数;Tl为负载力矩。
通过对式(1), (2), (3), (4)进行拉氏变换可得
| $ \begin{array}{l} {n_p}{q_p}(s) - {q_m}{n_m}(s) = \left[ {{C_t} + \frac{{{V_0}}}{{{\beta _e}}}s} \right]P(s), \\ {q_m}P(s) = (Js + B){n_m}(s) + {T_l}(s), \\ {q_p}(s) = {k_x}{x_p}(s), \end{array}$ |
其中Ct为泵和马达的总泄露系数,其计算公式为
| $ {C_t} = {C_{ip}} + {C_{ep}} + {C_{im}} + {C_{em}}, $ |
在理想工作条件下,假设马达负载力矩不变,即Tl(s)=0,消去式中其他变量,最终得到变量泵-定量马达关于输入xp和输出nm的传递函数
| $ {G_1}(s) = \frac{{{n_m}(s)}}{{{x_p}(s)}} = \frac{{\frac{{{k_x}{n_p}}}{{{q_m}}}}}{{\frac{{J{V_0}}}{{{\beta _e}q_m^2}}{s^2} + (\frac{{{V_0}B}}{{{\beta _e}{q_m}^2}} + \frac{{J{C_t}}}{{q_m^2}})s + 1}}。$ | (5) |
同理可得出定量泵变量马达关于输入ym和输出nm的传递函数
| $ {G_2}(s) = \frac{{{n_m}(s)}}{{{y_m}(s)}} = \frac{{{k_m}{V_0}{P_0}s + {k_m}{\beta _e}{C_t}{P_0} - {k_m}{q_m}{n_{m0}}{\beta _e}}}{{J{V_0}{s^2} + ({C_t}{\beta _e} + {V_0}B)s + q_m^2{\beta _e} + {C_t}{\beta _e}B}}, $ |
式中:ym为变量马达的调节参数;Km为马达的每转排量梯度;p0为初始状态的压力油腔压力;nm0为初始状态的马达转速。
1.3 HST仿真模型基于以上分析和数学模型,可设计变量泵定量马达系统的simulink仿真模型如图 2所示。对定量泵变量马达系统,主要采用Matlab进行编程建模。
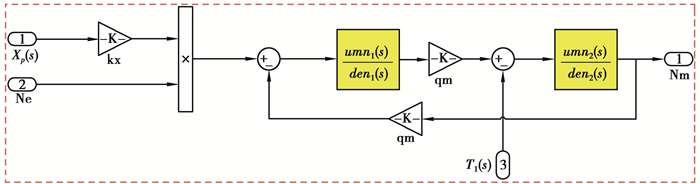
|
图 2 变量泵定量马达仿真模型 Fig. 2 Variable Pump-Quantitative Motor System Block Diagram |
为了明确BP神经网络PID控制方法在HST研究中的优势,引入PID、模糊自适应PID和BP神经网络PID 3种不同的控制方法,对HST中定量马达的转速控制进行了对比研究。3种控制器的结构与原理如下所述。
2.1 PID控制器PID是一种普遍应用的控制方法,将其偏差的比例(P)、积分(I)和微分(D)通过线性组合构成控制量,对被控对象进行控制[20]。先将纯比例控制器接入到闭环控制系统中,逐渐增加比例增益至系统出现震荡,此时的增益为临界增益(Ku),震荡周期为临界周期(Tu),根据经验得到PID控制的参数,再根据系统的输出响应曲线微调各参数,从而得到最佳控制结果。PID控制器采用的是增量式PID算法,其表达式为
| $ \Delta u(k) = {K_p}[e(k) - e(k - 1)] + {K_i}e(k) + {K_d}[e(k) - 2e(k - 1) + e(k - 2)], $ |
式中:Δu(k)为控制器在k时刻的输出增量;e(k), e(k-1), e(k-2)分别为k,k-1,k-2时刻的偏差大小;Kp、Ki、Kd分别为增量式PID算法的比例,积分,微分系数。在Simulink中设置的比例、积分、微分系数最终值分别为:Kp=0.077, Ki=0.158, Kd=0.0045。
2.2 模糊自适应PID控制器模糊自适应PID控制器主要引用了模糊数学的基本理论和方法,根据系统的实际响应情况,运用模糊推理,实现对PID参数的自动调整。模糊自适应PID控制器采用双输入三输出的控制机理,把偏差e以及偏差变化率ec模糊化作为输入,通过预先设定的模糊控制规则进行判断,输出Kp、Ki、Kd 3个参数的补偿量[20],控制结构如图 3所示。
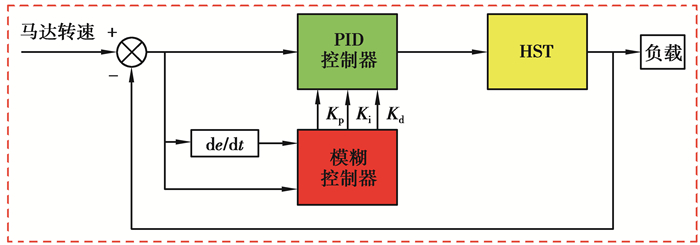
|
图 3 模糊自适应控制器结构 Fig. 3 Structure of fuzzy adaptive controller |
在采用模糊自适应PID对定量马达的转速控制研究中,设定马达转速偏差和偏差变化率的论域均为[-9, 9],并设置量化因子对该论域进行调整;设定相应的模糊子集同为{NB NM NS ZO PS PM PB},分别对应负大,负中,负小,零,正小,正中,正大。模糊控制器输出的控制参数补偿量为模糊化后的数值,论域均为[-6, 6],需要通过比例因子进行反模糊化得到实际补偿量。相应的Simulink模糊控制器结构如图 4所示。
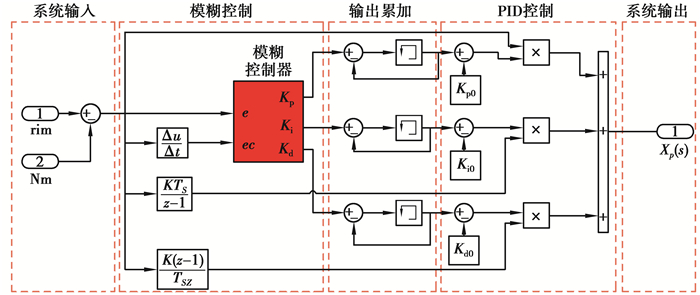
|
图 4 Simulink模糊控制器结构 Fig. 4 Simulink fuzzy controller structure |
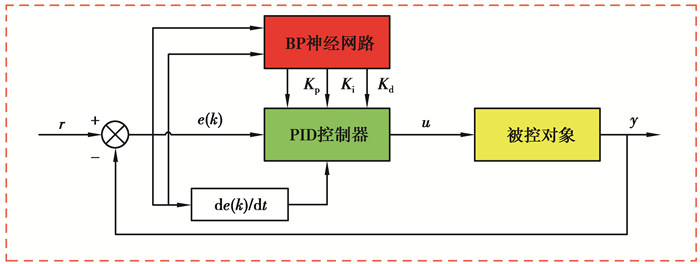
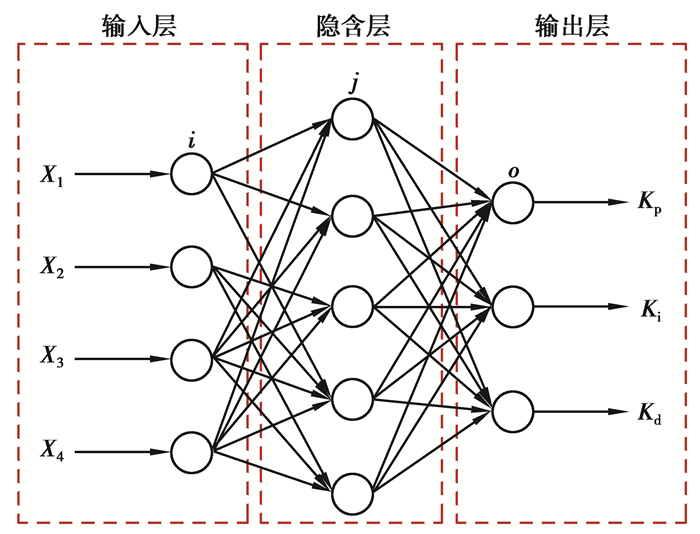
神经网络是模拟人脑思维方式的数学模型,其结构类似于大脑神经突触连接。通过不断调整大量神经元的权值,并在激活函数的作用下,达到处理信息的目的[21-23]。BP神经网络不同于结构简单的单神经元网络,它是由输入层,隐含层和输出层组成,并且隐含层的层数不定,根据控制要求进行适当选取。所采用的BP神经网络PID控制器是运用BP神经网络算法的一种4×5×3的三层前馈结构,输入层由4个神经元组成,分别是系统输出,期望值,偏差以及初始阈值,输出层节点分别为比例(P),积分(I),微分(D)单元,可以对PID控制器自动进行参数整定,其结构图如图 5、图 6所示。其中输入层的输入和输出相等,设输入表达式为
|
图 5 BP神经网络PID控制器结构框图 Fig. 5 Block Diagram of BP Neural Network PID Controller |
|
图 6 PID神经网络结构图 Fig. 6 Structure diagram of PID neural network |
| $ {x_i}(k) = [r(k), y(k), e(k), 1], (i - 1, 2, 3, 4)。$ |
式中:r(k)为系统期望输出值;y(k)为系统实际输出值;e(k)为马达转速偏差;1为初始阈值。隐含层和输出层的输入/输出表达式分别为
| $ \left\{ \begin{array}{l} {I_j}(k) = {{\omega }_j} \cdot {x_i}(k),(j = 1,2,3,4,5),\\ {h_j}(k) = \frac{{{e^{I(k)}} - {e^{I(k)}}}}{{{e^{I(k)}} + {e^{I(k)}}}},\\ {K_o}(k) = {\omega _o} \cdot h(k),(o = 1,2,3),\\ {O_o}(k) = \frac{{{e^{K(k)}}}}{{{e^{K(k)}} + {e^{K(k)}}}} 。\end{array} \right.$ |
式中:ωj为隐含层的权重值(5×4的矩阵);ω0为输出层的权重值(3×5的矩阵)。
BP神经网络采用反向传播学习算法,则其性能指标函数为
| $ E(k) = \frac{1}{2}{[r(k) - y(k)]^2} = \frac{1}{2}e{(k)^2}$ |
按照性能指标函数的负梯度方向修改权值通常容易陷入局部极小值状态,因此需要引入附加动量,通过附加动量使网络在修正权值时有可能滑过这些极小值[24]。带有附加动量因子的隐含层至输出层权值修正公式为
| $ \begin{array}{l} \Delta {\mathit{\boldsymbol{\omega }}_o}(k + 1) = - {\eta _2}\frac{{\partial E(k)}}{{\partial {\mathit{\boldsymbol{\omega }}_o}}} + \alpha \Delta {\mathit{\boldsymbol{\omega }}_o}(k), \\ \frac{{\partial E}}{{\partial {\mathit{\boldsymbol{\omega }}_o}}} = \frac{{\partial E}}{{\partial K}} \cdot \frac{{\partial K}}{{\partial {\mathit{\boldsymbol{\omega }}_o}}} = \frac{{\partial E}}{{\partial O}} \cdot \frac{{\partial O}}{{\partial K}} \cdot \frac{{\partial K}}{{\partial {\mathit{\boldsymbol{\omega }}_{nj}}}} 。\end{array}$ | (6) |
式中:η2为ωo的学习速率,取0.2;α为附加动量因子,一般取0.05。
将公式(6)简化为
| $ \begin{array}{l} \Delta {\mathit{\boldsymbol{\omega }}_o}(k + 1) = {\eta _2}\delta '(k) \cdot h(k) + \alpha {\mathit{\boldsymbol{\omega }}_o}(k)。\\ \delta '(k) = - e(k) \cdot {\mathop{\rm sgn}} \frac{{O(k) - O(k - 1)}}{{K(k) - K(k - 1)}} 。\end{array} $ | (7) |
同理可推出带有附加动量因子的输入层至隐含层的权值修正公式为
| $ \begin{array}{l} \Delta {\mathit{\boldsymbol{\omega }}_j}(k + 1) = {\eta _1}\delta (k) \cdot {x_i}(k) + \alpha {\mathit{\boldsymbol{\omega }}_j}(k), \\ \delta (k) = \delta '(k) \cdot {\mathop{\rm sgn}} \frac{{oh(k) - h(k - 1)}}{{K(k) - K(k - 1)}} \cdot ({\mathit{\boldsymbol{\omega }}_o}) 。\end{array} $ | (8) |
式中:η1为ωj的学习速率。
3 仿真结果及HST动态特性分析 3.1 3种控制方法下变量泵定量马达的动态特性超调量可以反映系统输出的最大偏差,为实现系统的快速响应,考虑静液压传动系统存在油液的泄露和传递效率的改变,可允许出现一定范围的超调量。但是超调量大会导致系统的稳定性差,不利于系统正常工作。因此,保证HST系统在安全超调量下的快速响应是对其控制研究中的一个重点。于Simulink分别采用传统PID控制、模糊PID控制和BP神经网络PID对HST中变量泵定量马达进行建模和控制仿真,并对比分析3种控制方法在期望转速提升下的动态响应特性。仿真采用的HST主要参数如表 1所示。
| 表 1 泵和马达主要仿真参数 Table 1 Main simulation parameters of pump and motor |
采用3种控制方法计算得到,系统从空载启动至马达转速为600 r/min的变化过程中,马达转速阶跃响应结果如图 7所示。从图 7中可以看出,3种控制方法均能使马达转速到达设定值:传统PID控制的超调量最大,为14%。模糊控制使得系统超调量有所降低,达到4%。但是,在预设的模糊规则下需要不断调整PID参数,会导致系统达到稳态的时间变长。而BP神经网络PID采用的反向传播法,每个神经元的权值都在负梯度方向上快速修正,使马达转速能较好地追踪给定转速。由图 7可知,BP神经网络PID基本无超调极大地增强了系统安全性,同时在0.2 s内即可在目标转速处稳定,响应迅速且无多余扰动。与传统PID控制和模糊PID控制结果相比,BP神经网络PID的超调量最小,响应速度更快,具有较大的优势。

|
图 7 变量泵定量马达阶跃响应曲线 Fig. 7 Step response curve of variable displacement pump quantitative |
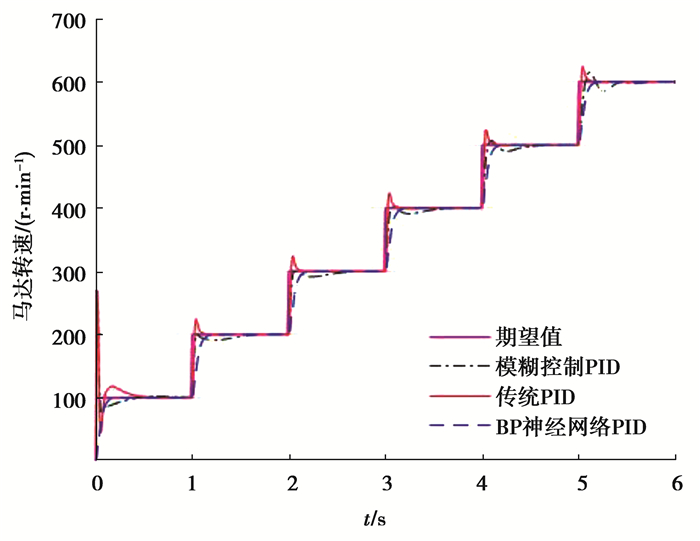
对于复杂多变的动态工况,对比分析了以上3种控制方法在不同阶跃期望转速下对马达转速的控制结果。在0~6 s内,马达转速设定值以每秒100 r/min的步长,由零逐步增加到600 r/min,采用3种控制方法获得的转速跟踪曲线如图 8所示。由于在不同阶跃转速下,PID控制的参数取转速为600 r/min的设定值,导致低转速阶段(0~0.1 s)系统阶跃响应曲线超调量过大,且容易波动。模糊控制的参数调整则受人为设定的控制规则的影响,在不同期望转速下的性能指标亦不同。而BP神经网络采用的是最小二乘法优化函数,通过梯度下降法不断调整权重值,使其在不同的转速下都能快速跟踪期望值。对图 8中三种方法的控制效果对比分析得到:在期望转速为100 r/min的状态下,PID控制和模糊控制的超调量和波动都很大,而BP神经网路具有较好的控制效果。期望转速递增的过程中(100~600 r/min),虽然PID控制和模糊控制效果的有所改善,但相比之下,BP神经网络控制方法仍为最佳。该仿真结果与3种控制方法的基本原理分析结果一致。
|
图 8 马达转速跟踪曲线 Fig. 8 Motor speed tracking curve |
以上研究结果表明,与传统控制方法相比,BP神经网络PID控制在不同的工况下,都有着良好的动态响应特性,控制效果更优。
3.2 BP神经网络PID对变量泵变量马达分段调节考虑到BP神经网络PID控制方法的优势,基于该方法对更大马达转速变化范围的变量泵变量马达进行分段控制研究,即变量泵定量马达和定量泵变量马达2个控制阶段。
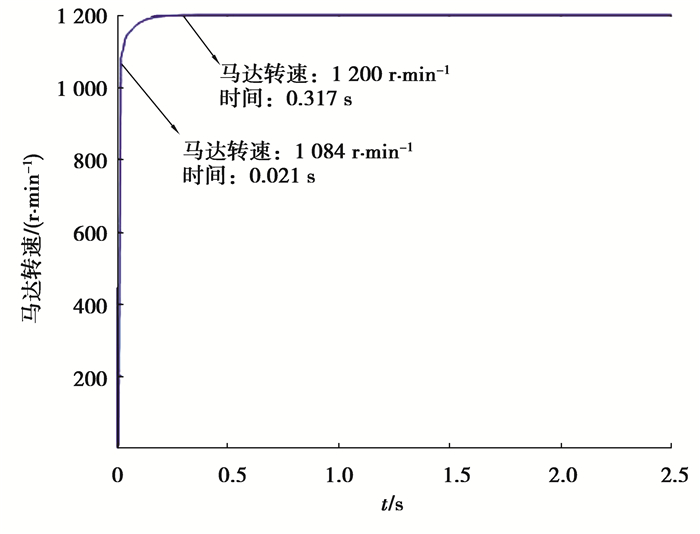
当系统中泵的输入转速为2 000 r/min,马达期望转速为1 200 r/min时,采用BP神经网络对变量泵变量马达分段控制的马达转速响应曲线如图 9所示。在0~0.5内,系统进行了2个控制阶段的快速切换,泵排量最大时所对应的马达转速在1 000r/min左右,并在0.317 s达到1 200 r/min的稳定转速。得益于BP神经网络良好的误差修正能力,马达输出转速能够快速地跟踪期望值,抑制波动,使系统达到稳定。这是传统的控制方法难以实现的。分析研究结果表明,变量泵变量马达系统的超调量为,调节时间为0.317 s。
|
图 9 变量泵变量马达阶跃响应曲线 Fig. 9 Variable Pump-Variable Motor Step Response Curve |
阮凌燕等[25]采用2个PID控制器单独控制变量泵和变量马达,其中PID参数值主要根据经验而设定,结果波动较大且达到稳定的时间较长。王岩提出改进的Bang-Bang控制算法对变量泵、变量马达排量快速控制,效果优于传统控制方法,但是由于Bang-Bang控制器的特性,使泵和马达的排量不断在最大、最小2个极端变化,造成控制难度增大,且排量变化频繁、不稳定。与文献[25]和[13]的结果相比,采用的BP神经网络PID控制的变量泵变量马达系统能自动调整控制参数,加快系统的响应速度,提高稳定性。
图 10为等效转动惯量(马达和负载部分的总转动惯量)分别为3.1、5.1、8.1、11.1下变量泵变量马达调速系统的马达输出转速曲线。从图中可知,不同负载的等效转动惯量对马达的响应转速产生影响。由于负载增大,使得马达进出口压差变大,相同输出转速下所需的马达排量越小,控制马达加速的时间越长,而稳定转速波动区间窄,产生的脉动也趋于减小。基于BP神经网络控制的分段调速系统在不同等效转动惯量下都能达到稳定状态,与文献[26]相比,所采用BP神经网络控制可以有效降低由负载引起的转速波动。
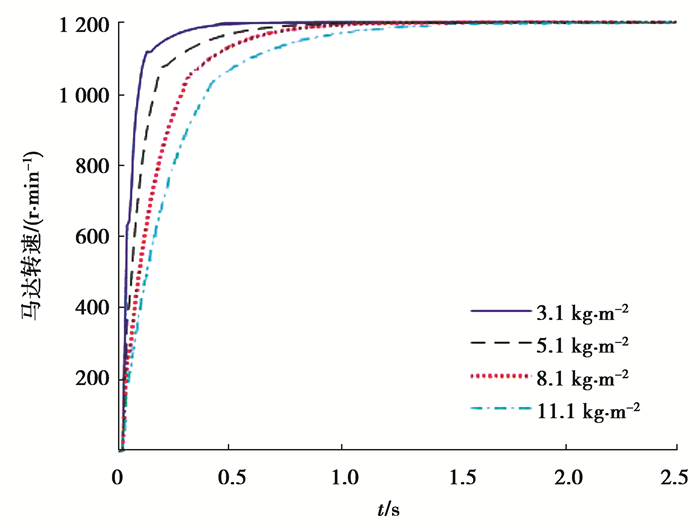
|
图 10 不同等效转动惯量下的马达转速 Fig. 10 Motor speed at different equivalent moment of inertia |
对变量泵和变量马达的排量也进行研究,变量泵的排量由零快速增加到24 ml/r所用的时间为0.13 s,此时马达转速为1 014 r/min,如图 11所示。采用BP神经网络PID控制方法,马达排量快速降低,从而使马达转速继续增加,最终达到设定转速1 200 r/min,此时马达排量为9.05 ml/r,符合马达最小排量不能低于最大排量的30%要求[13]。文献[18]提出变量泵变量马达自适应控制算法对HST进行研究,变量泵采用的是
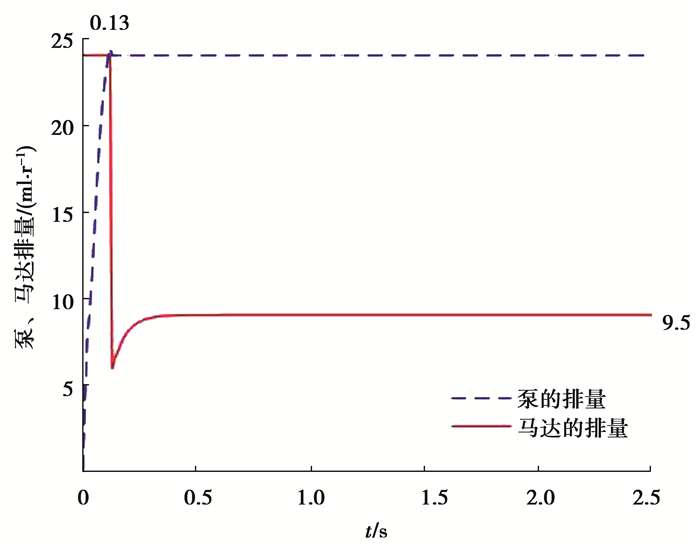
|
图 11 变量泵、变量马达排量大小 Fig. 11 Variable pump and variable motor displacement |
单神经元控制,变量马达排量则通过模糊控制进行排量预测,以变量泵控制量的变化率为输入,对马达控制信号的自动修正。忽略了静液压变速器由于压差而产生的油液泄露,把泵和马达的排量简化为线性关系,导致泵和马达排量自适应调整过程存在波动。所采用的BP神经网络PID则能准确地对变量泵变量马达模型进行控制,快速修正斜盘倾角,在最短的时间内使泵和马达排量达到当前期望马达转速下的最佳值,有效减小波动[27]。
4 结论引入BP神经网络控制方法对静液压变速器的动态特性进行了研究。主要对变量泵变量马达调速系统建立数学模型,并建模仿真。主要研究结果如下:
1) 引入BP神经网络对马达输出转速进行控制,能提高静液压传动系统的适用性和经济性。仿真试验结果表明:相对于传统的PID控制和模糊自适应PID控制,采用BP神经网络在减小超调量的同时可以稳定快速地跟踪目标转速,动态特性良好且具有较强的鲁棒性。
2) 针对变量泵变量马达分段控制,主要研究了目标转速下的系统响应,同时分析了等效转动惯量对系统控制性能的影响。研究结果表明,采用BP神经网络分别控制泵和马达可以增大系统的转速变化范围,减小系统因控制阶段的切换而产生的波动,使泵和马达排量的调节迅速而准确,并能有效降低由负载引起的转速波动。
BP神经网络控制适用于具有非线性、时变性的复杂系统,对今后的变量泵变量马达系统的同时控制有很好的指导性。
| [1] |
朱镇. 液压机械无级变速器性能优化研究[D]. 镇江: 江苏大学, 2016. Zhu Z. Study on Performance Optimization of Hydro-mechanical CVT[D]. Zhenjiang: Jiangsu University, 2016. (in Chinese) |
| [2] |
Dasgupta K. Analysis of a hydrostatic transmission system using low speed high torque motor[J]. Mechanism and Machine Theory, 2000, 35(10): 1481-1499. DOI:10.1016/S0094-114X(00)00005-7 |
| [3] |
田晋跃, 于英. 车辆静液压传动特性研究[J]. 农业机械学报, 2002, 33(4): 32-34. Tian J Y, Yu Y. Research on performance of hydrostatic transmissions of vehicles[J]. Transactions of the Chinese Society of Agricultural Machinery, 2002, 33(4): 32-34. (in Chinese) |
| [4] |
朱从民. 静液压传动车辆的复合控制[J]. 农业机械学报, 2005, 36(4): 26-29. Zhu C M. Complex control of hydrostatic transmission vehicle[J]. Transactions of the Chinese Society of Agricultural Machinery, 2005, 36(4): 26-29. (in Chinese) |
| [5] |
李和言, 陈宝瑞, 马彪, 等. 高速覆带车辆静液传动模糊自适应PID同步控制[J]. 农业机械学报, 2010, 41(3): 16-19, 45. Li H Y, Chen B R, Ma B, et al. Speed synchronization control of hydrostatic transmission based on fuzzy self-tuning PID[J]. Transactions of the Chinese Society for Agricultural Machinery, 2010, 41(3): 16-19, 45. (in Chinese) |
| [6] |
南英, 陈昊翔, 杨毅, 等. 现代主要控制方法的研究现状及展望[J]. 南京航空航天大学学报, 2015, 47(6): 798-810. Nan Y, Chen H X, Yang Y, et al. Primary methodologies of modern control: status and prospect[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(6): 798-810. (in Chinese) |
| [7] |
Liu P F, Zhang W. A fault diagnosis intelligent algorithm based on improved BP neural network[J]. International Journal of Pattern Recognition and Artificial Intelligence, 2019, 33(9): 1959028. DOI:10.1142/S0218001419590286 |
| [8] |
刘世平, 曹俊峰, 孙涛, 等. 基于BP神经网络的冗余机械臂逆运动学分析[J]. 中国机械工程, 2019, 30(24): 2974-2977, 2985. Liu S P, Cao J F, Sun T, et al. Inverse kinematics analysis of redundant manipulators based on BP neural network[J]. China Mechanical Engineering, 2019, 30(24): 2974-2977, 2985. (in Chinese) |
| [9] |
林超, 俞松松, 程凯, 等. 微纳传动系统的BP神经网络非线性控制[J]. 重庆大学学报, 2011, 34(11): 13-19. Lin C, Yu S S, Cheng K, et al. Non-linear control of mirco/nano-transmission system using BP neural network[J]. Journal of Chongqing University, 2011, 34(11): 13-19. (in Chinese) |
| [10] |
汪伟, 谭伦农, 杨泽斌, 等. 无轴承异步电机BP神经网络PID控制[J]. 电力电子技术, 2018, 52(11): 26-29. Wang W, Tan L N, Yang Z B, et al. The PID control for a bearingless induction motor based on BP neural network[J]. Power Electronics, 2018, 52(11): 26-29. (in Chinese) |
| [11] |
刘浩, 赵丁选, 张祝新, 等. 基于BP神经网络的高速开关阀多级电压控制策略[J]. 农业机械学报, 2019, 50(4): 420-426. Liu H, Zhao D X, Zhang Z X, et al. Control strategy of high-speed switch valve under multistage adaptive voltage based on BP neural network[J]. Transactions of the Chinese Society for Agricultural Machinery, 2019, 50(4): 420-426. (in Chinese) |
| [12] |
Eskii, YldrmŞ. Neural network-based fuzzy inference system for speed control of heavy duty vehicles with electronic throttle control system[J]. Neural Computing and Applications, 2017, 28(1): 907-916. |
| [13] |
王岩. 变量泵控制变量马达系统建模及控制[J]. 控制理论与应用, 2012, 29(1): 41-46. Wang Y. Modeling and control for variable-pump controlling variable-motor[J]. Control Theory & Applications, 2012, 29(1): 41-46. (in Chinese) |
| [14] |
郑琦, 李运华, 杨丽曼. 泵控并联变量马达速度系统复合控制策略[J]. 北京航空航天大学学报, 2012, 38(5): 692-696. Zheng Q, Li Y H, Yang L M. Compound control strategy for the pump-controlled-parallelvariable-displacement-motor speed system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(5): 692-696. (in Chinese) |
| [15] |
Liebenberg L, Krüger J J. Computer controlled hydrostatic transmission with traction control for vehicles[C]//SAE Technical Paper Series. 400 Commonwealth Drive, Warrendale, PA, United States: SAE International, 1990: 306-317.
|
| [16] |
李飞龙, 林勇刚, 李伟, 等. 风能静液压传动控制技术[J]. 吉林大学学报(工学版), 2014, 44(6): 1664-1668. Li F L, Lin Y G, Li W, et al. Energy hydraulic transmission system of wind turbine[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(6): 1664-1668. (in Chinese) |
| [17] |
陈宝瑞, 马彪, 李和言, 等. 高速履带车辆静液传动改进模糊控制[J]. 农业机械学报, 2009, 40(11): 18-21. Chen B R, Ma B, Li H Y, et al. Improved fuzzy control of high speed tracked vehicle hydrostatic transmission[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(11): 18-21. (in Chinese) |
| [18] |
王岩, 付永领, 牛建军. 变量泵-变量马达自适应控制算法研究[J]. China Mechanical Engineering (中国机械工程), 2009, 20(10): 1173-1175, 1179. Wang Y, Fu Y L, Niu J J. Adaptive control algorithm for variable pump-variable motor system[J]. China Mechanical Engineering China Mechanical Engineering, 2009, 20(10): 1173-1175, 1179. (in Chinese) |
| [19] |
左德龙. 静液压传动控制系统的研究[D]. 南京: 南京农业大学, 2009. Zuo D L. Research on hydrostatic transmission control system[D]. Nanjing: Nanjing Agricultural University, 2009. (in Chinese) |
| [20] |
刘金琨. 先进PID控制MATLAB仿真(4版)[M]. 北京: 电子工业出版社, 2016. Liu J K. Advanced PID control MATLAB simulation (4th)[M]. Beijing: Publishing House of Electronics industry, 2016. (in Chinese) |
| [21] |
Zeng G Q, Xie X Q, Chen M R, et al. Adaptive population extremal optimization-based PID neural network for multivariable nonlinear control systems[J]. Swarm and Evolutionary Computation, 2019, 44: 320-334. DOI:10.1016/j.swevo.2018.04.008 |
| [22] |
Eskii, Temürlenk A. Design of neural network-based control systems for active steering system[J]. Nonlinear Dynamics, 2013, 73(3): 1443-1454. DOI:10.1007/s11071-013-0875-y |
| [23] |
朱秋国, 熊蓉, 吕铖杰, 等. 新型串联弹性驱动器设计与速度控制[J]. 电机与控制学报, 2015, 19(6): 83-88. Zhu Q G, Xiong R, Lv C J, et al. Novel series elastic actuator design and velocity control[J]. Electric Machines and Control, 2015, 19(6): 83-88. (in Chinese) |
| [24] |
刘冰. MATLAB神经网络超级学习手册[M]. 北京: 人民邮电出版社, 2014. Liu B. Matlab neural network super learning manual[M]. Beijing: Posts & Telecom Press, 2014. (in Chinese) |
| [25] |
阮凌燕, 柯兵, 王岩. 变量泵驱动变量马达系统协调控制算法研究[J]. 机床与液压, 2017, 45(17): 94-98. Ruan L Y, Ke B, Wang Y. Study in coordinated control algorithm for variable pump driving variable motor system[J]. Machine Tool & Hydraulics, 2017, 45(17): 94-98. (in Chinese) |
| [26] |
高有山, 权龙, 黄家海, 等. 轴向柱塞液压马达机械液压耦合仿真分析[J]. 农业机械学报, 2016, 47(5): 395-400, 394. Gao Y S, Quan L, Huang J H, et al. Simulation analysis of axial piston hydraulic motors by mechanical coupling with hydraulic[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(5): 395-400, 394. (in Chinese) |
| [27] |
王岩, 张永龙, 秦绪情, 等. 车辆静液传动液压系统研究现状及发展趋势[J]. 机床与液压, 2015, 43(13): 149-155. Wang Y, Zhang Y L, Qin X Q, et al. Research status and development trend on vehicle hydrostatic transmission hydraulic system[J]. Machine Tool & Hydraulics, 2015, 43(13): 149-155. (in Chinese) |
 2021, Vol. 44
2021, Vol. 44


