2. 中国科学院自动化研究所, 北京 100190
2. Institute of Automation, Chinese Academy of Sciences, Beijing 100190, P. R. China
无线传感器网络融合了传感器技术、无线通信和电子技术等多个领域,从根本上解决了传感器网络庞大、布线困难的问题。无线传感器网络的基本功能是收集和返回传感器节点所在监测区域的信息。然而,网络节点的资源非常有限,主要是电池能量、处理能力、存储容量和通信带宽[1-3]。目前,无线传感器网络数据融合方法大多是基于查询模式的,适用范围比较窄[4]。应用中,需要对整个网络中各个区域的信息进行监控,聚合节点不仅需要获取整个网络节点采集到的数据,还需要对数据生成的区域信息进行更有针对性的分析,在这种情况下,有些融合方法不能满足实际需要。另外,当网络规模较小时,可以不使用融合方法来实现数据传输[5-7]。然而,当网络规模非常大且是异步的情况下,在整个网络中获取数据是非常耗费能量的,在传输数据时添加相应的精确位置信息会更消耗能量。如果不使用适当的融合方法,网络中的许多节点将因能量耗尽而迅速失效,严重时,整个网络可能崩溃[8-9]。因此,迫切需要设计一种有效的无线传感器网络数据融合方法。以下是目前主要的研究成果:
文献[10]提出了一种基于密度的无线传感器数据融合算法。通过对无线传感器网络在一定时间内的分析,有效数据和变化幅度主要集中在相对时间内,所需采样点更密集;而随机变化较小的数据则更分散、更需要采样点稀疏。在一定的数据采集时间内,根据数据的密度找到有效的采集中心点,收敛速度越接近中心点,数据融合速度离中心点越远。实验结果表明,该算法融合复杂度低,但融合能耗高。
文献[11]提出了一种基于多稀疏聚类压缩感知的无线传感器网络数据融合方法。利用改进的阈值对随机选取的传感器节点进行聚类,形成最优聚类。簇头利用Bernoulli随机观测矩阵对簇内节点进行线性压缩投影,将压缩后的信息传输到汇聚节点,减少数据传输,即降低通信能耗,从而提高网络的生命周期。根据传感器节点监测信号,它在有限差分和小波中都具有可压缩特性[12-15]。收敛节点在有限差分和小波的2个稀疏基约束下,利用OOMP算法重构线性压缩投影信息,并用最小二乘法重建数据。实验结果表明,该方法具有较高的数据采集和融合精度,但效率较低。
文献[16]提出了一种基于深度学习模型的数据融合算法。构建的特征提取模型CNNM在聚合节点处进行训练,然后通过CNNM提取每个终端节点的原始数据特征,最终将合并后的数据发送到聚合节点,从而减少数据传输量,延长网络寿命。实验结果表明,该算法具有较低的融合损失,但融合精度较差。
文献[17]提出了一种基于中继节点机制的聚类数据融合算法。根据不同簇的数据信任值和能量信任值选择簇头,并在每个簇中选择一个中继节点。集群成员的数据由簇头采集合并后发送到中继节点,中继节点用基站代替簇头进行数据通信等,大大降低了簇头每轮的能耗。实验结果表明,该算法具有良好的稳定性,但融合后的数据利用率较低,融合结果并不十分令人满意。
针对现有研究不能满足实际需要的情况,提出了一种基于无迹卡尔曼滤波(UKF)的无线传感器异步数据融合算法。具体流程如下:
1) 采用RNAT机制消除无线传感器异步数据中的冗余数据,降低数据融合的能耗,提高融合效率。
2) 通过四圆定位法确定目标的可能区域,并对待合并的数据进行跟踪定位,为数据融合奠定基础。
3) 采用无迹卡尔曼滤波算法实现异步数据融合。
4) 通过实验和讨论验证了该算法的正确性。
1 基于UKF的无线传感器异步数据融合算法设计 1.1 无线传感器异步数据冗余的消除为了降低数据融合能耗,提高融合效率,需要在数据融合前去除冗余数据。针对无线传感器异步数据的特殊性,采用RNAT机制去除冗余数据。具体流程如下:
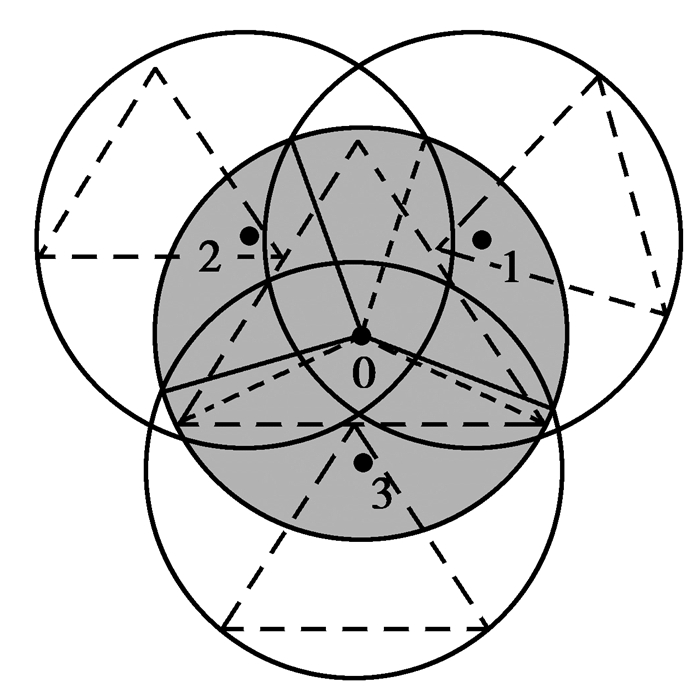
冗余节点识别:如果一个节点的检测区域可以被它的邻居完全覆盖,那么这个节点就是一个冗余节点。如图 1所示,假设节点i的检测区域是半径为r的圆,表示为S(i)。区域S(i)中的节点j是节点i的邻居,并且i的所有邻居的集合被记录为N(i)。相邻节点i和j的检测区域在点P1和P2处相交,使得S(i)和S(j)之间存在重叠。为便于计算,将重叠简化为半径为iP1、iP2和弧P1P2的扇区,表示为Sij。假设∪Sij⊇ S(i),j∈N(i),则节点i的检测区域可以被其邻居完全覆盖,即节点i是冗余节点。如图 2所示,节点0的检测区域被相邻节点1、2和3完全覆盖。根据上述判断方法,该节点为冗余节点。

|
图 1 探测区叠加示意图 Fig. 1 Schematic diagram of the overlay of the detection area |
|
图 2 探测范围示意图 Fig. 2 Schematic diagram of detection are coverage |
根据图 1和图 2,生成冗余树,通过网络中冗余节点的识别,来构造数据冗余树,具体过程如下:
簇内冗余节点的选择:簇中冗余节点的个数可能会比较多,根据距离和剩余能量判断冗余节点是否可以进行树的构建。通过簇内节点间的互相作用,如剩余能量或者位置,计算集群中的所有冗余节点都能成为树上节点的权重,广播并声明权重最高的节点为树上的一个节点,负责集群内监控数据的融合处理[18-20]。选定的冗余节点标识自己的级别,即级别为0。
Sink节点将自己的级别标记为1,并发送一条消息开始建立冗余节点树。消息格式为(ID,LEVEL)。此时,ID是Sink节点的ID,级别为1。在接收到该消息后,位于其通信范围内的冗余节点将Sink节点标记为其自己的父节点,并且其自身的级别是父节点LEVEL+1,它将成为次要节点。
辅助冗余节点广播消息(ID、FID、LEVEL),其中ID是辅助冗余节点本身的ID,FID是父节点的ID,LEVEL是2。接收此消息的冗余节点将检查其级别值。如果为0,则将次节点标记为自己的父节点,并将自己的级别修改为3。如果不是0,则表示它已经在冗余节点树上,并且节点不执行任何操作[21-22]。
根据这一级别的广播,直到网络不存在冗余节点(该级别为0),冗余树才完成。
根据上述方式检测无线传感器异步数据中的冗余数据。根据经验,当无线传感器网络中存在大量冗余节点时,如果不采用有效的处理机制,网络能量将主要消耗在数据的无线通信过程中,冗余数据的无线通信将极大地消耗网络能量。同时,集群网络中簇头节点的负担增加,网络寿命缩短[23-24]。在建立冗余节点的融合树机制后,由于冗余节点参与了簇头的任务,冗余节点和公共成员节点的能量发生了相应的变化[25]。冗余节点能量被移除,即冗余数据被消除。则冗余数据的消除公式可以表示为
| $ {E_{{\rm{rn}}}} = {E_{{\rm{ch}}}} - {E_{{\rm{men}}}}, $ | (1) |
其中:Ern表示冗余数据处理后的数据,Emen表示无线传感器的冗余能量数据,Ech表示无线传感器簇头节点的能量。
1.2 无线传感器的异步数据定位为了提高数据融合的精度,提高数据融合的利用率,有必要对待融合的无线传感器的异步数据进行跟踪定位。
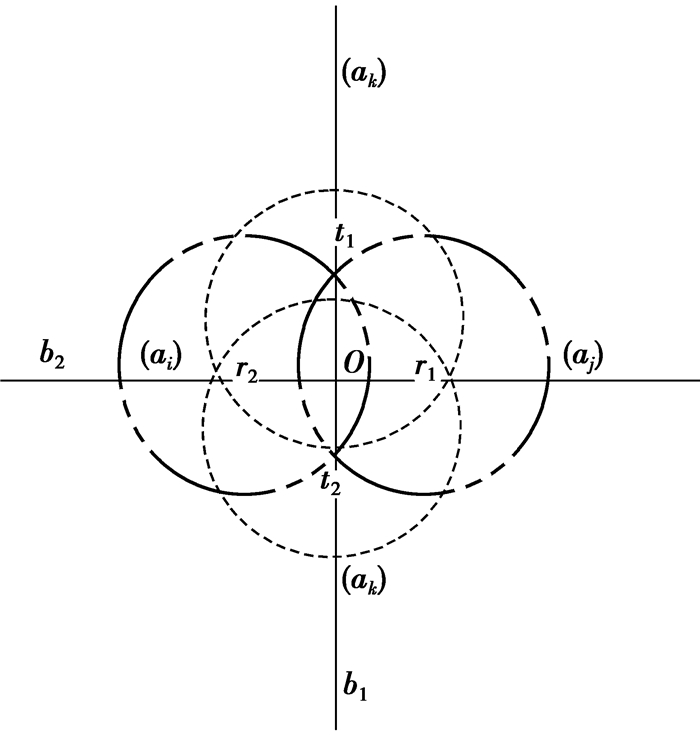
为了有效解决无线传感器的异步数据定位问题,假设每个传感器的探测范围半径相等,在计算目标区域时不必使用所有传感器信息,通过四圆定位法可以有效地确定目标可能出现的区域,如图 3所示。
|
图 3 定位图 Fig. 3 Positioning diagram |
假设Z表示包含目标的最小区域,D表示检测到所有目标的节点集,ai、aj和ak分别是以Ni、Nj和Nk为圆心的半径相等的圆。然后目标定位算法如下:Ni、Nj∈D,将t1和t2定义为满足式(2)的圆形区域内边界ai和aj的交点,通过t1和t2的直线定义为b1。
| $ \{ {t_1}, {t_2}\} = ({a_i}) \cap ({a_j}), $ | (2) |
在Nk∈D-{Ni,Nj}的所有节点中,在b1线的[t1,t2]区域寻找所有的圆形检测区域ak。假设只有1个节点的圆形检测区域as通过b1线上的区域[t1,t2],则
| $ Z = ({a_s}) \cap (({a_i}) \cap ({a_j})) 。$ | (3) |
根据式(3),算法结束。
假设有2个圆区域am和an通过直线b1上的区域[t1,t2],则计算这2个圆区域边界的交点,并将通过2点{r1,r2}的直线定义为b2。
| $ \{ {r_1}, {r_2}\} = ({a_m}) \cap ({a_n}) 。$ | (4) |
在Nk∈D-{Ni,Nj,Nm,Nn}的所有节点中,在b2上的{r1,r2}区域中寻找圆形检测区域。假设2个圆形区域通过b2上的{r1,r2}区域,则计算Z1=((am)∩(an))∩Z,算法结束;假设只有一个圆ar通过b2上的{r1,r2}区域,则Z=(ar)∩((ai)∩(aj)),算法结束。
上述算法的主要目的是计算出包含目标的最小区域。首先,任意选取2个检测目标信息的节点计算2个圆形检测区域边界的交集,然后迭代求出与[t1,t2]相交的圆形检测区域。经过以上步骤,可以找到满足条件的节点,并计算出通过2点{r1,r2}的直线b2。然后,使用相同的方法来计算穿过直线b2上的区域{r1,r2}的圆形检测区域。最后得到目标区域为ai、aj和ak的交叉区域,如图 3所示。O代表目标位置。通过上述异步数据目标定位,可以有效提高数据融合精度[26]。
1.3 基于UKF的无线传感器异步数据融合通过1.1节和1.2节的冗余数据去除和异步数据定位,采用UKF算法实现数据融合。
在无线传感器的异步数据融合中,传感器通常有一个或多个距离R、径向率R′、方位b′和俯仰角e的测量值[27-28]。由于在事后分析中提高数据融合的准确性,即数据分类的准确性和融合后的数据利用率非常重要,因此可以做一些必要的假设:
1) 不同传感器的原始测量值彼此独立。
2) 同一传感器的不同原始量测量值彼此独立。
基于上述2个一般可行性假设,可以对不同类型的传感器数据使用不同的测量进行有效的压缩融合。
假设H传感器的HR测量值为R,HR′测量值为R′,H′b测量值为b′,He测量值为e,Rjk表示第j个传感器在时间k时的距离测量值。R″jR′, k,k表示第j个传感器在时间k时相对于信道R的测量协方差,依此类推。根据这个假设,所有的数据都可以被统一的分类和合并,形成一种简单的分类数据压缩方法。压缩信道测量可以表示为
| $ {R_k} = \left[ {\sum\nolimits_{{j} = {1'}}^{{H_R}} {{{({R''}_{R,k}^j)}^{ - 1}}} } \right]\sum\nolimits_{j = 1}^{{H_R}} {{{({R''}_{R,k}^j)}^{ - 1}}R_k^j} , $ | (5) |
| $ {R_k}^\prime = \left[ {\sum_{{j} = {1'}}^{{{H'}_R}} {{{({R''}_{{R'}, k}^j)}^{ - 1}}} } \right]\sum_{j = 1}^{{{H'}_R}} {{{({R''}_{{R'}, k}^j)}^{ - 1}}{R'}_k^j} , $ | (6) |
| $ {b_k}^\prime = \left[ {\sum\nolimits_{j = {1'}}^{{{H'}_b}} {{{({R''}_{b', k}^j)}^{ - 1}}} } \right]\sum\nolimits_{j = 1}^{{{H'}_b}} {{{({R''}_{{b'}, k}^j)}^{ - 1}}{b'}_k^j} , $ | (7) |
| $ {e_k} = \left[ {\sum\nolimits_{j = {1'}}^{{H_e}} {{{({R''}_{R, k}^j)}^{ - 1}}} } \right]\sum\nolimits_{j = 1}^{{H_e}} {{{({R''}_{R, k}^j)}^{ - 1}}e_k^j} , $ | (8) |
方程(5)~(8)的计算结果经过无迹卡尔曼滤波,即用UKF实现数据融合。公式(5)到(8)的过滤器可以表示为
| $ {R''}_{R, k}^j = {R_k}K_k^{\rm{T}}, $ | (9) |
| $ {R''}_{{R'}, k}^j = {{R'}_k}K_k^{\rm{T}}, $ | (10) |
| $ {R''}_{{b'}, k}^j = {{b'}_k}K_k^{\rm{T}}, $ | (11) |
| $ {R''}_{e, k}^j = {e_k}K_k^{\rm{T}}, $ | (12) |
其中:Kk表示卡尔曼滤波的增益矩阵;T表示矩阵转置。信道测量通过式(9)~(10)进行融合,融合结果如式(13)所示
| $ {Z_k} = [{{R''}_{R, k}} + {{R''}_{R', k}} + {{R''}_{b', k}} + {{R''}_{e, k}}] \cdot [{a_i} \odot {a_j} \odot {a_k}], $ | (13) |
其中:Zk表示基于UKF的无线传感器异步数据融合的结果,⊙表示十字符号。
2 实验设计及算法性能分析通过利用matlab进行测试和仿真,验证所提出的无线传感器异步数据融合优化算法的有效性,并对算法的性能进行了比较和分析。仿真参数见表 1。
| 表 1 仿真参数 Table 1 Simulation parameters |
实验指标为:
1) 融合能耗;2)融合效率;3)融合精度。
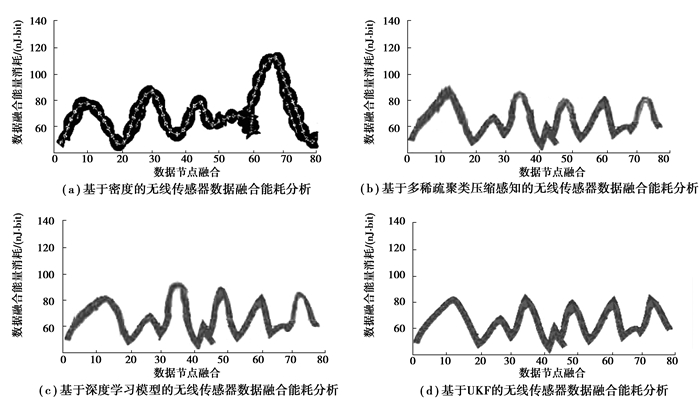
|
图 4 不同数据融合方法的能量消耗比较 Fig. 4 Comparison of energy consumption of different data fusion methods |
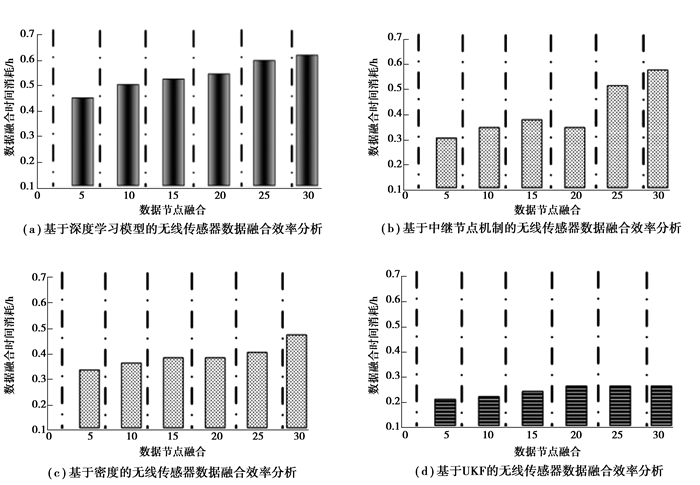
|
图 5 不同数据融合方法的融合效率比较 Fig. 5 Comparison of fusion efficiency of different data fusion methods |
从图 4和图 5的分析可以看出,基于UKF的无线传感器异步数据融合算法具有较高的融合效率,且融合能耗较低,说明该算法更具可行性。
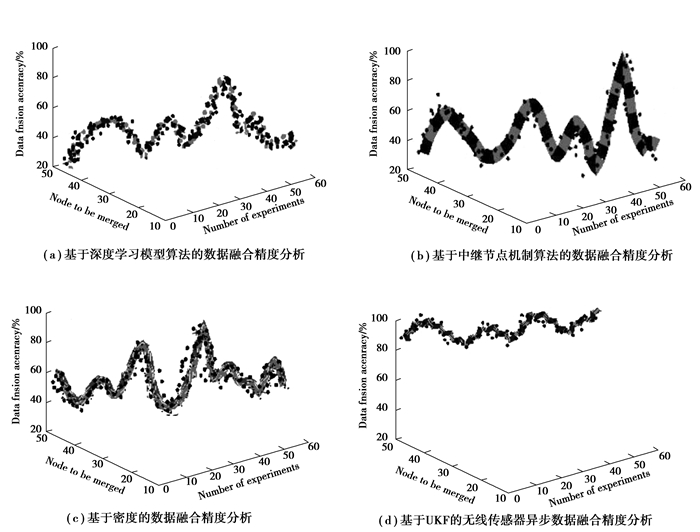
该算法在识别网络冗余节点的基础上,构造数据冗余树,去除冗余节点能量,有效地减少了数据融合时间和融合能耗。根据图 6的分析,与现有的无线传感器网络数据融合方法和算法相比,基于UKF的无线传感器异步数据融合算法具有更小的数据融合误差,即精度更高。在不同实验时间下,该算法融合的利用率较高。整个融合的准确率在90%以上。产生上述结果的主要原因是:通过异步数据定位,初步提高了数据融合精度和融合结果的利用率,并利用共同的可行假设对不同类型的传感器数据进行有效压缩,进一步提高了数据融合精度。
|
图 6 不同数据融合方法融合精度的比较 Fig. 6 Comparison of fusion accuracy of different data fusion methods |
根据UKF的无线传感器异步数据融合算法的数据定位精度研究,定位节点数量会影响定位精度,即使定位节点数一定,不同实验次数和定位干扰因素数也会影响定位精度。按照定位节点数一定,实验次数不同;定位节点数一定,定位干扰因素数不同;定位节点数为约束因子等3种情况,对数据定位精度进行观测,验证了该算法的数据融合效果。结果如图 7所示。

|
图 7 基于UKF的无线传感器异步数据融合算法在不同因素下的定位精度 Fig. 7 Data positioning accuracy of asynchronous data fusion algorithm based on UKF for wireless sensor under different factors |
从图 7可以看出,该算法具有较高的定位精度。在算法操作中,通过四圆定位法确定可能出现待定位目标的区域。其中,任意选择2个检测目标信息的节点,计算2个圆形检测区域边界的交集,然后用迭代法连续逼近待定位目标。根据这种随机性,该算法在不同影响因素下具有很强的定位精度。
4 结语提出了一种基于无迹卡尔曼滤波(UKF)的无线传感器异步数据融合算法,首先利用RNAT机制识别无线传感器网络中的冗余节点,然后采用四圆定位法进行异步数据跟踪定位,最后引入无迹卡尔曼滤波算法并结合异步数据定位结果实现异步数据融合。实验结果表明,提出的算法能耗低,且具有较高的数据融合效率和融合精度。
| [1] |
Ahmad Y, Ali U, Bilal M, et al. Some new standard graphs labeled by 3–total edge product cordial labeling[J]. Applied Mathematics and Nonlinear Sciences, 2017, 2(1): 61-72. DOI:10.21042/AMNS.2017.1.00005 |
| [2] |
De Paola A, Ferraro P, Gaglio S, et al. An adaptive Bayesian system for context-aware data fusion in smart environments[J]. IEEE Transactions on Mobile Computing, 2017, 16(6): 1502-1515. DOI:10.1109/TMC.2016.2599158 |
| [3] |
Rundel C W, Schliep E M, Gelfand A E, et al. A data fusion approach for spatial analysis of speciated PM2.5 across time[J]. Environmetrics, 2015, 26(8): 515-525. DOI:10.1002/env.2369 |
| [4] |
Castaldi F, Castrignanò A, Casa R. A data fusion and spatial data analysis approach for the estimation of wheat grain nitrogen uptake from satellite data[J]. International Journal of Remote Sensing, 2016, 37(18): 4317-4336. DOI:10.1080/01431161.2016.1212423 |
| [5] |
Gao W, Farahani M R, Aslam A, et al. Distance learning techniques for ontology similarity measuring and ontology mapping[J]. Cluster Computing, 2017, 20(2): 959-968. DOI:10.1007/s10586-017-0887-3 |
| [6] |
Qin Y, Luo Y Y, Zhao Y Q, et al. Research on relationship between tourism income and economic growth based on meta-analysis[J]. Applied Mathematics and Nonlinear Sciences, 2018, 3(1): 105-114. DOI:10.21042/AMNS.2018.1.00008 |
| [7] |
Yu D M, liu H N, Bresser C. Peak load management based on hybrid power generation and demand response[J]. Energy, 2018, 163: 969-985. DOI:10.1016/j.energy.2018.08.177 |
| [8] |
Novelli A, Tarantino E, Fratino U, et al. A data fusion algorithm based on the Kalman filter to estimate leaf area index evolution in durum wheat by using field measurements and MODIS surface reflectance data[J]. Remote Sensing Letters, 2016, 7(5): 476-484. DOI:10.1080/2150704X.2016.1154219 |
| [9] |
Zhang J F, Deng Y. A method to determine basic probability assignment in the open world and its application in data fusion and classification[J]. Applied Intelligence, 2017, 46(4): 934-951. DOI:10.1007/s10489-016-0877-9 |
| [10] |
许慧雅, 杨杨. 基于流量密度的无线传感器数据融合方案[J]. 控制工程, 2018, 25(1): 165-169. Xu H Y, Yang Y. Scheme of data aggregation based on data flow density for wireless sensor networks[J]. Control Engineering of China, 2018, 25(1): 165-169. (in Chinese) |
| [11] |
朱路, 刘媛媛, 慈白山, 等. 多稀疏基分簇压缩感知的WSN数据融合方法[J]. 传感技术学报, 2016, 29(3): 417-422. Zhu L, Liu Y Y, Ci B S, et al. The method of data aggregation for wireless sensor network based on cluster compressed sensing of multi-sparsity basis[J]. Chinese Journal of Sensors and Actuators, 2016, 29(3): 417-422. (in Chinese) DOI:10.3969/j.issn.1004-1699.2016.03.019 |
| [12] |
Di Nucci C, Russo Spena A. On the steady two-dimensional open channel flow[J]. Journal of Interdisciplinary Mathematics, 2018, 21(3): 579-594. DOI:10.1080/09720502.2015.1086136 |
| [13] |
Gao W, Zhu L L, Guo Y, et al. Ontology learning algorithm for similarity measuring and ontology mapping using linear programming[J]. Journal of Intelligent & Fuzzy Systems, 2017, 33(5): 3153-3163. |
| [14] |
Styugin M A, Kytmanov A A, Yamskikh T N. Formalization of the problem of protection against reconnaissance in conflict systems[J]. Journal of Discrete Mathematical Sciences and Cryptography, 2018, 21(3): 679-694. DOI:10.1080/09720529.2016.1226619 |
| [15] |
Yang Y S, Zhong M S, Yao H Q, et al. Internet of Things for smart Ports: Technologies and challenges[J]. IEEE Instrumentation & Measurement Magazine, 2018, 21(1): 34-43. |
| [16] |
马永军, 薛永浩, 刘洋, 等. 一种基于深度学习模型的数据融合处理算法[J]. 天津科技大学学报, 2017, 32(4): 71-74, 78. Ma Y J, Xue Y H, Liu Y, et al. Data aggregation algorithm based on the model of deep learning[J]. Journal of Tianjin University of Science & Technology, 2017, 32(4): 71-74, 78. (in Chinese) |
| [17] |
唐菁敏, 王超. 基于中继节点机制的分簇数据融合算法[J]. 云南大学学报(自然科学版), 2016, 38(5): 703-707. Tang J M, Wang C. Clustering data fusion algorithm based on relay node mechanism[J]. Journal of Yunnan University (Natural Sciences Edition), 2016, 38(5): 703-707. (in Chinese) |
| [18] |
Peng W X, Liu Z L, Motahari-Nezhad M, et al. A detailed study of oxy-fuel combustion of biomass in a circulating fluidized bed (CFB) combustor: Evaluation of catalytic performance of metal nanoparticles (Al, Ni) for combustion efficiency improvement[J]. Energy, 2016, 109: 1139-1147. DOI:10.1016/j.energy.2016.04.130 |
| [19] |
沙立成, 张岩, 张璇, 等. 电网多维异构数据融合三维可视化方法[J]. 自动化与仪器仪表, 2017(7): 201-203. Sha L C, Zhang Y, Zhang X, et al. Three dimensional visualization method for multi dimensional data fusion of power grid[J]. Automation & Instrumentation, 2017(7): 201-203. (in Chinese) |
| [20] |
安达, 梁智昊, 许守任. 基于大数据的智慧城市安全建设研究[J]. 中国电子科学研究院学报, 2016, 11(3): 229-232. An D, Liang Z H, Xu S R. Research on the construction of smart City safety based on big data[J]. Journal of China Academy of Electronics and Information Technology, 2016, 11(3): 229-232. (in Chinese) DOI:10.3969/j.issn.1673-5692.2016.03.003 |
| [21] |
Mohammadi-Nejad A R, Hossein-Zadeh G A, Soltanian-Zadeh H. Structured and sparse canonical correlation analysis as a brain-wide multi-modal data fusion approach[J]. IEEE Transactions on Medical Imaging, 2017, 36(7): 1438-1448. DOI:10.1109/TMI.2017.2681966 |
| [22] |
Gengler S, Bogaert P. Bayesian data fusion applied to soil drainage classes spatial mapping[J]. Mathematical Geosciences, 2016, 48(1): 79-88. DOI:10.1007/s11004-015-9585-y |
| [23] |
Tamboli P K, Duttagupta S P, Roy K. Particle filter-based recursive data fusion with sensor indexing for large core neutron flux estimation[J]. IEEE Transactions on Nuclear Science, 2017, 64(6): 1518-1525. |
| [24] |
Lee J. Optimal power allocating for correlated data fusion in decentralized WSNs using algorithms based on swarm intelligence[J]. Wireless Networks, 2017, 23(5): 1655-1667. DOI:10.1007/s11276-017-1454-9 |
| [25] |
Ferrin G, Snidaro L, Foresti G L. Data fusion and abductive inference for metaphor resolution: a bridging discussion[J]. The Knowledge Engineering Review, 2016, 31(3): 261-277. DOI:10.1017/S0269888916000060 |
| [26] |
Xing Z R, Xia Y Q. Comparison of centralised scaled unscented Kalman filter and extended Kalman filter for multisensor data fusion architectures[J]. IET Signal Processing, 2016, 10(4): 359-365. DOI:10.1049/iet-spr.2015.0205 |
| [27] |
Koupaee M, Kangavari M R, Amiri M J. Scalable structure-free data fusion on wireless sensor networks[J]. The Journal of Supercomputing, 2017, 73(12): 5105-5124. DOI:10.1007/s11227-017-2072-0 |
| [28] |
Cabral Farias R, Cohen J E, Comon P. Exploring multimodal data fusion through joint decompositions with flexible couplings[J]. IEEE Transactions on Signal Processing, 2016, 64(18): 4830-4844. DOI:10.1109/TSP.2016.2576425 |
 2021, Vol. 44
2021, Vol. 44

