轮式移动机器人是一种通过驱动轮子转动来实现运动功能的非完整约束结构,具有结构简单、能耗低和运动灵活等优点[1]。轮式移动机器人按轮子数量可分为独轮、两轮、三轮、四轮和多轮移动机器人。在实际应用中,会根据需要采用不同的轮式移动机器人。独轮和两轮机器人占地面积小且运动最为灵活,但竖直方向部分容易翻倒,是需要自平衡控制的倒立摆结构[2]。三轮移动机器人虽然灵活性不如独轮和两轮,但结构稳定不容易翻倒,且灵活性比四轮移动机器人要强很多。因此兼具稳定性和灵活性优点的三轮移动机器人在实际生活工作中应用非常广泛。
目前关于三轮移动机器人的控制研究大都侧重于其运动学方程[3-6],通过将其运动学方程转化为链式标准型,设计速度控制器跟踪给定的目标速度[7-9]。但在实际中一般是通过驱动力或力矩来实现控制目的,所以设计力或力矩控制器更符合实际。文[10]针对高速运动情况下,对轮式移动机器人进行了运动学、动力学模型重建,并利用反演控制方法设计了抗侧滑运动学反演控制器,同时利用逆动力学控制方法设计了抗扰动逆动力学控制器,完成了机器人对预定轨迹的跟踪。一般情况下,实际运动任务是控制三轮移动机器人精确沿给定目标轨迹曲线运动,而动力学方程只是单纯描述其运动速度和驱动力或力矩之间的关系。因此,需要将给定的目标轨迹曲线转化为速度目标形式,这样就可以将原来的运动控制问题转化为基于动力学方程的一般跟踪控制问题,从而使得问题变得简单且容易实现。文[11]利用平面曲线基本理论,将两轮式倒立摆的目标轨迹曲线转化为速度目标形式,结合其动力学方程为两轮式倒立摆设计了力矩控制器,精确实现往返运动控制。
随着科学技术的发展,轮式移动机器人的精确轨迹跟踪变得越来越重要,目前关于精确轨迹跟踪控制的研究主要侧重于先进控制器的设计,文[12]通过间接自适应模糊滑模控制方法,构造基于旋转子系统和纵向子系统的复合控制,实现速度跟踪和倾角稳定。文[13]设计了基于反步法的自适应控制,实现了轮式倒立摆的输出跟踪稳定。文[14]为解决平台与安装机器人之间的扰动、非线性和非完整约束之间的动力学耦合问题,提出了一种基于反步法的自适应滑模控制器用于移动机械臂的轨迹跟踪。从这些文献的仿真结果来看,无论控制设计方法多么先进,实际轨迹总是与目标轨迹曲线有一定的偏差,特别是在刚开始的一段时间内。主要原因是实际运动速度与目标速度之间的初始速度误差比较大,导致整个运动过程中的累积位置误差越来越大。因此,必须根据运动任务设计合适的速度跟踪目标,尽量减少初始速度误差。通过分析其侧向运动速度为零这一非完整约束,利用微分几何理论得到目标轨迹曲线与速度目标之间的一一对应关系。引入一个微分同胚的变量变换,将前向速度目标转化为和实际初始速度更接近的形式,通过减少初始速度误差来尽量减少三轮移动机器人运动时的累积位置误差。最后通过仿真说明所提轨迹跟踪目标设计和鲁棒控制设计方法的有效性。
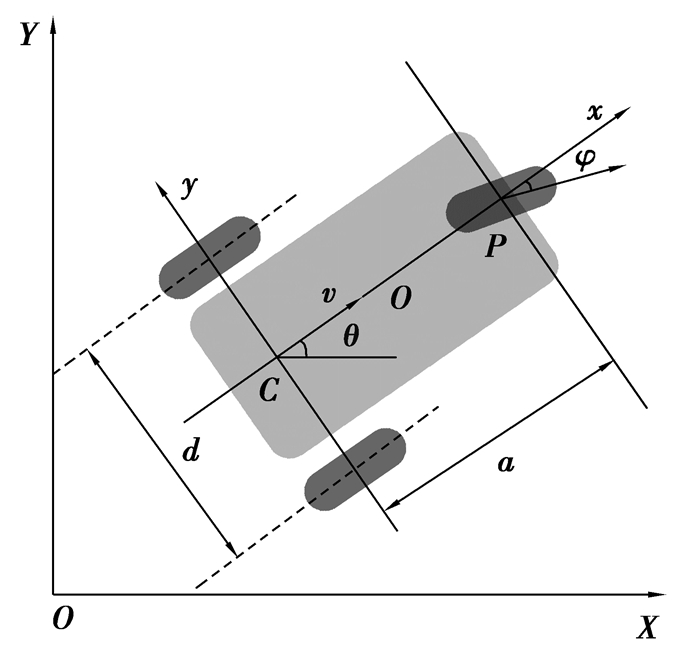
1 三轮移动机器人的运动学方程如图 1所示,三轮移动机器人的后2轮上各装有一个驱动马达,同时前轮通过控制方向盘来实现转向。当后2轮中心点C(x, y)随着三轮移动机器人在平面上做连续光滑运动时,点C的运动轨迹是一条光滑曲线,此时点C在与切向垂直方向的侧向速度为0,如若不然,其轨迹曲线会出现不光滑的尖点。因此三轮式移动机器人在平面上做光滑曲线运动时一般受到如下非完整约束
|
图 1 三轮移动机器人结构简图 Fig. 1 Schematic diagram of the three-wheeled mobile robot |
| $ -\dot{x} \sin \theta+\dot{y} \cos \theta=0。$ | (1) |
此时将点C的前向速度
| $ \left\{\begin{array}{l} -\dot{x} \sin \theta+\dot{y} \cos \theta=0 ,\\ v=\dot{x} \cos \theta+\dot{y} \sin \theta。\end{array}\right. $ | (2) |
根据方程(2)中的第二式可以知道,轨迹曲线的切向量长度就是点C沿该曲线运动的前向速度。因此,可以将方程(2)改写为
| $ \left\{\begin{array}{l} \dot{x}=v \cos \theta ,\\ \dot{y}=v \sin \theta。\end{array}\right. $ | (3) |
此外,当三轮移动机器人的后2轮不侧滑不空转时,需要满足下面2个完整约束
| $ \left\{\begin{array}{l} v=\frac{r}{2}\left(\dot{\theta}_{r}+\dot{\theta}_{l}\right), \\ \theta=\frac{r}{d}\left(\dot{\theta}_{r}-\dot{\theta}_{l}\right), \end{array}\right. $ | (4) |
其中:θ是三轮移动机器人的偏航角;θl和θr分别是左右两轮的转角;r是轮子的半径。
通过方程(4)反解出
| $ \left\{\begin{array}{l} \dot{\theta}_{r}=\frac{1}{r} v+\frac{d}{2 r} \dot{\theta} ,\\ \dot{\theta}_{l}=\frac{1}{r} v-\frac{d}{2 r} \dot{\theta}。\end{array}\right. $ | (5) |
然后将方程(2)的第二式代入方程(5)并结合方程(1),整理得到三轮移动机器人后两轮所受的运动约束方程
| $ \left\{\begin{array}{l} -\dot{x} \sin \theta+\dot{y} \cos \theta=0 ,\\ \dot{x} \cos \theta+\dot{y} \sin \theta+\frac{d}{2} \dot{\theta}-r \dot{\theta}_{r}=0 ,\\ \dot{x} \cos \theta+\dot{y} \sin \theta-\frac{d}{2} \dot{\theta}-r \dot{\theta}_{l}=0。\end{array}\right. $ | (6) |
接下来,分析三轮移动机器人前轮所受到的约束。
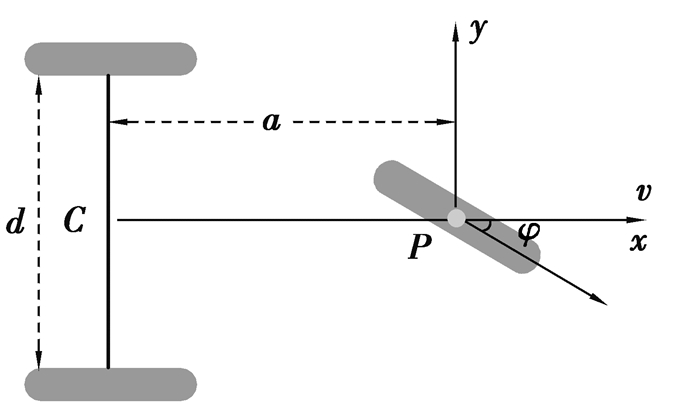
如图 2所示,P(xp, yp)点具有双重身份。一方面当P点作为前轮中心,在不发生侧滑运动时,其侧向速度为0,即满足方程
|
图 2 P点速度示意图 Fig. 2 Schematic diagram of the velocity of point P |
| $ -\dot{x}_{p} \sin \varphi+\dot{y}_{p} \cos \varphi=0。$ | (7) |
另一方面当P点作为中间体的前端点时,该点的速度满足如下关系
| $ \tan \varphi=\frac{\dot{\theta} a}{v} 。$ | (8) |
由方程(7)和(8)得到
| $ \dot{\theta}=\frac{v \tan \varphi}{a} 。$ | (9) |
方程(9)是一个重要的非完整约束,它描述了前轮转向和后轮运动速度之间的关系。将方程(3)的第一式代入方程(9),则方程(9)可改写为
| $ -\dot{x} \tan \varphi+a \dot{\theta} \cos \theta=0 。$ | (10) |
这里φ是前轮操舵转向角,将其看作一个控制变量,因为它是通过人为控制方向盘转向得到的。
结合方程(3)、(5)和(9),将三轮移动机器人的所有运动约束总结为
| $ \left\{\begin{array}{l} \dot{x}=v \cos \theta, \\ \dot{y}=v \sin \theta, \\ \dot{\theta}_{r}=\frac{1}{r} v+\frac{d}{2 r} \dot{\theta}, \\ \dot{\theta}_{l}=\frac{1}{r} v-\frac{d}{2 r} \dot{\theta}, \\ \dot{\theta}=\frac{v \tan \varphi}{a} 。\end{array}\right. $ | (11) |
令三轮移动机器人的广义坐标为q=(x, y, θ, θr, θl)T,方程(11)可以表示为以下矩阵形式
| $ \dot{\boldsymbol{q}}=\boldsymbol{S}(\boldsymbol{q}) \boldsymbol{V}, $ | (12) |
其中
| $ \boldsymbol{V}=(v, \dot{\theta})^{\mathrm{T}}, \boldsymbol{S}(\boldsymbol{q})=\left[\begin{array}{cc} \cos \theta & 0 \\ \sin \theta & 0 \\ \frac{\tan \varphi}{a} & 0 \\ \frac{1}{r} & \frac{d}{2 r} \\ \frac{1}{r} & -\frac{d}{2 r} \end{array}\right], $ |
利用非完整力学系统的Euler-Lagrange方程,三轮移动机器人的动力学方程为
| $ \frac{\mathrm{d}}{\mathrm{d} t}\left(\frac{\partial L}{\partial \dot{\boldsymbol{q}}}\right)-\frac{\partial L}{\partial \boldsymbol{q}}=\boldsymbol{E}(\boldsymbol{q}) \boldsymbol{T}+\boldsymbol{F}^{\mathrm{T}}(\boldsymbol{q}) \boldsymbol{\lambda}, $ | (13) |
其中:
方程(13)中的F(q)选取为
| $ \boldsymbol{F}(\boldsymbol{q})=\left[\begin{array}{ccccc} \sin \theta & -\cos \theta & 0 & 0 & 0 \\ \cos \theta & \sin \theta & 0 & -\frac{r}{2} & -\frac{r}{2} \\ -\tan \varphi & 0 & a \cos \theta & 0 & 0 \end{array}\right] 。$ |
这样选取得到的F(q)使得矩阵方程
| $ \boldsymbol{F}(\boldsymbol{q}) \boldsymbol{S}=0。$ | (14) |
接下来需要计算三轮移动机器人的动能。根据图 1所示,得到如下位置关系
| $ \left\{\begin{array}{l} x_{o}=x+\frac{a}{2} \cos \theta \\ y_{o}=y+\frac{a}{2} \sin \theta \end{array},\left\{\begin{array}{l} x_{p}=x+a \cos \theta \\ y_{p}=y+a \sin \theta \end{array}\right.\right., $ |
| $ \left\{\begin{array}{l} x_{w l}=x+\frac{d}{2} \sin \theta \\ y_{w l}=y-\frac{d}{2} \cos \theta \end{array},\left\{\begin{array}{l} x_{w r}=x-\frac{d}{2} \sin \theta \\ y_{w r}=y+\frac{d}{2} \cos \theta \end{array},\right.\right. $ |
其中,(xwl, ywl), (xwr, ywr)分别是左右轮的中心坐标。此时三轮移动机器人上的各中心点速度分别表示为
| $ v_{w l}^{2}=\dot{x}^{2}+\dot{y}^{2}+\frac{d^{2}}{4} \dot{\theta}^{2}+\mathrm{d} \dot{\theta}(\dot{x} \cos \theta+\dot{y} \sin \theta) , $ |
| $ v_{u r}^{2}=\dot{x}^{2}+\dot{y}^{2}+\frac{d^{2}}{4} \dot{\theta}^{2}-\mathrm{d} \dot{\theta}(\dot{x} \cos \theta+\dot{y} \sin \theta) , $ |
| $ v_{o}^{2}=\dot{x}^{2}+\dot{y}^{2}+\frac{a^{2}}{4} \dot{\theta}^{2}-a \dot{\theta}(\dot{x} \sin \theta+\dot{y} \cos \theta) , $ |
| $ v_{p}^{2}=\dot{x}^{2}+\dot{y}^{2}+a^{2} \dot{\theta}^{2}-a \dot{\theta}(\dot{x} \sin \theta+\dot{y} \cos \theta), $ |
因此,三轮移动机器人的后2轮的前向动能和转动动能之和表示为
| $ T_{w}=M_{w}\left(\dot{x}^{2}+\dot{y}^{2}+\frac{d^{2}}{4} \dot{\theta}^{2}\right)+\frac{1}{2} I_{w}\left(\dot{\theta}_{r}^{2}+\dot{\theta}_{l}^{2}\right)+I_{w d} \dot{\theta}^{2}。$ |
同样地,可以将三轮移动机器人的前轮和中间体的前向动能和转动动能之和分别表示为
| $ T_{f}=\frac{1}{2}\left(M_{w}+\frac{I_{w}}{r^{2}}\right)\left[\dot{x}^{2}+\dot{y}^{2}+a^{2} \dot{\theta}^{2}-2 a \dot{\theta}(\dot{x} \sin \theta-\dot{y} \cos \theta)\right] , $ |
| $ T_{B}=\frac{1}{2} M_{B}\left[\dot{x}^{2}+\dot{y}^{2}+\frac{1}{4} a^{2} \dot{\theta}^{2}-a \dot{\theta}(\dot{x} \sin \theta-\dot{y} \cos \theta)\right]+\frac{1}{2} I_{B} \dot{\theta}^{2}。$ |
其中:MB是中间体质量;Mw是轮子质量;Iwd是轮子绕z轴方向转动惯量;Iw是轮子绕轮轴方向转动惯量;IB是中间体绕z轴方向转动惯量。
将Lagrange函数L=Tw+TB+Tf代入方程(13),然后按状态变量的各阶导数整理得到
| $ \boldsymbol{A}(\boldsymbol{q}) \ddot{\boldsymbol{q}}+\boldsymbol{U}(\boldsymbol{q}, \dot{\boldsymbol{q}})=\boldsymbol{E}(\boldsymbol{q}) \boldsymbol{T}+\boldsymbol{F}^{\mathrm{T}}(\boldsymbol{q}) \boldsymbol{\lambda}, $ | (15) |
其中:
| $ \boldsymbol{A}(\boldsymbol{q})=\left[\begin{array}{ccccc} a_{11} & 0 & a_{13} & 0 & 0 \\ 0 & a_{22} & a_{23} & 0 & 0 \\ a_{31} & a_{32} & a_{33} & 0 & 0 \\ 0 & 0 & 0 & a_{44} & 0 \\ 0 & 0 & 0 & 0 & a_{55} \end{array}\right], \boldsymbol{U}(\boldsymbol{q}, \dot{\boldsymbol{q}})=\left[\begin{array}{ccccc} 0 & 0 & u_{13} & 0 & 0 \\ 0 & 0 & u_{23} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right], $ |
| $ a_{11}=a_{22}=3 M_{w}+M_{B}+\frac{I_{w}}{r^{2}}, a_{13}=a_{31}=-a\left(\frac{1}{2} M_{B}+M_{w}+\frac{I_{w}}{r^{2}}\right) \sin \theta, $ |
| $ a_{23}=a_{32}=a\left(\frac{1}{2} M_{B}+M_{w}+\frac{I_{w}}{r^{2}}\right) \cos \theta, a_{33}=a^{2} M_{w}+I_{B}+2 I_{w d}+\frac{a^{2}}{4} M_{B}+\frac{d^{2}}{2} M_{w}+\frac{I_{w}}{r^{2}} a^{2}, $ |
| $ a_{44}=a_{55}=M_{w} r^{2}+I_{w}, u_{11}=-\left(\frac{1}{2} M_{B}+M_{w}+\frac{I_{w}}{r^{2}}\right) a \dot{\theta} \cos \theta, u_{21}=-\left(\frac{1}{2} M_{B}+M_{w}+\frac{I_{w}}{r^{2}}\right) a \dot{\theta} \sin \theta。$ |
将方程(12)两边同时关于t求导,然后代入方程(15)得
| $ \boldsymbol{A}(\boldsymbol{q}) \dot{\boldsymbol{S}} \boldsymbol{V}+\boldsymbol{A}(\boldsymbol{q}) \boldsymbol{S} \dot{\boldsymbol{V}}+\boldsymbol{U}(q, \dot{q}) \boldsymbol{S} \boldsymbol{V}=\boldsymbol{E}(\boldsymbol{q}) \boldsymbol{T}+\boldsymbol{F}^{\mathrm{T}}(\boldsymbol{q}) \boldsymbol{\lambda}。$ | (16) |
在方程(16)的左右两边同时左乘ST(q),结合方程(14)消去等式中的Lagrange乘子得
| $ \boldsymbol{S}^{\mathrm{T}} \boldsymbol{A} \dot{\boldsymbol{S}} \boldsymbol{V}+\boldsymbol{S}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{S} \dot{\boldsymbol{V}}+\boldsymbol{S}^{\mathrm{T}} \boldsymbol{U}(q, \dot{q}) \boldsymbol{S} \boldsymbol{V}=\boldsymbol{S}^{\mathrm{T}} \boldsymbol{E}(\boldsymbol{q}) \boldsymbol{T}。$ |
整理上式,最终可以将三轮移动机器人动力学方程表示为如下状态方程形式
| $ \left\{\begin{array}{l} \dot{v}=\gamma_{1}-\gamma_{2} u_{2}, \\ \dot{\omega}=\ddot{\theta}=c u_{1}。\end{array}\right. $ | (17) |
其中
| $ \gamma_{1}=\frac{\beta_{1} \sin \varphi \dot{\varphi} \upsilon}{\beta_{2} \cos \varphi}, \gamma_{2}=\frac{4 r a^{2} \cos ^{2} \varphi}{\beta_{2}}, c=\frac{r}{d} I_{w}, u_{1}=T_{l}-T_{r}, u_{2}=T_{l}+T_{r} , $ |
| $ \beta_{1}=a^{2} r^{2} M_{B}+4 a^{2} r^{2} M_{w}+2 d^{2} r^{2} M_{w}+4 r^{2} I_{B}+4 a^{2} I_{w}+8 r^{2} I_{w d} , $ |
| $ \beta_{2}=\left(2 d^{2} r^{2} M_{w}+4 r^{2} I_{B}+8 I_{w d} r^{2}-3 a^{2} r^{2} M_{B}-8 a^{2} r^{2} M_{w}-8 a^{2} I_{w}\right) \cos \varphi-\beta_{1}。$ |
给定目标轨迹曲线
对给定的目标轨迹曲线
| $ \left\{\begin{array}{l} \dot{\tilde{x}}=\tilde{\upsilon} \cos \tilde{\theta} ,\\ \dot{\tilde{y}}=\tilde{\upsilon} \sin \tilde{\theta}, \end{array}\right. $ | (18) |
其中,
对方程(18)两边同时关于t求导得
| $ \left\{\begin{array}{l} \ddot{\widetilde{x}}=\frac{1}{\tilde{\upsilon}}(\dot{\tilde{x}} \ddot{x}+\dot{\tilde{y}} \ddot{\widetilde{y}}) \cos \tilde{\theta}-\tilde{\upsilon} \sin \tilde{\theta} \dot{\tilde{\theta}} ,\\ \ddot{\widetilde{y}}=\frac{1}{\tilde{\upsilon}}(\dot{\widetilde{x}} \ddot{\widetilde{x}}+\dot{\tilde{y}} \ddot{\widetilde{y}}) \sin \tilde{\theta}+\tilde{\upsilon} \cos \tilde{\theta} \dot{\tilde{\theta}}。\end{array}\right. $ | (19) |
将方程(18)和(19)交叉相乘并相减得
| $ \dot{\widetilde{x}} \ddot{\widetilde{y}}+\ddot{\widetilde{x}} \dot{\widetilde{y}}=\left(\dot{\widetilde{x}}{}^{2}+\dot{\widetilde{y}}{}^{2}\right) \dot{\widetilde{\theta}}。$ |
因此中心点C运动速度与运动轨迹曲线之间的关系式为
| $ \left\{\begin{array}{l} \tilde{\upsilon} =\sqrt{\dot{\tilde{x}}{}^{2}+\dot{\tilde{y}}{}^{2}}, \\ \widetilde{\omega}=\dot{\tilde{\theta}}=\frac{\dot{\widetilde{x}} \ddot{\widetilde{y}}-\ddot{\widetilde{x}} \dot{\tilde{y}}}{\dot{\widetilde{x}}^{2}+\dot{\tilde{y}}{}^{2}}=k(t) \tilde{\upsilon}=\frac{\dot{\tilde{x}} \ddot{\widetilde{y}}-\ddot{\widetilde{x}} \dot{\tilde{y}}}{\left(\dot{\tilde{x}}{}^{2}+\dot{\tilde{y}}{}^{2}\right)^{\frac{3}{2}}}\tilde{\upsilon}, \end{array}\right. $ | (20) |
其中
从方程(18)和(20)可以看出,中心点C运动的前向速度和偏航转速可以由相应的运动轨迹曲线确定;反之,其运动的轨迹曲线也可以由相应的前向速度和偏航转速所决定。因此,曲线
由于三轮移动机器人的动力学方程(17)是关于前向速度和偏航转速的,因此结合轨迹曲线
由于φ和u1之间有约束关系,本文将φ和u2看作控制变量。观察发现方程(17)是解耦的,可以先通过第二个方程将u1设计出来。然后结合方程(9)有
| $ \dot{\theta}=\frac{\nu \tan \varphi}{a}=\int_{0}^{t} c u_{1}(\eta) \mathrm{d} \eta。$ | (21) |
再利用方程(21)将控制器φ设计出来。然后将控制变量φ代入方程(17)的第一式,设计控制器u2实现最终的轨迹跟踪任务。
对目标轨迹曲线
| $ \left\{\begin{array}{l} \tilde{\nu}=\dot{\phi}(\eta) \sqrt{\dot{\widetilde{x}}^{2}+\dot{\widetilde{y}}^{2}} ,\\ \widetilde{\omega}=\dot{\tilde{\theta}}=k(\eta) \tilde{\nu}(\eta)。\end{array}\right. $ |
从上式可以看出,当参数变换后,前向速度目标也是随之而改变的。因此,上式中含有曲线相对曲率的第二式才是对轨迹曲线的本质刻画。
为了计算方便,假设原目标轨迹曲线
| $ \mathop {\lim }\limits_{\eta \to + \infty } \dot \phi (\eta ) = 0,\dot \phi (0) = 0。$ |
| $ \phi(\eta)=-\frac{(\beta \eta+1) \alpha e^{-\beta \eta}}{\beta^{2}}+r , $ |
其中,α>0, β>0,r>0,并且满足
| $ \left\{\begin{array}{l} \int_{0}^{+\infty} \dot{\phi}(\eta) \mathrm{d} \eta=l, \\ \dot{\phi}(0)=0。\end{array}\right. $ | (22) |
由方程(22)有r=l, α=lβ2。因此函数ϕ(η)可以设计为
| $ \phi(\eta)=-(\beta \eta+1) l e^{-\beta \eta}+l, $ |
其中l是目标轨迹曲线长度。
这样,在整个跟踪过程中,可以适当地调整前向速度目标的大小,使其更有利于减少速度误差,从而达到减少累积位置误差的目的。最终,对以弧长参数为变量的目标轨迹曲线
| $ \left\{\begin{array}{l} \tilde{\nu}=\dot{\phi}(t) ,\\ \widetilde{\omega}=\dot{\widetilde{\theta}}=k(\phi(t)) \tilde{\nu}, \end{array}\right. $ | (23) |
其中:s=ϕ(t)=-(βt+1)le-βt+l.
因此,对于一个目标轨迹曲线
由于方程(17)是解耦的,先考虑其偏航转速控制系统
| $ \dot{\omega}=c u_{1} . $ | (24) |
偏航转速控制系统(24)比较简单,容易设计反馈跟踪控制器。为了加强它的鲁棒性,采用积分滑模思想处理不确定性因素的影响[15]。
首先设计控制器的基础部分,令
| $ \dot{\tilde{e}}=c u_{1}-\dot{\tilde{\omega}}+d_{1}(t)=\widetilde{u}_{1}, $ |
其中d1(t)是偏航转速误差系统受到的不确定性因素。
将
| $ u_{10}=\frac{-k \tilde{e}+\dot{\tilde{\omega}}-d_{1}(t)}{c}, $ |
其中k是误差反馈控制增益参数。
再将轨迹跟踪目标设计成积分滑模面S1(ω(t))=0,且
| $ S_{1}(\omega(t))=G_{1}[\omega(t)-\omega(0)]-G_{1} \int_{0}^{t} \omega(\eta) \mathrm{d} \eta, $ |
其中G1>0是合适的常数。这样,切换控制部分设计为
| $ u_{11}=\left(-\mu\left(c G_{1}\right)^{-1}-\varepsilon\|\tilde{e}\|\right) \operatorname{sgn}\left(S_{1}(\omega(t))\right), $ |
其中: μ是滑模控制参数;ε是外部扰动最大振幅。因此,u1设计为
| $ u_{1}(t)=u_{10}(t)+u_{11}(t)。$ | (25) |
最后,结合方程(21)和(25),最终设计的操舵角控制器为
| $ \varphi=\arctan \left(\frac{a}{\upsilon } \int_{0}^{t} c u_{1}(\eta) \mathrm{d} \eta\right) 。$ | (26) |
接下来考虑前向速度控制系统
| $ \dot{\upsilon }=\gamma_{1}-\gamma_{2} u_{2}。$ | (27) |
对系统(27)利用反馈线性化思想处理,设
| $ u_{2}(t)=\frac{\gamma_{1}-h(t)}{\gamma_{2}}。$ | (28) |
得到一个简单的控制系统
| $ \dot{\upsilon }=h(t)。$ |
令X=[x1, x2]T=[s, υ]T,前向速度控制系统改写为
| $ \dot{\boldsymbol{X}}(t)=\boldsymbol{A} \boldsymbol{X}(t)+\boldsymbol{B} h(t), $ | (29) |
其中:
再将控制方程(29)转化成误差系统,令
| $ \tilde{s}=\int_{0}^{t} \upsilon(\tau) \mathrm{d} \tau, \widetilde{\boldsymbol{X}}=\left[\widetilde{x}_{1}, \widetilde{x}_{2}\right]^{\mathrm{T}}=[\widetilde{s}, \tilde{\upsilon}]^{\mathrm{T}}, $ |
| $ \boldsymbol{Y}(t)=\left[y_{1}, y_{2}\right]=\boldsymbol{X}(t)-\widetilde{\boldsymbol{X}}{(t)}, \boldsymbol{\eta}=\boldsymbol{A} \widetilde{\boldsymbol{X}}-\dot{\widetilde{\boldsymbol{X}}}。$ |
则前向速度误差系统为
| $ \dot{\boldsymbol{Y}}(t)=\boldsymbol{A} \boldsymbol{Y}(t)+\boldsymbol{B} h(t)+\boldsymbol{\eta}(t)+\boldsymbol{d}_{2}(t), $ |
其中d2(t)是前向速度误差系统受到的不确定性因素。
由于方程(23)中的前向速度目标
| $ J=\frac{1}{2} \int_{0}^{+\infty}\left[\boldsymbol{Y}^{\mathrm{T}}(t) \boldsymbol{QY}(t)+\boldsymbol{h}^{\mathrm{T}}(t) \boldsymbol{R} h(t)\right] \mathrm{d} t。$ |
为了使得前向速度误差尽量小,可以将前向速度误差的权重取得足够大[11]。利用线性二次型最优控制理论,h(t)设计为
| $ \boldsymbol{h}(t)=-\boldsymbol{R}^{-1} \boldsymbol{B}^{T}[\boldsymbol{P}(t) \boldsymbol{Y}(t)+\boldsymbol{b}(t)], $ |
其中:
| $ -\boldsymbol{P} \boldsymbol{A}-\boldsymbol{A}^{\mathrm{T}} \boldsymbol{P}+\boldsymbol{P} \boldsymbol{B} \boldsymbol{R}^{-1} \boldsymbol{B}^{\mathrm{T}} \boldsymbol{P}-\boldsymbol{Q}=0, $ |
| $ \dot{\boldsymbol{b}}=-\left[\boldsymbol{A}-\boldsymbol{B} \boldsymbol{R}^{-1} \boldsymbol{B}^{\mathrm{T}} \boldsymbol{P}\right]^{\mathrm{T}} \boldsymbol{b}-\boldsymbol{P} \boldsymbol{\eta}(t), \boldsymbol{b}(+\infty)=0。$ |
为了增强反馈控制的鲁棒性,同样采用积分滑模思想来处理不确定性因素。系统(29)的控制器基础部分设计为
| $ h_{20}(t)=-\boldsymbol{R}^{-1} \boldsymbol{B}^{\mathrm{T}}[\boldsymbol{P}(t) \boldsymbol{Y}(t)+\boldsymbol{b}(t)]。$ |
引入积分滑模函数
| $ S_{2}(\boldsymbol{X}(t))=\boldsymbol{G}_{2}[\boldsymbol{X}(t)-\boldsymbol{X}(0)]-\boldsymbol{G}_{2} \int_{0}^{t} \dot{\tilde{\boldsymbol{X}}}(\eta) \mathrm{d} \eta, $ |
其中,G2是适当的常矩阵。
积分滑模面设计为S2(X(t))=0,因此系统(29)的控制最终设计为
| $ h_{2}(t)=h_{20}(t)+h_{21}(t), $ | (30) |
其中:h21是切换的不连续控制,用来补偿系统不确定性因素和外部扰动的影响,
| $ h_{21}(t)=-\left(\mu+\varepsilon\|\boldsymbol{Y}\|_{1}\right)\left(\boldsymbol{G}_{2} \boldsymbol{B}\right)^{-1} \operatorname{sgn}\left(\boldsymbol{S}_{2}(\boldsymbol{X}(t))\right)。$ |
结合方程(28)和(30),前向速度控制器设计为
| $ u_{2}=\frac{\gamma_{1}-h(t)}{\gamma_{2}}=\frac{1}{\gamma_{2}}\left[\gamma_{1}-h_{20}(t)-h_{21}(t)\right]。$ | (31) |
最终,根据三轮移动机器人的动力学方程(17),可设计控制器(26)和(31)使得三轮移动机器人精确地沿着给定的目标轨迹曲线
考虑目标轨迹曲线是单位圆,假设初始时刻三轮移动机器人是静止的,且目标轨迹曲线为
| $ \tilde{r}=(\widetilde{x}(t), \widetilde{y}(t))=(\cos t, \sin t), t \in(0,2 {\rm{ \mathsf{ π}}})。$ |
由曲线基本理论,目标轨迹曲线的曲率为k(t)=1。
根据方程(20),轨迹曲线的速度目标形式表示为
| $ \left\{\begin{array}{l} \tilde{\upsilon }=1, \\ \widetilde{\omega}=1。\end{array}\right. $ | (32) |
再根据方程(23),改进的速度跟踪目标设计为
| $ \left\{\begin{array}{l} \tilde{\upsilon }=\dot{\phi}(t),\\ \widetilde{\omega}=\dot{\phi}(t)。\end{array}\right. $ | (33) |
假设三轮移动机器人的各部分参数选择如下
| $ M = 3{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{kg}},{M_w} = 2{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{kg}},a = 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{m}},r = 0.1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{m}},{I_w} = 0.01{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{kg}}{{\rm{m}}^2},{I_{wd}} = 0.005{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{kg}}{{\rm{m}}^2},I = 0.01{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{kg}}{{\rm{m}}^2}。$ |
| $ l = {\rm{ \mathsf{ π} }}/2,\beta = 0.5,k = 2,\mu = 0.01,\varepsilon = 2,{G_1} = 1.8,{\mathit{\boldsymbol{G}}_2} = {\mathop{\rm diag}\nolimits} (100,1)。$ |
若前向速度误差控制系统和偏航转速误差控制系统分别受到如下未知扰动影响
| $ {{d_1}(t) = 1.8\tilde e,{\mathit{\boldsymbol{d}}_2}(t) = {{\left( {5{y_1},9.2{y_2}} \right)}^{\rm{T}}}}。$ |
且将ϕ(t)设计为
| $ {\phi (t) = - {\rm{ \mathsf{ π} }}(t + 2){{\rm{e}}^{ - \frac{1}{2}t}} + 2{\rm{ \mathsf{ π} }}}。$ |
此时,关于控制器(26)和(31)中的所有量就都已知了,实验如图 3、4所示。
|
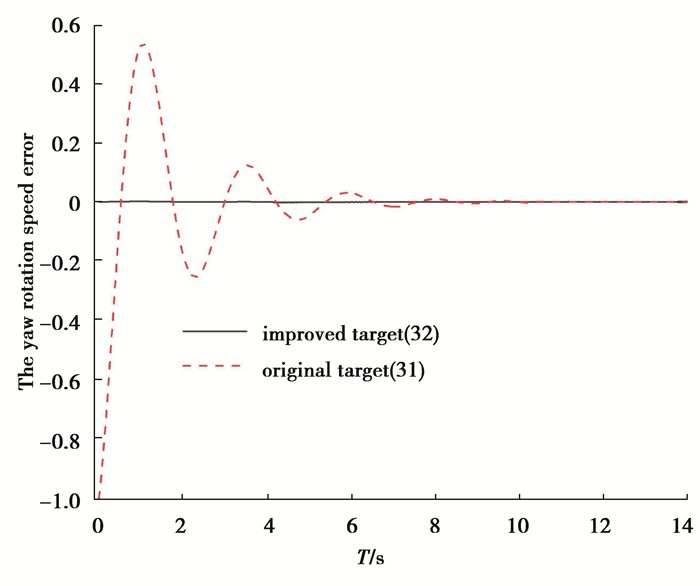
图 3 前向速度误差图 Fig. 3 Forward speed error of the three-wheeled robot |
|
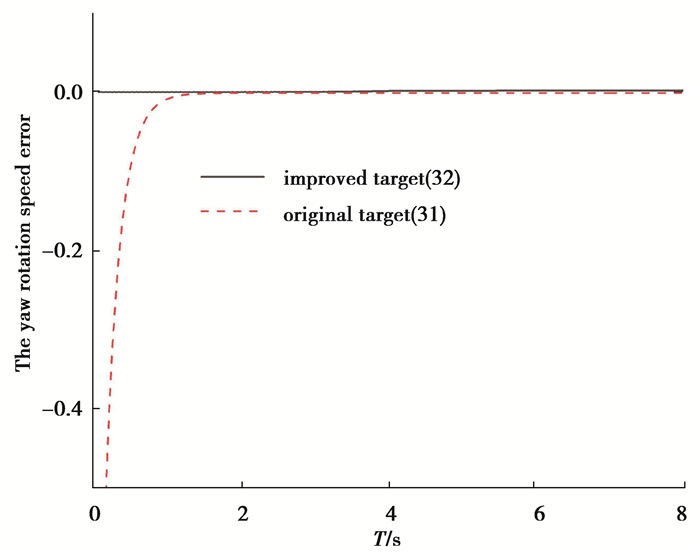
图 4 偏航转速误差图 Fig. 4 Yaw speed error of the three-wheeled robot |
从图 3和图 4可以看出,采用速度目标(32)会使得初始速度误差不为零,而改进后的速度跟踪目标(33) 从初始时刻开始速度误差为零。如若初始速度误差过大,自然会导致三轮移动机器人在整个运动过程中累积位置误差也很大,最终导致实际运动轨迹曲线严重偏离目标轨迹曲线。如图 5所示,由于笔者设计控制器时采用了积分滑模的思想,所设计的滑模控制器具有很强的鲁棒性。因此即使误差控制系统存在不确定性因素的影响,采用速度目标(33)和积分滑模控制器时,得到的实际运动轨迹几乎和目标轨迹重合,反之采用速度目标(32)时,即使同样采用积分滑模控制,得到的实际轨迹曲线也会严重偏离目标轨迹曲线,这主要是由于初始速度误差导致的累积位置误差太大所致。

|
图 5 三轮移动机器人在平面上的实际运动轨迹 Fig. 5 Actual motion trajectory of the three-wheeled robot |
通过分析三轮移动机器人的运动约束方程和运动规律,针对给定的目标轨迹曲线,给出了一种新的速度跟踪目标和控制器设计方法。该方法可以通过选择合适的光滑函数,为三轮移动机器人设计合适的前向速度和偏航转速目标,使得在控制过程中能够极大地减少误差控制系统的初始速度误差,从而达到减少累积位置误差的目的。仿真结果表明,采用文中所提出的速度跟踪目标和控制方法,可以使得三轮移动机器人能精确地沿着给定的目标轨迹曲线运动。
提出的精确轨迹运动控制方法完全可以推广到三维空间中的轨迹曲线跟踪运动,并应用于航天航空、机器人、机械制造等需要精确轨迹运动控制的领域。
| [1] |
谭跃刚. 非完整机器人的原理与控制[M]. 北京: 科学出版社, 2011. Tan Y G. Principle and control of non-holonomic robots[M]. Beijing: Science Press, 2011. (in Chinese) |
| [2] |
Chan R P M, Stol K A, Halkyard C R. Review of modelling and control of two-wheeled robots[J]. Annual Reviews in Control, 2013, 37(1): 89-103. DOI:10.1016/j.arcontrol.2013.03.004 |
| [3] |
Mirzaeinejad H. Optimization-based nonlinear control laws with increased robustness for trajectory tracking of non-holonomic wheeled mobile robots[J]. Transportation Research Part C: Emerging Technologies, 2019, 101: 1-17. DOI:10.1016/j.trc.2019.02.003 |
| [4] |
Zhai J Y, Song Z B. Adaptive sliding mode trajectory tracking control for wheeled mobile robots[J]. International Journal of Control, 2019, 92(10): 2255-2262. DOI:10.1080/00207179.2018.1436194 |
| [5] |
张少波. 非完整轮式移动机器人轨迹跟踪及避障控制研究[D]. 邯郸: 河北工程大学, 2019. Zhang S B. Research on trajectory tracking and obstacle avoidance control of nonholonomic wheeled mobile robots[D]. Handan, China: Hebei University of Engineering, 2019. (in Chinese) |
| [6] |
刘阳, 王忠立, 蔡伯根, 等. 基于单目视觉的移动机器人伺服镇定控制[J]. 华中科技大学学报(自然科学版), 2016, 44(10): 87-92. Liu Y, Wang Z L, Cai B G, et al. Monocular camera-based mobile robot visual servo regulation control[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2016, 44(10): 87-92. (in Chinese) |
| [7] |
沈智鹏, 张晓玲. 带扰动补偿的移动机器人轨迹跟踪反演控制[J]. 控制工程, 2019, 26(3): 398-404. Shen Z P, Zhang X L. Disturbance compensation based backstepping control for trajectory tracking of mobile robots[J]. Control Engineering of China, 2019, 26(3): 398-404. (in Chinese) |
| [8] |
Huang J, Chen J, Fang H, et al. An overview of recent progress in high-order nonholonomic chained system control and distributed coordination[J]. Journal of Control and Decision, 2015, 2(1): 64-85. DOI:10.1080/23307706.2015.1004803 |
| [9] |
Li H P, Yan W S, Shi Y. A receding horizon stabilization approach to constrained nonholonomic systems in power form[J]. Systems & Control Letters, 2017, 99: 47-56. |
| [10] |
李文科. 轮式移动机器人动力学轨迹跟踪控制研究[D]. 汉中: 陕西理工大学, 2019. Li W K. Trajectory tracking control for wheeled mobile robot based on dynamic[D]. Hanzhong, China: Shaanxi University of Technology, 2019. (in Chinese) |
| [11] |
周宇生. 时滞最优控制及其在轮式倒立摆中的应用[D]. 南京: 南京航空航天大学, 2016. Zhou Y S. Optimal control of delayed systems and its applications to wheeled inverted pendulum[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2016. (in Chinese) |
| [12] |
Yue M, An C, Du Y, et al. Indirect adaptive fuzzy control for a nonholonomic/underactuated wheeled inverted pendulum vehicle based on a data-driven trajectory planner[J]. Fuzzy Sets and Systems, 2016, 290: 158-177. DOI:10.1016/j.fss.2015.08.013 |
| [13] |
Cui R X, Guo J, Mao Z Y. Adaptive backstepping control of wheeled inverted pendulums models[J]. Nonlinear Dynamics, 2015, 79(1): 501-511. DOI:10.1007/s11071-014-1682-9 |
| [14] |
Chen N J, Song F Z, Li G P, et al. An adaptive sliding mode backstepping control for the mobile manipulator with nonholonomic constraints[J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(10): 2885-2899. DOI:10.1016/j.cnsns.2013.02.002 |
| [15] |
Zhou Y S, Wang Z H, Chung K W. Turning motion control design of a two-wheeled inverted pendulum using curvature tracking and optimal control theory[J]. Journal of Optimization Theory and Applications, 2019, 181(2): 634-652. DOI:10.1007/s10957-019-01472-4 |
 2021, Vol. 44
2021, Vol. 44


