2. 法国信息与系统国家重点实验室, UMR CNRS 7020, 法国 马赛 13397;
3. 中国重汽集团杭州发动机有限公司, 杭州 311232
2. LIS Laboratory, UMR CNRS 7020, Marseille 13397, France;
3. China National Heavy Truck Group Hangzhou Engine Co., Ltd., Hangzhou 311232, P. R. China
智能驾驶汽车能够提高汽车安全性,改善交通问题,并提升汽车舒适性和经济性,成为目前交通和汽车领域的重要研究热点[1-2]。但由于智能驾驶技术成熟性和智能驾驶背后法律问题,造成智能驾驶汽车将在很长时间内处于人车共驾的状态[3]。基于此,为了提高汽车安全和驾驶员舒适性,先碰撞预警再根据驾驶员反应进行变道避障控制,为人车共驾智能汽车避障重要控制方式之一。
进入21世纪,汽车碰撞预警系统得到广泛关注,国内外众多企业和研究机构对其进行了大量的研究[4-5]。在美国AHS(automated highway system)项目的推动下,开始广泛研究汽车避障预警和主动控制系统。由于安全距离模型能够直观反映两车之间的位置关系,具有广泛的适用性[6]。因此,很多碰撞预警研究的重点多集中设计纵向安全距离模型[7]。文献[8]通过获取汽车状态参数,提出了一种以所需安全距离为安全指标的汽车追尾预警算法。文献[9]通过对汽车超车时运动轨迹的分析,结合汽车的运动学模型,基于临界纵向安全距离,构建了超车汽车碰撞的预警模型。文献[10]构建了基于TTC(time to collision)碰撞时间理论的风险评估模型。但在真实行驶条件和环境下,路面状态、驾驶状态和驾驶干预将实时影响避障预警结果。并且,安全距离模型能实时计算两车应保持的期望安全车距,但无法反映出汽车当前行车状况的危险程度。
文献[11]利用3D虚拟危险势场规划避障轨迹,并基于多约束模型预测方法,实现了避障参考轨迹跟踪。文献[12]基于模拟退火优化算法,规划了能够绕过障碍物的避障轨迹,并基于主动前轮转向系统,设计了避障轨迹跟踪控制器。文献[13]采用人工势场方法规划了避障参考轨迹,并基于转向系统跟踪期望运动轨迹。但上述文献未研究驾驶员是否介入以及驾驶员对侧向避障起始时刻的影响,同时,控制策略也未考虑控制器参数摄动。
针对上述研究不足,笔者根据前方汽车速度动态变化,结合汽车的运动学模型,综合考虑了路面、驾驶状态和驾驶员干预,建立了纵向安全距离模型;并基于驾驶员反应时间和制动器反应时间等,提出了基于临界纵向安全距离和碰撞时间倒数(TTC1)融合互补的多级预警算法,有效处理多因素影响下的避障预警,并反映汽车当前危险程度和决定侧向避障触发时刻。同时,为了能够精准控制侧向避障轨迹跟踪,提出了考虑参数摄动的鲁棒控制策略。最终,通过预警和控制相结合,实现了根据驾驶员动态干预,实时修正预警算法,并决定是否需要侧向避障及侧向避障触发时刻,有效提高了人车共驾智能汽车安全性。
1 基于汽车制动过程分析的安全距离模型制动过程经历如下过程:驾驶员反应,驾驶员脚踩制动踏板到制动器开始起作用,制动器开始增压到最大压力,汽车持续制动到停车,汽车制动器解除;其对应时间分别为t1, t2, t3, t4, t5。从驾驶员反应到制动器开始起作用,即t1+t2时间内,汽车做匀速运动,制动距离为S1;t3时间内制动距离为S2;t4时间内制动距离为S3。具体推导过程见参考文献[14]。
总制动距离为
| $ S_{\mathrm{br}}=S_{1}+S_{2}+S_{3}。$ | (1) |
前车行驶的距离为SC,则安全预警距离表示为
| $ S_{\mathrm{w}}=S_{\mathrm{br}}-S_{\mathrm{C}}+d_{0}, $ | (2) |
式中d0为两车最小保持车距。
安全距离预警模型的影响因素主要有自车初始车速、制动过程各阶段历经时间、最大制动减速度和前车行驶距离。其中,制动过程各阶段时间除了与汽车制动系统性能有关外,还与驾驶员的驾驶状态密切相关。
最小保持车距为自车行驶或停车时与目标车之间的临界距离[15]。汽车避障过程中,将反映路面条件的附着系数和反映驾驶员特性的驾驶意图参数引入到最小保持车距中[16],以提高纵向主动避障系统对不同路面和驾驶员的适应能力,具体见公式(3)。
| $ d_{0}=k \frac{a}{\varphi_{\mu}+b}, $ | (3) |
式中:k为驾驶意图参数;φμ为附着系数;a,b为模型参数。
由公式(3)可知,当驾驶员驾驶状态相同且道路条件较好时,此时最小保持车距应较小以提高道路交通的利用率;当路面湿滑时,汽车易打滑,最小保持车距需较大以提升汽车行驶安全性。
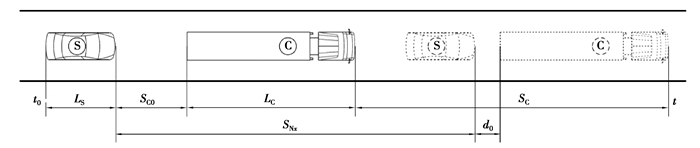
实时计算智能汽车与前车的纵向距离,为实时避障预警提供了基础,详见图 1。图中:t0为初始时刻,t为任意时刻,SC0为初始距离,LS为自车车长,LC为前车车长,SNx为自车纵向距离。
|
图 1 汽车纵向距离示意图 Fig. 1 Schematic diagram of vehicle longitudinal distance |
假设前车(C车)沿当前车道直线行驶,C车和S车(自车)的纵向行驶位移如下。
| $ S_{\mathrm{C}} =v_{\mathrm{C} 0} t+\int_{0}^{t} \int_{0}^{\lambda} a_{\mathrm{C}}(\tau) \mathrm{d} \tau \mathrm{d} \lambda , $ | (4) |
| $ S_{\mathrm{N} x} =v_{\mathrm{N} 0} t+\int_{0}^{t} \int_{0}^{\lambda} a_{\mathrm{N} x}(\tau) \mathrm{d} \tau \mathrm{d} \lambda。$ | (5) |
S车与C车在任意t时刻之间的实时间距
| $ S_{\mathrm{NC}}=\int_{0}^{t} \int_{0}^{\lambda}\left(a_{\mathrm{C}}(\tau)-a_{\mathrm{N} x}(\tau)\right) \mathrm{d} \tau \mathrm{d} \lambda+\left(v_{\mathrm{C} 0}-v_{\mathrm{N} x 0}\right) \cdot t+S_{\mathrm{C} 0}(0), $ | (6) |
式中:aC为前车加速度;aNx为自车加速度;vC为前车的实时车速;vNx为自车的实时车速;vC0为前车初始车速;vNx0为自车初始车速。
要使S车与C车在任意时刻都能安全避障,避障过程应实时满足式(7)。
| $ S_{\mathrm{NC}}>d_{0}, t \in(0, t)。$ | (7) |
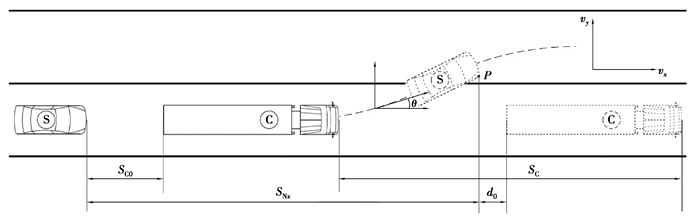
为了使变道完成时,车辆侧向加速度为零,采用正弦函数作为车道轨迹模型[17]。如图 2所示,图中P点为智能汽车变道过程中最易与前方汽车碰撞点。
|
图 2 智能汽车避障侧向变道轨迹俯视图 Fig. 2 Vertical view for lateral lane change of collision avoidance |
汽车侧向运动模型为
| $ {S_y} = \frac{{H{v_{{\rm{N}}x}}}}{{{S_{{\rm{C}}0}}}}t - \frac{H}{{2{\rm{ \mathsf{ π} }}}}\sin \left( {\frac{{2{\rm{ \mathsf{ π} }}{v_{{\rm{N}}x}}}}{{{S_{{\rm{C}}0}}}}t} \right), $ | (8) |
式中H为车道宽度。
为了使汽车侧向安全距离模型能够适应于不同路面条件和驾驶员的驾驶状态,将纵向安全距离模型中的最小保持距离代入式(8),可得S车侧向行驶轨迹为
| $ {{S_{{\rm{N}}y}} = \frac{{H{v_{{\rm{N}}x}}}}{{{S_{{\rm{C}}0}} - {d_0}}}t - \frac{H}{{2{\rm{ \mathsf{ π} }}}}\sin \left( {\frac{{2{\rm{ \mathsf{ π} }}{v_{{\rm{N}}x}}}}{{{S_{{\rm{C}}0}} - {d_0}}}t} \right)}。$ | (9) |
期望横摆角速度为
| $ {\gamma = \frac{{2{\rm{ \mathsf{ π} }}H{v_{{\rm{N}}x}}}}{{{{\left( {{S_{{\rm{C}}0}} - {d_0}} \right)}^2}}}\sin \left( {\frac{{2{\rm{ \mathsf{ π} }}{v_{{\rm{N}}x}}}}{{{S_{{\rm{C}}0}} - {d_0}}}t} \right)}。$ | (10) |
当汽车行驶到无法通过纵向制动避障时,此刻主动换道避障危险报警距离为
| $ S_{\mathrm{a}}=S_{2}+S_{3}-S_{C}+d_{0}。$ | (11) |
为确保预警系统不影响驾驶员驾驶状态,预警系统不能够设置过多预警状态。当SNC>SW时,此时处于安全行驶状态,预警设备不报警;当SNC≤SW时,进行持续不间断黄灯预警,提醒驾驶员控制汽车进行制动或转向操作,此时系统实际上未进行主动控制;当SNC≤Sa时,持续不间断红灯预警,此时无法通过制动安全避障,必须转向避障控制。
为实现转向避障控制,根据前后汽车实时车速,参考侧向行驶轨迹,建立了临界侧向避障安全距离模型,具体如下所示。
| $ {{S_{{\rm{N}}y}} = \frac{{H{v_{{\rm{N}}x}}}}{{{S_{{\rm{C}}0}} - {d_0}}}T - \frac{H}{{2{\rm{ \mathsf{ π} }}}}\sin \left( {\frac{{2{\rm{ \mathsf{ π} }}{v_{{\rm{N}}x}}}}{{{S_{{\rm{C}}0}} - {d_0}}}T} \right),} $ | (12) |
| $ {{S_{{\rm{N}}y}} = W,} $ | (13) |
式中:T为自车侧向位移等于前车宽度所用的时间;W为前车最大宽度。
汽车临界侧向避障极限的纵向安全距离为
| $ S_{\mathrm{s}}=v_{\mathrm{N} x} T+d_{0}-v_{\mathrm{C}} T。$ | (14) |
在此纵向安全距离之前,驾驶员可以自主控制汽车进行侧向避障;当SNC≤Ss时,驾驶员依然未干预,主动避障系统将自动接管汽车进行侧向变道避障控制。
汽车主动避障控制系统应能够根据当前汽车运动状态,判断安全状况并及时预警提醒驾驶员控制汽车。但安全距离模型只能够实时计算两车应保持的期望安全距离,无法反映出汽车当前危险程度[18]。基于上述原因,引入汽车碰撞时距TTC的倒数设计融合互补的多层预警算法。
汽车碰撞时距定义[19]为
| $ T_{\mathrm{TC} 1}=\frac{v_{\mathrm{N} x}-v_{\mathrm{C}}}{S_{\mathrm{CN}}}, $ | (15) |
式(15)也可表示为
| $ T_{\mathrm{TC1}}=\frac{\int_{0}^{t}\left(a_{\mathrm{N} x}(\tau)-a_{\mathrm{C}}(\tau) \mathrm{d} t\right.}{\int_{0}^{t} \int_{0}^{\lambda}\left(a_{\mathrm{C}}(\tau)-a_{\mathrm{N} x}(\tau)\right) \mathrm{d} \tau \mathrm{d} \lambda+\left(v_{\mathrm{C}}(0)-v_{\mathrm{N} x}(0)\right) \cdot t+S_{\mathrm{C0}}(0)}。$ | (16) |
由TTC1的定义可知,当TTC1>0时,自车大于目标车速,即自车正在接近目标车;当T TC1 < 0时,自车小于目标车速,说明自车正在远离目标车,此时为安全状态;当TTC1=0时,自车等于目标车速,说明两车处于相对静止状态,故为安全状态。
考虑到评价系统的实用性和通用性,融合互补的多级预警算法分为4个等级:安全、警告、危险及临界状态。并且,为了保证汽车实时安全,所提预警算法的预警等级由安全距离和碰撞时距早触发者决定。具体预警分级如表 1所示。
| 表 1 融合互补的多级预警算法 Table 1 Multi-layer warning algorithm based on fusion |
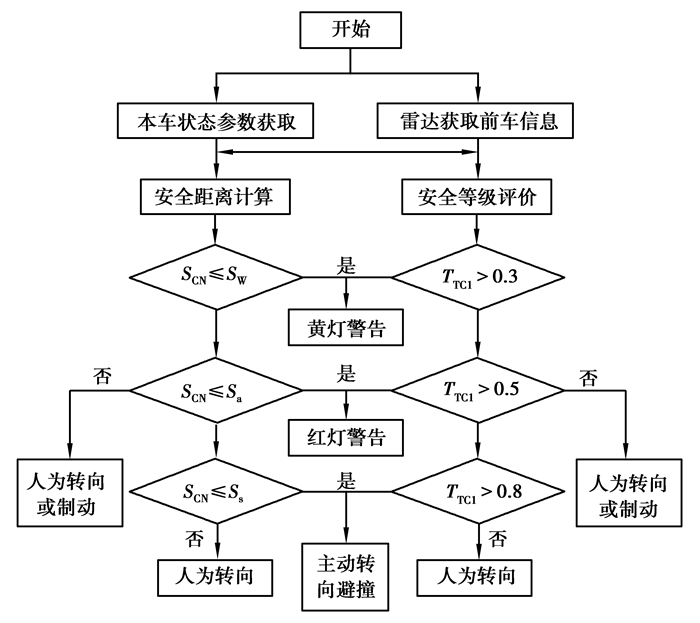
根据预警各级定义,设计了避障预警及避障方式切换流程图,见图 3。在动态环境不同前车和智能汽车状态下,两种方式预警时间节点不同,实际预警状态由两个预警方式中早触发的方式决定,形成了两种预警方式融合互补的多层预警算法,以确保驾驶员和控制器更多处理时间,进而保证汽车避障安全性。此多层预警算法既能够判断当前行驶与前车应保持的距离,也能够反映任一时刻的危险情况。
|
图 3 避障预警及避障方式切换流程图 Fig. 3 Flow chart of collision avoidance warning and mode switching strategy |
由图 3可知,当预警等级为2级时,发出黄灯警告,提醒驾驶员及时进行转向或制动干预;若驾驶员没有反应,到达3级危险状态时,发出持续不间断红灯警告,并只能通过转向避障;如果驾驶员未干预,到达4级临界状态时,避障系统将主动接管汽车进行主动换道,保证汽车避障安全。
3 汽车侧向避障控制如果从普通预警至4级(临界状态)预警,驾驶员一直未进行干预,此时控制系统将主动接管人车共驾智能汽车进行侧向避障。人车共驾智能汽车在侧向避障过程中,汽车状态变化将引起汽车垂直载荷动态变化,进而引起汽车前后侧偏刚度动态变化,影响控制策略精准控制。同时,人车共驾智能汽车在避障过程中可能存在外部干扰。因此,为了实现避障轨迹精准跟踪,设计了考虑参数动态摄动的侧向避障鲁棒控制策略。
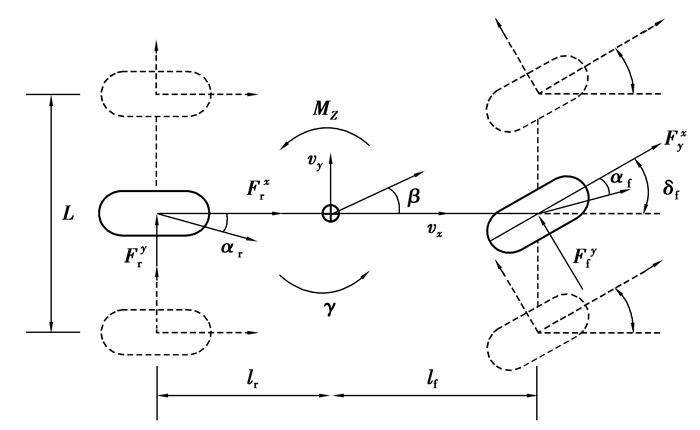
3.1 汽车侧向动力学模型为实现侧向避障轨迹跟踪,建立二自由度简化模型[20-21],如图 4所示。其二自由度分别为侧向运动和横摆运动。侧向运动由质心侧偏角表征,横摆运动由横摆角速度表征。
| $ m v_{x}(\dot{\beta}+\gamma)=\left(F_{\mathrm{fl}}^{x}+F_{\mathrm{fr}}^{x}\right) \sin \delta+\left(F_{\mathrm{fl}}^{y}+F_{\mathrm{fr}}^{y}\right) \cos \delta+F_{\mathrm{rl}}^{y}+F_{\mathrm{rr}}^{y}, $ | (17) |
| $ \left.I_{z} \dot{\gamma}=l_{f}\left(\left(F_{\mathrm{fl}}^{x}+F_{\mathrm{fr}}^{x}\right) \sin \delta+\left(F_{\mathrm{f} 1}^{y}+F_{\mathrm{fr}}^{y}\right) \cos \delta\right)\right)-l_{\mathrm{r}}\left(F_{\mathrm{rl}}^{y}+F_{\mathrm{rr}}^{y}\right)+M_{z}, $ | (18) |
|
图 4 简化模型 Fig. 4 Simple model |
式中:β为侧偏角;γ为横摆角速度;m为整车质量;vx为纵向速度;lf,lr分别为质心到前后轴的距离;Fflx,Ffrx,Frlx,Frrx,Ffly,Ffry,Frly和Frry分别为左右前后轮纵向力和侧向力;δ为前轮转角;Iz为横摆转动惯量;Mz为附加横摆力矩。
为了设计简化,设定前后轮轮距相等,假设前后轮的行驶条件相同,且左右轮的行驶条件也相同,则四轮汽车模型可化简为两轮简化汽车模型,对应的两轮汽车的侧向动力学方程为
| $ m v_{x}(\dot{\beta}+\gamma)=F_{\mathrm{f}}^{y} \cos \delta+F_{\mathrm{r}}^{y} , $ | (19) |
| $ I_{z} \dot{\gamma}=l_{\mathrm{f}} F_{\mathrm{f}}^{y} \cos \delta-l_{\mathrm{r}} F_{\mathrm{r}}^{y}+M_{z}, $ | (20) |
式中:Ffy为前轴侧向力;Fry为后轴侧向力。
当轮胎侧偏角较小时,侧向轮胎力可以线性近似地表示为
| $ F_{\mathrm{f}}^{y}=-2 C_{\mathrm{f}}\left(\beta+\frac{\gamma l_{\mathrm{f}}}{v_{x}}-\delta\right), $ | (21) |
| $ F_{\mathrm{r}}^{y}=-2 C_{\mathrm{r}}\left(\beta-\frac{\gamma l_{\mathrm{r}}}{v_{x}}\right), $ | (22) |
式中: Cf为前轴侧偏刚度;Cr为后轴侧偏刚度。
设车身侧偏角和横摆角速率为汽车模型的状态变量,并假设对于前轮转向角在汽车高速行驶时相对较小,结合小角近似,将式(21)(22)代入(19)(20)中,得到线性二自由度汽车模型,即
| $ m v_{x}(\dot{\beta}+\gamma)=-2\left(C_{\mathrm{f}}+C_{\mathrm{r}}\right) \beta-\frac{2\left(C_{\mathrm{f}} l_{\mathrm{f}}-C_{\mathrm{r}} l_{\mathrm{r}}\right)}{v_{x}} \gamma+2 C_{\mathrm{f}} \delta, $ | (23) |
| $ I_{z} \dot{\gamma}=-2\left(C_{\mathrm{f}} l_{\mathrm{f}}-C_{\mathrm{r}} l_{\mathrm{r}}\right) \beta-\frac{2\left(C_{\mathrm{f}} l_{\mathrm{f}}^{2}+C_{\mathrm{r}} l_{\mathrm{r}}^{2}\right)}{v_{x}} \gamma+2 C_{\mathrm{f}} l_{\mathrm{f}} \delta+M_{z}。$ | (24) |
状态空间表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{Bu}},}\\ {\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Cx}}。} \end{array}} \right. $ | (25) |
式中:
为确保汽车侧向避障精准控制,设计了考虑参数动态摄动的H∞鲁棒控制策略[20]。侧向避障过程中,汽车前轮侧偏刚度Cf和后轮侧偏刚度Cr动态变化,将影响路径跟随精准控制。但其取值区间已知,动态变化如式(26)。
| $ \left\{\begin{array}{l} C_{\mathrm{f}}=\overline{C}_{\mathrm{f}}\left(1+p_{\mathrm{f}} \delta_{\mathrm{f}}\right), \\ C_{\mathrm{r}}=\overline{C}_{\mathrm{r}}\left(1+p_{\mathrm{r}} \delta_{\mathrm{r}}\right)。\end{array}\right. $ | (26) |
式中:δf和δr分别为前轮侧偏刚度和后轮侧偏刚度的摄动,取值区间为[-1, 1];Cf和Cr分别为前轮侧偏刚度和后轮侧偏刚度的标称值;pf和pr分别为前轮侧偏刚度和后轮侧偏刚度的摄动范围。
将式(26)进行上线性分式变换,可得到式(27)。
| $ \left\{\begin{array}{l} C_{\mathrm{f}}=\overline{C}_{\mathrm{f}}\left(1+p_{\mathrm{f}} \delta_{\mathrm{f}}\right)=F_{u}\left(\boldsymbol{M}_{\mathrm{f}}, \delta_{\mathrm{f}}\right) ,\\ C_{\mathrm{r}}=\overline{C}_{\mathrm{r}}\left(1+p_{\mathrm{r}} \delta_{\mathrm{r}}\right)=F_{u}\left(\boldsymbol{M}_{\mathrm{r}}, \delta_{\mathrm{r}}\right)。\end{array}\right. $ | (27) |
式中Mf,Mr为上线性分式变换的系数矩阵。
结合汽车二自由度状态空间和汽车系统模型中摄动参数对应的上线性分时变换,可得到含有参数摄动的汽车系统模型结构,具体参考文献[20]。Gmds表示动力学标称模型,其输入为[uf1, uf2, ur1, ur1, u1, u2],输出为[yf1, yf2, yr1, yr1, y1, y2],状态变量为[β, γ],其状态空间表达式为
| $ \boldsymbol{G}_{\mathrm{mds}}=\left[\begin{array}{ccc} \tilde{A} & \tilde{B}_{1} & \tilde{B}_{2} \\ \widetilde{C}_{1} & \tilde{D}_{11} & \tilde{D}_{12} \\ \tilde{C}_{2} & \tilde{D}_{21} & \tilde{D}_{22} \end{array}\right], $ | (28) |
式中:
汽车系统模型摄动参数部分可由一个结构固定参数未知的不确定对角矩阵[22]表示:
| $ \boldsymbol{\varDelta}=\left[\begin{array}{cccc} \delta_{\mathrm{f}} & 0 & 0 & 0 \\ 0 & \delta_{\mathrm{f}} & 0 & 0 \\ 0 & 0 & \delta_{\mathrm{r}} & 0 \\ 0 & 0 & 0 & \delta_{\mathrm{r}} \end{array}\right],|\boldsymbol{\varDelta}| \leqslant 1。$ | (29) |
鉴于鲁棒稳定性,闭环系统对于所有的
| $ \left\|\left[\begin{array}{c} \boldsymbol{W}_{\mathrm{p}} \boldsymbol{S} \\ \boldsymbol{W}_{u} \boldsymbol{K} \boldsymbol{S} \end{array}\right]\right\|=\left\|\left[\begin{array}{c} \boldsymbol{W}_{\mathrm{p}}(\boldsymbol{I}+\boldsymbol{G} \boldsymbol{K})^{-1} \\ \boldsymbol{W}_{u} \boldsymbol{K}(\boldsymbol{I}+\boldsymbol{G} \boldsymbol{K})^{-1} \end{array}\right]\right\|<1, $ | (30) |
式中:
| $ \left[\begin{array}{c} e_{\mathrm{p}} \\ e_{u} \\ \overline{y} \end{array}\right]=\left[\begin{array}{cc} \boldsymbol{W}_{\mathrm{p}} & -\boldsymbol{W}_{\mathrm{p}} \boldsymbol{G} \\ \bf{0} & \boldsymbol{W}_{\mathrm{u}} \\ \boldsymbol{I} & -\boldsymbol{G} \end{array}\right]\left[\begin{array}{l} d \\ \overline{u} \end{array}\right] 。$ | (31) |
| $ \boldsymbol{P}(s)=\left[\begin{array}{cc} \boldsymbol{W}_{\mathrm{p}} & -\boldsymbol{W}_{\mathrm{p}} G \\ \bf{0} & \boldsymbol{W}_{u} \\ \boldsymbol{I} & -\boldsymbol{G} \end{array}\right]=\left[\begin{array}{ll} \boldsymbol{P}_{11} & \boldsymbol{P}_{12} \\ \boldsymbol{P}_{21} & P_{22} \end{array}\right], $ | (32) |
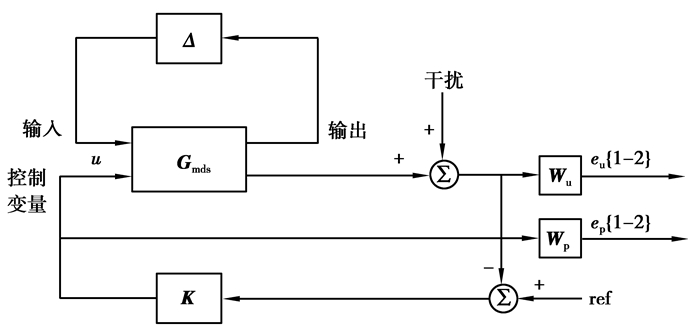
|
图 5 闭环系统关联结构图 Fig. 5 Association structure of the closed loop system |
式中:
从d到
| $ \boldsymbol{F}_{1}(\boldsymbol{P}, \boldsymbol{K})=\boldsymbol{P}_{11}+\boldsymbol{P}_{12} \boldsymbol{K}\left(\boldsymbol{I}-\boldsymbol{P}_{22}\right)^{-1} \boldsymbol{P}_{21}=\left[\begin{array}{c} \boldsymbol{W}_{\mathrm{p}}(\boldsymbol{I}+\boldsymbol{G} \boldsymbol{K})^{-1} \\ \boldsymbol{W}_{u} \boldsymbol{K}(\boldsymbol{I}+\boldsymbol{G} \boldsymbol{K})^{-1} \end{array}\right] 。$ | (33) |
因此,式(33)混合灵敏度问题即可转化为H∞标准控制问题,即:
| $ \left\|F_{1}(\boldsymbol{P}, \boldsymbol{K})\right\|_{\infty}<1。$ | (34) |
为验证基于碰撞预警的智能汽车侧向避障控制策略,搭建Carsim与Simulink联合仿真平台。根据驾驶员预警后的反应,设计了2个测试工况。工况1,预警后,驾驶员及时干预;工况2,预警后,驾驶员未干预,控制策略主动侧向避障控制。通过此2个工况,能够测试人车共驾状态下,预警算法预警效果;以及预警达到4级(临界状态)预警状态而驾驶员未干预时,验证控制策略自行侧向避障控制效果。人车共驾智能汽车基本参数如表 2所示。
| 表 2 汽车模型参数 Table 2 Parameters of vehicle model |
工况设置:前车以vC0=65 km/h的初速度行驶,自车初始车速vNx0=80 km/h,两车初始间距SC0=120 m,两车道间距H=3.5 m,驾驶员反应时间一般在0.4~1.0 s之间,考虑到不同驾驶员驾驶状态存在差异,取1.0 s;克服踏板自由行程、制动期间隙时间为0.2 s;轿车制动系统一般都为液压制动系统,则液压系统起作用时间为0.3 s,路面附着系数最大值为0.7。为了验证动态条件下有无驾驶员干预的预警效果,进行了无驾驶员和有驾驶员干预的两种模式仿真实验,验证结果如图 6所示。

|
图 6 驾驶员干预的自车预警响应图 Fig. 6 Warning response with driver intervention |
由图 6(a)(b)可知, 前车加速度和速度动态变化,有利于验证预警算法的动态预警能力。由6(c)(e)可知,每个预警级别参考值随着前车和后车加速度和速度变化而变化,因此,预警算法能够根据外界条件变化来实时决定不同预警层次的参考值,为人车共驾智能车精准预警和安全提供必要基础。由图 6(c)(d)可知,实时间距和碰撞时距随着前车和自车状态动态变化而变化,且各自实时预警级别参考值形成交点,获得了提醒报警点、危险报警点和临界点预警状态。图 6(e)(f)为驾驶员根据报警主动采取了干预,进行了制动操作后预警变化结果。由此两图可知,驾驶员采取行动后,危险报警点和临界点时间都会延后;并且驾驶员持续制动,汽车报警结果动态变化甚至解除报警。因此,融合互补的多级预警算法能够根据驾驶员动态介入,动态调整预警结果;并且,两种预警方式不同安全级别的报警时间不同,预警结果以两种预警方式早触发的为预警依据,有利于提高预警提前性,为驾驶员干预或者控制器控制获得更多控制时间。有无驾驶员干预的预警结果见图 6(g)(h)。
4.2 驾驶员未干预在实际交通环境下,由于驾驶员疲劳或者工况危险等原因,当汽车进入危险工况,驾驶员未对汽车进行干预,汽车将发生碰撞事故。针对此工况,所提控制策略在预警后,驾驶员未做出反应到达4级(临界状态)预警状态,将主动接管汽车进行主动侧向避障控制,保证智能汽车安全。测试工况展现了从开始检测到前方存在危险汽车,到最终实现智能汽车侧向安全避障全过程,仿真结果如图 7。

|
图 7 侧向避障控制仿真结果 Fig. 7 Simulation results of lateral collision avoidance |
由图 7(a)(b)可知,前车加速度和速度动态变化,有利于验证动态工况多级预警算法预警准确性。由图 7(c)(d)可知,随着前车速度急剧降低,多级预警算法先后实现了各种级别的预警。同时对比图 6(c)(d)和图 7(c)(d)上述两工况的预警方式,安全距离和碰撞时间预警时间节点接近,但不同行驶状态下,两种预警方式在同安全等级下预警时间互有早晚。因此,通过采用时间早的节点能够互补两种预警算法,更好地确保在不同行驶状态预警准确性,有效提高了人车共驾智能汽车避障安全性。融合互补的多级预警算法的预警结果见图 7(k)。
当4级(临界状态)触发后,避障系统主动接管了汽车,进行规划轨迹跟踪控制,实现智能汽车侧向避障控制。由图 7(e)(f)(g)(h)(i)可知,控制策略实现了位移、航向角和航向角速度良好跟踪。经过计算可知,侧向位移最大偏差量为0.077 m,最大误差率为2.2%;航向角峰值误差为0.26°,峰值误差率为7.5%;航向角速度峰值误差为0.05°/s,峰值误差率为2.2%。由图 7(j)可知,航向角速度变化平稳,并且值在正负2.27°/s范围内。因此,鲁棒控制策略能够保证避障过程中人车共驾智能车横摆稳定性。
综上所述,所提融合互补的多级预警算法能够根据外界状态的变化,实时调整各种级别的安全预警距离,为人车共驾智能车准确预警提供基础;同时,弥补了实时间距和碰撞时距两种方式不足,既能够体现距离变化又能够表示危险程度;并且能够根据驾驶员干预程度,实时修正预警结果。人车共驾智能车预警到四级(临界状态)且驾驶员未干预汽车,控制策略自动接管了智能车,并克服了前后侧偏刚度参数摄动,实现了侧向避障控制且确保了智能车横摆稳定性。
5 结论1) 针对前车和人车共驾智能车速度和加速度动态变化,考虑了驾驶员驾驶状态等因素,提出了汽车纵向安全距离模型。
2) 提出了基于纵向安全距离模型和避障时间融合互补的多级预警算法,实现了既保证汽车避障安全,又能够体现智能汽车危险状态。此预警算法实现了动态环境下各级预警,应对了预警过程中驾驶员干预,获得了多因素影响下实时准确的预警,为人车共驾智能车安全控制奠定了基础。人车共驾智能车到达4级(临界状态)且驾驶员未干预汽车,所提控制策略主动接管了汽车进行侧向避障,确保了汽车安全避障。
3) 考虑了侧向避障过程中参数动态摄动,设计侧向避障鲁棒控制器,实现了避障轨迹准确跟踪,从而实现了智能汽车侧向避障,并保证了避障过程智能汽车安全性和稳定性。
| [1] |
Wei S Y, Zou Y, Zhang X D, et al. An integrated longitudinal and lateral vehicle following control system with radar and vehicle-to-vehicle communication[J]. IEEE Transactions on Vehicular Technology, 2019, 68(2): 1116-1127. DOI:10.1109/TVT.2018.2890418 |
| [2] |
Bichiou Y, Rakha H A. Developing an optimal intersection control system for automated connected vehicles[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(5): 1908-1916. DOI:10.1109/TITS.2018.2850335 |
| [3] |
吴超仲, 吴浩然, 吕能超. 人机共驾智能汽车的控制权切换与安全性综述[J]. 交通运输工程学报, 2018, 18(6): 131-141. Wu C Z, Wu H R, Lyu N C. Review of control switch and safety of human-computer driving intelligent vehicle[J]. Journal of Traffic and Transportation Engineering, 2018, 18(6): 131-141. (in Chinese) DOI:10.3969/j.issn.1671-1637.2018.06.014 |
| [4] |
Song W J, Yang Y, Fu M Y, et al. Real-time obstacles detection and status classification for collision warning in a vehicle active safety system[J]. IEEE Transactions on Intelligent Transportation Systems, 2018, 19(3): 758-773. DOI:10.1109/TITS.2017.2700628 |
| [5] |
Xiang X H, Qin W H, Xiang B F. Research on a DSRC-based rear-end collision warning model[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(3): 1054-1065. DOI:10.1109/TITS.2013.2293771 |
| [6] |
Iranmanesh S M, Nourkhiz Mahjoub H, Kazemi H, et al. An adaptive forward collision warning framework design based on driver distraction[J]. IEEE Transactions on Intelligent Transportation Systems, 2018, 19(12): 3925-3934. DOI:10.1109/TITS.2018.2791437 |
| [7] |
Lian Y F, Zhao Y, Hu L L, et al. Longitudinal collision avoidance control of electric vehicles based on a new safety distance model and constrained-regenerative-braking-strength-continuity braking force distribution strategy[J]. IEEE Transactions on Vehicular Technology, 2016, 65(6): 4079-4094. DOI:10.1109/TVT.2015.2498949 |
| [8] |
Chen M L, Zhan X Q, Zhang X, et al. Localisation-based autonomous vehicle rear-end collision avoidance by emergency steering[J]. IET Intelligent Transport Systems, 2019, 13(7): 1078-1087. DOI:10.1049/iet-its.2018.5348 |
| [9] |
游峰, 张荣辉, 王海玮, 等. 基于纵向安全距离的超车安全预警模型[J]. 华南理工大学学报(自然科学版), 2013, 41(8): 87-92, 98. You F, Zhang R H, Wang H W, et al. Warning model for safety analysis of overtaking behavior based on longitudinal safety spacing[J]. Journal of South China University of Technology (Natural Science Edition), 2013, 41(8): 87-92, 98. (in Chinese) DOI:10.3969/j.issn.1000-565X.2013.08.014 |
| [10] |
杨为, 赵胡屹, 舒红. 自动紧急制动系统行人避撞策略及仿真验证[J]. 重庆大学学报, 2019, 42(2): 1-10. Yang W, Zhao H Y, Shu H. Simulation and verification of the control strategies for AEB pedestrian collision avoidance system[J]. Journal of Chongqing University, 2019, 42(2): 1-10. (in Chinese) |
| [11] |
Ji J, Khajepour A, Melek W W, et al. Path planning and tracking for vehicle collision avoidance based on model predictive control with multiconstraints[J]. IEEE Transactions on Vehicular Technology, 2017, 66(2): 952-964. DOI:10.1109/TVT.2016.2555853 |
| [12] |
Rodríguez-Seda E J, Tang C, Spong M W, et al. Trajectory tracking with collision avoidance for nonholonomic vehicles with acceleration constraints and limited sensing[J]. The International Journal of Robotics Research, 2014, 33(12): 1569-1592. DOI:10.1177/0278364914537130 |
| [13] |
Wahid N, Zamzuri H, Abdul Rahman M A, et al. Study on potential field based motion planning and control for automated vehicle collision avoidance systems[C]//2017 IEEE International Conference on Mechatronics (ICM). February 13-15, 2017, Churchill, VIC, Australia. IEEE, 2017: 208-213.
|
| [14] |
余志生. 汽车理论[M]. 6版. 北京: 机械工业出版社, 2018. Yu Z S. The theory of automobile[M]. 6th ed. Beijing: China Machine Press, 2018. (in Chinese) |
| [15] |
胡远志, 杨喜存, 刘西, 等. 基于驾驶员特性的主动避撞分级制动策略与验证[J]. 汽车工程, 2019, 41(3): 298-306. Hu Y Z, Yang X C, Liu X, et al. Hierarchic braking strategy for active collision avoidance and its verification based on driver's characteristics[J]. Automotive Engineering, 2019, 41(3): 298-306. (in Chinese) |
| [16] |
朱冰, 朴奇, 赵健, 等. 基于路面附着系数估计的汽车纵向碰撞预警策略[J]. 汽车工程, 2016, 38(4): 446-452. Zhu B, Piao Q, Zhao J, et al. Vehicle longitudinal collision warning strategy based on road adhesive coefficient estimation[J]. Automotive Engineering, 2016, 38(4): 446-452. (in Chinese) DOI:10.3969/j.issn.1000-680X.2016.04.009 |
| [17] |
Wang P, Chan C Y. Vehicle collision prediction at intersections based on comparison of minimal distance between vehicles and dynamic thresholds[J]. IET Intelligent Transport Systems, 2017, 11(10): 676-684. DOI:10.1049/iet-its.2017.0065 |
| [18] |
黄丽琼. 基于制动/转向的汽车主动避撞控制系统研究[D]. 南京: 南京航空航天大学, 2016. Huang L Q. Research on vehicle active collision avoidance control system based on longitudinal braking/steering lane-changing[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2016. (in Chinese) |
| [19] |
Han J, Heo O, Park M, et al. Vehicle distance estimation using a mono-camera for FCW/AEB systems[J]. International Journal of Automotive Technology, 2016, 17(3): 483-491. DOI:10.1007/s12239-016-0050-9 |
| [20] |
Lian Y F, Wang X Y, Tian Y T, et al. Lateral collision avoidance robust control of electric vehicles combining a lane-changing model based on vehicle edge turning trajectory and a vehicle semi-uncertainty dynamic model[J]. International Journal of Automotive Technology, 2018, 19(2): 331-343. DOI:10.1007/s12239-018-0032-1 |
| [21] |
李以农, 胡一明, 邹桃. 轮毂电机驱动电动汽车横摆稳定性控制[J]. 重庆大学学报, 2017, 40(12): 24-34. Li Y N, Hu Y M, Zou T. Yaw stability control of wheel-drive electric vehicle[J]. Journal of Chongqing University, 2017, 40(12): 24-34. (in Chinese) |
| [22] |
Gu D W, Petkov P H, Konstantinov M M. Robust control design with MATLAB[M]. London: Springer London, 2013.
|
 2021, Vol. 44
2021, Vol. 44

