2. 重庆长安汽车股份有限公司, 重庆 40023
2. Chongqing Chang'an Automobile Company Limited, Chongqing 400023, P. R. China
内燃机测得的缸内工质压力可用于爆震检测、燃烧放热分析和排气温度估计,运行过程中在线监控并反馈控制这些参数以优化热机性能已得到广泛应用[1-3]。其中放热率分析已被证明是汽油机燃烧放热过程可靠的诊断方式,燃烧相位和持续期是评估燃烧过程的重要参数[4-6]。
在进行放热率分析时,缸内压力变化除了工质放热外,还受到气缸容积变化、气壁间传热和余隙流动等过程的影响[7]。为此,国内外学者们提出了诸多数值模型来提高分析精度。Krieger等[8]提出的单区模型用平均状态来表示缸内工质的热力学特性,基于热力学第一定律计算放热参数,但比热比和传热量难以合理估计成为限制其发展的瓶颈。复杂的多区模型将气缸划分为一个未燃区和多个已燃区分别计算,分析时结合各区域界面随时间的演变,能更全面地描述燃烧过程[9]。近年来多区分析模型虽取得了诸多进展,但其精度很大程度上仍取决于所采用传热模型的可靠度,且计算的复杂性导致其并不适用于大量循环的在线计算[10-16]。
目前工程上应用于燃烧闭环控制的模型均为单区,比热比采用定值估计和忽略传热影响导致了一定的误差[17]。Tunestål [18]在单区模型的基础上提出了一种考虑传热影响的比热比估计方法,并在一台HCCI(homogeneous charge compression ignition)发动机进行了简单的验证。该方法依据缸压和容积曲线估计循环的比热比,但关于比热比如何进行合理插值并没有做进一步研究。笔者在此基础上研究了一种新的插值方法,并基于不同的燃烧分析角度研究和评价了这种方法对汽油机放热率计算的影响。
1 总放热率模型在单区放热率模型中,缸内的工质被视为热力学状态均匀的单一流体,燃烧过程被抽象为额外的热添加过程。忽略余隙流动和工质泄露,在IVC(intake valve closure)至EVO(exhaust valve opening)期间运用热力学第一定律得到
| $ \delta Q_{\mathrm{ch}}=\mathrm{d} U+\delta W+\delta Q_{\mathrm{ht}}, $ | (1) |
式中:δQch为燃烧过程中释放的化学能;dU为工质内能的变化;δW为活塞对外做的功;δQht为工质与汽缸壁间的传热量。将理想气体的状态方程式pV=mRgT代入式(1)中(这里p、V、m、Rg、T分别为气体的压力、容积、质量、理想气体常数和温度),并将传热部分δQht移至等式左侧,整个等式再依据曲轴转角进行差分,并结合比热比的定义cp/cv=γ(这里的cp和cv分别为定压比热和定容比热),得到模型1:
| $ \frac{\mathrm{d} Q_{\text {net }}}{\mathrm{d} \theta}=\frac{\mathrm{d} Q_{\text {ch }}}{\mathrm{d} \theta}-\frac{\mathrm{d} Q_{\mathrm{ht}}}{\mathrm{d} \theta}=\frac{\gamma}{\gamma-1} p \frac{\mathrm{d} V}{\mathrm{~d} \theta}+\frac{1}{\gamma-1} V \frac{\mathrm{d} p}{\mathrm{~d} \theta}, $ | (2) |
式中θ为曲轴转角相位。式(2)即为目前工程上在线燃烧分析中大规模运用的净放热率模型。此方法忽略了传热部分,且计算过程中比热比难以测定和准确估计,因此一般使用定值(1.32)进行近似,导致计算结果往往不能准确描述燃烧过程。
若在式(2)的基础上将传热部分δQht隐式地包纳于比热比γ中,则有:
| $ \delta Q_{\mathrm{ch}}=\left(\frac{c_{\mathrm{v}}+R_{\mathrm{g}} \frac{\delta Q_{\mathrm{ht}}}{\mathrm{d}(p V)}}{R_{\mathrm{g}}}+1\right) p \mathrm{~d} V+\left(\frac{c_{\mathrm{v}}+R_{\mathrm{g}} \frac{\delta Q_{\mathrm{ht}}}{\mathrm{d}(p V)}}{R_{\mathrm{g}}}\right) V \mathrm{~d} p。$ | (3) |
考虑使用修正的比热参数c′v和c′p,以及比热比γ′:
| $ c_{\mathrm{p}}^{\prime}=c_{\mathrm{p}}+R_{\mathrm{g}} \frac{\delta Q_{\mathrm{ht}}}{\mathrm{d}(p V)}, $ | (4) |
| $ c_{\mathrm{v}}^{\prime}=c_{\mathrm{v}}+R_{\mathrm{g}} \frac{\delta Q_{\mathrm{ht}}}{\mathrm{d}(p V)}, $ | (5) |
| $ c_{\mathrm{p}}^{\prime} / c_{\mathrm{v}}^{\prime}=\gamma^{\prime}。$ | (6) |
由cp-cv=Rg可知新定义的比热参数仍满足c′p-c′v=Rg。依据曲轴转角对式(3)进行差分,式(3)经简化可得模型2:
| $ \frac{\mathrm{d} Q_{\text {gross }}}{\mathrm{d} \theta}=\frac{\mathrm{d} Q_{\text {ch }}}{\mathrm{d} \theta}=\frac{\gamma^{\prime}}{\gamma^{\prime}-1} p \frac{\mathrm{d} V}{\mathrm{~d} \theta}+\frac{1}{\gamma^{\prime}-1} V \frac{\mathrm{d} p}{\mathrm{~d} \theta}。$ | (7) |
可知式(7)将传热δQht纳入新比热比γ′中,进而总放热率与净放热率计算公式达到了形式上的统一。
2 总放热率模型的算法实现在总放热率模型(模型2)的基础上,将构造的总放热率公式(7)运用到压缩和膨胀冲程中。与燃烧过程相比缺失了热添加部分,故式(7)可简化为:
| $ 0=\frac{\gamma^{\prime}}{\gamma^{\prime}-1} p \frac{\mathrm{d} V}{\mathrm{~d} \theta}+\frac{1}{\gamma^{\prime}-1} V \frac{\mathrm{d} p}{\mathrm{~d} \theta}, $ | (8) |
对等式两端进行变换和积分后可得:
| $ p V^{\gamma^{\prime}}=C=p V^{\kappa^{\prime}}, $ | (9) |
即压缩和膨胀过程中若将传热也隐式地包纳于比热比中,则可将此过程视为绝热的多变过程,γ′可用多变指数κ′来表示。虽然在压缩和膨胀过程中κ′是变化的,但在压缩终点和膨胀始点κ′与模型2燃烧区间端点处的γ′应是连续的。因此,燃烧过程中的γ′可用压缩和膨胀过程中的κ′进行近似估计。故总放热率模型的算法实现主要包括压缩与膨胀区间内κ′的估计、燃烧过程中γ′的插值和放热率计算等部分构成。
2.1 压缩和膨胀过程中κ′的估计参考了文献[17]所提出的模型来估算压缩和膨胀过程中κ′。基本思想为:由于缸压测量所用的压电式压力传感器为相对压力传感器,虽然各循环缸内压力数据均已经过两点法或进气道压力校正,但压缩或膨胀区间内压力传感器由于热应力及零点漂移等原因仍存在着一定的压力偏差Δp。因此对于估计区间内的各个数据点应满足:
| $ \left(p^{\prime}+\Delta p\right) V^{\kappa^{\prime}}=\left(p_{0}^{\prime}+\Delta p\right) V_{0}^{\kappa^{\prime}}, $ | (10) |
式中:p′为压力传感器测量到的压力值;下标0代表此参数为计算区间内的基准位置。
将式(10)进行归一化处理之后可得:
| $ F_{i}(x)=\frac{p_{i}^{\prime}}{p_{0}^{\prime}}-\left(\frac{V_{0}}{V_{i}}\right)^{\kappa^{\prime}}\left(1+\frac{\Delta p}{p_{0}^{\prime}}\right)-\frac{\Delta p}{p_{0}^{\prime}}=0。$ | (11) |
式中:Fi(x)为公式(10)归一化后的表达函数,x代表两个未知参数κ′和Δp,下标i代表此计算区间内的任一数据点。
将式(11)应用于估计区间内的诸多数据点,即可组成含有两个未知参数κ′和Δp的非线性方程组。求解此非线性方程组可使用最小二乘法对损失函数进行表示,见式(12)。
| $ \operatorname{Cost}(x)=\frac{1}{2} \sum\limits_{i=1}^{n} F_{i}^{2}(x), $ | (12) |
式中n为估计区间内的数据点总数。使用Levenberg-Marquardt方法构造梯度来降低损失函数,可获得满足迭代终止条件的κ′和Δp。为了提高计算效率,在估计压缩和膨胀过程中的κ′时对信号进行无相移的低通滤波,计算压缩和膨胀行程中的κ′只需迭代4次以内就可以满足收敛条件。
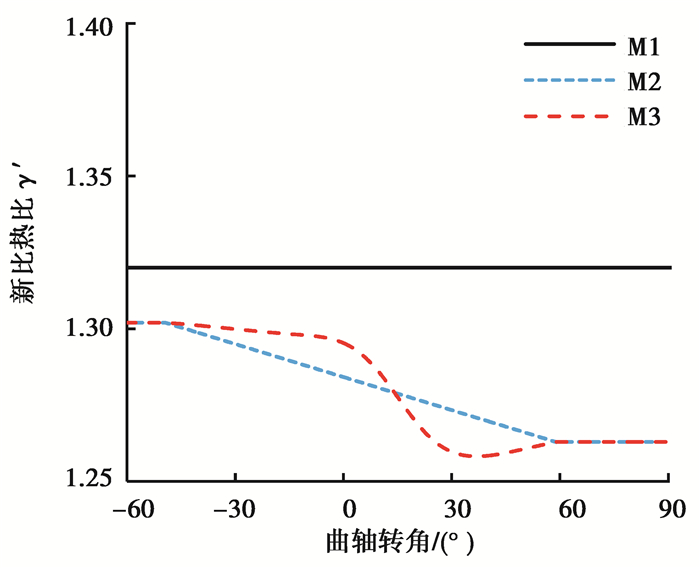
2.2 燃烧过程中γ′的插值由第1节可知两种模型经过简化已达到形式上的统一。关于模型2中燃烧过程γ′的插值方式,文献[17]中使用了基于曲轴转角进行线性插值的方法,如图 1中M2所示。考虑到γ′是由γ与δQht推演而来,这两个参数在发动机运行期间与缸内工质温度的变化接近线性相关[19],故提出了基于温度对燃烧过程中γ′进行插值的方法,用M3表示,其中工质温度可根据理想气体状态方程由IVC处进气温度与压力和容积曲线近似估计得到。将这两种不同的插值方式与模型1中广泛运用的恒定比热比法(M1)进行了放热率计算的对比。
|
图 1 γ′插值方法 Fig. 1 Interpolation method of γ′ |
与多缸机相比,单缸机气缸内进气量不受其他各缸影响,缸内有效燃油消耗能量的测定更加精准。考虑到这一点,本研究中用于算法验证的缸压数据是在1台压缩比为11的单缸高速汽油机上获得的。这款自然吸气式汽油机采用四气门结构,火花塞位于气缸盖中心。Kistler(6052C)压电式缸压传感器通过打孔齐平安装于气缸头部,采集到的缸内压力信号由DEWETRON-SIRIUS数据采集仪进行频率1 MHz的实时采样,用于后续的算法验证和评价。试验时通过调整节气门角度来改变负荷,ECU(engine control unit)采用MBT(maximum brake torque timing)点火角,空燃比均控制在当量比附近。缸压数据的曲轴转角分辨率设置为0.2°,并使用“两点法”对缸内压力进行了零点校正。
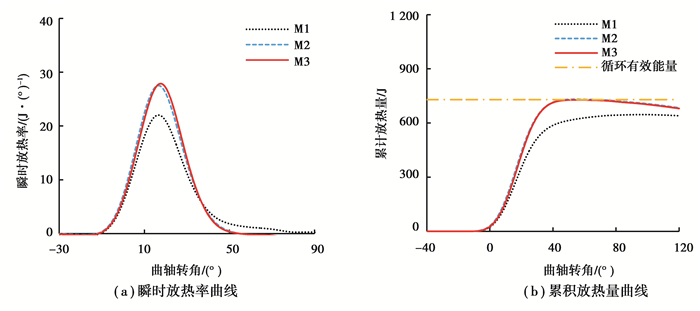
3 总放热率算法的评价验证 3.1 不同方法对循环释放能量的影响选取4 000 r/min外特性工况下的平均缸压数据,其中平均缸压曲线是360个循环缸内压力的平均值。分别使用M1、M2和M3这3种方法计算瞬时放热率和累计放热量,结果如图 2所示。由图 2(a)可知,相较于恒定比热比法M1计算所得的瞬时放热率曲线,M2和M3的放热率峰值均明显增高,且M2与M3的峰值差距较小。此外,可观察到M1计算的瞬时放热率在曲轴转角90° ATDC (after top dead center) 附近降低至0,但M2和M3计算的放热率的后半段均在曲轴转角60°ATDC左右迅速结束,这表明M2与M3方法的后半段燃烧均大幅缩短。累计放热量曲线是由瞬时放热率曲线积分所得,因此上述两个特征在图 2(b)中更加明显。
|
图 2 不同方法对放热率计算的影响 Fig. 2 Influence of different methods on heat-release rate calculation |
内燃机单个循环缸内有效释放能量可通过台架油耗与排气成分进行估算。比较不同算法累计放热量峰值与循环有效能量间的关系,可以对放热率算法的准确性提供一定的参考。由图 2(b)可知,M2与M3计算的累计放热量峰值非常接近循环有效能量,表明这两种方法比M1计算缸内累计释放能量更加准确。此外,可观察到M2与M3在曲轴转角60°ATDC后开始降低。这是因为在曲轴转角60° ATDC后M2与M3计算所得瞬时放热率均变为负值,M1在曲轴转角90° ATDC附近也逐渐降低。表明这两种方法并不具备“修平”累积放热量曲线的能力。
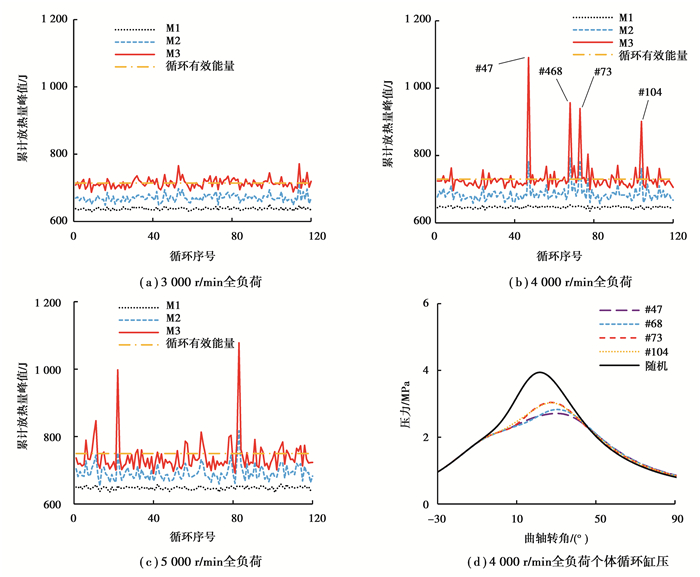
为进一步了解M2与M3对循环放热总量的修正效果,计算了3 000, 4 000, 5 000 r/min外特性工况下120个个体循环的累计放热量峰值,如图 3所示。相较于M1,M2与M3在不同转速下对个体循环放热总量均表现出了较好的修正效果,但累计放热量峰值随循环的变动率变大。相较于M2,M3累计放热量峰值更加接近循环有效能量,但循环变动率也变高。经过分析,M2与M3相较于M1累计放热量峰值循环变动率变大的原因在于压缩和膨胀过程中估计的κ′随循环变化存在变动。相较于M2的线性插值方法,M3使用温度插值的方法对放热率的“放大”效果更加突出,因此放热量峰值的波动程度更大。值得注意的是,图 3(b)与3(c)中均出现了个别循环放热量峰值异常的现象。选取4 000 r/min下的4个异常循环与随机选取循环进行对比,如图 3(d)所示,发现这些循环均为不正常燃烧循环。这些循环在进行参数估计时膨胀区间内的κ′值偏低,导致了放热量峰值被异常放大。总体而言,M2与M3对循环累计放热总量的估计更加精准,但并不适用于不正常燃烧循环的放热量计算。
|
图 3 不同方法对个体循环累计放热量峰值的影响 Fig. 3 Effects of different methods on cumulative heat-release peaks of different individual cycles |
燃烧控制参数表征了燃烧过程中对应的不同时间节点,汽油机的燃烧控制参数主要为:燃烧始点(CA05)、中点(CA50)及终点(CA90)[16]。CA05、CA50及CA90分别为累计放热量达到放热量峰值的5%、50%和90%时所对应的曲轴转角。此外,通常还可依据CA05和CA90计算燃烧持续期。研究不同计算方法对这些参数的影响可以系统地观察M2与M3对整个燃烧分析过程的影响。分别选取3 000, 4 000, 5 000 r/min外特性工况下120个个体循环的缸压进行分析。
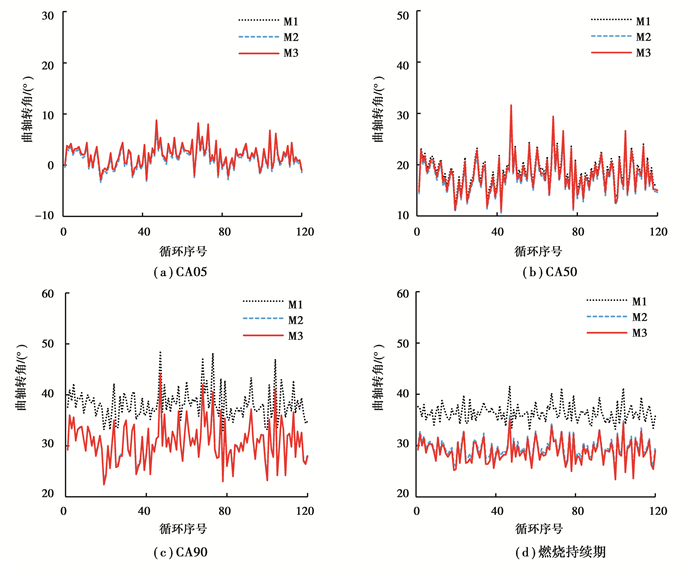
图 4为4 000 r/min外特性工况下3种方法计算所得的各循环燃烧控制参数。总体而言,不同方法并没有改变各参数的变化趋势,但它们的相位变动有所不同。由图 4(a)和(b)可知,相较于M1,M2的CA05和CA50相对提前;M3则相对延后,且M2与M3相位的变动值均较小。图 4(c)表明相较于M1,M2和M3的CA90均提前约8°左右,这与图 2(a)中放热率曲线提前结束的现象相吻合。M2与M3相较于M1的CA05变动不大且CA90提前,燃烧持续期也明显缩短,如图 4(d)所示。分析发现,M2与M3在燃烧区间内比热比的值均低于M1,如图 1所示,导致M2与M3计算的放热曲线结束较快,这与Brunt等[17]得到的结论一致。
|
图 4 不同方法对个体循环燃烧控制参数的影响 Fig. 4 Effects of different methods on combustion control parameters of different individual cycles |
汽油机的燃烧控制参数是燃烧过程始末的表征,它们之间存在互相影响,如相同条件下较早开始燃烧的循环通常结束较快。因此本研究中运用相关性分析,进一步探究M2及M3对CA05、CA50和CA90之间相关性的影响。图 5展示了4 000 r/min外特性工况下120个循环不同方法计算所得CA05与CA90间的相关性系数。M1的结果表明其非强相关(< 0.75),而M2与M3均加强了CA05与CA90之间的相关性,且M3比M2的改善效果略好。此相关性强表明燃烧始点越靠前则燃烧结束越快,与实际工程经验相符。

|
图 5 不同方法对全负荷4 000 r/min工况下CA05与CA90间相关性的影响 Fig. 5 Effects of different methods on the correlation between CA05 and CA90 under 4 000 r/min full load |
图 6给出了3 000,4 000,5 000 r/min外特性工况下不同方法所得各燃烧控制参数间的相关性系数,其中同一指标下从左至右3项分别为3 000, 4 000, 5 000 r/min下的结果。可见不同转速下M1方法仅CA05与CA50间存在着稳定的强相关性,其余参数间相关性均较弱。特别是CA50与燃烧持续期之间的相关性系数在0.3以下。使用M2与M3方法后,CA50与燃烧持续期之间的相关性被加强至中等程度,其余各参数间基本上均保持稳定的强相关,且两种方法对燃烧控制参数间相关性的改善效果差异较小。这表明M2与M3方法计算的各燃烧控制参数与缸内的实际燃烧历史更吻合。
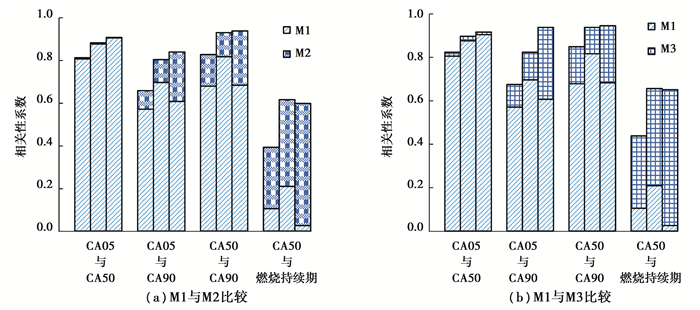
|
图 6 不同方法对燃烧控制参数间相关性的影响 Fig. 6 Effect of different methods on correlation between combustion control parameters |
目前工程上应用的单区放热率算法存在比热比和传热难以合理估计的问题,笔者在此背景下研究了一种考虑传热影响的比热比估计方法。首先估计压缩和膨胀期间的多变指数,进而依据曲轴转角(M2)或工质温度(M3)插值计算燃烧区间内的比热参数,用于总放热率的计算。从循环释放能量和燃烧控制参数的角度将这两种方法与恒定比热比法(M1)进行了对比验证,主要结论如下:
1) 相较于M1,M2与M3放热率曲线的峰值均明显升高,后半段放热持续期缩短。
2) 相较于M1与M2,所提出的M3方法估计的循环累计放热总量更加精准,但循环变动率也变大。对于不正常燃烧循环,M2与M3放热总量异常,这是由膨胀过程所估计的比热比参数相对偏低导致的。
3) 相较于M1,应用M2与M3方法得到的各循环CA90提前。M2与M3对燃烧控制参数的影响差异不大,燃烧控制参数间的相关性得到明显改善,能够更加准确地描述缸内燃烧历程。
| [1] |
Guardiola C, Olmeda P, Pla B, et al. In-cylinder pressure based model for exhaust temperature estimation in internal combustion engines[J]. Applied Thermal Engineering, 2017, 115: 212-220. DOI:10.1016/j.applthermaleng.2016.12.092 |
| [2] |
张力, 郑仁蔚, 张青, 等. 移动窗口域的VDO爆震燃烧识别扩展算法[J]. 重庆大学学报, 2017, 40(8): 19-26. Zhang L, Zheng R W, Zhang Q, et al. VDO knock diagnosis expansion algorithm based on moving window domain[J]. Journal of Chongqing University, 2017, 40(8): 19-26. (in Chinese) |
| [3] |
Guardiola C, Pla B, Bares P, et al. Closed-loop control of a dual-fuel engine working with different combustion modes using in-cylinder pressure feedback[J]. International Journal of Engine Research, 2020, 21(3): 484-496. DOI:10.1177/1468087419835327 |
| [4] |
Lee Y, Min K. Estimation of the polytropic index for in-cylinder pressure prediction in engines[J]. Applied Thermal Engineering, 2019, 158: 113703. DOI:10.1016/j.applthermaleng.2019.04.113 |
| [5] |
Juknelevicius R, Szwaja S, Pyrc M, et al. Influence of hydrogen co-combustion with diesel fuel on performance, smoke and combustion phases in the compression ignition engine[J]. International Journal of Hydrogen Energy, 2019, 44(34): 19026-19034. DOI:10.1016/j.ijhydene.2018.10.126 |
| [6] |
Fang C, Ouyang M G, Tunestal P, et al. Closed-loop combustion phase control for multiple combustion modes by multiple injections in a compression ignition engine fueled by gasoline-diesel mixture[J]. Applied Energy, 2018, 231: 816-825. DOI:10.1016/j.apenergy.2018.09.147 |
| [7] |
Irimescu A, Di Iorio S, Merola S S, et al. Evaluation of compression ratio and blow-by rates for spark ignition engines based on in-cylinder pressure trace analysis[J]. Energy Conversion and Management, 2018, 162: 98-108. DOI:10.1016/j.enconman.2018.02.014 |
| [8] |
Krieger R B, Borman G L. The computation of apparent heat release for internal combustion engines[R]. ASME, 1966.
|
| [9] |
Baratta M, Ferrari A, Zhang Q. Multi-zone thermodynamic modeling of combustion and emission formation in CNG engines using detailed chemical kinetics[J]. Fuel, 2018, 231: 396-403. DOI:10.1016/j.fuel.2018.05.088 |
| [10] |
Bissoli M, Frassoldati A, Cuoci A, et al. A new predictive multi-zone model for HCCI engine combustion[J]. Applied Energy, 2016, 178: 826-843. DOI:10.1016/j.apenergy.2016.06.062 |
| [11] |
Nazoktabar M, Jazayeri S A, Arshtabar K, et al. Developing a multi-zone model for a HCCI engine to obtain optimal conditions using genetic algorithm[J]. Energy Conversion and Management, 2018, 157: 49-58. DOI:10.1016/j.enconman.2017.12.001 |
| [12] |
Saeed K. A novel regenerative multiple zones model for modelling the premixed charge stirred chemical reactor based combustion engines[J]. Journal of the Energy Institute, 2017, 90(5): 680-695. DOI:10.1016/j.joei.2016.07.009 |
| [13] |
Neshat E, Honnery D, Saray R K. Multi-zone model for diesel engine simulation based on chemical kinetics mechanism[J]. Applied Thermal Engineering, 2017, 121: 351-360. DOI:10.1016/j.applthermaleng.2017.04.090 |
| [14] |
Tabatabaie T, Ehteram M A, Hosseini V. Investigating the effect of the heat transfer correlation on the predictability of a multi-zone combustion model of a hydrogen-fuelled spark ignition engine[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2016, 230(1): 70-81. DOI:10.1177/0954407015578047 |
| [15] |
Lashkarpour S M, Khoshbakhti Saray R, Najafi M. Multi-zone model for reactivity controlled compression ignition engine based on CFD approach[J]. Energy, 2018, 156: 213-228. DOI:10.1016/j.energy.2018.05.084 |
| [16] |
Yousefzadeh A, Jahanian O. Using detailed chemical kinetics 3D-CFD model to investigate combustion phase of a CNG-HCCI engine according to control strategy requirements[J]. Energy Conversion and Management, 2017, 133: 524-534. DOI:10.1016/j.enconman.2016.10.072 |
| [17] |
Brunt M F J, Emtage A L. Evaluation of burn rate routines and analysis errors[J/OL]. SAE Technical Papers, 1997: 970037[2020-02-05]. https://saemobilus.sae.org/content/970037. DOI: https://doi.org/10.4271/970037.
|
| [18] |
Tunestål P. Self-tuning gross heat release computation for internal combustion engines[J]. Control Engineering Practice, 2009, 17(4): 518-524. DOI:10.1016/j.conengprac.2008.09.012 |
| [19] |
Heywood J. Internal combustion engine fundamentals[M]. New York: McGraw-Hill, 1988.
|
 2021, Vol. 44
2021, Vol. 44


