b. 重庆大学 汽车工程学院, 重庆 400044
b. School of Automotive Engineering, Chongqing University, Chongqing 400044, P. R. China
多轴轮边电驱动型卡车可以省去变速箱、传动轴及差速器等结构,大大简化了传动系统结构,提升驱动效率,相比于传统机械传动结构车辆,可以显著提高整车经济性,已经成为当前研究的热点[1-2]。研究表明,双轴电驱动车辆的驱动模式(两驱或者四驱)对整车经济性具有较大的影响[3-4],当电驱动轴增加后,驱动力分配方式对整车经济性的影响将进一步增加。所以,为充分发挥多轴电驱动车辆高效驱动的特点,需要对其各轴间驱动力的分配方式进行深入研究。
目前,国内外针对多轴车辆驱动力分配的研究,已取得一些成果。文献[5]分析了多轴独立驱动车辆在各驱动工况下宜采用的驱动方式,并指出在一般良好路面上应采用基于经济性的驱动力分配方式。文献[6-7]针对3轴3电机独立驱动越野车,提出了一种基于电机系统效率最优的驱动力分配控制策略,并制定了驱动力分层控制方法来抑制驱动轮滑转,可以提高整车驱动经济性和通过性,但在优化过程中,预设前轴、中轴和后轴转矩分配系数(分别表示为Kf,Km,Kr)的关系为Kf≤Km≤Kr,无法涵盖所有分配情况,当驱动轴数继续增加时,是否仍然是驱动轮尽量在后更有利于车辆的驱动,有待进一步验证。文献[8]针对某6轮驱动纯电动车辆,在不同车速下,将每个电机的效率转化成其转矩的多项式函数,在此基础上对整车驱制动过程的转矩分配进行优化,该策略可以使车辆工作过程中6轮驱动系统效率最优,但未考虑驱制动过程中轴荷转移对车轮附着力的影响,当车轮发生滑转时可能无法响应最优转矩。
针对当前研究现状,提出一种应用于某型10×10增程式电动卡车(extended-range electric truck, ERET)的驱动力优化分配策略。在常规驱动模式下,以电驱动系统效率最优为核心,采用瞬时优化算法对驱动转矩的分配进行离线优化,生成可实时应用的驱动模式表并对其进行规则化处理,通过查表插值可以确定驱动轴数;基于整车轴荷分布情况,确定具体驱动轴,以充分利用地面附着力;利用Matlab/Simulink搭建整车后向仿真模型,在调整的世界重型商用车循环(adapted world transient vehicle cycle, C-WTVC)工况上进行仿真,分析所提出的驱动力优化分配策略对整车经济性的影响。
1 ERET结构简介ERET为10×10轮边电驱动形式,每根驱动轴上均配备2台相同的轮边永磁同步电机,整车结构如图 1所示,实线表示机械连接,虚线表示电气部件之间的电气连接。ERET的供电系统由柴油机辅助动力系统(auxiliary power unit, APU)和动力电池组成,其中APU系统由柴油机、变速机构和1台发电机组成,动力电池采用高性能锂电池。动力电池电量充足时可以单独为轮边电机提供动力,当其电量低于一定值时,APU会介入工作,为电池充电或者直接驱动轮边电机,从而延长续驶里程。
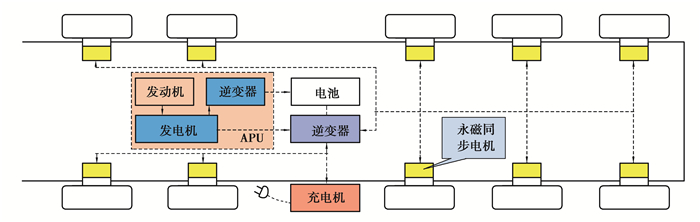
|
图 1 ERET整车结构简图 Fig. 1 Vehicle structure diagram |
APU与动力电池组单独或者协同向电驱动系统提供能量,当负载一定时,电驱动系统效率越高,则其对能量源的功率需求相对越低,即系统越节能。电驱动系统可以根据工况需求,灵活采用单轴驱动、双轴驱动、3轴驱动、4轴驱动或5轴驱动模式,不同驱动模式对应不同的功率分配方式,会影响电驱动系统的效率。当前ERET采用驱动力平均分配控制策略,控制简单,对控制器内存占用较小,但无法充分发挥电驱动系统的高效驱动能力。
因此,当负载一定时,需要对电驱动系统的驱动力进行优化分配。10台驱动电机通过路面进行耦合,轮边减速机构速比i0相同,在同一车速下,10台驱动电机的转速一样,对驱动力的分配即为对当前车速下的驱动电机转矩进行分配。笔者基于图 2所示永磁同步电机稳态效率图,采用瞬时优化算法对电驱动系统效率进行优化计算。
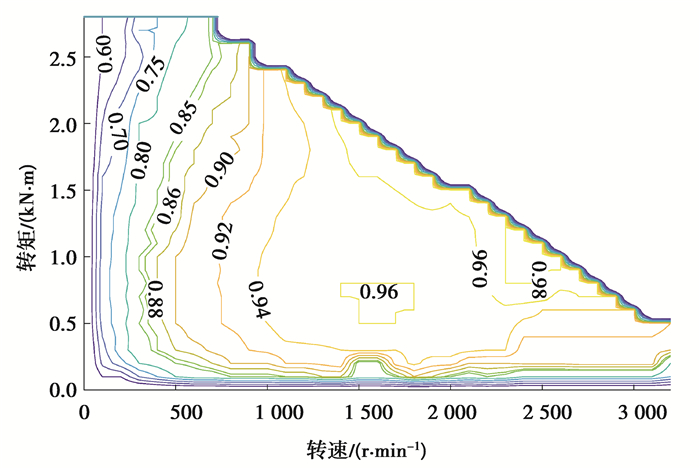
|
图 2 电机效率图 Fig. 2 Diagram of motor efficiency |
汽车行驶阻力包括滚动阻力、坡度阻力、空气阻力和加速阻力,其计算公式为
| $ F_{\mathrm{r}}=m g f \cos \alpha+m g \sin \alpha+\frac{C_{\mathrm{D}} A u_{\mathrm{a}}^{2}}{21.15}+\delta m \frac{\mathrm{d} u}{\mathrm{~d} t}, $ | (1) |
式中:Fr为车辆运行总阻力,N;m为整车质量,kg;g为重力加速度,m/s2;f为滚动阻力系数;α为坡度,(°);CD为空气阻力系数;A为迎风面积,m2;ua为车速,km/h;u为车速,m/s;r为车轮半径,m;δ为旋转质量转换系数。
整车需求功率Preq为
| $ P_{\mathrm{req}}=F_{\mathrm{r}} u / 1000。$ | (2) |
电驱动系统的输入功率Pin为
| $ P_{\mathrm{in}}=\sum T_{\mathrm{m} i} \omega_{\mathrm{m} i} / \eta_{\mathrm{m} i}, $ | (3) |
式中:Tmi为第i台驱动电机的转矩,N·m,i=1, 2,…,10;ωmi为第i台驱动电机转子的角速度,rad/s;ηmi为第i台驱动电机的驱动效率,通过实验数据插值获取,ηmi=f(Tmi, ωmi)。
因此电驱动系统效率ηm_sys可以定义为
| $ \eta_{\mathrm{m}_{-} \mathrm{sys}}=P_{\mathrm{req}} / P_{\mathrm{in}}。$ | (4) |
驱动电机转速与车速的关系为
| $ u_{\mathrm{a}}=0.377 \frac{n r}{i_{0}}, $ | (5) |
式中:n为驱动电机当前转速,r/min;i0为轮边减速机构的减速比。
电驱动系统效率优化的目标函数为
| $ \max \eta_{\mathrm{m}_{-} \mathrm{sys}}。$ | (6) |
公式(1)~(6)约束条件如下:
| $ \left\{ {\begin{array}{*{20}{l}} {0 \le \left| {{P_{{\rm{bat }}}}} \right| \le {P_{{\rm{bat\_max}}}}, }\\ {0 \le \left| {{P_{{\rm{APU}}}}} \right| \le {P_{{\rm{APU\_max}}}}, }\\ {{U_{{\rm{min}}\_{\rm{dis}}}} \le {U_{{\rm{bat}}}} \le {U_{\max \_{\rm{dis}}}}, }\\ {0 \le \left| {{T_{{\rm{m}}i}}\left( {{n_{{\rm{m}}i}}} \right)} \right| \le {T_{{\rm{m}}{i_ - }\max }}\left( {{n_{{\rm{m}}i}}} \right), }\\ {0 \le {n_{{\rm{m}}i}} \le {n_{{\rm{m}}{i_ - }\max }}。} \end{array}} \right. $ | (7) |
式中:Pbat为需求的动力电池放电功率,kW;Pbat_max为动力电池能提供的最大放电功率,kW;PAPU为需求的APU功率,kW;PAPU_max为APU能发出的最大功率,kW;Ubat为动力电池的端电压,V;Umax_dis和Umin_dis分别为动力电池端电压的最大和最小值,V;Tmi(nmi)为第i台驱动电机的需求转矩,N·m;Tmi_max(nmi)为转速nmi时驱动电机i能发出的峰值转矩,N·m;nmi_max为驱动电机i的最高转速,r/min。
2.2 优化过程基于上述优化目标函数和约束条件,在每一个工况点(车速—整车需求转矩)下,分别计算单轴驱动、双轴驱动、3轴驱动、4轴驱动和5轴驱动对应的电机系统驱动效率,选择效率最高的驱动方式为目标驱动模式,优化流程如图 3所示。
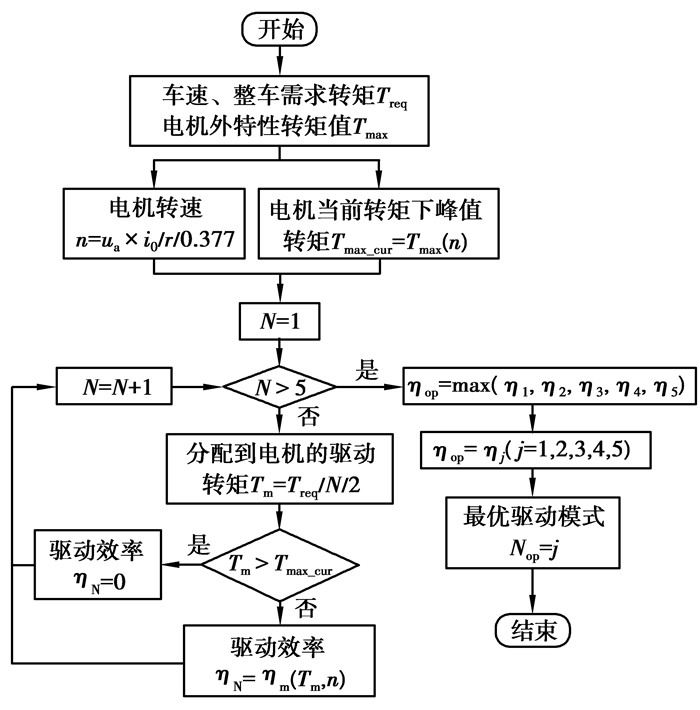
|
图 3 各工况点优化流程 Fig. 3 Optimization process of each operating point |
以动力源外特性为工作范围约束,比较各驱动模式的电驱动效率,将三维效率图向“车速-整车需求转矩”平面投影,可得到任意工况所对应的最优驱动效率,如图 4所示;电驱动系统效率最高的驱动模式,即为当前工况所对应的最经济工作模式[9-11]。所有可行工况点下最优的驱动模式表如图 5所示,其中,模式“1”表示单轴驱动,模式“2”表示双轴驱动,模式“3”表示3轴驱动,模式“4”表示4轴驱动,模式“5”表示5轴驱动,并且模式1~4中的驱动轴需要根据实时轴荷情况来进行选取(见第3节)。
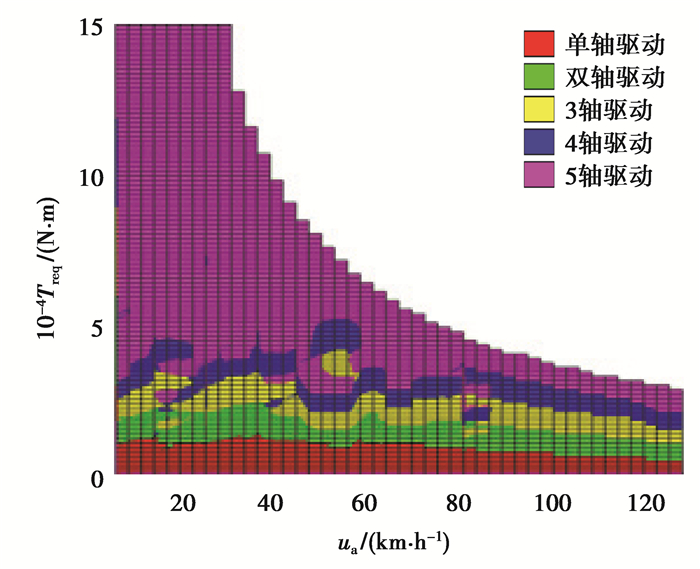
|
图 4 各模式下电驱动系统效率图 Fig. 4 Efficiency diagram of electric drive system in each mode |
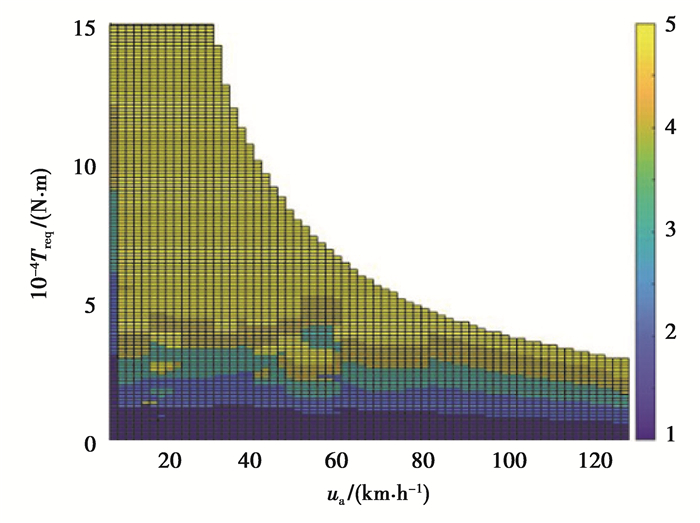
|
图 5 电驱动系统效率最优的驱动模式表 Fig. 5 Driving mode table for optimal efficiency of electric drive system |
分别采用转矩最优化分配策略和转矩平均分配策略,遍历所有可行工况范围内的工况点效率,可以得到图 6所示效率分布图。对比图 6(a)和(b),可以看出采用最优化转矩分配策略时,高效区(85%及以上)向中高速的低转矩区扩展,增大了高效工作区的范围,可以使车辆在低转矩区运行时保持较高的驱动效率。对两种策略下工作在高效区内的工作点比例进行统计,结果见表 1,可以看出,采用最优驱动力分配策略和转矩分配策略时,工作点在高效区的比例分别为70.57%和62.70%,经过优化的电驱动系统高效区比例提升了7.87%。
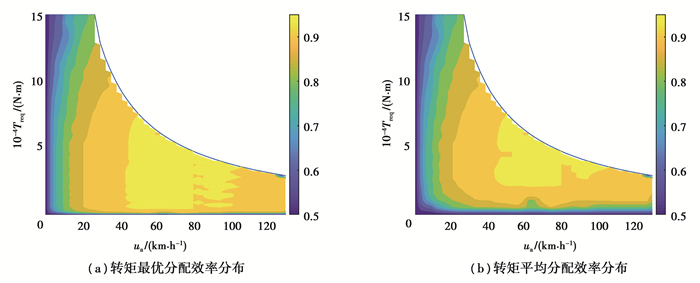
|
图 6 不同转矩分配方式下的电驱动系统效率分布 Fig. 6 Efficiency distribution of electric drive system with different torque distribution modes |
| 表 1 高效区对比 Table 1 Proportion of efficient areas |
由于所选用的高性能驱动电机存在局部高效区,使得驱动模式表分布不均匀,易引起驱动模式频繁切换。模式切换过程中,驱动轴会发生改变。当总的需求转矩增加时,低数量的驱动轴无法满足驱动力需求,需要更多的驱动轴介入工作;当总的需求转矩减小时,需要减少驱动轴数,以提高单个驱动电机的负荷率,从而保证整车运行的经济性。所以,模式切换时,会存在新工作电机的介入或者当前工作电机的退出。由于永磁同步电机在介入工作时升扭响应速度要慢于其在退出工作时的降扭响应速度,会导致切换过程中总的驱动转矩产生波动,进而可能引起较大的冲击[12-13]。如果频繁出现驱动电机的启停,也会增加对各电机控制器的控制难度。所以,应尽可能减少车辆运行过程中驱动模式的切换频率,以降低整车冲击和控制难度。这里采用两种措施来改善模式频繁切换的状况:
1) 两种不同驱动模式相交的区域,电驱动系统效率相差很小,所以,为了控制效果更佳,并改善模式频繁切换问题,将原始驱动模式表中出现的局部模式进行临近整合,使驱动模式表趋于规则化。
2) 若驱动模式边界为严格的单阈值线,当车辆运行工况在模式边界线上时,加速踏板的轻微抖动就可能使需求驱动模式发生切换。因此,需要对模式边界进行扩展,扩展的边界跨度速度维度为2 km/h,整车需求转矩维度为1 200 N·m。当控制器判定驱动模式落在模式交界的带状区域后(模式为“0”),不进行模式切换;当识别结果在上边界以上时,才会由模式Nop向模式(Nop+1)切换;当识别结果在下边界以下时,才会由模式Nop向模式(Nop-1)切换。通过这种方式可以在一定程度上降低模式切换的频率[14-15]。
按照上述两种措施对图 5中的最优驱动模式表进行处理,结果如图 7所示。
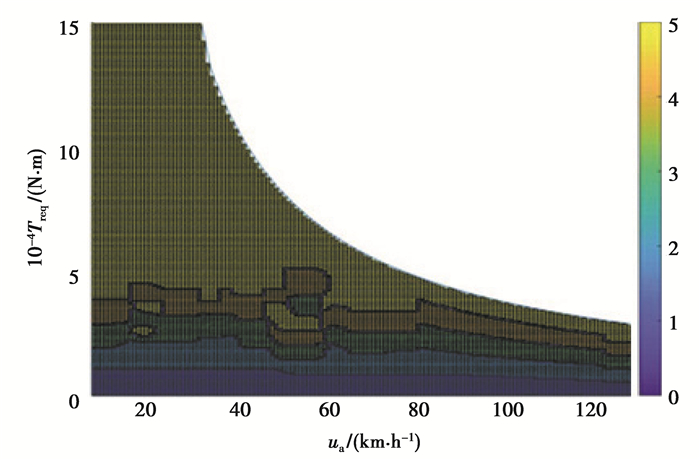
|
图 7 规则化的驱动模式表 Fig. 7 Regularized drive mode table |
从图 7可以插值得出最经济的驱动模式Nop(Nop=1,2,3,4或5),即采用几根驱动轴进行驱动,但具体采用哪些轴进行驱动需要考虑实时轴荷的变化,以保证车辆驱动过程中可以留有较大的附着余量,减小出现滑转的概率。
所研究的ERET工作时即为满载,驱动过程中可能会因速度变化引起轴荷转移。轴荷转移会造成某一轴甚至多轴出现垂向载荷不足,进而引起该轴上附着利用率减小,使车轮因滑转而无法响应最优驱动力。因此,需要在不考虑滑转带来的力矩重新分配基础上,根据实时轴荷分布情况优先选择质量较大的车轴作为驱动轴。将所制定的转矩分配控制策略用流程图 8表示。
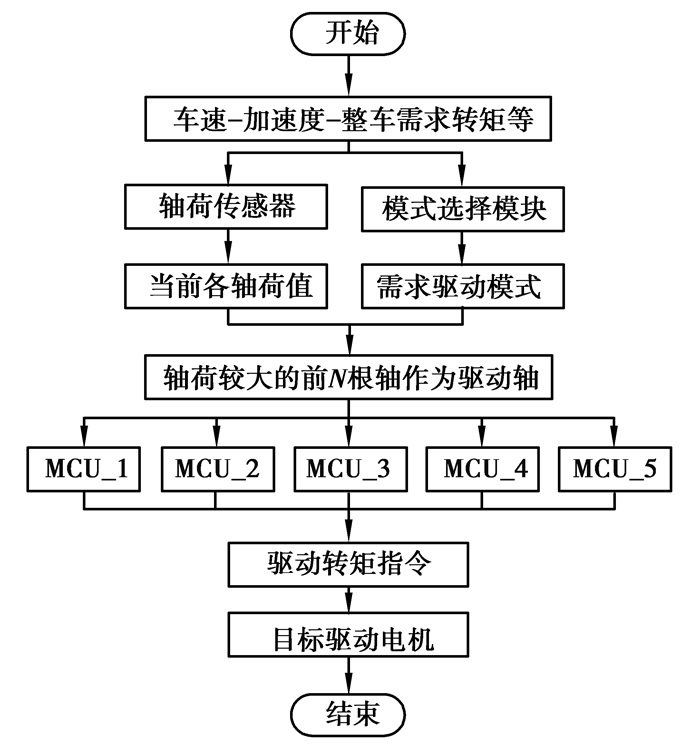
|
图 8 转矩分配控制策略流程图 Fig. 8 Flow chart of torque distribution control strategy |
轴荷传感器会将轴荷分布状态传递给控制器,控制器根据当前工况查表得到需求驱动轴数Nop,将驱动指令分配到轴荷大小排在前Nop位的轴。在确定了具体驱动轴以后,整车控制器会将总的需求转矩均分给目标驱动轴,这种分配方式有利于提高驱动效率[16-17]。同一根轴上对分配到的转矩,会再平均分配给左右2个轮边电机,保证车辆横向稳定性。
例如,当控制器确定的最优驱动轴数Nop=3,而轴荷传感器得到的轴荷大小顺序依次为第5轴、第3轴、第1轴、第2轴和第4轴,则控制器将选择第5轴、第3轴和第1轴为驱动轴,然后将整车需求转矩均分到3根轴上,每根驱动轴上的转矩经过折算后平均分配给左右2台轮边电机来对车辆进行驱动。
4 经济性仿真验证 4.1 仿真模型搭建目前最具代表性的2种电动汽车仿真方式为前向仿真和后向仿真,两者在建模的方法以及仿真的运行上均具有各自的优缺点。后向仿真不包括驾驶员模型,排除了驾驶行为对经济性的影响,较适合用于车辆设计阶段,可以用来指导零部件和控制策略选择;而前向仿真更适合于车辆设计的后期,用来调整、优化参数或控制策略,以完善车辆性能。考虑到经济性仿真更适合采用后向仿真,所以利用MATLAB/Simulink平台建立了后向仿真模型来对提出的驱动力优化分配策略进行验证。
由于ERET在电量充足情况下可以长时间工作在纯电动工作模式,当动力电池电量降低到某一设定值后APU系统才会介入工作,并且电驱动系统只能通过电能来进行驱动,故可在纯电动模式下对电驱动系统的最优化转矩分配策略进行验证,建模过程中可以假设APU始终处于关闭状态,车辆也就简化为多轴纯电动汽车,不必再对APU系统进行建模。
ERET后向仿真模型架构如图 9所示,在静态轴荷(见表 2)基础上,建立了动态轴荷转移模型[18-19]来模拟ERET运行时的轴荷状态,以轴荷转移引起的最大附着力的变化作为转矩分配模块的约束条件之一。转矩分配模块中,以经过离线优化的驱动模式表作为插值基准,得到各工况下最优的驱动模式,并在各约束条件下生成驱动指令,发送给相应驱动电机。由于从电机输出轴到车轮只有一个减速器和半轴,传动链短,效率高,所以将传动系统模型进行了简化,按照固定传动比和机械传动效率进行仿真计算。
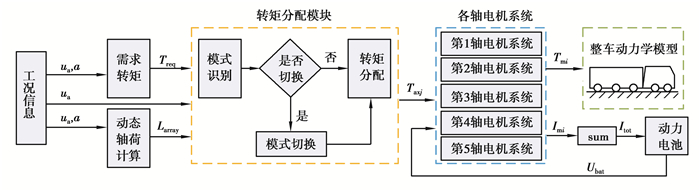
|
图 9 整车后向仿真模型框架 Fig. 9 Vehicle backward simulation model framework |
| 表 2 ERET满载时静态轴荷分布 Table 2 Static axle load distribution at full ERET load |
图 9中,a为车辆瞬时加速度,m/s2;Larray为动态轴荷大小排列序列;Taxj为分配到各轴的转矩,N·m;Imi为各电机工作电流,A;Itot为动力电池工作电流,A。
4.2 仿真结果对比分析选择C-WTVC工况进行经济性仿真,以对最优驱动力分配控制策略、转矩平均分配控制策略及基于轴荷比的转矩分配控制策略进行对比研究,工况特征如图 10所示。
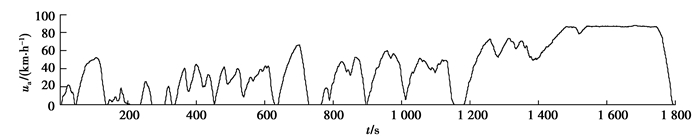
|
图 10 C-WTVC工况速度曲线 Fig. 10 Velocity curve of C-WTVC |
1) 工作点分布对比。
3种控制策略下各驱动电机工作点分布分别如图 11(a)(b)和(c)所示。从图 11(a)可以看出,采用转矩平分策略时,10台驱动电机的工作点始终相同,而且集中在低转矩范围,效率较低;图 11(b)显示按轴荷比进行分配时,在常规驱动工况下,动态载荷变化并不大,所以工作点仍然集中在低效区;而采用最优化转矩分配策略时,电机工作点则集中在较为高效的区域,如图 11(c)所示,在起步等低转矩工况下,优先采用第5轴上的电机进行驱动,这是因为起步时车辆重心会后移,而且随着需求转矩的变化,驱动轴也会相应发生变化,使得电驱动系统始终以最经济模式运行。
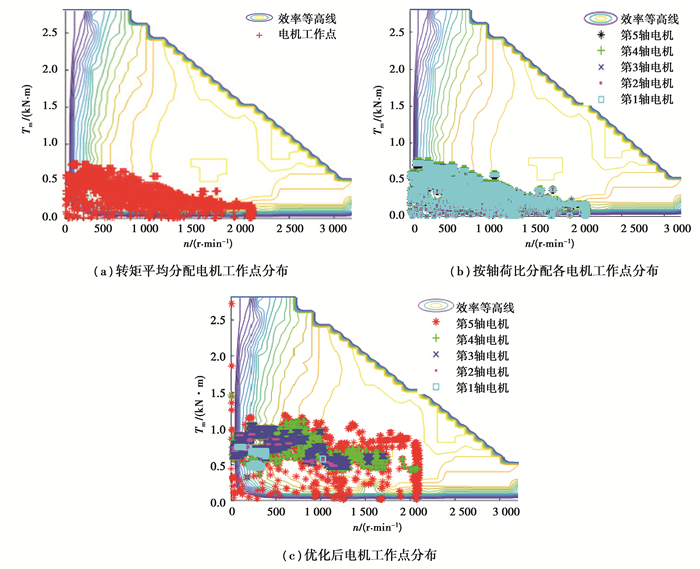
|
图 11 不同控制策略下驱动电机工作点分布 Fig. 11 Distribution of driving motor operating points under different control strategies |
2) 能耗对比。
采用3种控制策略所得百公里电耗值见表 3。可见,在C-WTVC工况下,采用电驱动系统效率最优化转矩分配控制策略时,较其他两种策略,可以节能6.12%~9.18%,效果明显。
| 表 3 经济性仿真结果 Table 3 Economic simulation results |
3) 模式识别结果分析。
以0~200 s工况段为例,对效率最优化转矩分配控制策略仿真分析过程中的模式识别问题进行分析。采用图 5所示不经处理的驱动模式表时,得到的模式识别结果如图 12(b)所示,采用图 7所示经规则化处理的驱动模式表时,得到的模式识别结果如图 12(c)所示,采用两种驱动模式表得到的C-WTVC工况能耗如表 4所示。
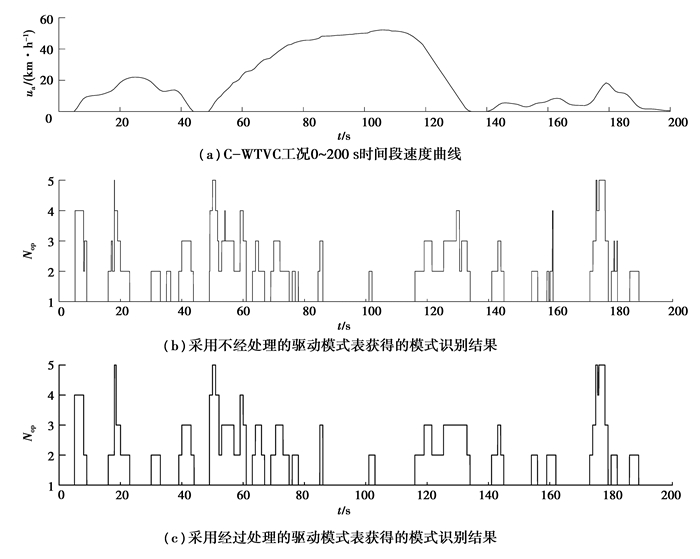
|
图 12 模式识别结果对比 Fig. 12 Comparison of mode recognition results |
| 表 4 驱动模式表处理前后能耗对比 Table 4 Energy consumption comparison before and after table processing |
可以看出,采用规则化处理的驱动模式表,可以有效地减少如图 12(b)中标注的瞬时模式,降低应用过程中的控制难度和模式切换频率,改善整车舒适性。而从能耗上来看,对驱动模式表处理前后百公里电耗变化量仅为0.1 kW · h/100 km,可以忽略不计。
5 结论为提高某5轴电驱动车辆的运行经济性,提出了一种基于电机系统效率最优的驱动力分配控制策略,该策略以电机系统效率最优为目标,分别计算同一工况点下单轴驱动、双轴驱动、3轴驱动、4轴驱动和5轴驱动模式下的电机系统效率,选择效率最高的驱动模式为目标模式,然后以电机外特性为约束条件,遍历计算所有工况点下的最优驱动模式,生成“车速—需求转矩—最优驱动模式表”,并对其进行规则化处理。在此基础上,考虑整车动态轴荷变化来选取目标驱动轴,实现对车辆的驱动控制。基于MATLAB/Simulink平台进行仿真,得出如下结论:
1) 采用基于电机系统效率最优的转矩分配控制策略可以提高各工作电机的负荷率及工作效率,相对转矩平均分配控制策略和按轴荷比例分配的控制策略具有更好的经济性。
2) 基于动态轴荷实时变化情况来选择驱动轴,可以使车辆充分利用轮胎与地面之间的附着力,保证车辆以最优驱动力稳定运行。
3) 采用“离线优化+在线应用”思想,首先对ERET驱动模式表进行离线优化,并对优化结果进行适当规则化处理,仿真结果表明该方案可以减小车辆运行过程中驱动模式切换的频率,在保证经济性的基础上兼顾车辆运行的舒适性,并降低了对电驱动系统的控制难度,有利于工程化应用。
| [1] |
龚贤武, 唐自强, 赵轩, 等. 轮边电机驱动型电动汽车动力系统参数优化设计[J]. 合肥工业大学学报(自然科学版), 2017, 40(1): 24-30. Gong X W, Tang Z Q, Zhao X, et al. Optimization design of powertrain parameter for in-wheel motor driven electric vehicles[J]. Journal of Hefei University of Technology (Natural Science), 2017, 40(1): 24-30. (in Chinese) DOI:10.3969/j.issn.1003-5060.2017.01.005 |
| [2] |
智晋宁, 项昌乐, 朱丽君, 等. 轮边电机驱动汽车性能仿真与控制方法的研究[J]. 汽车工程, 2012, 34(5): 389-393. Zhi J N, Xiang C L, Zhu L J, et al. A study on the performance simulation and control scheme for in-wheel motor driven vehicles[J]. Automotive Engineering, 2012, 34(5): 389-393. (in Chinese) DOI:10.3969/j.issn.1000-680X.2012.05.003 |
| [3] |
Sun B B, Gao S, Ma C, et al. System power loss optimization of electric vehicle driven by front and rear induction motors[J]. International Journal of Automotive Technology, 2018, 19(1): 121-134. DOI:10.1007/s12239-018-0012-5 |
| [4] |
Shen P H, Sun Z C, Zeng Y J, et al. Study on power ratio between the front motor and rear motor of distributed drive electric vehicle based on energy efficiency optimization[C]//SAE Technical Paper Series. 400 Commonwealth Drive, Warrendale, PA, United States: SAE International, 2016.
|
| [5] |
韦克康, 郝瑞祥, 孙湖, 等. 串联式混合动力多轴独立驱动车辆的电机驱动系统设计[J]. 电力电子, 2009, 7(2): 17-20. Wei K K, Hao R X, Sun H, et al. Design of the motor propulsion system for multiple- axiles-indenpently driver SHEV[J]. Power Electronics, 2009, 7(2): 17-20. (in Chinese) DOI:10.3969/j.issn.1000-100X.2009.02.008 |
| [6] |
范晶晶, 毛明. 基于经济性的三轴电传动车辆驱动力分配策略研究[J]. 车辆与动力技术, 2007(1): 49-51, 55. Fan J J, Mao M. A study of driving force distribution strategy for three-axles electric driving vehicle based on economics[J]. Vehicle & Power Technology, 2007(1): 49-51, 55. (in Chinese) DOI:10.3969/j.issn.1009-4687.2007.01.011 |
| [7] |
范晶晶, 罗禹贡, 张弦, 等. 多轴独立电驱动车辆驱动力的协调控制[J]. 清华大学学报(自然科学版), 2011, 51(4): 478-481. Fan J J, Luo Y G, Zhang X, et al. Coordinated control of driving torque for multi-axles independent driving vehicles[J]. Journal of Tsinghua University (Science and Technology), 2011, 51(4): 478-481. (in Chinese) |
| [8] |
Yun S, Yi K, Cheon S, et al. Development of a motor torque distribution strategy of six-wheel-driven electric vehicles for optimized energy consumption[C]//SAE Technical Paper Series. 400 Commonwealth Drive, Warrendale, PA, United States: SAE International, 2013.
|
| [9] |
初亮, 张培志, 林婷婷. 纯电动轿车模式识别及模式切换策略[J]. 华中科技大学学报(自然科学版), 2014, 42(6): 12-16. Chu L, Zhang P Z, Lin T T. Study on mode recognition and mode switching strategy of electric vehicle[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2014, 42(6): 12-16. (in Chinese) |
| [10] |
Hu M H, Zeng J F, Xu S Z, et al. Efficiency study of a dual-motor coupling EV powertrain[J]. IEEE Transactions on Vehicular Technology, 2015, 64(6): 2252-2260. DOI:10.1109/TVT.2014.2347349 |
| [11] |
Hu M H, Chen S, Zeng J F. Control strategy for the mode switch of a novel dual-motor coupling powertrain[J]. IEEE Transactions on Vehicular Technology, 2018, 67(3): 2001-2013. DOI:10.1109/TVT.2017.2769127 |
| [12] |
高松, 孙宾宾, 王鹏伟, 等. 双电机前后轴独立驱动电动车模式切换冲击度的测试分析[J]. 汽车工程, 2017, 39(5): 561-568. Gao S, Sun B B, Wang P W, et al. An experimental analysis on mode-switch jerk of front and rear motor drive electric vehicle[J]. Automotive Engineering, 2017, 39(5): 561-568. (in Chinese) |
| [13] |
杨阳, 杨文辉, 秦大同, 等. 强混合动力汽车驱动模式切换扭矩协调控制策略[J]. 重庆大学学报, 2011, 34(2): 74-81, 94. Yang Y, Yang W H, Qin D T, et al. Coordinated torque control strategy for driving-mode-switch of strong hybrid electric vehicle[J]. Journal of Chongqing University, 2011, 34(2): 74-81, 94. (in Chinese) |
| [14] |
巴特, 高印寒, 曾小华, 等. 混合动力汽车工作模式切换控制方案[J]. 吉林大学学报(工学版), 2016, 46(1): 21-27. Ba T, Gao Y H, Zeng X H, et al. Mode-switch control scheme for hybrid electric vehicle[J]. Journal of Jilin University (Engineering and Technology Edition), 2016, 46(1): 21-27. (in Chinese) |
| [15] |
Yin D J, Hori Y. Traction control for EV based on maximum transmissible torque estimation[J]. International Journal of Intelligent Transportation Systems Research, 2010, 8(1): 1-9. DOI:10.1007/s13177-009-0005-x |
| [16] |
陈浩, 袁良信, 郑四发, 等. 基于能耗优化的电动轮汽车转矩动态分配[J]. 清华大学学报(自然科学版), 2020, 60(2): 132-138. Chen H, Yuan L X, Zheng S F, et al. Dynamic torque allocation for in-wheel motor driven vehicle based on energy consumption optimization[J]. Journal of Tsinghua University (Science and Technology), 2020, 60(2): 132-138. (in Chinese) |
| [17] |
Yuan X, Wang J, Colombage K. Torque distribution strategy for a front and rear wheel driven electric vehicle[J]. 6th IET International Conference on Power Electronics, Machines and Drives (PEMD 2012), 2012, 1-6. |
| [18] |
赵刚, 王俊伟, 周福庚. 多轴车轴荷与制动性能分析[C]//安徽汽车工程学会2010学术年会. 安徽, 2010: 308-313. Zhao G, Wang J W, Zhou F G. Analysis of axle load and braking performance of multi-axle axle[C]//2010 Annual Meeting of Anhui Automobile Engineering Society. Anhui, 2010: 308-313. (in Chinese) |
| [19] |
Mutoh N, Akashi H, Suzuki K, et al. Front and rear wheel independent drive type electric vehicles (FRID EVs) with outstanding running performance suitable for next-generation electric vehicles[C]//2012 IEEE International Electric Vehicle Conference. March 4-8, 2012, Greenville, SC, USA. IEEE, 2012: 1-8.
|
 2021, Vol. 44
2021, Vol. 44


